《数据结构》第五章习题参考答案
数据结构第五章 查找 答案

数据结构与算法上机作业第五章查找一、选择题1、若构造一棵具有n个结点的二叉排序树,在最坏情况下,其高度不超过 B 。
A. n/2B. nC. (n+1)/2D. n+12、分别以下列序列构造二叉排序数(二叉查找树),与用其他3个序列所构造的结果不同的是 C :A. (100, 80, 90, 60, 120, 110, 130)B. (100, 120, 110, 130, 80, 60, 90)C. (100, 60, 80, 90, 120, 110, 130)D. (100, 80, 60, 90, 120, 130, 110)3、不可能生成下图所示的二叉排序树的关键字的序列是 A 。
A. 4 5 3 1 2B. 4 2 5 3 1C. 4 5 2 1 3D. 4 2 3 1 54、在二叉平衡树中插入一个结点造成了不平衡,设最低的不平衡点为A,并已知A的左孩子的平衡因子为0,右孩子的平衡因子为1,则应作 C 型调整使其平衡。
A. LLB. LRC. RLD. RR5、一棵高度为k的二叉平衡树,其每个非叶结点的平衡因子均为0,则该树共有 C 个结点。
A. 2k-1-1B. 2k-1+1C. 2k-1D. 2k+16、具有5层结点的平衡二叉树至少有 A 个结点。
A. 12B. 11C. 10D. 97、下面关于B-和B+树的叙述中,不正确的是 C 。
A. B-树和B+树都是平衡的多叉树B. B-树和B+树都可用于文件的索引结构C. B-树和B+树都能有效地支持顺序检索D. B-树和B+树都能有效地支持随机检索8、下列关于m阶B-树的说法错误的是 D 。
A. 根结点至多有m棵子树B. 所有叶子结点都在同一层次C. 非叶结点至少有m/2(m为偶数)或m/2+1(m为奇数)棵子树D. 根结点中的数据是有序的9、下面关于哈希查找的说法正确的是 C 。
A. 哈希函数构造得越复杂越好,因为这样随机性好,冲突小B. 除留余数法是所有哈希函数中最好的C. 不存在特别好与坏的哈希函数,要视情况而定D. 若需在哈希表中删去一个元素,不管用何种方法解决冲突都只要简单地将该元素删去即可10、与其他查找方法相比,散列查找法的特点是 C 。
数据结构(c语言版)第五章答案

数据结构(c语言版)第五章答案第五章1、设二维数组A【8】【10】是一个按行优先顺序存储在内存中的数组,已知A【0】【0】的起始存储位置为1000,每个数组元素占用4个存储单元,求:(1)A【4】【5】的起始存储位置。
A【4】【5】的起始存储位置为1000+(10*4+5)*4=1180;(2)起始存储位置为1184的数组元素的下标。
起始存储位置为1184的数组元素的下标为4(行下标)、6(列下标)。
2、画出下列广义表D=((c),(e),(a,(b,c,d)))的图形表示和它们的存储表示。
略,参考第5·2节应用题第5题分析与解答。
3、已知A为稀疏矩阵,试从时间和空间角度比较采用两种不同的存储结构(二维数组和三元组表)实现求∑a(i,j)运算的优缺点。
稀疏矩阵A采用二维数组存储时,需要n*n个存储单元,完成求∑ii a(1≤i≤n)时,由于a【i】【i】随机存取,速度快。
但采用三元组表时,若非零元素个数为t,需3t+3个存储单元(t个分量存各非零元素的行值、列值、元素值),同时还需要三个存储单元存储存稀疏矩阵A的行数、列数和非零元素个数,比二维数组节省存储单元;但在求∑ii a(1≤i≤n)时,要扫描整个三元组表,以便找到行列值相等的非零元素求和,其时间性能比采用二维数组时差。
4、利用三元组存储任意稀疏数组时,在什么条件下才能节省存储空间?当m行n列稀疏矩阵中非零元素个数为t,当满足关系3*t<m*n 时,利用三元组存储稀疏数组时,才能节省存储空间。
< bdsfid="74" p=""></m*n时,利用三元组存储稀疏数组时,才能节省存储空间。
<>5、求下列各广义表的操作结果。
(1)GetHead((a,(b,c),d))GetHead((a,(b,c),d))=a(2)GetTail((a,(b,c),d))GetTail((a,(b,c),d))=((b,c),d)(3)GetHead(GetTail((a,(b,c),d)))GetHead(GetTail((a,(b,c),d)))=(b,c)(4)GetTail(GetHead((a,(b,c),d)))GetTail(GetHead((a,(b,c),d)))=()第六章1、已知一棵树边的集合为{(i,m),(i,n),(e,i),(b,e),(b,d),(a,b),(g,j),(g,k),(c,g),(c,f),(h,l),(c,h),(a,c)}用树形表示法画出此树,并回答下列问题:(1)哪个是根结点?(2)哪些是叶结点?(3)哪个是g的双亲?(4)哪些是g的祖先?(5)哪些是g的孩子?(6)哪些是e的子孙?(7)哪些是e的兄弟?哪些是f的兄弟?(8)结点b和n的层次号分别是什么?(9)树的深度是多少?(10)以结点c为根的子树的深度是多少?(11)树的度数是多少?略。
数据结构第五章参考答案

习题51.填空题(1)已知二叉树中叶子数为50,仅有一个孩子的结点数为30,则总结点数为(___________)。
答案:129(2)3个结点可构成(___________)棵不同形态的二叉树。
答案:5(3)设树的度为5,其中度为1~5的结点数分别为6、5、4、3、2个,则该树共有(___________)个叶子。
答案:31(4)在结点个数为n(n>1)的各棵普通树中,高度最小的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
高度最大的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
答案:2 n-1 1 n 1 n-1(5)深度为k的二叉树,至多有(___________)个结点。
答案:2k-1(6)(7)有n个结点并且其高度为n的二叉树的数目是(___________)。
答案:2n-1(8)设只包含根结点的二叉树的高度为0,则高度为k的二叉树的最大结点数为(___________),最小结点数为(___________)。
答案:2k+1-1 k+1(9)将一棵有100个结点的完全二叉树按层编号,则编号为49的结点为X,其双亲PARENT (X)的编号为()。
答案:24(10)已知一棵完全二叉树中共有768个结点,则该树中共有(___________)个叶子结点。
答案:384(11)(12)已知一棵完全二叉树的第8层有8个结点,则其叶子结点数是(___________)。
答案:68(13)深度为8(根的层次号为1)的满二叉树有(___________)个叶子结点。
答案:128(14)一棵二叉树的前序遍历是FCABED,中序遍历是ACBFED,则后序遍历是(___________)。
答案:ABCDEF(15)某二叉树结点的中序遍历序列为ABCDEFG,后序遍历序列为BDCAFGE,则该二叉树结点的前序遍历序列为(___________),该二叉树对应的树林包括(___________)棵树。
《数据结构》习题集:第5章

第5章数组与广义表一、选择题1.在以下讲述中,正确的是(B )。
A、线性表的线性存储结构优于链表存储结构B、二维数组是其数据元素为线性表的线性表C、栈的操作方式是先进先出D、队列的操作方式是先进后出2.若采用三元组压缩技术存储稀疏矩阵,只要把每个元素的行下标和列下标互换,就完成了对该矩阵的转置运算,这种观点(A )。
A、正确B、错误3.二维数组SA 中,每个元素的长度为3 个字节,行下标I 从0 到7,列下标J 从0 到9,从首地址SA 开始连续存放在存储器内,该数组按列存放时,元素A[4][7]的起始地址为(B)。
A、SA+141B、SA+180C、SA+222D、SA+2254.数组SA 中,每个元素的长度为3 个字节,行下标I 从0 到7,列下标J 从0 到9,从首地址SA 开始连续存放在存储器内,存放该数组至少需要的字节数是( C )。
A、80B、100C、240D、2705.常对数组进行的两种基本操作是(B )。
A、建立与删除B、索引和修改C、查找和修改D、查找和索引6.将一个A[15][15]的下三角矩阵(第一个元素为A[0][0]),按行优先存入一维数组B[120]中,A 中元素A[6][5]在B 数组中的位置K 为( B )。
A、19B、26C、21D、157.若广义表A 满足Head(A)=Tail(A),则A 为(B )。
A、()B、(())C、((),())D、((),(),())8.广义表((a),a)的表头是( C ),表尾是(C )。
A、aB、bC、(a)D、((a))9.广义表((a,b),c,d)的表头是( C ),表尾是(D )。
A、aB、bC、(a,b)D、(c,d)10.广义表((a))的表头是( B ),表尾是(C )。
A、aB、(a)C、()D、((a))11.广义表(a,b,c,d)的表头是(A ),表尾是(D )。
A、aB、(a)C、(a,b)D、(b,c,d)12.广义表((a,b,c,d))的表头是(C ),表尾是(B )。
《数据结构及其应用》笔记含答案 第五章_树和二叉树

第5章树和二叉树一、填空题1、指向结点前驱和后继的指针称为线索。
二、判断题1、二叉树是树的特殊形式。
()2、完全二叉树中,若一个结点没有左孩子,则它必是叶子。
()3、对于有N个结点的二叉树,其高度为。
()4、满二叉树一定是完全二叉树,反之未必。
()5、完全二叉树可采用顺序存储结构实现存储,非完全二叉树则不能。
()6、若一个结点是某二叉树子树的中序遍历序列中的第一个结点,则它必是该子树的后序遍历序列中的第一个结点。
()7、不使用递归也可实现二叉树的先序、中序和后序遍历。
()8、先序遍历二叉树的序列中,任何结点的子树的所有结点不一定跟在该结点之后。
()9、赫夫曼树是带权路径长度最短的树,路径上权值较大的结点离根较近。
()110、在赫夫曼编码中,出现频率相同的字符编码长度也一定相同。
()三、单项选择题1、把一棵树转换为二叉树后,这棵二叉树的形态是(A)。
A.唯一的B.有多种C.有多种,但根结点都没有左孩子D.有多种,但根结点都没有右孩子解释:因为二叉树有左孩子、右孩子之分,故一棵树转换为二叉树后,这棵二叉树的形态是唯一的。
2、由3个结点可以构造出多少种不同的二叉树?(D)A.2 B.3 C.4 D.5解释:五种情况如下:3、一棵完全二叉树上有1001个结点,其中叶子结点的个数是(D)。
A.250 B. 500 C.254 D.501解释:设度为0结点(叶子结点)个数为A,度为1的结点个数为B,度为2的结点个数为C,有A=C+1,A+B+C=1001,可得2C+B=1000,由完全二叉树的性质可得B=0或1,又因为C为整数,所以B=0,C=500,A=501,即有501个叶子结点。
4、一个具有1025个结点的二叉树的高h为(C)。
A.11 B.10 C.11至1025之间 D.10至1024之间解释:若每层仅有一个结点,则树高h为1025;且其最小树高为⎣log21025⎦ + 1=11,即h在11至1025之间。
吉林省专升本数据结构习题及答案——第五章

吉林省专升本考试数据结构分章习题及参考答案———选择题(第五章)1、一棵完全二叉树上有1001个结点,其中叶子结点的个数是( )。
A、250B、500C、254D、5012、将一棵树t转换为孩子—兄弟链表表示的二叉树h,则t的后根序遍历是h 的A、前序遍历B、中序遍历C、后序遍历D、层序遍历3、采用邻接表存储的图,其深度优先遍历类似于二叉树的()。
A、中序遍历B、先序遍历C、后序遍历D、按层次遍历4、二叉树的第5层上最多含有结点数为()A、31B、16C、15D、325、某二叉树中序序列为A,B,C,D,E,F,G,后序序列为B,D,C,A,F,G,E则前序序列是:A、E,G,F,A,C,D,BB、E,A,C,B,D,G,FC、E,A,G,C,F,B,DD、上面的都不对6、若森林F有15条边、25个结点,则F包含树的个数是( )。
A、8B、9C、10D、117、有权值分别为2,3,5,8,7,4的叶子结点生成一棵哈夫曼树,其带权路径长度为()A、36B、72C、96D、1208、任何一棵二叉树的叶子结点在前序、中序、后序遍历序列中的相对次序()A、肯定不发生改变B、肯定发生改变C、不能确定D、有时发生变化9、为5个使用频率不等的字符设计哈夫曼编码,不可能的方案是( ).A、 111,110,10,01,00B、000,001,010,011,1C、100,11,10,1,0D、001,000,01,11,1010、给定二叉树1(2(4,5(6,7)),3)。
设N代表二叉树的根,L代表根结点的左子树,R代表根结点的右子树。
若遍历后的结点序列为3,1,7,5,6,2,4则其遍历方式是( )A、LRNB、NRLC、RLND、RNL11、若以{4,5,6,7,8}作为权值构造哈夫曼树,则该树的带权路径长度为()。
A、67B、68C、69D、7012、深度为k的完全二又树至少有( )个结点。
A、2k-2+1B、2k-1C、2k-1D、2k-1-113、一个具有1025个结点的二叉树的高h为()A、11B、10C、11至1025之间D、10至1024之间14、设F是一个森林,B是由F变换得的二叉树。
数据结构第五章考试题库(含答案)

第 5 章数组和广义表一、选择题为第一元素,其存储地址为1,1.设有一个10阶的对称矩阵A,采用压缩存储方式,以行序为主存储,a11的地址为()。
【燕山大学 2001 一、2 (2分)】每个元素占一个地址空间,则a85A. 13B. 33C. 18D. 402. 有一个二维数组A[1:6,0:7] 每个数组元素用相邻的6个字节存储,存储器按字节编址,那么这个数组的体积是(①)个字节。
假设存储数组元素A[1,0]的第一个字节的地址是0,则存储数组A的最后一个元素的第一个字节的地址是(②)。
若按行存储,则A[2,4]的第一个字节的地址是(③)。
若按列存储,则A[5,7]的第一个字节的地址是(④)。
就一般情况而言,当(⑤)时,按行存储的A[I,J]地址与按列存储的A[J,I]地址相等。
供选择的答案:【上海海运学院 1998 二、2 (5分)】①-④: A.12 B. 66 C. 72 D. 96 E. 114 F. 120G. 156 H. 234 I. 276 J. 282 K. 283 L. 288⑤: A.行与列的上界相同 B. 行与列的下界相同C. 行与列的上、下界都相同D. 行的元素个数与列的元素个数相同3. 设有数组A[i,j],数组的每个元素长度为3字节,i的值为1 到8 ,j的值为1 到10,数组从内存首地址BA开始顺序存放,当用以列为主存放时,元素A[5,8]的存储首地址为( )。
A. BA+141B. BA+180C. BA+222D. BA+225【南京理工大学 1997 一、8 (2分)】4. 假设以行序为主序存储二维数组A=array[1..100,1..100],设每个数据元素占2个存储单元,基地址为10,则LOC[5,5]=()。
【福州大学 1998 一、10 (2分)】A. 808B. 818C. 1010D. 10205. 数组A[0..5,0..6]的每个元素占五个字节,将其按列优先次序存储在起始地址为1000的内存单元中,则元素A[5,5]的地址是( )。
数据结构预算法 第5章习题解答
④
③
0 1 2 3 4 5
1 2 3 4 5 6 ^
3 0 3
^ 2 4 ^ 5 ^
0 1
1 4 ^
3 ^
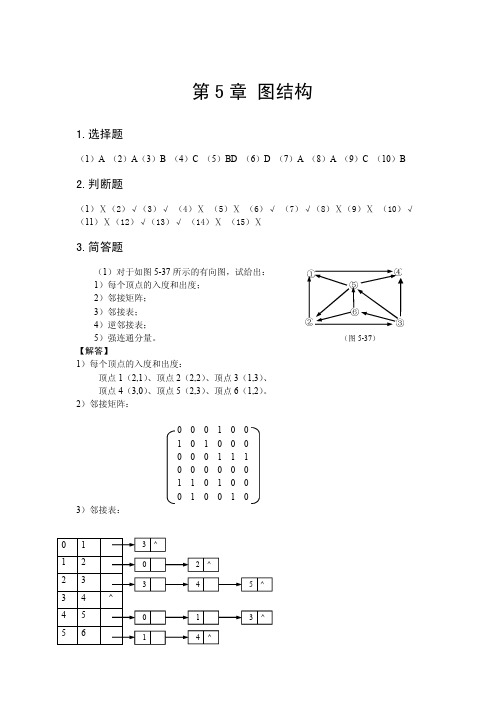
4)逆邻接表: 0 1 2 3 4 5 1 2 3 4 5 6 5)强连通分量:
1 4 1 0 2 2 ^ ^ 2 5 ^ 4 ^ 4 5 ^ ^
(2)设无向图 G 如图 5-38 所示,试给出: 1)该图的邻接矩阵; 2)该图的邻接表; 3)该图的多重邻接表; 4)从 V1 出发的“深度优先”遍历序列; 5)从 V1 出发的“广度优先”遍历序列。 【解答】 1) 该图的邻接矩阵: 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 0 1 1 0
{if(p!=s) p->next=s->next; else (G->adjlist[e->adjvex].firstedge=s->next;)} if(s) free(s); break; } } for(i=v;i<G->n;i++) /*删除顶点值*/ {G->adjlist[i].vertex=G->adjlist[i+1].vextex; G->adjlist[i].first[i].firstedge=G->adjlist[i+1].firstedge; } } void DeleteArc(AALGraph *G,int v,int w) /*在图 G 中删除序号为 v,w 的顶点之的边*/ {EdgeNode *s,*p; s=G->adjlist[v].firstedge; p=s; for(;s;s=s->next); /*在与 m 邻接的点中找 n*/ {if(s->adjvex==w) /*若找到邻接点 n,则将该边从边表中脱出*/ {if(p!=s) p->next=s->next; else G->adjlist[v].firstedge=s->next; } if(s) free(s); /*释放要删除的边结点*/ } s=G->adjlist[w].firstedge;p=s; for(;s;p=s,s=s->next) /*在与 n 邻接的点中找 m*/ {if(s->adjvex==v) /*若找到邻接点 m,则将该边从边表中脱出*/ {if(p!=s) p->next=s->next; else G->adjlist[w].firstedge=s->next; } if(s) free(s); /*释放要删除的边结点*/ } G->e--; } (3)试以十字链表为存储结构实现算法设计题(1)中所列图的基本操作。 算法略。 (4)试以邻接多重表为存储结构实现算法设计题(1)中所列图的基本操作。 算法略。 (5)对于含有 n 个顶点的有向图,编写算法由其邻接表构造相应的逆邻接表。 【解答】 Void InvertAdjList(ALGraph G, ALGraph *H) /*由有向图的邻接表 G 建立其逆邻接表 H*/ {for (i=1;i<=n;i++) /*设有向图有 n 个顶点,建逆邻接表的顶点向量*/ {H[i]->vertex=G.adjlist[i].vertex; H->firstedge=NULL;} for (i=0; i<n; i++) /*邻接表转为逆邻接表*/ {p= G.adjlist[i].firstedge; /*取指向邻接表的指针*/ while (p!=null) {j=p->adjvex;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数据结构》第五章习题参考答案一、判断题(在正确说法的题后括号中打“√”,错误说法的题后括号中打“×”)1、知道一颗树的先序序列和后序序列可唯一确定这颗树。
( ×)2、二叉树的左右子树可任意交换。
(×)3、任何一颗二叉树的叶子节点在先序、中序和后序遍历序列中的相对次序不发生改变。
(√)4、哈夫曼树是带权路径最短的树,路径上权值较大的结点离根较近。
(√)5、用一维数组存储二叉树时,总是以前序遍历顺序存储结点。
( ×)6、完全二叉树中,若一个结点没有左孩子,则它必是叶子结点。
( √)7、一棵树中的叶子数一定等于与其对应的二叉树的叶子数。
(×)8、度为2的树就是二叉树。
(×)二、单项选择题1.具有10个叶结点的二叉树中有( B )个度为2的结点。
A.8 B.9 C.10 D.112.树的后根遍历序列等同于该树对应的二叉树的( B )。
A. 先序序列B. 中序序列C. 后序序列3、二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG 。
该二叉树根的右子树的根是:( C )A. EB. FC. GD. H04、在下述结论中,正确的是( D )。
①具有n个结点的完全二叉树的深度k必为┌log2(n+1)┐;②二叉树的度为2;③二叉树的左右子树可任意交换;④一棵深度为k(k≥1)且有2k-1个结点的二叉树称为满二叉树。
A.①②③B.②③④C.①②④D.①④5、某二叉树的后序遍历序列与先序遍历序列正好相反,则该二叉树一定是( D )。
A.空或只有一个结点B.完全二叉树C.二叉排序树D.高度等于其结点数三、填空题1、对于一棵具有n个结点的二叉树,对应二叉链接表中指针总数为__2n____个,其中___n-1_____个用于指向孩子结点,___n+1___个指针空闲着。
2、一棵深度为k(k≥1)的满二叉树有_____2k-1______个叶子结点。
3、在完全二叉树中,编号为i和j的两个结点处于同一层的条件是「_┌㏒2 i┐= ┌㏒2j┐___ _。
4、某二叉树有20(n0)个叶子结点,有30个结点仅有一个孩子(n1),则该二叉树的总结点数为69 _。
(n=n0+n1+n2)(而n0=n2+1)5、完全二叉树中,结点个数为n,则编号最大的分支结点的编号为__└n/2┘____。
6、已知二叉树前序为ABDEGCF,中序为DBGEACF,则后序一定是_ DGEBFCA ___。
四、综合题1、设二叉树采用二叉链表存储结构,结点的数据域data为字符类型。
阅读下列算法,并回答问题:(1)对于如图所示的二叉树,写出执行函数function的输出结果;(2)简述函数function的功能。
void function(BinTree T){Stack< BinTreeNode*> S;BinTreeNode* p = T.GetRoot();BinTreeNode* q;if (p= =NULL) return;do {while (p!=NULL){S.Push(p);1if (p->leftChild!=NULL) p=p->leftChild;else p=p->rightChild;}while (!S.IsEmpty() && q=S.GetTop() && q-> rightChild = =p){p=S.Pop(); cout << p->data; }if(!S.IsEmpty ()){q=S.GetTop(); p=q-> rightChild; }} while (!S.IsEmpty ());}(1)DBFGECA(2) 函数function 的功能是对二叉树进行后序遍历。
2、课本P246 5.2题1234-156-17-18-1-1-1-193、课本P246 5.3题【解答】结点个数为n 时,深度最小的树的深度为2;它有n -1个叶结点,1个分支结点;深度最大的树的深度为n ;它有1个叶结点,n -1个分支结点。
4、课本P246 5.4题【解答】总结点数 n = n 0 + n 1 + n 2 + … + n m总分支数 e = n -1 = n 0 + n 1 + n 2 + … + n m -1 = m *n m + (m -1)*n m -1 + … + 2*n 2 + n 1则有 1)1(20+⎪⎭⎫ ⎝⎛-=∑=mi i n i n5、课本P246 5.5题 【解答】略6、课本P246 5.6题【解答】(1) 二叉树的前序序列与中序序列相同:空树或缺左子树的单支树; (2) 二叉树的中序序列与后序序列相同:空树或缺右子树的单支树; (3) 二叉树的前序序列与后序序列相同:空树或只有根结点的二叉树。
7、课本P246 5.7题(1)×(2)√(3)×(4)√8、课本P246 5.8题(1)×(2)×(3)√(4)×9、课本P247 5.14题【解答】略10、课本P247 5.17题11、课本P248 5.18题12、课本P248 5.19题WPL = (2+3)×5+6×4+(9+14+15)×3 +(16+17)×2 = 22913、课本P248 5.20题各字母的Huffman 编码: C1: 0110 C2: 10 C3: 0000 C4: 0111 C5: 00112 345 6 78 5-17答A B C D EF IG 5-18答 JH 16 5-19答179 14 1563 2C7 C5C6 C4 C2C1 C3C8C7C2C6: 010C7: 11C8: 0001电文总码长=4×(3+4+5+6)+3×(10+11)+2×(25+36)=25714、课本P248 5.23题【解答】(1) 统计二叉树中叶结点个数int BinaryTree<Type> :: leaf ( BinTreeNode<Type> * ptr ) {if ( ptr == NULL ) return 0;else if ( ptr->leftChild == NULL&&ptr->rightChild == NULL) return 1;else return leaf ( ptr->leftChild ) + leaf ( ptr->rightChild );}(2) 交换每个结点的左子女和右子女void BinaryTree<Type> :: exchange ( BinTreeNode<Type> * ptr ) {BinTreeNode<Type> * temp;if ( ptr->leftChild != NULL||ptr->rightChild != NULL ) {temp = ptr->leftChild;ptr->leftChild = ptr->rightChild;ptr->rightChild = temp;exchange ( ptr->leftChild );exchange ( ptr->rightChild );}}15、课本P248 5.24题【解答】template <class Type>void BinaryTree<Type> ::ConstructTree ( Type T[ ], int n, int i, BinTreeNode<Type> *&ptr ) { //私有函数:将用T[n]顺序存储的完全二叉树, 以i为根的子树转换成为用二叉链表表示的//以ptr为根的完全二叉树。
利用引用型参数ptr将形参的值带回实参。
if ( i >= n )ptr =NULL;else {ptr = new BinTreeNode<Type> ( T[i] ); //建立根结点ConstructTree ( T, n, 2*i+1, ptr->leftChild );ConstructTree ( T, n, 2*i+2, ptr->rightChild );}}16、课本P249 5.29题【解答】template <class Type> void BinaryTree<Type>::FullBinTree2Array(Type&* T){ Queue<BinTreeNode<Type> *> Q;BinTreeNode<Type> * p = GetRoot();Q.EnQueue(p);int index = 0;while(!Q.IsEmpty()){p = Q.DeQueue();T[index++]=p->data;if(p->leftChild != NULL) Q.EnQueue(p->leftChild);if(p->rightChild != NULL) Q.EnQueue(p->rightChild);}}17、课本P250 5.37题//缩格文本显示树template <class Type>void BinaryTree<Type> :: FormatDisplay( ) {Stack <BinTreeNode<Type>* > S;S.Push(NULL);Stack <int> S1;S1.Push(0);BinTreeNode<Type> * p = root; //初始化int level = 0;while(p !=NULL){for(int i = level; i > 0; i--) cout<<" ";cout << p->data << endl;if ( p->rightChild != NULL ){S.Push ( p->rightChild ); //预留右子树指针在栈中S1.Push(level);}if ( p->leftChild != NULL ){level++;p = p->leftChild; //进左子树}else //左子树为空, 进右子树{p = S.Pop();level=S1.Pop();}}}。
