数据结构第五章参考答案
数据结构第五章 查找 答案

数据结构与算法上机作业第五章查找一、选择题1、若构造一棵具有n个结点的二叉排序树,在最坏情况下,其高度不超过 B 。
A. n/2B. nC. (n+1)/2D. n+12、分别以下列序列构造二叉排序数(二叉查找树),与用其他3个序列所构造的结果不同的是 C :A. (100, 80, 90, 60, 120, 110, 130)B. (100, 120, 110, 130, 80, 60, 90)C. (100, 60, 80, 90, 120, 110, 130)D. (100, 80, 60, 90, 120, 130, 110)3、不可能生成下图所示的二叉排序树的关键字的序列是 A 。
A. 4 5 3 1 2B. 4 2 5 3 1C. 4 5 2 1 3D. 4 2 3 1 54、在二叉平衡树中插入一个结点造成了不平衡,设最低的不平衡点为A,并已知A的左孩子的平衡因子为0,右孩子的平衡因子为1,则应作 C 型调整使其平衡。
A. LLB. LRC. RLD. RR5、一棵高度为k的二叉平衡树,其每个非叶结点的平衡因子均为0,则该树共有 C 个结点。
A. 2k-1-1B. 2k-1+1C. 2k-1D. 2k+16、具有5层结点的平衡二叉树至少有 A 个结点。
A. 12B. 11C. 10D. 97、下面关于B-和B+树的叙述中,不正确的是 C 。
A. B-树和B+树都是平衡的多叉树B. B-树和B+树都可用于文件的索引结构C. B-树和B+树都能有效地支持顺序检索D. B-树和B+树都能有效地支持随机检索8、下列关于m阶B-树的说法错误的是 D 。
A. 根结点至多有m棵子树B. 所有叶子结点都在同一层次C. 非叶结点至少有m/2(m为偶数)或m/2+1(m为奇数)棵子树D. 根结点中的数据是有序的9、下面关于哈希查找的说法正确的是 C 。
A. 哈希函数构造得越复杂越好,因为这样随机性好,冲突小B. 除留余数法是所有哈希函数中最好的C. 不存在特别好与坏的哈希函数,要视情况而定D. 若需在哈希表中删去一个元素,不管用何种方法解决冲突都只要简单地将该元素删去即可10、与其他查找方法相比,散列查找法的特点是 C 。
数据结构(c语言版)第五章答案

数据结构(c语言版)第五章答案第五章1、设二维数组A【8】【10】是一个按行优先顺序存储在内存中的数组,已知A【0】【0】的起始存储位置为1000,每个数组元素占用4个存储单元,求:(1)A【4】【5】的起始存储位置。
A【4】【5】的起始存储位置为1000+(10*4+5)*4=1180;(2)起始存储位置为1184的数组元素的下标。
起始存储位置为1184的数组元素的下标为4(行下标)、6(列下标)。
2、画出下列广义表D=((c),(e),(a,(b,c,d)))的图形表示和它们的存储表示。
略,参考第5·2节应用题第5题分析与解答。
3、已知A为稀疏矩阵,试从时间和空间角度比较采用两种不同的存储结构(二维数组和三元组表)实现求∑a(i,j)运算的优缺点。
稀疏矩阵A采用二维数组存储时,需要n*n个存储单元,完成求∑ii a(1≤i≤n)时,由于a【i】【i】随机存取,速度快。
但采用三元组表时,若非零元素个数为t,需3t+3个存储单元(t个分量存各非零元素的行值、列值、元素值),同时还需要三个存储单元存储存稀疏矩阵A的行数、列数和非零元素个数,比二维数组节省存储单元;但在求∑ii a(1≤i≤n)时,要扫描整个三元组表,以便找到行列值相等的非零元素求和,其时间性能比采用二维数组时差。
4、利用三元组存储任意稀疏数组时,在什么条件下才能节省存储空间?当m行n列稀疏矩阵中非零元素个数为t,当满足关系3*t<m*n 时,利用三元组存储稀疏数组时,才能节省存储空间。
< bdsfid="74" p=""></m*n时,利用三元组存储稀疏数组时,才能节省存储空间。
<>5、求下列各广义表的操作结果。
(1)GetHead((a,(b,c),d))GetHead((a,(b,c),d))=a(2)GetTail((a,(b,c),d))GetTail((a,(b,c),d))=((b,c),d)(3)GetHead(GetTail((a,(b,c),d)))GetHead(GetTail((a,(b,c),d)))=(b,c)(4)GetTail(GetHead((a,(b,c),d)))GetTail(GetHead((a,(b,c),d)))=()第六章1、已知一棵树边的集合为{(i,m),(i,n),(e,i),(b,e),(b,d),(a,b),(g,j),(g,k),(c,g),(c,f),(h,l),(c,h),(a,c)}用树形表示法画出此树,并回答下列问题:(1)哪个是根结点?(2)哪些是叶结点?(3)哪个是g的双亲?(4)哪些是g的祖先?(5)哪些是g的孩子?(6)哪些是e的子孙?(7)哪些是e的兄弟?哪些是f的兄弟?(8)结点b和n的层次号分别是什么?(9)树的深度是多少?(10)以结点c为根的子树的深度是多少?(11)树的度数是多少?略。
数据结构作业系统_第五章答案

数据结构第五章作业答案

第5章数组和广义表1.选择题(1)假设以行序为主序存储二维数组A=array[1..100,1..100],设每个数据元素占2个存储单元,基地址为10,则LOC[5,5]=()。
A.808 B.818 C.1010 D.1020(2)设有数组A[i,j],数组的每个元素长度为3字节,i的值为1到8,j 的值为1到10,数组从内存首地址BA开始顺序存放,当用以列为主存放时,元素A[5,8]的存储首地址为()。
A.BA+141 B.BA+180 C.BA+222 D.BA+225(3)设有一个10阶的对称矩阵A,采用压缩存储方式,以行序为主存储,a11为第一元素,其存储地址为1,每个元素占一个地址空间,则a85的地址为()。
A.13 B.33 C.18 D.40(4)若对n阶对称矩阵A以行序为主序方式将其下三角形的元素(包括主对角线上所有元素)依次存放于一维数组B[1..(n(n+1))/2]中,则在B 中确定a ij(i<j)的位置k的关系为()。
A.i*(i-1)/2+j B.j*(j-1)/2+i C.i*(i+1)/2+j D.j*(j+1)/2+i (5)A[N,N]是对称矩阵,将下面三角(包括对角线)以行序存储到一维数组T[N(N+1)/2]中,则对任一上三角元素a[i][j]对应T[k]的下标k 是()。
A.i(i-1)/2+j B.j(j-1)/2+i C.i(j-i)/2+1 D.j(i-1)/2+1(6)设二维数组A[1.. m,1.. n](即m行n列)按行存储在数组B[1.. m*n]中,则二维数组元素A[i,j]在一维数组B中的下标为()。
A.(i-1)*n+j B.(i-1)*n+j-1 C.i*(j-1) D.j*m+i-1(7)数组A[0..4,-1..-3,5..7]中含有元素的个数()。
A.55 B.45 C.36 D.16(8)广义表A=(a,b,(c,d),(e,(f,g))),则Head(Tail(Head(Tail(Tail(A)))))的值为()。
《数据结构及其应用》笔记含答案 第五章_树和二叉树

第5章树和二叉树一、填空题1、指向结点前驱和后继的指针称为线索。
二、判断题1、二叉树是树的特殊形式。
()2、完全二叉树中,若一个结点没有左孩子,则它必是叶子。
()3、对于有N个结点的二叉树,其高度为。
()4、满二叉树一定是完全二叉树,反之未必。
()5、完全二叉树可采用顺序存储结构实现存储,非完全二叉树则不能。
()6、若一个结点是某二叉树子树的中序遍历序列中的第一个结点,则它必是该子树的后序遍历序列中的第一个结点。
()7、不使用递归也可实现二叉树的先序、中序和后序遍历。
()8、先序遍历二叉树的序列中,任何结点的子树的所有结点不一定跟在该结点之后。
()9、赫夫曼树是带权路径长度最短的树,路径上权值较大的结点离根较近。
()110、在赫夫曼编码中,出现频率相同的字符编码长度也一定相同。
()三、单项选择题1、把一棵树转换为二叉树后,这棵二叉树的形态是(A)。
A.唯一的B.有多种C.有多种,但根结点都没有左孩子D.有多种,但根结点都没有右孩子解释:因为二叉树有左孩子、右孩子之分,故一棵树转换为二叉树后,这棵二叉树的形态是唯一的。
2、由3个结点可以构造出多少种不同的二叉树?(D)A.2 B.3 C.4 D.5解释:五种情况如下:3、一棵完全二叉树上有1001个结点,其中叶子结点的个数是(D)。
A.250 B. 500 C.254 D.501解释:设度为0结点(叶子结点)个数为A,度为1的结点个数为B,度为2的结点个数为C,有A=C+1,A+B+C=1001,可得2C+B=1000,由完全二叉树的性质可得B=0或1,又因为C为整数,所以B=0,C=500,A=501,即有501个叶子结点。
4、一个具有1025个结点的二叉树的高h为(C)。
A.11 B.10 C.11至1025之间 D.10至1024之间解释:若每层仅有一个结点,则树高h为1025;且其最小树高为⎣log21025⎦ + 1=11,即h在11至1025之间。
数据结构预算法 第5章习题解答
④
③
0 1 2 3 4 5
1 2 3 4 5 6 ^
3 0 3
^ 2 4 ^ 5 ^
0 1
1 4 ^
3 ^
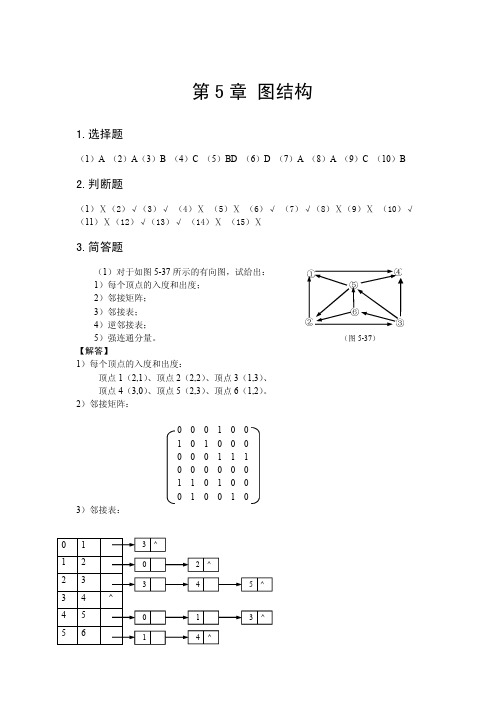
4)逆邻接表: 0 1 2 3 4 5 1 2 3 4 5 6 5)强连通分量:
1 4 1 0 2 2 ^ ^ 2 5 ^ 4 ^ 4 5 ^ ^
(2)设无向图 G 如图 5-38 所示,试给出: 1)该图的邻接矩阵; 2)该图的邻接表; 3)该图的多重邻接表; 4)从 V1 出发的“深度优先”遍历序列; 5)从 V1 出发的“广度优先”遍历序列。 【解答】 1) 该图的邻接矩阵: 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 0 1 1 0
{if(p!=s) p->next=s->next; else (G->adjlist[e->adjvex].firstedge=s->next;)} if(s) free(s); break; } } for(i=v;i<G->n;i++) /*删除顶点值*/ {G->adjlist[i].vertex=G->adjlist[i+1].vextex; G->adjlist[i].first[i].firstedge=G->adjlist[i+1].firstedge; } } void DeleteArc(AALGraph *G,int v,int w) /*在图 G 中删除序号为 v,w 的顶点之的边*/ {EdgeNode *s,*p; s=G->adjlist[v].firstedge; p=s; for(;s;s=s->next); /*在与 m 邻接的点中找 n*/ {if(s->adjvex==w) /*若找到邻接点 n,则将该边从边表中脱出*/ {if(p!=s) p->next=s->next; else G->adjlist[v].firstedge=s->next; } if(s) free(s); /*释放要删除的边结点*/ } s=G->adjlist[w].firstedge;p=s; for(;s;p=s,s=s->next) /*在与 n 邻接的点中找 m*/ {if(s->adjvex==v) /*若找到邻接点 m,则将该边从边表中脱出*/ {if(p!=s) p->next=s->next; else G->adjlist[w].firstedge=s->next; } if(s) free(s); /*释放要删除的边结点*/ } G->e--; } (3)试以十字链表为存储结构实现算法设计题(1)中所列图的基本操作。 算法略。 (4)试以邻接多重表为存储结构实现算法设计题(1)中所列图的基本操作。 算法略。 (5)对于含有 n 个顶点的有向图,编写算法由其邻接表构造相应的逆邻接表。 【解答】 Void InvertAdjList(ALGraph G, ALGraph *H) /*由有向图的邻接表 G 建立其逆邻接表 H*/ {for (i=1;i<=n;i++) /*设有向图有 n 个顶点,建逆邻接表的顶点向量*/ {H[i]->vertex=G.adjlist[i].vertex; H->firstedge=NULL;} for (i=0; i<n; i++) /*邻接表转为逆邻接表*/ {p= G.adjlist[i].firstedge; /*取指向邻接表的指针*/ while (p!=null) {j=p->adjvex;
数据结构第五章习题答案

1.二维数组A行下标i的范围从1到12,列下标j的范围从3到10,采用行序为主序存储,每个数据存储元素占用4个存储单元,该数组的首地址(既A[1][3]的地址)为1200,则A[6][5]的地址为(D)A.1400B.1404C.1372D.13682.有一个M*N的矩阵A,若采用行序为主序进行顺序存储,每个元素占用8个字节,则A ij (1≤i≤M,1≤i≤N)元素的相对字节地址(相对首元素地址而言)为(B)A.((i-1)*N+j)*8B.((i-1)*N+j-1)*8C.(i*N+j-1)*8D.((i-1)*N+j+1)*83.稀疏矩阵一般的压缩存储方法有两种,即(D)A.二维数组和三维数组B.三元组和散列C.散列和十字链表D.三元组和十字链表4.若采用三元组压缩技术存储稀疏矩阵,只要把每个元素的行下标和列下标互换,就完成了对该矩阵的转置运算,这种观点(B)A.正确B.错误5.广义表((a,b),c,d)的表头是(C),表尾是(D)。
A.aB.bC.(a,b)D.(c,d)6.一个广义表的表头总是广义表,这个断言是(B)A.正确B.错误7.二维数组A[10][20]采用列序为主方式存储,每个元素占一个存储单元,并且A[0][0]的存储地址是200,则A[6][12]的地址是(326)8.有一个10阶对称矩阵A,采用压缩存储方式(以行序为主存储,且A[0][0]=1),则A[4][3]的地址是(14)9.一个广义表为(a,(a,b),d,e,((i,j),k)),则该广义表的长度为(5),深度为(3)10.广义表((a),((b),c),(((d))))的表头是((a)),表尾是((((b),c),(((d)))))11.已知广义表A=((a,b,c),(d,e,f)),则广义表运算head(tail(tail(A)))=(e)12.已知广义表GL=(a,(b,c,d),e),运用head和tail函数取出GL中的原子b的运算是(head(head(tail(GL))))13.特殊矩阵和压缩矩阵哪一种压缩存储后会失去随机存取的功能?为什么?答:稀疏矩阵在进行压缩存储后会失去随机存取的功能,因为非零元素的位置没有办法确定。
《数据结构》吕云翔编著第5章树习题解答

第五章树课后习题讲解一、选择题⑴如果结点A有3个兄弟,B是A的双亲,则结点B的度是()。
A 1B 2C 3D 4【解答】D⑵设二叉树有n个结点,则其深度为()。
A n-1B nC +1D 不能确定【解答】D【分析】此题并没有指明是完全二叉树,则其深度最多是n,最少是 +1。
⑶二叉树的前序序列和后序序列正好相反,则该二叉树一定是()的二叉树。
A 空或只有一个结点B 高度等于其结点数C 任一结点无左孩子D 任一结点无右孩子【解答】B【分析】此题注意是序列正好相反,则左斜树和右斜树均满足条件。
⑷线索二叉树中某结点R没有左孩子的充要条件是()。
A R.lchild=NULLB R.ltag=0C R.ltag=1D R.rchild=NULL【解答】C【分析】线索二叉树中某结点是否有左孩子,不能通过左指针域是否为空来判断,而要判断左标志是否为1。
⑸深度为k的完全二叉树至少有()个结点,至多有()个结点,具有n个结点的完全二叉树按层序从1开始编号,则编号最小的叶子的序号是()。
A 2k-2+1B 2k-1C 2k -1 -1D 2k-1E 2k+1F 2k+1 -1G 2k -1+1H 2k【解答】B,C,A【分析】深度为k的完全二叉树最少结点数的情况应是第k层上只有1个结点,最多的情况是满二叉树,编号最小的叶子应该是在结点数最少的情况下,叶子结点的编号。
⑹一个高度为h的满二叉树共有n个结点,其中有m个叶子结点,则有()成立。
A n=h+mB h+m=2nC m=h-1D n=2m-1【解答】D【分析】满二叉树中没有度为1的结点,所以有m个叶子结点,则度为2的结点个数为m-1。
⑺任何一棵二叉树的叶子结点在前序、中序、后序遍历序列中的相对次序()。
A 肯定不发生改变B 肯定发生改变C 不能确定D 有时发生变化【解答】A【分析】三种遍历次序均是先左子树后右子树。
⑻如果T' 是由有序树T转换而来的二叉树,那么T中结点的前序序列就是T' 中结点的()序列,T中结点的后序序列就是 T' 中结点的()序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题5
1.填空题
(1)已知二叉树中叶子数为50,仅有一个孩子的结点数为30,则总结点数为(___________)。
答案:129
(2)3个结点可构成(___________)棵不同形态的二叉树。
答案:5
(3)设树的度为5,其中度为1~5的结点数分别为6、5、4、3、2个,则该树共有(___________)个叶子。
答案:31
(4)在结点个数为n(n>1)的各棵普通树中,高度最小的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
高度最大的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
答案:2 n-1 1 n 1 n-1
(5)深度为k的二叉树,至多有(___________)个结点。
答案:2k-1
(6)(7)有n个结点并且其高度为n的二叉树的数目是(___________)。
答案:2n-1
(8)设只包含根结点的二叉树的高度为0,则高度为k的二叉树的最大结点数为(___________),最小结点数为(___________)。
答案:2k+1-1 k+1
(9)将一棵有100个结点的完全二叉树按层编号,则编号为49的结点为X,其双亲PARENT (X)的编号为()。
答案:24
(10)已知一棵完全二叉树中共有768个结点,则该树中共有(___________)个叶子结点。
答案:384
(11)(12)已知一棵完全二叉树的第8层有8个结点,则其叶子结点数是(___________)。
答案:68
(13)深度为8(根的层次号为1)的满二叉树有(___________)个叶子结点。
答案:128
(14)一棵二叉树的前序遍历是FCABED,中序遍历是ACBFED,则后序遍历是(___________)。
答案:ABCDEF
(15)某二叉树结点的中序遍历序列为ABCDEFG,后序遍历序列为BDCAFGE,则该二叉树结点的前序遍历序列为(___________),该二叉树对应的树林包括(___________)棵树。
答案:EACBDGF 2
2.选择题
(1)在一棵度为3的树中,度为3的结点的个数为2,度为2的结点个数为1,则度为0的结点个数为()。
A. 4
B. 5
C. 6
D. 7
(2)下列陈述中正确的是()。
A. 二叉树是度为2的有序数
B. 二叉树中结点只有一个孩子时无左右之分
C. 二叉树中必有度为2的结点
D. 二叉树中最多只有两棵子树,并且有左右之分
(3)在K叉树中,如果结点M有3个兄弟,而且N是M的双亲,则N的度是()A. 3 B. 4 C. 5 D. 1
(4)设高度为h的二叉树上只有度为0和度为2的结点,则此类二叉树中所包含的结点数至少为()。
A. 2h
B. 2h-1
C. 2h+1
D. h+1
(5)高度为5的完全二叉树至少有()个结点。
A. 16
B. 32
C. 31
D. 5
(6)具有65个结点的完全二叉树的高度为()。
(根的层次号为0)
A. 8
B. 7
C.6
D. 5
(7)对一个满二叉树,m个树叶,n个结点,深度为h,则(无)。
A. n=h+m
B. h+m=2n
C. m=h-1
D. n=2h-1
(8)任一棵二叉树,其叶子结点数为n0,度为2的结点数为n2,则存在关系()。
A. n2 +1=n0
B. n0 +1=n2
C. 2n2 +1=n0
D. n2 =2n0 +1
(9)某二叉树的前序遍历结点访问顺序是abdgcefh,中序遍历的结点访问顺序是dgbaechf,则其后序遍历的结点访问顺序是()。
A. bdgcefha
B. gdbecfha
C. bdgaechf
D. gdbehfca
(10)设m、n为一棵二叉树上的两个结点,在中序遍历时,n在m前的条件是()。
A. n在m右方
B. n是m祖先
C. n在m左方
D.n是m子孙
(11)一棵二叉树的广义表表示为a(b(c,d),e(f(g))),则得到的层序遍历序列为()。
A. abcdefg
B. cbdaegf
C. cdbgfea
D. abecdfg
(12)若二叉树采用二叉链表作为存储结构,要交换其所有分支结点左右子树的位置,利用()遍历方法最合适。
A. 前序
B. 中序
C. 后序
D. 层序
说明:显然,如果按前序或后序遍历,当访问某结点时,交换其左右孩子,则可完成要求。
进行层序遍历时,当结点出队时,交换左右孩子,也可以完成题目要求。
因此该题有3个答案,谈不上哪个最合适。
建议该题目将“最合适”改为“不合适”,这样答案应该是唯一的。
(13)对二叉树进行()遍历,可以得到该二叉树所有结点构成的排序序列。
A. 前序 B. 中序 C. 后序 D. 层序
(14)设F是一个森林,B是由F转换得到的二叉树,F中有n个非叶结点,则B中右指针域为空的结点有()个。
A. n-1
B. n
C. n+1
D. n+2
(15)利用3,6,8,12,5,7这6个值作为叶子结点的权,生成一棵哈夫曼树,该树的深度为()。
A.3
B. 4
C.5
D. 6
(16)若度为m的哈夫曼树中,其叶结点个数为n,则非叶结点的个数为()。
A. n-1 B. [n/m]-1
C. [(n-1)/(m-1)]
D. [n/(m-1)]-1
说明:在这里度为m的哈夫曼树是指仅含有度为0和m的结点的m叉树。
因此有:
(1) N=n+n m
(2) N = 1 + mn m
3.试分别画出具有3个结点的树和二叉树的所有不同形态。
答案:树:
二叉树:
4.试找出分别满足下面条件的所有二叉树:
(1)前序序列和中序序列相同;
答案: 右斜树
(2)中序序列和后序序列相同;
答案:左斜树
(3)前序序列和后序序列相同。
答案:只有根结点的树
5.一棵高度为h的满k叉树有如下性质:第h层上的结点都是叶结点,其余各层上每个结点都有k棵非空子树,如果按层次自顶向下,同一层自左向右,顺序从0开始对全部结点进行编号,试问:
(1)各层的结点个数是多少?
答案:n层的结点个数为k n-1
(2)编号为i的结点的父结点(若存在)的编号是多少?
答案:|(i-1)/k| (|·|表示取下整)
(3)编号为i的结点的第m个孩子结点(若存在)的编号是多少?
答案:k*i+m
(4)编号为i的结点有右兄弟的条件是什么?其右兄弟结点的编号是多少?
答案:i%k!=0 i+1
(5)叶子结点数n0和非叶子结点数n k之间满足的关系。
答案:n k*(k-1)=n0-1
6.若一棵二叉树的前序序列为abdgcefh,中序序列为dgbaechf,请画出该二叉树,并写出其后序序列。
答案:gdbehfca
7.请将图5-42所示树T转换为二叉树T′。
答案:
8. 对于图5-43所示的二叉树,该树的三种遍历分别是什么?
答案:
前序 -+a*b-cd/ef
中序 a+b*c-d-e/f
后序 abcd-*+ef/-
9. 对于图5-44所示的二叉树,请画出和其对应的森林。
答案:
10. 假设用于通信的电文仅由9个字符组成,并且出现概率为0.07(A)、0.19(B)、0.02(C)、0.06(D)、0.32(E)、0.03(F)、0.21(G)、0.10(H):
(1)画出哈夫曼树;
答案:
(2)每个字符的哈夫曼编码; 答案: A 0010 B 10 C 00000 D 0001 E 01 F 00001 G 11 H 0011
(3)计算其带权路径长度;
答案:WPL=0.07*4+0.19*2+0.02*5+0.06*4+0.32*2+0.03*5+0.21*2+0.10*4=2.61
(4)如果电文是“ABCDEFGH ”压缩前每个字符使用8bit 的ASCII 编码,则采用上面的哈夫曼编码,其压缩比是多少? 答案:0.43758
84
2524524=⨯+++++++=
η
友情提示:部分文档来自网络整理,供您参考!文档可复制、编制,期待您的好评与关注!。
