基本条分法
条分法的基本原理

条分法的基本原理
首先,条分法的基本原理之一是分类。
分类是指将问题或者事物按照一定的标准进行划分,将其划分为不同的类别。
通过分类,可以使问题更加具体化,也可以使问题更加清晰。
例如,在讨论一个社会问题时,可以将其分为政治、经济、文化等不同的方面进行分类,从而更好地了解问题的全貌。
其次,条分法的基本原理之二是分析。
分析是指对分类下的具体情况进行深入研究和分析,找出问题的关键点和症结所在。
通过分析,可以找出问题的根源,并找到解决问题的方法。
例如,在对一个经济问题进行分析时,可以分别分析其产生的原因、影响的范围、可能的解决方案等,从而更好地理解和解决问题。
最后,条分法的基本原理之三是归纳。
归纳是指通过对分类和分析得出的结论和观点进行总结和归纳,从而得出最终的结论。
通过归纳,可以使问题的解决方案更加明确和有针对性。
例如,在对一个科学问题进行归纳时,可以将各种观点和结论进行总结,从而得出一个更加全面和准确的结论。
总之,条分法的基本原理包括分类、分析和归纳三个方面。
通
过这三个方面的运用,可以使问题的思路更加清晰,逻辑更加严密,从而更好地解决问题。
在实际生活和工作中,我们可以通过运用条
分法的基本原理,更好地理解和解决问题,提高自己的逻辑思维能力。
(1)土质边坡稳定分析之条分法

因为
dW dW p( x) q sin e' ru sec sin e' dx dx dW ' ' ce sec cos e cos e' dx
' e
c 'cos ht e' e' sin cos 4 2 4 2
N,可能得到负值。这一现象不仅不合理,而且有时 '
' e 1
会导致数值计算不收敛的问题
x p s d G a (2.20) G( x) sec s x a
N sin T cos Q G cos 0
中,对
的假定是指土条间的总作用力G,而不是上条骨架
。如果将土骨架作为研究对象,那么就要对 G' 作假定了。因此,两种处理方法,尽管具有相同的 '
间的有效作用力 的倾角 ' G 差别。
力学背景,但由于处理细节不完全—致,其结果仍会有微小的
2.3 对坡外水体的处理
对图2.8(a)所示坡外有水的情况。此时,通常采用下面 三种处理方案。
' e ' n
' e
(2.1)
其中:
c' c K
' e
(2.2)
tan ' tan K
' e
(2.3)
τ为沿滑动面的切向力, ' n 为垂直于滑动面的正应力,
c' '
为土的有效粘聚力, 为有效内摩擦系数
1.2 摩尔-库仑强度准则
当土坡沿破坏面滑动时,在滑动面上,土体处处达到 ' n 和剪应力τ满足摩 极限平衡。针对某一条土体其正应力 尔-库仑强度准则:
基本条分法

基本条分法基本条分法是基于均质粘性土,当出现滑动时,其滑动面接近圆柱面和圆锥面的空间组合,简化为平面问题时接近圆弧面并作为实际的滑动〔滑裂〕面。
将圆弧滑动面与坡面的交线沿组合的滑体部分,进行竖向分条,按不考虑条间力的作用效果并进行简化,将各个分条诸多力效果作用到的滑动圆弧上,以抗滑因素和滑动因素分析,用抗滑力矩比滑动力矩的极限平衡分析的方法建立整个坡体安全系数的评价方法。
基本条分法的计算过程通常是基于可能产生滑动〔滑裂〕圆弧面条件下,经过假定不同的滑动中心、再假定不同的滑动半径,确定对应的滑动圆弧,通过分条计算所对应的滑体安全系数,依此循环反复计算,最终求出最小的安全系数和对应的滑弧、滑动中心,作为对整个土坡的安全评价的度量。
计算研究说明,坡体的安全系数所对应的滑动中心区域随土层条件和土坡条件及强度所变化。
如图所示可见一斑。
圆弧基本条分法安全系数的定义为:Fs= 抗滑力矩/滑动力矩,即 =M R/M h图 9.2.1不同土层的 Fs 极小值区1 瑞典条分法如图所实示,瑞典条分法的安全系数Fs 的一般计算公式表达为:(cos )sin i iiiis iic l W tg F W θϕθ+=∑∑〔〕式中,Wi 为土条重力;θi 为土条底部中点与滑弧中心连线垂直夹角;抗剪强度指标c 、ϕ值是为总应力指标,也可采用有效应力指标。
工程中常用的替代重度法进行计算,即公式中分子的容重在浸润线以上部分采用天然容重,以下采用浮容重;分母中浸润线以上部分采用天然容重,以下采用饱和容重,这种方法既考虑了稳定渗流对土坡稳定性的影响,又方便了计算,其精度也能较好地满足工程需要,因此在实际工程中得到广泛应用。
应该指出,容重替代法只是一个经验公式,,可参见图所示,h 2i wi h ≠。
图 瑞典条分法当坡体在稳定渗流作用下,可采用容重替代法进行计算,其具体公式如下:1212[()cos tan ]()sin i iii i i i sisati i ic l h h b F hh b γγθϕγγθ'++=+∑∑〔〕式中:h 1i 为土条i 中线浸润线以上高度;h 2i 为土条i 中线浸润线以下高度;图 渗流孔隙水压力计算简图2 简化Bishop 计算公式:Bishop 考虑每一分条条间力的实际作用后,见图所示,其简化公式表为忽略条间力〔滑体内力〕作用,具体公式为1(cos tan )sin i i i i i is i ic l W m F W θθϕθ+=∑∑〔〕 其中sin tan cos i ii i m Fθθϕθ=+,〔〕简化Bishop 替代重度法公式:12121[()tan ]()sin i i i i i i is i sat i i ic b h h b m F h h b θγγϕγγθ'++=+∑∑〔〕式中各参数含义同上。
条分法 土条长度

条分法土条长度10cm 土条是一种常见的食材,具有多种用途。
在中国的餐桌上,土条既可以作为主食,也可以作为配菜。
它的制作方法简单,味道鲜美,因此备受喜爱。
我们来了解一下土条的制作过程。
制作土条的材料主要有面粉、水和食盐。
将面粉、食盐和适量的水混合在一起,搅拌均匀,揉成面团。
然后,将面团擀成薄片,切成宽约0.5cm的长条,用拇指压出纹路,使土条更有嚼劲。
最后,将土条放入开水中煮熟,捞出沥水即可。
土条的用途非常广泛。
首先,它可以作为主食。
将土条煮熟后,可以直接当做面食来食用。
可以搭配各种汤料,如牛肉汤、鸡汤等,制作成各种面条汤。
土条的口感劲道,能够增加整道菜的口感层次,让人食欲大增。
土条还可以作为配菜。
将土条切成段,炒熟后可以和蔬菜、肉类一起炒制,制作成各种美味的炒菜。
土条炒出的菜肴口感鲜嫩,搭配各种调料和配料,味道更加丰富多样。
除了作为食材,土条还具有一定的营养价值。
土条富含碳水化合物,能够为人体提供能量。
它还含有一定的蛋白质和脂肪,能够为人体提供必要的营养物质。
此外,土条中还含有丰富的维生素和矿物质,对身体健康有一定的保健作用。
在饮食文化中,土条也有一定的象征意义。
它代表着家庭的团聚和温暖。
在中国农村,人们常常在团年饭或其他重要的节日聚餐时,做一些土条来表示对亲友的关爱和祝福。
土条的制作过程需要耐心和细心,象征着人们对家庭和友情的用心和呵护。
总的来说,土条是一种美味可口的食材,具有多种用途。
无论是作为主食还是配菜,都能给人带来丰富的口感和美味的享受。
制作土条的过程简单,所需材料也容易获取。
无论是在家中烹饪还是在餐馆就餐,都可以尝试土条的美味。
让我们一起品尝这道美食,感受其中的独特魅力吧!。
岩土专业考试滑坡体计算常用条分法总结
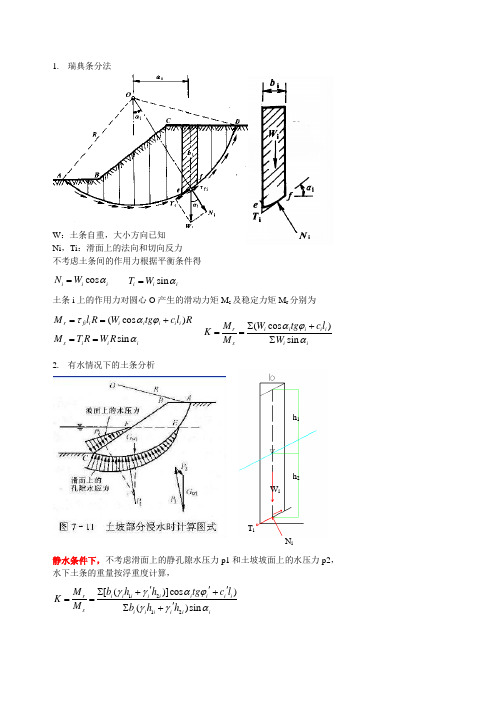
1212[()]cos )()sin i i i i i i i i i r s i i i i i i b h h tg c l M K M b h h γγαϕγγα'''∑++=='∑+(cos )r fi i i i i i i M l R W tg c l R ταϕ==+(cos )sin i i i i i r s i i W tg c l M K M W αϕα∑+==∑sin i i i T W α=cos ii i N W α=sin s i i i M T R W R α==1. 瑞典条分法W :土条自重,大小方向已知 Ni ,Ti :滑面上的法向和切向反力不考虑土条间的作用力根据平衡条件得土条i 上的作用力对圆心O 产生的滑动力矩M s 及稳定力矩M r 分别为2. 有水情况下的土条分析静水条件下,不考虑滑面上的静孔隙水压力p1和土坡坡面上的水压力p2, 水下土条的重量按浮重度计算,h 1W ih 2T iN isin i α=123123[()]cos )()sin i i i i i i i i i i i r s i i i sati i i i i b h h h tg c l M K M b h h h γγγαϕγγγα''''∑+++=='∑++2sin i w i iJ b h γα=∑['(cos )tan ']sin i i i i i i i s i i c l W u L F W αϕα+-=∑∑由荷载引起的超静孔隙水压力条件下(有效应力法) 当有超静孔隙水压力时,超静孔隙水压力作用在滑面上, 减小土条的有效法向应力由渗流引起的超静孔隙水压力条件下(代替法)流线平行坡面时, 用浸润线以下,坡外水位以上 所包围的同体积的水重对滑动圆心的力矩代替渗流力对 圆心的滑动力矩。
用条分法分析黄土地区路堑边坡的稳定性

图 2 路 堑横 断面 I
∑ ( i n +Qi ) w sq i
采 用 条 分 法 进 行 验 算 , 坡 坡 率 分 别 采 用 1: 边
0. 0 和 1 :0. 0 3 5
通 常 Qi w 数 值 相 比很 小 , 外 , 与 的 此 不考 虑 地 震 力 时 , 项 在 计 算 中不 计 入 , 此 因此 公 式 ( ) 化 为 : 1简
9 。 a ( —m) 9 。 2 . 。 ( 3. 。 4 3 ) 0一 一 O : 0 一 6 9 一 7 3 一 0. 。 =
3 1 0. 。
式中 : M稳=R∑ t i i =R2 at ̄ +C ) i R∑ L E[i i iL g
( t中+C L ) =R∑ ( f+CL ) Ni i ii] g Ni i ii
2 。 天 然 容 重 :1 . 9 N/  ̄ 5, 53 k m。
I
( 体 滑 动 ) 态 , 中 w 任 一 条 块 的 重 量 和 车 整 状 图 为
辆 荷 载 的 重 量 ; 为 水 平 力 ( 水 平 地 震 惯 性 力 ) Q 如 ; xi Z 分 别 为 W i Qi O 点 的 力 臂 , 注 意 : 和 i 和 对 ( xi 的 正 负号 ) 因此 , 据 条 分 法 原理 得 出 边坡 整体 安 。 根
按 所 求 出 的稳 定 系 数 K ~ K 这 6个 数 值 在 图 3上 绘 制 出 一 条 平 滑 的 K 值 曲线 , 找 出 最 小 的 稳 可
根 据 某 地 区路 线 通 过 的黄 土 地 段 出 现 的 深路 堑 的 边
坡 坡 率 的确 定 。 利 用 上 述 条 分 法 对 各 种坡 率 和 坡 高 边 坡 稳 定 性 进 行 分 析 验 算 , 取 得 了 一 些 有 实 用 参 并
毕肖普条分法

毕肖普条分法毕肖普条分法是一种常用的论证方法,它由英国哲学家毕肖普(Isaac Newton)提出,被广泛应用于各个领域的论述和思考中。
其核心思想是将一个复杂的问题或概念分解成若干个简单的部分,以便更好地理解和分析。
本文将从以下几个方面详细介绍毕肖普条分法。
一、毕肖普条分法的基本原理毕肖普条分法是一种归纳推理方法,其基本原理是将一个复杂的问题或概念分解成若干个简单的部分,以便更好地理解和分析。
具体而言,毕肖普条分法包括以下三个步骤:1. 将问题或概念拆解成若干个部分。
2. 对每个部分进行独立思考和讨论。
3. 将各部分综合起来得出总结性结论。
二、毕肖普条分法的应用场景毕肖普条分法可以应用于各种不同领域的论述和思考中。
以下列举几个常见的应用场景:1. 学术研究:在学术研究中,毕肖普条分法可以用来分析和解决复杂的理论问题。
例如,对于一个复杂的学术概念,可以将其拆分成若干个部分进行独立思考和讨论,最终得出总结性结论。
2. 商业决策:在商业决策中,毕肖普条分法可以用来分析和解决复杂的市场问题。
例如,对于一个新产品的市场推广计划,可以将其拆分成若干个部分进行独立思考和讨论,最终得出总结性结论。
3. 政策制定:在政策制定中,毕肖普条分法可以用来分析和解决复杂的社会问题。
例如,对于一个社会改革计划,可以将其拆分成若干个部分进行独立思考和讨论,最终得出总结性结论。
三、毕肖普条分法的优点毕肖普条分法有以下几个优点:1. 使问题更易理解:通过将一个复杂的问题或概念拆解成若干个简单的部分进行独立思考和讨论,在整体上使问题更易理解。
2. 便于深入探究:通过对每个部分进行独立思考和讨论,可以更深入地探究问题的本质和细节。
3. 有利于综合分析:通过将各部分综合起来得出总结性结论,可以更全面地分析问题并得出更准确的结论。
四、毕肖普条分法的局限性毕肖普条分法也存在一些局限性:1. 不适用于所有问题:毕肖普条分法适用于那些可以拆解成若干个简单的部分进行独立思考和讨论的问题,对于那些本身就比较简单或难以拆解的问题,该方法并不适用。
条分法的表解和图解

条分法的表解和图解条分法是一种表示数据结构的方法,可以以表或图的形式展示。
它是一种常用的数据存储技术,可用于识别元素之间的关系,进而更好地理解和处理数据。
条分法的表解和图解是常用的数据表示方法,被广泛应用于商业、技术、社会等各个领域。
一、表解表解,又称列解,是将不同的数据以表的形式进行整理。
每一列都表示相同种类的数据,每一行都表示不同类别的数据,以清晰的表格形式展示出来,以便更好地理解数据的相关性。
表解的背后逻辑是将数据分成不同的分类,然后逐一列出这些分类的数据内容,从而更好地识别出每组数据之间的关联性。
例如,在商店中可以用表解展示商品的清单:商品名称、类别、价格、库存量等,从而更加清晰地记录商品信息。
二、图解图解指的是将不同的数据以图表的形式进行展示。
可以用柱状图、折线图等形式来清晰表示数据之间的相互关系和变化,从而更好地发现其中的趋势和规律。
图解的优势在于数据的直观性,它可以直接以视觉形式表达出复杂的数据关系,让人一目了然。
例如,可以使用柱状图来表示某一商品的历史销售量,这样可以直观地看出该商品的销售情况和趋势。
三、条分法的应用条分法的应用极其广泛,在商业、技术、社会等各个领域都有着重要的应用价值。
在商业方面,条分法可用于对商品信息,市场行情,投资项目等进行统计分析,从而更好地帮助企业根据已有的信息来制定发展策略;同时,在供需领域的研究上,也可以利用条分法的表解和图解形式,更好地发现市场供需变化趋势,更有效地提高供需匹配效率。
另外,在技术领域,条分法也可以用于对运算结果、代码设计、计算机网络等信息进行分析。
例如,在网络路由技术中,可以使用条分法表明节点间的互联关系,以强化网络的运行效率,进而达到提高网络质量的目的。
最后,条分法还可以作为社会研究的分析工具,以图表的形式反映出社会及其事物之间的关系,从而发现社会变迁的趋势,加深人们对社会发展的认识。
综上所述,条分法的表解和图解是一种非常有效的数据表示方法,被广泛应用于各个领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本条分法
基本条分法是基于均质粘性土,当出现滑动时,其滑动面接近圆柱面和圆锥面的空间组合,简化为平面问题时接近圆弧面并作为实际的滑动(滑裂)面。
将圆弧滑动面与坡面的交线沿组合的滑体部分,进行竖向分条,按不考虑条间力的作用效果并进行简化,将各个分条诸多力效果作用到的滑动圆弧上,以抗滑因素和滑动因素分析,用抗滑力矩比滑动力矩的极限平衡分析的方法建立整个坡体安全系数的评价方法。
基本条分法的计算过程通常是基于可能产生滑动(滑裂)圆弧面条件下,经过假定不同的滑动中心、再假定不同的滑动半径,确定对应的滑动圆弧,通过分条计算所对应的滑体安全系数,依此循环反复计算,最终求出最小的安全系数和对应的滑弧、滑动中心,作为对整个土坡的安全评价的度量。
计算研究表明,坡体的安全系数所对应的滑动中心区域随土层条件和土坡条件及强度所变化。
如图 9.2.1所示可见一斑。
圆弧基本条分法安全系数的定义为:Fs= 抗滑力矩/滑动力矩,即 =M R/M h
图 9.2.1不同土层的 Fs 极小值区
1 瑞典条分法
如图9.2.2所实示,瑞典条分法的安全系数Fs 的一般计算公式表达为:
(cos )
sin i i
i
i
i
s i
i
c l W tg F W θϕθ
+=
∑∑
(9.2.1)
式中,Wi 为土条重力;θi 为土条底部中点与滑弧中心连线垂直夹角;抗剪强度指标c 、ϕ值是为总应力指标,也可采用有效应力指标。
工程中常用的替代重度法进行计算,即公式中分子的容重在浸润线以上部分采用天然容重,以下采用浮容重;分母中浸润线以上部分采用天然容重,以下采用饱和容重,这种方法既考虑了稳定渗流对土坡稳定性的影响,又方便了计算,其精度也能较好地满足工程需要,因此在实际工程中得到广泛应用。
应该指出,容重替代法只是一个经验公式,,可参见图9.2.3所示,h 2i wi h ≠。
图9.2.2 瑞典条分法
当坡体在稳定渗流作用下,可采用容重替代法进行计算,其具体公式如下:
1212[()cos tan ]()sin i i
i
i i i i s i
sat
i i i
c l h
h b F h
h b γγθϕγγ
θ'++=
+∑∑
(9.2.2)
式中:h 1i 为土条i 中线浸润线以上高度;
h 2i 为土条i 中线浸润线以下高度;
图 9.2.3 渗流孔隙水压力计算简图
2 简化Bishop 计算公式:
Bishop 考虑每一分条条间力的实际作用后,见图9.2.4所示,其简化公式表为忽略条间力(滑体内力)作用,具体公式为
1
(cos tan )
sin i i i i i i
s i
i
c l W m
F W θθϕθ
+=
∑∑
(9.2.3) 其
中
sin tan cos i i
i i m F
θθϕθ=+
,
(9.2.4)
简化Bishop 替代重度法公式:
12121
[()tan ]
()sin i i i i i i i
s i sat i i i
c b h h b m F h h b θγγϕγγθ'++=
+∑∑
(9.2.5)
式中各参数含义同上。
i l i
i+1
图9.2.4 bishop 计算简图
9.3 普遍条分法基本实现
9.3.1 普遍条分法的一般假定
在边坡稳定极限平衡分析中,普遍条分法主要的一项工作是对作用在滑动土体中的土条某些未知内力,引入适当的假定,减少这些未知力数目,使问题变得静定可解,未知力的假定较多的主要为土条的侧向力,根据这一侧向未知内力假定的特点,可将这些方法分为:
(1)对土条侧向力的倾角的分布形状作出假定,这类方法的代表是Morgenstern&Price 、
陈祖煜法。
(2)对土条侧向力的大小的分布函数作出假定,这一类方法代表是Sarma法;
(3)对土条侧向力的作用位置作假定,这一类方法的代表是Janbu法。
在侧向力作用土条的假定之后,应用极限平衡原理对边坡稳定分析建立普遍条分法的基本公式。
1、关于安全系数的定义
土坡沿着某一滑裂面滑动的安全系数定义:将土的抗剪强指标降低为c’/F和tanф/F,则土体沿着此滑裂面处处达到极限平衡,即
τ/
τ
F=或
f
(9.3.1)
·tan e
n e c τσφ'''=+
也可以表示为:
e
c c F ''=
(9.3.2)
tan
tan e F φφ'
'=
(9.3.3)
上述将强度指标的储备作为安全系数定义。
2、摩尔—库伦强度准则
假设土体的一部分沿着某一滑裂面滑动,在该滑裂面上,土体处处达以极限平衡,即正应力σ′n 和剪应力τ满足摩尔—库伦强强度准则。
在有些公式的实用中,对于孔隙水压力u ,通常定义孔隙水压力系数
dx dW u
r u /=
(9.3.4) 3、静力平衡条件
将滑动土体分成若干土条后,以每个土条和整个滑动土体都要满足力和力矩平衡方程的为必要条件,在建立的静力平衡方程组中,未知数的数目超过了方程式的数目,应用坡体的边界等条件为解决这一静不定问题的办法是对多余未知数作充分的假定,如前述对于侧向力的假定,使剩下的未知数和方程数目相等,从而解出安全系数的值。
4、合理控制条件
对多余未知数进行假定的具体方案可以是多种多样的,
但也不是完全任意的。
它必须使获得的解符合土的力学特性。
目前,被普遍接受的控制条件应该是:
(1)沿着划分的土条两侧垂直面上的剪应力不超过在这个面上所能发挥的抗剪能力,即也可以类似使用安全系数来表示。
(2)为保证在土条接触面上不产生拉力的作用效应,作用在土条上的有效力的合力作用点不应落在土条垂直面的外面。
