传热学第四版课件23第二章导热基本定律及稳态导热
合集下载
传热学第二章 稳态导热

(t)dxdydz
x x
dz+dz dy
dy+dy dz
dx+dx
x
dΦydydΦyy(yt)dxdyydz dΦzdzdΦzz( zt)dxdydz
单位时间内能增量 dUc t dxdydz
2019/10/1
19
微元体内热源的生成热为:
一般把导热系数仅仅视为温度 的函数,而且在一定温度范围 还可以用一种线性关系来描述。
0(1bT)
2019/10/1
14
记住常用物质的值:
2019/10/1
15
5 导热微分方程(Heat Diffusion Equation) ①一般形式
付里叶定律: qgradt
确定导热体内的温度分布是导热理论的首要 任务。 建立导热微分方程,可以揭示连续温度场随 空间坐标和时间变化的内在联系。
(b)无内热源,导热系数为常数时
t
a(x2t2
y2t2
z2t2)
(c)常物性、稳态
2t x2
y2t2
z2t2
0泊桑(Poisson)方程
(d)常物性、稳态、无内热源
2t 2t 2t 0 x2 y2 z2
拉普拉斯(Laplace)方程
2019/10/1
22
在同样加热条件下,物体的热扩散率越大,物 体内部各处的温度差别越小。
a 木 材 1 .5 1 0 7 m 2s , a 铝 9 .4 5 1 0 5 m 2s
a木材 a铝1600
2019/10/1
23
c t x( x t) y( y t) z( z t)
2019/10/1
传热学-第二章-导热基本定律及稳态导热

dQx qx dydz d
[J]
d 时间内、沿 x 轴方向、经 x+dx 表面导出的热量:
dQxdx qxdx dydz d [J]
ห้องสมุดไป่ตู้
qxdx
qx
qx x
dx
d 时间内、沿 x 轴方向导入与导出微元体净热量:
dQx
dQxdx
qx x
dxdydz d
气体的压力升高时:气体的密度增大、平均自由行程 减小、而两者的乘积保持不变。
除非压力很低或很高,在2.67*10-3MPa ~ 2.0*103MPa范围内, 气体的热导率基本不随压力变化
气体的温度升高时:气体分子运动速度和定容比热随T升高 而增大。 气体的热导率随温度升高而增大
混合气体热导率不能用部分求和的方法求;只能靠实验测定
热流密度矢量:等温面上某点,以通过该点处最大热流密度的
方向为方向、数值上正好等于沿该方向的热
流密度 q
直角坐标系中:
q
q
q qx i qy j qz k
q q cos
二、导热基本定律(Fourier’s law)
1822年,法国数学家傅里叶(Fourier)在实验研究基础上, 发现导热基本规律 —— 傅里叶定律
3、时间条件
说明在时间上导热过程进行的特点
x
y
z
直角坐标系:(Cartesian coordinates)
grad t t i t j t k
x
y
z
注:温度梯度是向量;正向朝着温度增加的方向
热流密度矢量 (Heat flux)
热流密度:单位时间、单位面积上所传递的热量;
第二章导热基本定律及稳态导热PPT课件

由(a)可得:
cw 1 说明热源与管子中心不重合。 由(a)、(b)可得:
将(c)代入(b)可得:
从而只能选正号,所以有: 等温线为一圆。
2 具有偏心空腔的圆柱体
由于是稳定导热,从而流过每一等温面的热流量是 相同的
对于等温面 1
y0
h2 h1
ε
对于等温面 2
热阻: 但h1和h2是未知的
下面用此方法求地下埋管与土壤间的导热量
有一热力管道,外径d=2r,
埋于地平面下h米深处。土 壤为均质且导热系数λ为常
数。管子表面温度及地表面
tf
y0
温度也是均匀的常量,为tW h 和tF,设管道很长,求单位 管道的热损失。
r” x
M
p(x,y)
r’
r
N y
因管道很长,从而可以看作是二维稳定导热
1项
2项
=控制体内内能的变化
3项
第一项 求沿x、y、z三个方向流入和流出的热量
把1、2、3项代入能量方程式
导温系数的物理意义:a越大,表明λ越大或ρC 越小,λ大,表示在相同的温度梯度下可以传 递更多的热量;ρC小表明温度上升1℃所吸收 的热量越小,从而可使相同的热量传递得更远 ,
物体内各点温度更快地随界面温度的升高而升 高。
三、利用“导热形状因子S”计 导热系数为算常数导,热无量内热源稳态导热体
内,两壁温度为定值,即有Q=λS(t1+t2)。
补充内容
稳定热传导的热源法 (虚拟热源法)
定义:如果一个物体有内热源作用时,我们可以通过
导热微分方程式和相应的单值性条件求温度分布。但 如果知道温度分布,我们反过来找导致这种温度分布 的原因—实际存在的热源或假想的热源。这种方法称 虚拟热源法或称映象法。
cw 1 说明热源与管子中心不重合。 由(a)、(b)可得:
将(c)代入(b)可得:
从而只能选正号,所以有: 等温线为一圆。
2 具有偏心空腔的圆柱体
由于是稳定导热,从而流过每一等温面的热流量是 相同的
对于等温面 1
y0
h2 h1
ε
对于等温面 2
热阻: 但h1和h2是未知的
下面用此方法求地下埋管与土壤间的导热量
有一热力管道,外径d=2r,
埋于地平面下h米深处。土 壤为均质且导热系数λ为常
数。管子表面温度及地表面
tf
y0
温度也是均匀的常量,为tW h 和tF,设管道很长,求单位 管道的热损失。
r” x
M
p(x,y)
r’
r
N y
因管道很长,从而可以看作是二维稳定导热
1项
2项
=控制体内内能的变化
3项
第一项 求沿x、y、z三个方向流入和流出的热量
把1、2、3项代入能量方程式
导温系数的物理意义:a越大,表明λ越大或ρC 越小,λ大,表示在相同的温度梯度下可以传 递更多的热量;ρC小表明温度上升1℃所吸收 的热量越小,从而可使相同的热量传递得更远 ,
物体内各点温度更快地随界面温度的升高而升 高。
三、利用“导热形状因子S”计 导热系数为算常数导,热无量内热源稳态导热体
内,两壁温度为定值,即有Q=λS(t1+t2)。
补充内容
稳定热传导的热源法 (虚拟热源法)
定义:如果一个物体有内热源作用时,我们可以通过
导热微分方程式和相应的单值性条件求温度分布。但 如果知道温度分布,我们反过来找导致这种温度分布 的原因—实际存在的热源或假想的热源。这种方法称 虚拟热源法或称映象法。
传热学(第四版)第二章:稳态热传导

t t t t ( ) ( ) ( ) Φ x x y y z z
1 单层平壁、第一类边界条件的导热
a 几何条件:单层平板; b 物理条件:、c、 已知;无内热源 c 时间条件: 稳态导热 : t 0 d 边界条件:第一类
2、微元体中内热源的发热量 d 时间内微元体中内热源的发热量:
[2] dxdydz
3、微元体热力学能的增量 内微元体中内能的增量:
t [3] c dxdydz
导热微分方程式、导热过程的能量方程 由 [1]+ [2]= [3]:
t t t t c ( ) ( ) ( ) x x y y z z
§2-2 导热问题的数学描述
根据傅里叶定律: - grad t q [ W m2 ]
要想确定热流密度,应知道物体内的温度场; 因此,确定导热体内的温度分布是导热理论的首要任务
根据热力学第一定律,对于任一微元体:
建立关于t的方程,求解温度分布
假设:(1) 所研究的物体是各向同性的连续介质; (2) 热导率、比热容和密度均为已知; (3) 物体内具有内热源;内热源均匀分布。
1、导入与导出微元体的净热量 沿 x 轴方向、经 x 表面导入的热量:
x qx dydz
沿 x 轴方向、经 x+dx 表面导出的热量:
() x dx qx dx dydz
qx dx qx qx dx x
qx dxdydz x
沿 x 轴方向导入与导出微元体净热量:
20
20
Temperature (C)
15
15
10
10
5
5
0
1 单层平壁、第一类边界条件的导热
a 几何条件:单层平板; b 物理条件:、c、 已知;无内热源 c 时间条件: 稳态导热 : t 0 d 边界条件:第一类
2、微元体中内热源的发热量 d 时间内微元体中内热源的发热量:
[2] dxdydz
3、微元体热力学能的增量 内微元体中内能的增量:
t [3] c dxdydz
导热微分方程式、导热过程的能量方程 由 [1]+ [2]= [3]:
t t t t c ( ) ( ) ( ) x x y y z z
§2-2 导热问题的数学描述
根据傅里叶定律: - grad t q [ W m2 ]
要想确定热流密度,应知道物体内的温度场; 因此,确定导热体内的温度分布是导热理论的首要任务
根据热力学第一定律,对于任一微元体:
建立关于t的方程,求解温度分布
假设:(1) 所研究的物体是各向同性的连续介质; (2) 热导率、比热容和密度均为已知; (3) 物体内具有内热源;内热源均匀分布。
1、导入与导出微元体的净热量 沿 x 轴方向、经 x 表面导入的热量:
x qx dydz
沿 x 轴方向、经 x+dx 表面导出的热量:
() x dx qx dx dydz
qx dx qx qx dx x
qx dxdydz x
沿 x 轴方向导入与导出微元体净热量:
20
20
Temperature (C)
15
15
10
10
5
5
0
第二章 导热基本定律及稳态导热1——传热学课件PPT

从物体中取出一个微元体 分析进入微元体的总能量 分析离开微元体的总能量 分析微元体中储存能的变化量 微元体自身产生的热量 写出微元体的能量平衡方程式
导热问题中的微元体
z dz
ydy
x y
dz
xdx
dx
dy
z
t dydz
x
x
x dx
x dx
x x
x
x
t x
三类边界条件的表示方法
第一类边界条件 t t x, y, z t t
w
w
(恒壁温)
第二类边界条件
qq w
(恒热流)
第三类边界条件 dt h t t
(换热)
dn w
w
f
关于导热微分方程的说明
热扩散(导温系数)系数的物理意义
a (m2/s) c
导热微分方程的使用条件 对于工程中遇到的大部分稳态和非稳态导热问 题导热方程均可适用;但对于在极短时间内产 生极大热流密度的传热问题,如激光加热过程, 导热微分方程不能使用;另外对于极低温度下 的导热问题,导热微分方程也不适用。
dxdydz
E c t dxdydz
导热微分方程
c
t
x
t x
t y
z
t z
c
不同条件下的导热微分方程
导热系数为常熟的 导热微分方程
t
a
2t x2
2t y2
2t z 2
c
常物性稳态有内热源的 导热微分方程
2t 2t 2t
x2 y2 z2 0
常物性没有内热源的 稳态导热微分方程
第二章 导热基本定律
及稳态导热
本章重点讨论稳态导热问题。为此首先 介绍一些相关的基本知识,如温度场、 温度剃度、导热基本定律等;然后应用 这些基本知识推导出求解导热问题的微 分方程;最后应用这些微分方程求解常 见的导热问题。
导热问题中的微元体
z dz
ydy
x y
dz
xdx
dx
dy
z
t dydz
x
x
x dx
x dx
x x
x
x
t x
三类边界条件的表示方法
第一类边界条件 t t x, y, z t t
w
w
(恒壁温)
第二类边界条件
qq w
(恒热流)
第三类边界条件 dt h t t
(换热)
dn w
w
f
关于导热微分方程的说明
热扩散(导温系数)系数的物理意义
a (m2/s) c
导热微分方程的使用条件 对于工程中遇到的大部分稳态和非稳态导热问 题导热方程均可适用;但对于在极短时间内产 生极大热流密度的传热问题,如激光加热过程, 导热微分方程不能使用;另外对于极低温度下 的导热问题,导热微分方程也不适用。
dxdydz
E c t dxdydz
导热微分方程
c
t
x
t x
t y
z
t z
c
不同条件下的导热微分方程
导热系数为常熟的 导热微分方程
t
a
2t x2
2t y2
2t z 2
c
常物性稳态有内热源的 导热微分方程
2t 2t 2t
x2 y2 z2 0
常物性没有内热源的 稳态导热微分方程
第二章 导热基本定律
及稳态导热
本章重点讨论稳态导热问题。为此首先 介绍一些相关的基本知识,如温度场、 温度剃度、导热基本定律等;然后应用 这些基本知识推导出求解导热问题的微 分方程;最后应用这些微分方程求解常 见的导热问题。
第二章 稳态导热ppt课件

.
第三节 通过圆筒壁的导热 l d 10
1. 第一类边界条件下单层圆筒壁的导热
假设;空心圆筒壁 l,内外径 r1, r2, 且 l>>d2, λ=常数,无内热源,内外表面维持均匀
恒定温度 tw1, tw2,且tw1> tw2。
t
确定(1)圆筒壁的温度分布; (2)通过径向的热流量。
λ
tw1
选取坐标系为圆柱坐标。 tf(r)
对于多层圆通壁的导热问题, 可根据热阻叠加原理,求得通过 多层圆筒壁的导热热流量:
ql
tw1 tw4 Rl1 Rl2 Rl3
tw1 tw4
1
21
ln
d2 d1
1
22
ln
d3 d2
1
23
ln
d4 d3
t
λ1 λ2λ3
tw1
tw2
tw3
tw4
ф
r1 r2 r3 r4
r
ΦL
.
tw1
R λl,1 tw2
1
n
tf1tf2 1 lnd(i1)
1
2r1h1
2 i1
i
di 2rn1h2
t
通过多层圆筒壁的总热流量:
2r11lh 1i n121 tfi1l ltnfd 2d(i i1)2rn11lh 2
ΦL
tw1 λ1 λ2 λ3
t f 1 h1 0
tw2
tw3 tw4 t f2 h2
ф r
t f1
R h1
tc1xc2
0 x dx δ x
由边界条件,求 c1,c2:
c2tw1, c1tw1tw2
.
平壁内的温度分布:
ttw1tw1tw2 x 温度梯度:
传热学(第二章)
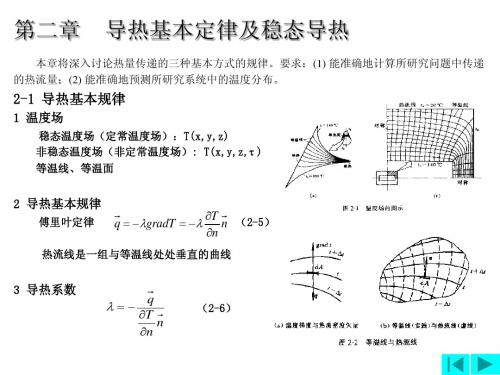
⒉ 通过圆筒壁的导热 由导热微分方程式(2—12)
边界条件:r=r1时,t=t1;r=r2时,t=t2 对(2-25)式积分两次,得其通解: t = c1 ln r + c2 将边界条件代入通解,确定积分常数
t2 − t1 t −t c2 = t1 − ln r 2 1 ln( r2 / r ) ln( r2 / r ) 1 1 t −t t = t1 + 2 1 ln( r / r ) (2-26) 1 ln( r2 / r ) 1 dt λ t1 − t2 q = −λ = (2-27) dr r ln( r2 / r ) 1 c1 =
2 1
λ1
第二章
导热基本定律及稳态导热
2-3 通过平壁、圆筒壁、球壳和其他变截面物体的导热 通过平壁、圆筒壁、
• 1∂ ∂T 1 ∂ ∂T ∂ ∂T ∂T (λr + 2 (λ ) + (λ ) + Φ = ρcp ∂τ r ∂r ∂r) r ∂ϕ ∂ϕ ∂z ∂z d dt 简化变为 dr (r dr ) = 0 (2-25)
⒉ 通过圆筒壁的导热 根据热阻的定义,通过整个圆筒壁的导热热阻为 (2-29) 29) 与分析多层平壁—样,运用串联热阻叠加的原则,可得通过图2-9所示的多层圆筒壁的 导热热流量 2πl(t1 − t4 ) Φ= (2-30) ln( d2 / d1) / λ1 + ln( d3 / d2 ) / λ2 + ln( d4 / d3) / λ3 ⒊ 通过球壳的导热 导热系数为常数,无内热源的空心球壁。内、外半径为r1、r2,其内外表面均匀 恒定温度为t1、t2,球壁内的温度仅沿半径变化,等温面是同心球面。 由傅立叶定律得: dt 各同心球面上的热流率q不相等,而热流量Φ相等。 Φ = −4πr2λ dr dr ⇒Φ 2 = −4πλdt r
工程传热学第二章稳态导热PPT课件
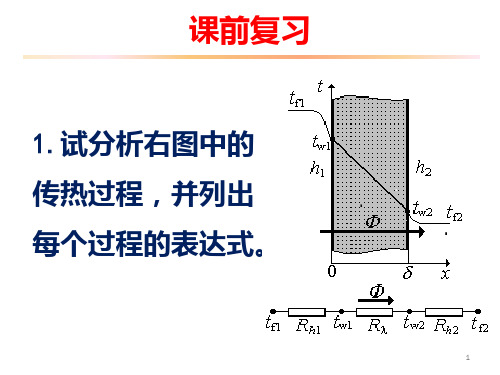
dΦy+dydΦyy( yt)dxdydz
31
沿x轴方向、经x+dx表面导出的热量:
qxdxqx+qxxdx+2xq2x d2x! 2+
qxdx
qx
qx x
dx
dΦx+dx
qx+dxdydz
(qx
qx x
dx)dydz
qxdydz
qx x
dxdydz
dΦx
x
(
t )dxdydz x
32
因此:
dΦ x+dxdΦ x x( x t)dxdydz
下,0.0257 W/(m﹒K) )
27
一般把导热系数仅 仅视为温度的函数, 而且在一定温度范围 还可以用一种线性关 系来描述。
0(1bT)
28
6.导热微分方程
应用能量守恒定律与傅里叶定律, 可建立导热微分方程式。
假设:
1) 所研究的物体是各向同性的连续介
质;
2) 物体内部具有内热源,内热源强度
qgradtt n
n
22
进一步表示为,
qt( titjtk)
x y z
热流密度在x, y, z 方向的投影的大小 分别为:
qx x t; qy y t; qz z t
热流密度是矢量,有方向。 23
5.导热系数
1)导热系数的定义式由下式
给出:
t1
- q
gradt
t2
x
导热系数在数值上等于单位温度 梯度时的热流密度的模(大小)。
FF22逆断层
孙孙氏氏店店正正断层断层
龙固背斜
46.5 47.8
49
50.3 51.5
31
沿x轴方向、经x+dx表面导出的热量:
qxdxqx+qxxdx+2xq2x d2x! 2+
qxdx
qx
qx x
dx
dΦx+dx
qx+dxdydz
(qx
qx x
dx)dydz
qxdydz
qx x
dxdydz
dΦx
x
(
t )dxdydz x
32
因此:
dΦ x+dxdΦ x x( x t)dxdydz
下,0.0257 W/(m﹒K) )
27
一般把导热系数仅 仅视为温度的函数, 而且在一定温度范围 还可以用一种线性关 系来描述。
0(1bT)
28
6.导热微分方程
应用能量守恒定律与傅里叶定律, 可建立导热微分方程式。
假设:
1) 所研究的物体是各向同性的连续介
质;
2) 物体内部具有内热源,内热源强度
qgradtt n
n
22
进一步表示为,
qt( titjtk)
x y z
热流密度在x, y, z 方向的投影的大小 分别为:
qx x t; qy y t; qz z t
热流密度是矢量,有方向。 23
5.导热系数
1)导热系数的定义式由下式
给出:
t1
- q
gradt
t2
x
导热系数在数值上等于单位温度 梯度时的热流密度的模(大小)。
FF22逆断层
孙孙氏氏店店正正断层断层
龙固背斜
46.5 47.8
49
50.3 51.5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b 2
602
)
c1
0.01
c2
0 (40
b 2
402
)
c1
0.02
c2
可否用
长江大学机械工程学院
School of Mechanical Engineering
0 0.892
b 0.009
一、通过平壁的稳态导热
长江大学机械工程学院
School of Mechanical Engineering
长江大学机械工程学院
School of Mechanical Engineering
➢第一类边界条件(
(0 1
bt))
无内热源,平壁厚δ
t
数学描述:
d(
dx
dt dx
)
0
x
0,
t t1
x , t t2
t1 t2
(0 1 bt) 0、b 为常数
o x
d(
dx
dt ) dx
0
dt dx
积分得:
0 (1
bt)
dt dx
c1
再次积分得:0
(t
1 2
bt
2
)
c1
x
c2
q
dt dx
0 (1 bt)
dt dx
c1
1000
代入边界条件:
x=0处,t=100℃; x=10mm = 0.01m处,t =60℃; x=20mm = 0.02m处,t =40℃
0
(100
b 2
1002
)
c2
0 (60
d2t dx2
0
q w1 q w2
q
hh((12twtt2fw12--ttwtwf112))( (twtt1wf 12--tttwwf212))11//hh12
/
qw1 qw2 =q
t
q
tf2 tf1
1 1
h1 h2
tf1,h1
tf2,h2
o x
一、通过平壁的稳态导热
长江大学机械工程学院
School of Mechanical Engineering
➢一侧为第一类边界,另一侧为第二或第三类边界
无内热源,λ为常数,平壁厚δ
d2t dx2
0
dt dx
c1
t
c1x c2
(a)另一侧为第二类边界
t
c2 t1
c1
qw
t
qw
x
t1
(b)另一侧为第三类边界
t1
t =? c1
qw
h(t2 t )
第 i 层的右侧壁温? t1 r1
t t1
t2 t3 t4
t2 r2 t3 r3 t4
一、通过平壁的稳态导热
➢第二类边界条件
无内热源,λ为常数,平壁厚δ
数学描述:
d2t dx2
0
qw const
dt dx
c1
t c1x c2
c1
qw
t
qw
o x
一、通过平壁的稳态导热
长江大学机械工程学院
School of Mechanical Engineering
➢第三类边界条件 无内热源,λ为常数,平壁厚δ
(3)给定物体边界与周围流体间的表面传热系数h
及周围流体的温度tf。
长江大学机械工程学院
School of Mechanical Engineering
§2-3 一维稳态导热
一、通过平壁的稳态导热 二、通过圆筒壁的稳态导热 三、变截面或变热导率的导热问题
一、通过平壁的稳态导热
长江大学机械工程学院
·
2t 0
2t 0
知识回顾:
长江大学机械工程学院
School of Mechanical Engineering
二、热扩散率(导温系数)
c
表征温度传递速度的快慢。
三、定解条件 ——几何、物理、时间、边界
(1)给定物体边界上任何时刻的温度分布; (2)给定物体边界上任何时刻的热流密度分布
平板材料导热系数λ=λ0(1+bt)(t为平板温度)中
的λ0及b。
t 100℃
q=1000W/m2
60℃ 40℃
x 0 0.01 0.02
长江大学机械工程学院
School of Mechanical Engineering
解:由题目条件可知,该问题为一维、稳态无内
热源问题。
d dt 0
dx dx
t4
三层平壁的稳态导热
一、通过平壁的稳态导热
长江大学机械工程学院
School of Mechanical Engineering
➢ 多层平壁,第一类边q
t1
t2 q
r2
2 2
t2
t3 q
r3
3 3
t3
t4 q
q
t1 tn1
n
ri
i1
t1 tn1
n i i1 i
已知q,如何计算其中
,c2
t1
t1
t2
o x
t
t2
t1
x
t1
温度分布
一、通过平壁的稳态导热
长江大学机械工程学院
School of Mechanical Engineering
t
t2
t1
x
t1
dt t2 t1
dx
热流密度:q t2 t1 t
t
热流量: t
(A)
t1 面积热阻
热阻
t2
o x
一、通过平壁的稳态导热
c2 t1
2
o
tf ,h
或qw
x
一、通过平壁的稳态导热
长江大学机械工程学院
School of Mechanical Engineering
2、通过多层平壁的导热
t1
多层平壁:由几层不同材料
组成的平壁。
例:房屋的墙壁 — 白灰 内层、水泥沙浆层、红砖 (青砖)主体层等组成。
t2
t3 t4
t1
t2
t3
知识回顾:
长江大学机械工程学院
School of Mechanical Engineering
一、导热微分方程
导入微 微元体内 导出微 微元体
元体的 + 热源的生 = 元体的 + 内能的
总热量 成热
总热量 增量
c t
(
t )
(
t )
(
t
)
•
x x y y z z
·
t a2t
c
t a2t
o
dt 随温度的升高而减小 上凸
dx
b 0,t 下凹
b>0
t2
x
长江大学机械工程学院
School of Mechanical Engineering
例 1 : q=1000W/m2 的 热 流 密 度 沿 x 方 向 通 过 厚
δ=20mm的平板。已知在x=0、10及20mm处的温
度分别为100℃、60℃及40℃。试据此数据确定
c1
(0 t
b 2
t 2)
c1x
c2
一、通过平壁的稳态导热
长江大学机械工程学院
School of Mechanical Engineering
t
b 2
t2
(t1
b 2
t12)
t1
t2
1
b2(t1
t2) x
t
二次曲线的凹向: A dt
dx
t1
b<0
b 0,t
1
dt1 dx1
2
dt 2 dx 2
School of Mechanical Engineering
1、通过单层平壁的导热 无内热源,λ为常数,平壁厚δ
➢第一类边界条件(λ=const)
t
数学描述: d2t dx2
0
x
0,
t t1
x , t t2
dt 积分得: dx c1 t c1x c2
代入边界条件:c1
t2
t1
