二叉树类模板的设计与实现
二叉树的实现实验原理

二叉树的实现实验原理二叉树是一种常见的数据结构,它由节点组成,每个节点最多有两个子节点,通常称为左子节点和右子节点。
二叉树的实现原理如下:1. 节点的定义:每个节点包含一个值和两个指针,分别指向左子节点和右子节点。
节点可以使用类或结构体来表示,具体的实现方式取决于编程语言。
2. 树的定义:树由节点组成,其中一个节点被指定为根节点。
根节点没有父节点,其他节点都有且只有一个父节点。
每个节点最多有两个子节点,即左子节点和右子节点。
3. 添加节点:向二叉树中添加节点时,需要遵循以下规则:- 如果树为空,将节点作为根节点添加到树中。
- 如果节点的值小于当前节点的值,将节点添加为当前节点的左子节点。
- 如果节点的值大于等于当前节点的值,将节点添加为当前节点的右子节点。
4. 遍历树:遍历二叉树可以按照不同的顺序进行,常见的遍历方式有三种:- 前序遍历(Preorder Traversal):先访问根节点,然后按照前序遍历方式遍历左子树,最后按照前序遍历方式遍历右子树。
- 中序遍历(Inorder Traversal):先按照中序遍历方式遍历左子树,然后访问根节点,最后按照中序遍历方式遍历右子树。
- 后序遍历(Postorder Traversal):先按照后序遍历方式遍历左子树,然后按照后序遍历方式遍历右子树,最后访问根节点。
遍历树的过程可以使用递归或迭代的方式来实现,具体的实现方法取决于编程语言和使用的数据结构。
5. 删除节点:删除二叉树中的节点时,需要考虑多种情况。
如果要删除的节点是叶子节点,可以直接删除它。
如果要删除的节点只有一个子节点,可以将子节点移动到要删除的节点的位置。
如果要删除的节点有两个子节点,可以选择将其中一个子节点替代要删除的节点,或者选择左子树的最大节点或右子树的最小节点替代要删除的节点。
根据上述原理,可以使用类或结构体等数据结构和递归或迭代的方式来实现二叉树。
具体的实现方法和细节可能因编程语言而异,但以上原理是通用的。
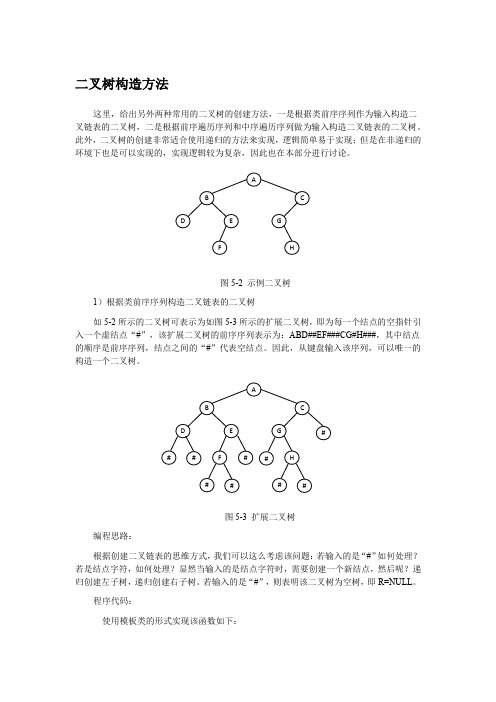
二叉树构造方法
பைடு நூலகம்
R->data = ch;
Create(R->lch); Create(R->rch);
//创建左子树 //创建右子树
}
}
2)根据前序遍历序列和中序遍历序列构造二叉链表的二叉树
如图 5-2 所示的二叉树的前序序列和中序序列为:ABDEFCGH 和 DBFEAGHC,则如 何创建二叉链表的二叉树呢?
编程思路:
递归实现创建操作时用来表示的结点的类型为指针的引用*&,这是通过函数参数传 递来使用的,目的是将指针本身传递给函数;非递归实现过程中没有参数调用,无法使 用*&类型,因此使用 **来传递结点指针的地址。
c.以类前序序列做为输入进行实现。
程序代码:
template <class T>
void BiTree<T>::Create(BiNode<T>** R)
{ BiNode<T>** stack[MAXSIZE]; int top =-1;
//定义顺序栈 //栈顶指针
char ch;
do
{
cin>>ch;
while(ch!=’#’)
{ *R = new BiNode<T>;
//创建结点,保存根结点指针的地址
(*R)->data=ch;
(*R)->lch =(*R)->rch = NULL;
b.使用非递归的方法创建二叉树必须要注意输入的参数类型**;
首先,**是指针的指针,也就是**类型的变量存储的数据是一个指针的地址。举个 例子,已知 int a=5;则 int *p=&a; int **pp = &p;则变量 a、p、pp 的关系如图所示:
数据结构二叉树应用课程设计含源代码实现

递归法的先序遍历:按照输出根、输出左孩子、输出右孩子的顺
序来递归的调用先序遍历函数。
递归法的中序遍历:输出左孩子、按照输出根、输出右孩子的顺
2 / 17
序来递归的调用中序遍历函数。 递归法的后序遍历:输出左孩子、输出右孩子、按照输出根的顺
序来递归的调用后序遍历函数。 二叉树的先序、中序、后序遍历的非递归方法是要借助数据结构
层序遍历。求二叉树的高度、宽度,结点数。判断是否为二叉排序树。
[ห้องสมุดไป่ตู้本要求]
(1) 从文件中读入建树信息,树的节点数目不小于 20 个,树的高
度不小于 4。
(2) 采用二叉链表结构。
(3) 至少 2 组输入数据,分别是二叉排序树和不是二叉排序树。
3.2 数据结构
***********************************************************
typedef struct
{
SElemType *base; //栈底指针
SElemType *top;
//栈顶指针
int stacksize;
//栈的容量
}SqStack;
//栈
3.3 算法设计思想
首先从文件中读取二叉树,按照先序遍历的顺序递归建树,先建
立它的左子树,再建立它的右子树,最后递归结束,整棵树构建成功!
cout<<"文件打开失败!请重试!"<<endl; exit(0); } ReadFile>>sum; while(sum--) { cout<<"case:"<<++case1<<endl; CreatBiTree(Head, ReadFile);
《二叉树模型》课件

二叉树的分类
01 满二叉树
如果一个二叉树的每个节点都有两个子节点,则 该二叉树称为满二叉树。
02 完全二叉树
如果一个二叉树的最后一层是满的,且除了最后 一层外,其他各层的节点数达到最大,则该二叉 树称为完全二叉树。
03 平衡二叉树
平衡二叉树是一种特殊的完全二叉树,它的左右 子树的高度差不超过1。
二叉树的应用场景
详细描述
在n叉树模型中,每个节点可以拥有任意数 量的子节点,而不仅仅是两个。这种模型在 处理具有多个分支的数据结构时非常有用, 例如决策树和知识图谱。n叉树模型在搜索 、排序和数据压缩等领域有广泛应用。
B树模型
要点一
总结词
B树模型是一种自平衡的多路搜索树,用于数据库和文件系 统的索引。
要点二
详细描述
详细描述
二叉树的插入操作包括节点的添加和位置调整两个步骤。在添加节点时,需要找到合适 的位置将其插入到二叉树中,并保持二叉树的平衡性。位置调整是为了维护二叉树的性
质,确保每个节点的左子树和右子树的高度差不超过1。
插入操作的时间复杂度
总结词
插入操作的时间复杂度取决于具体的实现方式和数据结构。
详细描述
在平衡二叉树中,插入操作的时间复杂度为O(log n),其中n为二叉树中节点的数量。而在一般的二 叉树中,插入操作的时间复杂度可能达到O(n),因为可能需要遍历整棵树才能找到合适的位置插入新 节点。因此,选择合适的二叉树数据结构和算法对于提高插入操作的效率至关重要。
05
二叉树算法的应用
堆排序算法
平衡二叉树的性质:平衡二叉树具有以下性质:1)它的左右子树的高度差不超过1;2)它的左 子树和右子树都是平衡二叉树;3)它的左子树和右子树的节点数相差不超过1。
二叉树课程设计报告

一、设计目标二叉树是形象地说既树中每个节点最多只有两个分支,它是一中重要的数据类型。
可以运用于建立家谱,公司所有的员工的职位图,以及各种事物的分类和各种机构的职位图表。
二叉树是通过建立一个链式存储结构,达到能够实现前序遍历,中序遍历,后序遍历。
以及能够从输入的数据中得知二叉树的叶子结点的个数,二叉树的深度。
在此,二叉树的每一个结点中必须包括:值域,左指针域,右指针域。
二、总体设计1.对程序中定义的核心数据结构及对其说明:typedef struct BiTNode{//创建二叉树char data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;在开头定义了二叉树的链式存储结构,此处采用了每个结点中设置三个域,即值域,左指针域和右指针域。
2.模块的划分及其功能:本程序分为:7大模块。
二叉树的建立链式存储结构、前序遍历、求叶子结点的个数计算、中序遍历、后序遍历、深度、主函数。
1、二叉树的建立链式存储结构;首先typedef struct BiTNode:定义二叉树的链式存储结构,此处采用了每个结点中设置三个域,即值域,*lchild:左指针域和rchild:右指针域。
2、二叉树的前序遍历;利用二叉链表作为存储结构的前序遍历:先访问根结点,再依次访问左右子树。
3、二叉树的求叶子结点的个数计算;先分别求得左右子树中各叶子结点的个数,再计算出两者之和即为二叉树的叶子结点数。
4、二叉树的中序遍历;利用二叉链表作为存储结构的中序遍历:先访问左子数,再访问根结点,最后访问右子树。
5、二叉树的后序遍历;利用二叉链表作为存储结构的前序遍历:先访问左右子树,再访问根结点。
6、求二叉树的深度:首先判断二叉树是否为空,若为空则此二叉树的深度为0。
否则,就先别求出左右子树的深度并进行比较,取较大的+1就为二叉树的深度。
7、主函数。
核心算法的设计:二叉树是n个节点的有穷个集合,它或者是空集(n=0),或者同时满足以下两个条件:(1):有且仅有一个称为根的节点;(2):其余节点分为两个互不相交的集合T1,T2,并且T1,T2都是二叉树,分别称为根的左子树和右子树。
线索二叉树课程设计说明书-模板

数学与计算机学院课程设计说明书课程名称: 数据结构与算法课程设计课程代码:题目: 线索二叉树的应用年级/专业/班: 2010级软件1班学生姓名:学号: 1127开始时间:2011 年12 月9 日完成时间:2011 年12 月23 日课程设计成绩:1指导教师签名:年月日摘要首先是对需求分析的简要阐述,说明系统要完成的任务和相应的分析,并给出测试数据。
其次是概要设计,说明所有抽象数据类型的定义、主程序的流程以及各程序模块之间的层次关系,以及ADT描述。
然后是详细设计,描述实现概要设计中定义的基本功操作和所有数据类型,以及函数的功能及代码实现。
再次是对系统的调试分析说明,以及遇到的问题和解决问题的方法。
然后是用户使用说明书的阐述,然后是测试的数据和结果的分析,最后是对本次课程设计的结论。
关键词:线索化;先序遍历;中序遍历;后续遍历线索二叉树的运用引言数据结构是计算机专业重要的专业基础课程与核心课程之一,在计算机领域应用广泛,计算机离不开数据结构。
数据结构课程设计为了能使我们掌握所学习的知识并有应用到实际的设计中的能力,对于掌握这门课程的学习方法有极大的意义。
本课程设计的题目为“线索二叉树的应用”,完成将二叉树转化成线索二叉树,采用前序、中序或后序线索二叉树的操作。
本课程设计采用的编程环境为Microsoft Visual Stdio 2008。
目录1需求分析 (3)2开发及运行平台 (4)3 概要设计 (5)4 详细设计 (7)5 调试分析 (12)6 测试结果 (13)7 结论 (18)致谢 (19)参考文献 (20)附录 (21)1、需求分析为了能更熟练精准的掌握二叉树的各种算法和操作,同时也为了开拓视野,综合运用所学的知识。
为此,需要将二叉树转化成线索二叉树,采用前序、中序或后序线索二叉树,以实现线索树建立、插入、删除、恢复线索等。
1.1任务与分析中次系统要实现对二叉树的建立,以及线索化该二叉树,同时实现对其先序、中序、后序线索话的并输出结果。
二叉树操作设计和实现实验报告

二叉树操作设计和实现实验报告一、目的:掌握二叉树的定义、性质及存储方式,各种遍历算法。
二、要求:采用二叉树链表作为存储结构,完成二叉树的建立,先序、中序和后序以及按层次遍历的操作,求所有叶子及结点总数的操作。
三、实验内容:1、分析、理解程序程序的功能是采用二叉树链表存储结构,完成二叉树的建立,先序、中序和后序以及按层次遍历的操作。
如输入二叉树ABD###CE##F##,链表示意图如下:2、添加中序和后序遍历算法//========LNR 中序遍历===============void Inorder(BinTree T){if(T){Inorder(T->lchild);printf("%c",T->data);Inorder(T->rchild);}}//==========LRN 后序遍历============void Postorder(BinTree T){if(T){Postorder(T->lchild);Postorder(T->rchild);printf("%c",T->data);}}3、调试程序,设计一棵二叉树,输入完全二叉树的先序序列,用#代表虚结点(空指针),如ABD###CE##F##,建立二叉树,求出先序、中序和后序以及按层次遍历序列,求所有叶子及结点总数。
(1)输入完全二叉树的先序序列ABD###CE##F##,程序运行结果如下:(2)先序序列:(3)中序序列:(4)后序序列:(5)所有叶子及结点总数:(6)按层次遍历序列:四、源程序代码#include"stdio.h"#include"string.h"#include"stdlib.h"#define Max 20 //结点的最大个数typedef struct node{char data;struct node *lchild,*rchild;}BinTNode; //自定义二叉树的结点类型typedef BinTNode *BinTree; //定义二叉树的指针int NodeNum,leaf; //NodeNum为结点数,leaf为叶子数//==========基于先序遍历算法创建二叉树==============//=====要求输入先序序列,其中加入虚结点"#"以示空指针的位置========== BinTree CreatBinTree(void){BinTree T;char ch;if((ch=getchar())=='#')return(NULL); //读入#,返回空指针else{T=(BinTNode *)malloc(sizeof(BinTNode)); //生成结点T->data=ch;T->lchild=CreatBinTree(); //构造左子树T->rchild=CreatBinTree(); //构造右子树return(T);}}//========NLR 先序遍历=============void Preorder(BinTree T){if(T) {printf("%c",T->data); //访问结点Preorder(T->lchild); //先序遍历左子树Preorder(T->rchild); //先序遍历右子树}}//========LNR 中序遍历===============void Inorder(BinTree T){if(T){Inorder(T->lchild);printf("%c",T->data);Inorder(T->rchild);}}//==========LRN 后序遍历============void Postorder(BinTree T){if(T){Postorder(T->lchild);Postorder(T->rchild);printf("%c",T->data);}}//=====采用后序遍历求二叉树的深度、结点数及叶子数的递归算法======== int TreeDepth(BinTree T){int hl,hr,max;if(T){hl=TreeDepth(T->lchild); //求左深度hr=TreeDepth(T->rchild); //求右深度max=hl>hr? hl:hr; //取左右深度的最大值NodeNum=NodeNum+1; //求结点数if(hl==0&&hr==0) leaf=leaf+1; //若左右深度为0,即为叶子。
二叉树的常用算法设计和实现

二叉树的常用算法设计和实现一、引言二叉树是一种重要的数据结构,广泛应用于计算机科学中。
掌握二叉树的常用算法设计和实现对于理解和应用二叉树具有重要意义。
本文档将介绍二叉树的常用算法设计和实现,包括二叉树的遍历、查找、插入和删除等操作。
二、算法设计1. 遍历算法:二叉树的遍历是二叉树操作的核心,常用的遍历算法包括先序遍历、中序遍历和后序遍历。
每种遍历算法都有其特定的应用场景和优缺点。
2. 查找算法:在二叉树中查找特定元素是常见的操作。
常用的查找算法有二分查找和线性查找。
二分查找适用于有序的二叉树,而线性查找适用于任意顺序的二叉树。
3. 插入算法:在二叉树中插入新元素也是常见的操作。
插入操作需要考虑插入位置的选择,以保持二叉树的特性。
4. 删除算法:在二叉树中删除元素也是一个常见的操作。
删除操作需要考虑删除条件和影响,以保持二叉树的特性。
三、实现方法1. 先序遍历:使用递归实现先序遍历,可以通过访问节点、更新节点计数器和递归调用下一个节点来实现。
2. 中序遍历:使用递归实现中序遍历,可以通过访问节点、递归调用左子树和中继判断右子树是否需要访问来实现。
3. 后序遍历:使用迭代或递归实现后序遍历,可以通过访问节点、迭代处理左子树和右子树或递归调用左子树和更新节点计数器来实现。
4. 二分查找:在有序的二叉搜索树中实现二分查找,可以通过维护中间节点和边界条件来实现。
5. 线性查找:在任意顺序的二叉树中实现线性查找,可以通过顺序遍历所有节点来实现。
6. 插入和删除:针对具体应用场景和删除条件,选择适当的插入位置并维护节点的插入和删除操作。
在有序的二叉搜索树中实现插入和删除操作相对简单,而在其他类型的二叉树中则需要考虑平衡和维护二叉搜索树的特性。
四、代码示例以下是一个简单的Python代码示例,展示了如何实现一个简单的二叉搜索树以及常用的二叉树操作(包括遍历、查找、插入和删除)。
```pythonclass Node:def __init__(self, data):self.data = dataself.left = Noneself.right = Noneclass BinarySearchTree:def __init__(self):self.root = Nonedef insert(self, data):if not self.root:self.root = Node(data)else:self._insert(data, self.root)def _insert(self, data, node):if data < node.data:if node.left:self._insert(data, node.left)else:node.left = Node(data)elif data > node.data:if node.right:self._insert(data, node.right)else:node.right = Node(data)else:print("Value already in tree!") # Value already in tree!def search(self, data):return self._search(data, self.root)def _search(self, data, node):if data == node.data:return Trueelif (not node.left and data < node.data) or (notnode.right and data > node.data):return Falseelse:return self._search(data, node.left) orself._search(data, node.right)def inorder_traversal(self): # inorder traversal algorithm implementationif self.root: # If the tree is not empty, traverse it in-order.self._inorder_traversal(self.root) # Recursive function call for in-order traversal.print() # Print a new line after traversal to clear the output area for the next operation.def _inorder_traversal(self, node): # Helper function for in-order traversal algorithm implementation. Traverse the left subtreefirst and then traverse the right subtree for a given node (start with root). This method handles recursive calls for traversal operations efficiently while keeping track of nodes already visited and。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
封皮(按学校要求手工填写)成绩评定表课程设计任务书摘要树结构在客观世界中广泛存在,如族谱、各种社会组织机构等都可以用树形结构来表示;树结构在计算机中应用也很广泛,如文件夹;其中二叉树结构是比较常用的一种数据结构,简单来说每个结点最多有两个孩子。
本文采用C++语言来描述二叉树类模板的设计并实现其功能,并且采用VS2010应用程序来实现程序。
关键词:二叉树类模板;MFC目录1 需求分析 (1)2 算法基本原理 (1)3 类设计 (1)4 基于控制台的应用程序 (2)4.1类的接口设计 (2)4.2类的实现 (3)4.3主函数设计 (8)4.4基于控制台的应用程序测试 (9)5 基于MFC的应用程序 (10)5.1基于MFC的应用程序设计 (10)5.1.1 MFC程序界面设计 (11)5.1.2 MFC程序代码设计 (13)5.2基于MFC的应用程序测试 (17)结论 (20)参考文献 (21)1需求分析进行二叉树类模板的设计并实现,数据元素可以是char,int,float等多种数据类型,包括以下功能:(1)采取顺序存储结构或链式存储结构实现二叉树的存储;(2)实现二叉树的建树;(3)实现二叉树的前序、中序、后序遍历;(4)能够求解二叉树的结点总数和叶子结点总数;(5)能够求解二叉树的高度;(6)将上述功能作为类的成员函数实现,编写主函数测试上述功能。
整个二叉树类模板程序中的存储采用的是链式存储结构。
在整个二叉树类中所有数据成员和成员函数均采用公有方式,类中有一个二叉树结点的定义,有建立二叉树的成员函数,有先序、中序、后序遍历的成员函数,有求解结点数、叶子节点数、二叉树深度的成员函数,它的功能在类里定义一个调用各个成员函数的成员函数来实现对二叉树的操作,然后在主函数中通过对模板的实例化产生对象,用对象调用成员函数的方式实现预期功能。
2算法基本原理一颗二叉树有许多个结点组成,每个结点有三个区域分别存有数据和它的左右孩子指针。
大体思路:先构造一棵二叉树,然后依次实现前序、中序、后序遍历,统计二叉树的结点总数,统计二叉树的叶子结点数,求出二叉树的高度这些功能。
在主函数中实例化char,int,float数据类型的类对象,然后根据类对象来实现功能。
3 类设计根据算法分析可以看到,本设计首先应该设计一个二叉树的模板类,可将ertree作为二叉树的类名,然后在这个类中定义各个成员函数来实现所需要的功能。
类的设计如下:template<class T>//声明模板classertree{public:typedefstruct node{//二叉树的节点T data;struct node *lchild,*rchild;}bitree;bitree *tree1();//建立二叉树Xxu(bitree *p);//先序遍历的结果Zxu(bitree *p);//中序遍历的结果Hxu(bitree *p);//后序遍历的结果JDS(bitree *p);//结点数YZJDS1(bitree *p);//叶子结点数height(bitree *p);//二叉树的高度fun();//调用成员函数}在实现过程中,需要访问ertree类数据成员,将其数据成员设置成公有的即可。
4 基于控制台的应用程序整个程序分为两个独立的文档,Debug 文件夹中包含有VS2010编译好的应用程序,可独立运行;其他文件夹整体包含程序所需要的各个组件,需要依靠VS2010才能运行。
4.1 类的接口设计#include<stdlib.h>//头文件给类的建立提供支持#include<malloc.h>#include<iostream>using namespace std;template<class T>classertree{public:typedefstruct node{//二叉树的节点T data;struct node *lchild,*rchild;}bitree;bitree *p;//定义一个类中的变量用来存储根结点bitree *tree1();//建立二叉树,从键盘由先序输入二叉树元素void Xxu(bitree *p);//先序遍历的结果void Zxu(bitree *p);//中序遍历的结果void Hxu(bitree *p);//后序遍历的结果int JDS(bitree *p);//结点数int YZJDS1(bitree *p);//叶子结点数int YZJDS2(bitree *p);//叶子结点数int YZJDS3(bitree *p);//叶子结点数int height(bitree *p);//二叉树的高度void fun1();//调用成员函数};在ertree类中没有定义构造函数和析构函数,因为这两个函数在运行时类可以自动生成,并不影响类的功能。
4.2 类的实现//用递归的方式来建立二叉树bitree *tree1(){//建立二叉树bitree *t;T a;cout<<"输入元素";cin>>a;if(a==0)t=NULL;else {t=(bitree *)malloc(sizeof(bitree));t->data=a;cout<<t->data<<"的左子树";t->lchild=tree1();cout<<t->data<<"的右子树";t->rchild=tree1();}return t;}bitree *tree2(){//建立二叉树bitree *t;T a;cout<<"输入元素";cin>>a;if(a=='0')t=NULL;else {t=(bitree *)malloc(sizeof(bitree));t->data=a;cout<<t->data<<"的左子树";t->lchild=tree2();cout<<t->data<<"的右子树";t->rchild=tree2();}return t;}//递归的调用方式进行先序遍历void Xxu(bitree *p){//先序遍历的结果if(p!=NULL){cout<<p->data<<' ';Xxu(p->lchild);Xxu(p->rchild);}}//递归的调用方式进行中序遍历void Zxu(bitree *p){//中序遍历的结果if(p!=NULL){Zxu(p->lchild);cout<<p->data<<' ';Zxu(p->rchild); }}//递归的调用方式进行后序遍历void Hxu(bitree *p){//后序遍历的结果if(p!=NULL){Hxu(p->lchild);Hxu(p->rchild);cout<<p->data<<' ';}}//递归的调用方式求解结点数int JDS(bitree *p){//结点数int c;if(p==NULL)c=0;elsec=1+JDS(p->lchild)+JDS(p->rchild);return c;}//递归的调用方式求解叶子结点数int YZJDS1(bitree *p){//叶子结点数if (p==NULL)return d1;else {if(p->lchild==NULL&&p->rchild==NULL)d1++;YZJDS1(p->lchild);YZJDS1(p->rchild);}}int YZJDS2(bitree *p){//叶子结点数if (p==NULL)return d2;else {if(p->lchild==NULL&&p->rchild==NULL)d2++;YZJDS2(p->lchild);YZJDS2(p->rchild);}}int YZJDS3(bitree *p){//叶子结点数if (p==NULL)return d3;else {if(p->lchild==NULL&&p->rchild==NULL)d3++;YZJDS3(p->lchild);YZJDS3(p->rchild);}}//求深度时调用该函数int max(intm,int n)//比较大小{if (m>n)return m;elsereturn n;}//递归的调用方式求解叶子结点数int height(bitree *p){//二叉树的高度if(p!=NULL){return (1+max(height(p->lchild),height(p->rchild)));} else return 0;}//这个成员函数用来调用其他成员函数void fun1(){//实现各种操作p=tree1();cout<<"\n先序遍历结果:";Xxu(p);cout<<"\n中序遍历结果:";Zxu(p);cout<<"\n后序遍历结果:";Hxu(p);cout<<"\n结点数:";cout<<JDS(p);cout<<"\n叶子结点数:";cout<<YZJDS1(p);cout<<"\n二叉树的高度为:";cout<<height(p);}void fun2(){p=tree2();cout<<"\n先序遍历结果:";Xxu(p);cout<<"\n中序遍历结果:";Zxu(p);cout<<"\n后序遍历结果:";Hxu(p);cout<<"\n结点数:";cout<<JDS(p);cout<<"\n叶子结点数:";cout<<YZJDS2(p);cout<<"\n二叉树的高度为:";cout<<height(p);}void fun3(){p=tree1();cout<<"\n先序遍历结果:";Xxu(p);cout<<"\n中序遍历结果:";Zxu(p);cout<<"\n后序遍历结果:";Hxu(p);cout<<"\n结点数:";cout<<JDS(p);cout<<"\n叶子结点数:";cout<<YZJDS3(p);cout<<"\n二叉树的高度为:";cout<<height(p);}在类的成员函数执行过程中,用一个类的公有制变量p来保存跟结点,然后在遍历时直接对根结点进行访问。
