泡利不相容原理
泡利不相容原理与洪特规则

泡利不相容原理与洪特规则泡利不相容原理与洪特规则是量子力学中两个重要的原则,它们对于电子在原子轨道中的排布和原子结构的稳定性起着关键作用。
泡利不相容原理由奥地利物理学家波尔斯·泡利于1925年提出,它指出相同的自旋量子数的两个电子不能在同一个原子轨道中同时存在。
这一原理保证了原子的稳定性,避免了电子之间的相互斥力过大,从而使原子结构能够保持相对稳定。
而洪特规则则是由美国物理学家罗伯特·洪特在1923年提出的,它总结了电子在原子轨道中填充的顺序规律,有助于理解原子的能级分布和化学性质。
泡利不相容原理与洪特规则的提出,彻底改变了人们对原子结构的认识。
在泡利不相容原理的指导下,我们可以确定原子中各个电子的排布方式,从而进一步推导出原子的化学性质和化学键的形成。
洪特规则则为我们提供了一个简单而有序的填充电子的方式,帮助我们理解原子中电子的能级分布和轨道角动量的排布规律。
这两个原理的相互配合,为我们解释原子结构和化学键提供了有力的理论支持。
泡利不相容原理的核心概念是电子的自旋量子数,它决定了电子的自旋状态以及电子之间的排斥能。
根据泡利不相容原理,相同自旋量子数的两个电子无法同时处于同一个原子轨道中,这意味着在一个原子轨道中最多只能容纳两个电子,并且这两个电子的自旋量子数必须相反。
这一原理的提出,解决了之前无法解释原子结构和化学性质的难题,为后来量子力学的发展奠定了基础。
洪特规则则为我们提供了填充电子的顺序规律。
根据洪特规则,电子在填充原子轨道时会优先填充能量较低的轨道,而不同轨道的填充顺序遵循一定的规律。
具体来说,s轨道先于p轨道填充,p轨道又先于d轨道填充,最后才是f轨道。
在每个轨道内,电子的填充顺序则遵循洪特规则中的“两电子自旋相反”的原则。
这一规律简洁而有序,帮助我们理解原子各能级之间的排布规律,以及不同能级之间的能级间隔。
泡利不相容原理与洪特规则的结合,使得我们能够更加深入地理解原子结构和化学键的形成。
泡利不相容原理证明

泡利不相容原理证明泡利不相容原理是量子力学中的一个重要概念,它解释了为什么相同类型的费米子无法存在于相同的量子态中。
费米子是一类具有半整数自旋的粒子,如电子、质子和中子等。
泡利不相容原理的证明可以通过考虑多粒子波函数的对称性来进行。
根据泡利不相容原理,任意两个相同类型的费米子不能处于完全相同的量子态中,也就是说它们的波函数在空间和自旋两个方面不能完全相同。
首先,考虑两个相同类型的费米子,我们可以将它们的波函数表示为:Ψ(1,2) = Φ(1)Φ(2)其中,Φ(1)和Φ(2)分别是第一个和第二个粒子的波函数。
由于费米子的自旋是半整数,因此它们的自旋波函数必须是反对称的。
也就是说,当交换两个粒子的标签时,波函数需要发生符号变化。
我们可以用符号来表示波函数的对称性。
如果波函数对于每一对交换的粒子都保持不变,那么波函数是对称的;如果波函数在每一对交换的粒子上发生了符号变化,那么波函数是反对称的。
对于费米子,其波函数必须是反对称的。
现在考虑两个相同类型的费米子,我们可以交换它们的标签,即交换粒子1和粒子2。
根据波函数的反对称性,我们得到:Ψ(2,1) = -Ψ(1,2)两个波函数的差异可以通过将它们相加和相减来揭示:Ψ(1,2) + Ψ(2,1) = 0Ψ(1,2) - Ψ(2,1) = 2Ψ(1,2)根据量子力学的原理,波函数的模的平方表示找到一个粒子在某个量子态的概率。
如果两个波函数的和为零,那么在这个量子态下的概率为零,也就是说两个粒子不能同时处于相同的量子态中。
由此可见,泡利不相容原理限制了相同类型的费米子处于相同的量子态中。
这一概念对于理解原子和分子的电子结构以及凝聚态物理中的电子行为非常重要。
泡利不相容原理 库珀对

泡利不相容原理库珀对
泡利不相容原理是量子力学中的一个基本原理,由奥地利物理学家沃纳·泡利于1925年提出。
这个原理主要描述了原子中电子的排布规律,指出在一个原子中,不可能有两个电子具有完全相同的四个量子数(主量子数、角量子数、磁量子数和自旋量子数)。
这一原理对于我们理解原子结构和原子光谱现象具有重要意义。
在原子物理中,泡利不相容原理的应用非常广泛。
例如,它解释了为什么原子中的电子会按照特定的能级分布,这是因为每个能级只能容纳一个电子。
此外,泡利不相容原理还解释了原子光谱线的复杂性,这是因为电子在能级之间跃迁时,会吸收或释放特定能量的光子。
与此同时,库珀对是另一种重要的量子现象。
1954年,美国物理学家约翰·库珀提出了库珀对的概念。
库珀对是指在超导体中,两个电子通过交换声子(晶格振动)产生的有效吸引力而成对。
在超导体中,库珀对的存在使得电子能够克服原子核的库仑排斥力,从而形成稳定的电子对。
这一现象是超导现象的基础,对于解释超导体的高温超导和高压超导具有重要意义。
泡利不相容原理与库珀对之间存在着密切的联系。
在超导体中,泡利不相容原理使得电子能够按照特定的规律排列,形成稳定的库珀对。
这种排列有助于提高超导体的临界温度,从而使超导现象更加显著。
此外,库珀对在超导体中的形成过程也受到泡利不相容原理的调控。
在现代科学研究中,泡利不相容原理和库珀对的重要性不言而喻。
它们为我们在原子物理、超导物理等领域的研究提供了基本理论依据。
泡利不相容定律(3篇)

第1篇一、引言在微观世界的探索中,科学家们发现了一系列神奇的现象。
其中,泡利不相容定律是量子力学中一个非常重要的原理,它揭示了微观粒子之间的一种特殊关系。
本文将详细阐述泡利不相容定律的内涵、起源、应用以及在我国科研领域的重要性。
二、泡利不相容定律的内涵泡利不相容定律,又称为泡利原理,是奥地利物理学家沃尔夫冈·泡利于1925年提出的。
该定律指出:在同一个原子中,不可能有两个电子的四个量子数完全相同。
这四个量子数分别是主量子数(n)、角量子数(l)、磁量子数(m)和自旋量子数(s)。
1. 主量子数(n):表示电子所处的能级,取值为正整数(1、2、3...)。
2. 角量子数(l):表示电子在原子轨道中的角动量大小,取值范围为0到n-1。
3. 磁量子数(m):表示电子在特定角动量状态下的磁矩方向,取值范围为-l到l。
4. 自旋量子数(s):表示电子自旋的取向,取值为+1/2或-1/2。
泡利不相容定律意味着,在同一个原子中,两个电子的四个量子数不能同时取相同值。
这保证了电子在原子中的稳定分布,为原子的化学性质提供了基础。
三、泡利不相容定律的起源泡利不相容定律的发现源于对原子结构的探索。
在20世纪初,科学家们发现,通过改变原子核的电荷数,可以产生不同元素。
然而,当时的原子模型无法解释元素周期表中的周期性规律。
泡利在研究电子在原子中的分布时,发现了这一神奇的现象,并提出了泡利不相容定律。
四、泡利不相容定律的应用泡利不相容定律在物理学、化学、材料科学等领域具有广泛的应用。
1. 物理学:泡利不相容定律是量子力学的基本原理之一,为研究原子、分子、固体等微观世界的性质提供了理论基础。
2. 化学:泡利不相容定律解释了元素周期表中元素的周期性规律,为化学元素的研究提供了重要依据。
3. 材料科学:泡利不相容定律在研究材料电子结构、导电性等方面具有重要意义。
五、泡利不相容定律在我国科研领域的重要性泡利不相容定律作为量子力学的基本原理之一,在我国科研领域具有重要地位。
1945年诺贝尔物理学奖──泡利不相容原理

1945年诺贝尔物理学奖──泡利不相容原理1945年诺贝尔物理学奖授予美国新泽西州普林斯顿大学的奥地利物理学家泡利(Wolfgamg Pauli,1900—1958),以表彰他发现了所谓泡利原理的不相容原理。
不相容原理是量子理论中的重要原理,是1925年1月由泡利提出的。
这一原理可以表述为:对于完全确定的量子态来说,每一量子态中不可能存在多于一个的粒子。
泡利后来用量子力学理论处理了h/4π自旋问题,引入了二分量波函数的概念和所谓的泡利自旋矩阵。
通过泡利等人对量子场的研究,人们认识到只有自旋为半整数的粒子(即费米子)才受不相容原理的限制,从而确立了自旋统计关系。
关于不相容原理的发现,泡利在他的诺贝尔奖演说中讲到,不相容原理发现的历史可以追溯到他在慕尼黑的学生时代。
在维也纳读中学时,他就掌握了经典物理学和相对论的知识。
在慕尼黑大学经索末菲引导接触到从经典的思想方法看来有些离奇的原子结构理论。
他和所有习惯于经典思想方法的物理学家一样,当第一次接触到玻尔的量子理论的基本假设时不免受到冲击。
他一方面接受了玻尔的原子理论;一方面了解索末菲企图用光谱定律的解释来克服使用动力学模型所遇到的困难。
泡利对这两种理论都不满意。
反常塞曼效应的解释问题,使物理学家倍感苦恼,泡利也不例外。
据说当时有一位友人看见泡利在哥本哈根的大街上闲逛,就问他为什么不高兴。
泡利回答说:“当一个人正在想到反常塞曼效应时,他怎么高兴得起来啊!”。
按照玻尔的想法,当分析原子的结构时,应该首先从内层开始。
可以设想有一个带正电荷Ze的原子核,在其周围是若干电子,这些电子一个接着一个被原子核俘获,直到它俘获了Z个电子而形成中性原子时为止。
最先被俘获的电子占据能量最低的量子轨道,这就是玻尔所谓的“组建原则”。
泡利不满意的原因在于他认为原子光谱的根源在于价电子的运动,不应该从原子实的结构去找。
泡利仔细研究了碱金属光谱的双重结构,引入了“经典不能描述的双重值”概念,在这基础上概括成一个重要结论,即原子中不能有两个电子具有相同的四个量子数。
泡利不相容原理与洪特规则

泡利不相容原理与洪特规则是量子力学中非常重要的概念,它们对于理解原子和分子的结构以及化学反应起着至关重要的作用。
泡利不相容原理是由意大利物理学家泡利于1925年提出的,它说明了相同自旋的两个费米子(如电子)不能同时处于同一量子态。
这一原理的提出,对于解释元素的电子排布以及化学键的形成都具有重要意义。
与泡利不相容原理相似的是洪特规则,它是由美国化学家洪特提出的,用于描述原子的电子排布规律。
洪特规则指出电子会优先填充能量较低的轨道,然后才会填充能量较高的轨道,这一规则帮助我们理解元素的电子排布及其性质。
在本文中,我们将深入探讨泡利不相容原理与洪特规则的本质、应用以及相关领域的研究进展。
泡利不相容原理和洪特规则的提出,彰显了量子力学在化学领域的重要性。
在传统的经典力学中,电子的轨道可以是任意填充的,而在量子力学中,由于波函数的对称性,相同自旋的两个费米子无法处于同一态。
这一原理的提出,极大地改变了我们对于原子结构和元素性质的认识。
借助泡利不相容原理,我们可以解释为什么每个电子壳层中有特定数量的电子,以及为什么元素会表现出不同的化学性质。
洪特规则则进一步完善了我们对于电子排布的认识,指导着化学家们设计新的材料和化合物。
泡利不相容原理和洪特规则的研究不仅仅停留在理论层面,更多的是在实际应用中得到体现。
例如,在材料科学领域,研究人员可以通过控制电子的排布来设计出具有特定性质的新材料。
另外,在化学反应的研究中,泡利不相容原理和洪特规则也起着关键的作用。
通过这些规则,人们可以预测某种化学反应中可能产生的产物,从而指导实验的进行。
可以说,泡利不相容原理和洪特规则是化学、物理领域不可或缺的基础知识。
泡利不相容原理和洪特规则所揭示的电子排布规律,也为我们提供了一种新的思维方式。
通过理解这些规则,我们可以更好地理解原子和分子的结构,从而为材料设计、催化剂开发以及环境保护等领域提供新的思路。
值得一提的是,随着技术的不断进步,人们对于泡利不相容原理和洪特规则的理解也在不断深入。
泡利不相容原理能量最低原理洪特规则

泡利不相容原理能量最低原理洪特规则泡利不相容原理是由奥地利物理学家沃尔夫冈·泡利于1925年提出的。
该原理主要描述的是在原子或分子中,不能有两个或两个以上的粒子(如电子)处于完全相同的量子状态。
根据泡利不相容原理,每个电子必须具有唯一的一组量子数,包括主量子数、角量子数、磁量子数和自旋量子数。
这意味着即使在同一原子中,两个电子也必须具有至少一个不同的量子数。
泡利不相容原理限制了电子的排布方式,使得原子和分子中的电子结构变得稳定和有序。
能量最低原理是在量子力学中的一个基本概念,它指出在任何系统中,自然趋向于取得能量最低的状态。
在原子和分子中,能量最低原理指出原子中的电子会按照一定规则填充能级。
电子首先填充较低能量的能级,然后逐渐向较高能量的能级填充。
这个填充顺序是根据洪特规则来确定的。
洪特规则是由洪特(Hund)于1925年提出的。
根据洪特规则,当填充原子中的电子时,电子首先会填充处于不同能级的轨道。
然后,在同一能级的轨道上填充电子时,电子趋向于尽可能地保持自旋方向相同,以最小化电子之间的相互排斥。
这种电子填充方式称为“单电子占据”或“零自旋规则”。
根据洪特规则,这一填充顺序能够使得原子和分子结构更加稳定和有序。
这三个原理为我们提供了理解原子和分子的结构以及元素周期表中特殊性质的重要理论基础。
泡利不相容原理限制了电子在原子和分子中的状态,使得不同元素和化合物具有不同的基本特性。
能量最低原理和洪特规则则解释了电子在原子和分子中的填充顺序,进一步揭示了原子和分子结构以及它们之间相互作用的基本规律。
这些原理不仅对于理解原子和分子的性质和行为有重要意义,也在化学、材料科学和纳米科学等领域中具有广泛应用。
泡利不相容原理
L l(l 1)
n一定时 有n种取值 l 越小能量越低 4
3.磁量子数 ml 0,1,2… l 引起磁场中能级的分裂
Lz ml
4.自旋磁量子数
ms
1 2
产生精细结构
Sz ms
5
需要说明的是 自旋量子数 s = 1/2 只有一个值 自旋角动量也只有一个值
S s(s 1) 3 2
不变 不必总提及 可不计入
原子中核外电子的排布要遵守 泡利不相容原理 能量最低原理
6
四个量子数小结
名称
取值
主量子数 n 1,2,
l 0,1,2,n 1
角量子数 L ll 1
磁量子数
自旋磁量 子数
ml 0,1, l
Lz ml
ms
1 2
SZ 2
物理意 义
高能级: 能量较高的能级 低能级: 能量较低的能级
基能级: 能量最低的能级
(相应的状态称基态) 激发能级: 能量高于基能
级的其它所有能级(相应 状态称激发态)
n
6
5 4 激发态 3
2
基态 1
3
一、原子中电子的四个量子数 描述原子中电子的运动状态 需要一组量子数( n,l,ml,ms )
1.主量子数 n = 1, 2, 3, 决定能量的主要因素
n=1 n=2
n=3
1
l
2 3d 1 3p 0 3s
1 2p 0 2s
0 1s
10
•一个支壳层内电子 可有(2l+1)× 2种量子态
∴ 主量子数为n的壳层
内可容纳的电子数为
Zn
n1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
13
各壳层可容纳的电子数
Nl n
l
0123 4 5 spdf g h
6 i
Nn
1K 2L 3M 4N 5O 6P 7Q
2
2
26
8
2 6 10
18
2 6 10 14
32
2 6 10 14 18
50
2 6 10 14 18 22
72
2 6 10 14 18 22 26 98
14
泡利
Wolfgang Pauli 奥地利人 1900-1958
同一个量子态
9
2.各壳层可容纳的电子数
•同一个n 组成一个壳层 对应于n = 1, 2, 3,…的各壳层 分别记做 K, L, M, N, O, P…
•相同 n, l 组成一个支壳层 对应于l = 0, 1, 2, 3,…的各支壳层 分别记做 s, p, d, f, g, h…
10
n 3
Ze K L M 2
例: 钠原子有11个核外电子,钠原子基态的电子组态为
1s2 2s2 2 p6 3s
1s2 2s2 2 p6
这10原子称原子实。原子实以外 的电子称为价电子,可以被激发
n≥3的激发态的钠原子电子组态为
(1s2 2s2 2 p6 3p) (1s2 2s2 2 p6 3d) (1s2 2s2 2 p6 4s) 等等
物理意 义
电子能量的主体
确定的能级 角动量的可 能取值 对总能量有一定 影响
“轨道”角动量在磁场中 可能的取向 能级分裂
谱线精细结构
8
二、泡利不相容原理
1.泡利不相容原理 一个原子内不可能有两个或两个以上的
电子具有完全相同的状态 或说 一个原子内不可能有四个量子数完全
相同的电子 或说 不可能有两个或两个以上的电子处于
n一定时 有n种取值 l 越小能量越低 5
3.磁量子数 ml 0,1,2… l 引起磁场中能级的分裂
Lz ml
4.自旋磁量子数
ms
1 2
产生精细结构
Sz ms
6
需要说明的是 自旋量子数 s = 1/2 只有一个值 自旋角动量也只有一个值
S s(s 1) 3 2
论的结果相同
3
玻尔理论的一条能级对 2 应于电子的一种轨道
量子力学的一条能级
1
则对应于电子的一种状态
每个状态用量子数 n , l , ml , ms 描述
3
能级: 粒子的内部能量值
高能级: 能量较高的能级 低能级: 能量较低的能级
基能级: 能量最低的能级
(相应的状态称基态) 激发能级: 能量高于基能
20
不变 不必总提及 可不计入
原子中核外电子的排布要遵守 泡利不相容原理 能量最低原理
7
四个量子数小结
名称
取值
主量子数 n 1,2,
l 0,1,2, n 1
角量子数 L ll 1
磁量子数
自旋磁量 子数
ml 0,1, l
Lz ml
ms
1 2
SZ
2
n=1 n=2
n=3
1
l
2 3d 1 3p 0 3s
1 2p 0 2s
0 1s
11
•一个支壳层内电子 可有(2l+1)× 2种量子态
∴ 主量子数为n的壳层
内可容纳的电子数为
Zn
n1
(2l
1) 2
2n2
l0
泡利原理是一个极为重要的自然规律是理 解原子结构和元素周期表的重要理论基础。
统中,不可能有两个电子具有相同的状态——
4对量子数 n、l、m、m s 至少有一对不同。
2、能量最小原理:基态原子中电子先填
满能量小的壳层。
例题:氯原子有
17个电子,写出 基态原子组态。
1s22s22p63s23p5
n l 2(2l+1)
10 2
1s2
20 2
2s2
16
2p6
30 2
3s2
15
3p5 19
获1945年诺贝尔 物理学奖
15
三、能量最低原理
“电子优先占据最低能态
”
n
3
Ze K L M 2
n=1
n=2
n=3
1
l
2 3d 1 3p 0 3s
1 2p 0 2s
0 1s
16
17
能 量
主量子数
电子能量水平随主量子数和次量子数的变化情况
18
四、原子的电子组态符号
Hale Waihona Puke 分配原则1、泡利不相容原理:一个多电子原子系
级的其它所有能级(相应 状态称激发态)
n
6
5 4 激发态 3
2
基态 1
4
一、原子中电子的四个量子数 描述原子中电子的运动状态 需要一组量子数( n,l,ml,ms )
1.主量子数 n = 1, 2, 3, 决定能量的主要因素
2.角(轨道)量子数 l = 0,1,2…(n-1) 对能量有一定影响
L l(l 1)
孤立原子的能级
围绕原子核旋转的电子能量不能任意取值,只能取特定 的离散值(离散轨道),这种现象称为电子能量的量子化。
原子核 电子
低能级
高能级 电子优先抢占低能级
1
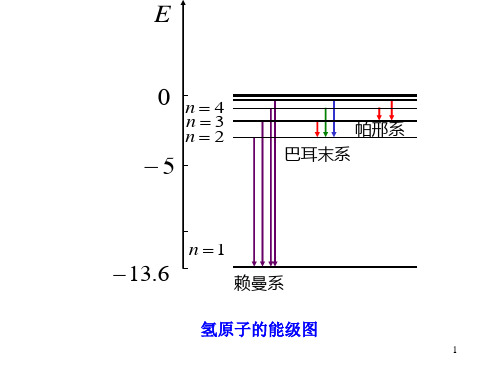
E
0 n4
n3 n2
5
帕邢系 巴耳末系
n 1
13.6
赖曼系
氢原子的能级图
2
n
由量子力学得出的氢 原子能级图和玻尔理
65 4
