气体分子运动论和热力学基础之玻尔兹曼分布律
合集下载
玻尔兹曼分布律重力场中粒子按高度分布

玻尔兹曼分布律在物理学中的应用
气体分子运动论
01
玻尔兹曼分布律是气体分子运动论的基础,可以用来描述气体
分子在平衡态下的速度分布和能量分布。
热力学
02
玻尔兹曼分布律在热力学中也有广泛应用,如热力学第二定律、
熵的概念等都涉及到玻尔兹曼分布律。
固体物理
03
在固体物理中,玻尔兹曼分布律可以用来描述电子在金属中的
05 结论与展望
研究结论
玻尔兹曼分布律在重力场中粒 子按高度分布的研究表明,在 一定条件下,粒子分布符合玻
尔兹曼分布。
随着高度的增加,粒子分布 逐渐稀疏,但仍保持玻尔兹
曼分布特征。
重力场对粒子分布的影响表现 为在低处粒子聚集,高处粒子 较少,这与玻尔兹曼分布的特
性相符合。
研究限制与不足
01
本研究仅限于理论分析和模拟,未能进行实际实验验证。
能量状态
根据能量守恒,可以得出 粒子在重力场中的能量状 态由动能和势能共同决定。
能量变化
在重力场中,粒子的能量 会发生变化,主要表现在 动能和势能之间的转换。
03 玻尔兹曼分布律与重力场 的结合
玻尔兹曼分布律在重力场中的适用性
玻尔兹曼分布律适用于粒子在平衡态 下的分布情况,当粒子受到重力作用 时,其分布情况同样适用玻尔兹曼分 布律。
玻尔兹曼分布律重力 场中粒子按高度分布
目录
CONTENTS
• 玻尔兹曼分布律的概述 • 重力场中粒子的运动规律 • 玻尔兹曼分布律与重力场的结合 • 实验验证与结果分析 • 结论与展望
01 玻尔兹曼分布律的概述
定义与特性
定义
玻尔兹曼分布律是描述粒子在平衡态下按能量分布的规律,其数学表达式为f(E) = exp(-E/kT),其中E为粒子能量,k为玻尔兹曼常数,T为绝对温度。
玻尔兹曼分布律

分布函数的概念有着普遍的意义,在速度空间有 麦克斯韦速度分布函数。
6
*力学量的平均值
x
xdN
N
xf ( x)dx
g( x)
g( x)dN
N
g( x) f ( x)dx
7
4.2 玻尔兹曼分子数密度分布
重力场中粒子按高度的分布( P )mgh
热运动使分子趋于均匀分布而重力使之位于低处。 在重力加速度可以认为不变的范围,取地面为势能 零点.分布在高度为h的地方单位体积内的分子数?
上式右方仅与速率有关.与速度方向无关.具有各向同性的特点.
分布在任一速率v ~ v +dv区间的体积是
4v2 dv 17
结论:在平衡态下,当气体分子间的相互作用 可以忽略时,分布在任一速率区间v ~ v +dv 的 分子数占总分子数的比率为
dN v (
m
3
) 2 e mv2 2kT 4v2 dv
§4 玻尔兹曼分布律
4.1 统计分布律与分布函数的概念 • 分布函数
4.2 玻尔兹曼分子数密度分布 • 等温大气压强公式(高度计原理)
• 玻尔兹曼密度分布律
• 玻尔兹曼分子按能量分布律
§5 麦克斯韦速度分布律
5.1 麦克斯韦速度分布律
5.2 麦克斯韦速率分布律
平均速率 v和方均根速率 v2, 最可几速率vp
3
• 分布函数 以伽尔顿板实验为例说明。
设一定量的分子总数为N
dN(x) 表示分布在某区间 x~ x +d x 内的分子数, dN (x) /N表示分布在此区间内的分子数占总分子数 的比率(或百分比)。
dN(x)/N 是 x 的函数,在不同区间附近取相等的 间隔,此比率一般不相等。
玻尔兹曼速度分布律

这个分布律描述了气体分子在各个方向上的速度分布情况,反映了气体分子运动 的统计规律。
分子平均动能与温度的关系
分子平均动能是气体分子动能的平均值,与温度T有关。根据 玻尔兹曼速度分布律,分子平均动能随着温度的升高而增大 。这是因为高温下气体分子运动速度更快,具有更高的动能 。
分子平均动能与温度的关系可以用公式E=3/2kT表示,其中E 是分子平均动能,k是玻尔兹曼常数,T是绝对温度。这个公 式反映了气体分子平均动能与温度的正比关系。
高温高压下的适用性
当温度和压力较高时,玻尔兹曼速度分布律可能不再适用。这是因为高温和高压条件下,气体分子间 的相互作用以及分子与容器壁之间的相互作用变得更加复杂,需要考虑量子效应和相对论效应的影响 。
在高温高压条件下,可能需要采用其他理论模型,如量子统计力学或相对论统计力学,来描述气体分 子的速度分布。
适用范围
玻尔兹曼速度分布律适用于稀薄气体,即在分子数密度较低的情况 下,气体分子的运动行为可以用该定律来描述。
02 玻尔兹曼速度分布律的数 学表达式
表达式概述
玻尔兹曼速度分布律是描述气体分子在平衡态下速度分布的统计规律,其数学表达 式为:f(v) = (m/2πkT)^(3/2) * 4πv^2 * e^(-mv^2/2kT),其中m是分子质量,k 是玻尔兹曼常数,T是绝对温度。
玻尔兹曼速度分布律
目录
CONTENTS
• 引言 • 玻尔兹曼速度分布律的数学表达式 • 玻尔兹曼速度分布律的物理意义 • 玻尔兹曼速度分布律的应用 • 玻尔兹曼速度分布律的局限性 • 玻尔兹曼速度分布律的发展与展望
01 引言
背景介绍
气体分子运动论
气体分子运动论是物理学的一个重要 分支,主要研究气体分子在空间中的 运动规律和相互作用。
分子平均动能与温度的关系
分子平均动能是气体分子动能的平均值,与温度T有关。根据 玻尔兹曼速度分布律,分子平均动能随着温度的升高而增大 。这是因为高温下气体分子运动速度更快,具有更高的动能 。
分子平均动能与温度的关系可以用公式E=3/2kT表示,其中E 是分子平均动能,k是玻尔兹曼常数,T是绝对温度。这个公 式反映了气体分子平均动能与温度的正比关系。
高温高压下的适用性
当温度和压力较高时,玻尔兹曼速度分布律可能不再适用。这是因为高温和高压条件下,气体分子间 的相互作用以及分子与容器壁之间的相互作用变得更加复杂,需要考虑量子效应和相对论效应的影响 。
在高温高压条件下,可能需要采用其他理论模型,如量子统计力学或相对论统计力学,来描述气体分 子的速度分布。
适用范围
玻尔兹曼速度分布律适用于稀薄气体,即在分子数密度较低的情况 下,气体分子的运动行为可以用该定律来描述。
02 玻尔兹曼速度分布律的数 学表达式
表达式概述
玻尔兹曼速度分布律是描述气体分子在平衡态下速度分布的统计规律,其数学表达 式为:f(v) = (m/2πkT)^(3/2) * 4πv^2 * e^(-mv^2/2kT),其中m是分子质量,k 是玻尔兹曼常数,T是绝对温度。
玻尔兹曼速度分布律
目录
CONTENTS
• 引言 • 玻尔兹曼速度分布律的数学表达式 • 玻尔兹曼速度分布律的物理意义 • 玻尔兹曼速度分布律的应用 • 玻尔兹曼速度分布律的局限性 • 玻尔兹曼速度分布律的发展与展望
01 引言
背景介绍
气体分子运动论
气体分子运动论是物理学的一个重要 分支,主要研究气体分子在空间中的 运动规律和相互作用。
气体分子运动论和热力学基础之玻尔兹曼分布律

kT
)dvx
dvy
dvz
dxdydz
在温度一定时,分子的平均动能是一定的, 所以,分子优先占据势能较低的位置。
如果对坐标 进行积分
N0 n0
V
exp( p )dxdydz
kT
上式就演化为麦克 斯韦速率分布律。
由于对速率的积
分是归一化的
(m 2πkT
)3/ 2
exp(
k kT
)dvxdvydvz
/
2
exp(
kT
)dvx
dvy
dvz
dxdydz
分布律,exp(-ε/kT) 称为概率因子。
其中n0表示εp = 0处单位体积内各种速度的总分子数。
在一定的速度和坐标范围内,在一定的温度下的 平衡状态中,分子的能量越低,分子数就越多态。
{范例8.6} 玻尔兹曼分布律
dN
n0
(
m 2πkT
)3
/
2
exp(
[解析](2)在重力场中,气体分子的密度 随高度的分布可用点的密集程度表示。
不论什么 分子,由 于重力的 作用,分 子数密度 在低空比 较大,在 高空比较 小。
氖气的分 子量比较 小,分子 数密度减 小得比较 慢,在同 样的高度 内,点数 相对比较 均匀。
氧气的 分子量 比较大, 分子数 密度减 小得比 较快, 在高空 比较稀 薄。
由于势能与位置有关,因此分子在空间的分布是不均匀的。
玻尔兹曼认为:气体在一定的温度下处于平衡状态时,在速
度间隔vx~vx + dvx、vy~vy + dvy、vz~vz + dvz和坐标间隔x~x + dx 、
y~ y + dy、z~z + dz中的分子数为
热学-统计物理3 第3章 气体分子热运动速率和能量的统计分布律
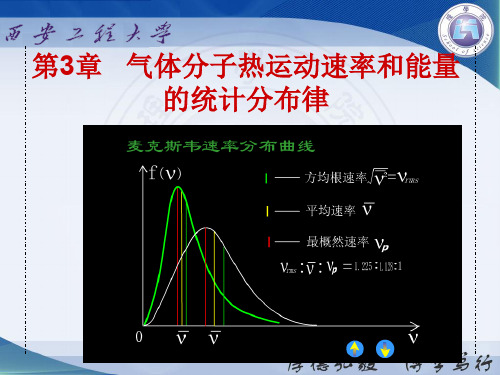
f v
v v pv v 2
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确?
(A) vp 是气体分子中大部分分子所具有的速率. (B) vp 是速率最大的速度值. (C) vp 是麦克斯韦速率分布函数的最大值.
(D) 速率大小与最概然速率相近的气体分子的比 率最大.
例1 计算在 27 C 时,氢气和氧气分子的方均
M
3.方均根速率 v2
v2
N
0
v2dN N
0
v2Nf N
(v)dv
o
v
v2 v2 f (v)dv 4 ( m )3 2 e mv2 2kT v4dv
0
2 kT
0
v4ev2 dv 3
0
8 5
v2 3kT m
v2 3kT 3RT
2kT
v
麦克斯韦速率分布函数的物理意义: f (v) dNv
Nd v
既反映理想气体在热动平衡条件下,分布在速率 v 附近单
位速率区间内的分子数占总分子数的百分比,又表示任意
一分子的速率出现在 v附近单位速率区间内的概率。
如果以速率为横坐标轴,速率分布函数为纵坐标轴,画 出的一条表示f(v) —v之间关系的曲线,称为气体分子的麦 克斯韦速率分布曲线。 ,它形象地描绘出气体分子按速率 分布的情况。
大量分子的速率的算术平均值叫做分子的平均速率.
v
vNf (v)dv
0
vf (v)dv
v 4 (
m
)3 e2 mv2 2kT v2dv
N
0
0
v v pv v 2
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确?
(A) vp 是气体分子中大部分分子所具有的速率. (B) vp 是速率最大的速度值. (C) vp 是麦克斯韦速率分布函数的最大值.
(D) 速率大小与最概然速率相近的气体分子的比 率最大.
例1 计算在 27 C 时,氢气和氧气分子的方均
M
3.方均根速率 v2
v2
N
0
v2dN N
0
v2Nf N
(v)dv
o
v
v2 v2 f (v)dv 4 ( m )3 2 e mv2 2kT v4dv
0
2 kT
0
v4ev2 dv 3
0
8 5
v2 3kT m
v2 3kT 3RT
2kT
v
麦克斯韦速率分布函数的物理意义: f (v) dNv
Nd v
既反映理想气体在热动平衡条件下,分布在速率 v 附近单
位速率区间内的分子数占总分子数的百分比,又表示任意
一分子的速率出现在 v附近单位速率区间内的概率。
如果以速率为横坐标轴,速率分布函数为纵坐标轴,画 出的一条表示f(v) —v之间关系的曲线,称为气体分子的麦 克斯韦速率分布曲线。 ,它形象地描绘出气体分子按速率 分布的情况。
大量分子的速率的算术平均值叫做分子的平均速率.
v
vNf (v)dv
0
vf (v)dv
v 4 (
m
)3 e2 mv2 2kT v2dv
N
0
0
3.5玻尔兹曼分布律

1.38 1023 300 kT 10 2 2 2 ( 3 . 7 10 ) 1 2d p
6.8 103 ( m )
此计算值大于热水瓶胆的两壁间距,所以氮气分子 的平均自由程为 0.4 cm。
例.试计算气体分子热运动速率的大小介于vp- vp/100 和vp+vp/100之间的分子数占总分子数的百分数。 vp 99 = vp 解:按题意 v v p 100 100
临界点 实际气体 等温线 临界等 温线
T
饱和蒸汽压
凝结线
范德瓦耳斯等温线 蒸发线
气体动理论
§3.7 气体分子的平均自由程
一个分子连续两次 碰撞之间经历的平 均自由路程叫平均 自由程 一个分子单位时间里 受到平均碰撞次数叫 平均碰撞频率 z
单位时间内分子经历的平均距离 v, 平均碰撞 z 次
v z
玻耳兹曼分布律:在温度为 T 的平衡态下,任何系 统的微观粒子按状态分布: dN E E/kT e N
玻耳兹曼分布律是麦克斯韦速率分布律的推广,其中状态 对应于一定能量值,也就是说,在能量越大的状态,粒子 数就越少,且随能量值增大按指数规律衰减。 重力场中分子按高度分布:
dN h e mgh/kT N0
平均碰撞频率 z
u
A d
d d
设有效直径为 d 的分子 A 以相对平均速率 u 运动, 其它分子可设为静止。在A运动方向上,以 d 为半 径的圆柱体内的分子都将与分子A碰撞。该圆柱体的 截面积 就叫碰撞截面
d
2
单位时间内分子A走 u ,相应的圆柱体体积为 u ,则 平均碰撞频率 统计理论可计算 平均自由程 对空气分子 标准状态下
§ 3.5 玻尔兹曼分布律
玻尔兹曼分布律

中分子数为 N 。设大气的温度为T ,空气分子的质量μ 。
就此空气柱求玻耳兹曼分布律中的n0
解 根据玻耳兹曼分布律,在重力场中,存在于x~x+dx , y~y+dy , z~z+dz 区间内,具有各种速度的分子数为
dN = ndV = n0e-e p / kTdxdydz
取z 轴垂直向上,地面处 z=0, 可得
求 27℃ 时单位体积内的空气分子数、平均自由程、平均碰撞 次数 。
解 由气体的状态方程, 有
n
=
p kT
=
1.33 ´ 10-3 1.38 ´10-23 ´ 300
=
3.21´1017 m-3
l=
1 2π d 2n =
1 2π (3´10-10 )2 ´ 3.21´1017
= 7.79 m
12/13
一. 分子的平均碰撞频率 Z
一个分子单位时间内 和其它分子碰撞的平 均次数,称为性小球,分子间的碰撞 为完全弹性碰撞。大量分子中,只有被考察的特定分子A
以平均速率 u 运动,其它分子都看作静止不动。
8/13
·单位时间内与分子 A 发生碰撞的分子数为 nπ d 2u
dN (rv,vv) = Ce-e / kTdvxdvydvzdxdydz
式中e =ek+ep 是分子的总能量, C 是与位置坐标和速度无关 的比例系数。 这一结论,称为麦克斯韦–玻耳兹曼分布定律。它给出了 分子数按能量的分布规律。
5/13
例 在大气中取一无限高的直立圆柱体,截面积为A , 设柱体
一. 重力场中粒子按高度的分布
dp = -r gdh dp = -nm gdh
平衡态下气体的温度处处 相同,气体的压强为
就此空气柱求玻耳兹曼分布律中的n0
解 根据玻耳兹曼分布律,在重力场中,存在于x~x+dx , y~y+dy , z~z+dz 区间内,具有各种速度的分子数为
dN = ndV = n0e-e p / kTdxdydz
取z 轴垂直向上,地面处 z=0, 可得
求 27℃ 时单位体积内的空气分子数、平均自由程、平均碰撞 次数 。
解 由气体的状态方程, 有
n
=
p kT
=
1.33 ´ 10-3 1.38 ´10-23 ´ 300
=
3.21´1017 m-3
l=
1 2π d 2n =
1 2π (3´10-10 )2 ´ 3.21´1017
= 7.79 m
12/13
一. 分子的平均碰撞频率 Z
一个分子单位时间内 和其它分子碰撞的平 均次数,称为性小球,分子间的碰撞 为完全弹性碰撞。大量分子中,只有被考察的特定分子A
以平均速率 u 运动,其它分子都看作静止不动。
8/13
·单位时间内与分子 A 发生碰撞的分子数为 nπ d 2u
dN (rv,vv) = Ce-e / kTdvxdvydvzdxdydz
式中e =ek+ep 是分子的总能量, C 是与位置坐标和速度无关 的比例系数。 这一结论,称为麦克斯韦–玻耳兹曼分布定律。它给出了 分子数按能量的分布规律。
5/13
例 在大气中取一无限高的直立圆柱体,截面积为A , 设柱体
一. 重力场中粒子按高度的分布
dp = -r gdh dp = -nm gdh
平衡态下气体的温度处处 相同,气体的压强为
分子动理论2(玻耳兹曼分布范氏自由程)

分子动理论2 - 玻耳 兹曼分布与范氏自由
程
目录
• 引言 • 玻耳兹曼分布 • 范氏自由程 • 玻耳兹曼分布与范氏自由程的关系 • 结论
01
引言
主题简介
玻耳兹曼分布
描述气体分子在平衡态下,分子 速度分布的概率密度函数。
范氏自由程
分子在连续两次碰撞之间所走的 平均距离。
重要性及应用领域
物理学
气体分子运动论、热力学、统计物理等领域的基 础理论。
对未来研究的展望
1
随着科学技术的发展,我们需要进一步深入研究 微观粒子的运动规律和相互作用机制,探索更深 入的理论和模型。
2
我们需要加强跨学科的合作和研究,将分子动理 论与其他学科的理论和方法相结合,科研人才,加强 科研队伍的建设,为未来的科学研究和发展提供 有力的人才保障。
03
范氏自由程
范氏自由程的定义
01
范氏自由程是指分子在两次碰撞之间所走的平均距离。
02
它与气体分子的平均碰撞频率和分子的平均热运动速度有关 。
03
范氏自由程是分子动理论中的一个重要概念,用于描述气体 分子间的相互作用和运动特性。
范氏自由程的推导
01
通过气体分子的平均碰撞频率和分子的平均热运动速
范氏自由程则可以用来研究气体分子的输运性质,如扩散、 热传导和黏滞等现象。通过对范氏自由程的研究,可以深 入了解气体分子的微观运动规律。
对微观世界理解的意义
01
玻耳兹曼分布和范氏自由程对 于我们理解微观世界具有重要 的意义。
02
通过这两个概念,我们可以更 好地理解分子之间的相互作用 和运动规律,从而深入探究物 质的本质和变化规律。
这个分布函数描述了分子在某一特定速度v下的概率密度,反 映了气体分子速度分布的概率特征。
程
目录
• 引言 • 玻耳兹曼分布 • 范氏自由程 • 玻耳兹曼分布与范氏自由程的关系 • 结论
01
引言
主题简介
玻耳兹曼分布
描述气体分子在平衡态下,分子 速度分布的概率密度函数。
范氏自由程
分子在连续两次碰撞之间所走的 平均距离。
重要性及应用领域
物理学
气体分子运动论、热力学、统计物理等领域的基 础理论。
对未来研究的展望
1
随着科学技术的发展,我们需要进一步深入研究 微观粒子的运动规律和相互作用机制,探索更深 入的理论和模型。
2
我们需要加强跨学科的合作和研究,将分子动理 论与其他学科的理论和方法相结合,科研人才,加强 科研队伍的建设,为未来的科学研究和发展提供 有力的人才保障。
03
范氏自由程
范氏自由程的定义
01
范氏自由程是指分子在两次碰撞之间所走的平均距离。
02
它与气体分子的平均碰撞频率和分子的平均热运动速度有关 。
03
范氏自由程是分子动理论中的一个重要概念,用于描述气体 分子间的相互作用和运动特性。
范氏自由程的推导
01
通过气体分子的平均碰撞频率和分子的平均热运动速
范氏自由程则可以用来研究气体分子的输运性质,如扩散、 热传导和黏滞等现象。通过对范氏自由程的研究,可以深 入了解气体分子的微观运动规律。
对微观世界理解的意义
01
玻耳兹曼分布和范氏自由程对 于我们理解微观世界具有重要 的意义。
02
通过这两个概念,我们可以更 好地理解分子之间的相互作用 和运动规律,从而深入探究物 质的本质和变化规律。
这个分布函数描述了分子在某一特定速度v下的概率密度,反 映了气体分子速度分布的概率特征。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其中n0表示εp = 0处单位体积内各种速度的总分子数。
在一定的速度和坐标范围内,在一定的温度下的 平衡状态中,分子的能量越低,分子数就越多态。
{范例8.6} 玻尔兹曼分布律
d N n 0 (2 π m k T )3 /2 e x p ( k T )d v x d v y d v z d x d y d z
[解析](2)在重力场中,气体分子的密度 随高度的分布可用点的密集程度表示。
不论什么 分子,由 于重力的 作用,分 子数密度 在低空比 较大,在 高空比较 小。
氖气的分 子量比较 小,分子 数密度减 小得比较 慢,在同 样的高度 内,点数 相对比较 均匀。
氧气的 分子量 比较大, 分子数 密度减 小得比 较快, 在高空 比较稀 薄。
{范例8.6} 玻尔兹曼分布律
(1)求证:在重力场中分子数 密度按高度分布的规律为
n
n0
exp(mgz) kT
其中z是高度。
氢气、氖气、氮气、氧气和氟气的分子量分别为2,20,28, 32和38,氢气、氖气、氮气、氧气和氟气在300K时分子数密度 按高度分布的曲线有什么异同?氧气在温度100K到400K(间隔 为50K)时分子数密度按高度分布的曲线有什么异同? (2)用点 表示分子,通过点的密集程度表示氖气,氮气和氧气分子按高 度分布的规律。(温度设为300K)
玻尔兹曼认为:气体在一定的温度下处于平衡状态时,在速
度间隔vx~vx + dvx、vy~vy + dvy、vz~vz + dvz和坐标间隔x~x + dx 、
y~ y + dy、z~z + dz中的分子数为
此式称为玻尔兹曼
d N n 0 (2 π m k T )3 /2 e x p ( k T )d v x d v y d v z d x d y d z分称布为律概,率因exp子(-。ε/kT)
n
n0
exp(mgz) kT
其中z是高度。
氢气、氖气、氮气、氧气和氟气的分子量分别为2,20,28, 32和38,氢气、氖气、氮气、氧气和氟气在300K时分子数密度 按高度分布的曲线有什么异同?氧气在温度100K到400K(间隔 为50K)时分子数密度按高度分布的曲线有什么异同?
由于势能与位置有关,因此分子在空间的分布是不均匀的。
{范例8.6} 玻尔兹曼分布律
(1)求证:在重力场中分子数 密度按高度分布的规律为
n
n0
exp(mgz) kT
其中z是高度。
氢气、氖气、氮气、氧气和氟气的分子量分别为2,20,28, 32和38,氢气、氖气、氮气、氧气和氟气在300K时分子数 密度按高度分布的曲线有什么异同?氧气在温度100K到 400K(间隔为50K)时分子数密度按高度分布的曲线有什么异 同? (2)用点表示分子,通过点的密集程度表示氖气,氮气 和氧气分子按高度分布的规律 (温度设为300K)。
在重力场中εp = mgz,因此在高 为z处的单位体积内的分子数为
n=dxddNyB dzn0exp(m kT gz)
在重力场中,气体分子的密度随高度的增加按指数规律减小。
分子的质量越大,分子数密 度随高度减小得越快,这是 因为重力的作用越显著。
气体的温度越高,分子数随 高度减小得越慢,这是因为 分子的无规则热运动加剧。
在温度一定时,分子的平均动能是一定的, 所以,分子优先占据势能较低的位置。
如果对坐标 进行积分
N0 n0
V
exp(p )dxdydz
kT
上式就演化为麦克 斯韦速率分布律。
由于对速率的积
分是归一化的
(2π m kT)3/2exp(k T k)dvxdvydvz1
可得玻尔兹曼分 布律的常用形式
dNBn0exp(kT p)dxdydz
[解析](1)麦克斯韦的速度分布律和速 率分布律的指数中都包含动能因子
k
1 mv2 2
这是不考虑分子受外力场影响的情况。
如果分子在保守力场中运动,分子的总 能量就是动能与势能之和ε = εk + εp。 玻尔兹曼认为:指数中的动能应该用总能量代替。
{范例8.6} 玻尔兹曼分布律
(1)求证:在重力场中分子数 密度按高பைடு நூலகம்分布的规律为
