第二次月考(B卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(下册)(原卷版)
月考(B卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(浙江版)(上册)(原卷版)

班级 姓名 学号 分数月考测试卷(B 卷)(测试时间:60分钟 满分:120分)一、选择题(每小题3分,总计30分)1.如果,那么下列各式中正确的是( )A 、 B、 C 、 D 、2.如图,已知AB=AD ,那么添加下列一个条件后,仍无法判定△ABC ≌△ADC 的是( )A .CB=CDB .∠BAC=∠DAC C .∠BCA=∠DCAD .∠B=∠D=90°3.在△ABC 中,三边长满足,则互余的一对角是( )A .∠A 与∠B B .∠C 与∠A C .∠B 与∠CD .∠A 、∠B 、∠C4.下列说法正确的是( )①三角形的角平分线是射线;②三角形的三条角平分线都在三角形内部,且交于同一点;③三角形的三条高都在三角形内部;④三角形的一条中线把该三角形分成面积相等的两部分。
A .①②B .②③C .③④D .②④5.在数轴上表示不等式2x <﹣4的解集,正确的是( )A.B. C. D. 6.如果点P (m ,1-2m )在第一象限,那么m 的取值范围是( )A .0<m<12B .-12<m<0C .m<0D .m>127.如图,已知DE 是直角梯形ABCD 的高,将△ADE 沿DE 翻折,腰AD 恰好经过腰BC 的中点,则AE :BE 等b a b a +-+-22 22b a b a -- b a 2121-- 222c a b =-于( )A.2:1B.1:2C.3:2D.2:38.等边三角形的高为23,则它的边长为( )A .1B .2C .21 D .4 9.已知不等式组⎩⎨⎧<>a x x 1无解,则a的取值范围是 ( ) (A)a >1 (B) a <1 (C)a ≤1 (D) a ≥110.如图,在△ABC 中,∠C=90°,AC=4,BC=2,点A 、C 分别在x 轴、y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动.在运动过程中,点B 到原点的最大距离是( ).A .6B .2C .2+2D . 2二、填空题(每小题4分,总计24分)11.若△ABC 的三边长分别为5、13、12,则△ABC 的形状是 .12.如图,直线a 、b 被直线c 所截.若b a //, 401=∠, 702=∠,则=∠3 度.13.已知不等式2x -a <0的正整数解只有2个,则a 的取值范围是 .14.对于任意实数m 、n ,定义一种运运算m ※n=mn ﹣m ﹣n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5﹣3﹣5+3=10.请根据上述定义解决问题:若a <2※x <7,且解集中有两个整数解,则a 的取值范围是 .15.如图,在 Rt △ABC 中, ∠C=90°,AD 平分∠BAC 交BC 于D, 若 BC=14cm ,且CD:DB=3:4,则D 到边AB 的距离是16.如图,在直角坐标系xOy 中,点A 在第一象限,点B 在x 轴的正半轴上,△AOB 为正三角形,射线OC ⊥AB ,在OC 上依次截取点P 1,P 2,P 3,…,P n ,使OP 1=1,P 1P 2=3,P 2P 3=5,…,P n ﹣1P n =2n ﹣1(n 为正整数),分别过点P 1,P 2,P 3,…,P n 向射线OA 作垂线段,垂足分别为点Q 1,Q 2,Q 3,…,Q n ,则点Q n 的坐标为 .三、解答题(总计66分)17.解不等式2+≥,并把它的解集表示在数轴上.18.如图,在平面直角坐标系中,P (a ,b )是△ABC 的边AC 上一点,△ABC 经平移后点P 的对应点为P 1(a +6, b +2)(1)请画出上述平移后的△A 1B 1C 1,并写出点A 、C 、A 1、C 1的坐标;(2)求出以A 、C 、A 1、C 1为顶点的四边形的面积.19.已知如图1,线段AB 、CD 相交于点O ,连结AC 、BD ,我们把形如图1的图形称之为“8字形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥聪明才智,解决以下问题:22x 3x(1)在图1中,请写出∠A、∠B、∠C、∠D之间的数量关系,并说明理由;(2)仔细观察,在图2中“8字形”的个数有个;(3)在图2中,若∠B=76°,∠C=80°,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB 分别相交于M、N利用(1)的结论,试求∠P的度数;(4)在图3中,如果∠B和∠C为任意角,并且AP和DP分别是∠CAB和∠BDC的三等分线,即∠PAO=13∠CAO,∠BDP=13∠BOD,那么∠P与∠C、∠B之间存在的数量关系是(直接写出结论即可).20.如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,BE、CD相交于点O.(1)若BD=CE,试说明:OB=OC.(2)若BC=10,BC边上的中线AM=12,试求AC的长.21.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B 在小正方形的顶点上.(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).22.已知:如图,点D在△ABC的边BC上,AB=AC=BD,AD=CD。
第二次月考(A卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(上册)(解析版)

(测试时间:90分钟 满分:120分)一、选择题(共10小题,每题3分,共30分)1.下列多项式的乘法中可以用平方差公式计算的是( )A.(2x+1)(-2x-1) B .)12)(12(++x xC .)22)(12(--x xD .(-2x+1)(-2x-1)【答案】D.【解析】考点:平方差公式.2.老师给出:a+b=1,22b a +=2, 你能计算出ab 的值为 ( )A .-1B .3C .-23 D .-21 【答案】D.【解析】试题分析:根据完全平方公式可得:12)(222=++=+ab b a b a ,即2+2ab=1,则ab=-21 考点:完全平方公式.3.等腰三角形一个底角是30°,则它的顶角的度数是( )A. 30°B. 60°C. 90°D. 120°【答案】D.【解析】试题分析:等腰三角形的两个底角相等,则顶角的度数=180°-30°×2=120°.考点:等腰三角形的性质.4.小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带第_____块去,这利用了三角形全等中的_____原理( )A.2;SAS B.4;ASA C.2;AAS D.4;SAS【答案】B【解析】试题分析:已知两角和一边可以得到唯一的一个三角形,则带第4块去是最好的.考点:作三角形.5.等腰三角形的两边分别为12和6,则这个三角形的周长是()A. 24 B. 18 C. 30 D. 24或30【答案】C.【解析】试题分析:根据三角形的三边关系可得:三角形的三边长为12、12和6,则三角形的周长=12+12+6=30. 考点:等腰三角形的性质.6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.∠B=∠D=90° B.∠BCA=∠DCA C.∠BAC=∠DAC D.CB=CD【答案】B【解析】考点:三角形全等的判定.7.把多项式2x2-8x+8分解因式,结果正确的是()A.(2x-4)2 B.2(x-4)2C.2(x-2)2 D.2(x+2)2【答案】C.【解析】试题分析:根据题意,先提公因式2,然后再利用完全平方求值,可得222882(2)x x x -+=-. 考点:因式分解.8.若(x 2-x+m)(x-8)中不含x 的一次项,则m 的值为( )A.8;B.-8;C.0;D.8或-8;【答案】B.【解析】试题分析:根据多项式的乘法计算法则可得:原式=x 3-9x 2+(8+m)x-8m ,根据不含一次项可得:8+m=0,解得:m=-8.考点:多项式的乘法.9.若9x 2-kxy+4y 2 是一个完全平方式,则 k 的值为( )A 、6B 、±6C 、12D 、±12【答案】D.【解析】试题分析:由题意可得,这个多项式9x 2-kxy+4y 2一定等于(3x ±2y)2,因此k 的值为±12.考点:完全平方式的运用.10.下列运算正确的是( )A .a 3+a 3=3a 6B .(-a )3·(-a )5=-a 8C .(-2a 2b )·4a=-24a 6b 3D .(-13a -4b )(13a -4b )=16b 2-19a 2 【答案】D【解析】考点:幂的有关计算二、填空题(共10小题,每题3分,共30分)11.如果式子 ()2x +与()x p +的乘积不含x 的一次项,那么p = .【答案】-2【解析】试题分析:根据题意可得:(x+2)(x+p)=2x +(2+p)x+2p ,根据题意得:2+p=0,解得:p=-2.考点:多项式的乘法计算.12.小明照镜子时,发现衣服上的英文单词在镜子呈现为“A P P L E ”,则这串英文字母是________;【答案】APPLE.【解析】试题分析:根据镜面效应可得:这串英文字母为“APPLE ”.考点:镜面效应.13.如图,已知点A 、C 、F 、E 在同一直线上,△ABC 是等边三角形,且CD=CE ,EF=EG ,则∠F= 度。
期末测试卷(二)(B卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(上册)(解析版)

(测试时间:90分钟满分:120分)一、选择题(共10小题,每题3分,共30分)1.已知△ABC中AD为中线,且AB=5、AC=7 ,则AD的取值范围为()A、2<AD<12 B、5<AD<7 C、1<AD<6 D、2<AD<10【答案】C.【解析】在△ADB和△EDC中,AD DEADB EDCBD DC=∠=∠=⎧⎪⎨⎪⎩,∴△ADB≌△EDC(SAS),∴CE=AB,∵AB=5,AC=7,∴CE=5,设AD=x,则AE=2x,∴7-5<2x<7+5,∴1<x<6,故选C.考点:1.全等三角形的判定与性质;2.三角形三边关系.2.如图,把一张三角形纸片沿DE折叠,当点A落在四边形BCDE的内部时,∠A、∠1、∠2之间的关系是()A.∠A=∠1+∠2 B.2∠A=∠1+∠2C.3∠A=∠1+∠2 D.3∠A=∠1+∠2【答案】B【解析】试题分析:连接AA ′,则△A ′ED 即为折叠前的三角形,由折叠的性质知:∠DAE=∠DA ′E .由三角形的外角性质知:∠1=∠DAA ′+∠DA ′A ,∠2=∠EAA ′+∠EA ′A ;则∠1+∠2=∠DAE+∠DA ′E=2∠DAE 即∠1+∠2=2∠A .故选C .考点:1.三角形内角和定理;2.翻折变换(折叠问题).3.如果把分式yx xy 3中的x 与y 都扩大2倍,那么这个分式的值( ) A .不变 B .扩大2倍 C .扩大4倍 D .扩大6倍【答案】B .【解析】考点:分式的基本性质.4.如图,三条直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A.一处B.两处C.三处D.四处【答案】D【解析】∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;综上,到三条公路的距离相等的点有4个,∴可供选择的地址有4个.考点:角平分线的性质5.如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的结论是()AFEDBA.①②③ B.①②③④ C.①② D.①【答案】A【解析】试题分析::∵DE ∥BC ,∴∠DFB=∠FBC ,∠EFC=∠FCB ,∵BF 是∠ABC 的平分线,CF 是∠ACB 的平分线,∴∠FBC=∠DFB ,∠FCE=∠FCB ,∵∠DBF=∠DFB ,∠EFC=∠ECF ,∴△DFB ,△FEC 都是等腰三角形.∴DF=DB ,FE=EC ,即有DE=DF+FE=DB+EC ,∴△ADE 的周长AD+AE+DE=AD+AE+DB+EC=AB+AC .综上所述,命题①②③正确.故选A.考点:1.等腰三角形的判定与性质;2.平行线的性质.6.如图,在ABC ∆中,AB=AC, A ∠=36︒,AB 的垂直平分线DE 交AC 于D ,交AB 于E ,下述结论:①BD 平分ABC ∠;②AD=BD=BC ;③BDC ∆的周长等于AB+BC ;④D 是AC 中点.其中正确的命题序号是( )A .①②③B .①②④C .②③④D .①③④【答案】A【解析】考点:线段垂直平分线的性质7.如图,在边长为a 的正方形中,剪去一个边长为b 的小正方形(a b >),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a 、b 的恒等式为( )A .222()2a b a ab b -=-+B .222()2a b a ab b +=++C .22()()a b a b a b -=+-D .2()a ab a a b +=+【答案】C .【解析】试题分析:第一个图形的阴影部分的面积=22a b -; 第二个图形是梯形,则面积是:1(22)()()()2a b a b a b a b +⋅-=+-.则22()()a b a b a b -=+-. 故选C .考点:平方差公式的几何背景.8.若多项式ax 2+bx +c 因式分解的结果为(x-2)(x +4),则abc 的值为A .-16B .16C .8D .-8【答案】A .考点:因式分解的意义.9.关于x 的分式方程15=-x m ,下列说法正确的是 ( ) (A )方程的解是5+=m x(B )m <-5时,方程的解是正数(C )m <-5时,方程的解是负数(D )无法确定【答案】C【解析】试题分析:去分母得:m=x-5,解得:x=m+5,检验:当m+5-5=0时,x=5是增根,原方程无解.当方程的解为负数∴m+5<0解这个不等式得:m <-5;方程的解是正数∴m+5>0解这个不等式得:m >-5.但当m+5-5=0,即m=0时,x=5是增根,原方程无解.故选C .考点:分式方程的解.10.如图所示,∠E=∠F=90°,∠B=∠C ,AE=AF ,结论:①EM=FN ;②CD=DN ;③∠1=∠2;④△ACN ≌△ABM .其中正确的有( )A .1个B .2个C .3个D .4个【答案】C考点: 全等三角形的判定.二、填空题(共10小题,每题3分,共30分)1.当m = 时,分式22m m --的值为零.【答案】-2【解析】试题分析:分式的值为零的条件:分式的分子为0且分母不为0时,分式的值为零. 解:由题意得⎩⎨⎧≠-=-0202m m ,解得⎩⎨⎧≠±=22m m ,则m=-2. 考点:分式的值为零的条件2.如图,l ∥m ,等边△ABC 的顶点A 在直线m 上,则∠α= .【答案】20°.【解析】试题分析:如图,延长CB交直线m于D,∵△ABC是等边三角形,∴∠ABC=60°,∵l∥m,∴∠1=40°.∴∠α=∠ABC-∠1=60°-40°=20°.考点:1.平行线的性质;2.等边三角形的性质.3.若△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=4,则AC= 。
专题05 特殊平行四边形(B卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(浙

班级姓名学号分数《特殊平行四边形》测试卷(B卷)(测试时间:60分钟满分:120分)一、选择题(每小题3分,总计30分)1.下列说法正确的是()A.对角线相等且互相垂直的四边形是菱形B.对角线互相垂直的梯形是等腰梯形C.对角线互相垂直的四边形是平行四边形D.对角线相等且互相平分的四边形是矩形2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是()A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠CC.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC3.如图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是A.10 B.16 C.18 D.204.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则)A. 35B.23C.38D.455.如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,下列说法错误的是()A .△EBD 是等腰三角形,EB=EDB .折叠后∠ABE 和∠CBD 一定相等C .折叠后得到的图形是轴对称图形D .△EBA 和△EDC 一定是全等三角形6.如图,点P 是正方形ABCD 的对角线BD 上一点,PE⊥BC 于点E ,PF⊥CD 于点F ,连接EF .给出下列五个结论:①AP=EF;②AP⊥EF;③△APD 一定是等腰三角形;④∠PFE=∠BAP;⑤PD=.其中正确结论的序号是( )A . ①②③④B . ①②④⑤C . ②③④⑤D . ①③④⑤7.如图,在正方形ABCD 的外侧,作等边三角形ADE ,AC ,BE 相交于点F ,则∠BFC 为( )A.45B.55C.60D.758.如图,已知菱形ABCD 的对角线AC 、BD 的长分别为6cm ,8cm ,AE ⊥BC 于点E ,则AE 的长是( ) A.35cm B.52cm C.548cm D.524cm 9.如图,E 是边长为l 的正方形ABCD 的对角线BD 上一点,且BE=BC ,P 为CE 上任意一点,PQ ⊥BC 于点Q ,PR ⊥BE 于点R ,则PQ+PR 的值为( )A BDA .B .C .D . 10.如图,在斜边为3的等腰直角三角形OAB 中,作内接正方形A 1B 1C 1D 1;在等腰直角三角形OA 1B 1中,作内接正方形A 2B 2C 2D 2;在等腰直角三角形OA 2B 2中,作内接正方形A 3B 3C 3D 3…依次作下去,则第2014个正方形A 2014B 2014C 2014D 2014的边长是( )A .201213 B .201313 C .201413 D .201513二、填空题(每小题4分,总计24分)11.用边长相等的三角形、四边形、五边形、六边形、七边形中的一种;能进行平面镶嵌的几何图形有 种.12.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,∠AOB=60°,点E 、F 分别是BO 、BC 的中点,若AB=6cm ,则△BEF 的周长为13.如图,四边形ABCD 是正方形,延长AB 到点E ,使AE=AC ,则∠BCE 的度数是 .14.如图,将一张长方形纸片沿EF 折叠后,点A 、B 分别落在A ’、B ’的位置,如果∠1=56°,那么∠2的度数是_______________.2221233215.如图平行四边形ABCD中AB=AD=6,∠DAB=60度,F为AC上一点,E为AB中点,则EF+BF的最小值为.16.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+其中正确的序号是______________三、解答题(总计66分)17.(4分)如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AE AF.求证:CE=CF.18.如图,正方形ABCD的对角线相交于点 O,点O也是正方形A′B′C′O的一个顶点,如果两个正方形的边长都是2,求两个正方形重叠部分的面积。
专题12 全等三角形(B卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(上册)(原卷版)
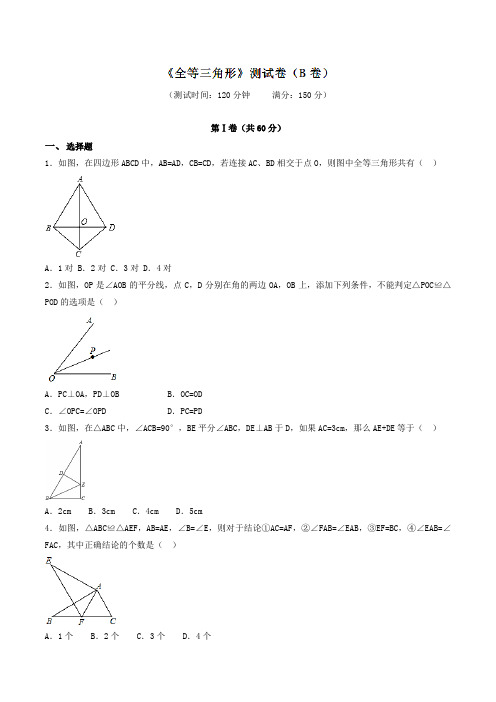
(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题1.如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有()A.1对 B.2对 C.3对 D.4对2.如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是()A.PC⊥OA,PD⊥OB B.OC=ODC.∠OPC=∠OPD D.PC=PD3.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于()A.2cm B.3cm C.4cm D.5cm4.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是()A.1个 B.2个 C.3个 D.4个5.如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFC的理由是()A.SSS B.AAS C.SAS D.HL6.如图,已知AE=CF,∠AFD=∠CEB,那么添加一个条件后,仍无法判定△ADF≌△CBE的是()A.AD=CB B.∠A=∠C C.BE=DF D.AD∥BC7.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是()A.8 B.6 C.4 D.28.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有()A.1个 B.2个 C.3个 D.4个9.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是()A .SASB .ASAC .AASD .SSS10.如图,在△ABC 中,∠ABC=45°,AC=8cm ,F 是高AD 和BE 的交点,则BF 的长是( )A .4cmB .6cmC .8cmD .9cm11.如图,已知AB ∥CF ,E 为DF 的中点,若AB=9 cm ,CF=5 cm ,则BD= cm .12.如图,在△ABC 和△BDE 中,点C 在边BD 上,边AC 交边BE 于点F .若AC=BD ,AB=ED ,BC=BE ,∠D=60°,∠ABE=28°,则∠ACB= .13.如图,DE ⊥AB 于E ,DF ⊥AC 于F ,若BD=CD ,BE=CF ,则下列结论:①DE=DF ;②AD 平分∠BAC ;③AE=AD ;④AB+AC=2AE 中正确的是 .14.如图,已知∠BAC=∠DAE=90°,AB=AD ,要使△ABC ≌△ADE ,还需要添加的条件是 .15.如图,在△ABC 和△EDB 中,∠C=∠EBD=90°,点E 在AB 上.若△ABC ≌△EDB ,AC=4,BC=3,则AE= .16.如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为.17.如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△ABC的面积是2,那么△A1B1C1的面积是.18.如图所示,直线a经过正方形ABCD的顶点A,分别过顶点B、D作DE⊥a于点E、BF⊥a于点F,若DE=4,BF=3,则EF的长为.19.如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB= .20.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,P、Q是边AC、BC上的两个动点, PD⊥AB于点D, QE ⊥AB于点E.设点P、Q运动的时间是t秒(t>0).若点P从C点出发沿CA以每秒3个单位的速度向点A 匀速运动,到达点A后立刻以原来的速度沿AC返回到点C停止运动;点Q从点B出发沿BC以每秒1个单位的速度向点C匀速运动,到达点C后停止运动,当t= 时,△APD和△QBE全等.三、解答题(21,22,23每题10分,24,25,26,27每题15分共60分)21.如图,点F、C在BE上,BF=CE,∠A=∠D,∠B=∠E.求证:AB=DE.22.如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点D在AB上,连接AC,求证:△AOC ≌△BOD.23.如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.24.如图,OC平分∠AOB,CD⊥OA于D,CE⊥OB于E,连接DE,猜想DE与OC的位置关系?并说明理由.25.已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:D在∠BAC的平分线上.26.如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过后,点P与点Q第一次在△ABC的边上相遇?(在横线上直接写出答案,不必书写解题过程)27.如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D 匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D 匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.(1)试说明:AD∥BC;(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.:。
20162017学年八年级数学同步单元双基双测AB卷
2016-2017学年八年级数学同步单元双基双测“ AB”卷、选择题 x 1 A. x 0 B. 2.若点( -5, y 〔)、 1.当分式 (-3,y 2)、(3,y 3)都在反比例函数3 .......................................... 、一土有意义时,字母X 应满足( X 0 C. x 1 D. y= -3的图像上,则( X A . y 1 > y 2 > y 3 C. y 3>y 1 >y23. ( 08年四川乐山中考题)如图,在直角梯形ABCD 中,AD // BC ,点E 是边CD 的中点,若4.函数y B . y 2 > y i > y3 D. yi>y 3>y 2 AB AD 的图象经过点(1, -2),则k 的值为( x B. A.- 25.如果矩形的面积为 - 2 6cmf,那么它的长 C. 2 D. -2 y cm 与宽x cm 之间的函数关系用图象表示大致(+十C ) B. 菱形 C. 矩形 D. 正方形 B 6.顺次连结等腰梯形各边中点所得四边形是( A.梯形 7 .若分式 -2^一— 的值为0,则x 的值为( x 4x 3 A. 3 8. (2004年杭州中考题)甲、乙两人分别从两地同时出发, 小时甲追上乙A a biA. ------- 倍 bB.3 或-3C.-3D.0 若相向而行,则a 小时相遇;若同向而行,则 bB. —倍 9.如图,把一张平行四边形纸片 Z BOD= .那么甲的速度是乙的速度的(八b a — C.b ab a —D. ------ 倍 b aABCD 替BD 对折。
使C 点落在E 处,BE 与AD 相交于点D.若/ DBC=15 ,则OA. 130 °B. 14010.如图,在高为3米,水平距离为4米楼梯的表面铺地毯,地毯的长度至少需多少米( C.150 ° D.160°A. 4B.5C.6D.7二、填空题11. 边长为7, 24, 25的^ ABC 内有一点P 到三边距离相等,则这个距离为212. 如果函数y=kx 2k是反比例函数,那么 k=,此函数的解析式是「时1 1 5 2a 3ab 2b 心13. 已知 _ _ _ = 5,贝U ------------- 的值是a ba 2ab b14.从一个班抽测了 6名男生的身高,将测得的每一个数据(单位:cm)都减去165.0cm,其结果如下:-1.2 , 0.1 , -8.3 , 1.2 , 10.8 , -7.0这6名男生中最高身高与最低身高的差是 ;这6名男生的平均身高约为 ===^ (结果保 留到小数点后第一位)215.如图,点P 是反比例函数y —上的一点,PDJ_X 轴于点D,则^ POD 勺面积为X三、计算问答题17.(08年宁夏中考题)汶川地震牵动着全国亿万人民的心,某校为地震灾区开展了 “献出我们的爱” 赈灾 捐款活动.八年级(1)班50名同学积极参加了这次赈灾捐款活动,下表是小明对全班捐款情况的统计表:捐款(元)10 15 30 , 50 60 人数3611*136因不慎两处被墨水污染,已无法看清,但已知全班平均每人捐款38元.(1) 根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程. (2) 该班捐款金额的众数、中位数分别是多少?18. 已知如图:矩形 ABCD 勺边BC 在X 轴上,E 为对角线BD 的中点,点B 、D 的坐标分别为 B (1, 0), D (3, 3),反比例函数y =- 的图象经过A 点,X(1)写出点A 和点E 的坐标; (2) 求反比例函数的解析式; (3) 判断点E 是否在这个函数的图象上16.先化简,再求值:1 X2 X 1,其中X=219.已知:CD为Rt ABC的斜边上的高,且BC a , AC b , AB c, CD h (如图)求证:1 b 2D参考答案 I. D 2. II. 3 3. A 4. D 5 . C 6 . B 7 . C 8 . C 9 . ,、1 12. — 1 或一 2 y= - x 1 或 y= 1x 1 2 13.1 14.19.1cm,164.3cm 15.1 16. 2x-1 17. 解: 答: 18.解:,3 (1)被污染处的人数为 11人 设被污染处的捐款数为 x 元,则 11 x +1460=50X 38解得x =40 (1) 被污染处的人数为 11人,被污染处的捐款数为(2) 捐款金额的中位数是 ........................................ 3 (1) A (1, 3), E (2, ^ 40元,捐款金额的众数是 40元. 50元.(2)设所求的函数关系式为 k y=_ x 把 x= 1, y= 3代入, 得:k = 3X 1 = 3 V =3为所求的解析式 ........... … 3 (3)当 x = 2 时,y = 2 ―,3、.••点 E (2,歹)在这个函数的图象上。
专题03 数据分析初步(B卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(浙江
班级 姓名 学号 分数《数据分析初步》测试卷(B 卷)(测试时间:60分钟 满分:120分)一、选择题(每小题3分,总计30分)1.关于数据:85,88,80,95,88,86的叙述中,错误的是( ) A.极差是15 B.众数是88 C.中位数是86 D.平均数是872.某校九年级有19名同学参加语文阅读知识竞赛,预赛成绩各不相同,要取前10名参加决赛, 小明已经知道了自己的成绩,他想知道自己能否进入决赛,还需要知道这19名同学成绩的( ) A .中位数 B .众数 C .平均数 D .极差3.已知一组数据x1、x2、x3、x4、x5的平均数是4,方差是5;那么另一组数据3x1-2、3x2-2、3x3-2、3x4-2、3x5-2的平均数和方差分别是( ) A .10,45 B .10,13 C .12,45 D .10,434.已知一组数据1a ,2a ,3a ,4a ,5a 的平均数为8,则另一组数据101+a ,102-a ,103+a ,104-a ,105+a 的平均数为( )(A )6 (B )8 (C )10 (D )125.已知A 样本的数据如下:72,73,76,76,77,78,78,78,B 样本的数据恰好是A 样本数据每个都加2,则A ,B 两个样本的下列统计量对应相同的是( )A .平均数B .标准差C .中位数D .众数6.某特警队为了选拔”神枪手”,举行了1 000米射击比赛,最后由甲、乙两名战士进入决赛,两人各射靶10次,经过统计计算,甲、乙两名战士的总成绩都是99.68环,甲的方差是0.28,乙的方差是0.21.则下列说法中,正确的是( ).A .甲的成绩比乙的成绩稳定B .乙的成绩比甲的成绩稳定C .甲、乙两人成绩的稳定性相同D .无法确定谁的成绩更稳定7.房山区体校甲、乙两队10名参加篮球比赛的队员的身高(单位:cm )如下表所示:设两队队员身高的平均数分别为x ,x 甲乙错误!未找到引用源。
期中测试卷(B卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(浙江版)(下册)(解析版)
班级 姓名 学号 分数(测试时间:60分钟 满分:120分)一、选择题(每小题3分,总计30分)1.下面关于x 的方程中①ax 2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=.一元二次方程的个数是( )A .1B .2C .3D .4 【答案】A 【解析】考点:一元二次方程的定义点评:本题属于基础应用题,只需学生熟练掌握一元二次方程的定义,即可完成. 2.下列计算结果正确的是( ) A 3= B 6=± C = D .3+=【答案】A . 【解析】试题分析:A 3==,故本选项正确;B 6=故本选项错误;C D .因为3和 故选A .考点:1.二次根式的性质与化简;2.二次根式的加减法. 3.下列调查的样本具有代表性的是 ( )A 、利用当地的七月份的日平均最高气温值估计当地全年的日最高气温B 、在农村调查市民的平均寿命1xC、利用一块实验水稻田的产量估水稻的实际产量D、为了了解一批洗衣粉的质量情况,从仓库中任意抽取100袋进行检验【答案】D.【解析】样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.根据样本的确定方法与原则,结合实际情况,依次分析选项可得答案.试题分析:A.抽取七月份的平均最高气温,样本太小,缺乏代表性B. 农村和城市人的寿命有差别,样本不具有代表性;C利用一块试验田,样本太小D从仓库中任意抽取100袋进行检验的样本是随机的,具有代表性.考点:样本估计总体.4.如果关于x的一元二次方程(m-1)x2+2x+1=0有两个不相等的实数根,那么m的取值范围是( ) A.m>2 B.m<2 C.m>2且m≠1 D.m<2且m≠1【答案】m<2且m≠1.【解析】考点:根的判别式.5.把方程x2﹣3x=10左边配成一个完全平方式,方程两边应同加上()A.9x2 B. C.9 D.【答案】B.【解析】试题分析:根据一元二次方程配方法则“方程两边都加上一次项系数一半的平方”可知方程两边同加上9 4 .故选B.考点: 一元二次方程的解法——配方法.6.方程x2_3x-2=0的根的情况是()A.方程有两个相等的实数根 B.方程有两个不相等的实数根C.方程没有实数根 D.方程的根的情况无法确定【答案】B【解析】试题分析::∵a=1,b=-3,c=-2, ∴△=b 2-4ac=(-3)2-4×1×(-2)>0, 所以方程有两个不相等的实数根. 故选B考点:根的判别式.7.王明同学随机抽某市10个小区所得到的绿化率情况,结果如下表:则关于这10个小区的绿化率情况,下列说法错误..的是( ▲ ) A .中位数是25% B .众数是25%C .极差是13%D .平均数是26.2%【答案】C8.某旅游景点三月份共接待游客25万人次,五月份共接待游客64万人次,设每月的平均增长率为x ,则可列方程为( )A 、225(1)64x +=B 、225(1)64x -=C 、264(1)25x +=D 、264(1)25x -= 【答案】A 【解析】试题分析:设每月的平均增长率为x ,依题意得25(1+x )2=64;故选A . 考点:一元二次方程9.设1x 、2x 是关于x 的一元二次方程22x x n mx ++-=的两个实数根,且10x <,2130x x -<,则 【 】 A .1,2m n >⎧⎨>⎩ B .1,2m n >⎧⎨<⎩ C .1,2m n <⎧⎨>⎩ D .1,2m n <⎧⎨<⎩【答案】C【解析】解:∵x 2-3x 1<0, ∴x 2<3x 1,∵x 1<0, ∴x 2<0.∵x 1,x 2是关于x 的一元二次方程x 2+x+n-2=mx 的两个实数根, ∴x 1+x 2=m-1,x 1x 2=n-2, ∴m -1<0,n-2>0, ∴1,2m n <⎧⎨>⎩故选C 。
专题04 因式分解(B卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(北师大版
班级姓名学号分数《因式分解》测试卷(B卷)(测试时间:120分钟满分:120分)一、选择题(每小题3分,共30分)1、a4﹣b4和a2+b2的公因式是()A、a2﹣b2B、a﹣bC、a+bD、a2+b22、下列等式从左到右的变形,属于因式分解的是()A、a(x﹣y)=ax﹣ayB、x2+2x+1=x(x+2)+1C、(x+1)(x+3)=x2+4x+3D、x3﹣x=x(x+1)(x﹣1)3、因式分解(x﹣1)2﹣9的结果是()A、(x+8)(x+1)B、(x+2)(x﹣4)C、(x﹣2)(x+4)D、(x﹣10)(x+8)4、下列因式分解正确的是()A、x2+2x﹣1=(x﹣1)2B、x2+1=(x+1)2C、2x2﹣2=2(x+1)(x﹣1)D、x2﹣x+1=x(x﹣1)+15、将下列多项式分解因式,结果中不含因式x+1的是()A、x2﹣1B、x2﹣2x+1C、x(x﹣2)+(x+2)D、x2+2x+16、如图,边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为m,则另一边长为()A、2m+6B、3m+6C、2m2+9m+6D、2m2+9m+97、若﹣2a n﹣1﹣4a n+1的公因式是M,则M等于()A、2a n﹣1B、﹣2a nC、﹣2a n﹣1D、﹣2a n+18、多项式(x+2)(2x﹣1)﹣2(x+2)可以因式分解成(x+m)(2x+n),则m﹣n的值是()A、2B、﹣2C、4D、59、小强是一位密码翻译爱好者,在他的密码手册中,有这样一条信息:a﹣b,x﹣y,x+y,a+b,x2﹣y2,a2﹣b2分别对应下列六个字:城、爱、我、宜、游、美,现将(x2﹣y2)a2﹣(x2﹣y2)b2因式分解,结果呈现的密码信息可能是()A、我爱美B、宜城游C、爱我宜城D、美我宜城10、设P=a2(﹣a+b﹣c),Q=﹣a(a2﹣ab+ac),则P与Q的关系是()A、P=QB、P>QC、P<QD、互为相反数二、填空题(每小题3分,共30分)11、分解因式:3x2﹣75=________.12、多项式24m2n2+18n各项的公因式是________.13、利用因式分解计算20142﹣20132﹣2014=________.14、15x2(y+4)﹣30x(y+4)=________,其中x=2,y=﹣2.15、a,b互为相反数,则a(x﹣2y)﹣b(2y﹣x)的值为________.16、若3x2﹣2x﹣1=0,则6x3+2x2﹣6x+1的值为________.17、若m2+2mn+2n2﹣6n+9=0,则的值为________.18、若△ABC的三边长为a,b,c,且c(a﹣b)+b(b﹣a)=0,则△ABC为________三角形.19、村民王富投资办养殖场,分大猪和小猪两个正方形养猪场.已知大猪场的面积比小猪场的面积大40m2,两个猪场的围墙总长为80m,试求小猪场的面积.________ m2.20、已知a=,b= ,c= ,则代数式2(a2+b2+c2-ab-bc-ac)的值是________.三、解答题(本大题共7小题,共60分)21、(7分)已知:A=4x+y,B=4x﹣y,计算A2﹣B2.22、(7分)已知三次四项式2x3﹣5x2﹣6x+k分解因式后有一个因式是x﹣3,试求k的值及另一个因式.23、(7分)给出三个多项式:x2+2x﹣1,x2+4x+1,x2﹣2x.请选择你最喜欢的两个多项式进行加法运算,并把结果因式分解.24、(7分)给定一列代数式:a3b2,ab4,a4b3,a2b5,a5b4,a3b6,….(1)分解因式:ab4﹣a3b2;(2)根据你发现的规律,试写出给定的那列代数式中的第100个代数式.25、(10分)两位同学将一个二次三项式分解因式,一位同学因看错了一次项系数而分解成2(x﹣1)(x﹣9),另一位同学因看错了常数项而分解成2(x﹣2)(x﹣4),请将原多项式分解因式.26、(10分)已知x2+bx+c(b、c为整数)是3(x4+6x2+25)及3x4+4x2+28x+25的公因式,求b、c的值.27、(12分)已知a,b,c为△ABC的三条边的长,当b2+2ab=c2+2ac时,(1)试判断△ABC属于哪一类三角形;(2)若a=4,b=3,求△ABC的周长.。
期末测试卷(二)(B卷)-2016-2017学年八年级数学同步单元双基双测“AB”卷(下册)(原卷版)
(测试时间:90分钟 满分:120分)一、选择题(共10小题,每题3分,共30分)1.函数y =x 的取值范围是 ( ) A .0x > B .2x >- C .2x -≥ D .2x ≠-2.如果0,0ab a b >+<,那么下面各式:①ba b a =,② 1=⋅a b b a ,③ b b a ab -=÷,其中正确的是( )A.①②B.②③C.①③D.①②③3.为参加 “2014年初中学业水平体育考试”,小明同学进行了刻苦训练,在立定跳远时,测得5次跳远的成绩(单位:m )为:2.3,2.5,2.4,2.3,2.1这组数据的众数、中位数依次是( )A .2.4,2.4B .2.4,2.3C .2.3,2.4D .2.3,2.34.已知:直角三角形的两条直角边的长分别为3和4,则第三边长为( ) A.5 B.7 C.7或5 D.5 5.给出的下列说法中:①以 1 ,2,3为三边长的的三角形是直角三角形;②如果直角三角形的两边长分别是3和4,那么斜边必定是5;③一个等腰直角三角形的三边长分别是a 、b 、c ,其中c 为斜边,那么a ︰b ︰c=1︰1︰2.其中正确的是( )A .①②B .①③C .②③D .①②③6.已知一矩形的两边长分别为7cm 和12 cm ,其中一个内角的平分线分长边为两部分,这两部分的长分别为( )。
A .6cm 和6cmB .7cm 和5cmC .4cm 和8cmD .3cm 和9cm7.下列给出的条件中,能判断四边形ABCD 是平行四边形的是( )A .∠A=∠C ,AD ∥BCB .AB ∥CD ,AD=BCC .∠B=∠C ,∠A=∠D D .∠A=∠C ,AD=BC8.对于函数y=-3x +1,下列结论正确的是( )A .它的图像必经过点(-1,3)B .它的图象经过第一、二、三象限C .当x >13时,y <0 D .y 的值随x 值的增大而增大9.下面四条直线中,直线上每个点的坐标都是方程x -2y=2的解的是( )A .B .C .D .10.小明、小宇从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小宇骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:①小宇先到达青少年宫;②小宇的速度是小明速度的3倍;③a=20;④b=600.其中正确的是( )A .①②③B .①②④C .①③④D .①②③④二、填空题(共10小题,每题3分,共30分)1.计算 ()()=+-2323 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(测试时间:90分钟 满分:120分)
一.选择题(共10小题,每题3分,共30分)
1.下列二次根式中,是最简二次根式的为( )
A
B
D
2.若正比例函数y=3x 的图象经过A (m ,4m+1),则m 的值为( ).
A .1
B .﹣1
C .25
D .﹣25
3.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y 与时间x 的关系的大致图象是( )
4.一次函数21y x =-+的图像不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5..如图,一次函数y 1=x+b 与一次函数y 2=kx+4的图像交于点P (1,3),则关于x 的不等式x+b >kx+4的解集是 ( )
A.x >﹣2
B.x >0
C.x >1
D.x <
1
6.如图,在Rt △ABC 中,∠ACB=90°,AC=6,BC=8,AD 是∠BAC 的平分线.若P ,Q 分别是AD 和AC 上的动点,则PC+PQ 的最小值是( )
A. 2.4
B. 4
C. 4.8
D. 5
7.若等腰三角形的周长是100cm,则能反映这个等腰三角形的腰长y(cm)与底边长x(cm)之间的函数关系式的图象是()
8.如图,在平面直角坐标系中,若有一点P(2,1)向上平移3个单位或者向左平移4个单位,恰好在直线y=kx+b上,则k的值是()
A.1
2
B.2 C.
3
4
D.
4
3
9.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPQ的面积是()
A.10 B.16 C.20 D.36
10.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是()
A.①②③ B.仅有①② C.仅有①③ D.仅有②③
二、填空题(共10小题,每题3分,共30分)
11.已知式子错误!未找到引用源。
有意义,则x的取值范围是_______________
12.直线y=﹣3x+5与x轴交点的坐标是.
13.某水池有水15m3,现打开进水管进水,进水速度5m3/h;xh后这个水池内有水y m3,则y关于x的关系式为.
14.一个y关于x的函数同时满足两个条件:①图象过(2,1)点;②当x>0时,y随x的增大而减小.这个函数解析式为.(写出一个即可)
15.将直线y=2x向下平移3个单位后所对应的函数关系式为.
16.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③甲队比乙队提前3天完成任务;④当x=2或6时,甲乙两队所挖管道长度都相差100米.正确的有.(在横线上填写正确的序号)[来
17.如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A
的对应点A′是直线y=4
5
x上一点,则点B与其对应点B′间的距离为.
18.如图,已知一次函数(0)y ax b a =+≠和(0)y kx k =≠的图象交于点P ,则二元一次方程组,0
y ax b y kx -=⎧⎨-=⎩的解是 .
19.如图,在矩形ABCD 中,AB =4,BC =6,点E 为BC 的中点,将△ABE 沿AE 折叠,使点B 落在矩形内点F 处,连接CF ,则CF 的长为___________.
20.小明在上学的路上(假定从家到校只有这一条路)发现忘带眼镜,立刻停下,往家里打电话,妈妈接到电话后立刻带上眼镜赶往学校.同时,小明原路返回,两人相遇后小明立即赶往学校,妈妈回家,妈妈要15分钟到家,小明再经过3分钟到校.小明始终以100米/分的速度步行,小明和妈妈之间的距离y (米)与小明打完电话后的步行时间t (分)之间函数图象如图所示,则下列结论:①打电话时,小明与妈妈的距离为1250米;②打完电话后,经过23分钟小明到达学校;③小明与妈妈相遇后,妈妈回家的速度为150米/分;④小明家与学校的距离为2550米.其中正确的有 .(把正确的序号都填上)
三、解答题(共60分)
21.(本题5分)已知一次函数y=kx+b 的图象经过点A (1,﹣1)和点B (﹣1,3),求这个一次函数的解析式.
22.(本题5分)如图,在ABC 中, AB BC =,D、E、F分别是BC 、AC 、AB 边上的中点.求证:四边形BDEF 是菱形;
23.(本题8分)如图,直线b y kx =+与x 轴交于点A (1,0),与 y 交于点B (0,-2).
(1)求直线AB 的表达式;
(2)点C 是直线AB 上的点,且CA=AB,过动点P(m ,0)且垂直于x 轴的直线与直线AB 交于点D ,若点D 不在线段BC 上,写出m 的取值范围.
24.(本题8分)已知y 是x 的一次函数,且当x=8时,y=15:当x=﹣10时,y=﹣3,求:
(1)这个一次函数的解析式;
(2)当y=﹣2时,求x 的值.
25.(本题8分)在平面直角坐标系xOy 中,一次函数的图象经过点A (2,3)与点B (0,5).
(1)求此一次函数的表达式;
(2)若点P 为此一次函数图象上一点,且△POB 的面积为10,求点P 的坐标.
26.(本题8分)如图,已知一次函数y =x +2与y =-2x +6的图象相交于点A ,函数y =-2x +6的图象分别交x 轴、y 轴于点B 、C ,函数y =x +2的图象分别与x 轴、y 轴交于点E 、D .
(1)求点A 的坐标;
(2)求△ABE 的面积.
27.(本题9分)甲、乙两车同时从M地出发,以各自的速度匀速向N地行驶.甲车先到达N地,停留1h 后按原路以原速匀速返回,直到两车相遇,乙车的速度为50km/h.如图是两车之间的距离y(km)与乙车行驶时间x(h)之间的函数图象.
(1)甲车的速度是 km/h,M、N两地之间相距 km;
(2)求两车相遇时乙车行驶的时间;
(3)求线段AB所在直线的解析式.
28.(本题9分)如图,直线l1的解析表达式为y=﹣3x+3,且l1与x轴交于点D.直线l2经过点A、B,直l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)在直线l2上存在异于点C的另一个点P,使得△ADP与△ADC的面积相等,求P点的坐标.。
