经典:统计学第三章--平均指标与变异指标-及习题
平均指标和变异指标练习题

平均指标和变异指标练习题题目一某班级共有40名学生,他们的身高数据如下:学生姓名身高(cm)小明160小红158小华165小李172小张155……请你使用平均指标和变异指标回答以下问题:1.计算这40名学生的平均身高。
2.计算这40名学生的身高的标准差。
3.根据平均身高和标准差,判断哪些学生的身高属于正常范围内(身高在平均身高的正负1个标准差范围内)。
题目二一家工厂连续30天生产的产品数量如下:日期产品数量2022-01-01 1002022-01-02 982022-01-03 1022022-01-04 992022-01-05 101……请你使用平均指标和变异指标回答以下问题:1.计算这30天内产品数量的平均值。
2.计算这30天内产品数量的极差。
3.根据平均值和极差,判断哪些天的产品数量与平均水平相差较大。
题目三某城市连续7天的气温数据如下:日期最高气温(℃)2022-01-01 102022-01-02 122022-01-03 82022-01-04 152022-01-05 20……请你使用平均指标和变异指标回答以下问题:1.计算这7天内最高气温的平均值。
2.计算这7天内最高气温的方差。
3.根据平均值和方差,判断这7天里的气温波动情况。
解答题目一1.计算这40名学生的平均身高。
使用平均指标,计算40名学生的平均身高可以通过求所有学生身高的和再除以学生人数得到。
平均身高 = (160 + 158 + 165 + 172 + 155 + ... + ... ) / 402.计算这40名学生的身高的标准差。
使用变异指标,计算40名学生的身高的标准差可以通过以下步骤进行:•计算每个学生身高与平均身高的差值。
•计算所有差值的平方和。
•求平方和的平均值。
•对平方和的平均值进行开方。
标准差可以描述数据的离散程度,数值越大表示数据的离散程度越大。
3.根据平均身高和标准差,判断哪些学生的身高属于正常范围内。
统计学第三章练习题(附答案)

统计学第三章练习题(附答案).单项选择题B.平均差 D.离散系数2.如果峰度系数k >3,表明该组数据是(A )0A. 64.5 和 78.5 D.64.5 和 67.55.对于右偏分布,平均数、中位数和众数之间的关系是( A)o7.在离散程度的测度中,最容易受极端值影响的是( A)08.在⽐较两组数据的离散程度时,不能直接⽐较它们的标准差,因为两组数据的 (D )oA.标准差不同C 数据个数不同1.⽐较两组数据的离散程度最合适的统计量是(D )。
A.极差 C 标准差A.尖峰分布B 扁平分布C 左偏分布 D.右偏分布3.某⼤学经济管理学院有 1200 名学⽣,法学院有 800 名学⽣,医学院有 320 名学⽣,理学院有 200 名学⽣0上⾯的描述中,众数是(B)0A.1200B.经济管理学院C.200D 理学院4. 某班共有 25 名学⽣ , 期末统计学课程的考试分数分别为:68,73,66,76,86,74,61,89,65,90,69,67,76,62,81,63,68,81,70,73,60,87,75,64,56考试分数下四分位数和上四分位数分别是( A)0B.67.5 和 71.5C.64.5和 71.5A.平均数>中位数>众数B. 中位数>平均数>众数 C 众数〉中位数〉平均数D.众数〉平均数〉中位数6.某班学⽣的统计学平均成绩是70分,最⾼分是 96分,最低分是 62分,根据这些信息,可以计算的测度离散程度的指标是(B)0A ⽅差B 极差C 标准差 D.变异系数A.极差B ⽅差C 标准差D.平均差B.⽅差不同 D.计量单位不同9.总量指标按其反应的内容不同,可分为( C)0A.总体指标和个体指标B.时期指标和时点指标c 总体单位总量指标和总体标识总量指标 D.总体单位总量指标和标识单位指标10.反映同⼀总体在不同时间上的数量对⽐关系的是(D.⽐例相对指标11.2003年全国男性⼈⼝数为 66556万⼈,2002年全国⾦融、保险业增加值为 5948.9亿元,2003年全社会固定资产投资总额为 55566.61亿元,2003年全国城乡居民⼈民币储蓄存款余额103617.7亿元。
《统计学原理》计算题
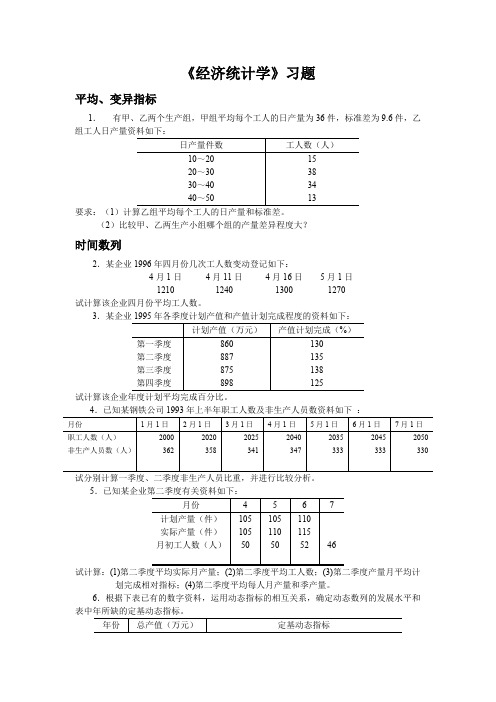
《经济统计学》习题平均、变异指标1.有甲、乙两个生产组,甲组平均每个工人的日产量为36件,标准差为9.6件,乙组工人日产量资料如下:日产量件数工人数(人)10~201520~303830~403440~5013要求:(1)计算乙组平均每个工人的日产量和标准差。
(2)比较甲、乙两生产小组哪个组的产量差异程度大?时间数列2.某企业1996年四月份几次工人数变动登记如下:4月1日4月11日4月16日5月1日1210124013001270试计算该企业四月份平均工人数。
3.某企业1995年各季度计划产值和产值计划完成程度的资料如下:计划产值(万元)产值计划完成(%)第一季度860130第二季度887135第三季度875138第四季度898125试计算该企业年度计划平均完成百分比。
4.已知某钢铁公司1993年上半年职工人数及非生产人员数资料如下:月份1月1日2月1日3月1日4月1日5月1日6月1日7月1日职工人数(人)2000202020252040203520452050非生产人员数(人)362358341347333333330试分别计算一季度、二季度非生产人员比重,并进行比较分析。
5.已知某企业第二季度有关资料如下:月份4567计划产量(件)105105110实际产量(件)105110115月初工人数(人)50505246试计算:(1)第二季度平均实际月产量;(2)第二季度平均工人数;(3)第二季度产量月平均计划完成相对指标;(4)第二季度平均每人月产量和季产量。
6.根据下表已有的数字资料,运用动态指标的相互关系,确定动态数列的发展水平和表中年所缺的定基动态指标。
年份总产值(万元)定基动态指标增长量(万元)发展速度(%)增长速度(%) 1986741-100-1987591988115.6198923.91990131.719912981992149.9199355.219944611995167.27.运用时间数列指标的相互关系,根据已知资料,确定某纺织厂棉布生产的各年发展水平、逐期增长量、环比发展速度、环比增长速度和增长1%的绝对值指标。
第三章平均指标练习及答案

第三章平均指标练习及答案第三章平均指数和标记变异指数1,填写问题1。
平均指数是一种统计指数,表明某个标记在特定的时间、地点和条件下达到_ _ _ _ _ _ _ _ _ _,也称为平均值2。
权重对算术平均值的影响不是由权重的大小决定的,而是由权重的大小决定的3。
几何平均数是n的n根。
这是最适合计算和平均速度的方法。
4。
当标记值较大且次数较多时,平均值接近标记值较大的一侧;当标志值小且次数大时,平均值接近标志值较小的一侧。
5。
当加权算术平均值等于简单算术平均值时6.使用组中值计算加权算术平均值时,假设每个组中的标记值都是分布的,计算结果为1 7。
中位数是位于可变序列中的标记值,模式是群体中出现次数的标记值中位数和众数也可以称为平均数8。
调和平均是一种平均,它是9。
当变量序列中的算术平均值大于模式时,变量序列的分布是分布的;另一方面,当算术平均值小于模式时,变量序列的分布是分布的10。
更常用的趋势指标是、、、、11.标准偏差系数是12。
据了解,XXXX一季度某一系列商品的平均销售数量按商品销售情况分为以下几类:按商品销售情况(低于2万-30元)公司20家店铺商品销售的平均差价是()如果店铺数量为1.530-40.9 40-50超过3 2(数)甲7万元乙10万元丙12万元丁3万元9当数据集高度倾斜时,哪个平均值更具代表性?()算术平均值b中值c模式d几何平均值14。
方差为()A绝对偏差平均值B平方偏差平均值C平方偏差平均值D绝对偏差平均值15。
一组数据的偏度系数为1.3。
显示这组数据的分布是()正态分布b 平顶分布c左偏置分布d右偏置分布16。
当一组数据属于左偏置分布时,则()A均值、中值和模式组合成左侧的一个B模式和右侧的C模式。
平均值越小,平均值越大。
d模式在右侧,平均值为17。
四分位偏差排除了序列两端()单位标志值的影响A1096B 15% C25 % D35 %18。
优势比是代表_ _ _ _ _ _ _ _ _ _ _规模的指标。
统计学 第三章练习题答案及解析

3%1%2%5.1++453025453025++++统计学第三章出题优课后习题答案原多项选择第三题D 选项解释有误,现在已经重新更改。
一、单项选择题1. 某商场某月商品销售额为1200万元,月末商品库存额为400万元,这两个总量指标( )。
A. 是时期指标B. 前者是时期指标,后者是时点指标C. 是时点指标2. 国民总收入与国内生产总值之间相差一个( )。
A. 出口与进口的差额B. 固定资产折旧C. 来自国外的要素收入净额3. 有三批产品,废品率分别为1.5%、2%、1%,相应的废品数量为25件、30件、45件,则这三批产品平均废品率的计算式应为( )。
A. B.C. D.4. 下列各项中,超额完成计划的有( )。
A. 利润计划完成百分数103.5%B. 单位成本计划完成百分数103.5%C. 建筑预算成本计划完成百分数103.5%5. 某厂某种产品生产量1月刚好完成计划,2月超额完成2%,3月超额完成4%,则该厂该年一季度各月平均超额完成计划的计算方法是( )。
A. 2%+4%=6%B. (2%+4%)÷2=3%C. (2%+4%)÷3=2%453025%1%2%5.1++++3%1%2%5.1⨯⨯6. 甲、乙两组工人的平均日产量分别为18件和15件。
若甲乙两组工人的平均日产量不变,但是甲组工人数占两组工人总数的比重下降,则两组工人总平均日产量( )。
A. 上升B. 下降C. 不变D.可能上升,也可能下降7. 当各个变量值的频数相等时,该变量的()。
A. 众数不存在B. 众数等于均值C. 众数等于中位数8. 如果你的业务是提供足球运动鞋的号码,那么哪一种平均指标对你更有用?( )A. 算术平均数B. 几何平均数9. 某年年末某地区城市和乡村平均每人居住面积分别为30.3和33.5平方米,标准差分别12.8和13.1平方米,则居住面积的差异程度( )。
A. 城市大B. 乡村大10. 下列数列的平均数都是50,在平均数附近散布程度最小的数列是( )。
统计学平均数与变异指标计算题答案

XH
Σm Σm
X
9150 2400 3150 3600
1.20 1.05 0.9
1.02(元)
第4页/共17页
2.某公司所属甲、乙两企业 职工的月工资水平如下:
按月工资 甲 企 业 乙 企 业 分组(元) 工人数(人) 工人结构(%)
350-400
50
5
400-450
80
12
450-500
100
合 计 — 630 328250 174493750 3465079.37
第8页/共17页
【解】五、2、(2)
σ甲 =
Σ(x - x)2f ∑f
3465079.37 =
630 = 74.16(元)
第9页/共17页
【解】五、2、(2)
Hale Waihona Puke σ甲 Σ x2f Σf
(ΣΣxff)2
1
7
4493 630
7
5
0
xf
18750 34000 47500 63000 115000 50000
x2 f ( x - x )2 f
7031250 1066238.05 14450000 737740.87 22562500 211876.09 33075000 1891.31 66125000 582552.18 31250000 864780.87
5
2
1
.
0
32
5501.95
74.18(元)
第10页/共17页
【解】五、2、(2)
某公司乙企业职工工资标准差计算表
按月工 组中 资分组 值x 350-400 375 400-450 425 450-500 475 500-550 525 550-600 575 600以上 625 合计 —
第3章-平均数、标准差与变异系数

50只小鸡出壳天数的频数分布表
出壳天数 频数(f) fx
19
2
38
20
3
60
21
10
210
22
24
528
23
9
207
24
2
48
合计
50
1091
x
fx f
1091 50
21.82
fmax=24, Mo=22
Md=22
表3-2 某纯系蛋鸡200枚蛋重的频数分布表
组别
44.25— 45.75— 47.25— 48.75— 50.25— 51.75— 53.25— 54.75— 56.25— 57.75— 59.25— 60.75—
• 极差(全距)
•
极差 = 最大值 - 最小值
• 只利用了资料中最大值和最小值, 不
能准确表达资料中各个观察值的变异程
度。
• 平均离差
xx
d
n 1
离均差
(x x)
它不能表示整个资
(x x) 0 料中所有观察值的 总偏离程度
标准差S
x x 使用不方便, 在统 S (x x)2 /(n 1) 计学中未被采用
n
(xi x)2
s 2 i1 n 1
样本标准差 s
n
(xi x)2
i 1
n 1
• 为了方便计算,将离均差平方和转化为另 一种形式,同时略去下标,上式可表示为:
s
x2
( x)2
n
n 1
• 在计算离散型频数资料的标准差时,
s
fx 2
( fx)2
N
N 1
• 式中x为组值, f为频数, N为总频数(∑f), k为组数。
第三章平均指数和变异指数

(一)简单算术平均数
(二)加权算术平均数
1、根据单项数列计算的
2、根据组距数列计算的
3、用比重权数计算的加权算术平均数
4、根据相对数(平均数)计算的加权 x
5、是非标志的平均数
(三) x 的数学性质
(四) x 的应用条件
返回
(一)简单算术平均数
计算公式: x x1 x2 x3 xn x
14 8 (14 8) (14 10)
5
123(个)
(二)中位数
1.定义:排序后处于中间位置上的值,集中趋 势的测度值之一。不受极端值的影响
50%
50%
Me
适用:主要用于定序数据,也可用数值型数据,但不能 用于定类数据
2.中位数计算
(位置的确定)
未分组数据:
中位数位置 N1 2
∑f 组距分组数据: 中位数位置
高了15%。计划完成相对指标为 (正指标)
115% 110%
104.5%
某企业计划某种产品成本今年比去年降低5%,实际
降低了6%。计划完成相对指标为 (逆指标)
94% 95%
98.95%
不同时期 比 较 不同现象 比较
同一时期比较 同类现象比较
动态 相对数
注: 又称发 展速度
强度 相对数
注: 复名数
如:
流通费用率(%)
流通费用总额 销售收入
返回
(六)计划完成相对指标
1、基本公式 计划完成相对指标
实际完成数 计划数
100%
2、短期计划的检查 (1)计划任务数为绝对数
计划完成相对指标
实际绝对水平 计划绝对水平
100%
某企业计划规定本年度销售收入达到1000万元, 实际为950万元,计划完成相对指标为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
第一节 平均指标
计算公式为:
X x1 x2 n
n
xn i1 xi
n
2. 加权算术平均数 根据分组整理而形成的变量数列计算算术平均数的 方法,称为加权算术平均法。
求这几年间国内生产总值的平均发展速度。
24
第一节 平均指标
(四)中位数(median) 将总体各单位标志值按大小顺序排列,居于 中点位置的那个标志值就是中位数。它是位 置平均数,不受极端值的影响。 1. 由未分组资料计算中位数
先按大小顺序排列,其次利用公式(N+1) /2确定中位数位次,最后确定中位数。
5
第一节 平均指标
计算公式为:
X x1 f1 x2 f2 f1 f2
n
xn fn fn
xi fi
i1 n
fi
i1
3. 算术平均数的性质
(1)各个变量值与平均数离差之和为0;(2)各个变量 值与平均数的离差平方和为最小值。
6
❖ 例:某厂工人各级别工资额和相应工 人数资料如表: 试计算工人平均工资。
15
例:求商品的平均价格
某商品的销售情况
销售价格 销售额 (元) (元)
3
90
4
80
5
50
16
第一节 平均指标
(三)几何平均数(geometric mean) 1. 简单几何平均数
n
Gn x1x2 xn n xi i1
17
例1:2001-2005年我国工业品的产量分别是上年的 107.6%、102.5%、100.6%、102.7%、102.2%,计 算这5年的平均发展速度。
工资额(元)
工人数(人)
460 520 600 700 850
合计
5 15 18 10 2
50
7
各组标志值 × 各组单位数 =各组标志总量
工资额(元) x
460 520 600 700 850
合计
工人数(人) 工资总额(元)
f
xf
5
2300
15
7800
18
10800
10
7000
2
1700
50
29600
25
第一节 平均指标
2. 由单项式分组资料计算中位数 经过分组的资料在确定中位数时,首先将变量数列
的频数或频率进行累加,然后用公式 f 来计算中
2
位数位次,确定中位数组,最后确定中位数。
26
家庭人口数(人) 家庭户数(户)
1
18
2
90
3
180
4
72
合计
360
向上累计频数(户)
18 108 288 360
21
例:某投资银行25年的年利率分别是:1年3%,4 年5%,8年8%,10年10%,2年15%,求平均年利 率。
22
XG f x1f1x2f 2...xnf n 251.031.0541.0881.1101.152 1.086108.6%
1.03,,(,1.05,yx,4,),,(,1.08,yx,8,),
企业的生产情况。 ❖分析现象之间的依存关系。 如商业企业规模的大小
和商品流通费用率之间存在的依存关系。
3
第一节 平均指标
三、平均指标的分类 在社会经济统计中,常用的平均指标有算术平均数、调和平均数、几何
平均数、中位数、众数 等。 (一)算术平均数(mean)
算 术 平 均 数 =总 总 体 体 标 单 志 位 总 总 量 量
,(,1.1,yx,10,),,(,1.15,yx,2,), =,2ndF,x y , 25,=
出现结果:1.086 即108.6% 平均年利率=108.6%-1=8.6%
23
练习:
年份
1998
1999
2000
2001
2002
国内生产总值 78345.2 82067.5 89468.1 97314.8 104790.6
1 xn
1x
2. 加权调和平均数
12
第一节 平均指标
2. 加权调和平均数
H
1
m1 m2
x1
x2
m1 m2
mn xn
mn
m m x
m为权数。
13
行驶速度 x
75 80 合计
行驶里程 m
225 160 385
行驶时间 M/x 3 2 5
14
X
m 38577
h
m5
X
❖ 即行使速度为77公里/小时
X XX X n G
1
...
2
n=
3 0.98*0.85*0.9
=90.8%
20
第一节 平均指标
2. 加权几何平均数
G x x f1 f2 fn
f1 f2
1
2
n
xfn f n
xfi i
i1
LnG f1Lnx1 fnLnxn
f
几何平均数也可用对数的算术平均形式表示。因 此,也称对数平均数。
可以证明: xGH
第三章 平均指标与变异指标
第一节 平均指标 第二节 变异指标 第三节 标准差、偏度和峰度
1
第一节 平均指标
2
第一节 平均指标
一、平均指标的含义 也称平均数,它表明同类现象在一定时间、地 点、条件下所达到的一般水平,是总体内各单 位参差不齐的标志值的代表值。
二、平均指标的作用
❖反映标志值的集中趋势。如农民家庭收入情况。 ❖便于比较分析。如用劳动生产率等平均数对比不同
甲企业
单位产品
产量比重
成本(元) (%)
1.0
10
1.1
20
1.2
70
乙企业
单位产品 产量比重 成本(元) (%)
1.2
30
1.1
30
1.0
40
10
x x f f
11
第一节 平均指标
(二)调和平均数(harmonic mean) 又称倒数平均数。 1. 简单调和平均数
H
1
1 1
x1 x2
n
n
18
X X X51.0761.0251.0061.0271.022
1.031103.1%
1.067,,1.025, ,1.006, ,1.027, ,1.022,=,2ndF,
x y , 5,=
出现结果:1.0309 即103.1%
19
例2:某企业生产某一产品,要经过铸造、金加工、电 镀三道工序,各工序产品合格率分别为98%、85%、 90%,求三道工序的平均合格率。
27
3. 由组距式分组资料计算中位数 确定中位数位次的方法同上,然后按下限公式或上限 公式计算中位数。
8
各组工( 资 x) 额 各 各组 组工 工( 资 ( 人 xx) 总 ) f数
平工 均资为:
xxf465 05210 56010 87010 0852 05( 92元/
f
51 51 81 02
9
❖ 甲乙两企业生产同种产品,1月份各批产量和 单位产品成本资料如下,求平均成本。
怎么做?
第一批 第二批 第三批
