第四章题解
近世代数第四章 环与域题解讲解

第四章环与域§1 环的定义一、主要内容1.环与子环的定义和例子。
在例子中,持别重要的是效域上的多项式环、n阶全阵环和线性变换环,以及集M的幂集环.2.环中元素的运算规则和环的非空子集S作成子环的充要条件:二、释疑解难1.设R是一个关于代数运算十,·作成的环.应注意两个代数运算的地位是不平等的,是要讲究次序的.所以有时把这个环记为(R,十,·)(或者就直接说“R对十,·作成一个环”).但不能记为R,·,十).因为这涉及对两个代数运算所要求满足条件的不同.我们知道,环的代数运算符号只是一种记号.如果集合只有二代数运算记为 ,⊕,又R对 作成一个交换群,对⊕满足结合律且⊕对 满足左、右分配律,即就是说,在环的定义里要留意两个代数运算的顺序.2.设R对二代数运算十,·作成一个环.那么,R对“十”作成一个加群,这个加群记为(R,十);又R对“·”作成一个半群,这个乍群记为(R,·).再用左、右分配律把二者联系起来就得环(R,十.·).三、习题4.1解答1.2.3.4.5.6.7.8.证明:循环环必是交换环,并且其子环也是循环环.§4.2 环的零因子和特征一、主要内容1.环的左、右零因子和特征的定义与例子.2.若环R 无零因子且阶大于1,则R 中所有非零元素对加法有相同的阶.而且这个相同的阶不是无限就是一个素数.这就是说,阶大于l 且无零因子的环的特征不是无限就是一个素数. 有单位元的环的特征就是单位元在加群中的阶.3.整环(无零因子的交换环)的定义和例子. 二、释疑解难1.由教材关于零因子定义直接可知,如果环有左零因子,则R 也必然有右零因子.反之亦然.但是应注意,环中一个元素如果是一个左零因子,则它不一定是一个右零因子.例如,教材例l 中的元素⎪⎪⎭⎫⎝⎛0001就是一个例子.反之,一个右零因子也不一定是一个左零因子.例如,设置为由一切方阵),(00Q y x y x ∈∀⎪⎪⎭⎫ ⎝⎛对方阵普通加法与乘法作成的环.则易知⎪⎪⎭⎫⎝⎛0001是R 的一个右零因子,但它却不是R 的左零因子.2.关于零因子的定义.关于零因子的定义,不同的书往往稍有差异,关键在于是否把环中的零元也算作零因子.本教材不把零元算作零因子,而有的书也把零元算作零因子.但把非牢的零因子称做真零因子.这种不算太大的差异,读者看参考书时请留意.3.关于整环的定义.整环的定义在不同的书中也常有差异.大致有以下4种定义方法: 定义1 无零因子的交换环称为整环(这是本教材的定义方法). 定义2 阶大于l 且无零因子的交换环,称为整环. 定义3 有单位元且无零因子的交换环,称为整环.定义4 阶大于1、有单位元且无零因子的交换环,称为整环.以上4种定义中,要求整环无零因子、交换是共同的,区别就在于是否要求有单位元和阶大于1.不同的定义方法各有利弊,不宜绝对肯定哪种定义方法好或不好.这种情况也许到某个时期会得到统一.但无论如何现在看不同参考书时应留意这种差异.本教材采用定义1的方法也有很多原因,现举一例。
现代控制理论习题解答(第四章)

第四章 控制系统的稳定性3-4-1 试确定下列二次型是否正定。
(1)3123212322212624)(x x x x x x x x x x v --+++= (2)232123222126410)(x x x x x x x x v ++---= (3)312321232221422410)(x x x x x x x x x x v --+++= 【解】: (1)04131341111,034111,01,131341111<-=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数不定。
(2)034101103031,0110331,01,4101103031<-=--->=--<-⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=P二次型函数为负定。
(3)017112141211003941110,010,1121412110>=---->=>⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=P 二次型函数正定。
3-4-2 试确定下列二次型为正定时,待定常数的取值范围。
312321231221211242)(x x x x x x x c x b x a x v --+++=【解】:312321231221211242)(x x x x x x x c x b x a x v --+++=x c b a x T ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=1112121110212111,011,0111111>---->>c b a b aa 满足正定的条件为:⎪⎩⎪⎨⎧++>+>>1111111114410ca b c b a b a a3-4-3 试用李亚普诺夫第二法判断下列线性系统的稳定性。
;1001)4(;1111)3(;3211)2(;1110)1(x x x x x x x x ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=【解】: (1)设22215.05.0)(x x x v +=⎩⎨⎧≠≤==-=--=+=)0(0)0(0222221212211)(x x x x x x x x x x x x x v为半负定。
第四章题解

4-1 在定态操作反应器的进口物料中脉冲注入示踪物料。
出口处示踪物浓度随时间变化的情况如下。
假设在该过程中物料的密度不发生变化,试求物料的平均停留时间与])(2)(4[3109753864210c c c c c c c c c c tdt c i +++++++++∆=⎰∞]0)5.20.1025.1(2)0.10.55.125.6(40[32++++++++==100min)/1(100)()(0tii c dtc t c t E ==⎰∞})(])()()()([2])()()()([4)({31010997755338866442211_t E t t E t t E t t E t t E t t E t t E t t E t t E t t E t tt +++++++++∆=]0)03.08.05.0(2)14.05.075.013.0(40[32+++++++++=min 187.6=⎰∞=-=-=02222971.8187.625.47)(t dt t E t tσmin 24-2 无量纲方差表达式的推导 (1)推导无量纲方差222/ttσσθ=;(2)推导CSTR 的22tt=σ。
1. τθt=2. ττtet E -=1)(证明:222)(i i i ittt t E t -∆=∑∞σ⎰∞--=221tdt e t t ττ22)()()()(ττθθττθ--=⎰∞-d t E()]1)1([022--=⎰∞θθθτd E22θστ= 222/τσσθt=∴ 220222)(1)(--∞-=-=⎰⎰t dt e tt dt t E t ttττσ222ττ-=2τ=22τσ=t4-3 设()θF 及()θE 分别为闭式流动反应器的停留时间分布函数及停留时间分布密度函数,θ为对此停留时间。
(1)若该反应器为平推流反应器,试求①F(1); ②E(1);③F(0.8);④E(0.8);⑤F(1.2) (2)若该反应器为全混流反应器,试求①F(1); ②E(1);③F(0.8);④E(0.8);⑤F(1.2) (3)若该反应器为非理想流动反应器,试求 ①F(∞); ②F(0);③E(∞);④E(0);⑤⎰∞0)(θθd E ;⑥⎰∞)(θθθd E解1平推流模型0)(=θF )(t t 〈 0)(=θE )(t t ≠1)(=θF )(t t≥ ∞=)(θE )(t t =)()(τθtF F =⎪⎩⎪⎨⎧===2.1,18.0,01,1θθθ⎩⎨⎧=====8.0,01,1)()(θθτθt E E2 全混流θθ-=e E )( , θθ--=e F 1)(==)()(τθt f F ⎪⎭⎪⎬⎫=-=-=----699.01551.01632.012.18.01e e e ⎪⎩⎪⎨⎧===2.18.01θθθ ==)()(τθtE E ⎪⎭⎪⎬⎫==--449.0368.08.01e e ⎩⎨⎧==8.01θθ3非理想流动模型a 多釜串联θθθN N N e N N E ---=1)!1()(, 0)(C C F N =θ()()1]!11)(!21)(!111[1)(12=-++++-=∞--N N N N N N e F θθθθ()()0]!11)(!21)(!111[1)0(12=-++++-=--N N N N N N eF θθθθ()()()0!11=-=∞--θθN N Ne N N E()()1,00!1001≠=-=-N e N N E N N()()1!1!1)(01010=-=-=⎰⎰⎰∞--∞--∞θθθθθθθθd e N N d e N N d E N N NN N N ()1!1)(0=-=⎰⎰∞-∞θθθθθθd e N N d E N N N4-4 C(t)t/min4-18图用阶跃法测定某一闭式流动反应器的停留时间分布,得到离开反应器的示踪剂浓度与时间的关系,如图4-18所示。
第四章刚体运动习题详解
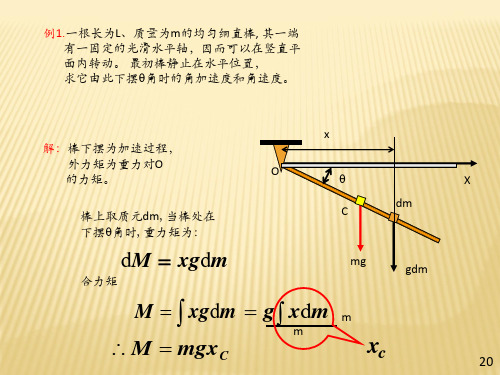
解:棒下摆为加速过程, 外力矩为重力对O 的力矩。
棒上取质元dm,当棒处在 下摆角时,重力矩为:
x
O
X
C
dm
dM xgdm
合力矩
mg
gdm
解:
因摩擦力产生的力矩是恒定的,故角速度均匀 减小。
0
0
t
0
0 t
dt t
0
f dS
r
σ
m πR2
R
dθ o
r
M J 1 mR2
2
dr
t 0mR2 / (2M ) (1) M ?
考虑面元dS对轴的摩擦力矩dM :
dM r0gdm r0g dS
26
t0mR2/(2M ) (1) dM r0g dS
mg 由(3)(4)(5)得
mgR sin
1 2
J02
1 2
J2
(5)
gh 2R2
cos2
g R
sin
1 2R
.
g 2
(h
4
3R)
M J
mgR 2mR2
g 2R
( 60 )
44
dt
O
X
C
即 d d
3g cos d d
mg
2L
θ
0
3gcos
2L
d
0
d
3g 2L
sin
1 2
2
3g sin
L
22
m 例2.质量为 、长为L的匀质细杆水平放置,一端
《理论力学》第四章 静力学应用专题习题解
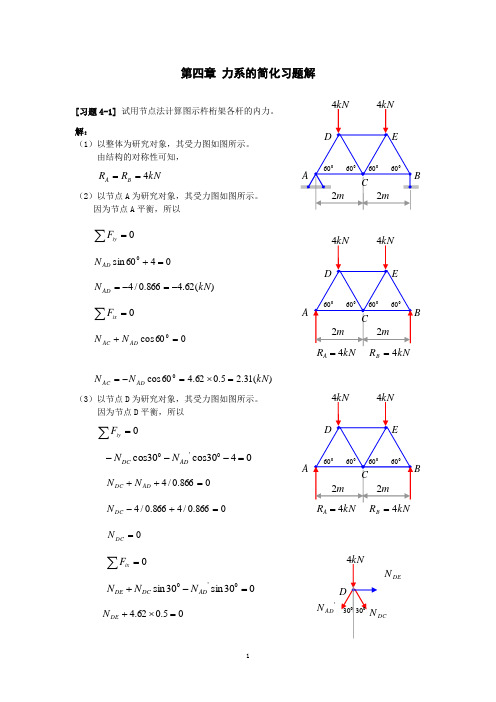
第四章 力系的简化习题解[习题4-1] 试用节点法计算图示杵桁架各杆的内力。
解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N)(31.25.062.460cos 0kN N N AD AC =⨯=-= (3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ixF030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE NkN4)(akN4AB RkN 2AC23N A )(31.2kN N DE -=(4)根据对称性可写出其它杆件的内力如图所示。
[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力以整体为研究对象,其受力图如图所示。
由对称性可知,kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =kN2AC23N A0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iyF02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。
无机化学(周祖新)习题解答 第四章

无机化学(周祖新)习题解答第四章第四章酸碱平衡和溶解沉淀平衡习题解答(4)思考题1.强电解质的水溶液有强的导电性,但AgCl和BaSO4水溶液的导电性很弱,它们属于何种电解质?1.答:AgCl和BaSO4水溶液的导电性虽很弱,溶液中离子浓度很小,这是由于AgCl和BaSO4本身溶解度小,致使溶液中自由离子浓度小,导电性弱。
而AgCl和BaSO4(溶解部分)在溶液中还是全部解离的,所以是强电解质。
2.在氨水中加入下列物质时,NH3?H2O的解离度和溶液的pH将如何变化?⑴NH4Cl ⑵NaOH ⑶HAc ⑷加水稀释 2.NH3?H2ONH4++OH-⑴加入NH4Cl,氨水解离度下降,pH减小。
⑵加入NaOH,氨水解离度下降,pH增加。
⑶加入HAc,氨水解离度增加,pH减小。
⑷加水稀释,氨水解离度增加,pH减小。
3.下列说法是否正确?若有错误请纠正,并说明理由。
⑴酸或碱在水中的解离是一种较大的分子拆开而形成较小离子的过程,这是吸热反应。
温度升高将有利于电离。
⑵1×10-5 mol?L-1的盐酸溶液冲稀1000倍,溶液的pH值等于8.0。
⑶将氨水和NaOH溶液的浓度各稀释为原来1/2时,则两种溶液中OH-浓度均减小为原来的1/2。
⑷pH相同的HCl和HAc浓度也应相同。
⑸酸碱滴定中等当点即指示剂变色点。
⑹某离子被完全沉淀是指其在溶液中的浓度为0。
3.⑴错。
在解离即较大的分子拆开而形成较小离子的吸热反应的同时,较小离子与水分子的水合是是放热的,总反应的吸放热取决于两过程热效应的相对大小,有吸热也有放热,故温度升高不一定有利于解离。
⑵错。
在pH值远离7的时候,溶液每稀释10倍,pH近视增加一个单位,这是没有计算水解离出的H+,当pH接近7的时候,水解离出的H+就不能再忽略了,所以酸性溶液不管怎么稀释,只能越来越接近中性,不可能变为碱性。
⑶错。
NaOH溶液稀释为原来1/2时OH-浓度确实减小为原来的1/2;但氨水在稀释过程中,其解离平衡向右移动,会解离出更多的OH-,稀释一倍后,其OH-浓度大于原来的一半。
第04章 集成运算放大电路题解

第四章集成运算放大电路自测题一、选择合适答案填入空内。
(1)集成运放电路采用直接耦合方式是因为。
A.可获得很大的放大倍数B. 可使温漂小C.集成工艺难于制造大容量电容(2)通用型集成运放适用于放大。
A.高频信号B.低频信号C.任何频率信号(3)集成运放制造工艺使得同类半导体管的。
A.指标参数准确B.参数不受温度影响C.参数一致性好(4)集成运放的输入级采用差分放大电路是因为可以。
A.减小温漂B. 增大放大倍数C. 提高输入电阻(5)为增大电压放大倍数,集成运放的中间级多采用。
A.共射放大电路B.共集放大电路C.共基放大电路解:(1)C (2)B (3)C (4)A (5)A二、判断下列说法是否正确,用“√”或“×”表示判断结果填入括号内。
(1)运放的输入失调电压U I O 是两输入端电位之差。
( ) (2)运放的输入失调电流I I O 是两端电流之差。
( ) (3)运放的共模抑制比cdCMR A A K =( ) (4)有源负载可以增大放大电路的输出电流。
( )(5)在输入信号作用时,偏置电路改变了各放大管的动态电流。
( ) 解:(1)× (2)√ (3)√ (4)√ (5)× 三、电路如图T4.3所示,已知β1=β2=β3=100。
各管的U B E 均为0.7V ,试求I C 2的值。
图T4.3解:分析估算如下: 100BE1BE2CC =--=RU U V I R μ AβCC B1C0B2C0E1E2CC1C0I I I I I I I I I I I I R +=+=+====1001C =≈⋅+=R R I I I ββμA四、电路如图T4.4所示。
图T4.4(1)说明电路是几级放大电路,各级分别是哪种形式的放大电路(共射、共集、差放……);(2)分别说明各级采用了哪些措施来改善其性能指标(如增大放大倍数、输入电阻……)。
解:(1)三级放大电路,第一级为共集-共基双端输入单端输出差分放大电路,第二级是共射放大电路,第三级是互补输出级。
近世代数第四章-环与域题解讲解

第四章环与域§1 环的定义一、主要容1.环与子环的定义和例子。
在例子中,持别重要的是效域上的多项式环、n阶全阵环和线性变换环,以与集M的幂集环.2.环中元素的运算规那么和环的非空子集S作成子环的充要条件:二、释疑解难1.设R是一个关于代数运算十,·作成的环.应注意两个代数运算的地位是不平等的,是要讲究次序的.所以有时把这个环记为(R,十,·)(或者就直接说“R对十,·作成一个环〞).但不能记为R,·,十).因为这涉与对两个代数运算所要求满足条件的不同.我们知道,环的代数运算符号只是一种记号.如果集合只有二代数运算记为 ,⊕,又R对 作成一个交换群,对⊕满足结合律且⊕对 满足左、右分配律,即就是说,在环的定义里要留意两个代数运算的顺序.2.设R对二代数运算十,·作成一个环.那么,R对“十”作成一个加群,这个加群记为(R,十);又R对“·〞作成一个半群,这个乍群记为(R,·).再用左、右分配律把二者联系起来就得环(R,十.·).三、习题4.1解答1.2.3.4.5.6.7.8.证明:循环环必是交换环,并且其子环也是循环环.§4.2 环的零因子和特征一、主要容1.环的左、右零因子和特征的定义与例子.2.假设环R 无零因子且阶大于1,那么R 中所有非零元素对加法有一样的阶.而且这个一样的阶不是无限就是一个素数.这就是说,阶大于l 且无零因子的环的特征不是无限就是一个素数. 有单位元的环的特征就是单位元在加群中的阶.3.整环(无零因子的交换环)的定义和例子. 二、释疑解难 1.由教材关于零因子定义直接可知,如果环有左零因子,那么R 也必然有右零因子.反之亦然.但是应注意,环中一个元素如果是一个左零因子,那么它不一定是一个右零因子.例如,教材例l 中的元素⎪⎪⎭⎫⎝⎛0001就是一个例子.反之,一个右零因子也不一定是一个左零因子.例如,设置为由一切方阵),(00Q y x y x ∈∀⎪⎪⎭⎫ ⎝⎛对方阵普通加法与乘法作成的环.那么易知⎪⎪⎭⎫⎝⎛0001是R 的一个右零因子,但它却不是R 的左零因子.2.关于零因子的定义.关于零因子的定义,不同的书往往稍有差异,关键在于是否把环中的零元也算作零因子.本教材不把零元算作零因子,而有的书也把零元算作零因子.但把非牢的零因子称做真零因子.这种不算太大的差异,读者看参考书时请留意.3.关于整环的定义.整环的定义在不同的书中也常有差异.大致有以下4种定义方法: 定义1 无零因子的交换环称为整环(这是本教材的定义方法). 定义2 阶大于l 且无零因子的交换环,称为整环. 定义3 有单位元且无零因子的交换环,称为整环.定义4 阶大于1、有单位元且无零因子的交换环,称为整环.以上4种定义中,要求整环无零因子、交换是共同的,区别就在于是否要求有单位元和阶大于1.不同的定义方法各有利弊,不宜绝对肯定哪种定义方法好或不好.这种情况也许到某个时期会得到统一.但无论如何现在看不同参考书时应留意这种差异.本教材采用定义1的方法也有很多原因,现举一例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题: 原理,有必要吗? 问题:有人应用 Babinet 原理,有必要吗?
补充题一:利用单缝夫琅和费衍射原理, 补充题一:利用单缝夫琅和费衍射原理,可以在线检测拉丝机生产的金属细 丝的直径误差。 (1 自行设计检测装置,画出原理示意图; 丝的直径误差。 1) 自行设计检测装置,画出原理示意图;说明其工作原 ( 理及装置构造。 理及装置构造。 (2) 设光波长 λ = 0.633µm ,透镜焦距 f = 3m ,金属细丝直径的设计值
回答:衍射图形不变;仅中央亮斑随之移动。 回答:衍射图形不变;仅中央亮斑随之移动。
2 是平行于狭缝的线光源。 是垂直于狭缝的线光源 结果又如何?) 于狭缝的线光源, ○S 是平行于狭缝的线光源。 若 S S 是垂直于狭缝的线光源,结果又如何?) (
4.11
(1) 试求在正入射照明下,图示两种衍射屏的夫琅和费衍射图形的复振幅分布 试求在正入射照明下,
x2 + y 2 jk f + 2f
K E ( x, y ) = e f
L ( x, y ) =
2 Lx L sin c λf
Lx sin c λf
2 lx − l sin c λf
lx sin c λf
解答:反射光的衍射( 解答:反射光的衍射( n2 = n1 = 1 ),
∆θ =
a0 cos β
λ0
∆θ 0 = 0.6 ×10−4 rad ∆θ 60 = 1.2 ×10−4 rad ∆θ89 = 3.4 ×10−3 rad
折射光的衍射( n1 = 1, 折射光的衍射(
n2 = 1.5 ),
题结论) (利用 4-6 题结论)
2
是衍射图形中心的辐照度。 其中 L0 是衍射图形中心的辐照度。 为例,分别计算近似值和实际值, (2) 以 m = 2 为例,分别计算近似值和实际值,求近似值的 ) 相对误差有多大? 相对误差有多大?
轴的衍射光强度分布为: (1)沿 x 轴的衍射光强度分布为 )
sin α L = L0 α
2
1 λ2 f 2
2 Lx L sin c λf
Lx sin c λf
2 lx − l sin c λf
lx sin c λ f
图(b)圆环 (b)圆环
r2 jk f + 2f
E (r ) =
K e f
Rr R r 2 J1 2π 1 2 J1 2π 2 λ f λ f − πR 2 (π R1 )2 ( 2) R1r R r 2π 2π 2 λf λf
2
Rr R r 2 J1 2π 1 2 J1 2π 2 λ f 1 2 λ f − πR 2 L ( r ) = 2 2 (π R1 ) ( 2) λ f R1r R2 r 2π λ f 2π λ f
∆θ =
λ0
a0 n2 − n sin β
2 2 1 2
∆θ 0 = 0.4 ×10−4 rad ∆θ 60 = 0.42 ×10−4 rad ∆θ89 = 0.54 ×10−4 rad
4.8 (1)试证明单缝夫朗和费衍射第 m 级次级大的辐照度可以近 ) 似地表示为: 似地表示为:
1 Lm = L0 ( m + 1 2) π
2
代入:
sin β ′ =
n1λ0 n1 sin β , λ2 = n2 n2
方法(2) 用等效狭缝概念。在 n2 介质中,等效狭缝宽度: 方法( 用等效狭缝概念。 介质中,等效狭缝宽度:
λ n12 ′ a0 = a0 cos β ′ = a0 1 − 2 sin 2 β , ∆θ = 2 n2 a′
物理光学
第四章习题解
第四章学习要点
• 1.掌握下述基本概念: 光的衍射,衍射的三要素,惠更斯-菲涅 耳原理,光的衍射与光的干涉的异同,菲 涅耳衍射,夫琅和费衍射,爱里分布,衍 射受限分辨本领,瑞利判据,巴比内原理, 光栅,光谱,光栅分辨本领,光栅色散, 色散范围,菲涅耳半波带,菲涅耳波带板。
2.在有限距离观察夫琅和费衍射的装置; 2.在有限距离观察夫琅和费衍射的装置; 在有限距离观察夫琅和费衍射的装置 3.应用标量衍射理论计算简单孔径的夫琅和费 3.应用标量衍射理论计算简单孔径的夫琅和费 衍射的方法(单缝,双缝,园孔,园屏, 衍射的方法(单缝,双缝,园孔,园屏,一维 振幅光栅) 夫琅和费衍射图形的特点。 振幅光栅),夫琅和费衍射图形的特点。 4.夫琅和费衍射的性质 夫琅和费衍射的性质。 4.夫琅和费衍射的性质。 5.光学系统的衍射受限分辨本领 光学系统的衍射受限分辨本领。 5.光学系统的衍射受限分辨本领。 6.应用半波带法分析园孔的菲涅耳衍射 应用半波带法分析园孔的菲涅耳衍射; 6.应用半波带法分析园孔的菲涅耳衍射; 7.菲涅耳波带板的设计和成像性质 菲涅耳波带板的设计和成像性质。 7.菲涅耳波带板的设计和成像性质。
(2)当 m=2 时, ) 实际计算所得的次级大值: L2 = 0.01694 L0 实际计算所得的次级大值:
1 而近似值: 而近似值: L2′ = L0 = 0.01621L0 ( m + 1 2)π
2
′ L2 − L2 所以相对误差: Hale Waihona Puke 4.5% 所以相对误差: ′ L2
λ
a cos β
。
a ( sin θ − sin β ) 解答: 解答: 1) I ( x ) = I ( x0 ) sinc ( λ
2
(2) x0 = f sin β
(3) 方法一: 方法一: 由第一极小条件
a
λ
( sin θ − sin β ) = 1 ,以及 θ = ∆θ + β
2
a0 x 其中 α = π λf
2
级次级大位于相邻两个暗点的中点, 相邻两个暗点的中点 近似计算时认为第 m 级次级大位于相邻两个暗点的中点,即:
1 1 α = m + π ,所以: Lm = L0 所以: 2 m + 1 2) π (
实际位置由下式决定 (2)次极大的实际位置由下式决定 )次极大的实际位置由下式决定:
α +β
2 sin
利用: 利用: sin α − sin β = 2 cos
α −β
2
θ θ sin ( β + ∆θ ) − sin β = 2sin cos β + 2 2
≈ ∆θ cos β =
λ
a0
→ ∆θ =
λ
a0 cos β
方法二:由等效狭缝宽度: 方法二:由等效狭缝宽度: a0′ = a0 cos β 和中央亮斑半角宽度: 和中央亮斑半角宽度: ∆θ =
误差越小 由图看出,m 越大 误差越小 看出 越大,误差越小.
4.9 试以单缝夫琅和费衍射装置 如图所示)为例,讨论装置作如下变化时对 试以单缝夫琅和费衍射装置(如图所示 为例 如图所示 为例, 衍射图形的影响。 衍射图形的影响。 (1) 透镜 L2:焦距变大; 焦距变大; (2) 衍射屏 :设为单缝。 衍射屏∑:设为单缝。
2 2 答案: 答案: (1) L ( x ) = L ( 0 ) sin c a0 fξ = L ( 0 ) sin c
(
)
a0 sin θ λ
a x = L ( 0 ) sin c 2 0 , λf
2 x1 = ω =
2λ f λ , ∆θ = a0 a0
(2)图(a)方环 (a)方环
2 2 L环 ( 0, 0 ) ( L − l ) 9 = = = 56.25% 4 L孔 ( 0, 0 ) 16 L 2
(3)图(b)圆环 (b)圆环
L环 ( 0, 0 ) ( R − R2 = L孔 ( 0, 0 ) R14
2 1
2 2
)
=
9 = 56.25% 16
式中 λ0 为光在真空中的波长。 为光在真空中的波长。 解答:方法( 题方法。 解答:方法(1)导出衍射图形辐照度分布,按 4.5 题方法。 导出衍射图形辐照度分布,
a λ2 I ( x ) = I ( 0 ) sinc ( sin θ − sin β ′ ) , ∆θ ≈ a cos β ′ λ2
d sin α =0, 即 dα α
ta n α
= α
这一方程可以利用图解法求解。如图所示, 这一方程可以利用图解法求解。如图所示,在同一坐标系中 其交点即为方程的解。 分别作出曲线 F=tanα和 F=α,其交点即为方程的解。
头几个次极大所对应的α 头几个次极大所对应的α值, 已列于表 3 - 1 中
λ
a0
,可导出结论. 可导出结论.
4.6 如果上题中其他条件不变,只是衍射屏左、右两侧媒质不同,折射率 如果上题中其他条件不变,只是衍射屏左、右两侧媒质不同, 试证明此时衍射图形中央亮斑半角宽度为: 分别为 n1 和 n2。试证明此时衍射图形中央亮斑半角宽度为:
∆θ ≈
λ0
2 a n2 − n12 sin 2 β
1 ○ ∑屏沿 ξ 轴平移,但不超出入射光照明范围; 屏沿 轴平移,但不超出入射光照明范围;
回答: ∑平移等价于光源 S 平移; ∑平移,衍射图形随之平移。 平移, 回答: 平移等价于光源 平移; 平移 衍射图形随之平移。
2 ○ ∑屏绕 z 轴旋转; 屏绕 轴旋转;
(3) 光源 S: :
1 是点光源, 方向有一移动; 方向平移,结果又如何?) ○ S 是点光源,但沿 x 方向有一移动; 若 S 沿 y 方向平移,结果又如何?) (
