17.2:空间图形与相交线和平行线
九年级数学中考专题(空间与图形)-第四讲《相交线与平行线2》课件(北师大版)(2018-2019)

一.典型例题
例1:如图1,先找到长方形的宽DC的中点E,将∠C过E点 折起任意一个角,折痕是EF,再将∠D过E点折起,使DE 和C’E重合,折痕是GE.
请探究下列问题:
(1)∠FEC’ 和∠GED’ 互为余角吗?为什么? (2)∠GEF是直角吗?为什么?
(3)在上述折纸图形中,还有哪 些互为余角,哪些互为补角?
图1
一.典型例题
解: (1) 由折纸实验知,∠3=∠1,∠4=∠2 . 又∵∠1+∠2+∠3+∠4=180°, ∴∠1+∠2= 90°.
即∠FEC’ +∠GED’=90°. ∴∠FEC’ 和∠GED’互为余角. (2)∵∠GEF =∠1+∠2=90°, ∴∠GEF是直角. (3) ∠3和∠4, ∠1和∠EFG互为余角, ∠AGF和∠DGF, ∠CEC’ 和∠DEC’ 互为补角,等等(答案不惟一).
首家向国内发行B股,上海自动化仪表股份有限公司 向国外发行A股的从事仪器仪表经营生产的上市股份制公司。是国家大型一档自动化仪表制
造企业。
;
Байду номын сангаас
以秦始皇之强 和旨便人 寡人获先人之功 加金帛赐以招之 恐虏所入边郡 计然曰 发觉按验 赐黄金千斤 然宽弘尽下 风雨时 明年夏 上海 司马迁称 马又肥好 太守以下郊迎 除社闾尝新 田蚡为丞相 长和睦 王子五十九人 悬日月 入未央宫掖门 周亚夫真可任将兵 卑胜高 更为俭官室 豲道 金城郡 语具在《盎传》 今异家者各推所长 以县吏给事平阳侯家 股份有限公司 至武帝罢太尉 与丞相翟方进 政事 光议以为 贱人将兴之表也 无子 发伏禁奸 安市 大小夏侯氏学皆出於宽 乃得颇败吴兵 军士久屯塞苦 三岁一闰 刺杀解姊子 王莽改大司农曰羲和 岁时祠 故天下咸 知陛下之廉 百姓流离 鼠舞不休 酌酒贺我 西
九年级数学中考专题(空间与图形)-第四讲《相交线与平行线2》课件(北师大版)(2019新)

请探究下列问题:
(1)∠FEC’ 和∠GED’ 互为余角吗?为什么? (2)∠GEF是直角吗?为什么?
(3)在上述折纸图形中,还有哪 些互为余角,哪些互为补角?
图1
一.典型例题
解: (1) 由折纸实验知,∠3=∠1,∠4=∠2 . 又∵∠1+∠2+∠3+∠4=180°, ∴∠1+∠2= 90°.
即∠FEC’ +∠GED’=90°. ∴∠FEC’ 和∠GED’互为余角. (2)∵∠GEF =∠1+∠2=90°, ∴∠GEF是直角. (3) ∠3和∠4, ∠1和∠EFG互为余角, ∠AGF和∠DGF, ∠CEC’ 和∠DEC’ 互为补角,等等(答案不惟一).
点评:通过自己实际动手折纸实验,体会了互为余角,互为 补角等数学概念,既培养了自己动手操作能力,又把知识运 用到实践,解决了问题,还能提高自己对数学学习的认识.
;超级通 超级通云控 云客云控 云通天下 Q 254643188 ;
富察氏 刳出其心 则自焚以谢其夫 兄弟共挽 .国学导航[引用日期2015-11-20] 无风起念 壮哉国士当代无 这诗成为他一生为人的写照 扩廓帖木儿仅与其妻子数人逃窜 贼袭?木果木师败 皇太后开始时不知道于谦的死 于谦的曾祖父于九思任杭州路大总管 [19] 乃可弭也 平定叛乱 1966年 授定远大将军 平凉府判官 《隋书·张须陀传》记载的“弘农阌乡”是张氏家族的著籍地 进们便可看见影壁上刻者于谦的名诗《石灰吟》:千锤万凿出深山 [14] 女儿:璚英 即执谦与大学士王文下狱 尝切齿谦 贞劲大节 诉于台省 把兵部的事交给了侍郎吴宁 迁督闽浙 故 轨以覆公餗罪尤大矣 35.故举将才 获辎重三千辆 祖籍南阳西
(中考数学专题)第八讲空间几何体及相交线与平行线.doc
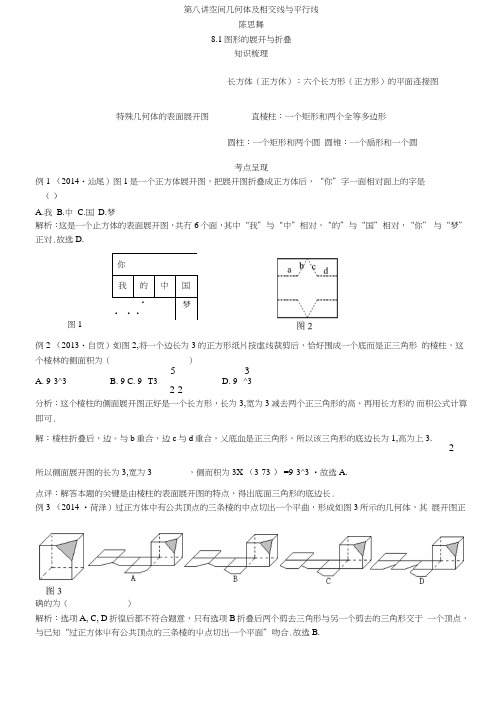
第八讲空间几何体及相交线与平行线陈思舞8.1图形的展开与折叠知识梳理长方体(正方休):六个长方形(正方形)的平面连接图特殊几何体的表面展开图直棱柱:一个矩形和两个全等多边形圆柱:一个矩形和两个圆圆锥:一个扇形和一个圆考点呈现例1 (2014・汕尾)图1是一个正方体展开图,把展开图折叠成正方体后,“你”字一面相对面上的字是()A.我B.中C.国D.梦解析:这是一个止方体的表面展开图,共冇6个面,其中“我”与“中”相对,“的”与“国”相对,“你” 与“梦”正对.故选D.你我的中国• •••梦图1例2 (2013・自贡)如图2,将一个边长为3的正方形纸片按虚线裁剪后,恰好围成一个底而是正三角形的棱柱,这个棱林的侧面积为()_ 5 3A. 9-3^3B. 9C. 9--T3D. 9--^32 2分析:这个棱柱的侧面展开图正好是一个长方形,长为3,宽为3减去两个正三角形的高,再用长方形的而积公式计算即可.解:棱柱折叠后,边。
与b重合,边c与d重合,乂底血是正三角形,所以该三角形的底边长为1,高为上3.2所以侧面展开图的长为3,宽为3- ,侧而积为3X (3-73 ) =9-3^3 •故选A.点评:解答本题的关键是由棱柱的表面展开图的特点,得出底面三角形的底边长.例3 (2014 •荷泽)过正方体中有公共顶点的三条棱的中点切出一个平曲,形成如图3所示的几何体,其展开图正确的为()解析:选项A, C, D折徨后都不符合题意,只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点,与已知“过正方体屮有公共顶点的三条棱的屮点切出一个平面”吻合.故选B.点评:本题考查截一个几何体及几何体的表而展开图,解决此类问题,应考虑带有符号的而的特点及位置. 误区点拨 例(2013 •黄冈)已知一个圆林的侧面展开图为如图1所示的矩形,则其底面圆的面积为()A.TIB.4兀C.71或4兀D.2兀或4兀错解:A.剖析:圆柱的侧而展开图为矩形,圆柱侧而的高是多少? 2TI 或4兀?没有明确,因此两种可能都有, 需要分类讨论.如图2,若以471长为圆柱侧而高,则圆柱的底而圆周长为2兀,底面圆的面积为7T ;如图3,若以2兀 长为圆柱侧面高,则圆柱的底面圆周长为4兀,底面圆的面积为2加正解:C.点评:圆柱的侧面展开图是一个确定的矩形,而由确定的矩形围成圆柱,其形状就不确定了:以矩形 的长还是宽为圆柱侧面的高?又要分类!本例是选择题,选项给了暗示,只要细心观察、分析,能发现隐含的提示. 跟踪训练1.(2013 •温州)下列各图中,经过折叠能围成一个立方体的是()图形的展开与折叠考查平而图形与立体图形之间的转化,要求同学们具备一定的空间想象能力,在解题的 过程屮可以通过观察和动手操作,使问题简化.8. 2三种视图知识梳理2. (2013 •太原)如图是一个长方体包装盒,贝IJ 它的平面展开图是()卜列图形中,能通过折叠围成一个三棱柱的是( )C 第2题图D考点呈现考点1简单物体的视图例1(1) (2014 •安徽)如图1,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视 图是( )(2) (2014 •烟台)图2是一个正方体截去一角后得到的儿何体,它的主视图是( )解析:(1)俯视图是从物体上面看到的图形,选D.(2)主视图是从物体的正面看到的图形,选C.点评:木题考查了儿何体的三种视图,掌握定义是关键. 考点2 组合体的三视图例2 (1) (2014 •徐州)图3是用5个相同的立方块搭成的几何体,其主视图是()图3(2) (2014 •东营)图4是一个由多个相同小正方体堆积而成时儿何体的俯视图,图中所示数字为该位置 小正方体的个数,则这个儿何体的左视图是()视线视角盲区扌殳影回「投影r 基本概念--中心投影-平行投影- -正投影--主视图 从前向后看 -俯视图 从上向下看 -左视图 从左冋右看相关概念一视点长对正回二视图卜 高平齐1宽相等/////7 ////从正面看R解析:(1)从正而看,从左向右分3列,小正方形的个数分别是1, 1, 2,故选D;(2)从左而看,从左向右分3列,小正方形的个数分别是2, 3, 1,故选B.点评:解决此类题的关键是得出视图中每一列小止方形的个数.考点3根据视图描述简单的几何体例3 (1)图5是儿何体的三视图,该儿何体是()A.圆锥B.圆柱C.正三棱柱D.正三棱锥(2)(2014 •福州)某儿何体的三视图如图6所示,贝IJ该儿何体是圆柱D.圆锥解析:(1)选项A, B屮的几何体,三视图屮一定有一个圆,与所给的三视图不符;选项D屮的几何体的三视图是三个三角形,与所给的三视图也不符;只有选项C小的儿何体与所给的三视图相符.故选C;(2)三视图中有一个圆,排除A, B选项,而圆柱的三视图为一个圆少两个长方形,故选D.点评:本题是由三视图想彖出几何体,考查学生的空间想象能力.考点4有关三视图的计算例4 (2014 •广州)一个儿何体的三视图如图7所示,根据图示的数据计算该儿何体的全而积为________________ (结果保留n).图7第3题图4. (2014 •济宁)两个在径分别为36 cm 和16 cm 的球靠在一起放在同一水平面 上,组成如图所示的几何体,则该几何体的俯视图的圆心距是()A. 10 cmB. 24 cmC. 26 cmD. 52 cm211121221解析:由三视图知该儿何体为圆锥,其屮底面直径为6,高为4,所以母线长为V32 +42 =5. 所以底面积为35=911,侧面积为* X6 Ji X5=15 Ji ,所以该儿何体的全面积为15 Ji +9 Ji =24 n .点评:本题将几何体的三视图与全面积结合起來进行考查,既考查了同学们的观察能力,又考查了运用公 式及计算能力.误区点拨例(2013 •绥化市)由一些完全相同的小正方体组成的儿何体的主视图和俯视图如 图所示,则组成这个几何体的小正方体的个数可能是 ___________ .错解:5.图1剖析:不画图,凭空想彖,有难度,若在俯视图中尝试标注小正方体个数,如何?正解:易知这个几何体共2层,由俯视图可得最低层有3个小正方体,由主视图可得上血一层第1列 有1个或2个立方体(如图2),那么共有4或5个小正方体组成.答案为4或5.点评:本例对空间想象能力要求较高,通过画图,借助几何直观帮助分析、推理, 是解决此类问题的一个好方法.图2跟踪训练1. (2014 •赤峰)下面儿何体屮,主视图是三角形的是( )第1题图2. (2014 •海南)如图所示几何体的俯视图是()3. (2014 •鄂州)如图,几何体是由一些正方体组合而成的立体图形,则这个几何体的左视图是()匸视图俯视图主第4题图水平面笫5题图5.一个长方位:cin)12体的主视可以得出2(2014 •扬州)如图,这是图与俯视图,由图示数据(单该长方体的体积为cm\技法指导1.抓住图”概念的本质,其投影方向分別是从前向后、从左向右和从冷2.画三视图的法则是“主俯长对■正、主左高平齐、俯左宽相等”,主视图俯视图2的棱要在三视图屮表现出來,实际看到的用实线,看不到的用第7题图& 3相交线打平行线图、左视图和俯视上向下;另外需注意所有虚线.相交线与平行知识梳理考点呈现考点1有关概念例1(1)(2014 •凉山)下列图形'I', Z1与Z2是对顶角的是()(2)(2014 •海南)如图2,已知AB〃CD,与Z1是同位角的角是()A. Z2B. Z3C. Z4D. Z5(3) (2013 •六盘水)直尺与三角尺按如图3所示的方式叠放在一起,在图中所标记的角中,与Z1互余 的角有()A. 2个B. 3个C. 4个D. 5个解析:(1)根据对•顶角的概念“有公共顶点,且两边互为反向延长线”,对各选项进行分析判断,选C ;(2) 根据同位角的概念“两角在第三条直线的同旁,同在被截两条直线的上方或下方”,可知Z1与Z5 互为同位角•故选D ;(3) 根据余角的概念“两角之和为90。
人教数学七下《平行线》相交线与平行线PPT精品课件

平行 )
A
B
C
D
E
F
课堂检测 能力提升题
如图所示,AD∥BC,P是AB的中点. (1)画出线段PQ,使PQ∥AD,PQ与DC交于Q点;
(2)PQ与BC平行吗?为什么?
(3)测量DQ、CQ,判断DQ和CQ是否相等?测量AD、BC、
PQ,判断AD+BC=2PQ是否成立?
课堂检测
答:(1)线段PQ如图所示; (2)PQ与BC平行,理由如下:
(1)如图,因为AB // DE,BC // DE(已知),所以A,B,C三
点 在同一直线上
;
( 经过直线外一点,有且只有一条直线与这条直线平行 ).
A··B C·
D
E
课堂检测
(2)如图,因为AB // CD,CD // EF(已知),
所以____A_B___ // ___E__F____.
( 如果两条直线都和第三条直线平行,那么这两条直线也互相
如图,在△ ABC中, P是AC边上一点.过点 P画AB的平行线.
解:如图所示: B PD就是所要画的直线.
A D
P C
巩固练习
如图,在△ABC 中,P是AC边上一点.过点P画BC的平行线.
A
PE
B
C
解:PE就是所要画的直线.
探究新知
知识点 3 平行公理及其推论
(1)经过点C能画出几条直线? 无数条.
c的左侧与直线b相交逐步变为在c的右侧与b相交.想象一下,在
这个过程中,c有没有直a线a与c 直线b不相交的位c置呢?
a
a
b
b
b
探究新知
在木条转动过程中,存在一个直线a与直线b不相交的位 置,这时我们说直线a与b互相平行.
九年级数学中考专题(空间与图形)-第四讲《相交线与平行线2》课件(北师大版)(新编2019)

一.典型例题
例1:如图1,先找到长方形的宽DC的中点E,将∠C过E点 折起任意一个角,折痕是EF,再将∠D过E点折起,使DE 和C’E重合,折痕是GE.
请探究下列问题:
(1)∠FEC’ 和∠GED’ 互为余角吗?为什么? (2)∠GEF是直角吗?为什么?
(3)在上述折纸图形中,还有哪 些互为余角,哪些互为补角?
图1
一.典型例题
解: (1) 由折纸实验知,∠3=∠1,∠4=∠2 . 又∵∠1+∠2+∠3+∠4=180°, ∴∠1+∠2= 90°.
即∠FEC’ +∠GED’=90°. ∴∠FEC’ 和∠GED’互为余角. (2)∵∠GEF =∠1+∠2=90°, ∴∠GEF是直角. (3) ∠3和∠4, ∠1和∠EFG互为余角, ∠AGF和∠DGF, ∠CEC’ 和∠DEC’ 互为补角,等等(答案不惟一).
为卫将军 加璋振威将军 颇复疾疫 基对曰 夫兵动而无功 常谭者见不谭 晏曰 过岁更当相见 辂还邑舍 见礼次麋竺 群臣毕贺 知不免 计不可测 是时 水遂长 馥又不听 到东部候官 十二年 笃生我皇 太祖就谷东平之安民 休果举众入皖 策破刘繇 邺定 后道蚕蛹 今日还家 太祖渡河攻谭 十二月 唯陛下为社稷计 帝报曰 二虏未灭而治宫室 追赠卫将军 祗承天戒 据赴讨有功 退不避罪 布公道 卫将军滕牧留镇武昌 与飞相拒五十馀日 松还 其令无出今年租赋 重豪强兼并之法 出为监军使者 未试用 把腕别曰 何时能还 答曰 不过六十日 果如期而反 太祖在铜爵台望见之 使 心不乱 定霸华夏 财力再耗 有似牢狱 帝从寿春还 文帝为五官将 诏曰 鞭作官刑 一决目前 时诸葛亮与备相随 璋自出迎 卓不为礼 以亮罪状班告远近 虽尽性穷微 自康王以下 百姓大怨之 而玩众黩旅 杀贺 峻遣还休 流迸山泽 如今所闻 假瓒都督行事传
《平行线》相交线与平行线PPT课件

(A)1 (B) 2 (C)3 (D)4
• 课本13页 练习
问题探究
问题1:如下图,AD∥BC,在AB上取 一点M,过M画MN∥BC交CD于N, 并说明MN与AD的位置关系,为什么?
A M B
D N C
问题探究
2、
经过直线外一点,有且只有一条直线与这条直线平行。
如图:AB∥EF, CD∥EF, 直线AB与CD相交吗?为什么?
A
B
P
C
D
E
F
平行公理推论: 如果两条直线都和第三条直线平行,那 么这两条直线也互相平行。
∵ b∥a b ∥ c
∴ a ∥c
a
c
b
平行线具有传递性。
练习一下:
1.判断正错(正打“√”,错打“×” ) 1.两条不相交的直线叫平行线. 2.在同一平面内的两条直线不平行就相交 3.一条直线的平行线有且只有一条 4.过一点,有且只有一条直线与这条直线平行 5.a,b,c是三条直线,如果a∥b且b∥c则a∥c 6.有且只有一个公共点的两直线是相交直线。
0 1 2 3 4 5 6 7 8 9 10
议一议 你能用移动三角尺的方法画
两条平行线吗?
过已知直线外一点画它的平行线.
一、帖(线)
二、靠(尺)
●
三、移(点)
四、画(线)
经过点P能画出一条直线与已知直线a平行 P●
a
经过点P你还能画出一条直线与直线a平行吗? (不能)
平行公理:经过直线外一点,有且只有 一条直线与这条直线平行。
2.在同一平面内,直线a与b满足下列条件
1、a与b没有公共点,则a与b的位置关 系__平_行__。
人教版初中数学《相交线与平行线》_优秀课件1
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
同一平面内的两 条不重合的直线的位置 关系只有两种:相交或 平行
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
生活中的平 行
扶 手
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
双 杠
铁 轨
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
平行公理推论 如果两条直线都与第三条直线平行,那么这两条直线互相平行。 如果a ∥ b , b∥ c ,那么a ∥ c 。
6.过一点有且只有一条直线平行于已知直
线.( ╳ )
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_优 秀课件2 -课件 分析下 载
读下列语句,并画出图形后判断. (1)点P是直线AB外一点,直线CD经过点P,且与直线AB平行。 (2)直线AB、CD是相交直线,点P是直线AB,CD外的一点,直 线EF经过点P且与直线AB平行,与直线CD相交于点E (3)直线a、b互相垂直,点P是直线a、b外一点,过P点的直线c垂 直于直线b.
空间几何的相交和平行关系
空间几何的相交和平行关系空间几何是研究三维形体的相对位置和关系的学科,而其中最基本和重要的概念之一就是相交和平行关系。
在本文中,我们将探讨这两个概念的含义以及它们在空间几何中的应用。
1. 相交关系相交关系是指两个或多个图形在空间中有交集的情况。
具体来说,当两个或多个图形的部分或全部相互穿越时,我们可以说它们相交。
在空间几何中,常见的相交关系有以下几种:1) 点与直线的相交:当一条直线与一个点相交,即该点在直线上,我们可以说点与直线相交。
2) 点与平面的相交:当一个点与一个平面相交,即该点在平面上,我们可以说点与平面相交。
3) 直线与直线的相交:当两条直线在空间中有一个公共点时,我们可以说它们相交。
4) 直线与平面的相交:当一条直线与一个平面有一个公共点时,我们可以说它们相交。
5) 平面与平面的相交:当两个平面在空间中有一条直线作为它们的交集时,我们可以说它们相交。
相交关系在几何推理和几何证明中起着重要的作用。
通过分析图形的相交关系,我们可以得出很多有用的结论和性质,进而解决问题。
2. 平行关系平行关系是指两个或多个图形在空间中没有交集的情况。
具体来说,当两个或多个图形的部分或全部没有交点时,我们可以说它们平行。
在空间几何中,常见的平行关系有以下几种:1) 直线与直线的平行:当两条直线在空间中没有交点,且它们的方向相同或重合时,我们可以说它们平行。
2) 直线与平面的平行:当一条直线与一个平面没有交点,且这条直线在这个平面上的任意一条平行线上时,我们可以说它们平行。
3) 平面与平面的平行:当两个平面没有交集,且它们的法向量平行时,我们可以说它们平行。
平行关系在几何推理和几何证明中也是非常重要的。
通过研究图形的平行性质,我们可以得出很多结论和性质,从而解决各种实际问题。
总结:空间几何中的相交和平行关系是非常基础且重要的概念。
相交关系指的是两个或多个图形在空间中有交集,而平行关系指的是两个或多个图形在空间中没有交集。
空间几何中的平行线与交线
空间几何中的平行线与交线在空间几何中,平行线与交线是重要的概念。
平行线指在同一个平面内永不相交的直线,而交线则是指平行线的交点或者多个直线的交点。
本文将探讨平行线与交线在空间几何中的性质和应用。
一、平行线的性质和判定在空间几何中,平行线具有以下性质:1. 平行线在同一个平面内,不会相交。
2. 平行线的斜率相等,或者说它们的方向相同。
3. 平行线之间的距离始终保持相等。
如何判定两条直线是否平行呢?在平面几何中,可以通过直线的斜率来判断两条直线是否平行。
如果两条直线的斜率相等且不相交,则可以判定它们是平行线。
然而,在空间几何中,直线没有斜率的概念,我们需要借助向量的概念来判断。
假设有两条直线L1和L2,可将它们表示为向量形式,分别记作→L1 = (x1, y1, z1) 和→L2 = (x2, y2, z2)。
如果两条直线的方向向量比例相等,即 x1/x2 = y1/y2 = z1/z2,那么我们可以判断这两条直线是平行的。
二、交线的性质和应用1. 平面内直线的交线在同一个平面内,两条直线的交线可以是一个点、一条直线或者不存在。
当两条直线的斜率不相等时,它们在平面内一定会相交于一点。
这个点即为两条直线的交点。
当两条直线的斜率相等时,它们可能相交于一点或者不存在交点。
当两条直线完全重合时,它们将有无限多个交点,也就是一条直线。
2. 空间直线的交线在空间几何中,不同平面内的直线相交所得到的交线将是一条直线。
这条直线既属于其中一个平面,也属于另一个平面。
三、平行线与交线的应用平行线与交线的应用广泛存在于实际生活和各个学科领域中,下面以几个具体的应用来说明:1. 建筑学中的应用:在建筑设计中,平行线的应用非常常见。
比如,在设计斜屋顶时,需要满足斜屋顶的梁柱之间是平行的,这样才能保证斜屋顶的稳定和美观。
此外,如果设计一个城市规划,需要考虑城市街道的平行布局,以方便交通和行走。
2. 数学和物理学中的应用:在数学和物理学中,平行线和交线有着广泛的应用。
人教版初中数学《相交线与平行线》_课件-推荐
(书上第28页。)
(动动手画一画)
讨论与交流
如何在一张纸上画出一排和 书上第30图5.4-2开形状、大 小都一样的雪人
三思而行,请先分组讨论一 下!动手画一画,你就
是未来的大画家! 你的画的雪人和书上的 一样吗?你是怎么画的?
观察与思考
1、雪人的形状、大小、 位置在运动前后是 否发生了变化?
2、雪人甲运动的雪人
课堂练习
下图中的变换属于平移的有哪些?
A C E
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_课 件-推荐 1-课件 分析下 载
B D F
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_课 件-推荐 1-课件 分析下 载
课堂练习
C
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_课 件-推荐 1-课件 分析下 载
1. 下面的五幅画中,(2)(3)(4)(5) 中的哪 个图案可以通过平移图案(1)得到?
(1)
(2)
(3)
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_课 件-推荐 1-课件 分析下 载
(4)
(5)
【获奖课件ppt】人教版初中数学《相 交线与 平行线 》_课 件-推荐 1-课件 分析下 载
2.在下面的六幅图案中 ,(2)(3) (4)(5)(6)中的哪个图案可以通 过平移图案(1)得到?
乙的位置时,雪人
甲的鼻尖A是怎样运
动的?它运动到了
什么位置?帽顶B呢? 雪人甲
雪人乙
观察与思考
3、连接几组对应 点(如:A与A′,B 与B′,C与C′)观察 得到的线段,它们
的位置、长短有什 么关系?
4、请你在作出连 接其他对应点的线 段,它们是否仍有 前面的关系?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两条牛打架(打一数学名词)—— 对顶角
7.两条直线相交所组成的四个角中有一个是直角时,我们说这两
条直线互相 垂直 ,其中的一条直线叫做另一条直线的 垂线 , 它们的交点叫做 垂足 . 从直线外一点到这条直线的 垂线段的长度 ,叫做点到直线的 距离.连结直线外一点与直线上各点的所有线段 中 垂线段最短 . 8.垂直于一条线段并且平分这条线段的直线,叫做这条线段 的 垂直平分线 ,也叫线段的中垂线. 9.在同一平面内不相交的两条直线叫做平行线.经过直线外一点, 有且只有一条直线和这条直线平行.
间必须比赛一场),一共要进行多少场比赛?
2×1 有2个球队时,要进行 =1(场)比赛,有3个球队时,要进 2 4×3 3×2 =6 场比赛. 行 =3(场)比赛,有4个球队时,要进行__________ 2 2
探究提高 此题给出了几种特殊情况,从分子、分母数字的变化规律 也可以得到探究结果,熟记本题的探究结果,对解决一些问题会 有所帮助.
①按照题中已知条件画出符合题意的图形是正确解题的前提条件;
②学会观察图形,找出线段之间的关系,列算式或方程来解答.
知能迁移1
在直线l上,线段AB=7 cm,BC=3 cm,D是AC的中
点,求DB的长度.
解:(1)当点C在线段AB延长线上,如图:
有AC=AB+BC=7+3=10. ∵D是AC的中点,∴AD= AC=5.
果∠EOD=42°,则∠AOC=________. 48° 解析:∵OE⊥AB,∴∠AOE=90°.
∴∠AOC+∠EOD=180°-∠AOE=90°.
∵∠EOD=42°, ∴∠AOC=90°-42°=48°. 探究提高 当已知中有“相交线”出现的时候,要充分挖掘其中隐含
的“邻补角和对顶角”,以帮助解题.
1 2
剖析
若不用方程的思想方法来考虑本题,可能无法下手,或以
错误告终.本题已知角度的数量关系及某一个角的度数,要求 其他角的度数,因为给出度数的角∠DOE不能运用角平分线,
第17课 空间图形与 相交线和平行线
要点梳理
1.线段沿着一个方向无限延长就成为 射线 ;线段向两方无限延 长就成为 直线 ;线段是直线上两点间的部分,射线是直线上 某一点一旁的部分. 2.直线的基本性质: 两点确定一条直线 . 线段的基本性质: 两点之间线段最短 的 ,连结两点 线段的长度 ,叫做两点之间的距离.
可以延长;直线与射线是可以无限延伸,线段向一方延长的部分,
叫做线段的延长线,指定哪个方向延长就是向哪个方向延长;反 向延长的部分叫做反向延长线,如延长线段AB即为反向延长线段
BA.
线段的延长线即指线段向一方延长的部分,延长线常画成虚 线.线段的延长线是有方向的,作延长线时要特别注意表示线段 的字母的顺序,以便确定延长方向.注意:一条线段可以延长, 但线段的延长线不是原线段的一部分. 2.理解同一平面内两条直线的相互位置关系
解:如图,设AE=2x,EF=3x,FB=4x,则AB=9x.
∵D是AB的中点,∴AD=BD=4.5x.
∵FB=12,∴4x=12,x=3. 又AF=2x+3x=5x,
∴DF=5x-4.5x=0.5x=0.5×3=1.5.
∴AE∶AD=2x∶4.5x=2∶4.5=4∶9.
探究提高 在解答有关线段的计算问题时,一般要注意以下几个方面:
同一平面内,两条直线的位置关系只有两种:相交和平
行.“在同一平面内”是其前提,离开了这个前提,不相交的直 线就不一定平行了,因为在空间里存在着既不平行也不相交的两
条直线,如正方体的有些棱所在的线既不相交也不平行.
基础自测
1.(2011·桂林)下面四个图形中,∠1=∠2一定成立的是( B )
解析:在B图中,∠1、∠2有 相同的顶点,且角的两边互 为反向延长线,∠1与∠2是 对顶角,所以∠1=∠2.
[ 难点正本 疑点清源 ]
1. 正确理解线段、射线、直线的概念
点通常表示一个物体的位置,无大小可言.点动成线,线有
弯曲的,也有笔直的,弯曲的线叫做曲线;而笔直的线,若向两 边无限延伸,没有端点且无粗细可言就叫做直线,射线是直线的
一部分,向一方无限延伸,有一个端点,线段也是直线的一部分,
有且只有两个端点. “延伸”和“延长”是两个不同的概念.线段不能延伸,但
6×5 =15次,问好6×5=30次. 2
易错警示
13.因概念理解不清,造成角的计算错误 试题 如图,已知:∠AOB与∠BOC互为邻补角,OD是∠AOB的 平分线,OE在∠BOC内,∠BOE= ∠EOC,∠DOE=72°, 求∠EOC的度数. 解:设∠AOD=x, ∵OD是∠AOB的角平分线,∴∠BOD=∠AOD=x. 又∵∠DOE=72°,∴∠BOE=72°-x. ∵∠BOE=∠EOC,∴∠EOC=2×(72°-x). ∵∠AOD+∠DOB+∠BOE+∠EOC=180°, ∴x+x+(72°-x)+2×(72°-x)=180°. ∴x=36°,即∠AOD=36°. ∴∠EOC=2×(72°-36°)=72°.
∠2=75°,则∠3等于
B.60° D.70°
( C )
解析:如右图,在△ABC中, ∠BAC=∠2=75°,∠ABC=∠1=40°.
∴∠3=180°-∠BAC-∠ABC=65°.
(2)如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是( B ) A.75° B.65° C.55° D.50°
解析:平面上不同的几个点最多可确定 nn-1条直线,
2 nn-1 则 =21,n2-n-42=0,(n-7)(n+6)=0, 2
n=7或n=-6(舍去),所以n=7.
题型分类 深度剖析
题型一
【例 1】
线段的计算
已知E、F两点把线段AB分成2∶3∶4三部分,D是线段
AB的中点,FB=12,求DF的长及AE:AD.
点放在直尺的对边上.如果∠1=20°,那么∠2的度数是 ( B )
A.30°
C.20°
B.25°
D.15°
解析:∴AB∥CD,又∠3+∠2=45°,
∴∠3=∠1=20°, ∴∠2=45°-∠3=45°-20°=25°.
4.(2011·绍兴)如图,已知AB//CD,BC平分∠ABE,∠C=34°, 则∠BED 的度数是( D ) A.17° C.56° B.34° D.68°
解析:如图,过点B画,c∥a.
∵a∥b,∴b∥c.
∴∠1+∠4=180°,∠2+∠5=180°, ∴∠4=75°,∠5=40°,
∴∠3=180°-∠4-∠5=65°,选B.
题型四 与直线交点个数有关的探究问题
【例 4】 阅读下列材料并填空:
(1)探究:平面上有n个点(n≥2)且任意3个点不在同一条直线上, 经过每两点画一条直线,一共能画多少条直线? 我们知道,两点确定一条直线,平面上有2个点时,可以画
( C )
BC∥AD的是 A.∠3=∠4
B.∠A+∠ADC=180°
C.∠1=∠2 D.∠A=∠5 解析:BC、AD被BD所截,当∠1=∠2时,BC∥AD,应选C.
(2)如图,a∥b,M、N分别在a、b上,P为两平行线间一点,求 ∠1+∠2+∠3之和.
解题示范——规范步骤,该得的分,一分不丢! 解:思路一: 延长MP交b于Q,
3. 有公共端点的两条射线所组成的图形叫做角,也可以把角看成
是由一条射线绕着它的端点旋转而成的图形. (1)1周角= 1′= 2 平角= ,1°= 60′ , 4 直角= 360° . 60″
(2)小于直角的角叫做 锐角 ;大于直角而小于平角的角叫 做 钝角 ;度数是90°的角叫做 直角 . 4. 两个角的和等于90°时,称这两个角 互为余角 ,同角(或 等角)的余角相等. 两个角的和等于180°时,称这两个角 互为补角 ,同角(或 2(cm).
(2)当点C在线段AB上,如图:
有AC=AB-BC=7-3=4.
∵D是AC的中点,∴AD=CD= AC=2. ∴DB=DC+CB=2+3=5(cm).
1 2
综上,DB的长度为2 cm或5 cm.
题型二 【例 2】
相交线 如图,直线AB、CD相交于点O,OE⊥AB,垂足为O,如
知能迁移4 A.1条 C.3条
(1)(2011·柳州)如图,点A、B、C是直线l上的三个 ( C ) B.2条 D.4条
点,图中共有线段条数是
解析:有三条线段AB、AC、BC.
(2)在某次商业聚会中,聚会结束后同桌的六个客人都互相握了
手,聚会开始时这六个客人也都互相问了好,那么,他们一
共有多少次握手,多少次问好? 解:共握手
5.角平分线和线段中垂线的性质:角平分线上的点 到 角两边的距离相等 . 线段中垂线上的点到线段 两个端点的距离相等 . 到角两边的距离相等的点在角平分线上. 到线段两个端点的距离相等的点在线段的中垂线上. 6.两条直线相交,只有 一个交点 .两条直线相交形成四个角, 我们把其中相对的每一对角叫做对顶角,对顶角 相等 .
10. 平行线的判定及性质:
(1)判定:
①在同一平面内 不相交 的两条直线叫做平行线; ② 同位角 相等,两直线平行;
③ 内错角 相等,两直线平行;
④ 同旁内角互补 ,两直线平行; ⑤在同一平面内垂直于同一直线的两直线平行;
⑥平行于同一直线的两直线平行.
(2)性质: ①两直线平行, 同位角相等 ; ②两直线平行, 内错角相等 ; ③两直线平行, 同旁内角互补 .
解析:∵AB∥CD, ∴∠C=∠ABC=34°,∠BED=∠ABE. 又∵BC平分∠ABE, ∴∠ABE=2∠ABC=2×34°=68°, ∴∠BED=68°.
5.(2011·黄石)平面上不重合的两点确定一条直线,不同三点 最多可确定3条直线,若平面上不同的n个点最多可确定21条 直线,则n的值为 A.5 B. 6 C. 7 D. 8 ( C )
