崇雅中学初中部2013-2014学年八年级下月考数学试卷(二)

合集下载

2013-2014学年八年级下月考数学试卷(二)

八年级第二学期数学段考（二）说明：1．全卷共4页，考试时间为100分钟，满分为120分。

2．用黑色字迹的钢笔或签字笔答题。

答案按各题要求写在答题卷上。

3、不能使用计算器。

一、选择题（共10小题，每题3分，共30分）1、若二次根式1-x 1-x 有意义，则x 的取值范围是( ) A ．x ≥1 B ．x ≤1 C ．x ＞1 D ．x ≠12、甲、乙两个样本的容量相同，甲样本的方差为0.102，乙样本的方差是0.06，那么（）．A ．甲的波动比乙的波动大B ．乙的波动比甲的波动大C ．甲、乙的波动大小一样D ．甲、乙的波动大小无法确定3、函数1+=x y 的图象上有两点),1(1y A 、),2(2y B -，那么下列结论正确的是（）A.21y y <B.21y y >C.21y y =D.1y 与2y 之间的大小关系不能确定4、下列各组数中，不能构成直角三角形的是（）A 、4，5，3B 、1，1，2C 、6，8，10D 、5，12，135、已知直线y=2x+1与直线 y=－x+4.则它们的交点是（）A ．（1，0）B ．（1，3）C ．（－1，－1）D ．（－1，5）6 ）A 、、、37、下列说法不正确的是（）A 、 3a 不是分式 B 、三边长比是3：4：5的三角形是直角三角形 C 、对角线相等的平行四边形是矩形 D 、数据3，2，1，3，4的中位数是18、函数y=－X+1的图象不经过（）A 、第一象限B 、第二象限C 、第三象限D 、第四象限9、服装销售商在进行市场占有率的调查时，他最应该关注的是（）A ．服装型号的平均数B ．服装型号的众数C ．服装型号的中位数D ．最小的服装型号10、平行四边形ABCD 的对角线交于点O ，有五个条件：①AC=BD ，②∠ABC=90°，③ AB=AC ， ④ AB=BC ， ⑤ AC ⊥BD ，则下列哪个组合可判别这个四边形是正方形（）A ．① ②B ．① ③C ．① ④D ．④ ⑤二、填空题（共6小题，每题4分，共24分）11、写出一个图象在二、四象限的正比例函数的解析式。

八年级6月月考数学试题及答案.docx

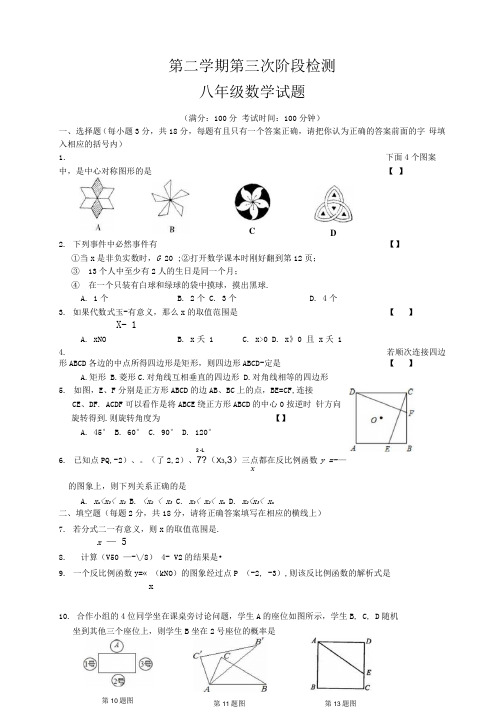
第二学期第三次阶段检测八年级数学试题（满分：100分考试时间：100分钟）一、选择题（每小题3分，共18分，每题有且只有一个答案正确，请把你认为正确的答案前面的字母填入相应的括号内）1.下面4个图案中，是中心对称图形的是【】C D2.下列事件中必然事件有【】①当x是非负实数时，G20 ;②打开数学课本时刚好翻到第12页；③13个人中至少有2人的生日是同一个月；④在一个只装有白球和绿球的袋中摸球，摸出黑球.A. 1个B. 2个C. 3个D. 4个3.如果代数式玉-有意义，那么x的取值范围是【】X- 1A. xNOB. x夭 1C. x>0D. x》0 且 x夭 14.若顺次连接四边形ABCD各边的中点所得四边形是矩形，则四边形ABCD-定是【】A.矩形B.菱形C.对角线互相垂直的四边形D.对角线相等的四边形5.如图，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF,连接CE、DF. ACDF可以看作是将ABCE绕正方形ABCD的中心0按逆时针方向旋转得到.则旋转角度为【】A. 45°B. 60°C. 90°D. 120°2 -L6.已知点PQ,-2）、。

（了2,2）、7?（X3,3）三点都在反比例函数y =-—X的图象上，则下列关系正确的是A. x x<x3< x2B. <x2 < x3C. x3< x2< x xD. x2<x3< x x二、填空题（每题2分，共18分，请将正确答案填写在相应的横线上）7.若分式二一有意义，则x的取值范围是.x— 58.计算（V50 —-\/8） 4- V2的结果是•9.一个反比例函数y=« （kNO）的图象经过点P （-2, -3）,则该反比例函数的解析式是x10.合作小组的4位同学坐在课桌旁讨论问题，学生A的座位如图所示，学生B, C, D随机坐到其他三个座位上，则学生B坐在2号座位的概率是第10题图第11题图第13题图11.如图，在AABC中，ZCAB=70°,在同一平面内，将AABC绕点A逆时针旋转50°到△ AB'C的位置，则Z CAB'=度.12.已知打的整数部分是a,小数部分是b,贝\\a--=b13.如图正方形ABCD中，点E在边DC上，DE=2, EC = 1 ,把线段AE绕点A旋转，使点E落在真线BC上的点F处，则F、C两点的距离为.9 _14.函数y r = x（x > 0） , y2 = —（x > 0）的图象如图所不，则结论：①两函数图象的交点xA的坐标为（3,3）；②当x>3时，y2>yi ；③当x二1时，BC=8；④当x逐渐增大时，yi随着x的增大而增大，y2随着x的增大而减小.其中正确结论的序号是第14题图15.如图，在函数（X〉O）的图象上有点Pl、P2> P3...、Pn、Pn+1，点Pl的横坐标为2,且后面每个点的横坐庙它前面相邻点的横坐标的差都是2,过点Pi、P2> P3...、Pn、Pn+1分别作X轴、y轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为S1、S2、S3...、Sn，则Sn=.（用含n的代数式表示）三、解答题（本大题8小题，共64分.把解答过程写在试卷相对应的位置上.解答时应写出必要的计算过程，推演步骤或文字说明）16.计算：（每小题4分，共8分）_ _ / 厂、2005 / 厂、2006（10V48-6V27+4712）^76 ⑵（2-丁5）（2 + J5）（1）17.（本题满分6分）先化简代数式（―+ 一^——）-—,然后选取一个使原式有意义的a值代入求值。

广东省崇雅中学12月份考试文科数学试题

广东省崇雅中学12月份考试文科数学试题一选择题（每题5分，共计50分）1、集合{}2,4,6M =的真子集的个数为（）A ．6B ．7C ．8D ．9 2、“m =21”是“直线(m +2)x +3my +1=0与直线(m －2)x +(m +2)y －3=0相互垂直”的( )。

A ．充分必要条件 B ．充分而不必要条件C ．.必要而不充分条件D ．既不充分也不必要条件 3、已知10<<a ，3log 21log ,5log 21,3log 2log a a a a az y x -==+=，则（） A. x>y>z B z>y>x C y>x>z D z>x>y 4、下列函数图象中，正确的是（）．5、已知=+-=+ni m i n m ni im是虚数单位，则是实数，，，其中11（） (A)1+2i (B) 1－2i (C) 2+i (D)2－i6、设函数)(x f 定义如下表，数列}{n x 满足50=x ，且对任意自然数n 都有)(1n n x f x =+，则=2010xx1 2 3 4 5 )(x f41352A ．1B ．2C ． 4D ．57、已知α，β是平面，m ，n 是直线，给出下列命题 ①若α⊥m ，β⊂m ，则βα⊥．②若α⊂m ，α⊂n ，β//m ，β//n ，则βα//． ③如果m n m ,,αα⊄⊂、n 是异面直线，那么α与n 相交． ④若m αβ=，n ∥m ，且βα⊄⊄n n ,，则n ∥α且n ∥β．其中正确命题的个数是A ．4B ．3C ．2D ．1y=x+ay=x+a 1 1 111ooo o xx xy =log a xy=x +ay=x ayy y=x+a y=x ay=a yy BC D8、设椭圆)0(,12222>>=+b a b y a x 的离心率为21，右焦点为)0,(c F ，方程02=-+c bx ax 的两个实根分别为1x 和2x ，则点),(21x x PA 必在圆222=+y x 内 B 必在圆222=+y x 上C 必在圆222=+y x 外 D 以上都有可能9、在电脑游戏中，“主角”的生命机会往往被预先设定。

3月八年级下月考数学试卷含答案解析

3月八年级下月考数学试卷含答案解析八年级（下）月考数学试卷（3月份）一、选择题（每小题3分，共30分）1．下列标志既是轴对称图形又是中心对称图形的是（）A．B．C．D．2．代数式﹣，，x+y，，，中是分式的有（）A．1个B．2个C．3个D．4个3．下列各式从左到右的变形正确的是（）A．=B．C．D．4．把分式中的x、y都扩大到原来的4倍，则分式的值（）A．扩大到原来的8倍B．扩大到原来的4倍C．缩小到原来的 D．不变5．能判定四边形ABCD为平行四边形的条件是（）A．AB=AD，CB=CD B．∠A=∠B，∠C=∠D C．AB=CD，AD=BC D．AB∥CD，AD=BC 6．顺次连结矩形四边的中点所得的四边形是（）A．矩形B．正方形C．菱形D．以上都不对7．关于x的方程可能产生的增根是（）A．x=1 B．x=2 C．x=1或x=2 D．x=一1或=28．如图，已知四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从C向D移动而点R不动时，那么下列结论成立的是（）A．线段EF的长逐渐增大B．线段EF的长逐渐减少C．线段EF的长不变12．下列4个分式：①；②；③；④，中最简分式有个．13．如果一个矩形较短的边长为5cm．两条对角线所夹的角为60°，则这个矩形的面积是cm2．14．若分式方程=5+有增根，则a的值为．15．若﹣=2，则的值是．16．已知关于x的方程的解是负数，则n的取值范围为．17．如图，在矩形ABCD中，对角线AC、BD 相交于点O，若DF⊥AC，∠ADF：∠FDC=3：2，则∠BDF=．18．如图，平行四边形ABCD中，BE⊥AD于E，BF⊥CD于F，BE=2，BF=3，平行四边形ABCD 的周长为20，则平行四边形ABCD的面积为．19．如图，矩形ABCD中，AB=6，BC=8，点E 是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为．20．如图，正方形ABCD的边长为6，点O是对角线AC、BD的交点，点E在CD上，且DE=2CE，过点C作CF⊥BE，垂足为F，连接OF，则OF的长为．三、解答题（本大题共70分，解答时应写出文字说明、证明过程或演算步骤）21．计算：（1）（2）（3）（4）．22．解下列方程．（1）=﹣1（2）+=．23．化简代数式，再从﹣2，2，0，1四个数中选一个恰当的数作为a的值代入求值．24．如图的正方形格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：（1）将△ABC沿x轴翻折后再沿x轴向右平移1个单位，在图中画出平移后的△AB1C1．若△ABC内有一点P（a，b），则经过两次变换后点P的坐标变为．（2）作出△ABC关于坐标原点O成中心对称的△A2B2C2．（3）若将△ABC绕某点逆时针旋转90°后，其对应点分别为A3（2，1），B3（4，0），C3（3，﹣2），则旋转中心坐标为．25．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．（1）试说明AC=EF；（2）求证：四边形ADFE是平行四边形．26．把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．（1）问四边形DEBF是什么特殊四边形？说明理由．（2）若AB=12cm，BC=18cm，求重叠部分的面积．27．阅读下列材料：我们定义：若一个四边形的一条对角线把四边形分成两个等腰三角形，则称这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如正方形，菱形都是和谐四边形．结合阅读材料，完成下列问题：如图，等腰Rt△ABD中，∠BAD=90°．若点C 为平面上一点，AC为凸四边形ABCD的和谐线，且AB=BC，请画出图形并求出∠ABC的度数．28．如图，矩形OABC顶点B的坐标为（8，3），定点D的坐标为（12，0），动点P从点O出发，以每秒2个单位长度的速度沿x轴的正方向匀速运动，动点Q从点D出发，以每秒1个单位长度的速度沿x轴的负方向匀速运动，PQ两点同时运动，相遇时停止．在运动过程中，以PQ为斜边在x轴上方作等腰直角三角形PQR．设运动时间为t秒．（1）当t=时，△PQR的边QR经过点B；（2）设△PQR和矩形OABC重叠部分的面积为S，求S关于t的函数关系式．2015-2016学年江苏省无锡市东湖塘中学八年级（下）月考数学试卷（3月份）参考答案与试题解析一、选择题（每小题3分，共30分）1．下列标志既是轴对称图形又是中心对称图形的是（）A．B．C．D．【考点】中心对称图形；轴对称图形．【分析】根据轴对称图形与中心对称图形的定义解答．【解答】解：A、是轴对称图形，不是中心对称图形；B、是中心对称图形，不是轴对称图形；C、是中心对称图形，不是轴对称图形；D、是中心对称图形，也是轴对称图形．故选D．2．代数式﹣，，x+y，，，中是分式的有（）A．1个B．2个C．3个D．4个【考点】分式的定义．【分析】根据分母中含有字母的式子是分式，可得答案．【解答】解；代数式是分式，故选；A．3．下列各式从左到右的变形正确的是（）A．=B．C．D．【考点】分式的基本性质．【分析】依据分式的基本性质进行变化，分子分母上同时乘以或除以同一个非0的数或式子，分式的值不变．【解答】解：A、a扩展了10倍，a2没有扩展，故A错误；B、符号变化错误，分子上应为﹣x﹣1，故B错误；C、正确；D、约分后符号有误，应为b﹣a，故D错误．故选C．4．把分式中的x、y都扩大到原来的4倍，则分式的值（）A．扩大到原来的8倍B．扩大到原来的4倍C．缩小到原来的 D．不变【考点】分式的基本性质．【分析】根据题意得出算式，再根据分式的基本性质化简，即可得出答案．【解答】解：根据题意得：==，即和原式的值相等，故选D．5．能判定四边形ABCD为平行四边形的条件是（）A．AB=AD，CB=CD B．∠A=∠B，∠C=∠D C．AB=CD，AD=BC D．AB∥CD，AD=BC 【考点】平行四边形的判定．【分析】平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．根据平行四边形的判定方法，采用排除法，逐项分析判断．【解答】解：A、若AB=AD，CB=CD，无法判定，四边形ABCD为平行四边形，故此选项错误；B、∠A=∠B，∠C=∠D，无法判定，四边形ABCD 为平行四边形，故此选项错误；C、AB=CD，AD=BC，可判定是平行四边形的条件，故此选项正确；D、此条件下无法判定四边形的形状，还可能是等腰梯形，故此选项错误．故选：C．6．顺次连结矩形四边的中点所得的四边形是（）A．矩形B．正方形C．菱形D．以上都不对【考点】中点四边形．【分析】因为题中给出的条件是中点，所以可利用三角形中位线性质，以及矩形对角线相等去证明四条边都相等，从而说明是一个菱形．【解答】解：连接AC、BD，在△ABD中，∵AH=HD，AE=EB∴EH=BD，同理FG=BD，HG=AC，EF=AC，又∵在矩形ABCD中，AC=BD，∴EH=HG=GF=FE，∴四边形EFGH为菱形．故选：C．7．关于x的方程可能产生的增根是（）A．x=1 B．x=2 C．x=1或x=2 D．x=一1或=2【考点】分式方程的增根．【分析】增根是化为整式方程后产生的不适合分式方程的根．所以应先确定增根的可能值，让最简公分母（x﹣1）（x﹣2）=0，根据解方程，可得答案．【解答】解：由关于x的方程可能产生的增根，得（x﹣1）（x﹣2）=0．解得x=1或x=2，故选：C．8．如图，已知四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从C向D移动而点R不动时，那么下列结论成立的是（）A．线段EF的长逐渐增大B．线段EF的长逐渐减少C．线段EF的长不变D．线段EF的长与点P的位置有关【考点】三角形中位线定理．【分析】因为AR的长度不变，根据中位线定理可知，线段EF的长不变．【解答】解：因为AR的长度不变，根据中位线定理可知，EF平行与AR，且等于AR的一半．所以当点P在CD上从C向D移动而点R不动时，线段EF的长不变．故选C．9．已知小明上学时，走上坡路，速度为m千米/时；放学回家时，沿原路返回，速度为n千米/时，则小明上学和放学时的平均速度为（）A．千米/时 B．千米/时C．千米/时 D．千米/时【考点】列代数式（分式）．【分析】设从家到学校的单程为1，那么总路程为2，根据平均速度=，列分式并化简即可得出答案．【解答】解：设上学路程为1，则往返总路程为2，上坡时间为，下坡时间为，则平均速度==（千米/时）．故选C10．如图，在矩形ABCD中，AB=4cm，AD=12cm，P点在AD边上以每秒1cm的速度从A向D运动，点Q在BC边上，以每秒4cm的速度从C 点出发，在CB间往返运动，二点同时出发，待P点到达D点为止，在这段时间内，线段PQ有（）次平行于AB．A．1 B．2 C．3 D．4【考点】一元一次方程的应用．【分析】易得两点运动的时间为12s，PQ∥AB，那么四边形ABQP是平行四边形，则AP=BQ，列式可求得一次平行，算出Q在BC上往返运动的次数可得平行的次数．【解答】解：∵矩形ABCD，AD=12cm，∴AD=BC=12cm，∵PQ∥AB，AP∥BQ，∴四边形ABQP是平行四边形，∴AP=BQ，∴Q走完BC一次就可以得到一次平行，∵P的速度是1cm/秒，∴两点运动的时间为12÷1=12s，∴Q运动的路程为12×4=48cm，∴在BC上运动的次数为48÷12=4次，∴线段PQ有4次平行于AB，故选D．二、填空题（本大题共有10个空格，每个空格2分，共20分.把答案直接写在横线上）11．当x=1时，分式的值为0．当x≠3时，分式有意义．【考点】分式的值为零的条件；分式有意义的条件．【分析】先根据分式的值为0的条件列出关于x 的不等式组，求出x的值，再根据分式有意义的条件列出关于x的不等式，求出x的取值范围即可．【解答】解：∵分式的值为0，∴，解得x=﹣1；∵分式有意义，∴x﹣3≠0，即x≠3．故答案为：=﹣1，≠3．12．下列4个分式：①；②；③；④，中最简分式有2个．【考点】最简分式．【分析】将题目中的式子能化简的先化简，不能化简的式子是最简分式．【解答】解：∵，，，，∴最简分式是①④，故答案为：2．13．如果一个矩形较短的边长为5cm．两条对角线所夹的角为60°，则这个矩形的面积是25 cm2．【考点】矩形的性质．【分析】根据矩形对角线相等且互相平分性质和题中条件易得△AOB为等边三角形，即可得到矩形对角线一半长，进而求解即可．【解答】解：如图：AB=5cm，∠AOB=60°，∵四边形是矩形，AC，BD是对角线，∴OA=OB=OD=OC=BD=AC，在△AOB中，OA=OB，∠AOB=60°，∴OA=OB=AB=5cm，BD=2OB=2×5=10cm，∴BC=cm，∴矩形的面积=25cm 2．故答案为：．14．若分式方程=5+有增根，则a的值为4．【考点】分式方程的增根．【分析】分式方程去分母转化为整式方程，根据分式方程有增根，得到最简公分母为0，求出x 的值，代入整式方程即可求出a的值．【解答】解：去分母得：x=5x﹣20+a，由分式方程有增根，得到x﹣4=0，即x=4，把x=4代入整式方程得：4=20﹣20+a，解得：a=4，故答案为：4．15．若﹣=2，则的值是﹣．【考点】分式的化简求值．【分析】先根据题意得出a﹣b=﹣2ab，再代入原式进行计算即可．【解答】解：∵﹣=2，∴a﹣b=﹣2ab，∴原式====﹣．故答案为：﹣．16．已知关于x的方程的解是负数，则n的取值范围为n＜2且n≠．【考点】分式方程的解．【分析】求出分式方程的解x=n﹣2，得出n﹣2＜0，求出n的范围，根据分式方程得出n﹣2≠﹣，求出n，即可得出答案．【解答】解：，解方程得：x=n﹣2，∵关于x的方程的解是负数，∴n﹣2＜0，解得：n＜2，又∵原方程有意义的条件为：x≠﹣，∴n﹣2≠﹣，即n≠．故答案为：n＜2且n≠．17．如图，在矩形ABCD中，对角线AC、BD 相交于点O，若DF⊥AC，∠ADF：∠FDC=3：2，则∠BDF=18°．【考点】矩形的性质．【分析】根据∠ADC=90°，求出∠CDF和∠ADF，根据矩形性质求出OD=OC，推出∠BDC=∠DCO，求出∠BDC，即可求出答案．【解答】解：设∠ADF=3x°，∠FDC=2x°，∵四边形ABCD是矩形，∴∠ADC=90°，∴2x+3x=90，x=18°，即∠FDC=2x°=36°，∵DF⊥AC，∴∠DMC=90°，∴∠DCO=90°﹣36°=54°，∵四边形ABCD是矩形，∴AC=2OC，BD=2OD，AC=BD，∴OD=OC，∴∠BDC=∠DCO=54°，∴∠BDF=∠BDC﹣∠CDF=54°﹣36°=18°，故答案为：18°．18．如图，平行四边形ABCD中，BE⊥AD于E，BF⊥CD于F，BE=2，BF=3，平行四边形ABCD 的周长为20，则平行四边形ABCD的面积为12．【考点】平行四边形的性质．【分析】根据平行四边形的周长求出AD+CD，再利用面积列式求出AD、CD的关系，然后求出AD的长，再利用平行四边形的面积公式列式计算即可得解．【解答】解：∵▱ABCD的周长为20，∴2（AD+CD）=20，∴AD+CD=10①，∵S▱ABCD=AD•BE=CD•BF，∴2AD=3CD②，联立①、②解得AD=6，∴▱ABCD的面积=AD•BE=6×2=12．故答案为：12．19．如图，矩形ABCD中，AB=6，BC=8，点E 是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为3或6．【考点】翻折变换（折叠问题）．【分析】当△CEB′为直角三角形时，有两种情况：①当点B′落在矩形内部时，如答图1所示．连结AC，先利用勾股定理计算出AC=10，根据折叠的性质得∠AB′E=∠B=90°，而当△CEB′为直角三角形时，只能得到∠EB′C=90°，所以点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，则EB=EB′，AB=AB′=6，可计算出CB′=4，设BE=x，则EB′=x，CE=8﹣x，然后在Rt△CEB′中运用勾股定理可计算出x．②当点B′落在AD边上时，如答图2所示．此时四边形ABEB′为正方形．【解答】解：当△CEB′为直角三角形时，有两种情况：①当点B′落在矩形内部时，如答图1所示．连结AC，在Rt△ABC中，AB=6，BC=8，∴AC==10，∵∠B沿AE折叠，使点B落在点B′处，∴∠AB′E=∠B=90°，当△CEB′为直角三角形时，只能得到∠EB′C=90°，∴点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，如图，∴EB=EB′，AB=AB′=6，∴CB′=10﹣6=4，设BE=x，则EB′=x，CE=8﹣x，在Rt△CEB′中，∵EB′2+CB′2=CE2，∴x2+42=（8﹣x）2，解得x=3，∴BE=3；②当点B′落在AD边上时，如答图2所示．此时ABEB′为正方形，∴BE=AB=6．综上所述，BE的长为3或6．故答案为：3或6．20．如图，正方形ABCD的边长为6，点O是对角线AC、BD的交点，点E在CD上，且DE=2CE，过点C作CF⊥BE，垂足为F，连接OF，则OF的长为．【考点】全等三角形的判定与性质；等腰直角三角形；正方形的性质．【分析】在BE上截取BG=CF，连接OG，证明△OBG≌△OCF，则OG=OF，∠BOG=∠COF，得出等腰直角三角形GOF，在RT△BCE中，根据射影定理求得GF的长，即可求得OF的长．【解答】解：如图，在BE上截取BG=CF，连接OG，∵RT△BCE中，CF⊥BE，∴∠EBC=∠ECF，∵∠OBC=∠OCD=45°，∴∠OBG=∠OCF，在△OBG与△OCF中∴△OBG≌△OCF（SAS）∴OG=OF，∠BOG=∠COF，∴OG⊥OF，在RT△BCE中，BC=DC=6，DE=2EC，∴EC=2，∴BE===2，∵BC2=BF•BE，则62=BF，解得：BF=，∴EF=BE﹣BF=，∵CF2=BF•EF，∴CF=，∴GF=BF﹣BG=BF﹣CF=，在等腰直角△OGF中OF2=GF2，∴OF=．故答案为：．三、解答题（本大题共70分，解答时应写出文字说明、证明过程或演算步骤）21．计算：（1）（2）（3）（4）．【考点】分式的混合运算．【分析】（1）在第二个分式的分母中提取符号，放在分式的前面，再根据同分母的分式的加减直接计算即可；（2）根据分式的除法法则，直接计算即可；（3）根据异分母分式加减的法则，先通分，再相加，即可解答；（4）根据分式的混合运算的法则，先计算括号里面的，再根据分式的除法法则计算即可．【解答】解：（1）原式====m+2；（2）原式==；（3）原式===；（4）原式==．22．解下列方程．（1）=﹣1（2）+=．【考点】解分式方程．【分析】两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：（1）去分母得：15x﹣12=4x+10﹣3x+6，移项合并得：14x=28，解得：x=2，经检验x=2是增根，分式方程无解；（2）去分母得：3x﹣3+2x+2=4，解得：x=1，经检验x=1是增根，分式方程无解．23．化简代数式，再从﹣2，2，0，1四个数中选一个恰当的数作为a的值代入求值．【考点】分式的化简求值．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a=0代入计算即可求出值．【解答】解：原式=•=•=，当a=0时，原式=2．24．如图的正方形格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：（1）将△ABC沿x轴翻折后再沿x轴向右平移1个单位，在图中画出平移后的△AB1C1．若△ABC内有一点P（a，b），则经过两次变换后点P的坐标变为（a+1，﹣b）．（2）作出△ABC关于坐标原点O成中心对称的△A2B2C2．（3）若将△ABC绕某点逆时针旋转90°后，其对应点分别为A3（2，1），B3（4，0），C3（3，﹣2），则旋转中心坐标为（0，2）．【考点】作图-旋转变换；作图-轴对称变换．【分析】（1）根据网格结构找出点A、B、C关于x轴对称并向右平移1个单位后的对应点A1、B1、C1的位置，然后顺次连接即可，再根据轴对称和平移的性质的性质写出点P的对应点的坐标；（2）根据网格结构找出点A、B、C关于原点O 成中心对称的点A2、B2、C2的位置，然后顺次连接即可；（3）根据网格结构找出点A3、B3、C3的位置，再根据旋转的性质找出旋转中心并写出坐标．【解答】解：（1）△A1B1C1如图所示；P（a+1，﹣b）；（2）△A2B2C2如图所示；（3）旋转中心（0，2）．故答案为：（a+1，﹣b）；（0，2）．25．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．（1）试说明AC=EF；（2）求证：四边形ADFE是平行四边形．【考点】平行四边形的判定；全等三角形的判定与性质；等边三角形的性质．【分析】（1）首先Rt△ABC中，由∠BAC=30°可以得到AB=2BC，又因为△ABE是等边三角形，EF⊥AB，由此得到AE=2AF，并且AB=2AF，然后即可证明△AFE≌△BCA，再根据全等三角形的性质即可证明AC=EF；（2）根据（1）知道EF=AC，而△ACD是等边三角形，所以EF=AC=AD，并且AD⊥AB，而EF⊥AB，由此得到EF∥AD，再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形．【解答】证明：（1）∵Rt△ABC中，∠BAC=30°，∴AB=2BC，又∵△ABE是等边三角形，EF⊥AB，∴AB=2AF∴AF=BC，在Rt△AFE和Rt△BCA中，，∴△AFE≌△BCA（HL），∴AC=EF；（2）∵△ACD是等边三角形，∴∠DAC=60°，AC=AD，∴∠DAB=∠DAC+∠BAC=90°又∵EF⊥AB，∴EF∥AD，∵AC=EF，AC=AD，∴EF=AD，∴四边形ADFE是平行四边形．26．把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．（1）问四边形DEBF是什么特殊四边形？说明理由．（2）若AB=12cm，BC=18cm，求重叠部分的面积．【考点】翻折变换（折叠问题）．【分析】（1）证得DE=DF，得四边形BFDE是平行四边形，根据折叠的性质知：BF=DF，得四边形BFDE是菱形；（2）根据折叠的性质知：AE=A′E，AB=A′D；可设AE为x，用x表示出A′E和DE的长，进而在Rt△A′DE中求出x的值，即可得到A′E的长，即可得到AE和DE长，再利用三角形的面积公式可得答案．【解答】解：（1）四边形DEBF是菱形，连接BE，由折叠的性质可得∠BFE=∠DFE，∵AD∥BC，∴∠BFE=∠DEF，∴∠DFE=∠DEF，∴DE=DF，∴四边形BFDE是平行四边形，由折叠知，BF=DF．∴四边形BFDE是菱形；（2）设AE=A′E=xcm，则DE=18﹣x；在Rt△A′ED中，A′E=xcm，A′D=AB=12cm，ED=AD﹣AE=（18﹣x）cm；由勾股定理得：x2+144=（18﹣x）2，解得x=5；∴S△DEF=×DE×DC=（18﹣5）×12=78（cm2）．27．阅读下列材料：我们定义：若一个四边形的一条对角线把四边形分成两个等腰三角形，则称这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如正方形，菱形都是和谐四边形．结合阅读材料，完成下列问题：如图，等腰Rt△ABD中，∠BAD=90°．若点C 为平面上一点，AC为凸四边形ABCD的和谐线，且AB=BC，请画出图形并求出∠ABC的度数．【考点】等腰三角形的判定与性质．【分析】首先根据题意画出图形，然后由AC是四边形ABCD的和谐线，可以得出△ACD是等腰三角形，从图1，图2，图3三种情况运用等边三角形的性质，正方形的性质和30°的直角三角形性质就可以求出∠ABC的度数．【解答】解：∵AC是四边形ABCD的和谐线，∴△ACD是等腰三角形，在等腰Rt△ABD中，∵AB=AD，∴AB=AD=BC，如图1，当AD=AC时，∴AB=AC=BC，∠ACD=∠ADC∴△ABC是正三角形，∴∠ABC=60°．如图2，当AD=CD时，∴AB=AD=BC=CD．∵∠BAD=90°，∴四边形ABCD是正方形，∴∠ABC=90°；如图3，当AC=CD时，过点C作CE⊥AD于E，过点B作BF⊥CE于F，∵AC=CD．CE⊥AD，∴AE=AD，∠ACE=∠DCE．∵∠BAD=∠AEF=∠BFE=90°，∴四边形ABFE是矩形．∴BF=AE．∵AB=AD=BC，∴BF=BC，∴∠BCF=30°．∵AB=BC，∴∠ACB=∠BAC．∵AB∥CE，∴∠BAC=∠ACE，∴∠ACB=∠BAC=∠BCF=15°，∴∠ABC=150°，综上：∠ABC的度数可能是：60°90°150°．28．如图，矩形OABC顶点B的坐标为（8，3），定点D的坐标为（12，0），动点P从点O出发，以每秒2个单位长度的速度沿x轴的正方向匀速运动，动点Q从点D出发，以每秒1个单位长度的速度沿x轴的负方向匀速运动，PQ两点同时运动，相遇时停止．在运动过程中，以PQ为斜边在x轴上方作等腰直角三角形PQR．设运动时间为t秒．（1）当t=1时，△PQR的边QR经过点B；（2）设△PQR和矩形OABC重叠部分的面积为S，求S关于t的函数关系式．【考点】四边形综合题．【分析】（1）△PQR的边QR经过点B时，△ABQ 构成等腰直角三角形，则有AB=AQ，由此列方程求出t的值；（2）在图形运动的过程中，有三种情形，当1＜t≤2时，当1＜t≤2时，当2＜t≤4时，进行分类讨论求出答案．【解答】解：（1）△PQR的边QR经过点B时，△ABQ构成等腰直角三角形，∴AB=AQ，即3=4﹣t，∴t=1．即当t=1秒时，△PQR的边QR经过点B．故答案为：1；（2）①当0≤t≤1时，如答图1﹣1所示．设PR交BC于点G，过点P作PH⊥BC于点H，则CH=OP=2t，GH=PH=3．S=S矩形OABC﹣S梯形OPGC=8×3﹣（2t+2t+3）×3=﹣6t；②当1＜t≤2时，如答图1﹣2所示．设PR交BC于点G，RQ交BC、AB于点S、T．过点P作PH⊥BC于点H，则CH=OP=2t，GH=PH=3．QD=t，则AQ=AT=4﹣t，∴BT=BS=AB﹣AQ=3﹣（4﹣t）=t﹣1．S=S矩形OABC﹣S梯形OPGC﹣S△BST=8×3﹣（2t+2t+3）×3﹣（t﹣1）2=﹣t2﹣5t+19；③当2＜t≤4时，如答图1﹣3所示．设RQ与AB交于点T，则AT=AQ=4﹣t．PQ=12﹣3t，∴PR=RQ=（12﹣3t）．S=S△PQR﹣S△AQT=PR2﹣AQ2=（12﹣3t）2﹣（4﹣t）2=t2﹣14t+28．综上所述，S关于t的函数关系式为：S=．。

13-14下八年级期中试卷.docx

2013-2014学年度下学期期中质量测试题八年级数学一、选择题（每小题3分，共30分）1、要使二次根式冇意义,那么/的取值范围是（）A. x> —1B. x<lC. x±l 2、下列计算屮，正确的是（7、下列二次根式屮属于最简二次根式的是（□ABCD 中，对角线AC 、BD 交于点0,点E 是BC 的中点.若0E=3 cm,则D.xWlA. 2V3+4V2 =6>/5B.C. 373x3^2 =3^6D.3. 下列各组线段屮，能够组成肓角三角形的是（A 、 3、4、5B 、 5、 6、 7C 、 4、 5、 6D 、 6、 7、 8SS 4、如图，下列条件中, 能判定四边形ABCD 是平行四边形的是A> AB//CD, AD=CB B 、 AB 二AD, CB 二CDC 、 Z A=ZB, ZC=ZD D 、 AB 二CD, AD=BC5、如图,已知0A=0B, 那么数轴上点A 所表示的数是（ A 、 -3 B 、 -5 C 、 D. 756、 3血一血等于（A. 3B. 2C. V2D. 2V2 A. V14 B. V48 C. a~b D. J4d +48、如图, AB 的长为A. 3 cmB. 6 cmC. 9 cm D ・ 12 cm)第5题笫8题9、如图，一棵人树在离地面9米高的B 处断裂，树顶A 落在离树底部C 的12米处，则大树数断裂之前的高度为（A ： 9 米B ： 15 米C ： 21 米D ： 24 米 10、将一张矩形纸片ABCD 如图那样折起，使顶点C 落在C'处, 其中AB=4A /5若AC ED = 30°则折痕FD 的长为（）A 、4^5B 、8A /5C 、4D 、8二、填空题（每小题3分，共18分）11、化简：JT 二 __________ o 12、如图，在平行四边形ABCD 中ZA=120°,则ZD 二 _________13. 如图，在RtAABC 屮，D 为AB 的中点，AB 二10,则CD 二14、己知 a 〈2, J(Q -2)2 = ___________15、如图，正方形A. B 的面积分别是25和169,则正方形M 的面积是_______________________________________________________________1 1 1 1+ ------------- ---------------- + ■ • • + ---------------------V3 + 1 V5+V3 V7+V5 V20B + V20H三、解答题（共52分。

2013-2014年八年级数学12月月考试题(有答案)

（ 2） a2 16( a b)2 .
解：（ 1）原式＝ ( x y)( x y 2)
（ 2）原式＝ (5a 4b)(4b 3a)
18. 先化简，再求值：（ 7 分）
y( x y) ( x y) ( x y) 2 ，x其中 x = - 2，y = 1 ． 2
解：原式＝ xy，当 x = - 2， y = 1 时，原式＝－ 1 2
22. 解下列方程与不等式（ (1)3x(7-x)=18-x(3x-15) ；解：（ 1） x＝ 3 （ 2） x＜－ 1
8 分）（ 2） (x+3)(x-7)+8
＞ (x+5)(x-1).
23. （ 7 分）如图， OC是∠ AOB的角平分线， P 是 OC上
一点． PD⊥ OA交 OA于 D， PE⊥ OB交 OB于 E， F 是
24. （ 8 分） D 是 AB 上一点， DF 交 AC 于点 E， DE=EF ，AE=CE ，求证： A B∥CF。
证明：
A
∵∠ AED 与∠ CEF 是对顶角， ∴∠ AED= ∠ CEF，在△ ABC 和△ CFE 中， ∵DE=FE ，∠ AED= ∠CEF， AE=CE ，
E
F
D
B 第 24 题 C
答案： D 2. 23 表示（★★★★★） .
A. 2 ×2× 2
B. 2 × 3
C. 3× 3 答案： A
D. 2+2+2
3. 在平面直角坐标系中。点 P（ - 2， 3）关于 x 轴的对称点在（★★★★★） .
A. 第一象限 C. 第三象限答案： C
B. 第二象限 D. 第四象限
4. 等腰但不等边的三角形的角平分线、高线、中线的总条数是（★★★★★）

2013～2014(上)八年级第二次质量检测数学A卷

第3题图图2 2013～2014(上)八年级第二次质量检测数学试卷（A 卷） (2013.12)（本卷满分150分，请在答题卷上作答）命题人：吴达辉一、选择题：（每小题4分,共40分）1. 下列说法中正确的是（） A ．9的平方根是3 B2 422. 在绝对值不超过100的数中，平方根和立方根都为整数的有（） A. 2个 B. 3个 C. 4个 D. 5个3. 若a 为正整数，且x 2a＝5，则（2x 3a）2÷4x 4a的值为（）A.25B.5C.25D.104. 如图1所示的图形面积由以下哪个公式表示（） A ．a 2－b 2＝a （a －b ）＋b （a －b ） B ．（a －b ）2＝a 2－2ab ＋b 2C ．（a ＋b ）2＝a 2＋2ab ＋b 2D ．a 2－b 2＝a （a ＋b ）－b （a ＋b ）5. 工人师傅常用角尺平分一个任意角．做法如下：如图2所示，∠AOB 是一个任意角，在边OA ，OB 上分别取OM =ON ，移动角尺，使角尺两边相同的刻度分别与M ，N 重合．过角尺顶点C 的射线OC 即是∠AOB 的平分线．这种做法的道理是（）A.HLB.SSSC.SASD.ASA6. 如图，ABC ∆≌BAD ∆，A 和B 以及C 和D 分别是对应点，如果︒=∠︒=∠35,60ABD C ，则BAD ∠的度数为（）A.︒35B.︒60C.︒80D.︒857.下列命题：：① 有一个角是60°的三角形是等边三角形；② 内错角相等； ③ 相等的角是对顶角；④ 两点之间线段最短；⑤直线比射线长.其中真命题有（）A.1个B.2个C.3个D.4个8. 已知△ABC，在下列条件：①∠A＝∠B－∠C；②∠A：∠B：∠C=3：4：5； ③222b 22229.Rt 10. 交BC 于11. 12. 13. 14. 15.为DE 、DF,CH ⊥AB,垂足为H,请写出线段DE 、DF 、CH 三者之间的数量关系 .16.如图是一个三级台阶，它的每一级的长宽和高分别为20dm 、3dm 、2dm ，A 和B 是这个台阶两个相对的端点，A 点有一只蚂蚁，想到B 点去吃可口的食物，则蚂蚁沿着台阶面爬到B 点最短路程是_____________.2032AB图12013～2014(上)八年级第二次质量检测数学答题卷（A 卷） (2013.12)二、填空题（每小题4分,共24分）11. 1 12. -8 13. 2021 14.外角和等于360°的图形是三角形，假 15. DE+CH=DF 16. 25dm 三、解答题（共86分）17.计算：（每小题5分，共10分）（1）3223)()(a a -⋅- （2）2[(34)3(34)](4)x y x x y y +-+÷-18.因式分解（每小题5分，共10分）（1）22)23(4)2(25x y y x --- （2）bc c a b 2222+-+-19.（本题6分）若a 、b 为实数，且471122++-+-=a a a b ，求b a +的值.20. （本题6分）如图，把长方形ABCD 沿直线BD 向上折叠，使点C 落在C ′的位置上，已知AB=•3，BC=7，求：重合部分△EBD 的面积．21.（本题6分）如图，△ABC 中，∠C=90°，M 是BC 的中点，MD ⊥AB 于D ．求证：AD 2=AC 2+BD 2．23. （本题8分）如图，在△ABC 中，BD=CD ，∠ABD=∠ACD,求证AD 平分∠BAC.23.（本题8分）如图,已知在△ABC 中,AB=AC,D 为BC 上一点,BF=CD,CE=BD,求∠EDF 与∠A 的关系．………………………………密………………………………………封………………………线………………………………班级：姓名：座号：ABCDADBCE24. （本题8分）如图，AD ∥BC ，点E 在线段AB 上，∠ADE =∠CDE ，∠DCE =∠ECB . 求证：CD =AD +BC .25. （本题10分）如图，长方形ABCD 中，AD=8cm,CD=4cm. (1)若点P 是边AD 上的一个动点,当PA=PC 时，PD 等于多少? (2)在(1)的情况下,当PA=PC 时，Q 是AB 边上的一个动点,若415AQ 时, QP 与PC 垂直吗？为什么？26.（本题14分）数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．∠AEF=90°，且EF 交正方形外角∠DCG 的平分线CF 于点F ，求证：AE=EF ．（1）经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ．请写出小明的完整证明过程。

2013-2014学年八年级数学上学期第二次月考试题(新人教版第8套)_PDF压缩

12.直角三角形中一个锐角为 30° ,斜边和最小的边的和为 12cm,
则斜边长为
cm
13.等腰三角形两个内角之比为解答题（共 48 分）
2:1，这个等腰三角形的顶角的度数是
14.(6 分）如图，铁路和公路都经过 P 地，曲线 MN 是一条河流，现欲在河上建一个货运码头 Q，使其到铁路和公路的距离相等，请用直尺和圆规通过画图找到码头 Q 的位置。（注意： ①保留作图痕迹；②在图中标出点 Q）
第 2题
第 4题
2. 如图，在△ ABC 中，∠ C=9 0°， AD 平分∠ BAC 交 BC 于 D ，若 BC=64 ，且 BD ： CD=
9： 7，则点 D 到 AB 边的距离为 ( )
A 、 18
B 、28
C、 32
D、 24
3.下列条件不能判定两个是（
）
A ． AB 和 BC 焊接点 B C． AB 和 AD 焊接点 A
B ．AB 和 AC 焊接点 A D． AD 和 BC 焊接点 D
二、填空题（每小题 4 分，共 28 分）
7.如图，△ ABC≌△ DEB， AB＝ DE ，∠ E＝∠ ABC，则∠ C 的对应角为
，
BD 的对应边为
A
求证：（ 1） AE=EC （ 2） AH=2BD
八年级（上）数学第二次月考试卷答案一、填空题（每题 4 分，共 24 分）
1.A 2.B 3.D 4.B 5.C 6.D 二填空题（每小题 4 分，共 28 分）
7. ∠DBE CA 8. 5
9. 3265 10. 6 11. 4 12. 8cm 13. 36 或° 90° 解答题（共 48 分） 14. 6 分 15. 8 分 16.证明：（1） AD 是 △ABC 的中线，

(数学试卷)2013-2014学年度下学期八年级数学第二次月考试题

八年级数学第二次月考试题（时间120分钟满分100分）一、选择题（共12小题，每小题2分，共24分）1. 如果分式x-11有意义，那么x 的取值范围是（）. A.x ＞1 B.x ＜1 C.x ≠1 D.x =12．下列计算正确的是( ).AB ．2=C ．(26= D ．3．下列各图象中，y 不是x 函数的是（）.4．下列命题中是真命题的是（）.A ．两边相等的平行四边形是菱形B ．一组对边平行一组对边相等的四边形是平行四边形C ．两条对角线相等的平行四边形是矩形D．对角线互相垂直且相等的四边形是正方形5. 计算(－34xy )·(－3xy )2的结果是（）. A ．4x 2y 2B ．－4x 2y 2C ．－12x 3y 3D ．12x 3y3 612a -，则( ). A B C DA ．12a < B ．12a ≤ C ．12a > D ． 12a ≥ 7. 如果0,<>cb a ，那么下列不等式成立的是（）.A ．c b c a +>+B ．b c a c ->-C ．bc ac >D ．cb c a > 8．如图，菱形ABCD 中，∠B =60°，AB =4，则以AC 为边长的正方形ACEF 的周长为（）.A ．14B ．15C ．16D ．179. 已知a 、b 、c 是三角形的三边长，如果满足(a －9)2c 15-＝0，则三角形的形状是( ).A ．底与腰不相等的等腰三角形B ．等边三角形C ．钝角三角形D ．直角三角形10. 已知点Ｐ坐标（63,2+-a a ），点Ｐ到两坐标轴的距离相等，则点Ｐ的坐标是（）.A ．（3，3）B ．（3，－3）C ．（6，－6）D ．（3，3）或（6，－6）11. 如图，将一张矩形纸片ABCD 沿直线MN 折叠，使点C 落在点A 处，点D 落在点E 处，直线MN 交BC 于点M ，交AD 于点N ，AB=4, AD=8, 则折痕MN 的长为（）.A ．5B ．52C ．32D ．5412. 如图，正方形ABCD 的边长为4，点P 在DC 边上且DP =1，点Q 是AC 上一动点，则DQ +PQ 的最小值为（）.A. 5 B ．24 C ．10 D ．32二、填空题（共6小题，每小题3分，共18分）13．已知一个正比例函数的图象经过点（－1，3），则这个正比例函数的表达式是 .14．在方程83=-ay x 中，如果⎩⎨⎧==13y x 是它的一个解，那么a 的值为．（第8题图）（第11题图） ( 第12题图)15. 一个多边形的内角和等于1080°，则这个多边形是边形.16．如图，今年的冰雪灾害中，一棵大树在离地面3米处折断，树的顶端落在离树杆底4米处，那么这棵树折断之前的高度是米．17. 如图，在四边形ABCD 中，对角线AC ⊥BD ，垂足为O ，点E 、F 、G 、H 分别为边AD 、AB 、BC 、CD 的中点．若AC =8，BD =6，则四边形EFGH 的面积为．18.如图，在平面直角坐标系中，矩形OABC 的顶点A 、C 的坐标分别为（10，0），（0，4），点D 是OA 的中点，点P 在BC 上运动，当△ODP 是腰长为5的等腰三角形时，点P 的坐标为．三、解答题(本大题共6题，共58分)19．（6分）计算： 312)2014(1210-++-+-π20．（10分）已知：AC 是平行四边形ABCD的对角线且BE ⊥AC ，DF ⊥AC ．求证：四边形BFDE 是平行四边形．（第16题图）（第22题图）（第17题图）（第18题图）21．（10分）如图，反映了小明从家到超市的时间与距离之间关系的一幅图.（1）图中反映了哪两个变量之间的关系？超市离家多远？（2）小明到达超市用了多少时间？小明往返用了多少时间？（3）小明离家出发后20分钟到30分钟内可能在哪里？（4）小明从家到超市时的平均速度是多少？返回时的平均速度是多少？（第21题图）22.（10分）已知：如图，在△ABC 中，AB =AC ，AD ⊥BC ，垂足为点D ，AN 是△ABC 外角 ∠CAM 的平分线，CE ⊥AN ，垂足为点E ，（1）求证：四边形ADCE 为矩形；（2）当△ABC 满足什么条件时，四边形ADCE 是一个正方形？并给出证明．（第22题图）钟)23.（10分）在四边形ABCD中，AD∥BC，∠B=90°，AD=24 cm，BC=26 cm，动点P从点A 出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿着CB方向向点B以3cm/s 的速度运动。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级第二学期数学段考（二）
说明：1．全卷共4页，考试时间为100分钟，满分为120分。

2．用黑色字迹的钢笔或签字笔答题。

答案按各题要求写在答题卷上。

3、不能使用计算器。

一、选择题（共10小题，每题3分，共30分）
1、若二次根式
1-x 1-x 有意义，则x 的取值范围是( ) A ．x ≥1 B ．x ≤1 C ．x ＞1 D ．x ≠1
2、甲、乙两个样本的容量相同，甲样本的方差为0.102，乙样本的方差是0.06，那么（）．
A ．甲的波动比乙的波动大
B ．乙的波动比甲的波动大
C ．甲、乙的波动大小一样
D ．甲、乙的波动大小无法确定
3、函数1+=x y 的图象上有两点),1(1y A 、),2(2y B -，那么下列结论正确的是（）
A.21y y <
B.21y y >
C.21y y =
D.1y 与2y 之间的大小关系不能确定
4、下列各组数中，不能构成直角三角形的是（）
A 、4，5，3
B 、1，1，2
C 、6，8，10
D 、5，12，13
5、已知直线y=2x+1与直线 y=－x+4.则它们的交点是（）
A ．（1，0）
B ．（1，3）
C ．（－1，－1）
D ．（－1，5）
6 ）
A 、、、3
7、下列说法不正确的是（）
A 、 3
a 不是分式 B 、三边长比是3：4：5的三角形是直角三角形 C 、对角线相等的平行四边形是矩形 D 、数据3，2，1，3，4的中位数是1
8、函数y=－X+1的图象不经过（）
A 、第一象限
B 、第二象限
C 、第三象限
D 、第四象限
9、服装销售商在进行市场占有率的调查时，他最应该关注的是（）
A ．服装型号的平均数
B ．服装型号的众数
C ．服装型号的中位数
D ．最小的服装型号
10、平行四边形ABCD 的对角线交于点O ，有五个条件：①AC=BD ，②∠ABC=90°，③ AB=AC ， ④ AB=BC ， ⑤ AC ⊥BD ，则下列哪个组合可判别这个四边形是正方形（）
A ．① ②
B ．① ③
C ．① ④
D ．④ ⑤
二、填空题（共6小题，每题4分，共24分）
11、写出一个图象在二、四象限的正比例函数的解析式。

12、数据1，2，8，5，3，9，5，4，5，4的众数是_________；中位数是__________。

13、菱形有一个内角是120°，有一条对角线为6cm ，则此菱形的边长是 .
14、有一个三角形的两边是3和2，使这个三角形为直角三角形，则第三边的长
为 .
15、如果最简二次根式a +1与24-a 是同类二次根式，那么a = ．
16、已知直线y 1=kx+1与直线 y 2=－k+4，
当x _____________时，y 1＞ y 2。

三、解答题（共3小题，每小题5分，共15分）： 17、 10318214.3-⎪⎭
⎫ ⎝⎛+--+∏-）（ 18、()2
632+；
19、已知一次函数的图象经过点（3，5）（－4.－9）两点，
（1）、求一次函数的解析式。

（2）、当y ＞0,求x 的取值范围。

四、解答题（共3小题，每小题8分，共24分） 20、（8分）一组数据：2，3，4，x 中，若中位数与平均数相等，求数x 的值是多少？
21、（8分）如图，有一个直角三角形纸片，两直角边AC=6cm ，BC=8cm ，现将直角边AC
沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，你能求出CD
22、（8分）下图是某篮球队队员年龄结构直方图，根据图中信息解答下列问题：
（1）该队队员年龄的平均数；
（2）该队队员年龄的众数和中位数．
．
五、解答题（共3小题，每小题9分，共27分）
23、等腰三角形周长40cm ，（1）、写出底边长与腰长的函数关系式，
（2）、写出自变量取值范围。

（3）、画出相应的函数图象。

24、（9分）如图，已知直线y=kx+b过点A（－1，5），且平行于直线y=－x+2.
（1）、求直线y=kx+b的关系式，（2）、若B （m,-5）在这条直线Array上，O为原点，求m 的值及S△AOB
25、（9分）如图所示，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，•交AB于E，F
在DE上，并且AF=CE．
（1）求证：四边形ACEF是平行四边形；
（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论．
（3）四边形ACEF有可能是正方形吗？为什么？。