第七讲卡方检验和方差分析
合集下载
第七章方差分析基础《卫生统计学》课件
方差分析简述方差分析也是统计检验的一种。
由英国著名统计学家：R.A.FISHER推导出来的，也叫F检验。
190240290340分组正常钙组中剂量钙(1.0%)高剂量钙(1.5%)1X 2X 3X X(2) 计算检验统计量可根据表7-5的公式来计算出离均差平方和、自由度、均方和F值。
从已知正态总体N(10,52)进行随机抽样，共抽取了k=10组样本，每组样本的样本含量n i=20，可算出各组的均数和标准差，得表7-7的结果。
如果采用t检验作两两比较，其比较次数为(1)10(101)45 222k k km⎛⎫--====⎪⎝⎭从理论上讲10个样本均来自同一正态总体N(10,52)，应当无差异，但我们用两样本t检验时，已经规定犯第一类错误的概率不超过α=0.05，本次实验实际犯第一类错误的频率为5/45≈0.11，显然比所要控制的0.05要大。
因此不能直接用前面学过的两样本t检验对多样本均数作两两比较，而应采用专用的两两比较的方法。
(2) 计算检验统计量首先将三个样本均数由大到小排列，并编组次：, =11()2A B A B A B X X A BX X X X q S MS n n νν---==+误差误差(3) 确定值并作出推断结论自由度ν误差和对比组内包含组数a查附表4的q界值表得q界值，将算得的q值与相应q界值进行比较得各组的p值。
(3) 确定P值并作出推断结论自由度ν误差和实验组数 (不含对照组)查附表5.2的Dunnett –t(q， )界值表,得q，临界值，用计算得到的q，与临界值进行比较，得P值 。
(2) 计算检验统计量=11()A B A B A B X X A BX X X X t S MS n n νν---==+误差误差。
第七讲卡方检验和方差分析
如果拟定假设为真，则各类农户的期望频数如下：
2 （观察值期望期值望值）2
D3：D5=B3：B5*$B$6
EXCEL的chitest函数计算卡方统计量 后直接报告P值。
由于P值非常 小，有足够的 信心拒绝拟定
假设。
C5:c8=binomdist(b5:b8, $b$2,$b$4,false)
处置内
差异
处置间 差异
X13 X23 X33 X43 X53
处置内
差异
如果处置间差异显著地大于处置内差异， 则认为各样本所来自的总体并非具有相等的平均数
差异的表述
绝对差异的表述：（离差）平方和 相对差异的表述：均方和=（离差）平方和
除以自由度
处置（列）间平方和 处置（列）内平方和 总平方和 总自由度：
Within Groups 427300.0
T o ta l
439835.7
包装 方式 促销 的数 据和 方差 分析 表
ANOVA
M ea n
df
Square
2 6267.857
11 38845.455
13
F .161
Si g. .853
圣地亚哥 25 31 18 23 27
洛杉矶 28 33 35 29 36
假定前提： (1)各总体都服从正态分布； (2)各总体方差相等； (3)样本间相互独立。
程序： (1)提出假设； (2)根据指定的显著水平和观察 值总数目、处置数目确定拒绝的
最小F 值； (3)求出SSC和SSE，计算样本F
值； (4)比较检验统计量，得出结论 。
SALES
Sum of Squares Between Groups 12535.714
2 （观察值期望期值望值）2
D3：D5=B3：B5*$B$6
EXCEL的chitest函数计算卡方统计量 后直接报告P值。
由于P值非常 小，有足够的 信心拒绝拟定
假设。
C5:c8=binomdist(b5:b8, $b$2,$b$4,false)
处置内
差异
处置间 差异
X13 X23 X33 X43 X53
处置内
差异
如果处置间差异显著地大于处置内差异， 则认为各样本所来自的总体并非具有相等的平均数
差异的表述
绝对差异的表述：（离差）平方和 相对差异的表述：均方和=（离差）平方和
除以自由度
处置（列）间平方和 处置（列）内平方和 总平方和 总自由度：
Within Groups 427300.0
T o ta l
439835.7
包装 方式 促销 的数 据和 方差 分析 表
ANOVA
M ea n
df
Square
2 6267.857
11 38845.455
13
F .161
Si g. .853
圣地亚哥 25 31 18 23 27
洛杉矶 28 33 35 29 36
假定前提： (1)各总体都服从正态分布； (2)各总体方差相等； (3)样本间相互独立。
程序： (1)提出假设； (2)根据指定的显著水平和观察 值总数目、处置数目确定拒绝的
最小F 值； (3)求出SSC和SSE，计算样本F
值； (4)比较检验统计量，得出结论 。
SALES
Sum of Squares Between Groups 12535.714
医学统计学：方差分析课件
H1：
各组样本的总体均数不等或不全相等；
如果H0 成立，即各处理组的样本来自相同的总体，无 处理因素的作用，则组间变异同组内变异一样，只反
映随机误差作用的大小。
F值接近于l，就没有理由拒绝H0；反之，F值越大， 拒绝H0的理由越充分。
数理统计理论证明，当H0成立时，F统计量服从F分布。
F 分布曲线
方差分析步骤
单因素方差分析
1. 建立检验假设，确定检验水准 H0：4组家兔的血清ACE浓度总体均数相等，
H1：4组家兔的血清ACE浓度总体均数不等或不 全相等，各 不等或不全相等
2. 计算统计量 F 值
单因素方差分析 计算步骤
方差分析步骤
单因素方差分析 计算步骤
方差分析表
3. 确定P值，并做出统计推断
设计方法
拉丁方设计
（四）优缺点
Байду номын сангаас
拉丁方设计
❖ 优点 1、精确性高
拉丁方设计在不增加试验单位的情况下，比随机 单位组设计多设置了一个单位组因素，能将横行和 直列两个单位组间的变异从试验误差中分离出来， 因而试验误差比随机单位组设计小，试验的精确性 比随机单位组设计高。
2、试验结果的分析简便
拉丁方设计
两因素方差分析
配伍组设计资料的方差分析
例 某医师研究A、B和C 3种药物治疗肝炎的效果， 将32只大白鼠感染肝炎后，按性别相同、体重接 近的条件配成8个配伍组，然后将各配伍组中4只 大白鼠随机分配到4个组。对照组不给药物，其余3 组为实验组，分别给予A、B和C药物治疗。一定 时间后，测定大白鼠血清谷丙转氨酶浓度(IU/L)， 见下表。问4组大白鼠的血清谷丙转氨酶浓度是否 相同？
7
方差分析基本思想
方差分析卡方检验spss.
10-1】 数据格式：3列4行。2个分组变量treat和effect，1 个频数变量freq。 过程： Data →Weight Cases…→Weight cases by:freq Analyze→ Descriptive Statistics → Crosstabs…→ Row(s):treat Column(s):effect → Statistics… R Chi-square → Cell(s)…RRow
Custom按钮，选择由用户自定义方差分析模型中的各个
效应—在Build Term(s)下拉列表中选择Main effects—选 择处理组变量到Model列表中，定义第一个主效应—选择 区组变量到Model列表中，定义第二个主效应—去除 Include intercept in model的勾—Continue—OK
方差分析、卡方检验
一、完全随机设计资料的方差分析 操作过程： Analyze—Compare Means—One-Way Anova…—选择 分析变量到Dependent List列表中—选择分组变量到
factor 列表中—点击Post Hoc，选择两两比较的方法
（LSD法） — OK
二、随机区组设计的方差分析 Analyze—General Linear Model—Univariate…—选择分 析变量到Dependent List列表中—选择处理组变量到 Fixed Factor(s)列表中—选择区组变量到Fixed Factor(s) 列表中—单击Model按钮，进入模型定义窗口—单击
2.配对卡方检验
2.线性趋势 检验
2
【案例10-8】 数据格式：3列9行。2个分组变量x和y,1个频数变 量freq。 过程： Data →Weight Cases…→Weight cases by:freq Analyze→ Descriptive Statistics → Crosstabs…→ Row(s): x Column(s): y → Statistics… R Chi-square → Cell(s)…RRow
Custom按钮，选择由用户自定义方差分析模型中的各个
效应—在Build Term(s)下拉列表中选择Main effects—选 择处理组变量到Model列表中，定义第一个主效应—选择 区组变量到Model列表中，定义第二个主效应—去除 Include intercept in model的勾—Continue—OK
方差分析、卡方检验
一、完全随机设计资料的方差分析 操作过程： Analyze—Compare Means—One-Way Anova…—选择 分析变量到Dependent List列表中—选择分组变量到
factor 列表中—点击Post Hoc，选择两两比较的方法
（LSD法） — OK
二、随机区组设计的方差分析 Analyze—General Linear Model—Univariate…—选择分 析变量到Dependent List列表中—选择处理组变量到 Fixed Factor(s)列表中—选择区组变量到Fixed Factor(s) 列表中—单击Model按钮，进入模型定义窗口—单击
2.配对卡方检验
2.线性趋势 检验
2
【案例10-8】 数据格式：3列9行。2个分组变量x和y,1个频数变 量freq。 过程： Data →Weight Cases…→Weight cases by:freq Analyze→ Descriptive Statistics → Crosstabs…→ Row(s): x Column(s): y → Statistics… R Chi-square → Cell(s)…RRow
卡方检验与方差分析
不太理想的办法
与邻近行或列中的实际频数合并 删去理论频数太小的格子所对切概率法
42
方差分析
为了进行两组以上均数的比较，通常可 以使用方差分析方法。本部分主要介绍 方差分析基本概念、单因素方差分析及 其在SPSS中的操作。
方差分析是R.A.Fister发明的，用于两 个及两个以上样本均数差别的显著性检 验。
卡方检验
在H0为真时，实际观察数与理论数之差
Ai－Ti 应该比较接近0。
所以在H0为真时，检验统计量
2 P
k i 1
( Ai
Ti )2 Ti
服从自由度为（r-1）×（c-1）的卡方分布。
当
2 P
2 ,v，拒绝H0。
上述卡方检验由此派生了不同应用背景的各种问
题的检验，特别最常用的是两个样本率的检验
进一步，在掌握关键影响因素，如品种、施肥量因素等之后，我们 还要对不同的品种、不同的施肥量条件下的产量进行对比分析，研究究 竟哪个品种的产量高，施肥量究竟多少最合适，哪种品种与哪种施肥量 搭配最优，等等。在这些分析研究的基础上，我们就可以计算出各个组 合方案的成本和收益，并选择最合理的种植方案，主动的在农作物种植 过程中对各种影响因素加以准确控制，进而获得最理想的效果。
方差分析分类
单因素方差分析 多因素方差分析 协方差分析
方差分析概述
方差分析的作用
在诸多领域的数量分析研究中，找到众多影响因素中重要的影响因 素是非常重要的。比如：在农业生产中，我们总是希望在尽量少的投入 成本下得到较高的农作物产量。这就需要首先分析农作物的产量究竟受 到哪些因素的影响。有许多因素会影响农作物的产量，如种子的品种、 施肥量、气候、地域等，他们都会给农作物的产量带来或多或少的影响。 如果我们能够掌握在众多的影响因素中，哪些因素对农作物的产量起到 了主要的、关键性的作用，我们就可以根据实际情况对这些关键因素加 以控制。
与邻近行或列中的实际频数合并 删去理论频数太小的格子所对切概率法
42
方差分析
为了进行两组以上均数的比较，通常可 以使用方差分析方法。本部分主要介绍 方差分析基本概念、单因素方差分析及 其在SPSS中的操作。
方差分析是R.A.Fister发明的，用于两 个及两个以上样本均数差别的显著性检 验。
卡方检验
在H0为真时，实际观察数与理论数之差
Ai－Ti 应该比较接近0。
所以在H0为真时，检验统计量
2 P
k i 1
( Ai
Ti )2 Ti
服从自由度为（r-1）×（c-1）的卡方分布。
当
2 P
2 ,v，拒绝H0。
上述卡方检验由此派生了不同应用背景的各种问
题的检验，特别最常用的是两个样本率的检验
进一步，在掌握关键影响因素，如品种、施肥量因素等之后，我们 还要对不同的品种、不同的施肥量条件下的产量进行对比分析，研究究 竟哪个品种的产量高，施肥量究竟多少最合适，哪种品种与哪种施肥量 搭配最优，等等。在这些分析研究的基础上，我们就可以计算出各个组 合方案的成本和收益，并选择最合理的种植方案，主动的在农作物种植 过程中对各种影响因素加以准确控制，进而获得最理想的效果。
方差分析分类
单因素方差分析 多因素方差分析 协方差分析
方差分析概述
方差分析的作用
在诸多领域的数量分析研究中，找到众多影响因素中重要的影响因 素是非常重要的。比如：在农业生产中，我们总是希望在尽量少的投入 成本下得到较高的农作物产量。这就需要首先分析农作物的产量究竟受 到哪些因素的影响。有许多因素会影响农作物的产量，如种子的品种、 施肥量、气候、地域等，他们都会给农作物的产量带来或多或少的影响。 如果我们能够掌握在众多的影响因素中，哪些因素对农作物的产量起到 了主要的、关键性的作用，我们就可以根据实际情况对这些关键因素加 以控制。
《卡方检验》课件
制作交叉表
确定交叉表的行列变量
根据研究目的和内容，选择合适的行列变量，构建交叉表。
制作交叉表
将分组后的数据按照行列变量制作成交叉表，以便于进行卡 方检验。
计算理论频数
确定期望频数
根据交叉表中的数据，结合各组 的概率计算期望频数。
计算理论频数
根据期望频数和实际频数计算理 论频数，为后续的卡方检验提供 依据。
计算卡方值
计算卡方值
使用卡方检验的公式计算卡方值，该 值反映了实际频数与理论频数的差异 程度。
自由度的确定
在计算卡方值时，需要确定自由度， 自由度通常为行数与列数的减一。
显著性水平的确定
选择显著性水平
显著性水平是衡量卡方值是否显著的指标，通常选择0.05或0.01作为显著性水 平。
判断显著性
根据卡方值和自由度，结合显著性水平判断卡方检验的结果是否显著，从而得 出结论。
3.84、6.63等），可以确定观测频数与期望频数之间的差异是否具有统
计学显著性。
02
卡方检验的步骤
收集数据
确定研究目的
制定调查问卷或收集程序
在开始收集数据之前，需要明确研究 的目的和假设，以便有针对性地收集 相关数据。
根据研究目的和内容，制定合适的调 查问卷或建立数据收集程序，确保数 据的完整性和准确性。
详细描述
例如，在市场调研中，我们可以通过卡方检验来分析不同年龄段、性别、职业等 人群对于某产品的态度或购买意愿是否有显著差异，从而为产品定位和营销策略 提供依据。
实际案例二：医学研究中的应用
总结词
在医学研究中，卡方检验常用于病例 对照研究和队列研究中的分类变量关 联性分析。
详细描述
例如，在病例对照研究中，我们可以 通过卡方检验来比较病例组和对照组 在某些基因型、生活方式或暴露因素 上的分布是否有统计学差异，从而探 讨病因或危险因素。
卡方检验与方差分析
第十三章 2χ检验与方差分析我们前面已经比较系统地讨论了双样本的参数和非参数检验的问题。
现在，我们希望利用一般的方法来检验三个以上样本的差异，2χ检验法和方差分析法就是解决这方面问题的。
2χ检验法可以对拟合优度和独立性等进行检验，方差分析法则可以对多个总体均值是否相等进行检验。
后者由于通过各组样本资料之间的方差和组内方差的比较来建立服从F分布的检验统计量，所以又称F 检验。
第一节 拟合优度检验1．问题的导出第十一章最后一节，我们将累计频数检验用于经验分布与理论分布的比较，实际已经提供了拟合优度检验的一种方法。
2χ拟合优度检验与累计频数拟合优度检验相对应，在评估从经验上得到的频数和在一组特定的理论假设下期望得到的频数之间是否存在显著差异时，是一种更普遍的检验方法。
2．拟合优度检验(比率拟合检验)据经验分布来检验总体分布等于理论分布的零假设，检验统计量是2o χ＝频数理论理论频数观察频数∑-/)(2 理论证明，当n 足够大时，该统计量服从2χ分布。
因此对给定的显著性水平α，将临界值2αχ与2o χ比较，可以就H o 作出检验结论。
对于拟合优度检验，在试验规模小时，否定零假设的意义大，接受零假设的意义不大；若试验规模大时，则接受零假设的意义大，否定零假设的意义不大。
3．正态拟合检验第二节 无关联性检验2χ检验的另一个重要应用是对交互分类资料的独立性检验，即列联表检验。
由于列联表一般是按品质标志把两个变量的频数进行交互分类的，所以，①2χ检验法用于对交互分类资料的独立性检验，有其它方法无法比拟的优点；②如何求得列联表中的理论频数就成了独立性检验的关键。
1．独立性、理论频数及自由度检验统计量 2oχ＝∑-e e o f f f 2)(＝∑∑==-c i r j eij eij oij f f f 112)( 进一步上式可变为 2o χ＝-∑∑==c i r j eij oij f f 112n在使用2χ检验法进行列联表检验之前，还必须确定与2o χ这个检验统计量相联系的自由度，即 (r ×c -1)-(r -1)-(c -1)＝(c -1)(r -1)。
《应用统计》教学课件 第7章 χ2检验和方差分析
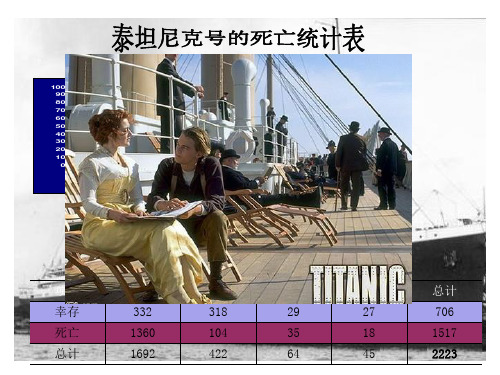
项目 幸存
死亡 总计
男人
妇女
332
318
（537.360） （134.022）
1360 （1154.640）
1692
104 （287.978）
422
男孩
29 （20.326）
35 （43.674）
64
女孩
27 （14.291）
18 （30.709）
45
总计 706
1517 2223
注：表中的括号内数字是期望频数，如， 537.360=（706×1692）/2223
二、独立性检验
所谓独立性，就是两个变量之间互不相关，一个变量的 取值不影响另一个变量的取值。
例：①是否吸烟与是否患肺癌有关； ②收入与受教育程度是否相关； ③从事的行业与所学专业有关； ④性别与体育运动偏好有关。
已知：
PA B PB P A B
如果变量A和变量B相互独立。
则：
PA B PA
PA B PB PA
一、多项分布的χ2 检验
多项分布：指实验结果多于两个的概率分布。
应用统计 理论分数 实际人数
优秀 10% 18
良好 30% 30
中等 40% 40
多项分布试验的条件：
及格 15% 22
不及格 5% 10
①有k个结果（k＞2）； ②每次进行的试验是相互独立的； ③每次有且仅有一个结果发生； ④每种可能出现结果的概率都保持不变。
使用步骤：①建立列联表； ②选择随机样本，记录每一单元格的频数； ③计算每一单元格的期望频数（＞5）； ④根据检验法则做出判断。
例2：在泰坦尼克号沉船事件中，各类别的幸存者与性别 之间关系是否相对独立？
H0 : 是否生还与乘客是男人、女人、男孩还是女孩是独立的； H1 : 乘客是否幸存与这个人是男人、女人、男孩、女孩相互依赖。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
57 206.7947
59
你的 结论 如何
？
方差分析的前提条件和程序
假定前提：
(1)各总体都服 从正态分布；
(2)各总体方差 相等；
(3)样本间相互 独立。
程序：
(1)提出假设； (2)根据指定的显著
水平和观察值总数目、
处置数目确定拒绝的
最小F 值； (3)求出SSC和SSE， 计算样本F 值；
(4)比较检验统计量， 得出结论 。
SSC k 1
处置（列）内均方和：
SSE MSE
nk
方差分析的逻辑
零假设：各样本（处置结果）来自平均数相等的总体。
若要推翻以上假设，则处置间差异必须显著地大于处置内差异。 两者对比采用列间均方和与列内均方和的比值形式表示。即：若要推翻 以上假设，则此比值必须“显著地大”。
此比值服从以ν1和ν2为自由度的F分布。所谓“比值显著地大”， 就是超过指定显著系数所对应的F分布临界值。
0
0. 05
10
20
30
40
Chi-square(d.f.=10)
?18.307
P( 2 10,0.05
18?.307)
0.05
已知自由度=10，右尾面积=0.05，求卡方变量值， 用EXCEL函数
CHIINV（右尾面积，自由度）
本例有
Probability
0.100 0.090 0.080 0.070 0.060 0.050 0.040 0.030 0.020 0.010 0.000
15.367
F 14.659
Si g. .001
样本成双比均值，独立配对法不一。 配对小样先算差，显著与否看t值。 样本独立路有歧：西格码已知直求z； 西格码未知s代，合并估计再求t。
处置是否有效果， 方差分析列表格。 组间组内均方比， F分布右尾拖。 P值偏大均值等， P值偏小拒假设。
卡方分布用处多， 非负分布右尾拖。 交叉列表判独立， 观察期望审拟合。
0.100
0.080
0.060
0.040
0.020
0.000
0
10
20
临界值 Fα
比值与1无显著差异
α
30
F40ν1，ν2
比值显著地大
F分布
两个独立的 t分布被各
F分布的图形
自的自由度去除，所得 P 之商的比率服从F分布.
F(10,4)
它是一种非对称分布,图
F(10,10)
形的形状取决于分子和
分母的自由度.
处置内
差异
处置间 差异
X13 X23 X33 X43 X53
处置内
差异
如果处置间差异显著地大于处置内差异， 则认为各样本所来自的总体并非具有相等的平均数
差异的表述
绝对差异的表述：（离差）平方和 相对差异的表述：均方和=（离差）平方和
除以自由度
处置（列）间平方和 处置（列）内平方和 总平方和 总自由度：
Within Groups 427300.0
T o ta l
439835.7
包装 方式 促销 的数 据和 方差 分析 表
ANOVA
M ea n
df
Square
2 6267.857
11 38845.455
13
F .161
Si g. .853
圣地亚哥 25 31 18 23 27
洛杉矶 28 33 35 29 36
SUMMARY 组
甲 乙 丙
计数 20 20 20
求和 779
1177 1458
平均 方差 38.95 196.1553 58.85 230.9763 72.9 193.2526
方差分析 差异源
组间 组内
SS 11640.1 11787.3
总计
23427.4
df
MS
F P-value F crit
2 5820.05 28.14409 3.15E-09 3.1总体上得分不一致呢？
或者说，样本数据反映的是随 机误差还是本质上的不同呢？
也可以问：三组数据是来自一 个总体，还是来自平均数不等 的三个总体呢？
处置1
处置2
处置3
X11
X21 X21 X21 X21
处置
内差
异
处置间 差异
X12 X22 X32 X42 X52
第七讲 卡方检验和方差分析
一、卡方检验 1. 拟合优度检验 1）指定分布率的拟合优度检验 2）理论概率分布的拟合优度检验 2. 独立性检验 1）列联表 2）独立性检验
Chi-square Curve
Probability
0.100 0.090 0.080 0.070 0.060 0.050 0.040 0.030 0.020 0.010 0.000
HOUR
Descriptiv es
1 2 3 T o ta l
Std. N Mean Deviation
5 24.80
4.82
5 32.20
3.56
5 18.80
3.19
15 25.27
6.73
Std. Error
2.15 1.59 1.43 1.74
95% Confidence Interval for Mean Lower Upper Bound Bound 18.82 30.78 27.78 36.62 14.83 22.77 21.54 29.00
如果拟定假设为真，则各类农户的期望频数如下：
2 （观察值期望期值望值）2
D3：D5=B3：B5*$B$6
EXCEL的chitest函数计算卡方统计量 后直接报告P值。
由于P值非常 小，有足够的 信心拒绝拟定
假设。
C5:c8=binomdist(b5:b8, $b$2,$b$4,false)
或：一个较小的P-值使得决策者更有信心拒绝“所有总 体平均数都相等”的假设。
F3:F22=(B3:B22-$B$23)^2 G3:G22=(C3:C22-$C$23)^2 H2:H22=(D3:D22-$D$23)^2
方差分析表（ANOVA）
航空公司满意分一例EXCEL输出
方差分析：单因素方差分析
k
2
SSC= n j X j X
j 1
k ni
2
SSE
X Xij
j1 i1
k nj
SST ( Xij X )2 j1 i1
n-1
处置（列）间自由度：ν1=k-1
处置（列）内自由度：ν2=（ n-1）-（ k-1）= n-k
处置（列）间均方和 ： MSC=
D5:d8=c5:c8*$b$9)
你将得 出什么 结论？
H0：行车意外独立于手 机使用情况。 H1：行车意外与于手机 使用情况有关。
B11=B6*$E$4/$E$6， 拖动到C11，D11。
B12=B6*$E$5/$E$6， 拖动到C12，D12。
对话框 内填入 什么？
这是什么数值？
本检验自由度是 多少？
假定前提： (1)各总体都服从正态分布； (2)各总体方差相等； (3)样本间相互独立。
程序： (1)提出假设； (2)根据指定的显著水平和观察 值总数目、处置数目确定拒绝的
最小F 值； (3)求出SSC和SSE，计算样本F
值； (4)比较检验统计量，得出结论 。
SALES
Sum of Squares Between Groups 12535.714
旧金山 23 18 21 17 15
一电台想了解在加利福尼亚州的三个
不同城市观众的收视习惯方面是否存在差异。 调研者随机从三个城市分别抽出5人组成随 机样本，要求每组人员报出其上周收看电视 所花的时间（小时），数据见表内。取显著 系数0.05，试问他能否得出三个城市在收看 电视上所花的时间方面存在差异吗？
0
Chi-square Curve
?0.5496
10
20
30
40
Chi-square(d.f.=11)
18
P( 2 10,0.05
18)
0.0?5496
已知自由度=10，卡方变量值=18，求右尾面积， 用EXCEL函数
CHIDIST（变量值，自由度）
本例有
自由度=分类数 - 1
卡方检验统计量
F(10,50)
F
一向方差分析的方差分析表
变异源 处置 误差 总
自由度
k-1
n-k n-1
平方和 均方和
F值
P-值
SSC MSC=SSC/(k-1)
SSE MSE=SSE/(n-k)
SST
MSC/MSE
当检验统计量（ MSC/MSE）超过对应于显著系数的F
值时，拒绝“所有总体平均数都相等”的假设。
Min Max im imu um m 18 31 28 36 15 23 15 36
HOUR
Between Groups Within Groups T o ta l
Sum of Squares 450.533 184.400 634.933
ANOVA
df 2
12 14
M ea n Square 225.267
本检验的结论是 什么？
第七讲 卡方检验和方差分析
二、方差分析 1. 方差分析的基本思想和原理 1） 处置的概念 2）平方和与均方和 3）F分布曲线 4）方差分析中的基本假设 2. 单因素方差分析的程序 3. 单因素方差分析方法的应用
三家航空公司顾客满意得分
100
80
60
甲
乙
40