理论力学第9章-刚体的平面运动
合集下载
理论力学习题册答案
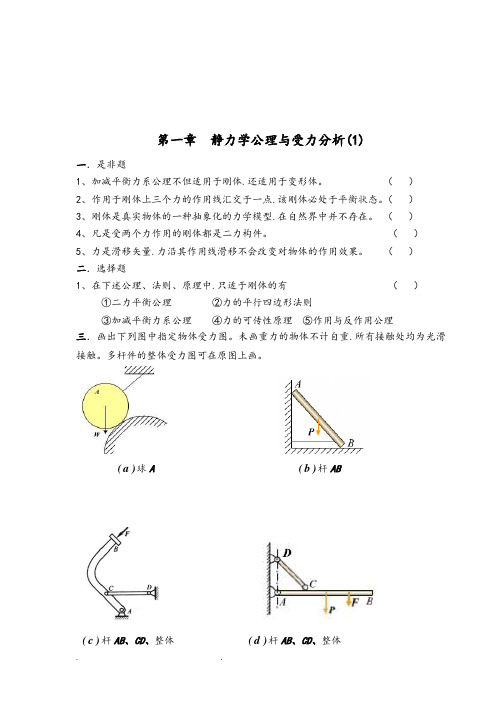
第一章静力学公理与受力分析(1)一．是非题1、加减平衡力系公理不但适用于刚体.还适用于变形体。
（）2、作用于刚体上三个力的作用线汇交于一点.该刚体必处于平衡状态。
（）3、刚体是真实物体的一种抽象化的力学模型.在自然界中并不存在。
（）4、凡是受两个力作用的刚体都是二力构件。
（）5、力是滑移矢量.力沿其作用线滑移不会改变对物体的作用效果。
（）二．选择题1、在下述公理、法则、原理中.只适于刚体的有（）①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三．画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆ABa(球A ))d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四．画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析（2）一．画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一．是非题1、因为构成力偶的两个力满足F= - F’.所以力偶的合力等于零。
（）2、用解析法求平面汇交力系的合力时.若选用不同的直角坐标系.则所求得的合力不同。
（）3、力偶矩就是力偶。
（）二．电动机重P=500N.放在水平梁AC的中央.如图所示。
理论力学课件-刚体平面运动
作速度 vA、vB的垂线，交点P即为该瞬时的
速度瞬心。
③ 已知某瞬时图形上两点A 、B 的速度 vA vB且 ⊥连线 AB， 则连线 AB与速度矢 vA、vB 端点连线的交点P即速度瞬心。 (a)
vA vB (a) 若vA 与vB 同向，则 AB
v A vB (b) 若v A 与vB 反向, 则 AB
但各点的加速度并不相等。 设匀角速度为，则 aB aB n AB 2 () 而 ac 的方向沿AC，故
aB ac ，瞬时平动与平动不同。
４. 速度瞬心法 利用速度瞬心求平面图形上点的速度的方法，称速度瞬心法。 平面图形任一瞬时的运动可以视为绕速度瞬心的瞬时转动， 故速度瞬心又称为平面图形的瞬时转动中心。 若P点为速度瞬心，则任意一点A的速度大小为 vA AP ， 方向 AP，指向与 一致。 5. 注意的问题 ① 速度瞬心在平面图形上的位置不是固定的，而是随时间 不断变化的。在任一瞬时是唯一存在的。 ② 速度瞬心处速度为零,但加速度不一定为零，不同于定轴 转动。 ③ 刚体作瞬时平动时，虽然各点速度相同，但各点加速度 不一定相同，不同于刚体作平动。
vB v A / sin
在Ｂ点做 速度平行四边形，如图示。
l / sin 45 2l ()
vBA vActg l ctg45 l
AB vBA / AB l / l （
）
根据速度投影定理 vB AB vA AB vB sin vA vB vA / sin
n 其中 aa aB , ae aA , ar aBA aBA aBA
于是
aB a A aBA aBA
n
aB a A aBA aBA n 其中：aBA AB ，方向 AB，指向与 一致； aBA n AB 2，方向沿AB，指向A点。
理论力学刚体的平面运动
B
A O vo C P
B ω
A O vo C vPO Pvo
解（1）∵轮子纯滚动 取O为基点
∴vP=0
vP vO vPO
∵ vP 0
vO vPO 0
vPO vO
由 vPO vO
且 vPO R
vO
R
B vAO vA ω
A voO vo C P
B vA
AO
C
P
（2）A点速度，取O为基点
于零？如果存在的话，该点如何确定？
２．速度瞬心的概念 一般情况，在每一瞬时，平面图形 上都唯一地存在一个速度为零的点，该 点称为平面图形在该瞬时的瞬时速度中
B
vB
vA
A O vo C vC
P
心，简称速度瞬心．
证明： vP vA vPA 取 AP vA /
vPA AP vA , 方向PA, 恰与vA反向. 所以
三、平面运动的分解• 刚体的平面运动方程
确定平面图形的位置------只需确定平面图形内任意 一条线段的位置．
任意线段AB的位置可 用A点的坐标和AB与x轴夹 角表示．因此图形S 的位
置决定于 xA, yA, 三个
独立的参变量，它们都是 时间的函数．
平面图形的运动方程
xA f1(t) yA f2 (t)
vA vO vAO vAO R vO
( vO )
R
vA vO2 vAO2
vO 2 vO 2
2vO 或取P为基点: vA vP vAP
vA vAP AP 2R 2vO
（3）B点速度，取O为基点
B vBO vo
vB
ω
A O vo C
P
vB vO vBO
哈工大理论力学教案 第9章
解:1, AB作平面运动 作平面运动
基点: 基点: A
2,
vB = vA + vBA ? √ √
大 ? vA 小 方 √ 向
vB = vA cot
vA vBA = sin
vBA vA ωAB = = l l sin
如图所示平面机构中, 例9-2 如图所示平面机构中,AB=BD= DE= l=300mm.在图示位置时,BD‖AE,杆AB的角速度为 .在图示位置时, , 的角速度为 ω=5rad/s. . 此瞬时杆DE的角速度和杆 中点C的速度 的角速度和杆BD中点 的速度. 求:此瞬时杆 的角速度和杆 中点 的速度.
解:1, AB作平面运动 作平面运动 2, vB = vA + vBA
大 ? ωr ? 小 方 √ 向
= 60
基点: 基点:A
√
√
vB = vA cos 30 = 2 3ωr 3
= 0
vB = 0
= 90
vB = vA = ωr, vBA = 0
如图所示的行星轮系中,大齿轮Ⅰ固定, 例9-4 如图所示的行星轮系中,大齿轮Ⅰ固定,半 径为r 行星齿轮Ⅱ沿轮Ⅰ只滚而不滑动,半径为r 径为 1 ,行星齿轮Ⅱ沿轮Ⅰ只滚而不滑动,半径为 2. 系杆OA角速度为 系杆 角速度为 ωO . 的角速度ω 及其上B, 两点的速度. 求:轮Ⅱ的角速度 Ⅱ及其上 ,C 两点的速度.
解:1 , BD作平面运动 作平面运动
2, vD = vB + vDB 大 ? ωl 小 方 √ 向 √ ? √
基点: 基点:B
vD = vDB = vB =ωl
vD vB ωDE = = = ω = 5rad s DE l vDB vB ωBD = = = ω = 5rad s BD l
理论力学_刚体的平面运动
(基点法： 恰当选取基点，作速度平行四边形，加速度矢量图； 速度投影法： 不能求出图形 ； 速度瞬心法：确定瞬心的位置是关键。）
16
[例1] 曲柄肘杆压床机构 已知：OA=0.15m , n=300 rpm ,AB=0.76m,
BC=BD=0.53m. 图示位置时, AB水平
AB 求该位置时的 BD 、
vo PO rsin 4sin30 2 3 4 3 m/s()
(
）
1 PB PO 2 OB 2 2 PO OB cos120 2 2 4 2 224 2 7 m 2
v B PB 2 7 2 3 4 21 18.3 m/s
研究AB, P１为其速度瞬心 v A OA 0.1510 1.5 m/s
AB vA 1.5 1.5 2 （ 7.16 rad/s AP ABsin 60 0.76 3 1
）
18
7.160.760.57.162.72 m/s vB BP AB cos 60 1 AB
求：当 =60º 时 (OAAB),滚轮的Ｂ，Ｂ．
翻页请看动画
13
分析: 要想求出滚轮的Ｂ, Ｂ 先要求出vB, aB
解：OA定轴转动,AB杆和轮B作平面运动
研究AB：
P1
n /3060 /30 2 rad/s v A OA 152 30 cm/s
P１为其速度瞬心 P2为轮速度瞬心
4
aa aB ; ae a A ; ar aBA aBA aBAn
于是,由牵连平动时加速度合成定理 aa ae ar 可得如下公式：
aB a A aBA aBA n
其中：aBA AB ， 方向AB，指向与 一致；
16
[例1] 曲柄肘杆压床机构 已知：OA=0.15m , n=300 rpm ,AB=0.76m,
BC=BD=0.53m. 图示位置时, AB水平
AB 求该位置时的 BD 、
vo PO rsin 4sin30 2 3 4 3 m/s()
(
）
1 PB PO 2 OB 2 2 PO OB cos120 2 2 4 2 224 2 7 m 2
v B PB 2 7 2 3 4 21 18.3 m/s
研究AB, P１为其速度瞬心 v A OA 0.1510 1.5 m/s
AB vA 1.5 1.5 2 （ 7.16 rad/s AP ABsin 60 0.76 3 1
）
18
7.160.760.57.162.72 m/s vB BP AB cos 60 1 AB
求：当 =60º 时 (OAAB),滚轮的Ｂ，Ｂ．
翻页请看动画
13
分析: 要想求出滚轮的Ｂ, Ｂ 先要求出vB, aB
解：OA定轴转动,AB杆和轮B作平面运动
研究AB：
P1
n /3060 /30 2 rad/s v A OA 152 30 cm/s
P１为其速度瞬心 P2为轮速度瞬心
4
aa aB ; ae a A ; ar aBA aBA aBAn
于是,由牵连平动时加速度合成定理 aa ae ar 可得如下公式：
aB a A aBA aBA n
其中：aBA AB ， 方向AB，指向与 一致；
理论力学第九章刚体的平面运动
O 基点
转角
基点的选取是任意的，平面图形的位置可由O’点 坐标及直线O’M与x’的夹角φ 完全确定。 基点的选择不同，其运动方程9-1a不同，平面图形随基 点平移的速度和加速度也不同。但平面图形绕不同基 点转动的角速度和角加速度却完全相同。证明如下
f (t ) f (t ) 3 3
结 论
刚体的平面运动可以简化为平面图形S 在其自身平面L上的运动。
6
2、运动分析
思考
刚体平面运动是复杂运动，考虑是否可以用 简单运动合成来分析？
Oxy 平移坐标系(动系) 平面运动=随 Oxy 的平移+绕 O 点的转动
=
+
7
3 运动方程
xO f1 t 9-1a yO f 2 t f3 t 9-1b
vB AB = vA
OA
vD
vB
vB
cos30 2 CD作定轴转动（C）
0.2309 m s
vE
vA
vB vD CD 3vB 0.6928 m s CB
vD vE DE = vD ,vE cos 30 vD , vE cos 30 0.8 m s
第九章 刚体的平面运动
本章重点：刚体平面运动的基本概念，求平面图形上各 点的速度与加速度的基点法，以及求速度的 速度投影法和瞬心法，运动学的综合应用。
1
刚体平面运动举例：行星齿轮中小齿轮运动情况
2
车轮运动情况
3
观察曲柄滑块机构中连杆AB的运动情况
4
§ 9-1
1、概念
刚体平面运动的概述和运动分解
30
理论力学第章刚体的平面运动
E
30
B vB
A vA
vD
vB CD CB
3vB
0.693
m s－1
vE60
CO
ω
轮E沿水平面滚动，轮心E的速度 水平，由速度投影定理，D，E 两
点的速度关系为
vE cos 30 vD
求得 vE 0.8 m s－1
§9.3 求平面图形内各点速度的瞬心法
一、问题的提出
B
vA vA
C
vD vA vDA
A Ⅱ
由于齿轮Ⅰ固定不动，接触点D不滑动，所以
ωO O
D
vDA ωⅡ
vD=0 ，因而有 vDA v A O r1 r2
Ⅰ
vDA为D点绕基点A的转动速度，应有
vDA Ⅱ DA
因此
Ⅱ
vDA DA
O (r1
r2
r2 )
（逆时针）
y
SM
O
o
x
§9.1 刚体平面运动的概述和运动分解
刚体平面运动方程
xo xo (t )
yo
yo (t )
(t)
刚体的平面运动可以看成是平动和转动的合成运动。
四、刚体的平面运动分解为平动和转动
刚体平面运动可以分解为随同基点的平动和绕基点
的转动，平面图形随同基点平动的速度和加速度与基点 的选取的有关。绕基点转动的角速度和角加速度则与基 点的选择无关。
动画
刚体平面运动分解
动画
平面运动
动画
平面运动
动画
平面运动分解
动画
平面运动
动画
理论力学复习总结(重点知识点)
第一篇静力学第1 章静力学公理与物体的受力分析1.1 静力学公理公理1 二力平衡公理：作用于刚体上的两个力，使刚体保持平衡的必要和充分条件是：这两个力大小相等、方向相反且作用于同一直线上。
F=-F’工程上常遇到只受两个力作用而平衡的构件，称为二力构件或二力杆。
公理2 加减平衡力系公理：在作用于刚体的任意力系上添加或取去任意平衡力系，不改变原力系对刚体的效应。
推论力的可传递性原理：作用于刚体上某点的力，可沿其作用线移至刚体内任意一点，而不改变该力对刚体的作用。
公理3 力的平行四边形法则：作用于物体上某点的两个力的合力，也作用于同一点上，其大小和方向可由这两个力所组成的平行四边形的对角线来表示。
推论三力平衡汇交定理：作用于刚体上三个相互平衡的力，若其中两个力的作用线汇交于一点，则此三个力必在同一平面内，且第三个力的作用线通过汇交点。
公理4 作用与反作用定律：两物体间相互作用的力总是同时存在，且其大小相等、方向相反，沿着同一直线，分别作用在两个物体上。
公理5 钢化原理：变形体在某一力系作用下平衡，若将它钢化成刚体，其平衡状态保持不变。
对处于平衡状态的变形体，总可以把它视为刚体来研究。
1.2 约束及其约束力１．柔性体约束２．光滑接触面约束３．光滑铰链约束第2章平面汇交力系与平面力偶系1.平面汇交力系合成的结果是一个合力,合力的作用线通过各力作用线的汇交点,其大小和方向可由失多边形的封闭边来表示,即等于个力失的矢量和,即F R=F1+F2+…..+Fn=∑F2.矢量投影定理：合矢量在某轴上的投影，等于其分矢量在同一轴上的投影的代数和。
3.力对刚体的作用效应分为移动和转动。
力对刚体的移动效应用力失来度量；力对刚体的转动效应用力矩来度量，即力矩是度量力使刚体绕某点或某轴转动的强弱程度的物理量。
（Mo（F）=±Fh）4.把作用在同一物体上大小相等、方向相反、作用线不重合的两个平行力所组成的力系称为力偶，记为（F,F’）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
点 A 称为基点(Base point)，一般选为已知点。当图形
S 在平面运动时，基点 A 的坐标 xA，yA 和夹角j 都随
时间而变化。
x y
A A
f1(t ) f2(t )
j f3(t )
（9-1）
y
y
B
yA
Aj
x
O
xA
x
刚体平面运动的运动方程（Equations of planar motion of rigid bodies）
竖直位置处点A、B、C、D的速度。
解：选轮心O为基点，先研
究点C的速度。由于圆轮沿直线 轨道作无滑动的滚动，点C的速 度为
vC vO vCO 0
圆轮的角速度为 vCO vO
RR
A
vDO
vD
D vO O
vO
vAO
vA
vO B vO
vCO
C
vBO vO
vB
各点相对基点的速度为 vAO vBO vDO R vO
[vB ]AB [v A ]AB
vB
vBA
j
vA
B
vB cos(90 j) vA cosj
vB vA cot j
vA
j
A
比较基点法和速度投影法可知，当已知平面图
形上一点速度的大小和方向以及另一点速度的方位
时，应用速度投影法求该点速度的大小和指向是很
方便的，但用速度投影法不能求出平面图形的角速
随着点 M 在垂线 AN 的位置不同，vM 的大小也不
同，总可以找到一点 C，这点的瞬时速度等于零。
vC vA ω AC 0
AC vA ω
刚体作平面运动时，在每一瞬时，图形内必有一 点为速度瞬心；速度瞬心是随时间而变化的，在不同 瞬时，平面图形有不同位置的速度瞬心。
9.4.2 平面运动图形内各点的速度及其分布
证明：设某瞬时，平面图形 S上点 A 的速度为 vA
，图形的角速度为 。若取点 A 为基点，则图形上任
一点 M 的速度
vM v A vMA
如果点 M 位于vA 的垂线 AN上， 则 vA和 vMA 在同一直线上，而方向相 反，故 vM 的大小为：
vCA N
vMA S
A
C
M
vA
vA
vM vA ω AM
则平面图形 S 绕基点 A 作定轴转动；
（2）若 j 为常数，平面图形 S 无转动，则平面图 形 S以方位不变的角 j 作平动。
平面图形 S 的运动可以看成是随着基点的平动和绕 基点的转动的合成。或者说，平面图形 S 的运动可以分 解为平动和转动。
一般的情况下，在基点 A 处建立平动坐标系 Axy。 图形 S的绝对运动（对于定系Oxy的运动）是平面运动， 相对运动（对于动系的运动）是绕基点A的转动，牵连 运动（动系对于静系Oxy的运动）为随基点A的平动。
平面图形内各点速度的大小与该点到速度瞬心的距 离成正比。速度的方向垂直于该点到速度瞬心的连线， 指向图形转动的一方。
平面图形上各点速度在某瞬时的分布情况，与图形 绕定轴转动时各点速度的分布情况类似。因此，平面图 形的运动可看成为绕速度瞬心的瞬时转动。
如果求出平面图形在某一瞬时的速度瞬心位置和 角速度，就可以很容易地确定该瞬时图形内各点的速 度。
常用的还有用瞬心法。 9.4.1 平面图形的速度瞬心 在某一瞬时，平面图形（或其延伸部分）上速度
等于零的点称为平面图形的瞬时速度中心（Instantane -ous center of velocity），简称为速度瞬心。
定理：一般情况，在每一瞬时，平面图形（或其 延伸部分）上都惟一地存在一个速度为零的点。
vA
j
A
速度 大小 方向
vB vA vBA
vB
vA
？
vA
铅直方位 水平向左
vBA
？ 垂直AB
作出速度平行四边形，vB位于速度平行四边形 的对角线上。由几何关系可得
vB vA cot j
vBA
vA
sin j
AB
vBA l
l
vA
sin j
例9-2 平面机构，AB = BD = DE = l = 30 cm，在
vBA 称为点 B 绕基点 A 转动
vB
v
BA
vA
B
vA
A
的速度，它的大小等于 O
x
vBA ω AB
方向垂直于转到半径AB，指向与平面图形的转向一致。
由速度合成定理得
vB vA vBA
（9-2）
平面图形内任一点的速度等于基点的速度与该点
绕基点转动的速度的矢量和。这种求平面图形内任一
点速度的方法称为基点法（Method of base point）。
结论：刚体的平面运动可以 简化为平面图形S 在其自身 平面内的运动。
9.1.3 刚体的平面运动方程
在平面图形S内建立平面直角坐标系Oxy，为确定
平面图形 S 在任意瞬时 t 的位置，只须确定其上任意
线段 AB 的位置，而线段 AB 的位置可由点 A 的坐标
xA，yA 和线段 AB 与 x 轴（或 y 轴）的夹角j 来确定。
A的速度为
vA vO vAO 2vO
B的速度为
vB vO2 vBO2 2vO
同理，可得D的速度为
A
vDO
vD
D vO O
vO
vAO
vA
vO B vO
vCO
C
vBO vO
vB
vD 2vO
9.3.2 速度投影法
应用矢量投影定理，将该矢量式 vB vA vBA向
AB连线投影 。
vA cos vB cos
根据机构的几何条件，确定速度瞬心位置的方法有 下列几种：
（1）当平面图形沿一固定面作无滑动的滚动（纯 滚动）时。平面图形与固定面的接触点 C 就是图形的 速度瞬心。
车轮在纯滚动的过程中，轮缘 上的各点相继与地面接触而成为车 轮在不同时刻的速度瞬心。
v C
（2）已知图形内任意两点 A 和 B 的速度的方向， 速度瞬心 C 的位置必在每一点速度的垂线上。
例如沿平直轨道作直线滚动的车轮，如图9-4所 示，设车轮的轮心 C 以速度 v0 作匀速运动，选点 C 为基点，初始时 C 点在 y 轴上，任一瞬时 CM 与 y
轴的夹角j，则车轮的运动方程为：
xc v0t,
yc R,
j v0t
R
y
y
C1
MR C
v0
j M1
O
K
x
x
9.2 平面运动分解为平动和转动 （1）若基点 A 不动，基点 A 坐标 xA，yA 均为常数，
A B
B A
B
j1
B
j2
A
A
dA dB
dt dt
A B
图形S绕基点转动的角速度、角加速度称为平面图形的角速
度和角加速度，而不必指明其基点。
9.3 求平面图形内各点速度的基点法
9.3.1 基点法 运用速度合成定理求平面图形内各点的速度。
取 A 为基点，牵连速度
y
ve vA
B点的相对速度 vr vBA
[vB ]AB [v A ]AB
（9-3）
速度投影定理：平面图形上任意两点的速度在 这两点连线上的投影相等。速度投影定理是刚体上任 意两点间的距离保持不变的必然结果。适用于任何形 式的刚体运动。
应用速度投影定理求速度的方法称为速度投影 法。
例9-4 用速度投影法求例9-1中点B的速度。
解： 依据
9.1.2 平面运动的简化
⑴ 作平面Ⅱ∥定平面Ⅰ且与 刚体相交成一平面图形S 。当刚体 运动时，平面图形S 始终保持在平 面Ⅱ内。平面Ⅱ称为平面图形S 自 身所在平面。
⑵ 在刚体上任取⊥平面图形S 的直线A1A2 ， A1A2 作平动，其上各 点都具有相同的运动。
⑶ A1A2 和图形S 的交点 A 的运动可代表全部A1A2 的运动， 而平面图形S 内各点的运动即可代表全部刚体的运动。
当 vA 和 vB 同向时，图 形的速度瞬心在 AB 的延长 线上；
9 刚体的平面运动
刚体的平面运动是机构中常见的一种运动，研 究刚体的平面运动具有重要的意义。
刚体的平面运动可以看成是随基点的平动（牵 连运动）与绕基点的转动（相对运动）的合成。
本章将研究刚体平面运动的描述方法，以及刚 体内各点的速度，加速度。
9.1 刚体平面运动的运动方程 9.1.1 刚体平面运动的定义 刚体运动时，如其上各点到某一固定平面的距离
BD vCB
C vB
vDB
60º vD
vC 60º
D
vB
vB
DE
60º E
vD vB vDB
作速度平行四边形。
16
vD vB 150cm/s
vDB vB 150 cm/s
DE
vD DE
vD l
5
rad /s
DB
vDB DB
5
rad/s
vDB
BD vCB
60º vD
vC
B
60º
C
D
vB
vB
度。
例9-5 已知 OA = 10 cm，以角速度 2 rad/s
转动，CD = 3 CB，在图示位置时，A、B、E 三点恰
在同一水平线上，且 CD ED 。
试求此瞬时点 E 的速度。
vD D
30º E
vE
B
vB
A vA
60
C
O
解：（1）运动分析：杆 OA、CD 作定轴转动， 杆 AB、DE 以及轮 E 作平面运动。
图示位置时，BD // DE，杆 AB 角速度为 5rad/s
S 在平面运动时，基点 A 的坐标 xA，yA 和夹角j 都随
时间而变化。
x y
A A
f1(t ) f2(t )
j f3(t )
（9-1）
y
y
B
yA
Aj
x
O
xA
x
刚体平面运动的运动方程（Equations of planar motion of rigid bodies）
竖直位置处点A、B、C、D的速度。
解：选轮心O为基点，先研
究点C的速度。由于圆轮沿直线 轨道作无滑动的滚动，点C的速 度为
vC vO vCO 0
圆轮的角速度为 vCO vO
RR
A
vDO
vD
D vO O
vO
vAO
vA
vO B vO
vCO
C
vBO vO
vB
各点相对基点的速度为 vAO vBO vDO R vO
[vB ]AB [v A ]AB
vB
vBA
j
vA
B
vB cos(90 j) vA cosj
vB vA cot j
vA
j
A
比较基点法和速度投影法可知，当已知平面图
形上一点速度的大小和方向以及另一点速度的方位
时，应用速度投影法求该点速度的大小和指向是很
方便的，但用速度投影法不能求出平面图形的角速
随着点 M 在垂线 AN 的位置不同，vM 的大小也不
同，总可以找到一点 C，这点的瞬时速度等于零。
vC vA ω AC 0
AC vA ω
刚体作平面运动时，在每一瞬时，图形内必有一 点为速度瞬心；速度瞬心是随时间而变化的，在不同 瞬时，平面图形有不同位置的速度瞬心。
9.4.2 平面运动图形内各点的速度及其分布
证明：设某瞬时，平面图形 S上点 A 的速度为 vA
，图形的角速度为 。若取点 A 为基点，则图形上任
一点 M 的速度
vM v A vMA
如果点 M 位于vA 的垂线 AN上， 则 vA和 vMA 在同一直线上，而方向相 反，故 vM 的大小为：
vCA N
vMA S
A
C
M
vA
vA
vM vA ω AM
则平面图形 S 绕基点 A 作定轴转动；
（2）若 j 为常数，平面图形 S 无转动，则平面图 形 S以方位不变的角 j 作平动。
平面图形 S 的运动可以看成是随着基点的平动和绕 基点的转动的合成。或者说，平面图形 S 的运动可以分 解为平动和转动。
一般的情况下，在基点 A 处建立平动坐标系 Axy。 图形 S的绝对运动（对于定系Oxy的运动）是平面运动， 相对运动（对于动系的运动）是绕基点A的转动，牵连 运动（动系对于静系Oxy的运动）为随基点A的平动。
平面图形内各点速度的大小与该点到速度瞬心的距 离成正比。速度的方向垂直于该点到速度瞬心的连线， 指向图形转动的一方。
平面图形上各点速度在某瞬时的分布情况，与图形 绕定轴转动时各点速度的分布情况类似。因此，平面图 形的运动可看成为绕速度瞬心的瞬时转动。
如果求出平面图形在某一瞬时的速度瞬心位置和 角速度，就可以很容易地确定该瞬时图形内各点的速 度。
常用的还有用瞬心法。 9.4.1 平面图形的速度瞬心 在某一瞬时，平面图形（或其延伸部分）上速度
等于零的点称为平面图形的瞬时速度中心（Instantane -ous center of velocity），简称为速度瞬心。
定理：一般情况，在每一瞬时，平面图形（或其 延伸部分）上都惟一地存在一个速度为零的点。
vA
j
A
速度 大小 方向
vB vA vBA
vB
vA
？
vA
铅直方位 水平向左
vBA
？ 垂直AB
作出速度平行四边形，vB位于速度平行四边形 的对角线上。由几何关系可得
vB vA cot j
vBA
vA
sin j
AB
vBA l
l
vA
sin j
例9-2 平面机构，AB = BD = DE = l = 30 cm，在
vBA 称为点 B 绕基点 A 转动
vB
v
BA
vA
B
vA
A
的速度，它的大小等于 O
x
vBA ω AB
方向垂直于转到半径AB，指向与平面图形的转向一致。
由速度合成定理得
vB vA vBA
（9-2）
平面图形内任一点的速度等于基点的速度与该点
绕基点转动的速度的矢量和。这种求平面图形内任一
点速度的方法称为基点法（Method of base point）。
结论：刚体的平面运动可以 简化为平面图形S 在其自身 平面内的运动。
9.1.3 刚体的平面运动方程
在平面图形S内建立平面直角坐标系Oxy，为确定
平面图形 S 在任意瞬时 t 的位置，只须确定其上任意
线段 AB 的位置，而线段 AB 的位置可由点 A 的坐标
xA，yA 和线段 AB 与 x 轴（或 y 轴）的夹角j 来确定。
A的速度为
vA vO vAO 2vO
B的速度为
vB vO2 vBO2 2vO
同理，可得D的速度为
A
vDO
vD
D vO O
vO
vAO
vA
vO B vO
vCO
C
vBO vO
vB
vD 2vO
9.3.2 速度投影法
应用矢量投影定理，将该矢量式 vB vA vBA向
AB连线投影 。
vA cos vB cos
根据机构的几何条件，确定速度瞬心位置的方法有 下列几种：
（1）当平面图形沿一固定面作无滑动的滚动（纯 滚动）时。平面图形与固定面的接触点 C 就是图形的 速度瞬心。
车轮在纯滚动的过程中，轮缘 上的各点相继与地面接触而成为车 轮在不同时刻的速度瞬心。
v C
（2）已知图形内任意两点 A 和 B 的速度的方向， 速度瞬心 C 的位置必在每一点速度的垂线上。
例如沿平直轨道作直线滚动的车轮，如图9-4所 示，设车轮的轮心 C 以速度 v0 作匀速运动，选点 C 为基点，初始时 C 点在 y 轴上，任一瞬时 CM 与 y
轴的夹角j，则车轮的运动方程为：
xc v0t,
yc R,
j v0t
R
y
y
C1
MR C
v0
j M1
O
K
x
x
9.2 平面运动分解为平动和转动 （1）若基点 A 不动，基点 A 坐标 xA，yA 均为常数，
A B
B A
B
j1
B
j2
A
A
dA dB
dt dt
A B
图形S绕基点转动的角速度、角加速度称为平面图形的角速
度和角加速度，而不必指明其基点。
9.3 求平面图形内各点速度的基点法
9.3.1 基点法 运用速度合成定理求平面图形内各点的速度。
取 A 为基点，牵连速度
y
ve vA
B点的相对速度 vr vBA
[vB ]AB [v A ]AB
（9-3）
速度投影定理：平面图形上任意两点的速度在 这两点连线上的投影相等。速度投影定理是刚体上任 意两点间的距离保持不变的必然结果。适用于任何形 式的刚体运动。
应用速度投影定理求速度的方法称为速度投影 法。
例9-4 用速度投影法求例9-1中点B的速度。
解： 依据
9.1.2 平面运动的简化
⑴ 作平面Ⅱ∥定平面Ⅰ且与 刚体相交成一平面图形S 。当刚体 运动时，平面图形S 始终保持在平 面Ⅱ内。平面Ⅱ称为平面图形S 自 身所在平面。
⑵ 在刚体上任取⊥平面图形S 的直线A1A2 ， A1A2 作平动，其上各 点都具有相同的运动。
⑶ A1A2 和图形S 的交点 A 的运动可代表全部A1A2 的运动， 而平面图形S 内各点的运动即可代表全部刚体的运动。
当 vA 和 vB 同向时，图 形的速度瞬心在 AB 的延长 线上；
9 刚体的平面运动
刚体的平面运动是机构中常见的一种运动，研 究刚体的平面运动具有重要的意义。
刚体的平面运动可以看成是随基点的平动（牵 连运动）与绕基点的转动（相对运动）的合成。
本章将研究刚体平面运动的描述方法，以及刚 体内各点的速度，加速度。
9.1 刚体平面运动的运动方程 9.1.1 刚体平面运动的定义 刚体运动时，如其上各点到某一固定平面的距离
BD vCB
C vB
vDB
60º vD
vC 60º
D
vB
vB
DE
60º E
vD vB vDB
作速度平行四边形。
16
vD vB 150cm/s
vDB vB 150 cm/s
DE
vD DE
vD l
5
rad /s
DB
vDB DB
5
rad/s
vDB
BD vCB
60º vD
vC
B
60º
C
D
vB
vB
度。
例9-5 已知 OA = 10 cm，以角速度 2 rad/s
转动，CD = 3 CB，在图示位置时，A、B、E 三点恰
在同一水平线上，且 CD ED 。
试求此瞬时点 E 的速度。
vD D
30º E
vE
B
vB
A vA
60
C
O
解：（1）运动分析：杆 OA、CD 作定轴转动， 杆 AB、DE 以及轮 E 作平面运动。
图示位置时，BD // DE，杆 AB 角速度为 5rad/s