3变精度粗糙集方法
第六讲 变精度粗糙集模型

P( E6 , X ) 0 ,故 m1 0.5 , m2 0.25 ,
从而 ( R, X ) 0.5 ,即使得 X 为 精确集的最小的 值为 0.5 , 或者说,对于任意 0.5 , X 为 粗糙集。
3 (2)令 X {x1 , x2 , x6 , x9},则 P( E1 , X ) , 5 2 3 P( E2 , X ) , P( E3 , X ) , P(E4 , X ) P(E5 , X ) P(E6 , X ) 1 , 3 4
R ( X ) {[ x]R ; P([ x]R , X ) 0.7} U E3.
从而 bnr ( X ) E1 E2 E4 , negr ( X ) E3.
0.3 0.3
0.3
0.3
3 基本性质
定理: 设 (U , R) 为近似空间。对于任意的 X , Y U ,
由于 P( E1 , X ) ,P( E2 , X ) 故
3 5
2 1 1 ,P( E3 , X ) 1 ,P( E4 , X ) ,P( E5 , X ) ,P( E6 , X ) 0 , 3 2 4
R ( X ) {[ x]R ; P([ x]R , X ) 0.3} E5 E6 {xi ;15 i 20},
第六讲: Ziarko变精度粗糙集模型
1 错分率与多数包含关系
设 U 为非空有限论域, X , Y U . 令
1 | X Y | , | X | 0 | X | P( X , Y ) | X | 0 0,
其中 | X | 表示集合 X 的基数。称 P( X , Y ) 为集合 X 关于集合 Y 的相对错误分类率。
一种利用属性序关系的变精度粗糙集知识约简方法

第32卷第4期2008年8月江西师范大学学报(自然科学版)J cI U R N A L0FⅡA N GⅪN O R l雌L I『r qⅣER SI TY(N A l r I瓜AI.ScI E N CE)、,01.32N o.4A I l g.2008一种利用属性序关系的变精度粗糙集知识约简方法张玉琢(云南师范大学计算机科学与技术系,云南昆明650092)摘要:变粗糙集模型主要用于包含错误信息或缺失一些重要信息的决策表的知识获取.该文引入了变粗糙集模型和卢上、下分布约简和分布约简(卢约简)的概念,并讨论了它们之间的关系;通过对约简的进一步研究,得到可辩识矩阵及其特性;在此基础上提供了利用属性序关系的约简算法,并通过含有噪声的实例验证了此方法的可行性和有效性.关键词:变粗糙集模型;知识约简;决策表;协调集中图分类号:TP18文献标识码:A自波兰数学家娜l ak提出粗糙集(R S)理论以来,它已被广泛应用于模式识别,机器学习,知识获取,人工智能等领域.但经典粗糙集理论存在一些局限[1.21;对此,研究者对经典粗糙集理论进行了不同的扩展.zi ar ko教授于1993年提出的变精度粗糙集模型心J是其中重要一分支.在该模型中,给定一个阈值,当对象所在的等价类在某种程度上包含于集合j中时,就认为这个对象属于X,这个推广在应用上是非常重要的,因为在实际应用中,绝对的包含有时是不必要的.知识约简是变精度粗糙集研究的重要内容,文献[1‘5]中对此问题有所讨论.归结所讨论的约简方法大致为两大类:一类是利用属性启发式约简算法求得属性约简集,其特点是以属性重要度作为启发式信息bo;二类是利用可辨识矩阵,通过对属性组合的合取和析取操作得到一个属性约简集u圳,但当得到的可辨识矩阵维数较高时。
该算法计算复杂度高,内存消耗量大,并且如何选取满意的特征属性组合是一个待商榷的问题怛12J.本文针对这个问题,提出了一个改进算法,在得出可辩识矩阵后,利用属性序关系求约简的算法,最后,通过具体实例验证该算法的有效性.1变精度粗糙集模型定义1【4】一个信息系统s可以表示为5=(u,C U D,y,.厂),其中u表示对象的非空有限集合,U= {石l,算2,…,‰I;C表示属性的非空有限集合,C={口I,口2,…,口。
基于随机抽样的变精度邻域粗糙集特征选择

廊坊师范学院学报(自然科学版) Journal of Langfang Normal University(Natural Science Edition)
Jun.2019 Vol.19 No.2
基于随机抽样的变精度邻域粗糙集特征选择
沈林
(莆田学院,福建莆田351100)
定义4决策系统的近似邻域依赖:
MDS) = |POS(QS)|/|U|
(2)
其中 POS(DS) = U^y,. ,Yj^U/D 是 D 对样本
U的划分,AsYj为决策类与在条件特征/的6邻
【摘要】在变精度邻域粗糙集的特征选择中,改进后的区分矩阵相较于依赖度,具有时间复杂度较低的优点,但由 于空间占用高,限制了其在大规模数据上的应用。减小数据规模虽然可以大幅降低空间消耗,但存在信息量丢失的风 险,为此,通过随机抽取多个小规模数据子集以降低空间占用,在分别进行特征选择后,选择权重高的特征子集进行了 测试。实验结果证明,可以将空间占用降低2-3个数量级,并保持精度和抽样前相当。 【关键词】邻域粗糙集;随机抽样;特征选择
• 14 •
第19卷•第2期
沈林:基于随卿样的删度
2019年6月
需要将样本离散化,这会掺杂进主观的因素,可能 会改变数据原有的含义。Hu用邻域关系代替了等 价关系,可以更加客观地描述样本之间的关系,在 这里先介绍邻域关系的定义。
定义2在上述DS中,对于特征Bu/ , U中样 本兀在特征B下的邻域关系可以记为
1基本概念
1.1邻域粗糙集和变精度邻域粗糙集模型 定义1 U为有限实数集合,d为特征集合,£>
为决策类,则{U,A,D)被称为决策信息系统DS。 邻域粗糙集是Hu为了弥补经典粗糙集理论的
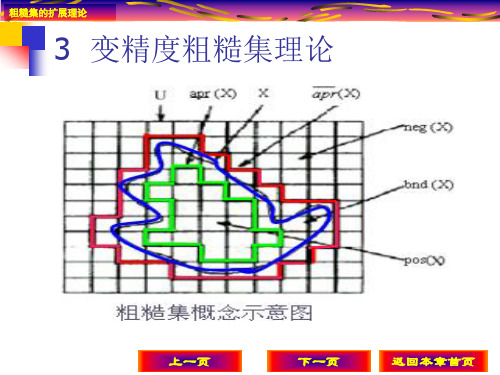
3变精度粗糙集方法
上一页
下一页
返回本章首页
粗糙集的扩展理论
β-粗糙近似
令:β=0.6,则β-粗糙近似分别为:
对论域进行划分,可得如下等价类 U/C={X1, X2, X3, X4, X5} 其中,X1={n1, n4,n6},X2={n2},X3={n3},X4={n5},X5={n7} U/D={YN,YP} 其中,YN={n1, n2,n3},YP={n4, n5,n6, n7}
上一页
U n1 n2 n3 n4 n5 n6 n7
a1
1 1 2 1 2 1 2
a3
1 2 1 1 2 1 2
d N N N P P P P
下一页
返回本章首页
粗糙集的扩展理论
由β-约简{a1 ,a3}构造的概率决策规则
表 2.6 由β-约简{a1 ,a3}构造的规则 规则 支持数 1 1 3 2
下一页
上一页 下一页 返回本章首页
粗糙集的扩展理论
β值与分类精度关系
上一页
下一页
返回本章首页
粗糙集的扩展理论
变精度粗糙集的分类质量
上一页
下一页
返回本章首页
粗糙集的扩展理论
变精度粗糙集中的近似约简
上一页
下一页
返回本章首页
粗糙集的扩展理论
概率规则获取
上一页
下一页
返回本章首页
粗糙集的扩展理论
算例 1
对论域进行划分,可得如下等价类: U/C={X1, X2, X3, X4, X5} 其中:X1={n1,n4,n6},X2={n2},X3={n3},X4={n5},X5={n7} U/D={YN,YP} 其中:YN={n1,n2,n3},YP={n4,n5,n6, n7} 求得一个β-约简为{a1,a3 }, β=0.6,则 β{a β=0.6
变精度软粗糙集

变精度软粗糙集石梦婷;刘文奇;余高锋;李磊【期刊名称】《计算机工程与应用》【年(卷),期】2014(000)001【摘要】According to the inclusion degree between two sets, a variable precision soft rough set based on the inclusion degree theory is constructed. Firstly, variable precision approximation operators with a parameter are defined. Then several important properties and theorems are proposed and proved. Secondly, double variable precision approximation operators with two parameters are presented, whose properties are also studied. Finally, the relation between the above-model and other rough set models is discussed, as well as the degeneration condition. At the same time, an example is illustrated to explain the applications in information processing.%从集合间的包含程度出发,构造了一种基于包含度的变精度软粗糙集模型。
提出带参数的变精度近似算子的定义,得到了它的基本性质和定理,并给出了证明;定义了双精度软粗糙集的近似算子,研究了其性质;讨论了该模型与其他粗糙集模型的关系以及退化条件;举例说明了在信息处理中的应用。
一种新的应用变精度粗糙集的决策树构造方法

一种新的应用变精度粗糙集的决策树构造方法
王越;万洪
【期刊名称】《重庆理工大学学报(自然科学版)》
【年(卷),期】2013(027)011
【摘要】决策树分类方法是一种有效的数据挖掘分类方法,但在构造决策树的过程中,节点属性选择的标准直接影响分类的效果.对此,应用变精度粗糙集的理论提出了变精度决策分类熵和信息决策熵的概念,并把信息决策熵作为节点属性选择的标准.信息决策熵综合考虑了属性的当前分类能力和属性之间的依赖关系,克服了只突出属性分类能力的缺点.理论和实例分析结果表明:与经典的ID3决策树算法及其他算法相比,该算法能得到简洁高效的决策树.
【总页数】7页(P58-64)
【作者】王越;万洪
【作者单位】重庆理工大学计算机科学与工程学院,重庆400054;重庆理工大学计算机科学与工程学院,重庆400054
【正文语种】中文
【中图分类】TP301.6
【相关文献】
1.一种新的应用变精度粗糙集的决策树构造方法 [J], 王越;万洪;
2.新的决策树构造方法 [J], 张凤莲;林健良
3.一种基于变精度粗糙集的C
4.5决策树改进算法 [J], 刘兴文;王典洪;陈分雄
4.一种基于粗糙集理论的决策树构造方法 [J], 于海平;朱玉全;陈耿;欧吉顺
5.基于变精度粗糙集的分类决策树构造方法 [J], 庞哈利;高政威;左军伟;卞玉倩因版权原因,仅展示原文概要,查看原文内容请购买。
基于对象阈值变精度概念的启发式推荐方法

基于对象阈值变精度概念的启发式推荐方法
张国锋;杨凯
【期刊名称】《计算机工程与设计》
【年(卷),期】2024(45)4
【摘要】针对启发式概念推荐方法进行优化,提出一种基于对象阈值变精度概念的启发式推荐方法。
将模糊形式背景转化为对象阈值可变的变精度形式背景,在此形式背景的基础上定义概念构造的启发式信息;利用内涵约束,在保证群组相似度的基础上,构造当前加权面积最大的概念,将这些概念组成强概念集合;在这个概念集合中利用组推荐方法对所有用户进行推荐。
实验在MovieLens系列数据集和FilmTrust数据集上的一系列结果验证这种优化是有效的,能够大幅加强推荐的精度和性能。
【总页数】8页(P1141-1148)
【作者】张国锋;杨凯
【作者单位】辽宁科技大学计算机与软件工程学院
【正文语种】中文
【中图分类】TP399
【相关文献】
1.变精度对象概念格的构造及其性质
2.基于变精度双论域粗糙集的个性化推荐方法
3.一种变精度粗糙集模型阈值选取的方法
4.基于多阈值的变精度邻域多粒度粗糙决策方法
5.启发式概念构造的组推荐方法
因版权原因,仅展示原文概要,查看原文内容请购买。
一种基于变精度粗糙集的规则提取方法研究

05 .
1
() 3
由 () 和 () 的定 义 , 对 于 给定 的 D 等 价 2式 3式 则 类[ D]定义 属性 集 C的 下 近似 集 为
收稿 日期 :0 50 —5 2 0— 90
基 金项 目: 教育部“ 世纪优秀人才支持计划 ”0 X 0 5 ) 新 (5 E 1 1 资助
_
g p ] [ / c
=
集 的下 近似集 和属 性 集 合基 数 之 间 的关 系 , 据该 根 关 系 提 出了一种 易实 现 的变精 度 粗糙 集决 策 表约简
算 法 。仿真实 验结 果 表 明本 文所 提 出的算 法计算 简 单、 易实现 。 容
{IrC ) 1 ‘ I‘ Cd ) ≥ , Cd ̄ _ , g ) c丽 (D _ 2a(cA an r _ J
关
键
词: 变精 度粗 糙 集 , 决策 表 , 性 属
文献 标识 码 : A 文 章编号 :0 02 5 ( O 6 O — 8 — 4 1 0 —7 8 2 O ) 33 00
中图分类 号 : 4 . V2 0 2
粗 糙集 理 论 是 1 8 9 2年 由波 兰 数 学 家 Z z lw dia s
和X 区分 开 。
变压 器故 障诊 断 中的应用 , 献 [ ] 究 了粗糙 集理 文 8研 论在航 空武 器系 统评 估 中的应 用 。 文献 [ ,] 7 8 均是 采 用 经 典 的 P wlk粗 糙 集模 型 , 模 型 所 处 理 的 分 a a 该 类 必 需是 完全 肯 定 的 , 不适 合 处理 具 有 干 扰 的决 策 表 数据 , 因此 Zak ir o提 出了 可处 理具 有 干 扰 的决 策 表数 据 的变精 度粗糙 集 模 型[ 。 9 ]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3变精度粗糙集方法
粗糙集方法是为了解决模糊或不确定性问题而发展的一种理论与方法。
在粗糙集方法中,对象的属性值可以是模糊的或精确的,而决策或分类规
则可以通过属性之间的相对约束关系来确定。
本文将介绍三个常用的变精
度粗糙集方法,并对其进行详细阐述。
1.粗糙集的数学模型:
粗糙集的数学模型是基于信息系统理论和近似推理理论。
它可以将不
精确或模糊的数据转化为一个或多个精确的决策或分类规则。
其数学模型
定义了粗糙集的三个基本元素:信息系统、下近似集和上近似集。
这三个
元素构成了粗糙集的主要特性和运算规则。
2.变精度粗糙集的基本概念:
在粗糙集方法中,为了处理不确定性或模糊性问题,可以使用变精度
技术来调整精确度。
变精度粗糙集是在标准粗糙集的基础上引入了多个精
度级别的概念,从而可以根据不同的应用要求对精确度进行调整。
3.粗糙集方法的三个变精度技术:
a.基于粗糙集的属性精度:
在传统粗糙集方法中,属性的精确度是预先定义的,而在基于粗糙集
的属性精度技术中,属性的精确度是由用户根据实际情况进行调整的。
通
过调整属性的精确度,可以提高粗糙集方法的分类或决策效果。
b.基于粗糙集的决策精度:
传统粗糙集方法中,决策的精确度是通过属性之间的相对约束关系来
确定的。
而在基于粗糙集的决策精度技术中,可以通过调整决策的精确度
来改善分类或决策结果。
这种技术常常会涉及到模糊推理或概率推理的方法。
c.基于粗糙集的规则精度:
在传统粗糙集方法中,规则的精确度是预先定义的。
而在基于粗糙集的规则精度技术中,可以通过调整规则的精确度来提高分类或决策的准确性。
这种技术通常涉及到规则的修剪或合并。
总结起来,粗糙集方法是一种基于信息系统理论和近似推理理论的模糊或不确定性问题处理方法。
它的数学模型定义了信息系统、下近似集和上近似集等三个基本元素,并通过属性精度、决策精度和规则精度等三个变精度技术来提高分类或决策的准确性。
这些方法在实际应用中具有较好的效果,并逐渐成为数据挖掘和智能决策等领域的重要研究方向。
