直线与圆的方程
圆的方程.直线与圆的方程

练习
平面上三个定点 A(-2 3, 0),B( 2 3 ,0) C(4 3 ,6), 点P是平面上满足 APB = 的一 3 个动点,求线段 PC 的长的最小值及点 P的坐标
再
见!
3、圆的参数方程
x a r cos (为参数) y b rsim
4、直线与圆的关系 1)直线L:y = k x + b 和圆 x2 + y2 = r2 相切、相交、相离 2)过圆x2 + y2 = r2上点P(x0,y0)的切线方 程:x0 x+y0 y=r2 3)直线被圆所截曲线方程:F1(x,y)=0和F2(x,y)=0,它们的交 点是P(x0,y0)求证:方程 F1(x,y)+λF2(x,y)=0 的曲线也经过点P( λ是任意实数 )
练习6.求经过两圆x2 +y2 +6x–4=0 和x2 + y2 +6y–28 = 0
的交点,且圆心在直线x – y – 4 = 0上的圆方程
练习2.如果直线L将圆x2 + y2 -2x-4y=0平分,且不过第 四象限,那么L的斜率的取值范围是___
(全国高考题)
例2.求当点(x,y)在以原点为圆心,a为半径的
圆上运动时,点(x+y,xy)的轨迹方程
练习3.求由曲线x2+y2=|x|+|y|所围成的图形 的面积
例3.如果直线l:y = x + b与曲线C: y 1 x 2 只有
圆方程及直线与 圆的位置关系
一、基本概念
1、圆的标准方程 以(a,b)为圆心,r为半径的圆的标准方程为: (x - a)2+(y - b)2 = r2
2、圆的一般方程:
x2 + y2 +D x + E y + F = 0
圆与直线方程的所有公式

圆与直线方程的所有公式
嘿呀,让我来给你讲讲圆与直线方程的那些公式哈!先来说说圆的标准方程,那就是$(x-a)^2+(y-b)^2=r^2$。
比如说,有个圆的圆心在(3,4),半径是 5,那这个圆的方程不就是$(x-3)^2+(y-4)^2=25$嘛!
再说说圆的一般方程$x^2+y^2+Dx+Ey+F=0$。
嘿,就好像每个圆都有自己独特的代码似的!
然后是直线方程呀,点斜式$y-y_1=k(x-x_1)$。
比如说已知直线上一点(2,3),斜率是 2,那直线方程不就是$y-3=2(x-2)$嘛!
还有斜截式$y=kx+b$,这就好比是直线的一种简洁表达。
两直线平行,它们的斜率相等哦!这就好像两个人走在平行的道路上。
两直线垂直,它们斜率的乘积为-1 呀!哇塞,是不是很神奇呢?咱可得把这些公式都记牢咯,在解决问题的时候就能派上大用场啦!。
直线与圆的方程
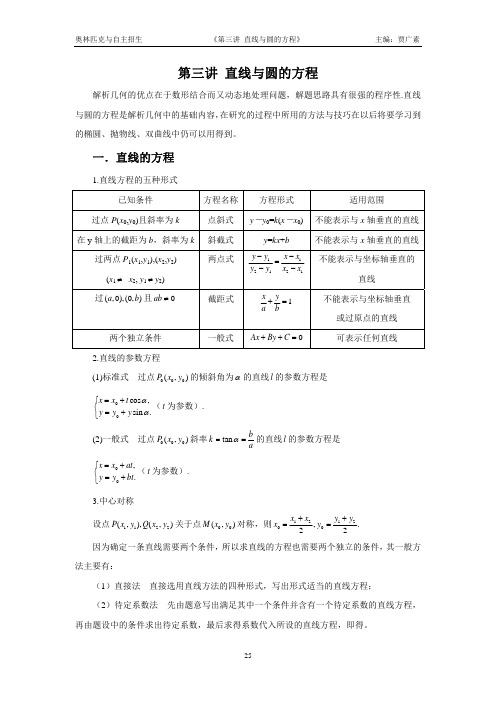
acr (c bk ) . cr acrk bcrk ack
2
同理考虑过点 B 的直线系方程,可得 xM 所以 | DM || DN | .
acr (c bk ) . cr acrk bcrk ack
2
类似的直线型几何问题, 有时用直线系方程处理比较简捷。 这里有一点需要向大家说明, 在竞赛数学中,用解析法处理平面几何问题,在计算过程中只要有一步计算错误,则整个解 答过程就算是错误的,这一点应该引起重视!
y c ( x a). ba
M P
C
A
所以过点 C 的直线系方程为
cx (a b) y ca (kx y ) 0,
E
D
F
N
1 ○
B
因为 PC 过点 P ,而 P(br , cr ) ,则 代入○ 1 式,并令 y 0, 解得 xN
bcr (a b)cr ac cr kbr
A y1 y2 ( ) 1, B x1 x2 A x1 x2 B y1 y2 C 0. 2 2
28
奥林匹克与自主招生
《第三讲 直线与圆的方程》
主编:贾广素
解关于 x1 , x2 的方程组,即可得 Q 点的坐标. 例 3.在直线 l : x y 5 0 上找一点 P ( x, y ) ,使得点 P ( x, y ) 对 A(1, 0), B(3, 0) 的视角 APB 最 大。 要使 APB 分析: 求点 P 的坐标, 一般来说通过三角函数值来刻画, 显然,APB 是锐角, 最大,只需求出夹角 APB 的正切的表达式,再去寻找最大值。凡是处理斜率问题都需要注 意斜率不存在的情况,故 AE,BF 垂直 AB 交 l 于 E、F,只需求当 P 不与 E、F 重合时夹角
直线与圆的方程

直线与圆的方程直线与圆是几何学中的基本概念,在解决几何问题时经常需要用到它们的方程。
本文将介绍直线与圆的方程的基本形式和求解方法,并通过实例加深理解。
一、直线的方程直线的方程可以使用点斜式、斜截式和两点式来表示。
下面逐一介绍这三种形式的方程表示方法。
1. 点斜式方程点斜式方程形式为 y-y₁=m(x-x₁),其中 (x₁,y₁) 是直线上的某一点,m 是直线的斜率。
通过已知点和斜率,可以轻松写出点斜式方程。
例如,如果已知直线过点 (2,3),斜率为 2/3,则点斜式方程为 y-3=(2/3)(x-2)。
2. 斜截式方程斜截式方程形式为 y=mx+b,其中 m 是直线的斜率,b 是直线与 y轴的截距。
通过已知斜率和截距,可以得到斜截式方程。
例如,如果已知直线斜率为 -1/2,截距为 2,则斜截式方程为 y=(-1/2)x+2。
3. 两点式方程两点式方程形式为 (y-y₁)/(y₂-y₁)=(x-x₁)/(x₂-x₁),其中 (x₁,y₁)和 (x₂,y₂) 是直线上的两个不同点。
通过已知两个点,可以计算出两点式方程。
例如,已知直线经过点 (1,3) 和 (4,7),则两点式方程为 (y-3)/(7-3)=(x-1)/(4-1)。
二、圆的方程圆的方程可以使用标准式和一般式来表示。
下面逐一介绍这两种形式的方程表示方法。
1. 标准式方程标准式方程形式为 (x-h)²+(y-k)²=r²,其中 (h,k) 是圆心坐标,r 是半径。
通过已知圆心和半径,可以直接写出标准式方程。
例如,如果已知圆心坐标为 (2,-3),半径为 5,则标准式方程为 (x-2)²+(y+3)²=25。
2. 一般式方程一般式方程形式为 x²+y²+Ax+By+C=0,其中 A、B、C 是常数。
通过已知圆心和半径,可以将一般式方程转化为标准式方程。
例如,如果已知圆心坐标为 (2,-3),半径为 5,则一般式方程为 x²+y²-4x+6y+20=0。
直线与圆的方程

直线与圆的方程方程是数学中重要的概念,是由变量、符号和数字组成的式子,它表示一种规律,可用来描述空间图形的形状和位置关系,其中最基本表示形状的方程是直线和圆的方程。
直线的方程是最基本的平面几何图形,它是两点之间最短的路径,用一元一次方程来表示,例如y=ax+b,其中a和b是实数。
值得注意的是,a是斜率,而b是截距,只有当两个参数都确定,才能确定一条直线,而不确定的参数只能确定一条平行于此直线的直线。
另一种形状的方程是圆的方程。
圆是有界的平面图形,由一个内切圆环和它的内切圆环组成,它的方程是(x-a)2+(y-b)2=r2,其中(a,b)是圆心坐标,r是半径,只有当圆心和半径都确定,才能确定一个圆,而不确定的参数只能确定一个相似的圆。
圆的表示方式又有两种,一种是非积分的极坐标形式,如r=a cos (θ)+b sin(θ),其中a和b是实数,θ代表角度。
另一种是标准形式,其方程为(x-x0)2+(y-y0)2=a2,其中(x0,y0)是圆心坐标,a是半径。
圆和直线这两种方程本质上是不同的,此外,它们在坐标系中表示出来的形状也是不同的,直线是一种平行于坐标轴的线,而圆则是一个有界的圆环,它的中心在坐标原点,其半径为a。
圆和直线的方程极大地丰富了几何图形的表达能力,通过对它们的方程的推导和求解,可以更好地理解图形的性质,从而推动几何学的发展,推动数学的发展。
从定义上讲,直线和圆的方程是可以相互转换的。
比如,可以将一元一次方程y=ax+b换成(x-a)2+(y-b)2=r2,这样,直线就可以转换成圆,圆也可以转换成直线。
另一方面,通过对直线和圆的方程求解,可以用它们来解决复杂的数学问题,比如求两个圆的位置关系,求一条直线与一个圆的位置关系,求一条直线与另一条直线的位置关系等等,这些复杂的数学应用可以用直线和圆的方程来解决。
由此可见,直线和圆的方程是数学中至关重要的概念,它丰富了图形的表达能力,并可用来解决复杂的数学问题,是数学发展的基础。
求直线与圆的交点坐标。

求直线与圆的交点坐标。
原题目:求直线与圆的交点坐标
问题描述
给定一条直线和一个圆,请求出它们的交点坐标。
解决方案
要求出直线和圆的交点坐标,我们可以先将直线和圆的方程表
示出来,然后解方程得到交点的坐标。
1. 直线的方程表示:设直线的方程为 Ax + By + C = 0,其中 A、
B、C 为常数,(x, y) 为直线上的任意一点。
根据直线的斜率和截距,我们可以求得直线的方程。
2. 圆的方程表示:设圆的方程为 (x - p)^2 + (y - q)^2 = r^2,其
中 (p, q) 为圆心坐标,r 为半径。
3. 解方程求交点坐标:将直线的方程代入圆的方程中,得到一
个关于 x 和 y 的二元二次方程,解这个方程可以得到交点的坐标。
4. 特殊情况处理:如果直线与圆没有交点或者直线与圆为切点,则交点个数为 0。
示例
假设直线的方程为 2x - 3y + 4 = 0,圆的方程为 (x - 1)^2 + (y - 2)^2 = 3^2。
将直线的方程代入圆的方程中:
(2x - 3y + 4)^2 + (y - 2)^2 = 3^2
展开并化简上述方程:
4x^2 - 12xy + 9y^2 - 8x + 12y - 4 = 0
这是一个关于 x 和 y 的二元二次方程,我们可以解这个方程来
得到交点的坐标。
总结
通过解方程,我们可以求出直线与圆的交点坐标。
需要注意的是,如果直线与圆没有交点或者直线与圆为切点,则交点个数为0。
【高中数学】秒杀秘诀---直线系和圆系方程
直线系和圆系方程定义:如果两条曲线方程是f 1(x ,y)=0和f 2(x ,y)=0,它们的交点是P (x 0,y 0),方程f 1(x ,y)+λf 2(x ,y )=0的曲线也经过点P (λ是任意常数)。
由此结论可得出:经过两曲线f 1(x ,y)=0和f 2(x ,y )=0交点的曲线系方程为:f 1(x ,y )+λf 2(x ,y )=0。
利用此结论可得出相关曲线系方程。
一.直线系概念:具有某种共同属性的一类直线的集合,称为直线系。
它的方程称直线系方程。
几种常见的直线系方程:(1)过已知点P (x 0,y 0)的直线系方程y -y 0=k (x -x 0)(k 为参数)(2)斜率为k 的直线系方程y =kx +b (b 是参数)(3)与已知直线Ax +By +C =0平行的直线系方程Ax +By +λ=0(λ为参数)(4)与已知直线Ax +By +C =0垂直的直线系方程Bx -Ay +λ=0(λ为参数)(5)过直线l 1:A 1x +B 1y +C 1=0与l 2:A 2x +B 2y +C 2=0的交点的直线系方程:A 1x +B 1y +C 1+λ(A 2x +B 2y +C 2)=0(λ为参数)例1:已知直线l 1:x +y +2=0与l 2:2x -3y -3=0,求经过的交点且与已知直线3x +y -1=0平行的直线分析:不论m 为何实数时,直线恒过定点,因此,这个定点就一定是直线系中任意两直线的交点。
解:由原方程得m(x +2y -1)-(x +y -5)=0,①即⎩⎨⎧-==⎩⎨⎧=-+=-+4y 9x 05y x 01y 2x 解得,∴直线过定点P (9,-4)例3:求过直线:210x y ++=与直线:210x y -+=的交点且在两坐标轴上截距相等的直线方程.概念:具有某种共同属性的圆的集合,称为圆系。
几种常见的圆系方程:(1)同心圆系:(x -x 0)2+(y -y 0)2=r 2,x 0、y 0为常数,r 为参数。
直线和圆的方程
直线和圆的方程在几何学中,直线和圆是两个基础的几何图形。
在解决几何问题时,了解直线和圆的方程是非常重要的。
本文将介绍直线和圆的方程,并提供一些示例来帮助读者更好地理解。
直线的方程一般式方程直线的一般式方程可以表示为:Ax + By + C = 0其中A、B和C是实数,并且A和B不能同时为零。
示例考虑一条过点P(x₁, y₁)和点Q(x₂, y₂)的直线。
我们可以通过计算斜率来得到直线的一般式方程。
首先,我们可以计算斜率:m = (y₂ - y₁) / (x₂ - x₁)然后,用点斜式方程来得到直线的一般式方程:y - y₁ = m(x - x₁)展开这个方程,我们得到:y - y₁ = ((y₂ - y₁) / (x₂ - x₁))(x - x₁)进一步化简得到直线的一般式方程:(y₂ - y₁)x + (x₁ - x₂)y + x₂y₁ - x₁y₂ = 0这个方程就是直线的一般式方程。
斜截式方程直线的斜截式方程可以表示为:y = mx + b其中m是斜率,b是y轴截距。
示例考虑一条通过点P(x₁, y₁)且斜率为m的直线。
我们可以用斜截式方程来表示这条直线。
直线的斜率为m,通过点P(x₁, y₁),所以直线方程为:y - y₁ = m(x - x₁)将方程展开,我们得到:y - y₁ = mx - mx₁移项整理得到直线的斜截式方程:y = mx - mx₁ + y₁进一步整理后得到:y = mx + (y₁ - mx₁)这个方程就是直线的斜截式方程。
圆的方程标准方程圆的标准方程可以表示为:(x - h)² + (y - k)² = r²其中(h, k)是圆心的坐标,r是圆的半径。
示例考虑一个圆心为C(h, k)且半径为r的圆。
圆心C(h, k),圆的半径为r,所以圆的方程为:(x - h)² + (y - k)² = r²这个方程就是圆的标准方程。
直线与圆的方程
直线与圆的方程
1 直线与圆
直线与圆是几何学中的一个基本概念,它是构成几何学中知识和技能的基础。
本文旨在详细介绍直线与圆的方程及其应用。
一、直线与圆的方程
直线与圆的方程是一种用来描述直线与圆的关系的数学方程式,它包含了圆的圆心坐标、半径、以及与圆的相交关系的参数,比如切点、关联直线本身的方程参数、直线的切点等。
其普通方程形式可总结为:
$$(x-a)^2+(y-b)^2=r^2$$
其中,$(a,b)$ 为圆心坐标,$r$ 为半径,$x,y$ 为直线参数。
二、应用
2.1 圆弧
圆弧,即圆周上的一部分,是根据圆曲线来定义从一点到另一点的弧形物体。
圆弧的弧度可由圆弧两端点以及圆心求出,以及圆弧方程
$$(x-a)^2+(y-b)^2=r^2$$
其中,$(a,b)$ 为圆心坐标,$r$ 为半径,$x,y$ 为直线参数,可得到弧线长度。
2.2 极坐标
极坐标是一明确的平面坐标及其表示方法,它设定一个坐标原点,然后由极径和极角构成一个坐标表示法。
而极坐标方程也可以由直线
与圆的方程得到:
$$(x-a)^2+(y-b)^2=r^2$$
其中,极径 $\rho=\sqrt{(x-a)^2+(y-b)^2}$,极角
$\varphi=\arctan\frac{y-b}{x-a}$。
三、总结
本文介绍了直线与圆的方程及其应用,明确了直线与圆的普通方
程形式,分析了圆弧的定义及圆弧方程,以及极坐标的应用。
这些概
念及方程应用在几何学及其它学科中都是至关重要的,让我们更好地
描述物体以及预测物体运动等。
直线与圆的方程
直线与圆的方程近些年,高等数学在数学领域中发挥着越来越重要的作用。
其中,直线与圆的方程是高等数学的重要知识点之一。
圆的方程和直线的方程都是用来表示几何图形的。
理解这两个方程,以及如何从一个表达式推导出另一个表达式,对于高等数学的学习都是十分重要的。
一、直线的方程直线是数学中最基本的几何图形,由两个不同的点组成,连接这两个点,即可形成一条直线。
直线的方程一般可以用一元一次方程的形式来表示:y=kx+b。
其中,K是直线斜率,B是截距。
给定任意一个点(x,y)可以推算出斜率K与截距B的值,从而确定直线的方程式。
此外,还可以使用参数方程的形式来表示直线的方程,如:x=at+b,y=ct+d,表示一条直线。
在此方程中,a,b,c,d定了这条直线的方向,t是参数。
二、圆的方程圆是由一系列的点的集合的闭合曲线组成的,其中心点(X0,Y0),是整个圆的中心点,其半径为R。
根据中心点坐标及半径,可以用极坐标系来表示一个圆,即:x = X0 + R*cosθy = Y0 + R*sinθ其中R是圆的半径,θ是弧度,一个圆上任一点坐标都可以用这个方程来表示。
此外,还可以使用标准的圆的方程来表示:(x-X0)+(y-Y0)=R在这个方程中,(X0,Y0)是圆心,R是半径,X,Y是圆上的一点,当X,Y给定时,可以求出该点到圆心的距离,从而确定该点是否在圆上。
三、直线与圆的相交在实际的计算中,有时需要求解直线与圆之间是否相交,以及相交的位置。
这里可以利用直线方程和圆方程来分析,首先用直线方程带入圆方程,并展开来求解。
(x-X0) + (kx+b-Y0) = R令a=k+1,b=2(b-Y0)k-2X0,c=X0+(b-Y0)-R,令f(x)= ax+bx+c,可以得到f(x) = 0解f(x)= 0,可以得到x1和x2,此时,(x1,y1)和(x2,y2)就是直线与圆的交点。
四、总结以上是关于直线与圆方程的介绍,主要介绍了用一元一次方程和参数方程表示直线,用极坐标系和标准圆的方程表示圆,以及求解直线与圆的交点的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线与圆的方程:
1.过点p (2,3),且在两坐标轴上的截距相等的直线方程为
2.过点p (2,3),倾斜角是135°的直线方程为
3.已知实数x,y 满足2x+y=8,当32≤≤x 时,求x
y 的最大和最小值 4.一条直线l 过点p (1,4)分别于两坐标轴正向交于两点A,B ,O 为坐标原点,求△AOB 面 积最小时直线的方程
5.求过点A (2,-3)且与直线2x+y-5=0平行的直线的方程
6.当a 为何值直线x+2y-1=0与直线(3a-1)x-ay-1=0平行
7.已知平行于直线2x+5y-1=0的直线l 与两坐标轴围成的三角形的面积为5,求直线l 的方程
8.已知直线1l 的斜率为3/4,直线2l 经过点A(3a,-2),B(o,12+a ),且21l l ⊥,求a 的值
9.过点(3,1)且与直线3x+2y-3=0垂直的直线方程
10.经过点C(2,-3),且垂直于过两点M(1,2),N(-1,-5)的直线方程为
11.与直线2x+y-3=0垂直,且与x 轴上的截距比在y 轴上的截距大2的直线方程为
12.已知直线l 经过两条直线2x-2y+10=0,3x+4y-2=0的交点,且垂直于直线3x-2y+4=0,求直线l 的方程
13.已知直线1l y=kx+k+2与2l ;y=-2x+4的交点在第一象限,求k 的取值范围
14.已知三角形ABC 的三个顶点A(-1,0),B(1,0),C(1/2,
2
3),判断三角形的形状
15.已知两点(0,m )(8,-5)之间的距离为17,则实数m 的值为
16.一条光线经过p(2,3)射在直线x+y+1=0上,反射后经过点A (1,1),求光线的
入射线和反射线方程
17.若A(7,8) ,B(10,4),C(2.,-4),求△ABC 的面积
18.点P (0,5)到直线y=2x 的距离是
19.直线l 在y 轴上的截距为10,且原点到直线l 的距离是8,则直线l 的方程
20.直线l 经过原点,且点M (5,0)到直线l 的距离等于3,求直线的方程
21.已知方程0916)41(2)3(24222=-+-++-+t y t x t y x
(1)t 为什么范围时,方程表示圆。
(2)方程表示圆时,t 为何值,圆的面积最大?求圆的方程
22.已知方程
01422=+-+x y x (1)求x y
的最大值和最小值 (2)求y-x 的最大值和最小值 (3)求22y x +的
最大值 和最小值
23.圆5)1(22=+-y x 的圆心到直线x y 3
3=的距离是 24.求过两点A(0,4)B(4,6),且圆心在直线x-2y-2=0上的圆的标准方程
25.求圆心在直线y=-2x 上,且与直线y=1-x 相切于点(2,-1)的圆的方程
26.已知圆C 满足:(1)截y 轴所得的弦长为2(2)被x 轴分成两段圆弧的弧长之比为3:1(3)圆心到直线l :x-2y=0的距离为5
5,求圆C 的方程 27.实数x,y 满足1)1(22=-+y x ,求(1)|3x+4y+16|的最值(2)22y x +的最值
(3)1
2++x y 的最值 28.求过圆422=+y x 上一点(13,)的圆的切线方程
29.自点(-1,4)作圆
1)3()2(22=-+-y x 的切线l,求切线l 的方程
30.求直线0323=+-y x 被圆
422=+y x 截得弦长 31.已知圆1)3()2(22=-+-y x ,求该圆与x 轴和y 轴的截距相等的切线l 的方程
32.从圆1)1()1(22=-+-y x 外一点P 向圆引切线,求切线长
33.求过点A (0,6)且与圆C:0101022=+++y x y x 切于原点的圆的方程
34.已知圆C 0162:221=+-++y x y x ,圆01124:222=-+-+y x y x C ,求两圆的公共弦所在的方程
35.已知一个圆经过直线l:2x+y+4=0与圆C:014222=+-++y x y x 的两个交点,并且有最小面积,求此圆的方程
36.两圆相交于两点(1,3)和(m ,-1),两圆圆心都在直线x-y+c=0上,则m+c=
37.已知过点A(-1,0)的动直线l 与圆C:4)3(22=-+y x 相交于P,Q 两点M 是PQ 的中点,l 与直线m:x+3y+6=0相较于N.
(1)求证:当l 与m 垂直时,l 必过圆心C
(2)当PQ=23时,求直线l 的方程
38.过圆O :422=+y x 外一点M(4,-1)引圆的两条切线,则经过两切点的直线方程是
39.直线l:4x-3y-12=0与x,y 轴的交点分别是A,B,O 为坐标原点,则△AOB 的内切圆的方程是
40.圆心在直线y=x 上,且与直线x+2y-1=0相切的圆,截y 轴所得的弦长是2,求此圆的方程
41.若圆02)1(222=-+-++m my x m y x 关于直线x-y+1=0对称,则实数m 的值为
42.已知圆C 过定点A (0,a ),(a>0),且在x 轴上截得的弦MN 的长为2a
(1求圆心C 的轨迹方程 (2)若MAN ∠=45°,求圆C 的方程
43.已知圆C 圆心为C(2,1),若此圆与圆0322=-+x y x 的公共弦所在直线过点(5,-2),求此圆的方程
44.已知圆922=+y x 的内接△ABC ,点A 的坐标是(-3,0),重心G 的坐标为(-2
1,-1)。
(1)求边BC 所在直线的方程 (2)求弦BC 的长
45.直线ax+by+1=0被圆2522=+y x 截得的弦长是8,则
2253b a +的最小值是 46.已知。
