材料力学 第七章弯曲正应力(1,2)分析
合集下载
秦飞编著《材料力学》第7章 弯曲应力

危险点发 生在什么 位置?
秦飞 编著《材料力学》 第7章 弯曲应力
14
7.1 弯曲正应力
弯曲正应力公式
各种型钢的Iz、Wz值均可以从附录的型钢规格表中查到。
常用截面:矩形截面
bh 3 Iz 12
y max
h 2
bh 2 Wz 6
h
b
对于直径为D的实心圆形截面
πD Iz 64
4
ymax
C
拉
z
M
z
C
压
拉 y y
秦飞 编著《材料力学》 第7章 弯曲应力 8
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(2)静力平衡关系 由平面假设,横截面上只有正应力σ。纯弯曲情况下,梁横 截面上的内力只有Mz=M,轴力和 My等其他内力均为零,则
dA 0
A
中性轴
z dA 0
A
由这3个静力平衡方
y
与y成正比,沿截面高
度线性变化。
秦飞 编著《材料力学》 第7章 弯曲应力
ρ为中性层曲率半径
10
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(4)物性关系
y 将 代入物性关系,得: y E E
可见,梁横截面上的弯曲正应力 (normal stress in bending) 与y成正比, 即 (1)沿截面高度线性分布; (2)在中性层处为零,在上、下表面 处最大。
My Iz
—弯曲正应力公式
此公式适用于所有横截面具有纵向对称轴的梁,如圆形截 面、工字形截面和T形截面。 由公式: 正比于y。 沿高度线性分布。 中性轴处=0。
秦飞 编著《材料力学》 第7章 弯曲应力 13
秦飞 编著《材料力学》 第7章 弯曲应力
14
7.1 弯曲正应力
弯曲正应力公式
各种型钢的Iz、Wz值均可以从附录的型钢规格表中查到。
常用截面:矩形截面
bh 3 Iz 12
y max
h 2
bh 2 Wz 6
h
b
对于直径为D的实心圆形截面
πD Iz 64
4
ymax
C
拉
z
M
z
C
压
拉 y y
秦飞 编著《材料力学》 第7章 弯曲应力 8
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(2)静力平衡关系 由平面假设,横截面上只有正应力σ。纯弯曲情况下,梁横 截面上的内力只有Mz=M,轴力和 My等其他内力均为零,则
dA 0
A
中性轴
z dA 0
A
由这3个静力平衡方
y
与y成正比,沿截面高
度线性变化。
秦飞 编著《材料力学》 第7章 弯曲应力
ρ为中性层曲率半径
10
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(4)物性关系
y 将 代入物性关系,得: y E E
可见,梁横截面上的弯曲正应力 (normal stress in bending) 与y成正比, 即 (1)沿截面高度线性分布; (2)在中性层处为零,在上、下表面 处最大。
My Iz
—弯曲正应力公式
此公式适用于所有横截面具有纵向对称轴的梁,如圆形截 面、工字形截面和T形截面。 由公式: 正比于y。 沿高度线性分布。 中性轴处=0。
秦飞 编著《材料力学》 第7章 弯曲应力 13
材料力学:第七章 弯曲变形

刚度设计依据
(1) 挠度w大小取决于M, E, I三个参数 应该取较小的M, 较大的E, I
(2) 弯矩M大小取决于载荷\约束分布及梁跨度大小
(3) 截面惯性矩I 大小和截面形状有关,
弹性模量E大小和材料有关
Iz =
y2dA,
A
当A大小一定时, y越大, I 越大
梁的合理刚度设计
选择I 较大的薄壁横截面形状
1 度静不定 选 FBy 为多余力, 去约 束, 写出位移边界条件
-变形协调条件 -物理方程
利用边界条件 解出未知力
列平衡方程,求其他约束力:
-补充方程
分析方法与步骤:
判断梁的静不定度
用多余力代替多余约
束的作用,得相当系统
相当系统
相当系统有多种选择:
计算相当系统在多余约
束处的位移,并根据变形 协调条件建立补充方程。
例题
解:
()
()
例题
例题
解:
()
()
()
例题
图示组合梁,EI=常数,求 wB 与qA
例题
解:
P378, 情况8
()
P377, 情况1,2
()
例题
图示刚架,求截面 C 的铅垂位移
例题
解:
位移w1包括AB弯曲 和AB扭转两部分
例题
矩形截面梁, 自由端承受集中载荷F作用, 该载荷与对 称轴y的夹角为θ, 用叠加法计算自由端求自由端截面形心C
的位移d
解:
例题
一般情况下
挠曲轴与外力作用面一般不重合
§6 简单静不定梁
静不定度与多余约束 简单静不定梁分析方法
静不定度与多余约束
静不定度 4-3= 1
(1) 挠度w大小取决于M, E, I三个参数 应该取较小的M, 较大的E, I
(2) 弯矩M大小取决于载荷\约束分布及梁跨度大小
(3) 截面惯性矩I 大小和截面形状有关,
弹性模量E大小和材料有关
Iz =
y2dA,
A
当A大小一定时, y越大, I 越大
梁的合理刚度设计
选择I 较大的薄壁横截面形状
1 度静不定 选 FBy 为多余力, 去约 束, 写出位移边界条件
-变形协调条件 -物理方程
利用边界条件 解出未知力
列平衡方程,求其他约束力:
-补充方程
分析方法与步骤:
判断梁的静不定度
用多余力代替多余约
束的作用,得相当系统
相当系统
相当系统有多种选择:
计算相当系统在多余约
束处的位移,并根据变形 协调条件建立补充方程。
例题
解:
()
()
例题
例题
解:
()
()
()
例题
图示组合梁,EI=常数,求 wB 与qA
例题
解:
P378, 情况8
()
P377, 情况1,2
()
例题
图示刚架,求截面 C 的铅垂位移
例题
解:
位移w1包括AB弯曲 和AB扭转两部分
例题
矩形截面梁, 自由端承受集中载荷F作用, 该载荷与对 称轴y的夹角为θ, 用叠加法计算自由端求自由端截面形心C
的位移d
解:
例题
一般情况下
挠曲轴与外力作用面一般不重合
§6 简单静不定梁
静不定度与多余约束 简单静不定梁分析方法
静不定度与多余约束
静不定度 4-3= 1
材料力学课件第七章变曲应力(机械专业)
A ydA M
yC ydA A ቤተ መጻሕፍቲ ባይዱ A
(c)
(a)(b)
A ydA 0
E
中性轴通过横截面形心
(a)(c)
A
y 2dA M
M EI z 1
Iz
A
y2dA-惯性矩
(d)
(d)(a)
( y )
My Iz
max
M Wz
max
Mymax Iz
静力学方面:
( y)
( y)d d y d
y
(a)
物理方面:
( y) E ( y)
dA0 (b) Fx 0, A M z 0, A ydA M (c)
第七章
弯曲应力
正应力分布
第七章
E
y
弯曲应力
(b)
(a)
dA 0 A
A
F
z
1)画弯矩图 跨中截面 C 为危险截面 危险截面上的最大弯矩
M max 1 Fl 280 kN m 4
M /kN m
C 8m
a
B
y
F
A
C
B
8m
280
x
第七章
2)计算正应力
弯曲应力
查型钢表,No. 50a 工字钢的惯性矩 Iz = 46500 cm4 ,抗弯截面 系数 Wz = 1860 cm3 危险截面 C 上的最大正应力
第七章
7.1 概 述
弯曲应力
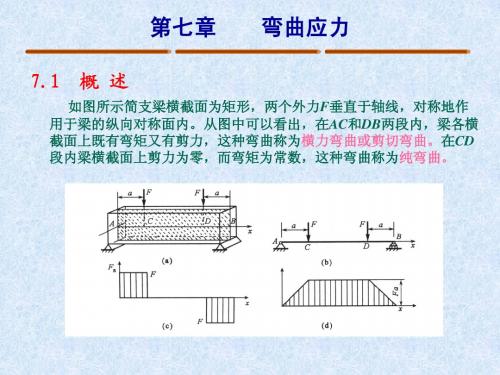
如图所示简支梁横截面为矩形,两个外力F垂直于轴线,对称地作 用于梁的纵向对称面内。从图中可以看出,在AC和DB两段内,梁各横 截面上既有弯矩又有剪力,这种弯曲称为横力弯曲或剪切弯曲。在CD 段内梁横截面上剪力为零,而弯矩为常数,这种弯曲称为纯弯曲。
材料力学 第07章 应力状态分析与强度理论

2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时,导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= -txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心,CD(CD') 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx- sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时,导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= -txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心,CD(CD') 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx- sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力
工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析,都需要求出应力的极值, 无论是强度分析还是刚度分析,都需要求出应力的极值,为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向, 到构件内最大应力的位置和方向,需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合,称为一点的 受力构件内一点处所有方位截面上应力的集合,称为一点的 研究一点的应力状态时, 应力状态 。研究一点的应力状态时,往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定: 主应力符号按代数值的大小规定:
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0
弯曲应力(剪应力6月9日)(1)

[1 12
16
283
16
28
(14
13)2 ]
[1 12
8 103
18 10
(19
13)2 ]
26200cm4
Wz
Iz ym a x
26200 (28 13)
1748cm3
(3)正应力校核
max
M Wz
1.2 105 1748 106
1.0 1.04 1.12 1.57 2.30
(四)切应力强度条件
max
(
FQ Sz,max
I z
)max
[
]
对于等宽度截面, m ax发生在中性轴上;对于宽度变化的截面,
m ax不一定发生在中性轴上。
在进行梁的强度计算时,需注意以下问题: (1)对于细长梁的弯曲变形,正应力的强度条件是主要的,剪应
S
* z
:y以外面积对中性轴的静矩
I z :整个截面对中性轴的惯性矩
b:y处的宽度
c
yc
y
z h
b
对于矩形:
S* z
A*
yc
b(h 2
y) [ y
h 2
2
y
]
b (h2 24
y2)
弯曲应力/弯曲时的剪应力
而
Iz
1 bh3 12
6FQ bh3
( h2 4
y2)
力的强度条件是次要的。但对于较粗短的梁,当集中力较大 时,截面上的剪力较大而弯矩较小,或是薄壁截面梁时,也 需要较核剪应力强度。
材料力学《第七章》应力状态分析

上海交通大学
受力: sadA、 tadA 受力: sxdAcosa、 txydAcosa
受力: sydAsina、 tyxdAsina
n
sx
txy
a
sa a
a
x
ta
tyx
e
切线方向上: Σ Fτ 0
σx σy σx σy σα cos2α τ xy sin2α 2 2
b
sy
τα d A ( σ x d A cos α )sin α ( τ xy d A cos α )cos α ( σ y d A sin α )cos α ( τ yx d A sin α )sin α 0
s1
一个主应力为零,其他二个主应力不为零。
3. 三向应力状态(空间应力状态): 三个主应力均不为零。
上海交通大学
一般要找出主应力后才能确定应力状态。
四、应力状态分析步骤
s2
1. 确定构件危险截面危险点;
2. 取危险点单元体;
s3
3. 计算单元体各面应力;
4. 截面法取部分单元体; 5. 由平衡条件确定单元体斜截面上的应力。 应力状态分析方法: 解析法、图解法。
上海交通大学
三、应力状态的分类 定义:单元体 上应力为零的面称为零应力面; 单元体上只有 s 而无 t 的面称为主平面。 主平面上的正应力 s 称为主应力。
s2
s3
单元体在某一特殊方向上,三个互相垂直的截面上只有 s,而 无 t ,即为单元体的三个主平面。 用 s1 ≥ s2 ≥ s3 表示三个主应力,此单元体称为主单元体。 1. 单向应力状态: 一个主应力不为零,其他二个主应力为零。如:轴向拉伸。 2. 二向应力状态(平面应力状态):
材料力学第07章应力状态与应变状态分析

以上由单元体公式
应力圆(原变换)
下面寻求: 由应力圆
单元体公式(逆变换)
只有这样,应力圆才能与公式等价
换句话,单元体与应力圆是否有一一对应关系?
为什么说有这种对应关系?
DE R sin[180o ( 2 20 )] R sin( 2 20 )
( R cos 20 ) sin 2 ( R cos 20 )cos 2
2
cos2
xy
sin 2
同理:
x
y
2
sin 2
xy
cos2
n
Ox
图2
二、极值应力
令:d
d
0
x
y
sin202 xycos200
由此得两个驻点:
01、(
01
2
)和两个极值:
tg20
2 xy x
y
y
mm
ax in
x
y ±(x
2
y
2
)2
2 xy
0 0极值正应力就是主应力 !
y
O
x
七、主单元体、主平面、主应力:
y
y
主单元体(Principal bidy):
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane):
剪应力为零的截面。 x
主应力(Principal Stress ):
主平面上的正应力。
1
主应力排列规定:按代数值大小,
1 2 3
三向应力状态( Three—Dimensional State of Stress): 三个主应力都不为零的应力状态。
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
E
ydA 0
A
A ydA Sz 0
中性轴Z必过截面形心
横截面对Z轴的静矩
M y
A
zdA
0
A
zE
y
dA
E
A
zydA
0
zydA I yz 0 截面的惯性积( y为对称轴)
A
M z y dA M
A
Байду номын сангаас
A
yE
y dA
M
y2dA Iz
截面对z轴的惯性矩
A
1 M
EI z
中性层的曲率公式
2)中性轴将截面分为受 拉、受压两个区域。
3)最大正应力发生在距
y
中性轴最远处。
3.简单截面的抗弯模量
dy
(1)矩形:
Wz
Iz h/2
bh3 12
2 h
y
Wz
1 6
bh2
(2)圆:
Wz
D 4
64(D / 2)
D 3
32
(3)圆环
WZ
(D4 d 4 )
64(D / 2)
D3
32
(1 4 )
式中 d
C
副梁CD:
Pa M max CD 4
M
由 (M m ax ) AB (M ) m ax CD
P (l a) P a
4
4
得 a l 2
P D
a
Pa (Mmax)CD 4
[例7-3]受均布载荷的外伸梁材料许用应力[ ] 160MPa 校核该梁的强度。
10kN / m
200
2m
4m
45 kN
1.正应力
My
IZ
2.横截面上的最大正应力
t
M y1 IZ
,
c
M y2 IZ
当中性轴是横截面的对称轴时:
若y1 y2 ymax
则 t c max
max
M ymax IZ
M
WZ
Wz
Iz y max
Wz 称为抗弯截面模量
1)沿y轴线性分布,同一 坐标y处,正应力相等。中 性轴上正应力为零。
(1) [ ]t [ ]c (等截面)只须校核Mmax处 (2) [ ]t [ ]c (等截面)
(a)对称截面情况只须校核Mmax处使
maxt [ ]t , maxc [ ]c
(b)非对称截面情况,具体分析,一般要校核 M+max与 M-max两处。
例4-14 图示简支梁由56a号工字钢制成,已知
后的轴线,横截面绕某一轴旋转了一个角度。
2.单向受力假设:
假设各纵向纤维之间互不挤压。于是各纵向纤维均 处于单向受拉或受压的状态。
中性层
梁在弯曲变形时,凹面部分纵向纤维缩短,凸面
部分纵向纤维伸长,必有一层纵向纤维既不伸长也不 缩短,保持原来的长度,这一纵向纤维层称为中性层.
中性层
中性轴
中性层与横截面的交线称为中性轴
[例7-1]:两矩形截面梁,尺寸和材料均相同, 但放置分别如图(a)、(b)。按弯曲正应力强度条 件确定两者许可载荷之比 P1/P2=?
l
解: max1
M max1 Wz1
P1l bh2 / 6
max2
M max2 Wz2
P2l hb2 / 6
由 max 1 max 2 [ ] 得:
P1 h P2 b
M
FS
三个方面:
jastin4.swf
静力学关系 变形几何关系 物理关系
一.几何变形
M
(1)aa、bb弯成弧
线,aa缩短,bb伸 长
(2)mm、nn变形后仍
保持为直线,且仍与M
变为弧线的aa,bb正
交;
(3)部分纵向线段缩短 ,另一部分纵向线段 伸长。
mn
M
aa
bb mn
M
1.平面假设:
梁各个横截面变形后仍保持为平面,并仍垂直于变形
M xy
二.梁弯曲正应力强度I条z 件
max [ ]
max
M max WZ
[ ]
利用上式可以进行三方面的强度计算:
①已知外力、截面尺寸、许用应力,校核梁的强度;
②已知外力、截面形状、许用应力,设计截面尺寸;
Wz
M max
[ ]
③已知截面形状尺寸、许用应力,求许可载荷
[M ] Wz[ ]
三.算例
D
y
D
0
Z
y
x d D
§7-2 横力弯曲时的正应力及正应力强度条件
一.横力弯曲时的正应力
My
IZ
上式是在平面假设和单向受力假设的基础上推 导的,实验证明在纯弯曲情况下这是正确的。
对于横力弯曲,由于剪力的存在,横截面产生剪 切变形,使横截面发生翘曲,不再保持为平面。理 论证明在L/h大于5时该式的精度能满足工程要求。
梁的强度。
9 kN 4 kN
52 C
zA
C
B D
88
1m 1m 1m
C截面
2.5kN
10.5kN
4
t
2.5 88 Iz
28.8MPa
< t
c
2.5 52 Iz
17MPa
< c
M
2.5
B截面
t
4 52 Iz
27MPa < t
c
4 88 Iz
46MPa < c
注:强度校核(选截面、荷载)
第七章 弯曲应力
§7-1纯弯曲时梁横截面上的正应力
一. 纯弯曲: 纯弯曲:
FS = 0,M = const
F
AC
Fa
l
F
Da B
F
FS
F
横力弯曲:
F
FS ≠0,M ≠0
M
Fa
CL8TU1
CL8TU2
M
dA M
FS
dA dA
dA FS
dA
在横截面上,只有法向内力元素σdA才能合成弯 矩M,只有切向内力元素τdA才能合成剪力FS
[例7-2]主梁AB,跨度为l,采用加副梁CD的方法提高
承载能力,若主梁和副梁材料相同,截面尺寸相同,则
副梁的最佳长度a为多少?
a Pa
解:
C2
2D
A
B
l P 22
A
l 2
P2
B
主梁AB:
M max AB
P (l a) 4
(l a)/2 M
M maxAB P(l a) / 4
(l a)/2
F=150kN。试求危险截面上的最大正应力max 和同 一横截面上翼缘与腹板交界处a点处的正应力a 。
12.5
F
A
FA
5m
C
10m
B z
FB
a
166
375 kN.m 21 560
M
Fl 解:1、作弯矩图如上, M max 4 375 kN m
2、查型钢表得
一.几何方程
y
y
z d
dx
y
dx
dx
(
y)d d d
y
y
二. 物理关系
E E y
dx
dx
一点的正应力与它到中性层的距离成正比。
三.静力学方程
FN dA 0 A
M y
z dA 0
A
M z
y dA M
A
E y
设中性轴为z
M
y
z dA
FN
dA 0
A
E y dA 0
FS 25
15kN
20
15
20
M
11.25
100
解:由弯矩图可见
Mmax 20 kN m
t
M max Wz
20 103 0.1 0.22 /
6
t 30MPa< [ ]
该梁满足强度条件,安全
[例7-4]图示铸铁梁,许用拉应力[σt ]=30MPa,许
用压应力[σc ]=60MPa,Iz=7.63×10-6m4,试校核此
E
ydA 0
A
A ydA Sz 0
中性轴Z必过截面形心
横截面对Z轴的静矩
M y
A
zdA
0
A
zE
y
dA
E
A
zydA
0
zydA I yz 0 截面的惯性积( y为对称轴)
A
M z y dA M
A
Байду номын сангаас
A
yE
y dA
M
y2dA Iz
截面对z轴的惯性矩
A
1 M
EI z
中性层的曲率公式
2)中性轴将截面分为受 拉、受压两个区域。
3)最大正应力发生在距
y
中性轴最远处。
3.简单截面的抗弯模量
dy
(1)矩形:
Wz
Iz h/2
bh3 12
2 h
y
Wz
1 6
bh2
(2)圆:
Wz
D 4
64(D / 2)
D 3
32
(3)圆环
WZ
(D4 d 4 )
64(D / 2)
D3
32
(1 4 )
式中 d
C
副梁CD:
Pa M max CD 4
M
由 (M m ax ) AB (M ) m ax CD
P (l a) P a
4
4
得 a l 2
P D
a
Pa (Mmax)CD 4
[例7-3]受均布载荷的外伸梁材料许用应力[ ] 160MPa 校核该梁的强度。
10kN / m
200
2m
4m
45 kN
1.正应力
My
IZ
2.横截面上的最大正应力
t
M y1 IZ
,
c
M y2 IZ
当中性轴是横截面的对称轴时:
若y1 y2 ymax
则 t c max
max
M ymax IZ
M
WZ
Wz
Iz y max
Wz 称为抗弯截面模量
1)沿y轴线性分布,同一 坐标y处,正应力相等。中 性轴上正应力为零。
(1) [ ]t [ ]c (等截面)只须校核Mmax处 (2) [ ]t [ ]c (等截面)
(a)对称截面情况只须校核Mmax处使
maxt [ ]t , maxc [ ]c
(b)非对称截面情况,具体分析,一般要校核 M+max与 M-max两处。
例4-14 图示简支梁由56a号工字钢制成,已知
后的轴线,横截面绕某一轴旋转了一个角度。
2.单向受力假设:
假设各纵向纤维之间互不挤压。于是各纵向纤维均 处于单向受拉或受压的状态。
中性层
梁在弯曲变形时,凹面部分纵向纤维缩短,凸面
部分纵向纤维伸长,必有一层纵向纤维既不伸长也不 缩短,保持原来的长度,这一纵向纤维层称为中性层.
中性层
中性轴
中性层与横截面的交线称为中性轴
[例7-1]:两矩形截面梁,尺寸和材料均相同, 但放置分别如图(a)、(b)。按弯曲正应力强度条 件确定两者许可载荷之比 P1/P2=?
l
解: max1
M max1 Wz1
P1l bh2 / 6
max2
M max2 Wz2
P2l hb2 / 6
由 max 1 max 2 [ ] 得:
P1 h P2 b
M
FS
三个方面:
jastin4.swf
静力学关系 变形几何关系 物理关系
一.几何变形
M
(1)aa、bb弯成弧
线,aa缩短,bb伸 长
(2)mm、nn变形后仍
保持为直线,且仍与M
变为弧线的aa,bb正
交;
(3)部分纵向线段缩短 ,另一部分纵向线段 伸长。
mn
M
aa
bb mn
M
1.平面假设:
梁各个横截面变形后仍保持为平面,并仍垂直于变形
M xy
二.梁弯曲正应力强度I条z 件
max [ ]
max
M max WZ
[ ]
利用上式可以进行三方面的强度计算:
①已知外力、截面尺寸、许用应力,校核梁的强度;
②已知外力、截面形状、许用应力,设计截面尺寸;
Wz
M max
[ ]
③已知截面形状尺寸、许用应力,求许可载荷
[M ] Wz[ ]
三.算例
D
y
D
0
Z
y
x d D
§7-2 横力弯曲时的正应力及正应力强度条件
一.横力弯曲时的正应力
My
IZ
上式是在平面假设和单向受力假设的基础上推 导的,实验证明在纯弯曲情况下这是正确的。
对于横力弯曲,由于剪力的存在,横截面产生剪 切变形,使横截面发生翘曲,不再保持为平面。理 论证明在L/h大于5时该式的精度能满足工程要求。
梁的强度。
9 kN 4 kN
52 C
zA
C
B D
88
1m 1m 1m
C截面
2.5kN
10.5kN
4
t
2.5 88 Iz
28.8MPa
< t
c
2.5 52 Iz
17MPa
< c
M
2.5
B截面
t
4 52 Iz
27MPa < t
c
4 88 Iz
46MPa < c
注:强度校核(选截面、荷载)
第七章 弯曲应力
§7-1纯弯曲时梁横截面上的正应力
一. 纯弯曲: 纯弯曲:
FS = 0,M = const
F
AC
Fa
l
F
Da B
F
FS
F
横力弯曲:
F
FS ≠0,M ≠0
M
Fa
CL8TU1
CL8TU2
M
dA M
FS
dA dA
dA FS
dA
在横截面上,只有法向内力元素σdA才能合成弯 矩M,只有切向内力元素τdA才能合成剪力FS
[例7-2]主梁AB,跨度为l,采用加副梁CD的方法提高
承载能力,若主梁和副梁材料相同,截面尺寸相同,则
副梁的最佳长度a为多少?
a Pa
解:
C2
2D
A
B
l P 22
A
l 2
P2
B
主梁AB:
M max AB
P (l a) 4
(l a)/2 M
M maxAB P(l a) / 4
(l a)/2
F=150kN。试求危险截面上的最大正应力max 和同 一横截面上翼缘与腹板交界处a点处的正应力a 。
12.5
F
A
FA
5m
C
10m
B z
FB
a
166
375 kN.m 21 560
M
Fl 解:1、作弯矩图如上, M max 4 375 kN m
2、查型钢表得
一.几何方程
y
y
z d
dx
y
dx
dx
(
y)d d d
y
y
二. 物理关系
E E y
dx
dx
一点的正应力与它到中性层的距离成正比。
三.静力学方程
FN dA 0 A
M y
z dA 0
A
M z
y dA M
A
E y
设中性轴为z
M
y
z dA
FN
dA 0
A
E y dA 0
FS 25
15kN
20
15
20
M
11.25
100
解:由弯矩图可见
Mmax 20 kN m
t
M max Wz
20 103 0.1 0.22 /
6
t 30MPa< [ ]
该梁满足强度条件,安全
[例7-4]图示铸铁梁,许用拉应力[σt ]=30MPa,许
用压应力[σc ]=60MPa,Iz=7.63×10-6m4,试校核此
