飞行器六自由度仿真
第二章_飞行器运动方程(1)

一个角运动 : 俯仰q
纵向两个线运动:高 航度 程HL
侧向两个角运动:滚 偏转 航pr 一个线运动 : 侧偏Y
坐标系选择
坐标系选择:选坐标系—机体系
飞机六自由度运动包括飞机绕三轴的转动(飞 机姿态变化),及飞机三个线位置的变化,在建 立六自由度方程时,选机体坐标系。
选体轴系下列好处:
2、线运动学方程式
线位置运动学方程 :地轴系与体轴系间线
速度关系:
让地轴系依次按 转动即可:
绕 oz 轴转 得到 x1 y1z g
x1 cos
y1
sin
z g 0
sin cos
0
0 x g
0
y
g
C
xg
y
g
1 z g
z g
2、线运动学方程式
再绕轴 oy1 转 得到 xy1 z2
飞行控制系统
第二章 飞行器运动方程 (一)
第二章 飞行器运动方程
刚体飞行器运动方程组 飞机的纵向运动 飞机的横侧向运动
2.1、飞行器运动方程组
一、建立飞机运动方程的基本假定 二、六自由度飞机运动方程 三、飞机运动方程的分组与线性化
一、建立飞机运动方程的基本假定:
认为飞机不仅是刚体,而且质量不变; 假定地球固定于空间,即略去地球自转、公转的
dV dt
1V
dV dt
V
dL dL dt 1H dt L
1、牵连运动
1V :沿 V 的单位向量; :动坐标系对惯性系的总角速度向量;
1L
:沿动量矩 :表示叉乘
L的单位向量;
v
是牵连加速度。
dV dH
dt 和 dt :表示在动坐标系内的相对导数。
六个自由度的四旋翼飞行控制原理
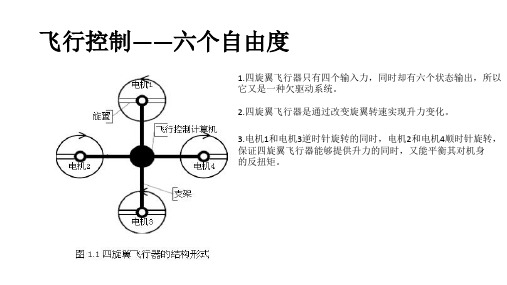
1.四旋翼飞行器只有四个输入力,同时却有六个状态输出,所以 它又是一种欠驱动系统。 2.四旋翼飞行器是通过改变旋翼转速实现升力变化。 3.电机1和电机3逆时针旋转的同时,电机2和电机4顺时针旋转, 保证四旋翼飞行器能够提供升力的同时,又能平衡其对机身 的反扭矩。
机载端控制电路版开发
• 红外接收装置——接收到发射装置的信息传递给单片机。
• 中央处理——单片机将接收到的红外信息处理,发送到PWM装置, 控制发动机的转速改变。
动力电路开发(PWM控制电流装置)
PWM电流控制电路: 每个PWM控制 器由一组电桥、及其外部一个感应电 阻(Rs)、一个内部比较器和一个单 稳多谐振荡器组成,来独立感应和控 制输出电流。
红外线接收器(接收信号)
反馈
单片机(中央处理)
PWM 步进电机(改变电流大小)
电机(转速改变) 飞行动作 轨道偏移外部扰动来自遥控电路开发(红外线装置)
• 四通道遥控器——上下、左右、前后、旋转 • 红外遥控装置——开关键,上升下降键,方向前后左右键。 (开关键:开启时,转速与飞行器重力刚好抵消,处于悬停 状态。关闭时,转速为零,处于停止状态。)
输出电流的逻辑控制:两个输入逻辑信号(l0 和 I1)用于数 字选择电机线圈电流在其最大水平的百分比,100%, 67%, 33%, or 0%。0%的输出电流值说明电桥关闭了所有驱动并且 也作为一个输出特性。
外界干扰因素
• 1.传感器噪声 • 2.外部扰动 • 3.摩擦 • 4.风速
基于模糊CMAC的飞行模拟机六自由度平台的复合控制

基于 模 糊 C C的飞 行模 拟机 六 自由度 平台 的复 合控 制 MA
高建树 ,刘 宪峰
( 中国民航 大学地 面特 种设 备研 究基地 ,天 津 30 0 ) 0 30
摘要 :针对飞行模拟机六 自由度平台 电液位置伺服 系统 的负载变 化大 、非线性程度 高、易受 外界干扰等特点 ,提 出采 用模糊 C C神经 网络控制策略来提高系统的性能 ,给出具体 的网络控制结构和算法 ,并在 MA L B上进行 了仿真 。仿 真 MA TA 结果表明 ,该方法具有较强 的 自适应能力和鲁棒性 ,适 用于六 自由度平 台的电液位置伺服系统。
.
t ATLAB r d he M wee ma e. Th i a in r s ls s w ha h tae y ha srng a a ie a lt a b sn s . I da s t h e smulto e u t ho t t te srt g s t o d pt biiy nd r u te s ta pt o t e v o
飞行器六自由度仿真

1 引言现在的战争已不是过去大刀长矛的时代,他早已成为国家综合实力的体现,这很大程度取决于军事高科技。
这其中导弹作为精确打击的利器关乎国家的战略安全。
而研究其包括导弹在内的飞行器精确制导与控制便显得十分的重要。
飞行器最优制导规律研究是进行武器系统总体方案论证和提高制导性能及精度的关键技术之一。
而要进行制导规律最优性研究一方面需要研究合适的制导规律,另一方面需要进行接近实际情况的全面的大量的仿真研究。
仿真验证包括建模与仿真两个方面。
在大型工程的方案论证阶段甚至包括实际研制的各个阶段,都要进行仿真检验以论证可行性、合理性和最优性。
仿真技术在工程应用特别在高端武器系统总体设计和方案论证中具有极为重要的作用。
对制导问题的研究在国外倍受重视。
在公开发表的文献中,专门讨论制导规律方面的研究论文很多,可见制导规律的研究是非常重要的。
但是仅有理论研究是远远不够的,因为设计的所谓最优制导规律大都是把实际系统进行了大量简化情况下推导出来的,因而与实际情况差别较大。
也就是说理论上是最优的制导规律或参数在实际系统中不一定是最优的。
因此,必须建立接近实际状态的数学模型和仿真软件。
通过仿真计算确定出制导系统的最优参数及制导规律的控制效果,才能最终确定制导规律的最优性。
目前国内外这类问题研究主要存在下列三个问题:其一是模型被简化。
从众多公开发表的文献资料看,大都是把控制系统简化为一阶、二阶、或三阶等根模型来推导制导规律,并据此模型进行仿真计算。
其二是把飞行器的六自由度空间运动状态简化为平面运动状态进行仿真研究,以这种把飞行器运动限制在平面范围内进行仿真计算是有局限性的。
其三是在全弹道数字仿真中仅选取几个特征点参数来代表全弹道的气动力参数,这些参数要表征全弹道动态过程是比较片面的,因而仿真结论的可信度是比较差的。
若把飞行器看成一个刚体,则它在空间的运动,可以看做是质心的移动和绕质心的转动的合成运动。
质心的移动取决于作用在飞行器上的力,绕质心的转动则取决于作用在飞行器上相对于质心的力矩。
飞机设计的基础:六自由度非线性运动方程的建立过程

飞机设计的基础:六自由度非线性运动方程的建立过程飞机飞行,涉及到力(力矩)平衡、静稳定和静操纵性等一系列的问题。
为了保证飞机的飞行安全和良好的飞行品质,还必须在静品质基础上研究飞机的动态特性。
可以说,飞机的各个系统设计都是围绕着飞机的飞行运动这一基本概念进行的,无论是总体设计、结构设计、气动设计、控制系统设计等等。
今天我们来简单介绍一下飞机运动方程建立的基本思路。
飞行中的歼-20从动力学观点来看,动态特性是研究飞机在外力或外力矩(外界扰动或飞行员操纵)作用下,各个运动参数随时间的变化规律,也就是求解飞机的运动方程,并在此基础上,对动态特性作进一步定量分析。
对于在三维空间运动的刚体飞机,具有6个自由度。
也就是说,如果要完整地描述飞机的运动,需要6个相互独立的微分方程组。
如果再加上空间位置和姿态,完整表征飞机的各个运动参数则需要15个微分方程。
对飞机运动进行受力分析可知,飞机运动要受到重力、发动机推力、空气动力以及三个轴向的滚转力矩作用。
这些力、力矩和运动参数的定义,不在同一坐标系下,因此求解时还需要经过坐标系转换变换到同一坐标系。
六自由度微分方程组加上复杂的坐标系变换,注定了飞机运动方程是复杂的。
飞行中的无人机不过,飞机运动方程能够真实地反映运动过程每一瞬间的情况,是对飞行性能、控制律设计以及运动仿真最基本的依据。
因此,有必要明白运动方程建立的基本方法和具体表现形式。
但是,现代控制理论主要是以传递函数和矩阵形式的状态方程作为分析对象进行研究和设计的。
因此,为了分析飞机稳定性、操纵性、控制律设计的方便,有必要研究建立飞机现行矩阵运动模型的方法。
垂直起降的F-35战机飞机的运动是一个复杂的动力学问题。
如果要全面考虑地球的曲率、燃油的消耗、武器的投射,飞机内部动力系统和操纵系统等机件的相对运动及飞机本身的弹性变形,外力使飞机外形、飞行姿态和运动参数变化等因素,会使飞机运动方程的推导变得极为复杂,并且很难进行解析处理。
民用飞机单发失效时仿真研究

民用飞机单发失效时仿真研究摘要:通过对六自由度运动方程进行仿真计算,研究了飞机非对称动力时的操稳特性,并总结了其飞行品质的验证方法。
仿真结果表明该方法的有效性,并具有一定的工程设计指导作用。
关键词:非对称动力;六自由度0 引言对于双发动机民用飞机,当其中一台发动机发生故障时,必然存在左右不平衡推力,造成不平衡力矩,飞机会产生侧滑角及滚转角并降低飞行高度。
此时需要偏转方向舵及副翼平衡不对称推力产生的横航向力矩,并保持飞机继续安全飞行。
目前,单台发动机的失效概率为1×10-5/飞行小时,相对于客机失事概率1×10-9/飞行小时要大得多。
因此,当客机发生动力的非对称损失时,要采取相应的补偿措施,保证其有效的操纵和安全飞行。
因此,有必要根据相关的飞行品质规范,对多发动机飞机的非对称动力的操稳特性进行深入研究。
本文以某典型的双发民用飞机为研究对象,依据运输类飞机适航标准,并结合空气动力学、理论力学及飞行力学等相关原理,确定仿真方法,并计算分析了单发失效时飞机相关的飞行品质,并验证该仿真方法的有效性。
1 非对称动力状态时飞行器飞行动力学模型建立非对称动力飞行指多发动机飞机一侧发动机发生故障,造成推力左右不对称时的飞行。
此时,要求飞机应能做定常直线飞行。
(1)飞行器动力学方程。
利用理论力学的动量定理可知,飞行器质心运动在任意动坐标系Oxyz上投影得质心动力学标量方程组为:m(+wq-vr)=F xm(+ur-wp)=F ym(+vp-uq=F z(1)根据理论力学中质点系的动量距定理知,dhdt=∑M(2)其中:h为质心系对所选择点的动量距;∑M 为合外力矩。
假设各坐标轴角速度的分量为ωX、ωY、ωZ,质量为d m的质心绕3个坐标轴的动量矩为:dh x=ωx(y2+z2)dm-ωyxydm-ωzzxdm dh y=ωy(z2+x2)dm-ωzzxdm-ωxxydmdh z=ωz(x2+y2)dm-ωxzxdm-ωyyzdm(3)引入惯性矩和惯性积,并对上式进行积分得,h x=ωxI x-ωyI xy-ωzI xzh y=ωyI y-ωzI yz-ωxI xyh z=ωzI z-ωxI xz-ωyI yz(4)对于飞机而言,xoz平面为对称面,因而I xy和I yz为零,所以得到转动动力学方程为:L=I x+(I z-I y)qrM=I y+(I x-I z)rpN=I z+(I y-I x)pq(5)(2)飞机运动学方程。
船舶拖航系统六自由度操纵运动仿真

船舶拖航系统六自由度操纵运动仿真船舶拖航系统六自由度操纵运动仿真船舶拖航系统是一种重要的海上运输设备,在海上货物运输中起到了非常关键的作用,而如何提高船舶拖航系统的操控能力是当前研究的热点。
船舶拖航系统的操纵运动仿真是一种非常有效的工具,可以模拟出各种不同的船舶拖航运动,对于提高系统的操纵能力具有重要意义。
船舶拖航系统的六自由度操纵运动是指在三个轴向分别进行平移和旋转的运动。
这六个自由度是:横向平移、纵向平移、垂直平移、绕X轴旋转、绕Y轴旋转和绕Z轴旋转。
在实际操作中,船舶拖航系统的操纵运动非常复杂,需要通过软件仿真来模拟出各种不同情况下的运动模式。
实现船舶拖航系统六自由度操纵运动仿真需要使用专业的仿真软件,如MATLAB/Simulink、ADAMS等。
这些软件具有良好的仿真性能和精度,可以精确地模拟出船舶拖航系统的各个运动指标。
以MATLAB/Simulink为例,其基于多体动力学理论,可以对船舶拖航系统进行六自由度动力学仿真,包括运动方程、力学方程和动力学方程等。
在进行船舶拖航系统六自由度操纵运动仿真时,需要考虑各种常见因素,并对其进行参数设置。
通常需要设置船舶的结构参数、物理参数、环境参数和控制参数等,以便精确地进行仿真分析。
其中结构参数包括船舶的长、宽、高等尺寸信息;物理参数包括船舶的质量、重心、惯性矩等;环境参数包括海洋水流、波浪等外部环境影响;控制参数包括船舶的操纵系统和控制策略等。
在仿真系统中,可以使用多种不同的仿真模式,如驱动模式、跟踪模式和预演模式等。
驱动模式是指在实际操纵情况下,通过对船舶各项指令进行控制,模拟出其对应的运动模式。
跟踪模式是指模拟出船舶跟随目标物体进行拖航操作的情况。
预演模式是指在不同环境条件下,模拟出船舶在某些特殊情况下的运动模式,以便用于系统优化和改进等方面。
总之,船舶拖航系统六自由度操纵运动仿真是一种非常重要的技术手段,对于提高船舶拖航系统的操纵能力具有重要意义。
动态系统建模(四旋翼飞行器仿真)实验报告-

动态系统建模(四旋翼飞行器仿真)实验报告:动态系统建模(四旋翼飞行器仿真)实验报告院(系)名称大飞机班学号学生姓名任课教师2021年 _月四旋翼飞行器的建模与仿真一、实验原理 I.四旋翼飞行器简介四旋翼飞行器通过四个螺旋桨产生的升力实现飞行,原理与直升机类似。
四个旋翼位于一个几何对称的十字支架前、后、左、右四端,如图1-1所示。
旋翼由电机控制;整个飞行器依靠改变每个电机的转速来实现飞行姿态控制。
在图1-1中,前端旋翼1 和后端旋翼3 逆时针旋转,而左端旋翼2 和右端的旋翼4 顺时针旋转,以平衡旋翼旋转所产生的反扭转矩。
由此可知,悬停时,四只旋翼的转速应该相等,以相互抵消反扭力矩;同时等量地增大或减小四只旋翼的转速,会引起上升或下降运动;增大某一只旋翼的转速,同时等量地减小同组另一只旋翼的转速,则产生俯仰、横滚运动;增大某一组旋翼的转速,同时等量减小另一组旋翼的转速,将产生偏航运动。
图1-1 四旋翼飞行器旋翼旋转方向示意图从动力学角度分析,四旋翼飞行器系统本身是不稳定的,因此,使系统稳定的控制算法的设计显得尤为关键。
由于四旋翼飞行器为六自由度的系统(三个角位移量,三个线位移量),而其控制量只有四个(4 个旋翼的转速),这就意味着被控量之间存在耦合关系。
因此,控制算法应能够对这种欠驱动(under-actuated)系统足够有效,用四个控制量对三个角位移量和三个线位移量进行稳态控制。
本实验针对四旋翼飞行器的悬浮飞行状态进行建模。
II.飞行器受力分析及运动模型(1)整体分析如图1-2所示,四旋翼飞行器所受外力和力矩为:Ø重力mg,机体受到重力沿-Zw方向Ø四个旋翼旋转所产生的升力Fi(i=1,2,3,4),旋翼升力沿ZB方向Ø旋翼旋转会产生扭转力矩Mi (i=1,2,3,4), Mi垂直于叶片的旋翼平面,与旋转矢量相反。
图1-2 四旋翼飞行器受力分析(2)电机模型Ø力模型(1.1)旋翼通过螺旋桨产生升力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 引言现在的战争已不是过去大刀长矛的时代,他早已成为国家综合实力的体现,这很大程度取决于军事高科技。
这其中导弹作为精确打击的利器关乎国家的战略安全。
而研究其包括导弹在内的飞行器精确制导与控制便显得十分的重要。
飞行器最优制导规律研究是进行武器系统总体方案论证和提高制导性能及精度的关键技术之一。
而要进行制导规律最优性研究一方面需要研究合适的制导规律,另一方面需要进行接近实际情况的全面的大量的仿真研究。
仿真验证包括建模与仿真两个方面。
在大型工程的方案论证阶段甚至包括实际研制的各个阶段,都要进行仿真检验以论证可行性、合理性和最优性。
仿真技术在工程应用特别在高端武器系统总体设计和方案论证中具有极为重要的作用。
对制导问题的研究在国外倍受重视。
在公开发表的文献中,专门讨论制导规律方面的研究论文很多,可见制导规律的研究是非常重要的。
但是仅有理论研究是远远不够的,因为设计的所谓最优制导规律大都是把实际系统进行了大量简化情况下推导出来的,因而与实际情况差别较大。
也就是说理论上是最优的制导规律或参数在实际系统中不一定是最优的。
因此,必须建立接近实际状态的数学模型和仿真软件。
通过仿真计算确定出制导系统的最优参数及制导规律的控制效果,才能最终确定制导规律的最优性。
目前国内外这类问题研究主要存在下列三个问题:其一是模型被简化。
从众多公开发表的文献资料看,大都是把控制系统简化为一阶、二阶、或三阶等根模型来推导制导规律,并据此模型进行仿真计算。
其二是把飞行器的六自由度空间运动状态简化为平面运动状态进行仿真研究,以这种把飞行器运动限制在平面范围内进行仿真计算是有局限性的。
其三是在全弹道数字仿真中仅选取几个特征点参数来代表全弹道的气动力参数,这些参数要表征全弹道动态过程是比较片面的,因而仿真结论的可信度是比较差的。
若把飞行器看成一个刚体,则它在空间的运动,可以看做是质心的移动和绕质心的转动的合成运动。
质心的移动取决于作用在飞行器上的力,绕质心的转动则取决于作用在飞行器上相对于质心的力矩。
在飞行中,作用在飞行器上的力主要有:总空气动力、发动机的推力和重力等。
作用在飞行器上的力矩有:空气动力引起的空气动力矩,由发动机推力(若推力作用线不通过飞行器质心时)引起的推力矩等。
作用在导弹上的空气动力和空气动力矩在其他条件相同的情况下,取决于飞行器的气动外形。
飞行器的推力,是由发动机内的燃气流以高速喷出而产生的反作用力等组成。
推力是飞行器飞行的动力。
火箭发动机推力只与火箭的飞行高度有关,而与火箭的其他运动参数无关,它的大小主要取决于发动机的性能参数。
根据万有引力定律,所有物体之间都存在着相互作用力。
飞行器在空间飞行就要受到地球、太阳、月球等等的引力。
对于贴近地球表面的大气层内飞行的飞行器,所以只计地球对其引力。
在考虑地球自转的情况下,除了受地心的引力外,还要受到因地球自转所产生的离心惯性力。
然而,高速飞行的飞行器一般是薄翼细长体弹性结构,因此有可能产生气动力和结构弹性的相互作用,造成弹体外形的弹性或塑性变形;操纵机构(如空气动力舵面)的不时偏转也相应改变飞行器的外形。
同时运动着的飞行器也不是常质量的,对于装有火箭发动机的导弹,工作着的火箭发动机不断地以高速喷出燃料燃烧后的产物,使导弹的质量不断发生变化;对于装有空气喷气发动机的导弹来说,一方面使用空气作为氧化剂,空气源源不断地进入发动机内部,另一方面燃烧后的燃气与空气的混合气又连续地往外喷出。
由此可见,每一瞬时工作着的反作用式发动机内部的组成不断地发生变化,即装有反作用式发动机的导弹是一个变组成系统。
由于导弹的质量、外形都随时间变化,因此研究导弹运动不能直接应用经典动力学理论,而采用变质量力学来研究,这比研究刚体运动要繁杂得多。
研究导弹的运动规律时,为使问题易于解决,可以把导弹质量与喷射出的燃气质量合在一起考虑,转换成为一个常质量系,即采用所谓“固化原理”,指在任意研究瞬时,设把变质量系的导弹视为虚拟刚体,把该瞬时在导弹所包围的“容积”内的质点“固化”在虚拟的刚体上作为它的组成。
同时,把影响飞行器运动的一些次要因素通常也略去,如弹体结构变形对运动的影响等。
这时,在这个虚拟的刚体上作用有如下诸力:对该物体的外力(如气动力、重力等)、反作用力(推力)、哥氏惯性力(液体发动机内流动的液体由于导弹的转动而产生的一种惯性力)、变分力(由火箭发动机内流体的非定态运动引起的)等。
其中后两种力较小,也常被略去。
采用了“固化原理”,可把所研究瞬时的变质量系的导弹的动力学基本方程可写成常质量刚体的形式,这时,要把反作用力作为外力来看待,把每研究瞬时的质量取代原来的常质量。
研究飞行器绕质心转动运动也可以用同样方式来处理。
为了验证这些问题,本文对六自由度飞行器进行了建模与仿真研究。
2 六自由度飞行器对象建模2.1 飞行器质心动力学模型仿真做如下假设:认为飞行器不仅是刚体,且质量是常数;假设地面为惯性参考系,即假设地坐标为惯性坐标;忽略地球曲率,把地球看成平面;假设重力加速度不随飞行高度而变化;假设机体X轴和Y轴处于飞行器对称面内,因此惯性积Jxz和Jxy等于0。
根据设计要求,我们来建立仿真飞行器质心运动动力学和飞行器绕质心转动的动力学方程的数学模型。
2.1.1 飞行器作用力仿真模块由于质心的运动动力方程是建立在弹道坐标系上的,根据{m dVdt=p cosαcosβ−X−mg cosθmV dθdt=P(sinαcosγv+cosαsinβsinγv)+Y cosγv−Zsinγv−mgcosθmV cosθdψvdt=P(sinαsinγv−cosαsinβcosγv)+Y sinγv+Z cosγv(2.1)将2.1方程三项作为一个向量来考虑,将右边作为力的分量F x,F y,F z,则为:[dV dtdθdtdψv dt ]=[F xm⁄F ymV⁄−F z mV cosθ⁄]=[10001V⁄000−1V cosθ⁄][F xF y−F z]/m(2.2)对上式2.2进行积分,可以算出来V,θ,φv,具体建立simulink仿真框图如下:图2.1 飞行器作用力仿真模块其中图2.1中“转换矩阵模块”子模块是[10001V ⁄000−1V cos θ⁄]的模型,如图2.2图2.2 飞行器作用力仿真模块2.1.2 飞行器运动学仿真模块由于飞行器运动学方程为:dxdt=V cos θcos ψvdydt=V sin θ dzdt=−V cos θsin ψv 其中V 是飞行器的运动速度;θ是飞行器弹道倾角; ψv 是飞行器弹道偏角; x ,y ,z 是飞行器相对于惯性坐标系三轴的位置坐标。
实现上式的仿真模块如图2.3所示:图2.3 飞行器运动学仿真模块通过图 2.3,可以得到飞行器在惯性坐标系的坐标值。
要转换到地面坐标系上。
弹道坐标系与地面坐标系的转换矩阵为:L(ψv ,θ)=[cos θcos ψvsin θcos ψv−sin ψv−sin θcos θ0cos θsin ψvsin θsin ψvcos ψv] 以上矩阵用Simulink 实现如下:首先用selector 把信号取出,再取正弦和余弦函数控件列出矩阵中每一项内容,最后用Reshape 形成矩阵,如图2.4所示:图2.4 地面坐标系和弹道坐标系转换矩阵仿真模块通过以上矩阵的转换,已知地面坐标系可求出弹道坐标系值,反之也可。
2.2 飞行器绕质心动力学方程仿真2.2.1 姿态运动学方程仿真模块绕质心转动的动力学方程是建立在飞行器坐标上的,其动力学方程为:{J x 1dωx 1dt +(J y 1−J z 1)ωz 1ωy 1=M x 1J y 1dωy 1dt +(J x 1−J z 1)ωz 1ωx 1=M y 1J z 1dωz 1dt +(J y 1−J x 1)ωx 1ωy 1=M z 1{J x 1dωx 1dt =M x 1−(J y 1−J z 1)ωz 1ωy 1J y 1dωy 1dt =M y 1−(J x 1−J z 1)ωz 1ωx 1J z 1dωz 1dt =M z 1−(J y 1−J x 1)ωx 1ωy 1对上式积分可以得ωz 1 ,ωx 1,ωy 1,{J x 1dωx 1dt =M x 1−(J y 1ωz 1ωy 1−J z 1ωz 1ωy 1)J y 1dωy dt =M y 1−(J x 1ωz 1ωx 1−J z 1ωz 1ωx 1)J z 1dωz 1dt =M z 1−(J y 1ωx 1ωy 1−J x 1ωx 1ωy 1)设 A =[ωx 1ωy 1ωz 1],B =[J x 1ωx 1J y 1ωy 1J z 1ωz 1],A1=[ωy 1ωz 1ωx 1],B2=[J y 1ωy 1J z 1ωz 1J x 1ωx 1],A2=[ωz 1ωx 1ωy 1],B1=[J z 1ωz 1J x 1ωx 1J y 1ωy 1],所以有:A1B1−A2B2=[J z 1ωy 1ωz 1−J y 1ωz 1ωy 1J x 1ωx 1ωz 1−J z 1ωz 1ωx 1J y 1ωx 1ωy 1−J x 1ωx 1ωy 1],此力矩模块由“Cross Product ”子模块提供。
根据姿态运动学方程求出三个姿态角ϑ,ψ,γ,其姿态运动学方程为:{dϑdt =ωy sin γ+ωz cos γdψdt =1cos ϑ(ωy cos γ−ωz sin γ)dγdt =ωx −tan ϑ(ωy cos γ−ωz sin γ)上式的数学模型如图2.5所示:图2.5姿态运动学方程仿真模块2.2.2 地面坐标系与弹体坐标系的转换矩阵仿真模块地面与弹体坐标系的转换矩阵为:L01=[cosϑcosψ−sinϑcosψcosγ+sinψsinγsinϑcosψsinγ+sinψcosγsinϑcosϑcosγ−cosϑsinγ−cosϑsinψsinϑsinψcosγ+cosψsinγ−sinϑsinψsinγ+cosψcosγ]其实现模块如下图2.6所示:图2.6地面坐标系与弹体坐标系的转换矩阵仿真模块图所以飞行器质心动力学方程和飞行器绕质心转动的动力学方程仿真模块图如图2.7,2.8所示:图2.7飞行器质心动力学方程仿真模块图图2.8飞行器绕质心转动的动力学方程仿真模块图3 仿真结果分析根据所绘制的仿真模型图运行所得结果:图3.1输出X de图3.2 输出V de图3.3输出ϑ,ψ,γ图3.4输出BoH图3.5 输出DCM图3.6输出ωx,ωy,ωz根据以上仿真结果,对比分析该数学模型能满足设计要求。
结论首先介绍了飞行器包括导弹的发展,进而介绍制导精度对于飞行器的控制具有十分重要的作用,开始查找资料,经过老师的指正,综合运用所学过的知识,根据飞行器六自由度模型的设计指标要求,基于Matlab/Simulink的仿真环境,采用了模块化的建模思想,建立了飞行器六自由度运动模型,根据对各个子模块分别采用Simulink建立单元仿真模型。
