高亚临界雷诺数圆柱绕流的尺度自适应模拟
不同雷诺数下的圆柱绕流数值模拟研究

不同雷诺数下的圆柱绕流数值模拟研究引言:圆柱绕流是流体力学领域中一个经典的、被广泛研究的问题。
在众多的工业应用中,圆柱绕流的研究对于风力发电机组的设计优化、管道内部液体运动的控制等方面具有重要实际意义。
雷诺数是描述流体流动的一个无量纲参数,它与流体的流速、流体的粘性有关。
本文将对不同雷诺数下的圆柱绕流进行数值模拟研究。
方法:数值模拟是一种有效的研究流体力学问题的方法,它能够通过计算机模拟得到流体的速度场、压力场等关键参数,从而进一步分析流体的特性。
在本文中,我们将使用计算流体力学方法进行圆柱绕流的数值模拟研究。
结果与讨论:我们选取了不同雷诺数的圆柱绕流作为研究对象,分别为200、400、600、800和1000,通过数值模拟得到了不同雷诺数下的圆柱绕流的速度场和压力场等关键参数。
首先,我们分析了速度场的分布。
通过数值模拟可以得到圆柱绕流过程中流体速度的分布情况。
随着雷诺数的增加,流体速度场呈现出不同的特征。
在雷诺数较低的情况下,流体绕圆柱流动的速度场分布较为简单,流速主要集中在圆柱前部和尾部。
随着雷诺数的增加,流体速度场呈现出更复杂的结构,流速分布更加均匀。
其次,我们研究了压力场的分布。
通过数值模拟可以得到圆柱绕流过程中流体压力的分布情况。
在不同雷诺数下,圆柱周围存在不同的压力区域。
当雷诺数较低时,圆柱前后表面存在较大的压差,压力分布较为不均匀。
而当雷诺数增加时,压力分布更加均匀,圆柱表面的压力变化较小。
最后,我们研究了绕流过程中的阻力情况。
通过数值模拟得到了不同雷诺数下圆柱绕流过程中的阻力系数。
我们发现,随着雷诺数的增加,阻力系数逐渐增大。
这是因为当雷诺数较低时,流体绕圆柱流动的速度较低,阻力较小;而当雷诺数增加时,流体流动速度较高,阻力也逐渐增大。
结论:本文通过数值模拟的方式研究了不同雷诺数下的圆柱绕流问题。
通过分析速度场、压力场和阻力系数等关键参数,我们得出了以下结论:随着雷诺数的增加,流体速度场更加复杂,流速分布更加均匀;压力场分布更加均匀,圆柱表面的压力变化较小;阻力系数随着雷诺数的增大而增加。
不同雷诺数下的圆柱绕流数值模拟研究

2 01 5在
中
国
水
运
VoI .1 5 Jul Y
No. 7
7月
Ch i n a Wa ter Tr a ns p or t
2 01 5
不 同雷诺数下 的圆柱绕流数值模拟研究
陈 禹,李 强 ,郭廷 凯
( 浙江海洋 学院 船舶与海洋I - 程系 ,浙江 舟 山 3 1 6 0 2 2 ) 摘 要:通过 a b a q u s的 CF D 模 块 ,在水动力作用下 ,对刚性 圆柱 展开了绕流三维仿真计算 ,同时也对 圆柱绕 流
的水动力特性进行了研究 。通过仿真计算得到了漩涡脱落形态、升力系数、 阻力系数 曲线 以及斯特劳哈尔数 ,经过 分析 比较可以看出 ,不同雷诺数情况下圆柱绕流在性质上存在着 比较大 的差异 。结果表 明,随着雷诺数 的增大 ,层 流变为紊 流 ,升力以及阻力系数 的变化 幅度出现 了不稳 定性 ,漩 涡的脱落 形态 也变得 不规则。 关键 词:圆柱 绕流 ;数值模 拟 ;升力 系数 ;阻力系数 ;漩涡 脱落 中图分类号:T H 3 1 1 文献标识码 :A 文章编号:1 0 0 8 - 7 9 7 3( 2 0 1 5 )0 7 — 0 0 8 8 — 0 3
王亚玲等为得到较高雷诺数 时圆柱绕流 的三维特性 , 采
用有限体积 法 , 选取 了 Re = 1 0 。 和 Re =1 0 , 对黏性 不可 压缩 流场条件下 的圆柱绕流展开 了了三维仿真 试验『 6 】 。苏铭德和 康 钦军 选取 Re = 1 0 和 2X 1 0 ,使 用大涡模拟 的方法 ,对 圆
收稿 日期 :2 0 1 5 — 0 5 — 0 3 作者简介 :陈
a
不同雷诺数下倾斜圆柱绕流三维数值模拟研究

不同雷诺数下倾斜圆柱绕流三维数值模拟研究近年来,研究倾斜圆柱绕流特性引起了学界的广泛关注。
圆柱绕流可分为水平和垂直两类,其中倾斜圆柱绕流为一种特殊的二维绕流状态,它在一定雷诺数范围内具有更复杂的流场结构特性,并且受水文物理过程的影响更为显著,研究其特性更为重要。
本研究使用时间和空间设置,以带边界流作为边界条件,利用基于六边形网格的数值模拟方法研究不同雷诺数下的倾斜圆柱绕流特性。
实验参数包括:倾斜角度α=20°,Re=1000 ~ 10000,向心轴比例范围为0.5 ~ 2.0,圆柱入口处外提升速度Um=0.3 ~ 0.8,及空气密度ρ=1。
有鉴于此,本研究根据不同雷诺数和向心轴比例,计算出倾斜圆柱绕流特性。
首先,主要考察不同雷诺数Re下倾斜圆柱绕流的流态特性,包括在不同位置的压力梯度,流场动量,温度梯度,流态结构以及涡度等信息。
其次,重点考察不同向心轴比例和轴向外提升速度下倾斜圆柱绕流的流态特性,包括压降,动量,温度梯度,以及不同方向的涡度分布。
结果表明,不同的雷诺数和向心轴比例会对倾斜圆柱绕流的流动特性产生明显不同的影响。
随着雷诺数的增大,压力梯度增大,动量梯度减小,温度梯度增大,涡度明显减少,圆柱内部的流场会变得更加复杂,气泡变小,而且其会从一种混合流场演变为一种逆流的流场结构。
另外,随着向心轴比例的增加,轴向外提升速度的变化会出现显著影响,但随着向心轴比例的增加,压力梯度会逐渐减小,动量梯度增大,温度梯度变化不大,涡度分布也会有较大变化。
研究结果表明,在不同雷诺数和向心轴比例范围内,倾斜圆柱绕流的流动特性会发生明显的变化。
本研究对于进一步理解流动特性和确定流动行为有重要的理论意义,同时也为实际工程的设计提供了参考。
总的来说,本研究通过应用数值模拟方法研究不同雷诺数下倾斜圆柱绕流特性,得出上述结论。
未来可以将此模拟实验方法应用于建立更复杂物理系统的研究,以更深入地理解绕流特性和其流动性质。
高雷诺数下方柱绕流特性的数值模拟

高雷诺数下方柱绕流特性的数值模拟周强;廖海黎;曹曙阳【摘要】为研究高雷诺数为22000下方柱周围流场形态及气动力特性,基于开源计算流体动力学(computational fluid dynamic,CFD)软件OpenFoam平台,采用基于动态亚格子模型的大涡模拟(large eddy simulation,LES)方法,对均匀来流作用下的方柱绕流迸行了三维数值模拟.首先,通过对基于时间积分的平均积分分量的比较,验证了本数值计算的准确性;其次,深人分析了方柱周围及其尾流区的流场结构,给出了流场结构的平均和湍流特征,并在此基础上,研究了其气动力特性;最后,分析了两种长径比下表面压力的展向空间相关性.研究结果表明:雷诺数为22000下方柱尾流区回转长度为1.37倍方柱宽度,Strouhal数为0.121,脉动升力系数为1.40;展向长度取8倍方柱宽度可更准确地获得周围湍流特性.%Three-dimensional large eddy simulations(LES)were performed at high Reynolds numbers (Re=22 000)and using the dynamic Smagorinsky sub-grid model to investigate uniform flow over a square cylinder. Meshing of the model was performed using Open Foam-an open-source computational tool. Mean integral quantities were compared against existing experimental and numerical results to validate the proposed numerical method. Subsequently,the flow structure around and aerodynamic forces acting on the cylinder were analysed to perform an in-depth investigation of mean-and turbulent-flow characteristics. Lastly,the influence of the grid system around the cylinder and span-wise length on the flow structure and spatial correlation were investigated via comparison between different cases. Results demonstrate that the recirculation length in the wake approximately measured1.37D(width of square),while the Strouhal number and RMS value of the lift coefficient are 0. 121 and 1. 40, respectively. In addition,domain length along the span-wise should be equal to 8D in order to obtain clear turbulent-flow characteristics.【期刊名称】《西南交通大学学报》【年(卷),期】2018(053)003【总页数】7页(P533-539)【关键词】方柱绕流;大涡模拟;流场特性;尾流结构;空间相关性【作者】周强;廖海黎;曹曙阳【作者单位】西南交通大学风工程四川省重点实验室,四川成都610031;西南交通大学风工程四川省重点实验室,四川成都610031;同济大学士木工程防灾国家重点实验室,上海200092【正文语种】中文【中图分类】U441长期以来,方柱绕流一直是风工程、钝体空气动力学、海洋工程等研究领域重要的、基础性的热点问题.在实际工程应用中,如桥梁的桥塔和桥墩、高层建筑、海洋平台等具有方柱形状的构件,在风或者水流作用下,会产生有规律的大尺度旋涡脱落现象,致使结构发生风致振动,进而导致其受损或发生疲劳破坏.因此,研究在方柱绕流问题及其尾流结构对于实际工程设计和建造具有十分重要的意义.不同雷诺数下,流体绕过方柱呈现出明显不同的流动特性.其中在高雷诺数下,流体经方柱前端边角后发生明显的流动分离,并伴随着回流或转捩,形成大尺度和不稳定的旋涡脱落,即与低雷诺数下流场相比,高雷诺数下的方柱绕流特性更加复杂,且表现出更加显著的三维特性.鉴于此,若采用雷诺时均方法,很难扑捉到准确的高雷诺数下方柱绕流特性;由于计算量太大,目前直接数值模拟还只限于雷诺数较低的流动.因此,对于高雷诺数方柱绕流问题,主要的数值研究方法就是大涡模拟(large eddy simulation, LES)方法.到目前为止,国内外学者针对方柱绕流问题开展了大量而丰富的实验和数值模拟研究.在实验研究方面,Lyn等[1]通过水洞实验,采用LDV(laser doppler velocimetry)技术研究了Re=21 400下的方柱绕流特性,详细分析了其尾流结构,同时其研究结果也广泛被作为数值模拟的参考标准;此后国外学者Saha等[2]在风洞中对高雷诺数下方柱的绕流特性进行了深入研究;近年来,Nishimura和Taniike[3]通过试验详细研究了不同攻角下方柱绕流特性;Yen等[4]利用粒子图像测速技术(particle image velocimetry, PIV)研究了方柱在4 000<Re<36 000、攻角0°~45°范围内的绕流结构和气动力特性.在数值研究方面,Sohankar等[5]对不同Re数下方柱绕流采用LES方法进行数值研究,其结果表明二维模拟与三维模拟的结果相差较大,而三维模拟结果明显更为准确;Okajima[6]也得到相类似的结论;Srinivas等[7]依据Lyn的实验,采用LES方法研究了方柱表面压力分布以及尾流区流场特性,发现LES 能够再现实验结果,但也发现数值模拟结果与实验结果在阻力系数、回转长度(回流区长度)等方面仍然存在一定的差别;Wang和Vanke[8]得到了相类似的结论;与此相似,Rodi等[9]总结了相关方面的研究进展,认为大多数数值算例得到的Strouhal 数(St)、流向平均速度均与实验结果接近,但是回转长度、阻力系数、速度脉动值以及表面压力分布相差很大,且与实验结果存在一定差别,其原因众说纷纭[9-11],认为有可能受到网格数量、来流条件、湍流模型参数等因素影响.张伟和葛耀君[12]采用κ-ω SST (shear-stress transport)模型,并与其PIV试验结果进行对比,得到了方柱的阻力系数、St以及流场的速度剖面和湍动能剖面,但是在脉动项上与实验结果还是存在差别.综上可见,对于高雷诺数下方柱绕流的数值模拟,因其流动的复杂性和明显的三维特性,此时,采用LES是比较合适的选择.然而如上文所述,大多采用LES方法模拟中展向长度的选取等细节问题还是存在不够明确的地方,导致一些流场速度、气动力等关键参数的脉动项与实验结果存在一定差别.为此,本文基于开源CFD软件OpenFoam平台,采用基于动态亚格子模型的大涡模拟方法,在Re=22 000情况下,对均匀来流条件下的不同网格系统、展向长度的方柱绕流问题进行了三维数值模拟,首先对数值结果的准确性进行验证,然后重点分析断面周围网格以及长径比对尾流区流场结构的影响,并给出不同长径比下气动力的展向空间相关性.1 控制方程与建模1.1 控制方程经过滤波后,大涡模拟的连续性和N-S方程为(1)(2)式中:t为时间;xi、xj为坐标的分量,i,j=1,2,3;ρ为流体密度;ui、uj分别为与xi、xj对应的速度分量;p为压力;μ为流体运动粘性;式中带有上划的量为滤波后的场变量,被定义为亚格子尺度应力,在Smagorinsky-lilly[13]亚格子模型中,(3)式中:τkk 为应力,k=1,2,3;δij为 Kroneker符号; Sij为变形速率张量;vSGS为亚格子模型涡粘系数,(4)其中:为格子过滤后的尺寸,和Δz为网格尺寸;(5)其中:Lkk为亚格子Leonard 应力;Lij和Mij的表达式分别为其中,Δ为格子过滤尺寸标准.1.2 建模与数值算法(1) 计算区域本文共计算3个算例,其中Case 1和Case 2的计算区域为30D×18D×4D(D为方柱断面宽度),Case 3则为30D×18D×8D.方柱模型上游来流区域长度为10D,下游尾流区长度为20D,即x方向上的长度为30D;模型离上下边界各为9D,即y方向上的宽度为18D;为了研究长径比的影响,展向长度分别取4D和8D两种长度,如图1所示.图1 计算区域示意图及边界条件Fig.1 Computational domain and boundary conditions(2) 边界条件(如图1所示)方柱表面边界条件:采用无滑移光滑固壁边界;入口边界条件:采用均匀来流速度条件,U=10 m/s;拟压(pseudo-pressure)φ采用Neumann条件;出口边界条件:速度满足格式为∂/∂t+c∂/∂x=0的对流边界条件,拟压取为0,这里c为任意常数;上下边界条件:采用自由流动边界条件;展向边界条件:采用周期边界条件.(3) 网格划分如图2所示,在方柱模型周围5D的范围内,采用贴体网格,并在方柱附近尤其是在尾流区,采用密集网格,而在远离方柱的区域使用稀疏的网格.为研究方柱表面周围网格的影响,在Case 1中,方柱表面附近的网格直接按照双曲切线间距分布由内向外伸展,如图3(a)所示;而在Case 2和Case 3中,则先在方柱表面附近采用厚度均匀的正交网格,然后再按照双曲切线间距分布由内向外伸展,如图3(b)所示.同时,为确保LES在边界层内计算的准确性,靠近方柱表面的第一层网格厚度Δd,设在展向布置上,Case 1和Case 2展向长度为4D,Case 3的展向长度为8D,三者的展向长度的解析度均为Δz/D=0.1,即在Case 1和Case 2中展向划分为40份,而在Case中展向划分为80份.因此,Case 1、Case 2和Case 3的网格总数分别为1 848 000、3 434 000和5 595 000.采用36核计算工作站,Case 1、Case 2和Case 3计算时间分别为192、240 h和320 h.(4) 数值算法在空间离散上,本文采用NVD(normalized variable diagram)格式,从而避免中心差分引起的非物理性振荡.对于时间的离散格式,采用二阶完全隐式法,以获得稳定并准确的结果.为避免计算中的数值振荡问题,本文在数值算法上采用了MIM(momentum interpolation method)方法[14];对N-S方程组采用Piso求解算法,并将连续性方程的收敛值设置为1×10-6;无量纲时间步长设置为Δt*=ΔtU/D=2.5×10-4,以确保柯朗数小于1,且保证每步计算可在20次迭代内完成.图2 整个计算区域内网格划分情况Fig.2 Grid system(a) Case 1(b) Case 2和Case 3图3 方柱表面周围网格划分情况Fig.3 Grid around square cylinder2 数值验证本节针对基于时间积分的平均积分分量,与其他实验和数值结果进行了比较,以确保本文数值计算的准确性.如表1所示,本文3个算例得到的St均与Lyn等[1]和Norberg[15]的实验值比较吻合;平均阻力系数CD与Sohankar等[5]的LES结果间误差小于1%,两者结果十分接近.需要指出的是,表1中计算气动力系数所采用的特征长度均为方柱断面宽度D.由此可见,本文进行的数值模拟是准确和可靠的.表1 平均积分分量对比表Tab.1 Comparison of integral parameters算例Re/×103StCD阻力系数脉动值C′L升力系数脉动值C′D平均背压Cpb平均回转长度LrCase 122.00.1242.340.311.521.711.32Case222.00.1212.300.321.471.621.37Case 322.00.1222.270.291.401.611.37Lyn等[1]21.40.1302.10——1.601.38Nishimura & Taniike[3]40.0—2.330.261.331.60—Norberg[15]22.00.1302.10——1.37—Sonhankar et al (LES)[5]22.00.1322.320.201.541.63—Wang & Vanke(LES)[8]21.40.1302.030.181.29—1.313 结果与讨论3.1 气动力特性表1给出并比较了其他基于时间积分的平均积分分量,包括Cpb、St和Lr (回转长度,其定义为圆柱体中心到中心线上最小流向速度Umin对应位置的距离,用于表征方柱后回流区的大小).由表1可见,本文3个数值算例得到的各项气动力统计值均与先前实验和数值结果比较吻合.对比Case 1和Case 2可以发现,前者的CD更大.原因在于Case 1的Lr更小,即方柱后方的回流区更靠近方柱后表面,这表明在方柱后方的旋涡更靠近方柱,因此导致方柱Cpb更小(如表1所示),从而使得方柱上的CD 更大.由此可见,与圆柱绕流相似,Lr是方柱绕流中的重要流场特征[16].对比Case 2和Case 3可以发现,两者的Cpb和Lr都几乎相同,但CD存在一定差别,其原因是两者的长径比不同,即Case 3中的展向长度更长,气动力的展向相关性更弱,使得其CD更小.此外,可以发现,随着展向长度的增加,均明显减小,且与实验值更为吻合.这是因为展向长度的增加导致相关性变弱,即脉动值对长径比更敏感.而先前数值计算大多考虑长径比的影响,使其计算结果在脉动项上与实验结果存在差别.同时由表1可以发现,与Case 1中各项气动力参数的结果相比,Case 2和Case 3结果更加准确,即在方柱表面附近先布置厚度均匀的正交网格,可有效改善数值结果.因此以下将主要针对后两者的结果进行说明.图4比较了方柱表面压力系数平均值Cp和脉动值的分布情况.(a) 平均值(b) 脉动值图4 方柱表面压力分布Fig.4 Surface pressure distribution on square cylinder由图4可见,本文结果与其他实验和数值结果基本吻合;且与Oka等[17]的数值结果相比,本文更加接近Nishmura等[3]的实验值.如图4(b)所示,与Case 2相比,Case 3中的脉动值与实验值更加吻合,特别是在方柱背面区域和靠近后方边角附近区域,也就是旋涡主要作用区域.这再次表明气动力系数的脉动值对展向长度更敏感. 3.2 流场特性图5给出并比较了中心平面(y=0的平面)上平均流向速度的分布情况.图5 中心线上的平均流向速度分布Fig.5 Stream-wise velocity at centreline由图5可以发现,平均流向速在方柱表面为0,在回转区域内逐渐减小直至最小值Umin;然后以近似渐近线的形式,单调地增加到外部流速U.通过对比发现本文的平均流向速度分布与Lyn等[1]的实验结果基本一致;且Lr/D=1.37与其他的数值结果(如表1所示)基本吻合.在尾流区,本文的结果较Wang等[8]的结果更加与实验值一致.但可以发现各个结果间的Lr偏差较小,而Umin/U比值偏差更大.其原因在于Umin/U较Lr对长径比更加敏感,因此,Case 2和Case 3的Umin/U比值也因为展向长度的不同而出现不同的结果.与此类似,Norberg[18]在研究圆柱绕流时,对比不同的长径比和阻塞率的试验结果后,也发现Umin对长径比更加敏感.图6给出了不同尾流位置上的分布情况(x=0对应的位置为方柱断面中心).由图可见,平均流向速度呈现为“U”形分布形态,且并随着流动向下游发展,速度分布趋于平缓,而平均竖向速度分布明显呈现出关于y=0轴的反对称性.与其他实验和数值结果对比可以发现,本文与Lyn等[1]实验值基本吻合,且明显好于Wang等[8]的数值模拟结果.同时还可以发现,在一些位置上,不同结果间存在微小差别,其主要原因在于方柱前方来流长度不同,以及早期试验设备的测量误差.对比Case 2和Case 3数据可以发现,两者结果基本一致,由此可见长径比对平均流场影响较小.流动速度的脉动值和雷诺应力分布都是流场结构中重要的湍流特征,因此可通过对速度脉动值和雷诺应力的分析,研究方柱尾流结构中的湍流特性.(a) 平均流向速度(b) 平均竖向速度图6 尾流区不同位置处平均速度分布Fig.6 Mean velocity profile in the wake由于旋涡的交替出现使得尾流区流向速度脉动值的峰值不在中心处,而是在两侧出现双峰值,如图7(a)所示.这说明在尾流区存在明显卡门涡街现象.然而随着流动向下游发展,峰值对应的尖角消失,变得更圆滑,甚至消失.这说明旋涡在下游发展中逐渐减弱.如图7(b)所示,尾流区不同位置处的脉动竖向速度均在在中心线上达到峰值,即存在单个峰值.因此表明交替出现的旋涡对流向和竖向上速度脉动值的影响是不同的.如图7(c)所示,由于交替旋涡的出现,雷诺应力(u′v′)呈现关于y=0轴的反对称性.此外以上三者均在位置x/D=1.5处达到峰值,然后随着流向而逐渐衰减,这表明旋涡强度最大值对应的位置在x/D=1.5附近,即回转长度大约为1.5D,再次证明了表1中得到的回转长度是合理准确的.同时可以发现,本文Case 2和Case 3结果均与其他结果基本吻合,但Case 3的结果更加接近Lyn等[1]实验值.由此可见,速度的脉动值对展向长度,即长径比更加敏感,因此为保证得到准确的湍流流场特性,需要选择合理长径比.为了进一步研究展向长度(长径比)对流场的影响,本文在方柱表面不同位置上,沿展向布置了一系列监测点,并通过分析得到其压力的相关性系数,如图8所示.由于展向采用周期边界条件,因此压力的相关性系数在两侧均等于1.同时可以发现随着长径比的增加,背面和侧面的压力相关性均减弱.背面压力相关性的减弱导致方柱的阻力系数的平均值和脉动值均有所减小,如表1所示;而侧面压力的减弱使得升力的脉动值明显减小,从而使得其值与实验结果更加吻合.因此,在对方柱绕流进行数值模拟时,为保证获取准确合理的平均和脉动气动力,以及准确的流场湍流特性,取8D的展向长度是十分必要的.(a) 脉动流向速度(b) 脉动竖向速度(c) 雷诺应力(u′v′)图7 尾流区不同位置处的脉动速度分布Fig.7 Fluctuating wake velocity(a) 方柱背面不同位置处(b) 方柱侧面不同位置处图8 方柱表面压力相关性系数Fig.8 Pressure correlation on cylinder surface4 结论在典型高雷诺数Re=22 000下,本文基于开源软件Openfoam平台,采用大涡模拟方法,对不同网格划分体系、不同展向长度下的方柱绕流进行三维数值模拟研究,在验证了数值结果的准确性基础上,深入分析了其尾流的流场结构和气动力特性,并给出了展向长度(长径比)对流场的影响,得到以下结论:(1) 在方柱表面附近先布置厚度均匀的正交网格,可获得更加准确的气动力结果.(2) 在方柱绕流中,回转长度是尾流结构的重要参考指标,其值大小直接影响着方柱气动力的表现,特别是断面的阻力系数.(3) 高雷诺数下,展向长度对回转长度影响较小,但对尾流流向速度分布中的Umin/U比值影响较大,即Umin/U比值对长径比更为敏感.(4) 长径比的大小直接影响方柱气动力的表现,特别是展向相关性,这使得气动力的脉动值对长径比也更加敏感,故为保证计算结果的准确性,特别为了获取更准确的湍流特性,展向长度取为8D是更为合理和有效.参考文献:【相关文献】[1] LYN D, EINAV S, RODI W, et al. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J]. Journal of Fluid Mechanics, 1995, 304: 285-319.[2] SAHA A, MURALIDHAR K, BISWAS G. Experimental study of flow past a square cylinder at high Reynolds numbers[J]. Experiments in Fluids, 2000, 29(6): 553-563.[3] NISHIMURA A, TANIIKE Y. Fluctuating wind forces of a stationary two dim. square prism[C]∥Proceedings of 16th National Symposium on Wind Engineering. Tokyo: Springer, 2000: 255-260.[4] YEN S C, YANG C W. Flow patterns and vortex shedding behavior behind a square cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(8): 868-878.[5] SOHANKAR A, NORBERG C, DAVIDSON L. Numerical simulation of flow past a square cylinder[C]∥The 3rd ASME/JSME Joint Fluids Engineering Conference. San Francisco: American Society of Mechanical Engineers, 1999: 18-23.[6] OKAJIMA A. Strouhal numbers of rectangular cylinders[J]. Journal of Fluid Mechanics, 1982, 123: 379-398.[7] SRINIVAS Y, BISWAS G, PARIHAR A, et al. Large-eddy simulation of high Reynolds number turbulent flow past a square cylinder[J]. Journal of Engineering Mechanics, 2006,132(3): 327-335.[8] WANG G, VANKA S. Large-eddy simulations of high Reynolds number turbulent flow over a square cylinder[J]. Dept. of Mechanical and Industrial Engineering Rep. No. CFD, 1996: 96-02.[9] RODI W, FERZIGER J, BREUER M, et al. Status of large eddy simulation: results of a workshop[J]. Transactions-American Society of Mechanical Engineers Journal of Fluids Engineering, 1997, 119: 248-262.[10] VOKE P R. Flow past a square cylinder: test case LES2[J]. Direct and Large Eddy Simulation Ⅱ, Spring, 1997, 5: 335-373[11] GRIGORIADIS D, BARTZIS J, GOULAS A. LES of the flow past a rectangular cylinder using the immersed boundary concept[J]. International Journal for Numerical Methods in Fluids, 2003, 41(6): 615-632.[12] 张伟,葛耀君. 方柱绕流粒子图像测速试验与数值模拟[J]. 同济大学学报:自然科学版,2009,37(7): 857-861,892.ZHANG Wei, GE Yaojun. Particle image velocimetry study and numerical simulation of turbulent near wake of square cylinder[J]. Journal of Tongji University: Natural Science, 2009, 37(7): 857-861, 892.[13] LILLY D K. A proposed modification of the Germano subgrid-scale closure method[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4(3): 633-635.[14] CHOI S K. Note on the use of momentum interpolation method for unsteady flows[J]. Numerical Heat Transfer: Part A: Applications, 1999, 36(5): 545-550.[15] NORBERG C. Flow around rectangular cylinders: pressure forces and wake frequencies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49(1/2/3): 187-196.[16] 周强,曹曙阳,周志勇. 亚临界雷诺数下圆柱体尾流结构的数值模拟[J]. 同济大学学报:自然科学版,2013,41(1): 33-38.ZHOU Qiang, CAO Shuyang, ZHOU Zhiyong. Numerical studies of wake characteristics on a circular cylinder at sub-critical reynolds number[J]. Journal of Tongji University: Natural Science, 2013, 41(1): 33-38.[17] OKA S, ISHIHARA T. Numerical study of aerodynamic characteristics of a square prism in a uniform flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009,97(11): 548-559.[18] NORBERG C. An experimental investigation of the flow around a circular cylinder: influence of aspect ratio[J]. Journal of Fluid Mechanics, 1994, 258: 287-316.。
高雷诺数下双圆柱绕流的数值模拟_廖俊

A辑第16卷第1期 水动力学研究与进展 Ser.A,V ol.16,N o.1 2001年3月 JOURNAL OF HYDRODYNAM ICS M ar.,2001文章编号:1000-4874(2001)01-0101-10高雷诺数下双圆柱绕流的数值模拟廖 俊1, 景思睿2(1.华中理工大学能源科学与工程学院,湖北武汉430074;2.西安交通大学能源与动力工程学院,陕西西安710049) 摘 要: 本文使用表面涡法研究高雷诺数下不同排列方式双圆柱绕流的流动状态。
计算了双圆柱在并列、串列及级列的情况下的各种流动结构,涡街的变化及作用在圆柱上的受力情况。
本文结果清楚地描述了双圆柱绕流复杂的流动状况,计算结果与实验显示的流动状况十分相似,斯特罗哈数和阻力系数与实验结果符合得很好。
关 键 词: 表面涡方法;圆柱绕流;数值模拟;涡街中图分类号: O357.1 文献标识码:A1 引言对多圆柱的绕流研究在工程实际中有很重大的意义,例如管束的热交换,反应堆,高大建筑物,海洋平台及桥梁等。
当流体流过圆柱体时,由于涡的脱落,使圆柱体上产生交变作用力。
这种作用力导致柱体的振动及材料的疲劳,而使结构损坏,产生严重的后果。
如水电站的蒸发塔,就曾经由于安装位置不正确,导致多个塔之间强烈影响、振动并使塔损坏,悬索桥也发生过类似事例,悬索共振而使桥倒塌。
由于多个柱体流动状况复杂、多变,导致对于柱体上作用力大小和方向极其复杂,实验测量非常困难,在实际工程中就需要用数值模拟的方式确定其流动状况,估计出柱体上的作用力大小、方向,以便工程参数的确定。
在多圆柱绕流研究中最多的是双圆柱绕流,双圆柱绕流按圆柱的不同排列方式可以分为三类:串列,两圆柱相对来流方向呈前后排列;并列,两圆柱相对来流方向呈并排排列;级列,两圆柱呈前后交叉排列。
对于柱体绕流的数值模拟方式可以分两大类,一类为网格法,另一类为无网格法。
网格法主要有有限差分法、有限元法。
流体力学Fluent报告——圆柱绕流

亚临界雷诺数下串列单圆柱与圆柱绕流的数值模拟之阳早格格创做目要:原文使用Fluent硬件中的RNG k-ε模型对付亚临界雷诺数下二维串列圆柱战圆柱绕流问题举止了数值钻研,通过截止对付比,分解了雷诺数、柱体形状对付柱体绕流阻力、降力以及涡脱频次的效率.普遍而止,Re数越大,圆柱的阻力越大,圆柱体则可则;而Re越大,二种柱体的降力均越大.相对付于圆柱,共种条件下,圆柱受到的阻力要大;好异天,圆柱涡脱降频次要小.Re越大,串列柱体的Sr数越靠近于单圆柱体的Sr数.闭键字:圆柱绕流、降力系数、阻力系数、斯特劳哈我数正在工程试验中,如航空、航天、航海、体育疏通、风工程及大天接通等广大的本量范畴中,绕流钻研正在工程本量中具备要害的意思.当流体流过圆柱时, 由于漩涡脱降,正在圆柱体上爆收接变效率力.那种效率力引起柱体的振荡及资料的疲倦,益坏结构,成果宽沉.果此,近些年去,稠稀博家战教者对付于圆柱绕流问题举止过细致的钻研,特天是圆柱所受阻力、降力战涡脱降以及涡致振荡问题.沈坐龙等[1]鉴于RNG k⁃ε模型,采与有限体积法钻研了亚临界雷诺数下二维圆柱战圆柱绕流数值模拟,得到了圆柱战圆柱绕流阻力系数Cd与Strouhal 数随雷诺数的变更顺序.姚熊明等[2]采与估计流体硬件CFX中LES模型估计了二维不可压缩匀称流中孤坐圆柱及串列单圆柱的火能源个性.使用非结构化网格六里体单元战有限体积法对付二维N- S圆程举止供解.他们着沉钻研了下雷诺数时串列单圆柱正在分歧间距比时的压力分集、阻力、降力及Sr数随Re数的变更趋势.费宝玲等[3]用FLUENT硬件对付串列圆柱绕流举止了二维模拟,他们采用间距比L/D(L为二圆柱核心间的距离,D为圆柱直径)2、3、4共3个间距举止了数值分解.估计均正在Re = 200 的非定常条件下举止.估计了圆柱的降阻力系数、尾涡脱降频次等形貌绕流问题的主要参量,分解了分歧间距对付圆柱间相互效率战尾流个性的效率.圆柱绕流的一个要害个性是震动形态与决于雷诺数.Lienhard[4]归纳了洪量的真验钻研截止并给出了圆柱体尾流形态随雷诺数变更的顺序.当Re<5时,圆柱上下游的流线呈对付称分集,流体本去不摆脱圆柱体,不旋涡爆收.此时与理念流体相似,若改变流背,上下游流形仍相共.当5<Re<40时,鸿沟层爆收分散,分散剪切层正在圆柱体里前产死一对付宁静的“附着涡”.当40<Re<150时,震动脆持层流状态而且流体旋涡接替天从圆柱后部做周期性的脱降并正在尾流中产死二列接叉排列的涡,即卡门涡街.从150<Re<300启初,旋涡里里启初由层流背湍流转捩,直至减少至3x105安排,此时圆柱体表面附近的鸿沟层仍为层流,所有涡街渐渐转化成湍流,及e<3xl05称为亚临界天区.当3xl05<Re<3.5x106时,鸿沟层的震动也渐渐趋于湍流状态,尾流中不明隐的涡街结构,称为临界状态.[5]圆柱绕流的另一个隐著个性是斯特劳哈我数是雷诺数的函数.早正在1878年,捷克科教家Strouhal[6]便对付风吹过金属丝时收出鸣喊声做过钻研,创造金属丝的风鸣音调与风速成正比,共时与弦线之细细成反比,并提出估计涡脱降频次f的体味公式:式中即斯特劳哈我数Sr由Re所唯一决定.原文使用Fluent硬件中的RNG k-ε模型对付亚临界雷诺数下二维串列圆柱战圆柱绕流问题举止了数值钻研,通过截止对付比,分解了雷诺数、柱体形状对付柱体绕流阻力、降力以及涡脱频次的效率.1.数教模型1.1统造圆程对付于停止圆柱绕流,原文钻研对付象为二维不可压缩震动.正在直角坐标系下,其疏通顺序可用N-S圆程去形貌,连绝性圆程战动量圆程分别为:其中ui为速度分量;p为压力;ρ为流体的稀度;ν为流体的能源黏性系数.对付于湍流情况,原文采与RNG k⁃ε模型,RNG k⁃ε模型是k⁃ε模型的矫正规划.通过正在大尺度疏通战建正后的粘度项体现小尺度的效率,而使那些小尺度疏通有系统天从统造圆程中去除.所得到的k圆程战ε圆程,与尺度k⁃ε模型非常相似,其表白式如下:其中Gk为由于仄衡速度梯度引起的湍动能的爆收项,,,体味常数=0.084 5,==1.39,=1.68.相对付于尺度k⁃ε模型,RNG k⁃ε模型通过建正湍动粘度,思量了仄衡震动中的转动及转动震动情况,RNG k⁃ε模型不妨更佳的处理下应变率及流线蜿蜒程度较大的震动.1.2相闭参数圆柱绕流的相闭参数主要有雷诺数Re、斯特劳哈我数Sr、降力系数Cl战阻力系数Cd,底下给出各个参数的估计公式战物理意思.雷诺数Re与圆柱绕流的状态战雷诺数有很大闭系,雷诺数代表惯性力战粘性力之比:其中U为去流速度;L为个性少度,原文与圆柱直径或者圆柱边少;为流体稀度;、分别为流体介量能源粘度战疏通粘度.斯特劳哈我数Sr是Strouhal 指出圆柱绕流后正在圆柱后里不妨出现接替脱降的旋涡,旋涡脱降频次、风速、圆柱直径之间存留一个闭系:式中:Sr为斯托罗哈数,与决于结构的形状断里;f 为旋涡脱降频次;L为结构的个性尺寸; U 为去流速度.阻力系数战降力系数是表征柱体阻力、降力的无量目参数.定义为:,式中ρ为流体稀度;V为去流速度;A为迎流截里里积;战.由于涡脱降的闭系,阻力系数将爆收振荡,原文采用仄衡脉动降力去钻研,即与圆均根值去钻研.2.数值估计2.1物理模型二维数值模拟单圆柱流场估计天区的采用如图1所示,圆柱绕流以圆柱体直径为个性尺度D,采用圆柱半径为1.5 mm,估计天区为9D×32D的矩形天区.柱1距上游少度图 1 串列圆柱战圆柱的估计天区5D,下游少度27D,脆持二柱间距 L/D= 2. 5D稳定 (L是二圆柱核心连线少度),二柱到上下鸿沟距离相等.对付于圆柱绕流,采用圆柱边少为个性少度,D=30mm.2.2网格区分估计天区采与分块结构化网格,柱体表面网格干加稀处理,鸿沟区网格相对付稠稀.简直网格区分情况睹图2.其中串列圆柱网格31116个节面,30615个四边形里单元;串图 2 圆柱绕流与圆柱绕流估计域的网格区分列圆柱46446个节面,46550个四边形里单元.2.3鸿沟条件管讲壁里战柱体表面均采与无滑移的停止壁里条件.而出心采用速度出心,出心采用自由出流.去溜速度大小根据Re去树坐,雷诺数分300、3000、12000、30000四个等第,速度大小依次为0.1m/s、1m/s、4m/s、10m/s.2.4估计模型原文湍流模型采与尺度壁里函数的RNG k-ε模型.采与有限容积法供解二维不可压缩粘性流体非定常震动统造圆程,即把估计天区分成很圆柱近壁里网格多小的统造体,对付每个统造体的各个变量举止积分.统造圆程的对付流项采与二阶迎风圆法失集,速度战压力采与SIMPLE算法耦合供解,将所有天区瞅成一个完全举止耦合估计.动量、湍动能战湍动耗集率均采与二阶迎风圆法.先定常估计流场,再用定常估计的截止动做非定常迭代的初初值举止估计.根据初略估计的涡脱频次,牢固树坐时间步少为0. 002s, 正在每个时间步内树坐迭代次数为20.流体介量为液态火.3.估计截止3.1网格模型考证为考证网格独力性,原文估计了网格节面数为8346,里单元为8932的细网格、节面数为31116,里单元为30615的稀网格、节面数为63432,里单元为67434的细稀网格下Re=200、L/D=2的串列网格的Sr数,截止隐现三套网格的估计截止分别为0.143、0.133、0.133.故稀网格可用.而圆柱绕流则采与共级别网格.[7]的估计数据相比较,比较图像如图3所示,最大缺面为2.2%.图3串列圆柱分歧间距的Sr数估计对付比3.2流线与涡量图图 6 Re=3000圆柱绕流流线图图 7 Re=3000圆柱绕流涡量等值线图图 4 Re=3000圆柱绕流流线图图 5 Re=3000圆柱绕流涡量等值线图原文给出了估计历程中雷诺数Re=3000,t=1s时的流线图战涡量图.3.3阻力系数图 9 Re=3000圆柱绕流脉动阻力系数图 8 Re=3000圆柱绕流脉动阻力系数原文给出了Re=3000时,圆柱绕流战圆柱绕流的脉动阻力系数图如下.由图9战错误!未找到引用源。
FLUENT仿真计算不同雷诺数下的圆柱绕流
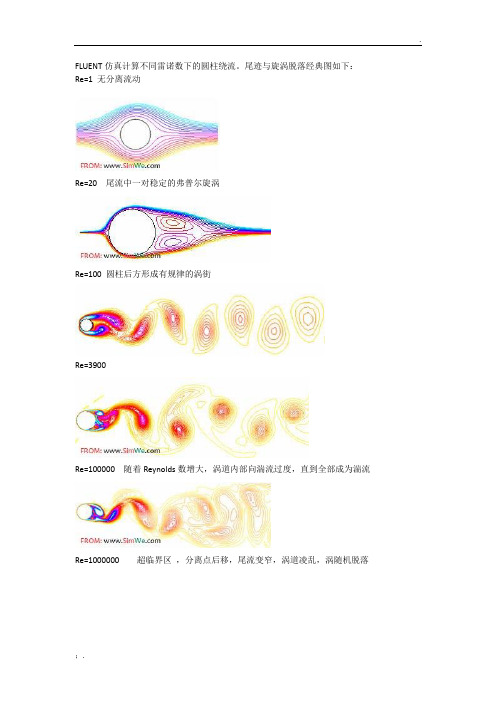
FLUENT仿真计算不同雷诺数下的圆柱绕流。
尾迹与旋涡脱落经典图如下:Re=1 无分离流动Re=20 尾流中一对稳定的弗普尔旋涡Re=100 圆柱后方形成有规律的涡街Re=3900Re=100000 随着Reynolds数增大,涡道内部向湍流过度,直到全部成为湍流Re=1000000 超临界区,分离点后移,尾流变窄,涡道凌乱,涡随机脱落Re=10000000 极超临界区,分离点继续后移,尾流变窄,湍流涡道重新建立。
图3 Cd随Re的变化曲线图3中实曲线是由Wieselsberger,A.Roshko以及G.W.Jones和J.J.Walker测量数据绘制得到,图中圆点部分是FLUENT计算值在Re=106(超临界区),从经典数据和我们的计算结果都可以看到,圆柱体的平均阻力系数急剧下降。
这是因为在Re=3×105附近,边界层流动由层流状态转变为湍流状态,虽然湍流边界层流动的摩擦阻力较层流边界层大,但它从物面的分离较晚,所以形成较小的尾流区。
由于钝体绕流的阻力主要是压差阻力,所以此时物体的总阻力有了一个明显的下降。
入口VELOCITY_INLET,出口OUTFLOW,上下WALL.Re=1,20,100,二维层流模型。
Re=3900后,三维大涡模型计算不准与网格划分与一些参数设置有关。
1。
圆柱中心离上下边界(wall)的距离大于10D(D为圆柱直径),影响较小。
2。
湍流模型采用大涡模型(LES)。
是目前最复杂,最完善的一种湍流模型。
试验曲线来自,《Boundary-Layer Theory》, Dr.HERMANN SCHLICHTING, Translated by Dr.J.KESTIN,Seventh Edition,用MATLB绘制4.阻力系数的求法请参考此论坛我发的教程FLUENT三分立系数的求法。
亚临界雷诺数下圆柱和方柱绕流数值模拟

亚临界雷诺数下圆柱和方柱绕流数值模拟最近,随着大规模流体动力学(LFD)和其他非结构性的方法的发展,数值模拟的重要性和应用也变得越来越广泛。
在绕流过程中,绕流模拟对于准确预测流体动力学行为至关重要。
近年来,圆柱和方柱绕流一直是重要的研究热点,其真实性受到广泛关注。
圆柱和方柱绕流数值模拟,是以相对低的雷诺数Re以及它们相对的相变过程的重要工具。
Re意味着流体动力学的影响,基于Re的亚临界状态共存精确研究流体动力学。
鉴于影响数值模拟精度的数值误差的存在,理论精度和实际应用的完整性和有效性是一个重要的问题。
亚临界状态下的圆柱和方柱绕流模拟,使用分布式交错网格(DMGs),以及完全控制差分过程(FDC),已被广泛应用于当前的数值模拟研究。
在这个过程中,FDC和DMG网格可以用来准确预测流体运动,这些预测可以用来更准确地预测流体动力学参数。
在这项研究中,我们提出了一种圆柱和方柱绕流模拟方法,以及用于仿真过程的FDC/DMG技术。
我们的方法基于亚临界雷诺数(Re),以及针对Re的相变过程。
通过引入非定常非均匀网格(CNG)来改进算法的准确性和实用性。
将计算结果与实验数据进行了比较和分析,以验证该模拟方法的有效性。
本研究的主要结论如下:(1)使用亚临界雷诺数可以准确预测圆柱和方柱绕流的流体动力学参数;(2)带有CNG的FDC/DMG可以更加准确地预测绕流过程中的数值模拟;(3)使用FDC/DMG可以更准确的描述实际流体动力学参数;(4)本研究的方法可以更加准确地预测不同Re下的流体动力学行为。
总的来说,本研究为亚临界雷诺数下圆柱和方柱绕流的模拟提供了一个可行的解决方案,它可以准确预测不同Re下的流体动力学行为。
本研究还提出了一种改进的算法,可以用来更加准确地模拟绕流,提高模拟的真实性和有效性。
通过本研究,我们有望更好地理解数值仿真,并将其用于实际的工程和科学应用中,为后续的更深入的研究提供更多的可能性。
经过本次研究,我们可以得出一个结论:亚临界雷诺数下的圆柱和方柱绕流数值模拟,使用FDC/DMG技术,可以更加准确地预测绕流的流体动力学参数,提高真实性和有效性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
489
γsep
Байду номын сангаас
Rev = min( s1 max 0, −1 · 3.135 · Reθc Freatt , 2)Fθt
4
Freatt = e−(RT /20) , γeff
(13) = max(γ, γsep ), s1 = 2
2
(8)
(5)
式中
√ L= k
1/4 Cµ ω
(9)
, LvK = κ
S , U = U
∂2 uk ∂2 uk ∂ xi2 ∂ x2 j
(6)
模型中源项分别为
Pγ = Flength ca1 ρS γ Fonset (1 − ce1 γ) (10) (11) (12)
模型常数为
C = 2.0, ξ = 3.51, κ = 0.41, σΦ = 2 , Cµ = 0.09 3
图 2 为计算中所采用的多块结构化网格. 在大涡 模拟特征最为显著的区域, 如图中接近 ( x/D, y/D) = (0.75, 0.5) 位置处的 P 点 [9] , 其网格尺度为 ∆/D = 0.026; 近壁面加密使得第一层网格单元中心处的 y+ < 1.0; 展向取 51 个均匀分布的网格点. 最后, 总 的网格单元数约为 3.3 × 106 . 计算中物理时间步长取 ∆t = 0.02t∗ , 参考时间 t∗ = D/U∞ , 此步长大小可使分 离区以及下游尾迹中的 CFL 数不大于 1. 根据实验, 来流湍流度取 T u = 0.6%, 相对分子 黏性 RT = µT /µL = 0.1. 在此条件下, γ–Reθ 模型给 出的间歇因子分布如图 3 所示. 可以看到, 在分离前 的边界层内 γ 为小量, 湍动能耗散远大于生成, 因此 不会出现湍动能的增长, 流动保持为层流, 如图 4 所 示. 当出现分离后, γ 在分离转捩模式作用下快速增
1 ∂ui ∂u j + 2 ∂ x j ∂ xi
模型常数 α, a1 , β∗ , β, σk , σω , σω2 取值以及函数 F1 , F2 的具体形式与 SST 模型一致, 具体可见文献 [18]. SST-SAS 模型中发挥尺度自适应作用的 QSAS 定 义为 [19]
QSAS = ρ · max ξκS 2 L − LvK 1 ∂ω ∂ω 1 ∂k ∂k 2k max 2 , ,0 C σΦ ω ∂ x j ∂ x j k2 ∂ x j ∂ x j
∂ (ρk) ∂ ρu j k ˜ k − β∗ ρωk + + =P ∂t ∂x j ∂k ∂ (µ + σk µT ) ∂x j ∂x j ρ ˜ ∂ (ρω) ∂ ρu j ω 2 + =α P k − βρω + ∂t ∂x j µT ∂ ∂ω (µ + σω µT ) + ∂x j ∂x j 1 ∂k ∂ω + QSAS 2 (1 − F1 ) ρσω2 ω ∂ xi ∂ xi ˜ k = min(Pk , 10 · β∗ ρωk), P ∂ui ∂ui ∂u j Pk = µT + ∂ x j ∂ x j ∂ xi ρk a1 ρk , , S = 2S i j S i j µT = min ω S F2
LvK = max κ S , CSAS ∆ , ∆ = Vol1/3 U (7)
(2)
(3) (4)
其中
S ij =
式中, Vol 为控制体单元体积, 常数 CSAS 可通过对各 项均匀同性湍流的模拟进行标定 [20] , 最后取 CSAS = 0.26.
1.2 转捩模型 Menter 和 Langtry 提出的基于经验关系式的 γReθ 转捩模型为 [14] ∂ (ργ) ∂ ρu j γ + = Pγ − Dγ + ∂t ∂x j ∂ µT ∂γ µ+ ∂x j σ f ∂x j ˜ θt ˜ θt ∂ ρRe ∂ ρu j Re + = Pθt + ∂t ∂x j ˜ θt ∂ ∂Re σθt (µ + µT ) ∂x j ∂x j
第 46 卷 第 4 期 2014 年 7 月
力
学
学
报
Vol. 46, No. 4 July, 2014
Chinese Journal of Theoretical and Applied Mechanics
研究论文
1)
高亚临界雷诺数圆柱绕流的尺度自适应模拟
杜 磊 宁方飞 2)
(北京航空航天大学能源与动力工程学院, 北京 100191)
k,trip eff
图 1 计算域及边界条件示意 Fig. 1 Schematic of the computational domain and boundary conditions
正是通过结合 SST-SAS 和 γ–Reθ 转捩模型实现了对 圆柱绕流的层流分离流态的模拟, 而对于湍流分离 则只单独求解 SST-SAS.
1.3 数值求解
本文工作采用了课题组自主开发的并行气动模 拟程序 MAP[26] . 非定常计算使用双重时间步方法, 物 理时间项采用三点欧拉格式离散, 在虚拟时间步内 为隐式推进求解. 对流通量使用混合格式计算其大 小, 主流区以及近壁面为迎风格式, 而在需要尺度分 辨的分离区中则切换为低耗散中心格式. 分区特点 使得混合格式非常适合 SAS, DES 等此类 RANS/LES 混合模拟, 格式的详细构造可参见文献 [21]. 黏性通 量采用二阶中心差分格式求解. 计算中用到的迎风格式为 LDFSS [22] , 并采用 MUSCL 插值获得高阶精度, 中心格式为有限差分形 式的四阶偏斜对称格式 [23] , 且添加了各项异性的标 量人工黏性, 二、四阶人工黏性系数分别取为 k(2) = 0.0 和 k(4) = 1.0 × 10−4 . 混合格式只在求解流动方程 时使用, 对于所有模型方程则使用纯迎风格式计算 对流通量.
以上模型中各函数的构造以及常数取值可参见文献 [14], 这里不再详述. 在转捩模拟中, 需要联立求解 γ–Reθ 转捩模型和 SST 湍流模型, 通过间歇因子控制湍动能的生成和发 展, 从而实现对转捩流动的模拟, 该思路同样也适用 于 SST-SAS, 可将方程 (1) 中的生成项和耗散项替换 为 ˜k Pk,trip = γeff P (14) ∗ D = min(max(γ , 0.1), 1.0)β ρωk
(1)
尺度由流动本身决定, 这与 DES 中使用固定的网格 尺度不同, 这是尺度自适应的第一层含义; LvK 对定 常和非定常性的不同响应则是尺度自适应的第二层 含义. 具体来说, 对于流场中的定常部分, 如主流区, 此时 LvK 将远大于模型尺度 L, 所以有 QSAS = 0, 模 型处于完全 RANS 模式 (SST 模型); 而在大分离湍流 区, 流动的强非定常性将使得 LvK 减小至远小于 L, 此时 QSAS 定义中前项将占主导, QSAS 不再为零, 模 型计算得到的 ω 增加, 涡黏性则会下降, 从而分离区 中能够出现更多的湍流脉动, SAS 就转换为具有湍 流尺度分辨能力的 LES 模式. 此外, 在近壁面边界层 内, QSAS 中的后项将始终大于前项, 从而保证了 SST 模型对边界层湍流的模拟能力不受影响. 实际使用中发现, 某些情况下 LvK 会出现小于 网格尺度的情况, 造成 SST-SAS 对网格所能分辨的 最小尺度湍流耗散不足的问题, 可对其进行如下最 小限制
2013–11–14 收到第 1 稿, 2014–02–13 收到修改稿.
1) 国家自然科学基金资助项目 (50506001)
将使用转捩模型来达到层流分离流动的目的; 其二, 对于圆柱分离后的大分离湍流进行的是尺度自适应 模拟 (scale adaptive simulation) [10-13] . 由于 γ-Reθ 转捩模型 [14-16] 所包含的模型方程均 为完全当地型的输运方程, 所以容易程序实现, 且在 三维流动模拟中不存在特殊困难. 同时, 大量数值计 算结果也表明该模型能够较为准确地模拟各类转捩 流动; Menter 提出的尺度自适应模拟中虽不显含网 格尺度, 但依赖于冯卡门长度尺度对流动非定常性 的响应使得该方法在分离湍流区中具备大涡模拟能 力, 因而用以模拟存在大分离流动的圆柱绕流是比较 合适的选择. 注意到, 常用的尺度自适应模型为 SSTSAS, 可由 SST 湍流模型添加尺度自适应项后得到, 而 γ-Reθ 同样联立 SST 使用, 因此两者可通过 SST 湍 流模型实现 “无缝” 结合, 能够方便地实现圆柱层流 分离流动的数值模拟. 本文模拟的圆柱绕流雷诺数 Re = 1.4 × 105 , 为进 行对比, 同时模拟了层流分离和湍流分离两种流态. 选取此雷诺数主要是考虑: 首先, 该雷诺数已接近亚 临界流动的极限, 这时层流分离和湍流分离流动差 别非常显著, 可以直观看到 “阻力危机” 的存在; 其 次, 已有的该雷诺数模拟结果可用以和本文模拟结 果的比较;最后, Cantwell [17] 对 Re = 1.4 × 105 圆柱 层流分离流动做了详细的实验研究, 给出了较为详
引 言
圆柱绕流由于包含丰富的流动现象, 特别是高 雷诺数亚临界流动时存在分离、流动转捩以及大分 离湍流等复杂过程, 使其成为计算流体力学领域非 常有挑战性的问题, 同时也是测试计算模型、 数值方 法等有效性的理想对象. 理论上直接数值模拟 (direct numerical simulation, DNS) 和大涡模拟 (large eddy simulation, LES) 是圆柱绕流计算的理想方法 [1-2] . 随着 计算能力的提高, 出现了雷诺数高达 1.4 × 105 甚至 1.0 × 106 的圆柱绕流大涡模拟 [3-4] . 大量的 DNS 和 LES 模拟结果加深了人们对圆柱绕流的机理认识, 同 时丰富了可供参考的数据库. 凭借计算量比 LES 小而计算精度高于 RANS 的 综合优势, RANS/LES 混合方法成为当前模拟高雷诺 数下大分离湍流的主要途径, 自然该方法也被用于 圆柱绕流的模拟当中 [5-7] . 然而, 混合方法在近壁面 边界层内的 RANS 特性使其无法直接模拟圆柱亚临 界绕流, 这是因为亚临界流动是层流分离, 而混合方 法只能模拟湍流分离, 即类似于发生了 “阻力危机” 的超临界流动. 为此, Travin [8] 采用 “Trip-Less (TL)” 技术, 强制流动在分离前为层流, 分离发生后为湍流, 如此, 实现了对 Re = 5.0 × 104 和 1.4 × 105 圆柱绕流层 流分离的 SA-DES 模拟 [9] . 本文也将对圆柱层流分离 流动进行数值模拟, 但策略与 Travin 不同. 其一, 这里
