第5章 三元合金相图
9材料科学基础课件-第五章三元相图

e1
A
L+α
2016/2/12
α+β
返回
• 三相区: L+α+β、 L+α+γ、 L+β+γ、 α+β+γ f=1 L→α+β、L→α+γ、 L→β+γ
在TE等温四相面以上有三个三相区,以下有一个, 称为3/1转变。 三相区由三相平衡三角形滑动而成。三相区棱边 为三个相的浓度变温线。
E
e
α β γ β
P O
β
Q C
R
w RP = w
P
RQ Q
A
• 成分为O的合金,分解为αβ两相,则αβ连线必过O点。
w % = 100%
2016/2/12
o
w % = 100%
返回
o
二、重心定律
• 已知成分的三个合金P、Q、N, 熔配成一个新的合金R,R成分 点必在△PQN内,且在△重量 重心上。
B Q n R P A q p N C
wP · RQ RP = w Q ·
=
RN wN ·
• 证:将PQ合金按直线定律熔配 成n,再由n和N按直线定律熔 配成R。
2016/2/12
返回
• 由合金O,分解成αβγ三个相, 则O位于△αβγ的重量重心处。
B
• 各相相对量:
o ' w % = 100% ' o ' w % = 100% ' o ' w % = 100% '
2016/2/12
β
γ’ O α’
α
A
β’
γ
C
返回
三元合金相图
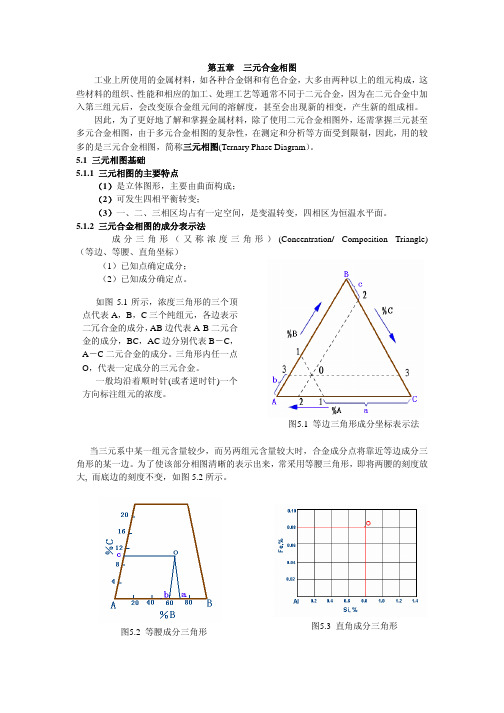
图5.3 直角成分三角形
如图 5.3 所示,当三元系成分以某一组元为主,其他两个组元含量很少时,合金成分点 将靠近等边三角形某一顶点。若采用直角坐标表示成分,则可使该部分相图更为清楚的表示 出来,一般用坐标原点代表高含量组元,而两个互相垂直的坐标轴代表其他两个组元的成分。 5.1.3 成分三角形中特殊的点和线
接。
三相平衡区的特点:直边三角形;两相区与之线接;单相区与之点接。
图 5.24 组元在固态有限互溶的三元相图的等温截面示意图 (3)变温截面
图 5.25 是组元在固态有限互溶的三元相图的变等温截面示意图。
图 5.8 三元相图中的重心定律
如图 5.8 所示,R 合金的重量与三个相的重量有如下关系
WR ⋅ Rd = Wα ⋅αd
Wα
= S∆Rβγ S ∆αβγ
= Rd αd
WR ⋅ Re = Wβ ⋅ βe
Wβ
= S∆Rαγ S ∆αβγ
= Re βe
WR ⋅ Rf = Wγ ⋅ γd
Wγ
= S∆Rαβ S ∆αβγ
以图 5.19 中合金 O 为例,可定量 计算其室温平衡组织的各组织组成物 的相对含量。
WA
=
oq Aq
×100%
WL
=
Ao Aq
×100%
W( A+C) = Eq × Ao ×100% W0 Ef Aq
W( A+B+C) = qf × Ao ×100%
W0
Ef Aq
图 5.20 是合金 o 的室温组织示意
(A+B+C)
5.3.2 固态有限互溶的三元共晶相图 固态下有限互溶的三元相图是由三对在液态无限互溶,而在固态有限互溶的二元共晶相
第五章 三元合金相图

第五章三元合金相图本章主要内容:成分表示方法:等边三角形,等腰三角形,直角坐标,成分三角形特殊线,直线法则与杠杆定律,重心法则;三元匀晶相图:相图分析,等温截面,变温截面;固态完全不溶三元共晶相图:相图分析,等温截面,变温截面,投影图;固态有限溶解的三元共晶系:相图分析,等温截面,变温截面,投影图及凝固过程;有包共晶反应的三元系:相图分析,投影图及凝固过程;有三元包晶反应的三元系:相图分析,投影图及凝固过程分析;生成化合物的三元相图;三元相图总结:三元系的单相区,三元系的两相区,三元系的三相区,三元系的四相平衡三元系的液相面投影,三元系的相区接触法则;三元相图实例:Fe-Cr-C系,Al-Cu-Mg系,CaO-SiO2-Al2O3系1 填空1. 三元相图等温截面的三相区都是___________________形。
2. 图1是A-B-C三元系成分三角形的一部分,其中X合金的成分是_____________________。
图2是三元系某变温截面的一部分,其中水平线代表________________反应,反应式为______________________ 。
4.图3为A-B-C三元系的一个等温截面, 固溶体中C组元的最大含量是_____________;X合金中A,B,C三组元的含量分别是_____________________________;在X合金的相组成物中,α相的百分含量是______,δ相的百分含量是____________。
图4图315图4是Cu-Zn-Al三元相图2%Al的一个变温截面,合金凝固时,L+α+β三相区将发生____________反应。
图中X合金的化学成分是______________________。
6图5是某三元系变温截面的一部分,合金凝固时,L+M+C将发生_________________反应。
7 三元相图的成分用__________________________表示。
第五章 三元合金相图

第五章 三元合金相图1 根据Fe -C -Si 的3.5%Si 变温截面图(5-1),写出含0.8%C 的Fe-C-Si 三元合金在平衡冷却时的相变过程和1100℃时的平衡组织。
图5-12 图5-2为Cu-Zn-Al 合金室温下的等温截面和2%Al 的垂直截面图,回答下列问题:1) 在图中标出X 合金(Cu-30%Zn-10%Al )的成分点。
2) 计算Cu-20%Zn-8%Al 和 Cu-25%Zn-6%Al 合金中室温下各相的百分含量,其中α相成分点为Cu-22.5%Zn-3.45%Al ,γ相成分点为Cu-18%Zn-11.5%Al 。
3) 分析图中Y 合金的凝固过程。
Y%图5-23 如图5-3是A-B-C 三元系合金凝固时各相区,界面的投影图,A 、B 、C 分别形成固溶体α、β、γ。
1) 写出P p '',P E '1和P E '2单变量线的三相平衡反应式。
2) 写出图中的四相平衡反应式。
3) 说明O 合金凝固平衡凝固所发生的相变。
图5-3 图5-44 图5-4为Fe-W-C三元系的液相面投影图。
写出e1→1085℃,P1→1335℃,P2→1380℃单变量线的三相平衡反应和1700℃,1200℃,1085℃的四相平衡反应式。
I,II,III三个合金结晶过程及室温组织,选择一个合金成分其组织只有三元共晶。
5 如图5-5为Fe-Cr-C系含13%Cr的变温截面1)大致估计2Cr13不锈钢的淬火加热温度(不锈钢含碳量0.2%, 含Cr量13%)2)指出Cr13模具钢平衡凝固时的凝固过程和室温下的平衡组织(Cr13钢含碳量2%)3)写出(1)区的三相反应及795 时的四相平衡反应式。
图5-5 图5-66 如图5-6所示,固态有限溶解的三元共晶相图的浓度三角形上的投影图,试分析IV区及VI区中合金之凝固过程。
写出这个三元相图中四相反应式。
图5-77 分析如图5-7所示的三元相图,该合金中E 点成分为27Pb18Sn55Bi ,γ相成分取100%Bi 。
5 三元相图
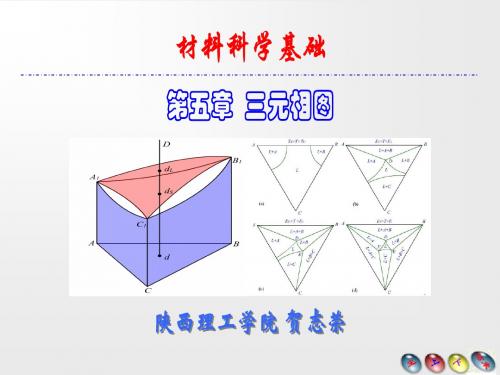
图 含稳定化合物的三元系的简化分割
第七节 三元合金相图应用举例
5.7.1 Fe-C-Si三元系的垂直截面
L
L
5.1.2 浓度三角形中具有特定意义的线
C
A% C% d c
Bc C% 100% BC
B
A
B% 图 平行于浓度三角形某一条边的直线
C c
A%
C% d
A% PB B % PA
P B B%
A
图 通过三角形顶点的任一直线
思考题1
下图的成分三角形中有 P、R、S、T 四个材料点, 问哪个点的材料,其成分 为: A=20%, B=10%,C=70% P R S T
图 过成分三角形顶点的变温截面图
图 平行于成分三角形一边的变温截面图
用垂直截面图可以分析合金的平衡结晶过程,了解合金在 平衡冷却过程中发生相变的临界温度,以及可以了解合金在 一定温度下所处的平衡状态。 但是,用垂直截面图不能了解合金在一定温度下的平衡相 成分和平衡相的重量。
图 变温截面图的应用
第五章 三元相图
为什么要用到三元相图?
二元相图只适用于二元合金或二个组元的陶瓷材料,对 于三组元的合金或陶瓷材料需用三元相图分析。 工程实用材料多是三组元或三组元以上的,三组元的合 金可举例如下:轴承钢中的Fe-C-Cr合金;高锰耐磨钢中的 Fe-C-Mn合金;不锈钢中的Fe-Cr-Ni合金;铸铁中的Fe-CSi合金;铝合金中的Al-Mg-Si合金,Al-Cu-Mg合金等等。
图 三元固溶体合金的平衡凝固过程分析
§5.3.2 等温截面图(水平截面图)
图 三元匀晶相图的水平截面图
如图合金O处于L+α两相 平衡。 图中的PQ线是连接两平 衡相成分点的直线,称为连 接线或共轭线。
第五章 三元合金相图

变温截面同二元相图的区别: 变温截面同二元相图的区别
根据三元固溶体合金结晶时的蝴蝶形规律,在两相平衡时 根据三元固溶体合金结晶时的蝴蝶形规律 在两相平衡时, 平衡相的成分点 在两相平衡时 不是落在一个垂直面上. 因此,变温截面的液 变温截面的液(固 相线不能表示平衡相的成分 相线不能表示平衡相的成分, 不是落在一个垂直面上 因此 变温截面的液 固)相线不能表示平衡相的成分 不能应用杠杆定律计算相的相对含量. 不能应用杠杆定律计算相的相对含量
五.投影图 投影图
5.4 三元共晶相图 一.组元在固态完全不溶的共晶相图 组元在固态完全不溶的共晶相图 (一).相图分析 一 相图分析
液相面( 个);固相面 个);二元共晶点 固相面( 二元共晶点(线 条);二元共晶面 个 二元共晶面( 液相面(3个);固相面(1个);二元共晶点 线3条);二元共晶面(6个); 三元共晶点(面 个 三元共晶点 面1个).
注意:在同一温度下 尽管三元合金的液相和固相成分的连接线是条水平线, 注意 在同一温度下, 尽管三元合金的液相和固相成分的连接线是条水平线 在同一温度下 但是,液相和固相成分的变化轨迹不在同一个平面上 液相和固相成分的变化轨迹不在同一个平面上. 但是 液相和固相成分的变化轨迹不在同一个平面上
等温截面(水平截面 三.等温截面 水平截面 在某一温度下的状态 等温截面 水平截面): 在某一温度下的状态. 单相区, 两相区, 相等温线(或者称 相线). 单相区 两相区 液(固)相等温线 或者称 液(固)相线 固 相等温线 或者称:液 固 相线
三个液相面、六个二元功晶面、 三个液相面、六个二元功晶面、一个三元 共晶面将相图分成九个相区: 共晶面将相图分成九个相区: 液相区: L 液相区: 两相区:( :(L+A、L+B、L+C) 两相区:( 、 、 ) 三相区:( :(L+A+B、L+B+C、L+C+A) 三相区:( 、 、 ) 三相区:( :(A+B+C) 三相区:( ) 四相区:( :(L+A+B+C) 四相区:( )
第五章 三元合金相图
二元共晶
三元共晶
第四节三元共晶相图
通过成分三角形 顶点的变温截面
第四节三元共晶相图
(四) 投影图 1. 投影图分析
2. 合金O结晶过程 L----L+A------------L+A+(A+B)---------------A+(A+B)+(A+B+C)
二元共晶 三元共晶
第四节三元共晶相图
3.合金O在室温下的相和 组织含量
第一节三元合金相图的表示方法
B (1)确定O点的成分 1)过O作A角对边的平行线 B% C% 2)求平行线与A坐标的截距 得组元A的含量 3)同理求组元B、C的含量 O A C
← A%
第一节三元合金相图的表示方法
C B
A
Oa+Ob+Oc=AB=AC=BC=100% A浓度:Oa=Of=Cb B浓度:Ob=Od=Ac C浓度:Oc=Ba A浓度:55% B浓度:20% C浓度:25%
90 • 标出 50%A+20%B+30%C 的合金 60 B% 50 40 30 20 10 A 90 80 70 60
B
10 20 30 40
80
70
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
第一节三元合金相图的表示方法
二、在成分三角形中具有特定意义的直线 B 成分三角形中特殊的点和线
第五章 三元合金相图
三元系相图简介
相图基本知识
三元相图的主要特点——立体图形,主要由曲面构成
三元系相图简介
垂直轴表示温度。 成分表示在棱柱底,通常是 一等边三角形。 棱柱的每个侧面表示三个二 元系统,如AB,BC,AC。
第5章-三元相图PPT课件
2、结晶过程分析 O 自液态缓冷至于液互
相相交时,开始从液相中结晶出 α 固溶体,此时液相的成分l1即为合金成分, 而固相的成分为固相面某一点 s。
α 相越来 越多,固相的成分由s1点沿固相面移至s2 点,液相成分自l1点移至 l2点,由直线法则可知,合金的成分点必落 在l2和s2的连线上。
Ca=WA=30% Ac=WC=60% Ab=WB=10%。
中都有应用,但应用最为广泛的还是等边 三角形。
•10
2、等边成分三角形中特定意义的线 (1) 平行 于三角形某一边的直线 凡成分位于该线上的所有合金,它们 所含的由这条边对应顶点所代表的组元的 含量为一定值。如图5-103中ef直线上代表 B组元的含量均为Ae。
•15
•16
•17
由直线法则可得到以下规律: a、 当温度一定时,若已知两平衡相的 成分,则合金的成分必位于两平衡相成分 的连线上; b、 当温度一定时,若已知一相的成分 及合金的成分,则另一平衡相的成分必位 于两已知成分点的连线的延长线上; c、 当温度变化时,两平衡相的成分变 化时,其连线一定绕合金的成分点而转动。
•1
三元相图与二元相图比较,组元数增加 了1个,即成分变量是两个,故表示成分的坐 标轴应为2个,需要用一个平面表示,再加上 垂直于该平面的温度轴,这样三元相图就 演变成一个在三维空间的立体图形,分隔 相区的是一系列空间曲面,而不是二元相 图的平面曲线。
•2
1、三元相图的成分表示方法 (1) 等边成分三角形 这样的三角形称为浓度三角形或成分三角 形(Composition Triangle)。常用的成分三 角形是等边三角形和直角三角形。
•38
•11
•12
(2)通过三角形顶点的任一直线 凡成分位于该直线上的所有合金
三元合金相图.ppt
本章知识结构
三元相图的基础 三元相图分析 三元相图举例
三元相图成分表示方法
三元相图的空间模型
三元相图的截面图和投影图 三元相图中的杠杆定律 及重心定律
小结
3
5.1 三元合金相图的表示方法
组元数 C=3 根据相律: F=3-P+1=4-P 完整的三元相图是三维的立体模型
4
三元相图的基本特点
三元相图与二元相图的差别,在于增加了一个成分 变量。三元相图的基本特点为: 是立体图形,主要由曲面构成; 可发生四相平衡转变; 一、二、三相区为一空间。
19
其它浓度三角形
1) 等腰浓度三角形
组元B的含量很少
B
成分点靠近AC边
按比例放大AB、BC边
A
C
20
2) 直角浓度三角形
组元A占绝大多数时
原点为基体组元A
纵、横坐标为组元B和C
↑ B%
B、C的浓度可以直接读出 A的浓度不能直接读出
A
N C%→
21
3)部分浓度三角形
22
5.2 三元系平衡相的定量法则
B%
C%
P
Q
A
← A%
C
15
课堂练习
B
4 绘出A =40%的
90
合金
80
5 绘出C =30%的
70
合金
60 B% 50
10
20
30
40 C%
50
40
60
30 20
70 80
10
90
A 90 80 70 60 50 40 30 20 10 C
← A%
16
过某一顶点的直线
A% Ca1 Ba'1 Ba'2 Ca2 常数
第五章 三元相图
5.1
三元相图的成分表示法
C
二元系的成分可用一条 直线上的点来表示;三元 系合金有两个独立的成分 参数,所以必须用一个平 面三角形来表示,这个三 角形叫做成分三角形或浓 度三角形。常用的成分三 角形是等边三角形,有时 也用直角三角形或等腰三 角形。 A
A%
C%
B%
B
浓度三角形
5.1.1 浓度三角形 1. 等边三角形 三角形的三个顶点A,B, C分别表示3个纯组元, 三角形的边AB,BC, CA分别表示3个二元系 的成分坐标,三角形内 的任一点都代表一定成 分的三元合金. A 一般按顺时针(或逆时针) 标注组元浓度。
L(三元) ΔT α(三元)
自由度:f=c-P+1=3-2+1=2 故三元匀晶转变区可有两个自由度: 温度和相成分。
5.3.1 相图分析
1 画图 (1) 先画一成份三角形 (应为正三角形) (2) 画温度轴 (3) 画二元匀晶相图(每 两个合金上存在一个二 元相图) ---三元系立体图可视为三 个二元系在空间的延伸 液相面----三个二元系的液相线 所围成的面. 固相面----三个二元系的固相线 所围成的面.
5.4
三元共晶相图
TA A2 A3 A1 E3 E C2 C3 C1 C TB
5.4.1 组元在固态互不溶,具有共晶转变的相图
一、相图分析
1. 画图 (1) 先画一成份三角形
(2) 画温度轴
(3) 画二元共晶相图
E1 TC E2
B2 B3
B1 B
三个二元共晶相图向空间 A 延伸 (4) 画出四相平衡共晶转变平 面A1B1C1 (5) 三个二元系共晶点向空间 延伸为三条共晶沟线,交 A1B1C1面于E点,称为共晶点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L1’、L2’、…和S1’ 、S2’、… 连成的 曲线称为共轭曲线。
3. 三相平衡(three-phase equilibrium)
三元系中三相平衡时,三个自由能—成分曲面 只有唯一的公切面。
三个公切点投影到成分三角形上构成的成分点 即三个平衡相在该温度下的成分点。当温度一 定,三个平衡相的成分将是确定不变的。连接 三个平衡相的成分点的三角形称为连接三角形。
线上的L2, α相的成分变到mp线上的α2 , α2在 L2和 x 两点连线的延长线上,根据杠杆定律可 算出此时两相相对量为:
L2 %
x 2 L2 2
100 %
2%
L2 x L2 2
100 %
在此温度下发生三相共晶反应
L2 2 2
在反应过程中L、α、β三相的成分分别沿着ee’、mp、nq线变化。冷
3. 三元相图的投影图(projections)
● 把三元立体相图中所有相区的交线都垂直投影 到浓度三角形中,就得到三元相图的投影图, 可利用它分析合金在加热和冷却过程中的转变。
● 如果把一系列不同温度的水平截面中的相界线 投影到浓度三角形中,并在每一条投影上标注 相应的温度,就得到等温线投影图;类似地图 上的等高线。
● 以等边成分三角形表示三元系的成分, 在浓度三角形的各个顶点分别作与浓度 平面垂直的温度轴,构成外形是一个三 棱柱体的三元相图;
● 三棱柱体的三个侧面是三组二元相图, 三棱柱体内部,有一系列空间曲面分隔 出若干相区。
● 三元相图复杂,不易描述相变过程和确 定相变温度。因此,实现三元相图实用 化的方法是使之平面化。
当 x 点在α3β的连线上,包晶反应结束而进入α+β两相区。反应结束 时α和β两相的相对量为
% 3 x 100 % 3 3
% x 3 100 % 3 3
包晶反应和共晶反应一样,合金的成分点进入共轭三角形是反应开始,
退出共轭三角形时反应结束。其差别是三相包晶反应的合金成分是从共轭三
六、自由能-成分曲面及公切面法则
(free energy-composition relationship)
1. 单相
● 二元合金中的溶体在给定温度下的自由能 与成分间的关系表现为下凹曲线。
● 三元合金中的溶体在给定温度下的自由能 与成分间的关系表现为下凹曲面。
2. 两相平衡(two-phase equilibrium)
第五章 三元合金相图
5.1 三元 相图基础 一、三元相图的基本特点
1) 完整的三元相图是三维的立体模型,合金成 分用成分三角形表示;
2) 三元系中可以发生四相平衡转变,四相平衡 区是恒温水平面;
f=C–P+1 f=3–4+1=0 3) 除了单相区和两相平衡区外,三元相图中三 相平衡区也占有一定空间,三相区中有一个自 由度,三相平衡转变是变温过程。
固定一个成分变量并保留温度变量的截面图,它与浓度三角形垂直, 所以称为垂直截面,也称为变温截面;
垂直截面的两种形式:
● 通过浓度三角形的一个顶点, 其它两组元的含量比不变。
● 固定一个组元的成分,其它 两组元成分可以相对变动。
● 三元相图的垂直截面与二元相图相似,可以用来了解 材料的结晶过程,但不能用杠杆定律来计算两相的相对 量。
包晶型: 是指降温时存在两个反应相和一个生成相这一类的总称。包括包 晶、包析等,反应式为:
二、共晶型三相平衡转变类型
1. 共晶型三相平衡区的空间形状
三相区的水平截面应为直边连接三角形, 随着温度的变化,三角形的位置、大小在不 断的改变,连接三角形的轨迹为组成了三相 区,它是一曲面的三棱柱体。
其中三个顶点的轨迹是三条曲线,构成三 棱柱体的三条棱,表示平衡的成分随温度的 变化规律,称为成分变温线,它将和单相区 相邻。三条边轨迹是构成三棱柱体的侧面曲 面。
如果这三点在一直线上,三角形变成缩成 一直线。
2. 共晶型三相平衡区在成分平面上的投影
在e和e′之间作若干个等距的水平截面,各截面上三相区三角形在浓度 三角形上的投影如图。随着温度的降低,三相区三角形的三个顶点都分 别沿mp、ee’和nq发生平移。移动时三角形顶点朝前,与降温方向一致。
合金 x 冷却时从液相L中析出成分为α1的固 溶体进入两相区,继续冷却,液相成分变到ee’
五、三元系中四相平衡转变的类型
● 同时平衡析出两种沉淀相:α→βII +γII ● 四相平衡共晶转变:L→αa +βb +γc ● 四相平衡包晶转变:L +αa +βb →γc ● 包共晶转变:L +αa →βb +γc ● 四相平衡偏共晶转变:L0→L2 +αa +βb ● 四相平衡共析转变:δ0→αa +βb +γc ● 四相平衡包析转变:δ0 +αa +βb→γc ● 包共析转变:δ0 +αa →βb +γc
二元系中两相平衡时,两个平衡相的成 分由公切线的切点确定,两个自由能与 成分曲线只有一条公切线。
三元系中两相平衡时,两个平衡相的成 分由公切面的切点确定,而且两个自由 能与成分曲面有许多公切面。
公切面沿两个曲面滚动,得到一系列对 应的切点L1–S1、L2–S2、…,它们投影 到成分三角形上构成一系列对应的成分 点L1’– S1’、L2’–S2’、…,
连接三角形是在一定的温度下,处于三相平衡 的三个相成分点组成的直边三角形。
5.2三元相图中的杠杆定
律和重心定律
1. 直线法则
当三元系统两相平衡共存时,在某一温度 下,合金的成分点与两平衡相的成分点必在 一条直线上。
如图合金成分o,两相α、β成分分别为 m、n,三点在同一直线上。
2. 杠杆定律(lever rule)
三、等温截面(水平截面图)
研究在一定温度下的相区结构、平衡 相的成分和相对量之间的关系。
在三元匀晶相图的等温截面上, l1l2、 s1s2共轭曲线。平衡相对应成分点的连接直 线称为共轭连线;
通过给定的合金成分点,只能有唯一的 一条共轭连线;
水平截面图——柯氏法则
在给定温度下,平衡的液相 和固相之间,低熔点的组元在 液相中的分数应高于在固相中 的分数。
1. 包晶型三相平衡区的空间形状
2. 共晶型三相平衡区在成分平面上的投影
在E1和E2之间作若干个等距的水平 截面,各截面上三相区三角形在浓度三 角形上的投影如图。随着温度的降低, 三相区三角形的三个顶点L、α、β分别 沿nq、mp和E1E2发生平移。移动时共轭 三角形的底边朝向温度降低的方向。
成分在mE1nqE2p范围内的合金结晶时,都发生 三相包晶反应。例如合金 x 冷至1点开始从液相L中析
f=3–3+1=1
二、三元相图成分表示方法
1. 等边成分三角形(composition triangle) 三角形的三个顶点A、B、C分别表示三个组元;
三角形的三条边分别表示3个二元系 的成分坐标;
三角形内的任一点表示三元系的某 一成分。
三元系成分确定方法(如合金 x ): 由 x 点出发,向A顶角对应边BC引平行线,相交于A组元的成分
四、三元相图的截面图和投影图
三元相图的使之平面化方法是通过减少变量的方法(如固定温度或 成分),将三维立体相图分解为二维平面图形。 1. 水平截面(horizontal section)
固定温度的截面图称为水平截面, 也称为水平截面。 它平行于浓度三角形。
2. 垂直截面(vertical section)
3. 重心法则(graHale Waihona Puke ity-center rule):
当三元系统三相平衡共存时,在某一温度 下,合金成分点应位于三个平衡相的成分点 所连成的三角形(共轭三角形)中,且必位于
γ
此三角形的重心位置。
对于在某一温度下处于三相共存状态的材 料,可以用重心法则计算三个平衡相的质量 分数。
α β
如图合金成分O,三相α、β、γ成分分别为P、Q、S,则各相的质 量分数为 :
用杠杆定律计算等温截面上两平衡相的质量
百分数
wα = mo/mn × 100%
wβ = on/mn × 100%
直线法则和杠杆定律的推论:
● 当给定材料在一定温度下处于两相平衡时,若其中一相的成分给 定,另一相的成分点必在两已知成分点连线的延长线上;
● 若两个平衡相的成分已知,材料的成分点必位于此两个成分点的 连线上。
线(CA),线段Cb即为A组元的成分。同理,Ac为B组元的成分, Ba 为C组元的成分。
2. 等边成分三角形中的特殊线
(special lines in equilateral composition triangle)
平行于三角形某一条边的直线:
成分位于该线上的材料,它们所含
与此线对应顶角代表的组元的质量分
3. 共晶型三相平衡区的垂直截面图
当垂直截面通过三相区时,成分和 截面相交得三个点,和三个侧面相交 得三条曲线,所以三相区在垂直图上 为一曲边三角形。在三相区的外侧, 以顶点与单相区相邻,以曲线边与双 相区相邻。
共晶型三相区在垂直截面上是一个顶点朝上的正立曲边三角形,上顶 点与液相区相连接。
三、包晶型三相平衡转变类型
出成分为α1的固溶体而进入两相区。冷至2点液相的 成分变到nq线上的L2点, α相的成分变到mp线上的α2 点,此时 x 点位于L2α2的连线上。因此,可以利用杠 杆定律计算出此时的α和L相的相对量。
% L2 x 100 % L2 2
L2 %
x 2 L2 2
100 %
在此温度下开始包晶反应: L 2 2
数相等;
wC% = Bb
wA%
