第5章三元匀晶和共晶相图123
合集下载
第五章三元相图-PPT精品.ppt
3 等温界面（水平截面） （1）做法：某一温度下的水平面与相图中各面的交线。 （2）截面图分析 3个相区：L, α, L+α; 2条相线：L1L2, S1S2（共轭曲线）; 若干连接线：可作为计算相对量的杠杆（偏向低熔
点组元；可用合金成分点与顶点的连线近似代替，过给定合 金成分点，只能有唯一的共轭连线。）
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （1）相图分析
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （2）等温截面 应用：可确定平衡相及其成分；可运用杠杆定律和重心定律。
是直边三角形 三相平衡区 两相区与之线接 （水平截面与棱柱面交线）
单相区与之点接 （水平截面与棱边的交点，表 示三个平衡相成分。）
类型： 包共晶转变 包晶转变
与4个单相区点接触； 相区邻接（四相平衡面） 与6个两相区线接触；
与4个三相区面接触。
第四节 三元相图总结
二 组元在固态有限溶解的共晶相图 3 四相平衡
两相共晶线 液相面交线 线：EnE 两相共晶面交线 液相单变量线 液相区与两相共晶面交线 固相单变量线
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （1）相图分析
液相面 固相面(组成) 面： 二相共晶面 三相共晶面 溶解度曲面：6个 两相区：6个 区： 单相区：4个 三相区：4个 四相区：1个
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图
（4）投影图 律）
定律）
合金结晶过程分析； 相组成物相对量计算（杠杆定律、重心定
组织组成物相对量计算（杠杆定律、重心
第四节 三元相图总结
二 组元在固态有限溶解的共晶相图
1 两相平衡
立体图：共轭曲面。 等温图：两条曲线。
点组元；可用合金成分点与顶点的连线近似代替，过给定合 金成分点，只能有唯一的共轭连线。）
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （1）相图分析
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （2）等温截面 应用：可确定平衡相及其成分；可运用杠杆定律和重心定律。
是直边三角形 三相平衡区 两相区与之线接 （水平截面与棱柱面交线）
单相区与之点接 （水平截面与棱边的交点，表 示三个平衡相成分。）
类型： 包共晶转变 包晶转变
与4个单相区点接触； 相区邻接（四相平衡面） 与6个两相区线接触；
与4个三相区面接触。
第四节 三元相图总结
二 组元在固态有限溶解的共晶相图 3 四相平衡
两相共晶线 液相面交线 线：EnE 两相共晶面交线 液相单变量线 液相区与两相共晶面交线 固相单变量线
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图 （1）相图分析
液相面 固相面(组成) 面： 二相共晶面 三相共晶面 溶解度曲面：6个 两相区：6个 区： 单相区：4个 三相区：4个 四相区：1个
第三节 三元共晶相图
二 组元在固态有限溶解的共晶相图
（4）投影图 律）
定律）
合金结晶过程分析； 相组成物相对量计算（杠杆定律、重心定
组织组成物相对量计算（杠杆定律、重心
第四节 三元相图总结
二 组元在固态有限溶解的共晶相图
1 两相平衡
立体图：共轭曲面。 等温图：两条曲线。
三元合金相图PPT课件
• 根据直线法则，合金的成分点R位
B
于两平衡相的成分点P、Q之间。
• 按杠杆定律对含量进行计算:
P1R1 = PR= 1
C%
R1Q1 RQ 3
B%
代入数据，得
60R1 = PR=1 R120 RQ 3
Q2 R2
Q
计算，得到：
P2
R P
直R1接=5计0算%A组元：60A%×75%. +20%×2P51%=R510%
•三元相图的类型多而复杂，目前比较完整的三元相
图只测出了十几种，更多的是关于三元相图中的各
种截面图和投影图。
.
3
恒压条件下，相律数学表达式为：F = C - P + 1。
• 纯金属成分固定不变，只有温度可以改变，所以纯金属自 由度数最多只有1个。
• 对于二元合金，其中一个组元含量确定，合金成分随即确 定（B%=100%-A%），所以合金成分变量只有一个，加 上温度变量，二元合金自由度数最多有2个。
第五章 三元合金相图
5.1 三元合金相图的表示方法 5.2 平衡相的定量法则 5.3 三元匀晶相图 5.4 固态互不溶解的三元共晶相图 5.5 三元相图总结
.
1
本章要求
• 1、熟悉成分三角形、直线法则和重心法则。 • 2、认识等温截面、变温截面和投影图。 • 3、了解三元匀晶相图和固态互不溶解的三
(2)当给定的合金在一定温度下处于两相平衡状 态时，若其中一相的成分给定，另一相的成分 点必在两已知成分点的延长线上。
(3)若平衡两相的成分点已知，合金成分点必然 位于此两成分点的连线上。
.
21
直线法则和杠杆法则的应用（一）
B
• 将两个已知成分的合金P、Q，
9材料科学基础课件-第五章三元相图
E
e1
A
L+α
2016/2/12
α+β
返回
• 三相区： L+α+β、 L+α+γ、 L+β+γ、 α+β+γ f=1 L→α+β、L→α+γ、 L→β+γ
在TE等温四相面以上有三个三相区，以下有一个， 称为3/1转变。 三相区由三相平衡三角形滑动而成。三相区棱边 为三个相的浓度变温线。
E
e
α β γ β
P O
β
Q C
R
w RP = w
P
RQ Q
A
• 成分为O的合金,分解为αβ两相，则αβ连线必过O点。
w % = 100%
2016/2/12
o
w % = 100%
返回
o
二、重心定律
• 已知成分的三个合金P、Q、N， 熔配成一个新的合金R，R成分 点必在△PQN内，且在△重量 重心上。
B Q n R P A q p N C
wP · RQ RP = w Q ·
=
RN wN ·
• 证：将PQ合金按直线定律熔配 成n，再由n和N按直线定律熔 配成R。
2016/2/12
返回
• 由合金O，分解成αβγ三个相， 则O位于△αβγ的重量重心处。
B
• 各相相对量：
o ' w % = 100% ' o ' w % = 100% ' o ' w % = 100% '
2016/2/12
β
γ’ O α’
α
A
β’
γ
C
返回
e1
A
L+α
2016/2/12
α+β
返回
• 三相区： L+α+β、 L+α+γ、 L+β+γ、 α+β+γ f=1 L→α+β、L→α+γ、 L→β+γ
在TE等温四相面以上有三个三相区，以下有一个， 称为3/1转变。 三相区由三相平衡三角形滑动而成。三相区棱边 为三个相的浓度变温线。
E
e
α β γ β
P O
β
Q C
R
w RP = w
P
RQ Q
A
• 成分为O的合金,分解为αβ两相，则αβ连线必过O点。
w % = 100%
2016/2/12
o
w % = 100%
返回
o
二、重心定律
• 已知成分的三个合金P、Q、N， 熔配成一个新的合金R，R成分 点必在△PQN内，且在△重量 重心上。
B Q n R P A q p N C
wP · RQ RP = w Q ·
=
RN wN ·
• 证：将PQ合金按直线定律熔配 成n，再由n和N按直线定律熔 配成R。
2016/2/12
返回
• 由合金O，分解成αβγ三个相， 则O位于△αβγ的重量重心处。
B
• 各相相对量：
o ' w % = 100% ' o ' w % = 100% ' o ' w % = 100% '
2016/2/12
β
γ’ O α’
α
A
β’
γ
C
返回
第五章 三元相图
B
B%
C%
A
← A% C% →
C
b c
a
图 部分浓度三角形
§5.1.2 浓度三角形中具有特定意义的线
1）与某一边平行的直线
C
含对角组元浓度相等
A% d C% c
Bc C% 100% BC
A
B B% 图 平行于浓度三角形某一条边的直线
确定O点的成分 1）过O作A角对边的平行线 2）求平行线与A坐标的截距 得组元A的含量 3）同理求组元B、C的含量
三元系中如果任意两个组 元都可以无限互溶,那么它们 所组成的三元合金也可以形 成无限固溶体,这样的三元合 金相图,叫三元匀晶相图。
相图概况
[1] 特征点： ta, tb, tc- 三个纯组 元的熔点； [2]特征面：液相面、固相面； [3]相区：L, α, L+α。
图 三元匀晶相图
§5.3.1 相图分析
( A B )
Ax nE nA Ee
( A B C )
Ax ne nA Ee
§5.4.2 组元在固态下有限溶解，具有共晶转变的三 元相图
1.相图分析
从占有空间的角度看,固态有限互溶三元共晶相图比固态 完全不互溶三元共晶相图要多三个单相区(α、 β、 γ)和三个 固态两相区(α+β、 β+ γ、 α+ γ)。
图 过成分三角形顶点的变温截面图
图 平行于成分三角形一边的变温截面图
用垂直截面图可以分析合金的平衡结晶过程，了解合金在 平衡冷却过程中发生相变的临界温度，以及可以了解合金在 一定温度下所处的平衡状态。 但是，用垂直截面图不能了解合金在一定温度下的平衡相 成分和平衡相的重量。
图 变温截面图的应用
5三元相图
重心法则
三元合金N处于α、β和γ三相平 衡，三相平衡成分为D、E和F， 质量为Ｗα、Ｗβ 和Ｗγ，则合金 N的成分点必落在三角形DEF的 质量重心上。 Ｗα ＝ Nd / Dd × WN Ｗβ ＝ Ne / Ee × WN Ｗγ = Nf / Ff × WN DEF称连接三角形(共轭三角形)
5.3 三元匀晶相图
mo L% = × 100% mn
no α% = × 100% mn
β:
Co,Ni
Al
γ′:
Al Co,Ni
Fe-Co-Al phase diagram at 650 °C
三元匀晶体系垂直截面图
T
L+α
T
WB 只有一个独立成分变量！ 过FE的垂直截面图
WB 过GB的垂直截面图
三元匀晶体系垂直截面图
三元匀晶体系等温截面图
f=1 固相线 液相线
T温度下的等温截面图
三元匀晶体系等温截面图
开始结晶
WL/WS=OS2/OL2
结晶结束
三元匀晶体系等温截面图
水平(等温)截面图表示在某一温度下三元系的相平衡。 等温截面图上连接两个相互平衡的相成分点的直线叫共轭 线 (tie-line)。 两相区可看作是由一系列共轭线组成的区域，共轭线之间 不能交叉。 在两相区，根据共轭线可以确定两相平衡体系中各相的相 对量，例如合金O，在t温度下L和α相的相对量为：
三元共晶相图的投影图
• • • •
单变量线降温的方向 四相反应类型 三相反应类型 初晶面的划分
三元共晶相图的投影图
三元合金O随温度降低： （1）析出初晶A，进入到L+A； （2）L相成分从O到m，达到m点 析出初晶A结束； （3）Lm→A+B，进入到L+A+B； （4）L相成分从m到E，达到E点 二元共晶结束； （5）LE ↔ A+B+C 组织组成物： 初晶A+二元共晶（A+B）+ 三元共晶（A+B+C）
第5章三元匀晶和共晶相图PPT课件
A1-B1-C1 TA
A3
A-B-C A-B-C
A2
A1
E3
TC
A
BA
E
e
C3
C2
L A+B L B+C L C+A
L A+B+C
TB
E1
B3
B2
E2 B1
B
C1
C
A e3
e1
B
e
e2
C
1、 E点合金
1）结晶过程
L
L A+B+C
A+B+C
相组成： A + B + C 组织组成： ( A + B + C )
三 相
L+B+C
区 L+C+A
A1A2-A2E1B2-B2B1-B1EA1-E1E B1B3-B3E2C2-C2C1-C1EB1-E2E C1C3-C3E3A3-A3A1-A1EC1-E3E
A-e-B B-e-C C-e-A
四 A+B+C 相 L+A+B+C 区
AA1-BB1-CC1-ABC-A1B1C1
相 区
L+B L+C
TB-E1-E-E2-B3-B1 TC-E2-E-E3-C3-C1
B-e1-e-e2-B C-e2-e-e3-C
TA
A e3
e1 e
C
A3 A2 A1
B A E3
e2
TC
E C3 C2
C1
C
相变类型
LA LB LC
TB
E1
B3
B2
E2 B1
A3
A-B-C A-B-C
A2
A1
E3
TC
A
BA
E
e
C3
C2
L A+B L B+C L C+A
L A+B+C
TB
E1
B3
B2
E2 B1
B
C1
C
A e3
e1
B
e
e2
C
1、 E点合金
1）结晶过程
L
L A+B+C
A+B+C
相组成： A + B + C 组织组成： ( A + B + C )
三 相
L+B+C
区 L+C+A
A1A2-A2E1B2-B2B1-B1EA1-E1E B1B3-B3E2C2-C2C1-C1EB1-E2E C1C3-C3E3A3-A3A1-A1EC1-E3E
A-e-B B-e-C C-e-A
四 A+B+C 相 L+A+B+C 区
AA1-BB1-CC1-ABC-A1B1C1
相 区
L+B L+C
TB-E1-E-E2-B3-B1 TC-E2-E-E3-C3-C1
B-e1-e-e2-B C-e2-e-e3-C
TA
A e3
e1 e
C
A3 A2 A1
B A E3
e2
TC
E C3 C2
C1
C
相变类型
LA LB LC
TB
E1
B3
B2
E2 B1
第五章 三元相图
B1
AБайду номын сангаас
B
C
（二）等温截面及其投影
L+C L
L+C L
L+A
L+A+C L+A L+C L
L+A+C L L+B
L+B
L+A+C L+A+B+C
C B
A+B+C
A
L+A+C L+A+B+C L+A+C L L+B
1.等温截面上的三相平衡区都是直边三角形，与 三角形相邻接的是两相平衡区 2.三角形的顶点与单相区相接，分别表示该温度 下三个平衡相的成分
LA+ C
TA C1 A3 A2 A1
E
L B + C
四三 相相 平平 衡衡 共共 晶晶 转 变 结 束
——
TB E1 B3 B2 E2 E B1
A
E3
TC
B
C3 C2 C1
C
中 转平 间 变衡 开 共 三面
始晶相
A3
A2 A1
E1
B2
B1
LA+ B
——
TA
A3 A2 A1
E TB E1 E3 TC E2 B3 B2 B1 B3 E2 B1 E C2 C1
B 10 20 30 40
50
C% 60 70 80 90
50 40 ← A%
30
20 10
C
课堂练习
90 3. 标出 50%A+20%B+30%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
大学材料科学基础第五章三元相图(3)
第五节 三元相图和类型
生产中使用的合金除了二元之外，还有三元、 甚至多元，即使是二元合金，由于杂质元素的 存在，在偏析区它们也不能看成是二元的。三 元合金的性质不同于二元，也不能简单的从二 元相图来推断，必须使用三元相图进行研究。 本章重点是建立三元相图的空间概念，三元相 图的识别和使用。 三元相图比二元相图复杂，但基础还是二元相 图。
C
连接线法则 1) 在等温截面上，通过给出的 合金成分点，只能有唯一的 一条共轭连线。 温度不变时，给定成分的合金 处于两相平衡时其成分不能 随意变动。当合金成分沿共 轭连线变化时，两平衡相的 成分是不变化的 2) 共轭连线不可能位于从三角 形顶点引出的直线上 (图中 所示的Af线)。
选分结晶原理 液、固两相平衡共存时，液相中低 熔点组元与高熔点组元含量的比 值，应大于与之共存的固相中低、 高熔点组元含量的比值：
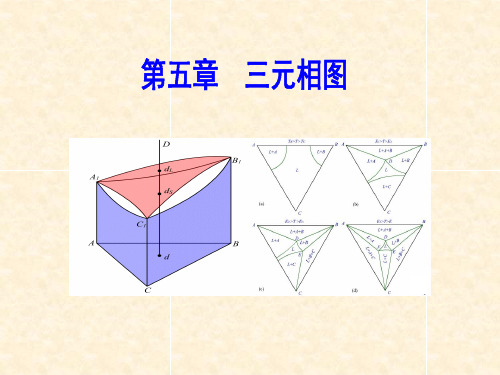
2．三相平衡及三相平衡反应
由相律可知，恒温下的 三相平衡，三个共存相 的成分任意一相都不可 变动，即在等温截面上 是满足热力学平衡条件 的三个成分点 三相平衡时，三个相也两两平衡，按两相平衡时的直线法 则，两两平衡相间可做出三条共轭连线 (图5—90b)，这三条 共轭连线在等温截面上围成一直边三角形，称为共轭三角形。 位于共轭三角形内的合金，其成分在共轭三角形内变动时三 个平衡相成分固定不变。 • 三相区的三条棱边线，分别表示了三相平衡共存时每一相 的成分随温 度的变化迹线，故称为成分变温线；又因为三相 共存时各相的成分和 温度只有一个独立变量，所以又称为单 变量线。
A
注意该图与二元相图的区别，两者只是在 形式上相似。在变温截面图上不能使用杠杆定 律，也不能确定多相平衡时各相的成分，因为 在图上无法确定连接线。
垂直截面图的用途：
生产中使用的合金除了二元之外，还有三元、 甚至多元，即使是二元合金，由于杂质元素的 存在，在偏析区它们也不能看成是二元的。三 元合金的性质不同于二元，也不能简单的从二 元相图来推断，必须使用三元相图进行研究。 本章重点是建立三元相图的空间概念，三元相 图的识别和使用。 三元相图比二元相图复杂，但基础还是二元相 图。
C
连接线法则 1) 在等温截面上，通过给出的 合金成分点，只能有唯一的 一条共轭连线。 温度不变时，给定成分的合金 处于两相平衡时其成分不能 随意变动。当合金成分沿共 轭连线变化时，两平衡相的 成分是不变化的 2) 共轭连线不可能位于从三角 形顶点引出的直线上 (图中 所示的Af线)。
选分结晶原理 液、固两相平衡共存时，液相中低 熔点组元与高熔点组元含量的比 值，应大于与之共存的固相中低、 高熔点组元含量的比值：
2．三相平衡及三相平衡反应
由相律可知，恒温下的 三相平衡，三个共存相 的成分任意一相都不可 变动，即在等温截面上 是满足热力学平衡条件 的三个成分点 三相平衡时，三个相也两两平衡，按两相平衡时的直线法 则，两两平衡相间可做出三条共轭连线 (图5—90b)，这三条 共轭连线在等温截面上围成一直边三角形，称为共轭三角形。 位于共轭三角形内的合金，其成分在共轭三角形内变动时三 个平衡相成分固定不变。 • 三相区的三条棱边线，分别表示了三相平衡共存时每一相 的成分随温 度的变化迹线，故称为成分变温线；又因为三相 共存时各相的成分和 温度只有一个独立变量，所以又称为单 变量线。
A
注意该图与二元相图的区别，两者只是在 形式上相似。在变温截面图上不能使用杠杆定 律，也不能确定多相平衡时各相的成分，因为 在图上无法确定连接线。
垂直截面图的用途：
材料科学基础三元相图
材料科学基础三元相图
一．三元相图的成分表示法：等腰三角形
材料科学基础三元相图
一．三元相图的成分表示法：直角坐标系
材料科学基础三元相图
3．浓度三角形中特殊线： 3.1 平行浓度三角形任一边的直线
3.2 从浓度三角形的一个顶点到对边的任意直线
材料科学基础三元相图
二、杠杆定律及重心法则
单相平衡勿须计算，四相平衡无从计算 1．两相平衡：杠杆定律
2．合金的凝固过程和组织
各点合金的组织
如表4-3（表中nmp区需修正） 如合金I：L→A 剩余液相交np于n1：L+A→M 至n2点，A消失，L→M 液相沿e1E：L→M+B 液相成分在E点：L→M+B+C
材料科学基础三元相图
材料科学基础三元相图
3．等温截面
材料科学基础三元相图
4。变温截面
材料科学基础三元相图
2.三元相图分析 法 总 结 --- 三 相 平 衡 -- 三 相
反应的判定--：
投影图判断三 相反应
液相单变量线穿 过两旁固相成分点连 线的为二元共晶型， 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应，且靠近单变线 的为生成相
材料科学基础三元相图
3．三元相图分析法总结---四相平衡
x合金结晶：
L→A，L+A→M，L→M，L→M+C，L→M+B+C
y合金结晶： L→A，L+A→M，L+A→M+C，L→M+C，L→M+B+C 5．固相有固溶度时的包共晶 包共晶：Lα+P→Md1+γc1 包晶反应 LE→Md2+βb+γc2 d1d2，c2c1为M+γ二元共晶结 束面投影
一．三元相图的成分表示法：等腰三角形
材料科学基础三元相图
一．三元相图的成分表示法：直角坐标系
材料科学基础三元相图
3．浓度三角形中特殊线： 3.1 平行浓度三角形任一边的直线
3.2 从浓度三角形的一个顶点到对边的任意直线
材料科学基础三元相图
二、杠杆定律及重心法则
单相平衡勿须计算，四相平衡无从计算 1．两相平衡：杠杆定律
2．合金的凝固过程和组织
各点合金的组织
如表4-3（表中nmp区需修正） 如合金I：L→A 剩余液相交np于n1：L+A→M 至n2点，A消失，L→M 液相沿e1E：L→M+B 液相成分在E点：L→M+B+C
材料科学基础三元相图
材料科学基础三元相图
3．等温截面
材料科学基础三元相图
4。变温截面
材料科学基础三元相图
2.三元相图分析 法 总 结 --- 三 相 平 衡 -- 三 相
反应的判定--：
投影图判断三 相反应
液相单变量线穿 过两旁固相成分点连 线的为二元共晶型， 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应，且靠近单变线 的为生成相
材料科学基础三元相图
3．三元相图分析法总结---四相平衡
x合金结晶：
L→A，L+A→M，L→M，L→M+C，L→M+B+C
y合金结晶： L→A，L+A→M，L+A→M+C，L→M+C，L→M+B+C 5．固相有固溶度时的包共晶 包共晶：Lα+P→Md1+γc1 包晶反应 LE→Md2+βb+γc2 d1d2，c2c1为M+γ二元共晶结 束面投影
三元共晶相图
c1 c2 E F C%
B%
A
← A%
D a2 a1
C
13
课堂练习
6. 绘出C / B ＝1/3的合金
C 1 25% B 3 75%
B 90 80 70 60 B% 50 40 30 20 10 20 30 40 C%
7. 绘出A / C ＝1/4的合金
50
60 70 80 90
10 A 90 80 70 60 50 40 ← A% 30 20 10
II点： A%=20% B%=50% C%=30% 70 60 B% 50 40 30 20 10 A 90 80 70 60 90 80
B 10 20 30 40 II C% 60 70 80 90 50 40 ← A% 30 20 10
5
50
C
课堂练习
1. 确定合金I、II、 III、IV的成分
40 30 20 10 A 90 80 70 70 60 90 80
B 10 20 30 40 C%
B% 50
50
60 70 80 90 60 50 40 ← A% 30 20 10
12
C
2） 过某一顶点作直线
B
A% Ca1 Ba '1 Ba '2 Ca2 常数 a1′ C % Bc1 Bc1 Bc 2 Bc 2 a2 ′
LA
A
E3
TC
E e1
B
e2
e3
C3 C2 C1
e
C LC
50
E1
LB
B
LA
A
LA
e1
LB
e e2 E2
LC
e3 E3
第5章-2---三元相图1
5.13 四相平衡共晶系
5.13.4 综合投影图
冷却过程中有 四相反应
L-a+b+
5.13 四相平衡共晶系
5.13.4 综合投影图
5.13 四相平衡共晶系 L
L－a
合金 o
L－a+b
L－a+b+
a+a + b+a+b++b+
L
合金 o’
L－b
L－a+b
a+b
b+a+b+a+
5.13.4 综合投影图
5.13 四相平衡共晶系
5.13.3、垂直截面
5.13 四相平衡共晶系
5.13.4 综合投影图
1、作法：将立体图中 各空间曲面、曲线投 影到成分三角形
2、用途： a、可得到各个面的投影 b、可得到各相区的投影 c、各种成分的平衡冷却
过程 d、组织分区图
5.13 四相平衡共晶系
5.13.4 综合投影图
5.13 四相平衡共晶系
5.13.4 综合投影图
5.13 四相平衡共晶系
I a; II a + bII ; III a + bII + II ; IV a + (a + b ) + bII ; V a + (a + b ) + bII + II ; VI a + (a + b ) + (a + b + ) + bII + II
用杠杆定理
5.12 三相平衡三元
5.12.2 几种典型的三相平衡三元系
5.12 三相平衡三元系
第5章-三元相图PPT课件
•20
2、结晶过程分析 O 自液态缓冷至于液互
相相交时，开始从液相中结晶出 α 固溶体，此时液相的成分l1即为合金成分， 而固相的成分为固相面某一点 s。
α 相越来 越多，固相的成分由s1点沿固相面移至s2 点，液相成分自l1点移至 l2点，由直线法则可知，合金的成分点必落 在l2和s2的连线上。
Ca＝WA＝30％ Ac＝WC＝60％ Ab＝WB＝10％。
中都有应用，但应用最为广泛的还是等边 三角形。
•10
2、等边成分三角形中特定意义的线 (1) 平行 于三角形某一边的直线 凡成分位于该线上的所有合金，它们 所含的由这条边对应顶点所代表的组元的 含量为一定值。如图5-103中ef直线上代表 B组元的含量均为Ae。
•15
•16
•17
由直线法则可得到以下规律： a、 当温度一定时，若已知两平衡相的 成分，则合金的成分必位于两平衡相成分 的连线上； b、 当温度一定时，若已知一相的成分 及合金的成分，则另一平衡相的成分必位 于两已知成分点的连线的延长线上； c、 当温度变化时，两平衡相的成分变 化时，其连线一定绕合金的成分点而转动。
•1
三元相图与二元相图比较，组元数增加 了1个,即成分变量是两个，故表示成分的坐 标轴应为2个,需要用一个平面表示，再加上 垂直于该平面的温度轴，这样三元相图就 演变成一个在三维空间的立体图形，分隔 相区的是一系列空间曲面，而不是二元相 图的平面曲线。
•2
1、三元相图的成分表示方法 (1) 等边成分三角形 这样的三角形称为浓度三角形或成分三角 形(Composition Triangle)。常用的成分三 角形是等边三角形和直角三角形。
•38
•11
•12
(2)通过三角形顶点的任一直线 凡成分位于该直线上的所有合金
2、结晶过程分析 O 自液态缓冷至于液互
相相交时，开始从液相中结晶出 α 固溶体，此时液相的成分l1即为合金成分， 而固相的成分为固相面某一点 s。
α 相越来 越多，固相的成分由s1点沿固相面移至s2 点，液相成分自l1点移至 l2点，由直线法则可知，合金的成分点必落 在l2和s2的连线上。
Ca＝WA＝30％ Ac＝WC＝60％ Ab＝WB＝10％。
中都有应用，但应用最为广泛的还是等边 三角形。
•10
2、等边成分三角形中特定意义的线 (1) 平行 于三角形某一边的直线 凡成分位于该线上的所有合金，它们 所含的由这条边对应顶点所代表的组元的 含量为一定值。如图5-103中ef直线上代表 B组元的含量均为Ae。
•15
•16
•17
由直线法则可得到以下规律： a、 当温度一定时，若已知两平衡相的 成分，则合金的成分必位于两平衡相成分 的连线上； b、 当温度一定时，若已知一相的成分 及合金的成分，则另一平衡相的成分必位 于两已知成分点的连线的延长线上； c、 当温度变化时，两平衡相的成分变 化时，其连线一定绕合金的成分点而转动。
•1
三元相图与二元相图比较，组元数增加 了1个,即成分变量是两个，故表示成分的坐 标轴应为2个,需要用一个平面表示，再加上 垂直于该平面的温度轴，这样三元相图就 演变成一个在三维空间的立体图形，分隔 相区的是一系列空间曲面，而不是二元相 图的平面曲线。
•2
1、三元相图的成分表示方法 (1) 等边成分三角形 这样的三角形称为浓度三角形或成分三角 形(Composition Triangle)。常用的成分三 角形是等边三角形和直角三角形。
•38
•11
•12
(2)通过三角形顶点的任一直线 凡成分位于该直线上的所有合金
第5章 三元合金相图
相对应成分点的连接直线称为连接线， 或称共轭连线；
L1’、L2’、…和S1’ 、S2’、… 连成的 曲线称为共轭曲线。
3. 三相平衡(three-phase equilibrium)
三元系中三相平衡时，三个自由能—成分曲面 只有唯一的公切面。
三个公切点投影到成分三角形上构成的成分点 即三个平衡相在该温度下的成分点。当温度一 定，三个平衡相的成分将是确定不变的。连接 三个平衡相的成分点的三角形称为连接三角形。
线上的L2， α相的成分变到mp线上的α2 ， α2在 L2和 x 两点连线的延长线上，根据杠杆定律可 算出此时两相相对量为：
L2 %
x 2 L2 2
100 %
2%
L2 x L2 2
100 %
在此温度下发生三相共晶反应
L2 2 2
在反应过程中L、α、β三相的成分分别沿着ee’、mp、nq线变化。冷
3. 三元相图的投影图(projections)
● 把三元立体相图中所有相区的交线都垂直投影 到浓度三角形中，就得到三元相图的投影图， 可利用它分析合金在加热和冷却过程中的转变。
● 如果把一系列不同温度的水平截面中的相界线 投影到浓度三角形中，并在每一条投影上标注 相应的温度，就得到等温线投影图；类似地图 上的等高线。
● 以等边成分三角形表示三元系的成分， 在浓度三角形的各个顶点分别作与浓度 平面垂直的温度轴，构成外形是一个三 棱柱体的三元相图；
● 三棱柱体的三个侧面是三组二元相图， 三棱柱体内部，有一系列空间曲面分隔 出若干相区。
● 三元相图复杂，不易描述相变过程和确 定相变温度。因此，实现三元相图实用 化的方法是使之平面化。
当 x 点在α3β的连线上，包晶反应结束而进入α＋β两相区。反应结束 时α和β两相的相对量为
L1’、L2’、…和S1’ 、S2’、… 连成的 曲线称为共轭曲线。
3. 三相平衡(three-phase equilibrium)
三元系中三相平衡时，三个自由能—成分曲面 只有唯一的公切面。
三个公切点投影到成分三角形上构成的成分点 即三个平衡相在该温度下的成分点。当温度一 定，三个平衡相的成分将是确定不变的。连接 三个平衡相的成分点的三角形称为连接三角形。
线上的L2， α相的成分变到mp线上的α2 ， α2在 L2和 x 两点连线的延长线上，根据杠杆定律可 算出此时两相相对量为：
L2 %
x 2 L2 2
100 %
2%
L2 x L2 2
100 %
在此温度下发生三相共晶反应
L2 2 2
在反应过程中L、α、β三相的成分分别沿着ee’、mp、nq线变化。冷
3. 三元相图的投影图(projections)
● 把三元立体相图中所有相区的交线都垂直投影 到浓度三角形中，就得到三元相图的投影图， 可利用它分析合金在加热和冷却过程中的转变。
● 如果把一系列不同温度的水平截面中的相界线 投影到浓度三角形中，并在每一条投影上标注 相应的温度，就得到等温线投影图；类似地图 上的等高线。
● 以等边成分三角形表示三元系的成分， 在浓度三角形的各个顶点分别作与浓度 平面垂直的温度轴，构成外形是一个三 棱柱体的三元相图；
● 三棱柱体的三个侧面是三组二元相图， 三棱柱体内部，有一系列空间曲面分隔 出若干相区。
● 三元相图复杂，不易描述相变过程和确 定相变温度。因此，实现三元相图实用 化的方法是使之平面化。
当 x 点在α3β的连线上，包晶反应结束而进入α＋β两相区。反应结束 时α和β两相的相对量为
§5-6 三元相图
典型合金的凝固过程
（4）投影图
e3
A α E β B
液相区投影
l
γ
e2 A
C
A l C
C
e1
l e3 m e1 n B
固相区投影
p B
e
2
各典型区域凝固过程和室温组织
五. 三元相图的一些规律
1. 单相区 自由度是3，其形状不受温度、成分对应关系的制约， 截面可以是多种形状的平面图形。 2. 双相区
分析合金在加热和冷却过程中的转变。
四. 三元共晶相图
1. 组元在固态完全不溶的三元共晶相图
（1）相图分析
A
B
A C
B C
点：熔点 tA，tB，tC 二元共晶点 E1，E2，E3 三元E2E，E3E
面：3个液相面
1个固相面
固相面
（三元共晶面）
6个二元共晶面
杠杆定律
由二种合金合成一种合金成分
由一种合金分解成二种合金成分
PR / RQ Wq / Wp
W / W R / R
2.重心法则
合金o分解为α 、β 和L三个平衡相，a、b、c 分别是 α 、β 和L的成分点。
则
oa ' w 100% aa ' ob' w 100% bb' oc ' wL 100% cc '
3 等温截面（水平截面）
T
共轭曲线及直线规则
共轭曲线
液、固相 等温线
两相区平衡两 相的成分连线
共轭连线
在等温截面的两相区内，根据相律 F=3-2=1， 说明两个相的成分只有一个是独立可变的。两个平 衡相的成分对应关系由直线法则决定。
第五章 三元相图
5.1
三元相图的成分表示法
C
二元系的成分可用一条 直线上的点来表示；三元 系合金有两个独立的成分 参数，所以必须用一个平 面三角形来表示，这个三 角形叫做成分三角形或浓 度三角形。常用的成分三 角形是等边三角形，有时 也用直角三角形或等腰三 角形。 A
A%
C%
B%
B
浓度三角形
5.1.1 浓度三角形 1. 等边三角形 三角形的三个顶点A，B， C分别表示3个纯组元， 三角形的边AB，BC， CA分别表示3个二元系 的成分坐标，三角形内 的任一点都代表一定成 分的三元合金. A 一般按顺时针(或逆时针) 标注组元浓度。
L(三元) ΔT α(三元)
自由度：f=c-P+1=3-2+1=2 故三元匀晶转变区可有两个自由度： 温度和相成分。
5.3.1 相图分析
1 画图 (1) 先画一成份三角形 (应为正三角形) (2) 画温度轴 (3) 画二元匀晶相图(每 两个合金上存在一个二 元相图) ---三元系立体图可视为三 个二元系在空间的延伸 液相面----三个二元系的液相线 所围成的面. 固相面----三个二元系的固相线 所围成的面.
5.4
三元共晶相图
TA A2 A3 A1 E3 E C2 C3 C1 C TB
5.4.1 组元在固态互不溶,具有共晶转变的相图
一、相图分析
1. 画图 (1) 先画一成份三角形
(2) 画温度轴
(3) 画二元共晶相图
E1 TC E2
B2 B3
B1 B
三个二元共晶相图向空间 A 延伸 (4) 画出四相平衡共晶转变平 面A1B1C1 (5) 三个二元系共晶点向空间 延伸为三条共晶沟线，交 A1B1C1面于E点，称为共晶点
第5章 三元合金相图PPT课件
8
五、三元系中四相平衡转变的类型
● 同时平衡析出两种沉淀相：α→βII +γII ● 四相平衡共晶转变：L→αa +βb +γc ● 四相平衡包晶转变：L +αa +βb →γc ● 包共晶转变：L +αa →βb +γc ● 四相平衡偏共晶转变：L0→L2 +αa +βb ● 四相平衡共析转变：δ0→αa +βb +γc ● 四相平衡包析转变：δ0 +αa +βb→γc ● 包共析转变：δ0 +αa →βb +γc
9
六、自由能-成分曲面及公切面法则
(free energy-composition relationship)
1. 单相
● 二元合金中的溶体在给定温度下的自由能与 成分间的关系表现为下凹曲线。
● 三元合金中的溶体在给定温度下的自由能 与成分间的关系表现为下凹曲面。
10
2. 两相平衡(two-phase equilibrium)
● 以等边成分三角形表示三元系的成分， 在浓度三角形的各个顶点分别作与浓度 平面垂直的温度轴，构成外形是一个三 棱柱体的三元相图；
● 三棱柱体的三个侧面是三组二元相图， 三棱柱体内部，有一系列空间曲面分隔 出若干相区。
● 三元相图复杂，不易描述相变过程和确 定相变温度。因此，实现三元相图实用 化的方法是使之平面化。
线（CA），线段Cb即为A组元的成分。同理，Ac为B组元的成分， Ba 为C组元的成分。
2
2. 等边成分三角形中的特殊线
(special lines in equilateral composition triangle)
平行于三角形某一条边的直线： 成分位于该线上的材料，它们所含
五、三元系中四相平衡转变的类型
● 同时平衡析出两种沉淀相：α→βII +γII ● 四相平衡共晶转变：L→αa +βb +γc ● 四相平衡包晶转变：L +αa +βb →γc ● 包共晶转变：L +αa →βb +γc ● 四相平衡偏共晶转变：L0→L2 +αa +βb ● 四相平衡共析转变：δ0→αa +βb +γc ● 四相平衡包析转变：δ0 +αa +βb→γc ● 包共析转变：δ0 +αa →βb +γc
9
六、自由能-成分曲面及公切面法则
(free energy-composition relationship)
1. 单相
● 二元合金中的溶体在给定温度下的自由能与 成分间的关系表现为下凹曲线。
● 三元合金中的溶体在给定温度下的自由能 与成分间的关系表现为下凹曲面。
10
2. 两相平衡(two-phase equilibrium)
● 以等边成分三角形表示三元系的成分， 在浓度三角形的各个顶点分别作与浓度 平面垂直的温度轴，构成外形是一个三 棱柱体的三元相图；
● 三棱柱体的三个侧面是三组二元相图， 三棱柱体内部，有一系列空间曲面分隔 出若干相区。
● 三元相图复杂，不易描述相变过程和确 定相变温度。因此，实现三元相图实用 化的方法是使之平面化。
线（CA），线段Cb即为A组元的成分。同理，Ac为B组元的成分， Ba 为C组元的成分。
2
2. 等边成分三角形中的特殊线
(special lines in equilateral composition triangle)
平行于三角形某一条边的直线： 成分位于该线上的材料，它们所含
第5章 三元合金相图
第5章 三元合金相图由A-B-C 三组元组成的合金称三元合金，其相图称三元相图。
要确定三元合金的成分，必须给出其中两个组元的成分。
所以，在三元相图中表示成分的坐标轴有两个。
5-1 三元相图成分表示方法在三元相图中表示成分的两个坐标轴原则上可以交成任何角度，但一般采用等边三角形的三个边表示。
设P 为等边三角形内任意点，从P 点分别做三条边的平行线，交三条边于a 、b 、c 点。
根据等边三角形的几何性质：%100==++=++AB Ba Ac Cb Pc Pb Pa 因此，可用Cb 、Ac 、Ba 表示A 、B 、C 的成分。
这样，三角形中每一点都表示一个三元合金的成分。
该三角形称浓度三角形，或成分三角形。
5-2 三元相图中的定量法则一、直线法则二元合金处于两相平衡时，自由度f =2-2+1=1，温度和成分两个变量中只有一个可以独立改变，如当温度一定时，两个平衡相的成分是确定的。
三元合金处于两相平衡时，f =3-2+1=2，当温度一定时，两个平衡相中，只有一个相的成分可独立改变。
当温度和其中一个相的成分一定时，剩余相的成分是确定的。
假设某三元合金的成分点为P ，在某一温度下，该合金处于α、β两相平衡，两相的成分点为a 、b （P133图4）。
可以证明（P133），此时，a 、b 、P 三成分点在一条直线上，且P 点位于a 、b 之间。
这一规律称直线法则。
二、杠杆定律三元相图中的杠杆定律与二元相图中的类似，即同样也只适用于两相区，但形式上略有不同，在直线法则的基础上：%100%⨯=ab Pb α， %100%⨯=abPa β 三、重心法则三元合金处于α、β、γ三相平衡时，f =3-3+1=1。
当温度一定时，三个平衡相的成分是确定的，其成分点a 、b 、c 构成一个三角形。
若将成分比喻成重量，则合金的成分点P 一定落在成分点a 、b 、c三角形的重心处，这一规律金属学原理称重心法则。
其数学表达式为（证明见P135）%100%⨯''=a a a P α %100%⨯''=b b b P β %100%⨯''=cc c P γ 其实，重心法则可看作是直线法则和杠杆定律的变形。
材料学基础第5章三元相图
材料科学基础
第五章
5.6三元相图小结
材料科学基础
第五章
一、单相状态 f＝3－1＋1＝3，而一个温度变量和两个成分变量之间没有任何
相互制约的关系，因此，不论是等温截面还是变温截面，单相区可能具 有多种多样的形状。 二、两相平衡 立体图：共轭曲面。 成分变化：蝶形规则。 等温图：共轭曲线（可用杠杆定律） 变温截面：判定转变温度范围和相转变过程，不能用杠杆定律。 三、三相平衡 立体图：三棱柱，棱边是三个平衡相单变量线。
二、投影图
材料科学基础
第五章
投影图的作用：合金结晶过程分析、相组成物相对量计算、组织组成 物相对量计算。
图8.17 三元共晶相图的投影区
表8.2 各典型区域合金的凝固组织过程及室温组织
材料科学基础
第五章
区
凝固过程
室温组织
Ⅰ
L→α
α
Ⅱ
L→α ，α→βⅡ
α＋βⅡ
Ⅲ
L→α ，α→βⅡ，α β
α＋βⅡ＋γⅡ
(1)当给定合金在一定温度下处于两相平衡状态时，若其中一相的成分 给定，则根据直线法则，另一相的成分点必位于两已知成分点连线的 延长线上。 (2)如果两个平衡相的成分点已知，则合金的成分点必然位于两平衡相 成分点的连线上，根据两平衡相的成分，可用杠杆定律求出合金的成 分。
5.2.2重心定律
x，y，z分别为α，β，γ成分点，则
材料科学基础
第五章
投影图有两种。一种是把空间相图中所有相区间的交线部投影到浓度 三角形中，借助对立体图空间构造的了解，可以用投影图来分析合 金的冷却和加热过程。另一种是把一系列水平截面中的相界线投影 到浓度三角形中。每一条线上注明相应的温度，这样的投影图叫等 温线投影图。等温线可反映空间相图中各种相界面的变化趋势，等 温线越密，表示这个相面越陡。
第5章三元匀晶和共晶相图123
二元相图与三元相图的关系：
二元相图
（二维平面图） 平面相区 线 点
＋ 1维 ＋ 1维 ＋ 1维
＋1维
三元相图
（三维立体图） 立体相区 面 线
1. 三元匀晶相图
B
C
A
tC 液相面
固相面 tB
B C
tA
A
液相面 固相面
—— 由液相线演化而来
L
tC
—— 由固相线演化而来
tB
单相区：
L、 B
L+
C
双相区：
L+ A
tA
2. 结晶过程
L
t1
L→
B
t2
C
A
3. 等温截面及其投影
B
C
A
L+
L
4. 垂直截面
类型一：
L L+
B
C
C
A
类型二：
L
L+
B
C
A
本章重点：
成分三角形； 直线法则和重心定律； 等温截面、变温截面、投影图； 直线法则和重心定律的应用； 三元共晶相图分析； 变温截面的画法
Cr-Ni合金；铸铁中的Fe-C-Si合金；铝合金中的
Al-Mg-Si合金，Al-Cu-Mg合表示方法
三元相图的基础
三元相图中的杠杆定律 及重心定律
三元匀晶相图
三元相图分析
三元相图举例 小结
第六章 三元匀晶相图
三元匀晶相图的相图分析
三元匀晶 相图
结晶过程分析
投影图 水平截面图 垂直截面图
第六章 三元合金相图
6.1三元相图的成分表示法 6.2三元系平衡相的定量法则 6.3三元匀晶相图
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章 三元合金相图
6.1三元相图的成分表示法 6.2三元系平衡相的定量法则 6.3三元匀晶相图
为什么要用到三元相图?
二元相图只适用于二元合金或二个组元的陶瓷材 料，对于三组元的合金或陶瓷材料需用三元相图 分析。
工程实用材料多是三组元或三组元以上的，三组 元的合金可举例如下：轴承钢中的Fe-C-Cr合金； 高锰耐磨钢中的Fe-C-Mn合金；不锈钢中的FeCr-Ni合金；铸铁中的Fe-C-Si合金；铝合金中的 Al-Mg-Si合金，Al-Cu-Mg合金等等。
L
4. 垂直截面
类型一：
L
L+
B
C
C
A
类型二：
L
B
C
L+
A
本章重点：
成分三角形； 直线法则和重心定律； 等温截面、变温截面、投影图； 直线法则和重心定律的应用； 三元共晶相图分析； 变温截面的画法
所以我们要勤恳读书，广泛阅读， 古人说“书中自有黄金屋。
”通过阅读科技书籍，我们能丰富知识， 培养逻辑思维能力；
过阅读文学作品，我们能提高文学鉴赏水平 培养文学情趣；
读报刊，我们能增长见识，扩大自己的知识
本章知识结构
三元相图的基础 三元相图分析
三元相图成分表示方法
三元相图中的杠杆定律 及重心定律
三元匀晶相图
三元相图举例
小结
第六章 三元匀晶相图
三元匀晶相图的相图分析
三元匀晶 相图
结晶过程分析 投影图
水平截面图
垂直截面图
二元相图与三元相图的关系：
二元相图
（二维平面图）
平面相区 线 点
＋1维
＋1维 ＋1维 ＋1维
三元相图
（三维立体图）
立体相区 面 线
1.
固相面 tB
B
C
tA
A
液相面
—— 由液相线演化而来 L
tC
固相面
—— 由固相线演化而来
tB
L+
单相区：
B
L、
双相区：
L+
C
tA
A
2. 结晶过程
L B
L→
t1
t2
C
A
3. 等温截面及其投影
B
C
A
L+
6.1三元相图的成分表示法 6.2三元系平衡相的定量法则 6.3三元匀晶相图
为什么要用到三元相图?
二元相图只适用于二元合金或二个组元的陶瓷材 料，对于三组元的合金或陶瓷材料需用三元相图 分析。
工程实用材料多是三组元或三组元以上的，三组 元的合金可举例如下：轴承钢中的Fe-C-Cr合金； 高锰耐磨钢中的Fe-C-Mn合金；不锈钢中的FeCr-Ni合金；铸铁中的Fe-C-Si合金；铝合金中的 Al-Mg-Si合金，Al-Cu-Mg合金等等。
L
4. 垂直截面
类型一：
L
L+
B
C
C
A
类型二：
L
B
C
L+
A
本章重点：
成分三角形； 直线法则和重心定律； 等温截面、变温截面、投影图； 直线法则和重心定律的应用； 三元共晶相图分析； 变温截面的画法
所以我们要勤恳读书，广泛阅读， 古人说“书中自有黄金屋。
”通过阅读科技书籍，我们能丰富知识， 培养逻辑思维能力；
过阅读文学作品，我们能提高文学鉴赏水平 培养文学情趣；
读报刊，我们能增长见识，扩大自己的知识
本章知识结构
三元相图的基础 三元相图分析
三元相图成分表示方法
三元相图中的杠杆定律 及重心定律
三元匀晶相图
三元相图举例
小结
第六章 三元匀晶相图
三元匀晶相图的相图分析
三元匀晶 相图
结晶过程分析 投影图
水平截面图
垂直截面图
二元相图与三元相图的关系：
二元相图
（二维平面图）
平面相区 线 点
＋1维
＋1维 ＋1维 ＋1维
三元相图
（三维立体图）
立体相区 面 线
1.
固相面 tB
B
C
tA
A
液相面
—— 由液相线演化而来 L
tC
固相面
—— 由固相线演化而来
tB
L+
单相区：
B
L、
双相区：
L+
C
tA
A
2. 结晶过程
L B
L→
t1
t2
C
A
3. 等温截面及其投影
B
C
A
L+