必修一基本初等函数
人教版高中数学必修一-第二章-基本初等函数知识点总结
人教版高中数学必修一第二章基本初等函数知识点总结第二章 基本初等函数一、指数函数(一)指数与指数幂的运算 1.根式的概念:负数没有偶次方根;0的任何次方根都是0=0。
注意:(1)na =(2)当 n a = ,当 n 是偶数时,0||,0a a a a a ≥⎧==⎨-<⎩2.分数指数幂正数的正分数指数幂的意义,规定:0,,,1)m na a m n N n *=>∈>且正数的正分数指数幂的意义:_1(0,,,1)m nm naa m n N n a*=>∈>且0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质 (1)(0,,)rsr s a a aa r s R +=>∈(2)()(0,,)r s rsa a a r s R =>∈ (3)(b)(0,0,)rrra ab a b r R =>>∈注意:在化简过程中,偶数不能轻易约分;如122[(1]11≠ (二)指数函数及其性质1、指数函数的概念:一般地,函数xy a = 叫做指数函数,其中x 是自变量,函数的定义域为R .注意:指数函数的底数的取值范围,底数不能是负数、零和1.即 a>0且a ≠1 2a>1注意: 指数增长模型:y=N (1+p)指数型函数: y=ka 3 考点:(1)a b =N, 当b>0时,a,N 在1的同侧;当b 〈0时,a,N 在1的 异侧.(2)指数函数的单调性由底数决定的,底数不明确的时候要进行讨论。
掌握利用单调性比较幂的大小,同底找对应的指数函数,底数不同指数也不同插进1(=a 0)进行传递或者利用(1)的知识。
(3)求指数型函数的定义域可将底数去掉只看指数的式子,值域求法用单调性. (4)分辨不同底的指数函数图象利用a 1=a ,用x=1去截图象得到对应的底数。
(5)指数型函数:y=N (1+p)x 简写:y=ka x 二、对数函数 (一)对数1.对数的概念:一般地,如果x a N = ,那么数x 叫做以a 为底N 的对数,记作:log a x N = ( a - 底数, N — 真数,log a N — 对数式)说明:1。
高一数学必修一第二章基本初等函数知识点总结
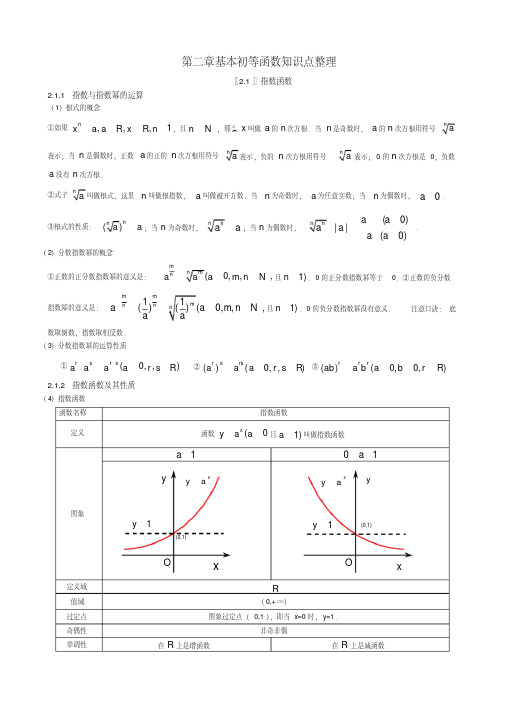
在 R 上是减函数
函数值的 变化情况
a 变化对
图象的影 响
y>1(x > 0), y=1(x=0), 0 < y<1(x < 0)
y> 1(x < 0), y=1(x=0), 0 < y< 1(x > 0)
在第一象限内, a 越大图象越高,越靠近 y 轴; 在第一象限内, a 越小图象越高,越靠近 y 轴; 在第二象限内, a 越大图象越低,越靠近 x 轴. 在第二象限内, a 越小图象越低,越靠近 x 轴.
y
f ( x) 中反解出 x
1
f ( y) ;
③将 x f 1( y ) 改写成 y f 1 ( x) ,并注明反函数的定义域.
( 8)反函数的性质
①原函数 y
f (x) 与反函数 y
1
f ( x) 的图象关于直线 y
x 对称.
②函数 y f ( x) 的定义域、值域分别是其反函数 y f 1 (x ) 的值域、定义域. ③若 P(a,b) 在原函数 y f (x ) 的图象上,则 P' (b, a) 在反函数 y f 1(x ) 的图象上.
③根式的性质: (n a )n a ;当 n 为奇数时, n an
a ;当 n 为偶数时, n an | a |
a (a 0)
.
a (a 0)
( 2)分数指数幂的概念
m
①正数的正分数指数幂的意义是: a n n a m (a 0, m, n N , 且 n 1) . 0 的正分数指数幂等于 0.②正数的负分数
设一元二次方程 ax 2 bx c 0( a 0) 的两实根为 x1, x2 ,且 x1 x2 .令 f ( x) ax 2 bx c ,从以下四个方
面来分析此类问题:①开口方向: a ②对称轴位置: x
高考《基本初等函数》 完整版课件PPT

高考调研 ·新课标 ·数学(必修一)
要点2 根式的性质 (1)当n为任何正整数时,(n a)n=a. (2)当n为奇数时,n an=a.
当n为偶数时,n an=|a|.
第4页
高考调研 ·新课标 ·数学(必修一)
要点3 分数指数幂的概念
(1)正数的正分数指数幂:a
m n
=
n
am
(a>0,m,n∈N*,且n
第11页
高考调研 ·新课标 ·数学(必修一)
思考题1 求下列各式的值.
3 (1)
-27;
4 (2)
(-9)2.
【答案】 (1)-3 (2)3
第12页
高考调研 ·新课标 ·数学(必修一)
例2 求使等式 (a-3)(a2-9)=(3-a) a+3成立的实 数a的取值范围.
【解析】 ∵3a+-3a≥ ≥00, ,∴aa≤ ≥3-,3,∴-3≤a≤3.
第21页
高考调研 ·新课标 ·数学(必修一)
3 【解析】 (1)-(-a)2. (2)原式=(yx2)12·(xy3)14·(xy36)112 =y1-14+12×x-12+34-14
5 =y4.
第22页
高考调研 ·新课标 ·数学(必修一)
课后巩固
第23页
高考调研 ·新课标 ·数学(必修一)
1.已知 (a-b)2=a-b,则( )
第15页
高考调研 ·新课标 ·数学(必修一)
【解析】 原式= ( 3- 2)2+ ( 3+ 2)2 =| 3- 2|+| 3+ 2| = 3- 2+ 3+ 2 =2 3.
第16页
高考调研 ·新课标 ·数学(必修一)
思考题3 求值 5+2 6+ 7-4 3- 6-4 2. 【解析】 5+2 6+ 7-4 3- 6-4 2 = ( 3+ 2)2+ ( 3-2)2- (2- 2)2 = 3+ 2+2- 3-(2- 2) =2 2. 【答案】 2 2
高一数学必修1第一章第二节基本初等函数

精心整理第二章:函数及其表示第一讲:函数的概念:知识点一:函数的概念:典型例题:判断下列对应关系是否为集合A到集合B的函数:A=z,B=Z,A=Z,B=Z,A={-1,1},B={0},f:)))巩固练习:已知函数f(-3),的值时,求知识点三:函数相等:如果两个函数的定义域相等,并且对应关系完全一致,那么我们称这两个函数一致。
典型例题3:下列函数中,f(x)与g(x)相等的是()A、B、C、D、巩固练习:)(2))(4)知识点四:区间的表示:零售量是否为月份的函数?为什么?知识点二:分段函数:典型例题1:作出下列函数的图像:(1)f(x)=2x,x∈Z,且|x|≤2(2)y=|x|典型例题2:某市“招手即停”公共汽车票价按下列规则制定:(1)5公里以内(含5公里),票价2元(2)5公里以上,每增加5公里,票价增加一元(不足5公里按5f:(1)集合A={P|P是数轴上的点},集合B=R,对应关系f:数轴上的点所代表的实数对应。
(2)集合A={P|P是平面直角坐标系中的点},集合B={(x,y)|x ∈R,y∈R},对应关系f:平面直角坐标系中的点与它的坐标对应;(3)集合A={x|x是三角形};集合B={x|x是圆};对应关系f:每个三角形都有对应它的内切圆。
课堂练习:1、如图,把截面半径为25cm的圆形木头据成矩形木料,如果中元素作业布置:1、求下列函数的定义域:(1)2、下列哪一组中的函数f(x)与g(x)相等?3、画出下列函数的图像,并说明函数的定义域和值域(1)y=3x(2)(3)y=-4x+5(4)x2-6x+74、已知函数f(x)=3x2-5x+2,求的值。
高中数学必修一基本初等函数知识点与典型例题总结
( a ,c ( 0 ,1 ) U ( 1 , ) ,b 0 )
c
2) 对数恒等式
a lo g a N N ( a 0 且 a 1 , N 0 )
3) 四个重要推论
①logabllggabllnnab; ②logamNnm nlogaN;
③logablog1ba;
④ lo g ab lo g bc lo g ac.
由f x是奇函数,图像关于原点对称.
所以f x在( ,- a )是增函数,
在(- a ,0)是减函数.
综上,函数 f x x a(a>0)的单调
区间是
x f x在(- a ,0),(0, a )是减函数.
在( ,- a ),( a ,+)是增函数,
单调区间的分界点为: a的平方根
5.函数f x x a (a>0)的值域
①找不到证明问题的切入口.如第(1)问,很 多考生不知道求其定义域.
②不能正确进行分类讨论.若对数或指数的 底数中含有参数,一般要进行分类讨论.
一般地,函数 y x x 是 自 变 量 , 是 常 数
叫做幂函数
y
y x, y x2, y x3,
1
y x2, y x1
的图象.
O
x
幂函数的性质
当x1x2 >a时,由x1,x2是任意的,知x1,x2可 无限接近.而x1,x2在同一个区间取值, 知x1,x2 ( a,+)时,x1x2 >a都成立. 此时,f(x2 )>f (x1). 所以x ( a,+)时,f(x)是增函数.
同时可知,x (0, a )时,f(x)是减函数.
⑵. 当x∈ (-∞,0)时,确定某单调区间
数学必修一基本初等函数知识点

数学必修一基本初等函数知识点
1. 线性函数:y = kx + b(k和b为常数),其中k称为斜率,b称为截距。
2. 幂函数:y = x^n(n为常数),其中n可以是正整数、零、负整数。
3. 指数函数:y = a^x(a为正实数且a≠1)。
4. 对数函数:y = loga(x)(a为正实数且a≠1),其中x为正实数。
5. 三角函数(正弦函数、余弦函数、正切函数、余切函数等):y = sinx,y = cosx,y = tanx,y = cotx等。
6. 反三角函数(反正弦函数、反余弦函数、反正切函数、反余切函数等):y = arcsinx,y = arccosx,y = arctanx,y = arccotx等。
7. 绝对值函数:y = |x|。
8. 双曲函数(双曲正弦函数、双曲余弦函数、双曲正切函数等):y = sinh(x),y = cosh(x),y = tanh(x)等。
9. 分段函数:根据不同条件定义函数的不同表达式,例如:y = f(x) =
{ x+1, (x≤0)
{ x^2, (0<x≤1)
{ 2x-1, (x>1)
10. 复合函数:将一个函数的输出作为另一个函数的输入进行运算,例如:f(g(x))。
以上是数学必修一中较为基本的初等函数知识点,只覆盖了一部分内容。
学习初等函数的重点是掌握其基本性质、图像和应用。
高中必修一数学第二章_基本初等函数(Ⅰ)ppt课件-人教版
x-13,x<2.
有两个不同的实根,则实数 k 的取值范围是______.
高中数学
解析:(1)作出
的图象,如
示.再把 f(x)的图象向左平移一个单位长度,可得到 y=
的图象.故选 B.
高中数学
(2)作出函数 f(x)=2x,x≥2,
的简图,如图
x-13,x<2.
方程 f(x)=k 有两个不同的实根,也就是函数 f(x)的图象 =k 有两个不同的交点,所以 0<k<1.
• (4)采用数形结合的方法,通过函数的图象解决
高中数学
比较下列各组数的大小:
(1)0.65.1,5.10.6,log0.65.1;
(2)log712,log812;
1
1
1
1
(3) a=0.22 ,b=0.32 ,c=331)因为 0<0.65.1<1,5.10.6>1,log0.65.1<0,
+
lg 42-lg 16+1-lg 14+log5 35-log
解:(1)原式=53212
3 +
-287-3÷(24)
3 -4
1
+25 ×
-1
=53-23-24+2-1=-22.
高中数学
1
(2)原式=(3-3) -3 + lg 42-2lg 4+1
-lg 4-1+log5
35 7
=3+ lg 4-12+lg 4+log5 5 =3+1-lg 4+lg 4+1
要题型,主要考查幂函数、指数函数、对数函 与性质的应用及差值比较法与商值比较法的应 用的方法有单调性法、图象法、中间搭桥法、 作商法. • (2)当需要比较大小的两个实数均是指数幂或对 可将其看成某个指数函数、对数函数或幂函数 值,然后利用该函数的单调性比较.
必修一第二章基本初等函数223
金品质•高追求 我们让你更放心!
返回
◆数学•必修1•(配人教A版)◆
基础梳理 1.一般地,把________叫做对数函数,其中 x是________,
函数的定义域是________,值域是________.
1.函数y=logax(a>0且a≠1) 自变量 (-∞,+∞) 2.对数函数y=logax(a>0,a≠1).
3.反函数 直线y=x对称 5.反函数 反函数 金品质•高追求 我们让你更放心!
返回
◆数学•必修1•(配人教A版)◆
6.互为反函数的两个函数的图象关于直线 __________对称.
例如:y=2x与y=log2x的图象关于直线________对
称.在同一直角坐标系中,函数y=2x与y=log2x以及函数y
金品质•高追求 我们让你更放心!
返回
◆数学•必修1•(配人教A版)◆ 自测自评
1.
,则a的取值范围是( B )
A.0,23∪(1,+∞)
B.23,+∞
C.23,1
D.0,23∪23,+∞
2.下列函数中,在(0,2)上为增函数的是( D )
A.y=log12x
②x>1,________; 0<x<1,________
2.(1)(0,+∞) (2)R (3)(1,0) (4)①(0,+∞) 增 ② (0,+∞) 减 (5)①y>0 y<0 ②y<0 y>0
金品质•高追求 我们让你更放心!
返回
◆数学•必修1•(配人教A版)◆
3.y=logax与y=ax互为________图象关于________对称.
返回
◆数学•必修1•(配人教A版)◆ 跟踪训练
分析:画出草图,结合图象解决.
金品质•高追求 我们让你更放心!
必修一第二章基本初等函数阶段复习课课件
解得 a=12,满足题意.综合①②知,a=21.
课堂小结
1.函数是高中数学极为重要的内容,函数思想和函数 方法贯穿整个高中数学的过程,纵观历年高考试题, 对本章的考查是以基本函数形式出现的综合题和应用 题,一直是常考不衰的热点问题. 2.从考查角度看,指数函数、对数函数概念的考查 以基本概念与基本计算为主;对图象的考查重在考查 平移变换、对称变换以及利用数形结合的思想方法解 决数学问题的能力;对幂函数的考查将会从概念、图 象、性质等方面来考查.
2.对于函数y=f(t),t=g(x). 若两个函数都是增函数或都是减函数,则其复合函数是增函 数;如果两个函数中一增一减,则其复合函数是减函数,即 “同增异减”,但一定要注意考虑复合函数的定义域.
求函数y (1)82xx2的单调区间 2
解令t 8 2x x2 (x 1)2 9,则y ( 1)t, 2
比较下列各组数的大小
a
log
1 2
3,
b
(1)0.2,c 3
2
1 3
解析
a=log
1 2
3<0,0<b=130.2<1,c=2
1 3
>1,故有
a小. (1) 0.213,0.233;(2)log32,log23,log25
解(1)∵y=x3 在 R 上是增函数,
课后作业: 导学案上的小题
5 +5
log52
+16
3 4
的值.
解
lg
8+lg 125-lg 2-lg log54·log25
5 +5
log52
+16
3 4
3lg 2+3lg 5-lg 2-lg 5
3
= 2log52·log25 +2+(24) 4
高一数学 基本初等函数(对、指、幂函数)高考考纲及典型例题高考真题解析
.
2
a 3 3a
【法二】 8 x 8 x 2 x
2
3 2
x 3
2 2 2 x 2 x 2 x 2 x 2 x 2 x
1
2 3
3
37 48
5 9 37 100 3 100 . 3 16 48
4
(4)原式 0.4 1 1 2 2 3 0.1
5 1 1 1 143 . 1 2 16 8 10 80
4.函数 f x a 2 7a 7 a x 是指数函数,求实数 a 的值. 【解析】∵函数 f x a 2 7a 7 a x 是指数函数,
1
0 a2 a1 1 a4 a3 . 1 又由题知: 0 10 1 3 10 ,∴ A 项正确. 3
1 x
a1 a2
O
x 1 x
b 7.已知二次函数 y ax 2 bx 与指数函数 y 的图象只能是下列图形中的 a y
1 1
1 2
1 1 , y x 2 的图像,了解它们的变化情况. x
二、重点知识总结
1.指数与指数幂运算 (1)①
a
n n n
n
a. a , 当n是奇数时 . a , 当n是偶数时
② a
(2)分数指数幂 ①a ②a
m n
n a m ( a 0 , m, n N * ,且 n 1 )
x y
2
是非负数,故④对.
7 (3) 2 9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本初等函数
指数函数、对数函数的概念和意义,指数函数、对数函数的图象和性质,会利用函数的单调性解决问题,几种简单的幂函数的图象和性质。
根式的运算,指数函数性质的应用,对数的运算法则,对数函数的图象及其性质的应用,幂函数性质的应用。
1.定点问题
①函数()21x f x a +=-过定点________
②函数()log (21)3a f x x =+-过定点________
③函数()()222a f x x x =++过定点________
归纳方法:
指数型函数: 令 指数式子=0,解出x ,再解出y
对数型函数: 令 真数式子=1,解出x ,再解出y
幂函数型函数:令 底数式子=1,解出x ,再解出y
2.比较大小
①单调性:
(2009全国卷Ⅱ文)设2lg ,(lg ),a e b e c ===则
(A )a b c >> (B )a c b >> (C )c a b >> (D )c b a >> ②中间值:
(2009全国卷Ⅱ理)设32log ,log log a b c π===
A. a b c >>
B. a c b >>
C. b a c >>
D. b c a >>
③图像法:
(2009天津卷文)设3.02131)2
1(,3log ,2log ===c b a ,则 A a<b<c B a<c<b C b<c<a D b<a<c
3.图像问题
指数函数底按逆时针增大,对数函数的底按顺时针增大,
幂函数的指数在直线x=1的右侧按逆时针增大。
