水力学资料
水力学-消能

(2)出池落差△z :
以下游河底0—0为基准面,对消力池出口处的上游断面 1及下游断面2列能量方程,其中两断面间的水头损失
vt2 ,则有 为 hj 2g
vt2 H1 ht hj ht ( ) 2g 2g 2g
2 vt2 v1 H1 ht ( ) 2g 2g
挑流鼻坎型式
• 挑流鼻坎型式有连续式和差动式两种。
连续式鼻坎设施简单,不易气蚀,在相同水力条件下, 挑距比差动式稍远,但水舌较集中,空中扩散较差,对河 床冲刷较深。 在挑流鼻坎内设置通气孔主要是为了避免挑流时高水 流带走水舌下面的空气而形成真空,影响挑射距离。
挑流鼻坎为什么容易被破坏?
泄水建筑在泄洪时,挑流鼻坎表面要承 受高速水流的冲刷,磨损很大。而许多工 程因施工等原因,挑流鼻坎表面不平整, 混凝土强度及耐磨达不到设计要求,经常 造成鼻坎表面混凝土脱落,钢筋裸露,影 响工程正常运行。
10.2 底流式衔接与消能
10.2.1 泄水建筑物下游收缩断面水深的计算
列坝前断面0-0及收缩断面c-c的能量方程: v02 vc0 2 vc0 2 H a1 hc0
2g 2g 2g
令,T为有效水头,T0称为有效总水头,则有
H a1
v02
2g
T
v02
(3) 临界水跃的跃后水深hc02 hc0和hc02都与池深d有关
d ' hc02
q2 ht 2g
1 (1ht )2 ( ' hco 2 ) 2
将与d有关的项放在等式左边,已知项放在等式右边,可得
' hc02
q2 q2 d ht 2 2 g ( ' hc02 ) 2 g (1ht ) 2
水力学

流线为什么不能相交? 因流线上任一点的切线方向代表该点的流速方向,如果流 线相交,在交点出就会出现两个切线方向,而同一时刻同 一点流体质点不可能同时向两个方向运动。
3.3.3 均匀流与非均匀流
①定义:总流中沿同一流线各点流速矢量相同 ②性质:1流线相互平行;2过水断面是平面;3沿流程过水断面形 状和大小不变,流速分布图相同 非均匀流 :沿同一根流线各点流速向量不同 在均匀流中,位于同一流线上各质点的流速大小和方向均相同。
有空间点上的运动情况,构成整个液体的运动。
用欧拉法描述液体运动时,液体质点的加速度应是当地加 速度与迁移加速度之和。
3.2 水流的分类
表征液体运动的物理量,如 流速、加速度、动水压强等 恒定流
按运动要素是否随时间变化
非恒定流
一元流 按运动要素随空间坐标的变化 二元流
三元流
均匀流 按流线是否为彼此平行的直线 非均匀流 急变流
Px hc Ax
曲面上静水总压力的水平分力等于曲面在铅垂投影面上 的静水总压力。
Pz Vp
曲面上静水总压力的垂直压力等于压力体内的水体重。 静水总压力
P Px2 Pz2
Pz tan Px
Pz arctg Px
例:某半圆柱面挡水建筑物,半径R=2m,宽度 b 2 m
代入到上式
0.6 pa 0.6 98060 V2 2 g H 2 9.806 2.8 20.78(m/s) g 9806
• 所以管内流量
qV
4
d 2V2 0.785 0.12 2 20.78 0.235(m 3/s)
水力学期末考试复习题及答案

水力学期末考试复习题及答案1、选择题:(每小题2分)(1)在水力学中,单位质量力是指( c )a、单位面积液体受到的质量力;b、单位体积液体受到的质量力;c、单位质量液体受到的质量力;d、单位重量液体受到的质量力。
(2)在平衡液体中,质量力与等压面( d )a、重合;b、平行c、相交;d、正交。
(3)液体中某点的绝对压强为100kN/m2,则该点的相对压强为ba、1 kN/m2b、2 kN/m2c、5 kN/m2d、10 kN/m2(4)水力学中的一维流动是指( d )a、恒定流动;b、均匀流动;c、层流运动;d、运动要素只与一个坐标有关的流动。
(5)有压管道的管径d与管流水力半径的比值d /R=( b )a、8;b、4;c、2;d、1。
(6)已知液体流动的沿程水力摩擦系数 与边壁相对粗糙度和雷诺数Re都有关,即可以判断该液体流动属于ca、层流区;b、紊流光滑区;c、紊流过渡粗糙区;d、紊流粗糙区(7)突然完全关闭管道末端的阀门,产生直接水击。
已知水击波速c=1000m/s,水击压强水头H = 250m,则管道中原来的流速v0为ca、1.54m b 、2.0m c 、2.45m d、3.22m(8)在明渠中不可以发生的流动是( c )a、恒定均匀流;b、恒定非均匀流;c、非恒定均匀流;d、非恒定非均匀流。
(9)在缓坡明渠中不可以发生的流动是( b )。
a、均匀缓流;b、均匀急流;c、非均匀缓流;d、非均匀急流。
(10)底宽b=1.5m的矩形明渠,通过的流量Q =1.5m3/s,已知渠中某处水深h =0.4m,则该处水流的流态为ba、缓流;b、急流;c、临界流;(11)闸孔出流的流量Q与闸前水头的H( d )成正比。
a、1次方b、2次方c、3/2次方d、1/2次方(12)渗流研究的对象是( a )的运动规律。
a、重力水;b、毛细水;c、气态水;d、薄膜水。
(13)测量水槽中某点水流流速的仪器有ba、文丘里计b、毕托管c、测压管d、薄壁堰(14)按重力相似准则设计的水力学模型,长度比尺λL=100,模型中水深为0.1米,则原型中对应点水深为和流量比尺为da、1米,λQ =1000;b、10米,λQ =100;c、1米,λQ =100000;d、10米,λQ=100000。
水 力 学 绪论

模型试验
当实际水流运动复杂,而理论分析困 难,无法解决实际工程的水力学问题时采 用。
指在实验室内,以水力相似理论为指 导,把实际工程缩小为模型,在模型上预 演相应的水流运动,得出模型水流的规律 性,再把模型试验成果按照相似关系换算 为原型的成果以满足工程设计的需要。
系统试验
在实验室内,小规模的造成某种水 流运动,用已进行系统的实验观测,从 中找到规律。
水
力
学
的
主
要
任 务
3.分析水流流动的形态。譬如修建一栏 河坝形成水库,需要计算上游河道中水
面的壅水长度,从而计算淹没范围,这
些都需要掌握水流的运动规律。
4.水能利用和消能问题。
水 力
供水系统中
学 的水箱、水塔
的 主 要
都建的很高, 根据能量方程
任 将位能或压能
务 转化为动能。
当水流从泄水孔泄到下游时,由于具
液体中的一切物理量都可以视为空 间坐标和时间的连续函数,因此可采用 连续函数的分析方法。
长期的生产和科学实验证明:利 用连续介质假定所得出的有关液体运 动规律的基本理论与客观实际是十分 符合的。
§0.3 液体的主要物理性质
➢ 惯性、质量与密度 ➢ 万有引力特性、重力与容重 ➢ 粘滞性 ➢ 压缩性 ➢ 表面张力
du dy
称为流速梯度,
是单位面积上的内摩擦力(切应力)。
作层流运动的液体,相互邻近层间单位面积
上所作用的内摩擦力(或粘滞力),与流速梯 度成正比,同时与液体的性质有关。
d tan( d ) dudt
dy
du d
dy dt
d
dt
液体的粘滞切应力与剪切变形速度成正比。
粘度
《水力学》期末考试实验指导书
X
=
3 5
4 6
水
或
X
=
1 5
2 6
水
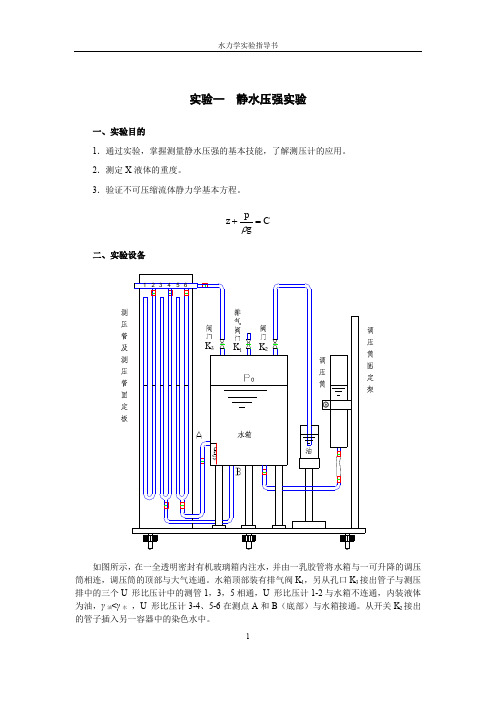
3.若水箱内气体压强 p0≠pa,则 p1≠p2、p3≠p4、p5≠p6。 当 p0<pa 时,则水箱液体表面真空度 pk=γ 水(▽2-▽1) 用水柱高来表示为:hk=▽2-▽1 四、实验步骤 1.认真阅读实验目的要求、实验原理和注意事项。 2.熟悉仪器,记录常数。 3.将调压筒放到最底位置,打开排气阀 K1,使水箱内部气压等于大气压,待水面稳定 后,观察各测管中的液面位置,以验证等压面原理。 关闭排气阀 K1,分三次调高调压筒。每次调高后,等到水位稳定后,记录各测压管水 位读数。 4.打开排气阀 K1,待液面稳定后再关闭 K1(此时不要移动调压筒)。 分三次调低调压筒。每次调低后,等到水位稳定后,记录各测压管水位读数。 5.打开真空管上的开关 K2,可见到容器中的染色水被吸上一个真空高度。
5
水力学实验指导书
水头的连线,即为总水头线。
微型比托管所测的水头为比托管管嘴所在位置的总水头。
四、实验步骤
1.熟悉实验设备后,打开尾阀,接通电源,启动供水系统。
2.等到供水稳定后,用吸耳球排除测压管中的气体。关闭尾阀,观察测压管中的水位 是否在同一水平面上,判断是否排完气体。再关闭出水阀门和给水阀,此时能量方程试验管 上各个测压管的液柱高度相同,因管内的水不流动没有流动损失,因此静水头的连线为一平 行基准线的水平线,将其读数记入表格静水头行中。
2.接通电源,开启水泵给水箱供水。
3.到水箱里的水开始溢流后,轻轻打开尾阀,使管道通过小流量,再打开指示剂开关, 使颜色水流入管道。
4.反复缓慢增大(或减小)流量,仔细观察层流和紊流现象。
水力学吴持恭第四版课件2 水静力学学习资料

公式 p = DP 平均压强
DA
p = lim DP DA 0 DA
单位:N/m2 (Pa)
点压强
二、静水压强的特性
第一特性:静水压强垂直于作用面,并指 向作用面。
第二章 水静力学
证明:取一处于静止或相对平衡的某一液体
P Ⅰ
N
AB
Ⅱ τ
N P
Pn
静水压强的方向与作用面的内法线方向重合, 静水压强是一种 压应力
=
p y
=
p z
=
p n
上式表明任一点的静水压强 p是
各向等值的,与作用面的方位无
关。第二特性得到证明
Z D Pn Px A Py C
O B Pz X
Y
第二章 水静力学
§2-2 液体的平衡微分方程及 其积分
液体处于平衡状态时,作用于液体上 的各种力及其坐标间的微分关系
第二章 水静力学 Z
A(x,y,z)
量(1
p
x
1
p y
1
p
z
)是对应相等的。
又称欧拉平衡微分方程
第二章 水静力学
将X
1
p x
=
0
Y
1
p y
=
0
Z 1
p z
=
0
依次乘以dx,dy,dz后相加得:
1
(
p x
dx
p y
dy
p z
dz)
=
Xdx
Ydy
Zdz
因为 ( p dx p dy p dz) 是P(x,y,z)的全微分 x y z
( p 1 p dx)dydz 2 x
( p 1 p dx)dydz 2 x
长沙理工大学水力学考研复习资料第九章 堰闸
1堰流及闸孔出流0.65 为闸孔出流0.75 为闸孔出流否则为堰流=堰顶水头或闸前水头。
水利水电学院赵昕3水舌下缘与堰顶为线接触。
形状:矩形,三角形,……: 水舌与堰顶为面接触曲线形,折线形)一段水流近似与堰顶平行;二次水面跌落ζ+α=11太小时水舌附壁(一般应使H>2.5cm)二、三角形薄壁堰优点:在小流量时仍然能够保持一定的稳定水头,适合用作量水堰。
将每个宽度db看成一个矩形薄壁堰的设计是关键,要求:流量系数尽可能地大体型较瘦堰面不产生大的负压13一、曲线型实用堰的剖面形状实用堰的外形轮廓基本上参照矩形薄壁堰的水舌下缘曲线设计(略向上凸出一点以消除壁面摩擦产生的负压)★实用堰的堰顶与薄壁堰的堰顶不同,水头H 约为后者的0.888倍。
问题:水头随流量改变,薄壁堰水舌随之改变,但实用堰外形不可能改变。
14时流量系数增大。
要求选取的剖面即使在高水头是也不产生大的负压。
17yH x d 85.085.12=xy与下游直线段(坡度m l )的切点C :C H x .dx dy 9250⎜⎜⎝⎛=⎟⎠⎞⎜⎝⎛19随着水头设计水头20三、侧收缩系数(1)弗朗西斯公式(Francis )([([⎪⎩⎪⎨⎧+−−+−=2.012.01n nn K K c ξξσ或[[⎪⎩⎪⎨⎧−+−==2.02.0b nb nb B B K K c c ξξσ2223[]nbH k n k pa 0)1(2−+−24252627实用堰水力计算问题的基本类型设计已知Q d ,确定:H d →堰剖面,堰顶高程堰宽B →b ,校核已知H ,计算Q →Q ~ H 关系已知Q ,计算H,10002H P m b H H h H P d c s ⎜⎜⎝⎛⎟⎠⎞⎜⎝⎛σ⎟⎟⎠⎞⎜⎜⎝⎛中行进流速水头含流量,计算时需要试算或迭代28P 1/H d ≧1.33 时为高堰:H 0≈H ,,2m b H H h H P Q c s s ⎟⎠⎞⎜⎝⎛σ⎟⎠⎞⎜⎝⎛σ=29五、低实用堰:过流能力大于宽顶堰堰0241.01)(4988.0dd H P m =驼峰堰折线实用堰流量系数32有底坎的宽顶堰1. 矩形宽顶堰无侧向收缩的自由溢流()gv h g v H H cc 222200∑ζ+α+ξ=α+=流量系数kk m ξ−ϕ=12/302H g mb Q =()00112k k k gH bkH Q −ϕ=ξ−ϕ=3638390.3550.3460.3400.3340.3300.3270.80.70.60.50.40.340八字形翼墙进口的平底宽顶堰流量系数0.3730.3750.3760.3750.3650.3690.3700.3690.3600.3640.3660.3640.3560.3640.3660.3640.3520.3580.3600.3580.3500.3560.3580.3560.3480.3540.3570.3540.3460.3520.3550.3520.3440.3510.3540.3510.3430.3500.3530.3500.51.02.03.00.80.70.60.50.40.30.20.10.0b/B41m s边孔流量系数m = 0.385,用弗朗西斯公式43.宽顶堰流动的淹没系数(有坎、无坎)求流经直角进口无侧收缩宽顶堰的流量Q。
水力学与桥涵水文
地观察和室内试验,建立实用的经验公式,以解决实际工程
问题。这些成果被总结成以实际液体为对象的重实用的水力 学
代表人物有皮托(H.Pitot)、谢才(A.de Chezy)、达西
(H.Darcy)等
1732年皮托发明了量测流体流速的皮托管
1769年谢才建立了计算均匀流的谢才公式
1856年达西提出了线性渗流的达西定律
理论方法中,流体力学引用的主要定理有: (1)质量守恒定律: (2)动量守恒定律:
(3)牛顿运动第二定律:
(4)机械能转化与守恒定律:动能+压能+位能+能量损失 =const 由于纯理论研究方法在数学上存在一定的困难,因 此亦采用数理分析法求解,即总流分析方法与代数方程为 主的求解方法:理论公式+经验系数,经验公式,二维微分 方程,基础流体力学(应用流体力学)、水力学。
绪
论
主要内容
§1.1 水力学与桥涵水文的性质与任务 §1.2 水力学的任务及其发展简史和研究方法
§1.3 液体的主要物理力学性质
§1.4 作用在流体上的力 §1.5 流体的力学模型
§1.1 水力学与桥涵水文的性质与 任务
《水力学与桥涵水文》是公路与城市道路、桥梁、交通工程 专业的一门技术基础课,侧重介绍有关基础原理与方法,为 专业课作前期理论应用训练及业务素质的培养。桥涵是跨越 河渠、宣泄洪水、沟通两侧灌溉水路及保证道路运行安全的 泄水建筑物,其有关水力水文计算原理与方法则是本学科的 任务。随着我国改革开放的深入,城镇建设日新月异,高等 级立体交叉交通枢纽日益增多,高速公路的里程在迅速增长, 上世纪末,我国已建成贯穿全国的两纵两横国道主干线,这 对路桥工程的等级及设计标准提出了新的要求,合理进行水 力水文计算亦更 具重要意义。
《水力计算手册》
《水力计算手册》水力计算手册第一章:引言1.1 背景介绍水力计算是水利工程领域中的重要内容,它是设计、建设和维护水利设施的基础。
水力计算手册是为了系统地介绍水力计算的基本原理、方法和应用而编写的。
本手册旨在帮助工程师和技术人员更好地理解和应用水力学知识,提高水力计算的准确性和可靠性。
1.2 基本概念本章将介绍水力计算手册中常用的基本概念,包括水力学、水流特性和水力计算的定义和分类。
第二章:水力学基础2.1 流体力学基础本节将介绍流体力学的基本概念和方程,包括流体静力学和流体动力学的基本原理和公式。
2.2 流体流动特性本节将介绍流体在不同条件下的流动特性,包括稳恒流动和非稳恒流动的特点和计算方法。
2.3 流量计算本节将介绍水力计算中常用的流量计算方法,包括流速计算、流量测量和河流横截面面积计算等。
第三章:水力计算方法3.1 水力元件计算方法本节将介绍水力计算中常用的水力元件计算方法,包括管道流动、水泵和水轮机的计算方法。
3.2 液压计算方法本节将介绍液压计算中的基本原理和方法,包括压力计算、流速计算和水力损失计算等。
3.3 水力模型计算方法本节将介绍水力模型计算中的基本原理和方法,包括模型试验的设计和数据处理等。
第四章:水力计算实例4.1 管道网络计算实例本节将给出管道网络计算的实例,包括水流速度计算、管道阻力计算和管道压力计算等。
4.2 水泵计算实例本节将给出水泵计算的实例,包括水泵性能曲线计算和水泵选型等。
4.3 水轮机计算实例本节将给出水轮机计算的实例,包括水轮机效率计算、水轮机功率计算和水轮机设计等。
第五章:水力计算应用5.1 水利工程设计本节将介绍水力计算在水利工程设计中的应用,包括渠道设计、堤坝设计和船闸设计等。
5.2 水资源管理本节将介绍水力计算在水资源管理中的应用,包括河流流量调控、水库调度和灌溉规划等。
5.3 水环境保护本节将介绍水力计算在水环境保护中的应用,包括水污染控制、水质保护和水生态修复等。
水力学基本概念
目录绪论: (1)第一章:水静力学 (1)第二章:液体运动的流束理论 (3)第三章:液流形态及水头损失 (3)第四章:有压管中的恒定流 (5)第五章:明渠恒定均匀流 (5)第六章:明渠恒定非均匀流 (6)第七章:水跃 (7)第八章:堰流及闸空出流 (8)第九章:泄水建筑物下游的水流衔接与消能 (9)第十一章:明渠非恒定流 (10)第十二章:液体运动的流场理论 (10)第十三章:边界层理论 (11)第十四章:恒定平面势流 (11)第十五章:渗流 (12)第十六章:河渠挟沙水流理论基础 (12)第十七章:高速水流 (12)绪论:1 水力学定义:水力学是研究液体处于平衡状态和机械运动状态下的力学规律,并探讨利用这些规律解决工程实际问题的一门学科。
2 理想液体:易流动的,绝对不可压缩,不能膨胀,没有粘滞性,也没有表面张力特性的连续介质。
3 粘滞性:当液体处在运动状态时,若液体质点之间存在着相对运动,则质点见要产生内摩擦力抵抗其相对运动,这种性质称为液体的粘滞性。
可视为液体抗剪切变形的特性。
(没有考虑粘滞性是理想液体和实际液体的最主要差别)4 动力粘度:简称粘度,面积为1m2并相距1m的两层流体,以1m/s做相对运动所产生的内摩擦力。
5 连续介质:假设液体是一种连续充满其所占空间毫无空隙的连续体。
6 研究水力学的三种基本方法:理论分析,科学实验,数值计算。
第一章:水静力学要点:(1)静水压强、压强的量测及表示方法;(2)等压面的应用;(3)压力体及曲面上静水总压力的计算方法。
7 静水压强的两个特性:1)静水压强的方向与受压面垂直并指向受压面2)任一点静水压强的大小和受压面方向无关,或者说作用于同一点上各方向的静水压强大小相等。
8 等压面:1)在平衡液体中等压面即是等势面2)等压面与质量力正交3)等压面不能相交4)绝对静止等压面是水平面5)两种互不相混的静止液体的分界面必为等压面6)不同液体的交界面也是等压面9 静水压强的计算公式:p=p0+10 绕中心轴作等角速度旋转的液体:11 绝对压强:以设想没有大气存在的绝对真空状态作为零点计量的压强,称为绝对压强。
