2023年九年级中考数学复习++几何图形动点与函数图像综合讲义
2023中考数学综合复习知识点

2023中考数学综合复习知识点中考数学综合复习知识点1、二次函数的概念一般地,如果,那么y叫做x 的二次函数。
叫做二次函数的一般式。
2、二次函数的图像二次函数的图像是一条关于对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向;②有对称轴;③有顶点。
3、二次函数图像的画法五点法:(1)先根据函数解析式,求出顶点坐标,在平面直角坐标系中描出顶点M,并用虚线画出对称轴(2)求抛物线与坐标轴的交点:当抛物线与x轴有两个交点时,描出这两个交点A,B及抛物线与y轴的交点C,再找到点C的对称点D。
将这五个点按从左到右的顺序连接起来,并向上或向下延伸,就得到二次函数的图像。
当抛物线与x轴只有一个交点或无交点时,描出抛物线与y轴的交点C及对称点D。
由C、M、D三点可粗略地画出二次函数的草图。
如果需要画出比较精确的图像,可再描出一对对称点A、B,然后顺次连接五点,画出二次函数的图像。
初中中考数学知识点梳理二次函数的解析式有三种形式:(1)一般式:(2)顶点式:(3)当抛物线与x轴有交点时,即对应二次好方程有实根和存在时,根据二次三项式的分解因式,二次函数可转化为两根式。
如果没有交点,则不能这样表示。
注意:抛物线位置由决定.(1)决定抛物线的开口方向①开口向上.②开口向下.(2)决定抛物线与y轴交点的位置.①图象与y轴交点在x轴上方.②图象过原点.③图象与y轴交点在x轴下方.(3)决定抛物线对称轴的位置(对称轴:)①同号对称轴在y轴左侧.②对称轴是y轴.③异号对称轴在y轴右侧.(4)顶点坐标.(5)决定抛物线与x轴的交点情况.、①△0抛物线与x轴有两个不同交点.②△=0抛物线与x轴有的公共点(相切).③△0抛物线与x轴无公共点.(6)二次函数是否具有、最小值由a判断.①当a0时,抛物线有最低点,函数有最小值.②当a0时,抛物线有点,函数有值.(7)的符号的判定:表达式,请代值,对应y值定正负;对称轴,用处多,三种式子相约;轴两侧判,左同右异中为0;1的两侧判,左同右异中为0;-1两侧判,左异右同中为0.(8)函数图象的平移:左右平移变x,左+右-;上下平移变常数项,上+下-;平移结果先知道,反向平移是诀窍;平移方式不知道,通过顶点来寻找。
中考数学动点问题专题讲解

专题一:建立动点问题的函数解析式36xPHOP--236211x -2222233621419xxx MHPH+-++N G P O B xy∴y =GP=32MP=233631x + (0<x <6).(3)(3)△△PGH 是等腰三角形有三种可能情况是等腰三角形有三种可能情况: : ①GP=PH 时,x x =+233631,解得6=x . . 经检验经检验经检验, , 6=x 是原方程的根是原方程的根,,且符合题意且符合题意. .②GP=GH 时,2336312=+x ,解得0=x . . 经检验经检验经检验, , 0=x 是原方程的根是原方程的根,,但不符合题意但不符合题意. . ③PH=GH 时,2=x .综上所述综上所述,,如果△如果△PGH PGH 是等腰三角形是等腰三角形,,那么线段PH 的长为6或2.二、应用比例式建立函数解析式例例2(2006年²山东)如图2,2,在△在△在△ABC ABC 中,AB=AC=1,,AB=AC=1,点点D,E 在直线BC 上运动上运动..设BD=,x CE=y . (1) (1)如果∠如果∠如果∠BAC=30BAC=30BAC=30°°,∠DAE=105DAE=105°°,试确定y 与x 之间的函数解析式;之间的函数解析式; (2) (2)如果∠如果∠如果∠BAC BAC 的度数为a ,∠DAE 的度数为b ,当a ,b 满足怎样的关系式时满足怎样的关系式时,(1),(1),(1)中中y 与x 之间的函数解析式还成立数解析式还成立??试说明理由试说明理由. .解:(1):(1)在△在△在△ABC ABC 中,∵AB=AC,AB=AC,∠∠BAC=30BAC=30°°,∴∠∴∠ABC=ABC=ABC=∠∠ACB=75ACB=75°°, , ∴∠∴∠∴∠ABD=ABD=ABD=∠∠ACE=105ACE=105°°. ∵∠∵∠BAC=30BAC=30BAC=30°°,∠DAE=105DAE=105°°, , ∴∠∴∠∴∠DAB+DAB+DAB+∠∠CAE=75CAE=75°°, 又∠又∠DAB+DAB+DAB+∠∠ADB=ADB=∠∠ABC=75ABC=75°°, ∴∠∴∠CAE=CAE=CAE=∠∠ADB, ∴△∴△ADB ADB ADB∽△∽△∽△EAC, EAC, EAC, ∴∴ACBD CEAB =,∴11xy =, , ∴∴x y 1=.(2)(2)由于∠由于∠由于∠DAB+DAB+DAB+∠∠CAE=a b -,又∠又∠DAB+DAB+DAB+∠∠ADB=ADB=∠∠ABC=290a-°,且函数关系式成立函数关系式成立, ,∴290a-°=a b -, , 整理得整理得=-2a b °90. 当=-2a b °90时,函数解析式xy 1=成立成立. .例3(2005年²年²上海上海上海))如图3(1),3(1),在△在△在△ABC ABC 中,∠ABC=90ABC=90°°,AB=4,BC=3. 点O 是边AC 上的一个动点上的一个动点,,以点O 为圆心作半圆为圆心作半圆,,与边AB 相切于点D,交线段OC 于点E.E.作作EP EP⊥⊥ED,ED,交射线交射线AB 于点P,P,交射线交射线CB 于点F.(1)(1)求证求证求证: : : △△ADE ADE∽△∽△∽△AEP. AEP.(2)(2)设设OA=x ,AP=y ,求y 关于x 的函数解析式的函数解析式,,并写出它的定义域义域. . (3) (3)当当BF=1时,求线段AP 的长的长. . 解:(1):(1)连结连结OD.根据题意根据题意,,得OD OD⊥⊥AB,AB,∴∠∴∠∴∠ODA=90ODA=90ODA=90°°,∠ODA=ODA=∠∠DEP.又由OD=OE,OD=OE,得得∠ODE=ODE=∠∠OED.∴∠∴∠ADE=ADE=∠AEP, AEP, ∴∴△ADE ADE∽△∽△AEP.(2)∵∠ABC=90°,AB=4,BC=3, ∴AC=5. ∵∠ABC=∠A E D C B 图 2●P D E A C B 3(2) O F O ●F P D E A C B 3(1) ADO=90ADO=90°°, , ∴∴OD OD∥∥BC, BC, ∴∴53x OD =,54x AD =,∴OD=x 53,AD=x 54. . ∴∴AE=x x53+=x 58. ∵△∵△ADE ADE ADE∽△∽△∽△AEP, AEP, AEP, ∴∴AE ADAP AE=, , ∴∴xx yx585458=. . ∴∴x y 516=(8250£<x ).(3)(3)当当BF=1时,时,①若EP 交线段CB 的延长线于点F,F,如图如图3(1)3(1),则,则CF=4.∵∠∵∠ADE=ADE=ADE=∠∠AEP, AEP, ∴∠∴∠∴∠PDE=PDE=PDE=∠∠PEC. PEC. ∵∠∵∠∵∠FBP=FBP=FBP=∠∠DEP=90DEP=90°°, , ∠∠FPB=FPB=∠∠DPE,∴∠∴∠F=F=F=∠∠PDE, PDE, ∴∠∴∠∴∠F=F=F=∠∠FEC, FEC, ∴∴CF=CE. ∴5-x 58=4,=4,得得85=x .可求得2=y ,即AP=2.②若EP 交线段CB 于点F,F,如图如图3(2), 3(2), 则则CF=2. 类似①类似①,,可得CF=CE. ∴5-x 58=2,=2,得得815=x .可求得6=y ,即AP=6.综上所述综上所述, , , 当当BF=1时,线段AP 的长为2或6. 三、应用求图形面积的方法建立函数关系式例4(2004年²上海)如图,在△在△ABC ABC 中,∠BAC=90BAC=90°°,AB=AC=22,⊙A 的半径为1.1.若点若点O 在BC 边上运动运动((与点B 、C 不重合不重合),),),设设BO=x ,△AOC 的面积为y .(1)(1)求求y 关于x 的函数解析式的函数解析式,,并写出函数的定义域并写出函数的定义域. .(2)(2)以点以点O 为圆心为圆心,BO ,BO 长为半径作圆O,O,求当⊙求当⊙求当⊙O O 与⊙与⊙A A 相切时相切时, , △AOC 的面积的面积. .解:(1):(1)过点过点A 作AH AH⊥⊥BC,BC,垂足为垂足为H.∵∠∵∠BAC=90BAC=90BAC=90°°,AB=AC=22, , ∴∴BC=4,AH=21BC=2. BC=2. ∴∴OC=4-x . ∵AH OC SAOC×=D 21, , ∴∴4+-=x y (40<<x ). (2)(2)①当⊙①当⊙①当⊙O O 与⊙与⊙A A 外切时外切时, ,在Rt Rt△△AOH 中,OA=1+x ,OH=x -2, , ∴∴222)2(2)1(x x -+=+. . 解得解得67=x .此时此时,,△AOC 的面积y =617674=-.②当⊙②当⊙O O 与⊙与⊙A A 内切时内切时, , 在Rt Rt△△AOH 中,OA=1-x ,OH=2-x , , ∴∴222)2(2)1(-+=-x x . . 解得解得27=x .此时此时,,△AOC 的面积y =21274=-.综上所述综上所述,,当⊙当⊙O O 与⊙与⊙A A 相切时相切时,,△AOC 的面积为617或21.A B C O 图8 H FABED专题二:动态几何型压轴题2x321017217ABCDEOlA ′ABCDEO lF 392+x 9412+x x 9+339412+x 3F GE AB D图3-2K F GE KF G E FGE U KFG EF GE AAA AA D D D DB D A BF MN332OBACOBACGFED CBAAD O33333COCOC1O则PC BP的值为的值为 (A )2 (B )3 (C )23 (D )26分析:本题是一道选择题,给出四个答案有且只有一个是正确的,因此可以取一个特殊位置进行研究,当点P 满足PB ⊥AB 时,可以通过计算得出PB=221322=-BC ³AP=BP ³AB ,因此,因此BC=62462288162822==+=+´BPAB BP AB , 在三角形BPC 中,PC=36222=-BC BP,所以,PC BP=3选(B )当然,本题还可以根据三角形相似得BP APPCBP=,即可计算出结论。
2023年九年级中考数学高频考点突破--二次函数与动态几何综合题

2023年中考数学高频考点突破--二次函数与动态几何综合题1.抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC 的面积最大时,求点P的坐标;(3)如图2,抛物线顶点为E,EF△x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若△MNC=90°,请指出实数m的变化范围,并说明理由.2.综合与探究如图,抛物线y=34x2−154x+3与x轴交于A,B两点,且点A在点B的左侧,与y轴交于点C.(1)求点A,B和C的坐标;(2)点E是直线BC上的动点,过点E作x轴的垂线交抛物线于点F,当EF=OC时,求点E的横坐标;(3)点P从点B出发沿BC以1个单位长度/秒的速度向终点C运动,同时,点Q从点O出发以相同的速度沿x轴的正半轴向终点B运动,一点到达,两点同时停止运动.连接PQ,当△BPQ是等腰三角形时,请直接写出运动的时间.3.如图,抛物线y=﹣x2+bx+c(a≠0)与x轴、y轴分别交于点A(3,0)、B(0,3)两点.(1)试求抛物线的解析式和直线AB的解析式;(2)动点E从O点沿OA方向以1个单位/秒的速度向终点A匀速运动,同时动点F沿AB方向以√2个单位/秒的速度向终点B匀速运动,E、F任意一点到达终点时另一个点停止运动,连接EF,设运动时间为t,当t为何值时△AEF为直角三角形?(3)抛物线位于第一象限的图象上是否存在一点P,使△PAB面积最大?如果存在,请求出点P的坐标;如果不存在,请说明理由.4.如图,抛物线y=ax2+bx+ 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.(1)求抛物线的函数解析式,并写出顶点D的坐标;(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,△EFK的面积最大?并求出最大面积.5.已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C.(1)求抛物线的解析式;(2)如图,设抛物线与x轴的另一个交点为D,在抛物线上是否存在点P,使△PAB的面积是△BDA面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由.(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合),经过A、E、O 三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求面积的最小值及E点坐标.6.如图,在平面直角坐标系中,直线y=−12x+2与x轴交于点A,与y轴交于点B,抛物线y=−23x2+bx+c过点B且与直线相交于另一点C(52,34).(1)求抛物线的解析式;(2)点P是抛物线上的一动点,当∠PAO=∠BAO时,求点P的坐标;(3)点N(n,0) (0<n<52)在x轴的正半轴上,点M(0,m)是y轴正半轴上的一动点,且满足∠MNC=90°.①求m与n之间的函数关系式;②当m在什么范围时,符合条件的N点的个数有2个?7.已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C.(1)求抛物线的解析式;(2)如图(1),设抛物线与x轴的另一个交点为D,在抛物线的对称轴上找一点H,使△CDH的周长最小,求出H点的坐标并求出最小周长值.(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合),经过A、E、O 三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求面积的最小值及E点坐标.8.如图,二次函数y=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),与y轴相交于点C,点G是二次函数图象的顶点,直线GC交x轴于点H(3,0),AD平行GC交y 轴于点D.(1)求该二次函数的表达式(2)求证:四边形ACHD是正方形(3)①作ME△x轴于点E,作MF△y轴于点F,根据四边形ADCM的面积为S,可得S=S四边形AOCM+S△AOD,再分别求出S四边形AOCM、S△AOD即可.②首先设点N的坐标是(t1,p1),则NI=|t1|,所以S△CMN=S△COM+S△CON=32(|t|+|t1|),再根据t<0,t1>0,可得S△CMN=32(|t|+|t1|)=32(t1-t)=214,据此求出t1﹣t=72;然后求出k1、k2的值是多少,进而求出t1、t2的值是多少,再把它们代入S关于t的函数表达式,求出S的值是多少即可.9.如图,抛物线y=14x2−32x−4与x轴交于A、B点(点B在点A的右侧),与y轴交于点C.连结BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.(1)求点A、B、C的坐标;(2)当点P在线段OB上运动时,直线l分别交BD、BC于点M、N.试探究m为何值时,四边形CQMD是平行四边形;(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.10.《函数的图象与性质》拓展学习片段展示:(1)(问题)如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a=,点A的坐标为.(2)(操作)将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式:.(3)(探究)在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是.(4)(应用)结合上面的操作与探究,继续思考:如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.①求A、B两点的坐标;(用含h的式子表示)②当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.11.如图,抛物线y=ax2+bx+c与x轴交于A(√3,0),B两点(点B在点A 的左侧),与y轴交于点C,且OB=3OA=√3OC,∠OAC的平分线AD交y轴于点D,过点A且垂直于AD的直线l交y轴于点E,点P是x轴下方抛物线上的一个动点,过点P作PF⊥x轴,垂足为F,交直线AD于点H.(1)求抛物线的解析式;(2)设点P的横坐标为m,当FH=HP时,求m的值;(3)当直线PF为抛物线的对称轴时,以点H为圆心,12HC为半径作⊙H,点Q为⊙H上的一个动点,求14AQ+EQ的最小值.12.如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F 旋转180°,得到新的抛物线C′.(1)求抛物线C的函数表达式;(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N 能否成为正方形?若能,求出m的值;若不能,请说明理由.13.如图1,抛物线y=−x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点B坐标为(2,0),点C坐标为(0,2).(1)求抛物线的表达式;(2)如图2,点P为直线BC上方抛物线上的一个动点,当△PBC的面积最大时,求点P的坐标;(3)如图3,过点M(1,3)作直线MD⊥x轴于点D,在直线MD上是否存在点N,使点N到直线MC的距离等于点N到点A的距离?若存在,求出点N的坐标;若不存在,请说明理由.14.如图,抛物线y=﹣13x2+bx+c经过点B(2 √3,0)、C(0,2)两点,与x轴的另一个交点为A.(1)求抛物线的解析式;(2)点D从点C出发沿线段CB以每秒√3个单位长度的速度向点B运动,作DE△CB 交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).①当点F落在抛物线上时,求t的值;②若点D在运动过程中,设△ABC与矩形CDEF重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出自变量t的取值范围.15.如图,在平面直角坐标系中,抛物线y=−12x2+bx+c与直线AB交于点A(4,5),B(0,1).(1)求该抛物线的函数表达式;(2)点C为该抛物线的顶点,连接AC,点P为抛物线上点B,C之间的任意一点,连接BP,CP,过点P作PE//AC交直线AB于点E,连接CE,求四边形CPBE面积的最大值;(3)设该抛物线沿射线AB方向平移2√2个单位后得到的抛物线为y1=a1x2+b1x+c1(a1≠0),平移后的抛物线与原抛物线交于点G,连接AG、BG,将△ABG 沿直线AB方向平移,平移后得到△A′B′G′,其中点A的对应点为点A′,点B的对应点为点B′,点G的对应点为点G′.在平移过程中,是否存在点B′,使得△OG′B′是以B′G′为腰的等腰三角形,若存在,请直接写出点B′的横坐标,若不存在,请说明理由.16.如图,已知抛物线y=ax 2+ 85x+c 与x 轴交于A ,B 两点,与y 轴交于点C ,且A (2,0),C (0,﹣4),直线l :y=﹣ 12 x ﹣4与x 轴交于点D ,点P 是抛物线y=ax 2+ 85x+c 上的一动点,过点P 作PE△x 轴,垂足为E ,交直线l 于点F.(1)试求该抛物线表达式;(2)如图(1),若点P 在第三象限,四边形PCOF 是平行四边形,求P 点的坐标; (3)如图(2),过点P 作PH△y 轴,垂足为H ,连接AC. ①求证:△ACD 是直角三角形;②试问当P 点横坐标为何值时,使得以点P 、C 、H 为顶点的三角形与△ACD 相似?答案解析部分1.【答案】(1)解:由题意得: {−1−b +c =0c =3 ,解得: {b =2c =3, ,∴抛物线解析式为 y =−x 2+2x +3 (2) 解:令 −x 2+2x +3=0 , ∴x 1= -1,x 2=3,即B (3,0), 设直线BC 的解析式为y=kx+b′,∴{b ′=33k +b ′=0,解得: {b ′=3k =−1, ,∴直线BC 的解析式为 y =−x +3 , 设P (a ,3-a ),则D (a ,-a 2+2a+3), ∴PD=(-a 2+2a+3)-(3-a )=-a 2+3a , ∴S △BDC =S △PDC +S △PDB ,=12PD ⋅a +12PD ⋅(3−a)=3 2PD=32(−a2+3a)=−32(a−32)2+278∴当a=32时,△BDC的面积最大,此时P(32,32)(3)解:由(1),y=-x2+2x+3=-(x-1)2+4,∴OF=1,EF=4,OC=3,过C作CH△EF于H点,则CH=EH=1,当M在EF左侧时,∵△MNC=90°,则△MNF△△NCH,∴MFNH=FNBC,设FN=n,则NH=3-n,∴1−m3−n=n1,即n2-3n-m+1=0,关于n的方程有解,△=(-3)2-4(-m+1)≥0,得m≥ −54,当M在EF右侧时,Rt△CHE中,CH=EH=1,△CEH=45°,即△CEF=45°,作EM△CE交x轴于点M,则△FEM=45°,∵FM=EF=4,∴OM=5,即N为点E时,OM=5,∴m≤5,综上,m的变化范围为:−54≤m≤5.2.【答案】(1)解:把x=0代入y=34x2−154x+3中,得y=3.∴点C的坐标是(0,3).把y=0代入y=34x2−154x+3中,得34x2−154x+3=0.解得x1=1,x2=4.∴点A的坐标是(1,0),点B的坐标是(4,0).∴点A的坐标是(1,0),点B的坐标是(4,0),点C的坐标是(0,3).(2)解:设直线BC的解析式是y=kx+3.∵过点B(4,0),∴0=4k+3.解得k=−3 4.∴直线BC的解析式是y=−34x+3.∵点E是直线BC上的动点,过点E作x轴的垂线交抛物线于点F,∴设点E的坐标是(m,−34m+3),则点F的坐标是(m,34m2−154m+3).∵EF=OC,点C的坐标是(0,3),∴|34m2−154m+3−(−34m+3)|=3.∴34m2−3m=3,或34m2−3m=−3.解得m1=2+2√2,m2=2−2√2,m3=m4=2.∴点E的横坐标是2+2√2,2−2√2和2.(3)解:设运动时间为t,根据题意,若要构成△BPQ,则P、Q不与点B重合,t的取值范围为0<t<4,∴PB=OQ=t,BQ=4−t,如图,过点P作PD⊥x轴于点D,设点P的坐标为(a,−34a+3),则BD=4−a,PD=−34a+3,根据勾股定理,在Rt △PDB 中, PD 2+DB 2=PB 2,(−34a +3)2+(4−a)2=t 2,解得a 1=4−45t ,a 2=4+45t (不符合题意,舍去),∴点P 的坐标为(4−4t 5,3t5),∵点Q 的坐标为(t ,0)∴PQ 2=(4−4t 5−t)2+(3t 5)2=9025t 2−72t5+16,∵PB =OQ =t ,BQ =4−t ,PQ 2=(4−4t 5−t)2+(3t 5)2=9025t 2−72t5+16,①当BP =BQ 时, 即t =4−t , 解得:t =2; ②当BP =PQ 时,t 2=9025t 2−72t5+16,解得:t 1=2013,t 2=4(不符合题意,舍去),③当BQ =PQ 时,(4−t)2=9025t 2−72t5+16,解得:t 1=3213,t 2=0(不符合题意,舍去),综上所述:当△BPQ 是等腰三角形时,时间为2秒,2013秒,3213秒.3.【答案】(1)解:∵抛物线y=﹣x 2+bx+c (a≠0)经过A (3,0),B (0,3),∴{−9+3b +c =0c =3 ,解得 {b =2c =3,∴抛物线解析式为y=﹣x 2+2x+3, 设直线y=kx+n ,∴{3k +n =0n =3 ,解得 {k =−1n =3 ,∴直线AB 的解析式为y=x+3(2)解:由题意可知OE=t ,则AF= √2 t ,AE=3﹣t , ∵△AEF 为直角三角形,∴有△AEF=90°和△AFE=90°两种情况, ①当△AEF=90°时,则有△AOB△△AEF ,∴AB AF = AO AE ,即√2√2t= 33−t ,解得t= 32 ; ②当△AFE=90°时,则有△AOB△△AFE ,∴OA AF = AB AE ,即 3√2t = 3√23−t,解得t=1; 综上可知当t 为 32或1时△AEF 为直角三角形(3)解:如图,过P 作PC△y ,AB 于点C ,交x 轴于点D ,设P (x ,﹣x 2+2x+3)(0<x <3),则C (x ,﹣x+3), ∵P 为抛物线在第一象限内的点, ∴PC=﹣x 2+2x+3﹣(﹣x+3)=﹣x 2+3x ,∴S △PAB =S △PBC +S △PAC = 12 PC•OD+ 12 PC•AD= 12 PC•OA= 32 PC= 32 (﹣x 2+3x )=﹣ 32(x﹣ 32 )2+ 278 ,∵﹣ 32<0,∴当x= 32 时,S △PAB 有最大值 278 ,此时P 点坐标为( 32 , 154),综上可知存在满足条件的点P ,其坐标为( 32 , 154)4.【答案】(1)解:由题意,得 {16a −4b +4=04a +2b +4=0解得 a =−12 ,b=-1.所以抛物线的解析式为 y =−12x 2−x +4 ,顶点D 的坐标为(-1, 92 ).(2)解:设抛物线的对称轴与x 轴交于点M .因为EF 垂直平分BC ,即C 关于直线EG 的对称点为B ,连结BD 交于EF 于一点,则这一点为所求点H ,使DH+CH 最小,即最小为DH+CH=DH+HB=BD= √BM 2+DM 2=32√13 .而 CD =√12+(92−4)2=√52.∴△CDH 的周长最小值为CD+DR+CH= √5+3√132.设直线BD 的解析式为y=k 1x+b ,则 {2k 1+b 1=0−k 1+b 1=92 解得 k 1=−32 ,b 1= 3.所以直线BD 的解析式为y= −32x+ 3.由于BC= 2 √5 ,CE=BC∕2 = √5 ,Rt△CEG△△COB , 得CE:CO=CG:CB ,所以CG= 2.5,GO= 1.5.G (0,1.5).同理可求得直线EF 的解析式为y= 12 x+ 32.联立直线BD 与EF 的方程,解得使△CDH 的周长最小的点H ( 34 , 158).(3)解:设K (t , −12t 2−t +4 ),x F <t <x E .过K 作x 轴的垂线交EF 于N .则KN=y K -y N = −12t 2−t +4 -( 12 t+ 32 )= −12t 2−32t +52.所以S △EFK =S △KFN +S △KNE = 12 KN (t+ 3)+ 12 KN (1-t )= 2KN= -t 2-3t+ 5 =-(t+ 32)2+ 294. 即当t=- 32 时,△EFK 的面积最大,最大面积为 294 ,此时K (- 32 , 358).5.【答案】(1)解:将点A (3,0),B (4,1)代入可得: {9a +3b +3=014a +4b +3=1 ,解得: {a =12b =−52, 故函数解析式为 y =12x 2−52x +3 ;(2)解:∵抛物线与x 轴的交点的纵坐标为0, ∴12x 2−52x +3=0 ,解得:x 1=3,x 2=2,∴点D 的坐标为(2,0),取点E (1,0),作EP△AB 交抛物线于点P ,∵ED=AD=1,∴此时△PAB的面积是△DAB的面积的两倍,∵直线AB解析式为y=x﹣3,∴直线EP为y=x﹣1,由{y=x−1y=12x2−52x+3解得{x=7−√172y=5−√172或{x=7+√172y=5+√172,∴点P坐标(7−√172,5−√172)或(7+√172,5+√172).(3)解:如图2中,作BD△OA于D.∵A(3,0),C(0,3),B(4,1),∴OA=OC=3,AD=BD=1,∴△OAC=△BAD=45°,∵△OAF=△BAD=45°,∴△EAF=90°,∴EF是△AEO的外接圆的直径,∴△EOF=90°,∴△EFO=△EAO=45°,∴△EOF是等腰直角三角形,∴当OE最小时,△EOF的面积最小,∵OE△AC 时,OE 最小,OC =OA ,∴CE =AE ,OE = 12 AC = 3√22,∴E ( 32 , 32 ),S △EOF = 12×3√22×3√22=94.∴当△OEF 的面积取得最小值时,面积的最小值为 94 ,E 点坐标( 32 , 32).6.【答案】(1)解:∵直线 y =−12x +2 与x 轴交于点A ,与y 轴交于点B ,令x=0,则y=2,令y=0,则x=4, ∴A (4,0),B (0,2),∵抛物线 y =−23x 2+bx +c 经过B (0,2), C(52,34) ,∴{2=c34=−23×254+52b +c ,解得: {b =76c =2 ,∴抛物线的表达式为: y =−23x 2+76x +2 ;(2)解:当点P 在x 轴上方时,点P 与点C 重合,满足 ∠PAO =∠BAO ,∵C(52,34) ,∴P(52,34) ,当点P 在x 轴下方时,如图,AP 与y 轴交于点Q ,∵∠PAO =∠BAO , ∴B ,Q 关于x 轴对称, ∴Q (0,-2),又A (4,0),设直线AQ 的表达式为y=px+q ,代入,{−2=q 0=4p +q ,解得: {p =12q =−2, ∴直线AQ 的表达式为: y =12x −2 ,联立得:{y =12x −2y =−23x 2+76x +2,解得:x=3或-2,∴点P的坐标为(3,−12)或(-2,-3),综上,当∠PAO=∠BAO时,点P的坐标为:(52,34)或(3,−12)或(-2,-3);(3)解:①如图,△MNC=90°,过点C作CD△x轴于点D,∴△MNO+△CND=90°,∵△OMN+△MNO=90°,∴△CND=△OMN,又△MON=△CDN=90°,∴△MNO△△NCD,∴MOND=NOCD,即m52−n=n34,整理得:m=−43n2+103n;②如图,∵△MNC=90°,以MC为直径画圆E,∵N(n,0) (0<n<5 2),∴点N在线段OD上(不含O和D),即圆E与线段OD有两个交点(不含O和D),∵点M在y轴正半轴,当圆E与线段OD相切时,有NE= 12MC,即NE2= 14MC2,∵M(0,m),C(52,34),∴E(54,38+m2),∴(38+m2)2= 14[(52)2+(m−34)2],解得:m= 25 12,当点M与点O重合时,如图,此时圆E与线段OD(不含O和D)有一个交点,∴当0<m<2512时,圆E与线段OD有两个交点,故m的取值范围是:0<m<25 12.7.【答案】(1)解:将点A(3,0),B(4,1)代入可得:{9a+3b+3=014a+4b+3=1,解得:{a=12b=−52,故函数解析式为y= 12x2﹣52x+3(2)解:如图1中,连接DC、AC,AC交对称轴于H,连接DH,此时△CDH的周长最小.∵A、D关于对称轴对称,HD=HA,x∴DH+CH=AC= √32+42=5,CD= √22+32= √13,∴△CDH的周长的最小值为5+ √13,∵A(3,0),C(3,0),∴直线AC的解析式为y=﹣x+3,∴H(52,12)(3)解:如图2中,作BD△OA于D.∵A(3,0),C(0,3),B(4,1),∴OA=OC=3,AD=BD=1,∴△OAC=△BAD=45°,∵△OAF=△BAD=45°,∴△EAF=90°,∴EF是△AEO的外接圆的直径,∴△EOF=90°,∴△EFO=△EAO=45°,∴△EOF是等腰直角三角形,∴当OE最小时,△EOF的面积最小,∵OE△AC时,OE最小,OC=OA,∴CE=AE,OE= 12AC=3√22,∴E(32,32),S△EOF=12•3√22• 3√22= 94.∴当△OEF的面积取得最小值时,面积的最小值为94,E点坐标(32,32)8.【答案】(1)解:(1)∵二次函数y=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0), ∴{9a −3b +3=0a +b +3=0 解得{a =−1b =−2∴二次函数的表达式为y=﹣x 2﹣2x+3. (2)解:如图1,,∵二次函数的表达式为y=﹣x 2﹣2x+3, ∴点C 的坐标为(0,3), ∵y=﹣x 2﹣2x+3=﹣(x+1)2+4, ∴点G 的坐标是(﹣1,4), ∵点C 的坐标为(0,3),∴设CG 所在的直线的解析式是y=mx+3, 则﹣m+3=4, ∴m=﹣1,∴CG 所在的直线的解析式是y=﹣x+3, ∴点H 的坐标是(3,0), 设点D 的坐标是(0,p ),则p−00−(−3)=3−00−3=−1,∴p=﹣3,∵AO=CO=DO=HO=3,AH△CD , ∴四边形ACHD 是正方形.(3)解:①如图2,作ME△x 轴于点E ,作MF△y 轴于点F ,,∵四边形ADCM 的面积为S ,∴S=S 四边形AOCM +S △AOD ,∵AO=OD=3,∴S △AOD =3×3÷2=4.5,∵点M (t ,p )是y=kx 与y=﹣x 2﹣2x+3在第二象限内的交点,∴点M 的坐标是(t ,﹣t 2﹣2t+3),∵ME=﹣t 2﹣2t+3,MF=﹣t ,∴S 四边形AOCM =12×3×(﹣t 2﹣2t+3)12×3×(-t)=﹣32t 2﹣92t+92,∴S=﹣32t 2﹣92t+92+4.5=﹣32t 2﹣92t+9,﹣3<t <0.②如图3,作NI△x 轴于点I ,,设点N 的坐标是(t 1,p 1),则NI=|t 1|,∴S △CMN =S △COM +S △CON =32(|t|+|t 1|),∵t <0,t 1>0,∴S △CMN =32(|t|+|t 1|)=32(t 1-t)=214,∴t 1-t=72,联立{y =kxy =−x 2−2x +3可得x 2﹣(k+2)x ﹣3=0,∵t 1、t 是方程的两个根,∴{t 1+t =k +2t 1t =−3∴t (t 1−t)2=(t 1+t)2﹣4t 1t=(k+2)2﹣4×(﹣3)=(72)2=494,解得k 1=−32,k 2=−52,a 、k=﹣32时,由x 2+(2﹣32)x ﹣3=0,解得x 1=﹣2,或(舍去).b 、k=﹣52时,由x 2+(2﹣52)x ﹣3=0,解得x 3=﹣32,或x 4=2(舍去),∴t=﹣2,或t=﹣32,t=﹣2时,S=﹣32t 2﹣92t+9=﹣32×4﹣92×(﹣2)+9=12t=﹣32时,S=﹣32×94﹣92×(-32)+9=998,∴S 的值是12或998.9.【答案】(1)解:当 y =0 时, 14x 2−32x −4=0 ,解得 x 1=−2 , x 2=8 ,∵ 点 B 在点 A 的右侧,∴ 点 A 的坐标为 (−2,0) ,点 B 的坐标为 (8,0) . 当 x =0 时, y =−4 , ∴ 点 C 的坐标为 (0,−4) .(2)解:由菱形的对称性可知,点 D 的坐标为 (0,4) . 设直线 BD 的解析式为 y =k x +b ,则 {b =48k +b =0,解得 k =−12, b =4 .∴ 直线 BD 的解析式为 y =−12x +4 .∵l ⊥x 轴,∴ 点 M 的坐标为 (m,−12m +4) ,点 Q 的坐标为 (m,14m 2−32m −4) .如图,当 MQ =DC 时,四边形 CQMD 是平行四边形,∴(−12m +4)−(14m 2−32m −4)=4−(−4) .化简得: m 2−4m =0 ,解得 m 1=0 (不合题意舍去), m 2=4 . ∴ 当 m =4 时,四边形 CQMD 是平行四边形.(3)解:抛物线上存在两个这样的点Q ,分别是Q 1(-2,0),Q 2(6,-4). 若△BDQ 为直角三角形,可能有三种情形,如答图所示:①以点Q 为直角顶点.此时以BD 为直径作圆,圆与抛物线的交点,即为所求之Q 点. ∵P 在线段EB 上运动,∴-8≤x Q ≤8,而由图形可见,在此范围内,圆与抛物线并无交点,故此种情形不存在. ②以点D 为直角顶点.连接AD ,∵OA=2,OD=4,OB=8,AB=10, 由勾股定理得:AD=2 √5 ,BD=4 √5 , ∵AD 2+BD 2=AB 2,∴△ABD 为直角三角形,即点A 为所求的点Q . ∴Q 1(-2,0); ③以点B 为直角顶点.如图,设Q 2点坐标为(x ,y ),过点Q 2作Q 2K△x 轴于点K ,则Q 2K=-y OK=x ,BK=8-x . 易证△Q 2KB△△BOD ,∴Q 2K OB =BK OD,即−y 8=8−x4 ,整理得:y=2x-16. ∵点Q 在抛物线上,∴y= 14x 2−32x −4∴14x 2−32x −4 =2x-16,解得x=6或x=8, 当x=8时,点Q 2与点B 重合,故舍去; 当x=6时,y=-4, ∴Q 2(6,-4).综上所述,正确的点Q 的坐标为(-2,0)或(6,-4).10.【答案】(1)1;(4,0)(2)y=-(x-2)2+4(3)0<x <2(填0≤x≤2也可以)或x >4(4)解:①令y =(x −ℎ)2−4=0,解得:x 1=ℎ−2,x 2=ℎ+2. 故点A ,B 的坐标为:A(ℎ−2,0),B(ℎ+2,0). ②当1<x <2时,新图象的函数值y 随x 增大而增大, 则:{ℎ−2≤1ℎ≥2 或ℎ+2≤1.解得:2≤ℎ≤3或ℎ≤−1.11.【答案】(1)解:由题意A ( √3 ,0),B (﹣3 √3 ,0),C (0,﹣3),设抛物线的解析式为y =a (x+3 √3 )(x −√3 ),把C (0,﹣3)代入得到a =13,∴抛物线的解析式为y =13 x 2+23√3 x ﹣3(2)解:在Rt△AOC 中,tan△OAC =OCOA =√3 ,∴△OAC =60°.∵AD 平分△OAC ,∴△OAD =30°,∴OD =OA•tan30°=1,∴D (0,﹣1),∴直线AD 的解析式为y =√33 x ﹣1,由题意P (m , 13 m 2+2√33m ﹣3),H (m , √33 m ﹣1),F (m ,0).∵FH =PH ,∴1 −√33m =√33 m ﹣1﹣( 13 m 2+2√33m ﹣3)解得m =−√3 或 √3 (舍弃),∴当FH =HP 时,m 的值为 −√3 (3)解:如图,∵PF 是对称轴,∴F ( −√3 ,0),H ( −√3 ,﹣2). ∵AH△AE ,∴△EAO =60°,∴EO =√3 OA =3,∴E (0,3).∵C (0,﹣3),∴HC =√(√3)2+12= 2,AH =2FH =4,∴QH =12 CH =1,在HA上取一点K ,使得HK =14 ,此时K ( −78√3,−158).∵HQ 2=1,HK•HA =1,∴HQ 2=HK•HA ,∴HQ AH =KHHQ .∵△QHK =△AHQ ,∴△QHK△△AHQ ,∴KQ AQ =HQ AH =14 ,∴KQ =14AQ ,∴14 AQ+QE =KQ+EQ ,∴当E 、Q 、K 共线时, 14AQ+QE 的值最小,最小值 =(7√38)2+(158+3)2=√4174.12.【答案】(1)解:由题意抛物线的顶点 D(0,4),A(−2,0) ,设抛物线的解析式为 y =ax 2+4 ,把 A(−2,0) 代入可得 a =−1 ,∴抛物线C 的函数表达式为 y =−x 2+4 .(2)解:由题意抛物线 C ′ 的顶点坐标为 (2m,−4) ,设抛物线 C ′ 的解析式为 y =(x −2m)2−4 ,由 {y =−x 2+4y =(x −2m)2−4 ,消去y 得到 x 2−2mx +2m 2−4=0 , 由题意,抛物线 C ′ 与抛物线C 在y 轴的右侧有两个不同的公共点, 则有 {(2m)2−4(2m 2−4)>02m >02m 2−4>0 ,解得 √2<m <2 , ∴满足条件的m 的取值范围为 √2<m <2 . (3)解:结论:四边形 PMP ′N 能成为正方形.理由:1情形1,当 0<m <√17−12时,如图,作 PE ⊥x 轴于 E, MH ⊥x 轴于H .由题意P 点在二次函数上,且横纵坐标相等, x =−x 2+4 ,解得 x =√17−12(舍去负值),∴P(√17−12,√17−12) ,当 △PFM 是等腰直角三角形时,四边形 PMP ′N 是正方形, ∴PF =FM, ∠PFM =90° ,可证 △PFE ≌△FMH ,可得 PE =FH =√17−12, EF =HM =√17−12−m ,∴M(m +√17−12,m −√17−12) ,∵点M 在 y =−x 2+4 上, ∴m −√17−12=−(m +√17−12)2+4 ,解得 m =−√17+√13+4√172或 −√17−√13+4√172(舍弃),∴m =−√17+√13+4√172时,四边形 PMP ′N 是正方形,情形2,如图,当 m >√17−12 时,四边形 PMP ′N 是正方形,同法可得 M(m −√17−12,√17−12−m) ,把 M(m −√17−12,√17−12−m) 代入 y =−x 2+4 中,√17−12−m =−12(m −√17−12)2+4 ,解得 m =√17 或0(舍弃), ∴m =√17 时,四边形 PMP ′N 是正方形. 综上,四边形 PMP ′N 能成为正方形,m =−√17+√13+4√172或 √17 .13.【答案】(1)∵ 点 B(2,0) ,点 C(0,2) 在抛物线 y =x 2+bx +c 图象上,∴{−4+2b +c =0c =2 ,解得 {b =1c =2 ,∴ 抛物线解析式为: y =−x 2+x +2 . (2)设直线BC 的解析式为y=kx+n , ∵ 点 B(2,0) ,点 C(0,2) , ∴{2k +n =0n =2 ,解得 {k =−1n =2 ,∴ 直线 BC 解析式为: y =−x +2 ,如图,过点 P 作 PH ⊥x 轴于 H ,交 BC 于点 G ,设点 P(m,−m 2+m +2) ,则点 G(m,−m +2) ,∴PG =(−m 2+m +2)−(−m +2)=−m 2+2m ,∵S △PBC =12×PG ×OB =12×2×(−m 2+2m)=−(m −1)2+1 ,∴ 当 m =1 时, S △PBC 有最大值, ∴ 点 P(1,2) .(3)存在 N 满足条件,理由如下:∵ 抛物线 y =−x 2+x +2 与 x 轴交于 A , B 两点, ∴ 点 A(−1,0) ,∵点 M 为 (1,3) ,点 C(0,2) ,设直线MC 解析式为y=ax+z , ∴{a +z =3z =2 ,解得 {a =1z =2,∴ 直线 MC 的解析式为: y =x +2 ,如图,设直线 MC 与 x 轴交于点 E ,过点 N 作 NQ ⊥MC 于 Q ,连接AN ,∴ 点 E(−2,0) , ∴DE =3=MD ,∴∠NMQ =45° . NQ =√22MN ,设点 N(1,n) , ∴NQ 2=AN 2 ,∴(√22MN)2=AN 2 , ∴(√22|3−n|)2=4+n 2 ,∴n2+6n−1=0,∴n=−3±√10,∴存在点N满足要求,点N坐标为(1,−3+√10)或(1,−3−√10).. 14.【答案】(1)解:把B(2√3,0),C(0,2)两点代入抛物线解析式得:{−4+2√3b+c=0c=2,解得:b=√33,c=2,则抛物线解析式为y=−13x 2+√33x+2;(2)解:①如图1所示,点F在抛物线上,作DG△y轴,FH△y轴,易得△CDG△△EFH,即CG=HE,GD=FH,由题意得:CD=EF=√3t,∵△CGD△△COB,∴CG2=√3t4=2√3,即CG=HE=√32t,DG=FH=32t,∵CE=2CD=2√3t,∴OH=3√32t−2,即F(−32t,−2+3√32t),代入抛物线解析式得:−2+3√32t=−13×94t2+√33×(−32)+2,解得:t= 4√33;②分三种情况考虑:(i)如图2所示,△ABC与矩形CDEF重叠部分为矩形CDEF,在Rt△CDE中,CD=√3t,∠ECD=60°,∴DE=3t,∴S=3t⋅√3t=3√3t2(0<t≤√3 3).(ii)如图3所示,△ABC与矩形CDEF重叠部分为五边形CDHGF,由题意得:CD=√3t,在Rt△CED中,△ECD=60°,∴CE=2√3t,∴OE=2√3t−2,在Rt△OGE中,GE=2OE=4√3t−4,同理可得EH=4t−4√33,即S△GEH=12GE⋅EH=(2√3t−2)(4t−4√33),则S=√3t⋅3t−(2√3t−2)(4t−4√33)=−5√3t 2+16t−8√33(√33<t≤4√39);(iii)如图4,△ABC与矩形CDEF重叠部分为四边形CDMN,由题意得:CN=2√32=4√33,CD=√3t,BD=4−√3t,在Rt△BMD 中, DM =√3t√3,则 S =S △BCN −S △BDM ,=12CN ⋅BC −12BD ⋅DM ,=12×4√33×4−12×(4−√3t)√3t √3,=−√32t2+4t(4√39<t ≤4√33).15.【答案】(1)∵y=- 12x 2+bx+c把A (4,5)B (0,1)代入{−12×16+4b +c =5c =1{b =3c =1∴y= −12x 2+3x +1(2)过点P 作PM△x 轴交AB 于F ,如图∵PE//AC ∴S △PEC =S △APE直线 AB 交于点 A(4,5) , B(0,1) . S 四边形BPCE =S △PBE +S △PEC =S △PBE +S △APE =S △APB 设AB 的解析式为y=kx+b∵直线 AB 经过点 A(4,5) , B(0,1) . ∴{4k +b =5b =1解得{k =1b =1∴y=x+1设点P (x ,- 12x 2+3x +1 ) 则点F(x ,x+1)∴PF=(- 12x 2+3x +1)−(x +1)=−12x 2+2x △ABP 的面积S = 12 PF×BK= 12×4PF=- x 2 +4x 当x=- b 2a=2 时,S △ABP 最大值=-22+4×2=4 ∴四边形CPBE 面积的最大值为4(3)如图,该抛物线沿射线 AB 方向平移 2√2 个单位,即沿x 轴负方向平移2个单位,沿y 轴负方向平移2个单位.∴平移后抛物线解析式为:y=- 12(x +2)2+3(x +2)+1−2 =- 12x 2+x+3 { y =−12x 2+x +3y =−12x 2+3x +1 {x =1y =72∴G(1, 72) ∴BG= √(1−0)2+(72−1)2=√292=B′G′ 分两种情况讨论,第一种情况当OB '=B 'G '= √292设点B`的坐标为(x,x+1)√x 2+(x +1)2=√292解得x= −12−3√64 ,或- 12 + 3√64 第二种情况当OG '=B 'G '∴K GG`=K AB =1∴y- 72 =x-1 ∴GG`的解析式为y=x+ 52设点B`的坐标为(x,x+1),则点G`的坐标为(x+1, x+ 72) ∵OG '=B 'G '∴√(x +1)2+(x +72)2=√292解得x= −94−√334 或 −94+√334综上:B`的横坐标为 −12−3√64 ,- 12 + 3√64 , −94−√334 ,或 −94+√334. 16.【答案】(1)解:由题意得: {4a +85×2+c =0c =−4 ,解得: {a =15c =−4, ∴抛物线的表达式为y= 15 x 2+ 85x ﹣4. (2)解:设P (m , 15 m 2+ 85 m ﹣4),则F (m ,﹣ 12m ﹣4). ∴PF=(﹣ 12 m ﹣4)﹣( 15 m 2+ 85 m ﹣4)=﹣ 15 m 2﹣ 2110m. ∵PE△x 轴,∴PF△OC.∴PF=OC 时,四边形PCOF 是平行四边形.∴﹣ 15 m 2﹣ 2110 m=4,解得:m=﹣ 52或m=﹣8. 当m=﹣ 52时, 15 m 2+ 85 m ﹣4=﹣ 274 , 当m=﹣8时, 15 m 2+ 85m ﹣4=﹣4. ∴点P 的坐标为(﹣ 52,﹣ 274 )或(﹣8,﹣4). (3)①证明:把y=0代入y=﹣ 12 x ﹣4得:﹣ 12x ﹣4=0,解得:x=﹣8. ∴D (﹣8,0).∴OD=8.∵A (2,0),C (0,﹣4),∴AD=2﹣(﹣8)=10.由两点间的距离公式可知:AC2=22+42=20,DC2=82+42=80,AD2=100,∴AC2+CD2=AD2.∴△ACD是直角三角形,且△ACD=90°.②解:由①得△ACD=90°.当△ACD△△CHP时,ACCD=CHHP,即2√54√5=|−15n2−85n||−n|,解得:n=0(舍去)或n=﹣5.5或n=﹣10.5.当△ACD△△PHC时,ACCD=PHCH,即2√54√5=|n||−15n2−85n|,解得:n=0(舍去)或n=2或n=﹣18.综上所述,点P的横坐标为﹣5.5或﹣10.5或2或﹣18时,使得以点P、C、H为顶点的三角形与△ACD相似。
2024年九年级中考数学一轮复习大纲课件

指数与对数的运算
学习指数与对数的定 义及其运算规则,掌 握它们在代数式中的
应用。
函数与关系的建立
了解函数与关系的概 念,学会建立函数关 系式并进行相关运算。
代数式的综合应用
综合运用所学知识, 解决复杂的代数式问 题,提高解决问题的
能力。
一元一次方程与不等式
反比例函数
反比例函数的图像与性质
反比例函数基础
详解反比例函数的定义、性质和图像特征
反比例函数应用
阐述反比例函数在实际问题中的应用和解题技巧
反比例函数综合
探讨反比例函数的综合问题和解题策略
函数图像的识别与应用
函数图像的特点和应用场景
函数图像的基本性质
图像变换、对称性、单调性、最值问题
函数图像的识别
• 学习如何用区间表示一元一次方程和 一元一次不等式的解集。
二元一次方程与不等式
二元一次方程和不等式的解法与应用
二元一次方程基本概念
01
介绍二元一次方程的定义、组成及解法
解二元一次方程组
02
解析二元一次方程组的解法及应用
不等式基本概念
03
阐述不等式的定义、性质及解集表示
解二元一次不等式组
04
讲解二元一次不等式组的解法及应用
中考数学一轮复习
全面提高数学素养,备战中考
目录 1.实数与函数 2.几何 3.代数 4.统计与概率 5.综合应用题 6.数学思想与方法
实数与函数
实数与函数的基础知识和应用
实数概念及运算
实数的定义、分类和运算规则
实数的分类与表 示
实数分为有理数和无理数, 有理数可以表示为分数或 整数,无理数不能表示为
2023年中考数学高频考点训练——动点问题的函数图象
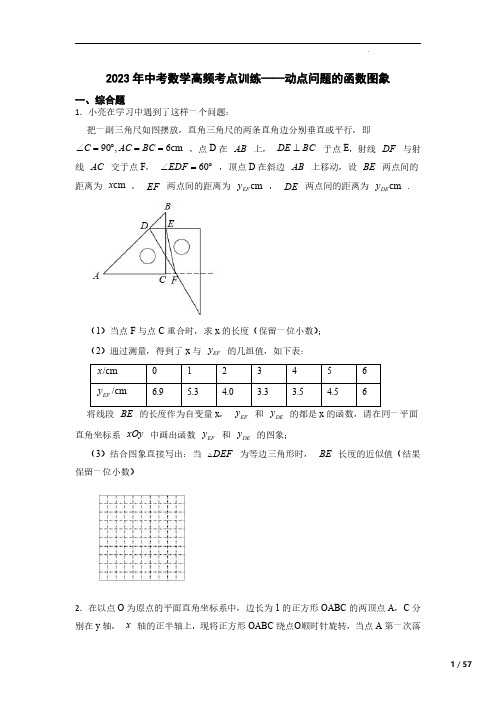
2023年中考数学高频考点训练——动点问题的函数图象一、综合题1.小亮在学习中遇到了这样一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,即90,6cm C AC BC ∠=︒==,点D 在AB 上,DE BC ⊥于点E ,射线DF 与射线AC 交于点F ,60EDF ∠=︒,顶点D 在斜边AB 上移动,设BE 两点间的距离为cm x ,EF 两点间的距离为cm EF y ,DE 两点间的距离为cm DE y .(1)当点F 与点C 重合时,求x 的长度(保留一位小数);(2)通过测量,得到了x 与EF y 的几组值,如下表:将线段BE 的长度作为自变量x ,EF DE 直角坐标系xOy 中画出函数EF y 和DE y 的图象;(3)结合图象直接写出:当DEF 为等边三角形时,BE 长度的近似值(结果保留一位小数)2.在以点O 为原点的平面直角坐标系中,边长为1的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,现将正方形OABC 绕点О顺时针旋转,当点A 第一次落在直线y x =上时,停止转动,旋转过程中,AB 边交直线y x =于点M ,BC 边交轴于点N.(1)旋转停止时正方形旋转的度数是.(2)在旋转过程中,当MN 和AC 平行时,①OAM 与OCN 是否全等?此时正方形OABC 旋转的度数是多少?②直接写出MBN 的周长的值,并判断这个值在正方形OABC 的旋转过程中是否发生变化.3.如图,点C 是以点O 为圆心,AB 为直径的半圆上的动点(不与点A ,B 重合),AB =6cm ,过点C 作CD ⊥AB 于点D ,E 是CD 的中点,连接AE 并延长交 AB 于点F ,连接FD .小腾根据学习函数的经验,对线段AC ,CD ,FD 的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:(1)对于点C 在 AB 上的不同位置,画图、测量,得到了线段AC ,CD ,FD 的长度的几组值,如表:位置1位置2位置3位置4位置5位置6位置7位置8AC /cm 0.10.5 1.0 1.9 2.6 3.2 4.2 4.9CD /cm 0.10.5 1.0 1.8 2.2 2.5 2.3 1.0FD /cm 0.2 1.0 1.8 2.8 3.0 2.7 1.80.5在AC ,CD ,FD 的长度这三个量中,确定的长度是自变量,的长度和的长度都是这个自变量的函数;(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;(3)结合函数图象,解答问题:当CD>DF时,AC的长度的取值范围是.4.如图,在△ABC中,∠C=90°,BC=6cm,AC=8cm,点D是AB的中点,以D 为顶点作∠MDN=∠A,∠MDN的两边分别与线段AC交于点M.N(点M在点N左边).设A,M两点间的距离为xcm,C、N两点间的距离为ycm.小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.(1)列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:x/cm00.6 1.2 1.8 2.3 2.9 3.4 3.5 4.0 4.3 4.5 4.7 4.8 y/cm a 4.6 4.3 3.9 3.6 3.1 2.6 2.4b 1.20.90.40.2请你补全表格:a=;b=.(2)描点、连线:在平面直角坐标系xOy中,描出表中各组数值所对应的点(x,y),并画出函数y关于x的图象:(3)探究性质:随着自变量x的不断增大,函数y的变化趋势:.(4)解决问题:当AM=CN时,A、M两点间的距离大约是cm.(保留一位小数)中,D为AB的中点,P是BC边上一动点,连接5.如图1,在Rt ABC,,设PC x=(当点P与点C重合时,x的值为0),==BC AC,.若43PD PA+=.PA PD y小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.(1)通过取点、画图、计算,得到了x与y的几组值,如下表:(参考数据: 1.414 3.162 3.606≈≈).(2)如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.(3)观察图象,下列结论正确的有_.①函数有最小值,没有最大值②函数有最小值,也有最大值③当43x >时,y 随着x 的增大而增大④当 1.5x <时,y 随着x 的增大而减小6.如图如图1,在矩形ABCD 中,3cm AB =,4cm BC =,圆弧 AE 过点A 和AD 延长线上的点E ,圆心R 在CD 上, AE 上有一个动点P ,PQ AC ⊥,交直线AC 于点Q .线段AP 的长cm x 与PQ 的长cm PQ y 以及RQ 的长cm RQ y 之间的几组对应值如下表所示.(1)将线段AP 的长度作为自变量,在平面直角坐标系中画出了函数PQ y 的图象,如图2所示.请在同一坐标系中画出函数RQ y 的图象.(2)结合函数图象填空:(结果精确到0.1)线段PQ 的长度的最大值约为;线段RQ 的长度的最小值约为;圆弧 AE 所在圆的半径约等于;连结PC ,PAC 面积的最大值约为.(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当以点P 、Q 、R 为顶点构成的三角形为等腰三角形时,线段AP 的长度的近似值.(结果精确到0.1)7.动点P 在□ABCD 边上沿着A→B→C→D 的方向匀速移动,到达点D 时停止移动.已知P 的速度为1个单位长度/s ,其所在位置用点P 表示,P 到对角线BD 的距离(即垂线段PQ 的长)为d 个单位长度,其中d 与t 的函数图象如图2所示.(1)若a =3,求当t =8时△BPQ 的面积;(2)如图3,点M ,N 分别在函数第一和第三段图象上,线段MN 平行于横轴,M 、N 的横坐标分别为t 1、t 2,设t 1、t 2时点P 走过的路程分别为12l l 、,若12l l +=16,求t 1、t 2的值.8.如图1,已知四边形OABC 的顶点O 在坐标原点,点A 在y 轴上,点C 在x 轴上,AB x 轴,动点P 从点O 出发,以每秒1单位的速度,沿O A B C O →→→→运动一周,顺次连结P ,O ,C 三点所围成图形的面积为S ,点P 的运动时间为t 秒,S 与t 之间的函数关系如图2中折线ODEFG 所示已知4AB =,点D ,点F 横坐标分别为8和22.(1)求a 和b 的值.(2)求直线EF 的函数解析式.(3)当P 在BC 上时,用t 表示P 点的纵坐标.9.“低碳环保、绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车沿同一路线去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m 米/分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程(y 米)与时间(x 分钟)的关系如图.请结合图象,解答下列问题:(1)a=;b=.(2)求出m 的取值是多少?(3)若小军的速度是120米/分,求小军在图中与爸爸第二次相遇时的时间.10.如图1,在菱形ABCD 中,1cm AB =,连结AC BD ,.设DAB x ∠=()0180x y AC BD <<=- ,,小宁根据学习函数的经验,对变量y 与x 之间的关系进行了如下探究.(1)【探究】列表:通过观察补全下表(精确到0.01)./x153045607590105120135150165/cm y 1.72 1.080.3700.73 1.08 1.41 1.72描点、连线:在图2中描出表中各组数值所对应的点() x y ,,并画出y 关于x的函数图象.(2)【发现】结合画出的函数图象,写出该函数的两条性质:①;②.(3)【应用】有一种“千斤顶”,它是由4根长为30cm 的连杆组成的菱形ABCD ,当手柄顺时针旋转时,B D 、两点的距离变小(如图3).在这个过程中,当33cm AC BD -=时,BAD ∠的度数约为.(精确到1°).11.快、慢两车分别从相距360km 的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h 后出发,到达佳市后停止行驶;快车到达哈市后,立即按原路原速返回佳市(快车掉头的时间忽略不计).快、慢两车距哈市的路程1y (单位:km ),2y (单位:km )与快车出发时间x (单位:h )之间的函数图象如图所示,请结合图象信息解答下列问题:(1)直接写出慢车的行驶速度和a 的值;(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?(3)快车出发多少小时两车相距100km ?请直接写出答案.12.如图,在Rt △ABC 中,∠B =90°,点P 从点A 出发,以12cm/s 的速度沿AB 向终点B 运动;2s 后,又有一动点Q 从点B 出发,沿B→C→A 方向以3cm/s 的速度向终点A 运动.第二幅图是△PQC 的面积S (cm 2)关于点P 的运动时间t (s )的函数图象,请结合图中提供的信息解决下面的问题;(1)线段AB =cm ,a=,m=;(2)求当t 为何值时,PQ ∥AC ;(3)求图中EF 段函数解析式.13.如图,在ABC 中,60C ∠=︒,3BC =厘米,4AC =厘米,点P 从点B 出发,沿B C A →→以每秒1厘米的速度匀速运动到点A .设点P 的运动时间为x 秒,B 、P 两点间的距离为y 厘米.小新根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究.下面是小新的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x与y的几组值,如下表:x(s)01234567y(cm)0 1.0 2.0 3.0 2.7 2.7m 3.6m的值是.(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;中画出(3ABC点P所在的位置,此时P运动的时间为▲秒14.已知图形ABCDEF的相邻两边垂直,AB=8cm.当动点M以2cm/s的速度沿图①的边框按B→C→D→E→F→A的路径运动时,△ABM的面积S随时间t的变化如图②所示.回答下列问题:(1)求a的值和EF的长度;(2)当点M运动到DE上时,求S与t的关系式.15.已知动点P以每秒2㎝的速度沿图甲的边框按从的路径移动,相应的△ABP 的面积S 与时间t 之间的关系如图乙中的图象表示.若AB=6cm,试回答下列问题:(1)图甲中的BC 长是多少?(2)图乙中的a 是多少?(3)图甲中的图形的面积是多少?(4)图乙中的b 是多少?16.对于平面直角坐标系xOy 中的任意点()P x y ,,如果满足x y a +=(x ≥0,a 为常数),那么我们称这样的点叫做“特征点”.(1)当2≤a ≤3时,①在点(1,2),(1,3),(2.5,0)A B C 中,满足此条件的特征点为;②⊙W 的圆心为(,0)W m ,半径为1,如果⊙W 上始终存在满足条件的特征点,请画出示意图,并直接写出m 的取值范围;(2)已知函数()10Z x x x =+>,请利用特征点求出该函数的最小值.17.如图,在正方形ABCD 中,1AB =,延长BC 至M ,使5BM =.以BD BM ,为邻边作DBMN .动点P 从点D 出发,以每秒1个单位的速度沿DN 向终点N 运动,过点P 作PQ ⊥BM 交BM 或BM 的延长线于点Q ,以PQ 为边向右作正方形PQRS .设正方形PQRS .设正方形PQRS 与DBMN 的重叠部分的面积为y ,点P 运动的时间为x (0x >.单位:秒).(1)用含x 的代数式表示线段PN 为;(2)当点S 与点N 重合时,求x 的值;(3)当正方形PQRS 与DBMN 的重叠部分不是正方形时,求y 与x 之间的函数关系式;(4)当DQS 或PRN 是直角三角形时,直接写出x 的值.18.如图,已知在平面直角坐标系中,矩形ABCD 的边AB//x 轴,AD//y 轴,点A 的坐标为(2,1),AB=4,AD=3.(1)求直线BD 的解析式.(2)已知双曲线(0)ky k x =>与折线ABC 的交点为E ,与折线ADC 的交点为F .①连接CE ,当S △BCE =3时,求该双曲线的解析式,并求出此时点F 的坐标;②若双曲线(0)ky k x =>与矩形ABCD 各边和对角线BD 的交点个数为3,请直接写出k 的取值范围.19.如图①,在矩形ABCD 中,AB <AD ,对角线AC ,BD 相交于点O,动点P 由点A 出发,沿AB→BC→CD 向点D 运动,设点P 的运动路程为x ,△AOP 的面积为y ,y与x的函数关系图象如图②所示:(1)AD边的长为.(2)如图③,动点P到达点D后从D点出发,沿着DB方向以1个单位长度/秒的速度匀速运动,以点P为圆心,PD长为半径的⊙P与DB、DC的另一个交点分别为M、N,与此同时,点Q从点C出发,沿着CD方向也以1个单位长度/秒的速度匀速运动,以点Q为圆心、2为半径作⊙Q.设运动时间为t秒(0<t≤5).①当t为何值时,点Q与点N重合?②当⊙P与BC相切时,求点Q到BD的距离.20.已知:在矩形ABCD中,E为边BC上的一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF.如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上.如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ.当点N到达终点B时,△GMNP和点同时停止运动.设运动时间为t秒,解答问题:(1)在整个运动过程中,当点G在线段AE上时,求t的值;(2)在整个运动过程中,是否存在点P ,使△APQ 是等腰三角形,若存在,求出t 的值;若不存在,说明理由;(3)在整个运动过程中,设△GMN 与△AEF 重叠部分的面积为S ,请直接写出S 与t 的函数关系式以及自变量t 的取值范围.21.如图,直角三角形ABC ∆中,90 4 60ACB AC A ∠︒=∠︒=,,=,O 为BC 中点,将ABC ∆绕O 点旋转180︒得到DCB ∆.一动点P 从A 出发,以每秒1的速度沿A B D →→的路线匀速运动,过点P 作直线PM ,使PM AC ⊥.(1)当点P 运动2秒时,另-动点Q 也从A 出发沿A-→B→D 的路线运动,且在AB 上以每秒1的速度匀速运动,在BD.上以每秒2的速度匀速运动,过Q 作直线QN 使//QN PM ,设点Q 的运动时间为t 秒,(0<t<10)直线PM 与QN 截四边形ABDC 所得图形的面积为S ,求S 关于t 的函数关系式,并求出S 的最大值(2)当点P 开始运动的同时,另一动点R 从B 处出发沿B C D →→的路线运动,且在BC 上以每秒32的速度匀速运动,在CD 上以每秒2的速度匀度运动,是否存在这样的P,R ,使BPR ∆为等腰三角形?若存在,直接写出点P 运动的时间m 的值,若不存在请说明理由.22.如图,直线l :243y x =-+分别与x 轴,y 轴交于A ,B 两点,在OB 上取一点()01C ,,以线段BC 为边向右作正方形BCDE ,正方形BCDE 沿CD 的方向以每秒1个单位长度的速度向右作匀速运动,设运动时间为t 秒()0t >.(1)求A,B两点的坐标;(2)在正方形BCDE向右运动的过程中,若正方形BCDE的顶点落在直线l 上,求t的值;(3)设正方形BCDE两条对角线交于点P,在正方形向右运动的过程中,是否存在实数t,使得OP PA+有最小值?若存在,求出t的值:若不存在,请说明理由.23.如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.(1)写出数轴上点A、C表示的数;(2)点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN=23CQ.设运动的时间为t(t>0)秒.①求数轴上点M、N表示的数(用含t的式子表示);②t为何值时,M、N两点到原点的距离相等?24.一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:(注:圆周率π的值取3)(1)请直接写出:花坛的半径是米,a=.(2)当2t<时,求s与t之间的关系式;(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:①蚂蚁停下来吃食物的地方,离出发点的距离.②蚂蚁返回O所用时间.答案解析部分1.【答案】(1)解:在Rt DEB 中,DE BE x ==,在Rt DEF 中,6EF BF BE x =-=-,60EDF ∠=︒tan EFEDF DE∠=∴6xx -=,解得 2.2x ≈将 2.2x ≈代入分式方程左边中得6 2.23.8=1.732.2 2.2-=≈故x 的长约为 2.2cm(2)解:由题意可知DE BE x ==,∴DE y x=又根据EF y 经过表中的那些点,所以取点,画图即可得到其图象.(3)解:如图所示,当△DEF 为等边三角形时,EF=DE∵∠B=45°,射线DE ⊥BC 于点E∴BE=EF∴EF=DE∴在(2)中EF y 与DE y 的交点横坐标即为BE 的长经测量可知 3.2x ≈∴BE 的长约为3.2.【解析】【分析】(1)由题意得出△ABC 为等腰直角三角形,结合DE ⊥BC ,得出BE=DE=x ,当点F 与点C 重合时,在Rt △DEF 中,EF=6-x ,∠EDF=60°,利用正切函数列构建方程求解即可;(2)根据△ABC 为等腰直角三角形,推出△BDE 为等腰直角三角形,则可求出y DE 与x 的函数关系并画出图象,根据表格提供的数据,并通过描点法画出在同一个平面直角坐标系中函数yEF 的图象;(3)根据等边三角形的性质得出EF=DE ,结合∠B=45°,DE ⊥BC ,得出BE=EF ,即y=x ,再根据y EF 与y DE 相交时,交点的横坐标即为BE 的长度,得出BE 的近似值.2.【答案】(1)45°(2)解:①∵//MN AC ,∴45BMN BAC ∠=∠=︒,45BNM BCA ∠=∠=︒,∴BMN BNM ∠=∠,∴BM BN =,又∵BA BC =,∴AM CN =,∵在OAM 和OCN 中,AM CNOAM OCN AO CO=⎧⎪∠=∠⎨⎪=⎩,∴()SAS OAM OCN ∆ ≌,∴1()2AOM CON AOC MON ∠=∠=∠-∠1(9045)22.52︒=⨯-︒=︒,∴旋转过程中,当MN 和AC 平行时,正方形OABC 旋转的度数为4522.522.5︒-︒=︒.②MBN 的周长的值为2,且在正方形OABC 的旋转过程中不发生变化.理由如下:如图所示,延长BA 交y 轴于点E,则45AOE EOM AOM AOM ∠=∠-∠=︒-∠,∵904545CON AOC MON AOM AOM AOM ∠=∠-∠-∠=︒-︒-∠=︒-∠,∴AOE CON ∠=∠,又∵OA OC =,1809090OAE OCN ∠=︒-︒=︒=∠,在OAE 和OCN 中,AOE CONOA OC OAE OCN∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASA OAE OCN ≌,∴OE ON =,AE CN =.在OME 和OMN 中,OE ONEOM NOM OM OM=⎧⎪∠=∠⎨⎪=⎩,∴()SAS OME OMN ≌,∴MN ME AM AE ==+.∴MN AM CN =+,∴MBN 的周长为2MN BN BM AM CN BN BM AB BC ++=+++=+=.∴在正方形OABC 的旋转过程中,MBN 的周长不发生变化.【解析】【解答】解:(1)∵A 点第一次落在直线y x =上时停止旋转,直线y x =与y轴的夹角是45 ,∴OA旋转了45°;【分析】(1)根据直线y=x图象上点的特点,得出线y=x与y轴的夹角是45°,即可得出求得边OA旋转的角度;(2)①利用SAS得出全等,根据正方形一个内角的度数求出∠AOM的度数,即可得出答案;②利用全等把△MBN的各边整理到成与正方形的边长有关的式子即可.3.【答案】(1)AC;CD;FD(2)解:函数图象如图所示:(3)3.5cm<x<5cm【解析】【解答】解:(1)由题意可知:AC是自变量,CD,DF是自变量AC的函数.故答案为:AC,CD,FD.(3)观察图象可知CD>DF时,3.5cm<x<5cm.故答案为:3.5cm<x<5cm.【分析】(1)根据函数的定义可得结论;(2)利用描点法画出函数图象即可;(3)利用图象法,观察图象写出函数CD的图象在函数DF的图象上方时,自变量的取值范围即可。
中考数学专题复习动点型问题(含详细参考答案)

专题十动点型问题一、中考专题诠释所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.“动点型问题”题型繁多、题意创新,考察学生的分析问题、解决问题的能力,内容包括空间观念、应用意识、推理能力等,是近几年中考题的热点和难点。
二、解题策略和解法精讲解决动点问题的关键是“动中求静”.从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理。
在动点的运动过程中观察图形的变化情况,理解图形在不同位置的情况,做好计算推理的过程。
在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
三、中考考点精讲考点一:建立动点问题的函数解析式(或函数图像)函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.例1(2013•兰州)如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为()A.B.C.D.思路分析:分析动点P的运动过程,采用定量分析手段,求出S与t的函数关系式,根据关系式可以得出结论.解:不妨设线段AB长度为1个单位,点P的运动速度为1个单位,则:(1)当点P在A→B段运动时,PB=1-t,S=π(1-t)2(0≤t<1);(2)当点P在B→A段运动时,PB=t-1,S=π(t-1)2(1≤t≤2).综上,整个运动过程中,S与t的函数关系式为:S=π(t-1)2(0≤t≤2),这是一个二次函数,其图象为开口向上的一段抛物线.结合题中各选项,只有B符合要求.故选B.点评:本题结合动点问题考查了二次函数的图象.解题过程中求出了函数关系式,这是定量的分析方法,适用于本题,如果仅仅用定性分析方法则难以作出正确选择.对应训练1.(2013•白银)如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O.与∠α 的两边相切,图中阴影部分的面积 S 关于⊙O 的半径 r (r >0)变化的函数图象大致 是( )A .B .C .D . 1.C考点二:动态几何型题目点动、线动、形动构成的问题称之为动态几何问题 . 它主要以几何图形为载体,运动变化为主线,集多个知识点为一体,集多种解题思想于一题 . 这类题综合性强,能力要求 高,它能全面的考查学生的实践操作能力,空间想象能力以及分析问题和解决问题的能力 动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊 位置。
2024年广东九年级中考数学专题复习课件专题八+++动点轨迹、路径长问题

解:如图,连接OM,OC,MC, ∵∠POQ=90°,OM=CM= 1 PQ.BC的中位线.
∴点M所经过的路线长为 1 AB=1.
2
故答案为1;
(2)连接MA,MB,则MA+MB的最小值为____5____.
7.如图,已知线段AB=6,P是AB上的动点,在AB的 同侧分别以AP,PB为斜边作等腰直角三角形APC和 BPD,连接CD.
(1)CD的最小值为__3___; (2)G为线段CD的中点,当点P由点
A移动到点B时,点G移动的路径 长度为__3__.
8.如图,以点O为圆心,1为半径的圆上有一动点B,A 是圆外一点,AO=2,△ABC是以线段AB为边所作 的等边三角形,连接OC,当点B在圆O上运动一周时, 则点C走过的路径长为__2_π__, OC的最大值是_3__.
坐标为(6-t,0),点Q的坐标为(0,2t).
∴在运动过程中PQ的中点M的坐标为
6
2
t
,
t
.
当x= 6 t 时,y=-2× 6 t +6=t.
2
2
∴点M在直线M′M″上.
如图,作M″N⊥x轴于点N,则M″N=4,M′N=2, 由勾股定理得M′M″= 42 22 2 5 , ∴线段PQ中点M所经过的路径长为2 5 .
解:以C为原点,以AC所在的直线为x轴,建立如图所
示的平面直角坐标系,依题意,得0≤t≤4, 当t=0时,点M′的坐标为(3,0),
当t=4时,点M″的坐标为(1,4),
设直线M′M″的解析式为y=kx+b,则
解得3kkbb4,0,
k 2, b 6.
∴直线M′M″的解析式为y=-2x+6.依题意,得点P的
2023年中考数学专题复习:二次函数综合压轴题(动点问题)

2023年中考数学专题复习:二次函数综合压轴题(动点问题)1.抛物线2y x bx c =-++与x 轴交于点()10A -,,()30B ,,与y 轴交于点C .(1)求抛物线的解析式;(2)点D 为第一象限内抛物线上的一动点,作DE x ⊥轴于点E ,交BC 于点F ,过点F 作BC 的垂线与抛物线的对称轴、x 轴、y 轴分别交于点G ,N ,H ,设点D 的横坐标为m .①当DF HF +取最大值时,求点F 的坐标;②连接EG ,若45GEH ∠=︒,求m 的值.2.如图,已知抛物线2y x bx c =-++与x 轴交于()1,0A -,()5,0B 两点(点A 在点B 的左侧),与y 轴交于点C .(1)求抛物线的解析式;(2)在抛物线的对称轴上存在一点P ,使得PA PC +的值最小,求此时点P 的坐标;(3)点D 是第一象限内抛物线上的一个动点(不与点C 、B 重合),过点D 作DF x ⊥轴于点F ,交直线BC 于点E ,连接BD ,直线BC 把BDF V 的面积分成两部分,若:3:2BDE BEF S S =V V ,请求出点D 的坐标.3.如图1,对于平面内小于等于90︒的MON ∠,我们给出如下定义:若点P 在MON ∠的内部或边上,作PE OM ⊥于点E ,PF ON ⊥于点F ,则将PE PF +称为点P 与MON ∠的“点角距”,记作(),d MON P ∠.如图2,在平面直角坐标系xOy 中,x 、y 正半轴所组成的角为xOy ∠.(1)已知点()5,0A 、点()3,2B ,则(),d xOy A ∠=______ ,(),d xOy B ∠=______.(2)若点P 为xOy ∠内部或边上的动点,且满足(),5d xOy P ∠=,在图2中画出点P 运动所形成的图形.(3)如图3,在平面直角坐标系xOy 中,抛物线212y x mx n =-++经过()5,0A 与点()3,4D 两点,点Q 是A 、D 两点之间的抛物线上的动点(点Q 可与A 、D 两点重合),求当(),d xOD Q ∠取最大值时点Q 的坐标.4.如图,抛物线2134y ax bx =++与x 轴交于点()30A -,和点B ,点D 是抛物线1y 的顶点,过点D 作x 轴的垂线,垂足为点()10C -,.(1)求抛物线1y 所对应的函数表达式;(2)如图1,点M 是抛物线1y 上一点,且位于x 轴上方,横坐标为m ,连接MC ,若MCB DAC ∠=∠,求m 的值;(3)如图2,将抛物线1y 平移后得到顶点为B 的抛物线2y .点P 为抛物线1y 上的一个动点,过点P 作y 轴的平行线,交抛物线2y 于点Q ,过点Q 作x 轴的平行线,交抛物线2y 于点R .当以点P ,Q ,R 为顶点的三角形与ACD V 全等时,请直接写出点P 的坐标.5.如图,抛物线()20y ax bx c a =++≠与x 轴交于A 、B 两点,与y 轴交于点()0,6C ,顶点为D ,且()1,8D .(1)求抛物线的解析式;(2)若在线段BC 上存在一点M ,过点O 作OH OM ⊥交BC 的延长线于H ,且MO HO =,求点M 的坐标;(3)点P 是y 轴上一动点,点Q 是在对称轴上一动点,是否存在点P ,Q ,使得以点P ,Q ,C ,D 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.6.如图,已知二次函数24y x bx =+-的图像经过点()3,4A -,与x 轴负半轴交于点B ,与y 轴交于点C ,连接AB ,BC .(1)填空:b =______;(2)点P 是直线AB 下方抛物线上一个动点,过点P 作PT x ⊥轴,垂足为T ,PT 交AB 于点Q ,求线段PQ 的最大值;(3)点D 是y 轴正半轴上一点,若∠=∠BDC ABC ,求点D 的坐标.7.如图,抛物线2y x bx c =++(b ,c 是常数)的顶点为C ,与x 轴交于A ,B 两点,()1,0A ,4AB =(1)求该抛物线的解析式;(2)点P 为线段AB 上的动点,过P 作PQ BC ∥交AC 于点Q ,求CPQ V 面积的最大值,并求此时P 点坐标;(3)如图,设抛物线与y 轴交于点D ,平行于BD 的直线MN 交抛物线于点M ,N ,作直线MB ND 、交于点G ,问点G 是否在某一定直线上运动,若在求此直线的解析式,若不在说明理由.8.如图,已知抛物线23y ax bx =+-的图象与x 轴交于点A ()10,和B ()30,,与y 轴交于点C ,D 是抛物线的顶点,对称轴与x 轴交于E .(1)求抛物线的解析式;(2)如图1,在抛物线的对称轴DE 上求作一点M ,使A M C V 的周长最小,M 的坐标__________周长的最小值______.(3)如图2,点P 是x 轴上的动点,过P 点作x 轴的垂线分别交抛物线和直线BC 于F 、G .设点P 的横坐标为m .是否存在点P ,使FG 最长?若存在,求出m 的值;若不存在,请说明理由.9.如图1,抛物线()230y ax bx a =+->交x 轴于点A ,B (点A 在点B 左侧),交y 轴于点C ,且3O B O C O A ==,点D 为抛物线上第四象限的动点.(1)求抛物线的解析式.(2)如图1,直线AD 交BC 于点P ,连接AC BD ,,若ACP △和BDP △的面积分别为1S 和2S ,当12S S -的值最小时,求直线AD 的解析式.(3)如图2,直线BD 交抛物线的对称轴于点N ,过点B 作AD 的平行线交抛物线的对称轴于点M ,当点D 运动时,线段MN 的长度是否会改变?若不变,求出其值;若变化,求出其变化的范围.10.已知抛物线23y ax bx =++(0a ≠)交x 轴于()0A 1,和()30B -,,交y 轴于C .(1)求抛物线的解析式;(2)若M 为抛物线上第二象限内一点,求使MBC V 面积最大时点M 的坐标;(3)若F 是对称轴上一动点,Q 是抛物线上一动点,是否存在F 、Q ,使以B 、C 、F 、Q 为顶点的四边形是平行四边形?若存在,直接写出点Q 的坐标.11.如图,在平面直角坐标系中,二次函数的图象交坐标轴于()20A -,,()40B ,,()08C ,三点,点P 是直线BC 上方抛物线上的一个动点.(1)求这个二次函数的解析式;(2)动点P 运动到什么位置时,PBC V 的面积最大,求此时P 点坐标及PBC V 面积的最大值;(3)在y 轴上是否存在点Q ,使以O ,B ,Q 为顶点的三角形与AOC V 相似?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.12.如图,抛物线2y x bx c =++与x 轴交于()1,0A -,()3,0B 两点,与y 轴交于点C .(1)求该抛物线的解析式;(2)若点E 是线段BC 上的一个动点,平行于y 轴的直线EF 交抛物线于点F ,求FBC V 面积的最大值;(3)设点P 是(1)中抛物线上的一个动点,是否存在满足6PAB S =△的点P ?如果存在,请求出点P 的坐标;若不存在,请说明理由.13.如图,抛物线2y ax bx =+经过()()3,0,2,10A B -两点.(1)求抛物线的解析式;(2)点P 是直线AB 下方抛物线上的一个动点,求PAB V 面积的最大值;(3)点M 是直线AB 上的一个动点,将点M 向左平移3个单位长度得到点N ,设点M 的横坐标为m ,若线段MN 与抛物线只有一个公共点,请直接写出m 的取值范围.14.如图,在平面直角坐标系中,直线122y x =-与x 轴交于点A ,与y 轴交于点C ,抛物线212y x bx c =++经过A ,C 两点,与x 轴的另一交点为点B ,点P 为抛物线上的一个动点.(1)求抛物线的函数表达式;(2)当ACP △的面积与ABC V 的面积相等时,求点P 的坐标;(3)是否存在点P ,使得ACP ABC BAC ∠=∠-∠,若存在,请直接写出点P 的横坐标;若不存在,请说明理由.15.如图,已知拋物线2y ax bx c =++与x 轴交于点()1,0A ,()3,0B -,与y 轴交于点()0,3C -.点P 是抛物线上一动点,且在直线BC 的下方,过点P 作PD x ⊥轴,垂足为D ,交直线BC 于点E .(1)求抛物线的函数解析式;(2)连接CP ,若45CPD ∠=︒,求点P 的坐标;(3)连接BP ,求四边形OBPC 面积的最大值.16.如图,在平面直角坐标系中,抛物线28y x bx =-++与x 轴交于点A ,B ,与y 轴交于点C ,直线y x t =-过点B ,与y 轴交于点D ,点C 与点D 关于x 轴对称.点P 是线段OB 上一动点,过点P 作x 轴的垂线交抛物线于点M ,交直线BD 于点N .(1)求抛物线的解析式;(2)当MDB △的面积最大时,求点P 的坐标;(3)在(2)的条件下,在y 轴上是否存在点Q ,使得以Q ,M ,N ,D 为顶点的四边形是平行四边形,若存在,求出点Q 的坐标;若不存在;说明理由17.如图,抛物线21262y x x =--与x 轴相交于点A 、点B ,与y 轴相交于点C .(1)请直接写出点A ,B ,C 的坐标;(2)若点P 是抛物线BC 段上的一点,当PBC V 的面积最大时求出点P 的坐标,并求出PBC V 面积的最大值.(3)点F 是抛物线上的动点,作FE AC ∥交x 轴于点E ,是否存在点F ,使得以A 、C 、E 、F 为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F 的坐标;若不存在,请说明理由.18.如图,在平面直角坐标系中,抛物线21=2y x bx c ++经过点()4,0A -,点M 为抛物线的顶点,点B 在y 轴上,直线AB 与抛物线在第一象限交于点()2,6C .(1)求抛物线的解析式;(2)连接OC ,点Q 是直线AC 上不与A 、B 重合的点,若2OAQ OAC S S =V V ,请求出点Q 的坐标;(3)在x 轴上有一动点H ,平面内是否存在一点N ,使以点A 、H 、C 、N 为顶点的四边形是菱形?若存在,直接写出点N 的坐标,若不存在,请说明理由.参考答案:1.(1)223y x x =-++(2)①点F 的坐标为⎝⎭;②1或952.(1)245y x x =-++(2)()2,3P (3)335,24D ⎛⎫ ⎪⎝⎭3.(1)5,5 (3)54,2⎛⎫ ⎪⎝⎭4.(1)21113424y x x =--+(2)2-(3)304⎛⎫ ⎪⎝⎭,或524⎛⎫- ⎪⎝⎭,5.(1)2246y x x =-++ (2)126,55⎛⎫ ⎪⎝⎭(3)(1,8或(1,8或271,4⎛⎫ ⎪⎝⎭6.(1)3-(2)PQ 的最大值是4 (3)50,3⎛⎫ ⎪⎝⎭7.(1)223y x x =+-(2)CPQ V 面积的最大值为2,此时P 点坐标为()1,0-(3)在,3y x =--8.(1)2=+43y x x --(2)()21-,(3)存在,m 的值为329.(1)2=23y x x --(2)22y x =--(3)不变,值为810.(1)223y x x =--+ (2)31524⎛⎫- ⎪⎝⎭, (3)存在,点Q 的坐标为()23-,或()45-,-或()25,-11.(1)228y x x =-++(2)当P 点坐标为()28,时,PBC V 的最大面积为8; (3)存在,点Q 的坐标为()016,或()016-,或()01,或()01-,.12.(1)2=23y x x -- (2)278(3)存在,点P 的坐标为()1或()1或()0,3-或()2,3-13.(1)23y x x =-(2)PAB S V 最大值为1258(3)23m -≤<或34m <<或338m =14.(1)抛物线的函数表达式为213222y x x =-- (2)点P 的坐标为(5,3)P(3)存在,点P 的横坐标为2911或7.15.(1)223y x x =+- (2)(14)--, (3)63816.(1)278y x x =-++(2)()3,0(3)存在,()0,17Q 或()0,33-17.(1)()2,0A -,()6,0B ,()0,6C - (2)点P 的坐标为153,2⎛⎫- ⎪⎝⎭时,PBC S V 有最大值272(3)存在,点F 的坐标为()4,6-或()2+或()2-18.(1)21=22y x x + (2)()8,12或()16,12--(3)()2N +或()2N -或()2,6N -或()4,6-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何图形动点与函数图像综合考向一判断函数图像(1)面积问题:①函数类型:与面积相关的量如果有一个变化的量为一次函数,如果有两个变化的量为二次函数;②节点、自变量取值范围及函数值;③函数的增减性等(2)线段长度问题:①根据相似性质对应边成比例或面积公式等确定函数关系式;②节点、自变量取值范围及函数值;③函数的增减性等1.如图,在Rt △ABC中,△C=900,AC=1cm,BC=2cm,点P从A出发,以1cm/s的速沿折线AC→ CB→ BA运动,最终回到A点。
设点P的运动时间为x(s),线段AP的长度为y(cm),则能反映y与x之间函数关系的图像大致是()2.如图,点E、F、G、H是正方形ABCD四条边(不含端点)上的点,DE=AF=BG=CH。
设线段DE的长为x cm,四边形EFGH的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是()3.如图,菱形ABCD的边长为5cm,sinA=,点P从点A出发,以1cm/s的速度沿折线AB→BC→CD运动,到达点D停止;点Q同时从点A出发,以1cm/s的速度沿AD运动,到达点D停止.设点P运动x(s)时,△APQ的面积为y(cm2),则能够反映y与x之间函数关系的图象是()A B C D4.如图,在菱形ABCD中,△B=60°,AB=2.动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一点也随之停止.设△APQ的面积为y,运动时间为x 秒.则下列图象能大致反映y与x之间函数关系的是()A B C D5.如图,在等边三角形ABC中,BC=4,在Rt△DEF中,△EDF=90°,△F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E 重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是()6.如图,在四边形ABCD中,AD△BC,△A=45°,△C=90°,AD=4cm,CD=3cm.动点M,N同时从点A出发,点M以cm/s的速度沿AB向终点B运动,点N以2cm/s的速度沿折线AD﹣DC向终点C运动.设点N的运动时间为ts,△AMN的面积为Scm2,则下列图象能大致反映S与t之间函数关系的是()A.B.C.D.7.如图,四边形ABCD是边长为1的正方形,点E是射线AB上的动点(点E不与点A,点B重合),点F在线段DA的延长线上,且AF=AE,连接ED,将ED绕点E顺时针旋转90°得到EG,连接EF,FB,BG.设AE=x,四边形EFBG的面积为y,下列图象能正确反映出y与x的函数关系的是()A.B.C.D.8.如图,在矩形ABCD中,AB=2,BC=3,动点P沿折线BCD从点B开始运动到点D.设运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是()9.如图,O是边长为4 cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A—B—M方向匀速运动,到M时停止运动,速度为1 cm/s,设P点的运动时间为t(s),点P的运动路径与OA,OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是()10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为()11.如图,AD、BC是△O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设△APB=y(单位:度),那么y与P运动的时间x(单位:秒)的关系图是()12.一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的AB,BC,CA,OA,OB,OC组成。
为记录寻宝者的进行路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为()A.A→O→B B.B→A→C C.B→O→C D.C→B→O考向二 函数图像与几何图形性质综合1.如图1,在直角梯形ABCD 中,动点P 从点B 出发,沿BC ,CD 运动至点D 停止.设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则△BCD 的面积是( )A .3B .4C .5D .62.如图①,在正方形ABCD 中,点E 是AB 的中点,点P 是对角线AC 上一动点.设PC 的长度为x ,PE 与PB 的长度和为y ,图②是y 关于x 的函数图象,则图象上最低点H 的坐标为 .3.如图1,点P 从△ABC 的顶点B 出发,沿B →C →A 匀速运动到点A 。
图2是点P 运动时,线段BP 的长度随时间变化的关系图象,其中M 为曲线部分的最低点,则△ABC 的面积是 .4.如图1,点F 从菱形ABCD 的顶点A 出发,沿A→D→B 以1cm/s 的速度匀速运动到点B ,图2是点F 运动时,△FBC 的面积y (cm 2)随时间x (s )变化的关系图象,则a 的值为( )OyxA .B .2C .D .25.如图①,正方形ABCD 中,AC ,BD 相交于点O ,E 是OD 的中点.动点P 从点E 出发,沿着E →O →B →A 的路径以每秒1个单位长度的速度运动到点A ,在此过程中线段AP 的长度随着运动时间的函数关系如图②所示,则AB 的长为( )A.24B.4C.D.6.如图1,矩形ABCD 中,点E为BC 的中点,点P 沿BC 从点B 运动到点C ,设B ,P 两点间的距离为x ,PA-PE=y ,图2是点P 运动时y 随x 变化的关系图象,则BC 的长为( )A .4B .5C .6D .77.如图1,在菱形ABCD 中,△A=60°,动点P 从点A 出发,沿折线AD→DC→CB 方向匀速运动,运动到点B 停止,设点P 的运动路程为x ,△APB 的面积为y ,y 与x 的函数图象如图2所示,则AB 的长为( )y xA.B.C.D.8.【2022三门峡二模10,3】如图1,矩形ABCD中,AB=6,BC=4,点P以每秒2个单位长度沿AD→DC→CB运动,点Q沿AB以每秒1个单位长度运动,当点Q运动到点B时,P,Q停止运动,设运动时间为x(秒),△APQ的面积为y,图2是y随x变化的关系图象,则a的值为()A.6B.8C.10D.129.【2022河南名校联盟10,3】如图1,在四边形ABCD中,AD//BC,AD=2BC,∠D=90°,动点M沿A→B→C→D的路线运动,到点D时停止。
过点M作MN⊥AD,垂足为点N,设点M运动的路程为x,△AMN的面积y与x之间的函数关系图象如图2所示,当x=10时,y的值是()13 C.5 D.6A.8B.210.【2022河南抢分卷10,3】如图1,在四边形ABCD中,∠B=∠C=90°,点P从四边形ABCD的顶点A出发,沿A→B→C→D 以1cm/s的速度匀速运动到点D.图2是点P运动时△ABP的面积y(cm²)随时间x(s)变化的关化的关系图象,则m的值为()A.10B.16C.12D.2411.【2022河南一模10,3】如图,在▱ABCD中,点P沿A→B→C方向从点A移动到点C,设点P移动路程为x,线段AP的长为y,图2是点P运动时y随x变化的关系图象,则BC 的长为()A.4B.4.8C.5D.1012.【2022河南二模9,3】如图,△ABC 中,tan ∠B==34,点D 为边BC 上一个不与B 、C 重合的一个动点,过点D 作DE ⊥AB 与点E ,作Rt △DEA 的中线EF ,当点D 从B 点出发匀速运动到点C 时,设△AEF 的面积为y ,BD=x ,y 与x 的函数图象如图2所示,则△ABC 的面积为( ) A.596 B.548 C.19 D.1813.【2023河南模拟一10,3】如图1,在△ABC 中,∠C=90°,AC=BC ,点D 从点A 出发沿线段AB 向终点B 运动,过点D 作DE ⊥AB ,交△ABC 的直角边于点E.△ADE 的面积y 与线段AD 的长x 之间的函数图象如图2所示,当△ADE 的面积为1时,线段AD 的长为( ) A.2 B.22- C.2或22- D.2或22+14.【2023河南重点中学内部摸底卷二10,3】如图1所示,动点P 从正六边形的A 点出发,沿A→B→C→D→E 以1cm/s 的速度匀速运动到点E ,图2是点P 运动时,△APE 的面积y (cm2)随着时间x (s )的变化的关系图象,则图2中的m 为( ) A.338cm ² B.33cm ² C.439cm ² D.34cm ² 15.【2023郑州名校联考16,3】如图1,点P 从扇形AOB 的O 点出发,沿O →A →B —O以1cm/s 的速度匀速运动,图2是点P 运动时,线段OP 的长度y 随时间x 变化的关系图象,则扇形AOB 中弦AB 的长度为_______cm.16.【2023安阳一模14,3】如图1,则等边三角形ABC 中,点P 为BC 边上的任意一点,且∠APD=60°,PD 交AC 于点D ,设线段PB 的长度为x ,CD 的长度为y ,若y 与x 的函数关系的大致图象如图2,则等边三角形ABC 的面积为_________。
17.【2023西安雁塔区一模12,3】如图1,在菱形ABCD 中,∠BAD=60°,点E 在AB 的延长线上,在∠CBE 的角平分线上取一点F (含端点B ),连接AF 并过点C 作AF 所在直线的垂线,垂足为G.设线段AF 的长为x ,CG 的长为y ,y 关于x 的函数图象及有关数据如图2所示,点Q 为图象的端点,则3 y 时,BF=_________。
