2-6-1 谱理论
仪器分析化学 第一章 色谱基本理论

n理5.54 (Yt1R /2)216 (tYR)2
n有效
5.54( tR' Y1/ 2
)2
16(tR' Y
)2
H有效
L n有效
(二) 塔板数和塔板高度
组分在固定相中的浓度 K 组分在流动相中的浓度
一定温度下,组分的分配系数K越大,出峰越慢; 试样一定时,K主要取决于固定相性质; 选择适宜的固定相可改善分离效果; 试样中的各组分具有不同的K值是分离的基础; 某组分的K = 0时,即不被固定相保留,最先流出。 同一条件下,若两组分的K值相等,则色谱峰重合, 差别越大,色谱峰的距离越大
三. 速率理论-影响柱效的因素
(一). 范.弟姆特(Van Deemter)方程式- 气相色谱速率理论
H = A + B/u + C·u
H:理论塔板高度, u:载气的线速度(cm/s)
减小A、B、C三项可提高柱效; 存在着最佳流速; A、B、C三项各与哪些因素有关?
A─涡流扩散项(eddy diffusion)
(四) 分配比与保留时间的关系
tR = tM(1+k) tR’=ktM
(五) 分配比、分配系数与选择性因子的关系
a = t´R(2)/ t´R(1)= k2 /k1= K2 /K1
讨论:如何使A、B组分完全分离
浓
度
A
B
A
B
组分A、B在沿柱移动时不同位置的浓度轮廓
1.两组分的分配系数必须有差异 2.区域宽度的扩展速度应小于区域分离的速度 3.在保证快速分离的前提下,提供足够长的色谱柱
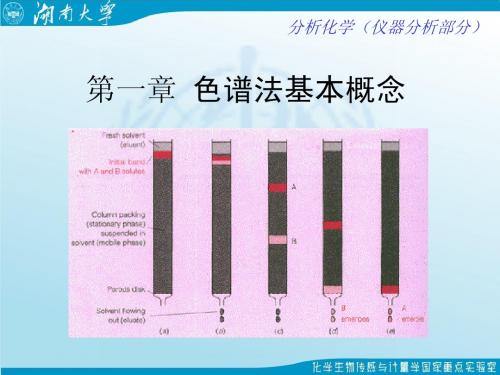
第10章 色谱分析基本概念
c
c0 σ 2π
e
当色谱峰为非正态分布时,可按正态分布函数加指数衰 减函数构建关系式。
目 录
1-1 色谱法概述
1-1-1 色谱法的特点、分类和作用 1-1-2 色谱分离过程 1-1-3 色谱流出曲线与术语
1-2 色谱理论基础
1-2-1 塔板理论 1-2-2 速率理论 1-2-3 分离度 1-3 定性定量方法 1-3-1 色谱定性分析 1-3-2 色谱定量分析
色谱柱长:L, 虚拟的塔板间距离:H,
色谱柱的理论塔板数:n,
则三者的关系为: n=L/H
理论塔板数与色谱参数之间的关系为:
tR 2 tR 2 n 5.54( ) 16( ) Y1/ 2 Wb
保留时间包含死时间,在死时间内不参与分配!
2.有效塔板数和有效塔板高度
• 单位柱长的塔板数越多,表明柱效越高。
调整保留时间(tR'):tR'= tR-tM
(2)用体积表示的保留值 保留体积(VR): VR = tR×F0 F0为柱出口处的载气流量,
单位:m L / min。
死体积(VM):
VM = tM ×F0
调整保留体积(VR'):
V R' = VR -VM
3. 相对保留值r21 组分2与组分1调整保留值之比: r21 = t´R2 / t´R1= V´R2 / V´R1 相对保留值只与柱温 和固定相性质有关,与其 他色谱操作条件无关,它 表示了固定相对这两种组 分的选择性。
式中为相比。 填充柱相比:6~35;毛细管柱的相比:50~1500。 容量因子越大,保留时间越长。 VM为流动相体积,即柱内固定相颗粒间的空隙体积; VS为固定相体积,对不同类型色谱柱, VS的含义不同; 气-液色谱柱: VS为固定液体积; 气-固色谱柱: VS为吸附剂表面容量;
色谱基础理论分配系数与分配比

1 分配系数
• 分配过程
物质在固定相和流动相(气相)之间发生的吸 附、脱附和溶解 、挥发的过程
• 分配系数
在一定的温度和压力下,组分在两相之间达到 分配平衡时的浓度比
2
1 分配系数
K cs
式中 :
cM
•cs :组分在固定相中的浓度; •cM:组分在流动相中的浓度;
气相色谱分析原理:
不同物质在两相间具有不同的分配系数 分配系数是色谱分离的依据
RS
w mM ms mM
1
1 ms / mM
1 1 k
7
3 分配系数分配比之间关系
假设色谱柱长为L
则组分和流动相通过色谱柱所需要的时间分别为:
tR
L us
由以上各式可得
tM
L u
tR tM (1 k)
k tR tM tR'
tM
tM
据上式可知:k可由实验测得
8
4 分配系数、分配比的应用
(
1)
(
k
)
式中 : 4
k 1
•R:分离度;
•n:理论塔板数;
•α: 相对保留值;
•k:分配比;
根据上述关系以及实验对分离度的要求,可以通过改变
柱温、相比等条件,得到合适的分配比,从而达到实验
要求的分离度
10
4 分配系数、分配比的应用
3o 在液液分配色谱中的应用
与在气相色谱中的应用对比:
相同点:分离顺序取决于分配系数的大小,分配 系数大的组分保留值大 不同点:气相色谱中流动相的性质对分配系数影 响不大;而液液分配色谱中,流动相的种类对分 配系数有较大的影响
3
2 分配比
• 分配比(容量因子或容量比)
色谱基本概念和理论

Ⅱ 基本概念和理论一、基本概念和术语1.色谱图和峰参数⊕色谱图(chromatogram)--样品流经色谱柱和检测器,所得到的信号-时间曲线,又称色谱流出曲线(elution profile).⊕基线(base line)--流动相冲洗,柱与流动相达到平衡后,检测器测出一段时间的流出曲线。
一般应平行于时间轴。
⊕噪音(noise)――基线信号的波动。
通常因电源接触不良或瞬时过载、检测器不稳定、流动相含有气泡或色谱柱被污染所致。
⊕漂移(drift)基线随时间的缓缓变化。
主要由于操作条件如电压、温度、流动相及流量的不稳定所引起,柱内的污染物或固定相不断被洗脱下来也会产生漂移。
⊕色谱峰(peak)--组分流经检测器时相应的连续信号产生的曲线。
流出曲线上的突起部分。
正常色谱峰近似于对称性正态分布曲线(高斯Gauss曲线)。
不对称色谱峰有两种:前延峰(leading peak)和脱尾峰(tailing peak ).前者少见。
⊕拖尾因子(tailing factor,T)--T=B/A,用以衡量色谱峰的对称性。
也称为对称因子(symmetry factor)或不对称因子(asymmetry factor)《中国药典》规定T应为0.95~1.05。
T<0.95为前延峰,T>1.05为拖尾峰。
⊕峰底――基线上峰的起点至终点的距离。
⊕峰高(Peak height,h)――峰的最高点至峰底的距离。
⊕峰宽(peak width,W)--峰两侧拐点处所作两条切线与基线的两个交点间的距离。
W=4σ。
⊕半峰宽(peak width at half-height,Wh/2)--峰高一半处的峰宽。
W h/2=2.355σ。
⊕标准偏差(standard deviation, σ)--正态分布曲线x=±1时(拐点)的峰宽之半。
正常峰宽的拐点在峰高的0.607倍处。
标准偏差的大小说明组分在流出色谱柱过程中的分散程度。
『科学的认识调式,小调主音唱6与唱1的两种情况』(转)

『科学的认识调式,⼩调主⾳唱6与唱1的两种情况』(转)(注:这⾥所有的唱名法指的是⾸调唱名!)过去玩乐队的时候我们⼀直在争论,⼩调主⾳唱6还是唱1?学古典的⼈说,⾸调唱法的话,当然唱6,简谱⾥都是这么标记的,6 7 1 2 3 4 5 6。
另⼀⽅则认为⾃然⼩调⽤⾸调唱名也可表述成1 2 b3 4 5 b6 b7 1(五声⼩调则是1 b3 4 5 b7 1)。
关于这个问题,我想很多玩⾳乐的朋友是莫衷⼀是的,特别是学院派⾳乐⼈与草根或者“现代”爵⼠派的⾳乐⼈之间此分歧特别严重。
于是乎我们很多⼈⾃然就会说,尼玛古典理论和现代理论他们是⽭盾的,他们互为体系(其实这句话是不对的哦,也是不科学的),但显然需要解释⼀个问题,为什么会出现这样的⽭盾?⾸先,在具体的⾳乐作品中,⽤⾸调唱名的话,调式的主⾳唱什么,得看⾳乐作品按什么“调”记谱,或者说在五线谱⾥是什么“调号”,那么同样都是⼩调,为什么会有两种不同的唱法呢,换句话说,为什么⼩调会有两种不同的记谱情况?因为在不同的⾳乐类型中,以⼩调调式为素材的⾳阶使⽤上,会搭配不同体系的和声织体,因此,如果按传统的记谱法,⽆法定义其属于什么“调”,或者说,⽆法直接描述其调性本质。
也就是说,两者由于和声织体不同⽽造成记谱⽅式的不同。
很多国内学院派教育的标准还停留在前苏联⾳乐教育体系,在调与调式的很多具体标准上,还没有做到与国际接轨,造成很多现代流⾏⾳乐专业的⾳乐家与正统科班出来的⾳乐家之间沟通存在⼀定障碍,于是争论就出现了。
其实呢,这两年我也⼀直在纠结这个问题。
主要是国内的⼏本主流基本乐理教材,包括李重光编的(⽆意冒犯,其实是有历史原因的,当时国内的⾳乐理论体系都是照搬前苏联),都有很多上下章节互为⽭盾的地⽅。
具体来说,就是"调",“调式”和“调性”的定义上,概念很模糊。
武汉⾳乐学院的李⾦华教授曾经写过⼀篇《调、调式和调式的概念辨析》,这个百度上有,⼤家可以搜索下,⼤意就是批评国内⼗多个不同版本的基本乐理教程对于调与调式概念解释上的模糊。
音乐理论基础课程—2、记谱法

Part 1 音符
1.单纯音符 以全音符为一个整体,按照平均二等份的规则逐级细分所形 成的音符,称为单纯音符。
第6页
Part 1 音符
2.附点音符 写在符头右面的小圆点,称为附点,它与所跟随的音符形成 一个整体,具有增长时值的作用。 计算方法为:附点的时值,代表所跟随音符时值的二分之一。
第7页
1.表示大段落需要反复演奏。
小节演奏顺序 1234 5678 5678 2、反复跳跃记号:在小节上方标明。反复后跳过1,直接演 奏2 2
第、Dal segno(D.S.)乐曲从头演奏到谱乐结束记录的地方, 再从处反复,结束在Fine
5、Coda 结束部分 6、小节反复记号:1小节反复,记在小节中间
第 16 页
Part 1 谱号和谱表
同样是弦乐器的重奏总谱,用垂直线与直括号连结即可。 不同声部的合唱总谱也用这种方法记谱,并具体标明不同声部的 名称。
第 17 页
Part 1 谱号和谱表
4、管弦乐队总谱记法:(自上而下) 木管乐器四行谱 铜管乐器四行谱 打击乐器一行谱 弓弦乐器五行谱
5、民族管弦乐队总谱记法:(常用简谱) 吹奏乐器 弹拨乐器 拉弦乐器 打击乐器
第 24 页
Part 2 省略记号
1、移高八度记号:记在五线谱或简谱的上面,表示虚线以内 的音移高八度演奏8---------
2、移低八度记号:记在五线谱或简谱的下面,表示虚线以内 的音移低八度演奏8--------
3、高八度重复记号:记在五线谱或简谱的上面,表示虚线以内 的音移高八度重复Con8------
第 29 页
Part 2 与速度有关的术语、记号
2.有关速度的术语
除了用数字表示速度,还可以用固定的词汇表达,称为术语。
自共轭算子的谱定理

自共轭算子的谱定理自共轭算子的谱理论是现代数学中重要的研究内容之一,它既是经典数学理论的延伸与发展,又在很多领域中得到了广泛的应用。
本文将介绍自共轭算子的谱定理的基本概念、性质以及应用。
一、自共轭算子的定义与性质在谈论自共轭算子的谱定理之前,首先需要了解自共轭算子的定义与性质。
1.自共轭算子的定义设H是一个Hilbert空间,T:H→H是一个线性算子。
如果存在一个算子S:H→H,满足对于任意的x,y∈H,都有⟨Tx, y⟨=⟨x, Sy⟨,则称算子T是自共轭的,而S则称为T的共轭算子。
2.自共轭算子的性质(1)自共轭算子是线性的:如果T是一个自共轭算子,那么对于任意的x,y∈H,a,b∈C,有T(ax+by)=aTx+bTy。
(2)共轭算子是封闭的:如果T是一个自共轭算子,那么T的共轭算子S也是一个自共轭算子。
(3)共轭算子的共轭与自共轭算子相等:如果T是一个自共轭算子,那么T的共轭算子S的共轭算子与T相等,即(S*)* =T。
(4)自共轭算子的范数等于原算子的范数:如果T是一个自共轭算子,那么||T||=||T*||,其中||T||表示算子T的范数,||T*||表示算子T的共轭算子的范数。
二、自共轭算子的谱定理的基本概念1.谱对于自共轭算子T,我们定义其谱σ(T)为所有使得(T-λI)不可逆的复数λ的集合,其中I表示H上的单位算子。
2.点谱与连续谱对于自共轭算子T的谱σ(T),我们可以按照以下方式分类:(1)点谱:对于每一个λ∈σ(T),都存在一个非零向量u∈H,使得(T-λI)u=0。
称这样的λ为T的特征值,而u称为T相应于特征值λ的特征向量,此时记T的点谱为σp(T)。
(2)连续谱:对于每一个λ∈σ(T),不存在一个非零向量u∈H,使得(T-λI)u=0。
称这样的λ为T的连续谱,此时记T的连续谱为σc(T)。
(3)剩余谱:对于每一个λ∈σ(T),存在一个非零向量u∈H,使得(T-λI)u=0,但是(T-λI)u≠0。
谱理论

第六章
点款
§1.豫解式与自伴性.................................................................................................89 §2.Parseval 公式的反演...........................................................................................92 §3.特征值问题.........................................................................................................97 §4.豫解式的积分表现...........................................................................................100 §5.点收敛...............................................................................................................104 §6.算子 T 的谱表示...............................................................................................105
第四章 Titchmarsh 公式
§1.谱函数存在性的另一证明.................................................................................64 §2. Titchmarsh 公式.................................................................................................65 §3. M (λ ) 与 ρ (u ) 的关系..........................................................................................67 §4.离散谱情形....... .................................................................................................69 §5.谱函数的唯一性.................................................................................................71 §6.例子.....................................................................................................................73
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例4、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → tu(t)。讨论 A 的谱集。 解: (2) 考虑方程 u(t) – tu(t) = v(t), a.e. t [0,1]。 同例3,当 >1或 (3) < 0 时,h(t) = ( - t)-1 连续,
1
从而 h X。
因此,方程 (3) 有解 u(t) = h(t)v(t)。
r(A)
= [0,1] ,
(A) = R\[0,1]。
例4、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → tu(t)。讨论 A 的谱集。 解:A 是有界线性算子,由无限维情形的分 类可知只需要讨论 (1) I – A 是否为单射;以及
1
(2) I – A 的值域与 X 的关系。
y( t )
t
(A)。并且有
(t s)
t s
e
(t
)
x( )d
e
(t
)
x( )d
0
e
x(t
)d
(3) 命题:设 A 为 Banach 空间 X 上的线性算 子,满足 (A) 非空,则 A 为闭算子。 证明:设 xn → x,Axn = yn → y。 目标:Ax = y。设 (A),则
-1
xn – Axn → x – y
R( I A) X ,剩余谱 单,
r(A) p(A) c(A)
。
无限维情形
例1、设 X = BUC(R,C),即全体从 R 到 C
的有界一致连续函数按照上确界范数构成的
Banach 空间。设A为微分算子,即
A : x( t ) x (t ),
p(A)
则 A 为闭算子,且 (A) =
= iR。
目标分三部分: 证明对任何 b R,ib
2
其中
M max
n Z
|
1 (2n )2 |2
例5、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → u”(t),其中 D(A) = {u C2[0,1]:u(0) = u(1),u’(0) = u’(1)}。 则 A 是闭算子。讨论 A 的谱集。
2
2
结论: (A) =
p(A)
xn → ( I – A) ( x – y)
x = ( I – A)-1( x – y)
x – Ax = x – y
Ax = y 。
例2、设 X = l 。 设 A 为右移位算子,则 0 设 B 为左移位算子,则 0
r(A); p(B)。
2
证明:(1) 令 M = span{e1},e1 = (1,0,
2
是 X 的一组正交规范基。并且
Aen en
2 (2n ) 由此可知:-
(2n )2 en
p(A)。
例5、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → u”(t),其中 D(A) = {u C2[0,1]:u(0) = u(1),u’(0) = u’(1)}。 则 A 是闭算子。讨论 A 的谱集。 解: -(2n )2时,考虑方程
射。由此可知点谱为空集。
例3、设 X = C[0,1],定义 X 上的线性算子 A:u(t) → tu(t)。讨论 A 的谱集。 解: (2) 任取 v(t) X,考虑方程 u(t) – tu(t) = v(t), 当 > 1 或者 t [0,1]。 (2) < 0 时,h(t) = ( - t)-1 X。
子的谱的结构不同。
例5、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → u”(t),其中 D(A) = {u C2[0,1]:u(0) = u(1),u’(0) = u’(1)}。 则 A 是闭算子。讨论 A 的谱集。 解:由无限维情形的分类可知只需要讨论
2
(1) I – A 是否为单射;以及
此时,R( I – A) = X,可知
(A)。
例4、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → tu(t)。讨论 A 的谱集。 解: (2) 考虑方程 u(t) – tu(t) = v(t), a.e. t [0,1]。 若 [0,1],令 v = 1,则
-1
1
(3)
u(t) = ( - t) ,
a.e. t [0,1]。
显然 u X,即 R( I - A) ≠ X。
因此,
(A)。
例4、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → tu(t)。讨论 A 的谱集。 解: (2) 考虑方程 u(t) – tu(t) = v(t), a.e. t [0,1]。 另一
un(t) – tun(t) = vn(t), a.e. t [0,1]。
c(A)。
因此, R( I A) ,即 X
例4、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → tu(t)。讨论 A 的谱集。
1
结论: (A) =
c(A)
= [0,1],
(A) = R\[0,1] 。 可见,在不同的函数空间里面,形式相同的算
[
n
2
(2n ) ]( u,en )en
n
2
(v,en )en
(5)
在(5)中对比 en 之前的系数可得 (v,en ) ( u,en ) (2n )2
例5、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → u”(t),其中 D(A) = {u C2[0,1]:u(0) = u(1),u’(0) = u’(1)}。 则 A 是闭算子。讨论 A 的谱集。 (v,en ) e D ( A) , 解:直接验证可知 u 2 n (2n ) n 并且 2 | (v,en ) | 2 2 || u || M || v || 2 2 | (2n ) | n
2
u(t) – u”(t) = v(t)。
(4)
由于 {en:n 为整数} 是 X 的正交规范基,可得
u
n
( u,en )en,v
n
(v,en )en
例5、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → u”(t),其中 D(A) = {u C2[0,1]:u(0) = u(1),u’(0) = u’(1)}。 则 A 是闭算子。讨论 A 的谱集。 解:于是可得
p(A);
证明若 a ≠ 0,则 a+ib 证明 A 为闭算子。
(A);
(1) ib
p(A),即方程
(ib - A)x = 0 有非 0 解,
ibt ( ) x ( t ) = e 令 直接解微分方程 ,则
(Ax)(t) = ibeibt = ibx(t),
即 Ax = ibx,ib 为点谱,x为对应特征向量。
= {-(2n ) :n 为整数},
(A) = C\{-(2n )2:n 为整数} 。
A 是闭算子由 (A) 非空即得。
例4、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → tu(t)。讨论 A 的谱集。 解: (1) 考虑方程 u(t) – tu(t) = 0, a.e. t [0,1], 函数 f(t) = – t 最多只有一个零点,可知
1
u(t) = 0,
a.e. t [0,1]。
即 I - A为单射,由此可知点谱为空集。
线性算子的谱理论
谱理论的重要性
1、考虑线性常微分方程组:
x ( t ) Ax( t )。
一方面,求方程的解只需要求出矩阵 A 的特 征值即得解为 x(t) = eAtx0;另一方面,解的 稳定性等价于矩阵 A 的特征值实部为负。 2、特征子空间是不变子空间,在更小的空间 讨论算子的性质往往要方便些……
若 y(t) 有界,令 s + ,则 t y( t ) e ( t ) x( )d e
0
(2) 由于 a > 0,可知积分 y(t) 收敛,并且 | y(t)| ≤ a-1|| x ||, t R。
由 x 一致连续,知 y 一致连续。从而,y X。 因此, ( I - A)y = x 有解,即 ||( I - A)-1|| ≤ a-1。 若 a < 0,在 y(t ) y( s )e 令s - ,类似地讨论
因此,方程 (2) 有解 u(t) = h(t)v(t)。
此时,R( I – A) = X,而在 (1) 中已经证明了
I – A 是单射,因此
(A)。
例3、设 X = C[0,1],定义 X 上的线性算子 A:u(t) → tu(t)。讨论 A 的谱集。 解: (2) 任取 v(t) X,考虑方程 u(t) – tu(t) = v(t), 当 t [0,1]。 (2)
(2) I – A 的值域与 X 的关系。
例5、设 X = L [0,1],定义 X 上的线性算子 A:u(t) → u”(t),其中 D(A) = {u C2[0,1]:u(0) = u(1),u’(0) = u’(1)}。 则 A 是闭算子。讨论 A 的谱集。 解:由例1.6.26,令en = e2n it,则 {en:n 为整数}
[0,1]时,只有当 v( ) = 0 时方程 (2) 才可
解。否则令 t =
上式即矛盾。
显然,非 0 常数函数不能由这一类函数逼近,
即 R( I A) X ,从而,
r(A)。
例3、设 X = C[0,1],定义 X 上的线性算子 A:u(t) → tu(t)。讨论 A 的谱集。
结论: (A) =
(2) 证明若 a ≠ 0,则 = a+ib 设 a > 0,对 x X,证明
(A)。
y X,使得
( I - A) y = x, 即如下常微分方程在 X 中有解
