投资组合的预期收益率的计算
证券投资理论(6学时)

图9-5阴影区域中所有证券组合的收益与风险都可以进 行比较,以便从中选择出最佳组合:即在一定风险条 件下获得最大收益或在一定收益条件下将风险水平降 到最低。
根据这个准则,可以确定位于阴影区域中最左上面的 曲线NB为有效边界:在NB边界上的所在点代表的投资 组合满足上述的准则,同种风险水平下期望收益最高; 同等期望收益水平下风险最小。这个有效边界便是投 资者进行多种证券投资时应选择的有效投资组合。
(2)
AB
1。这表示两种证券期望收益之间是完全负相
关关系,证券组合的风险会大大降低,因为这是A、B两种证券
风险相互抵消的结果。如果适当地选择组合中A、B证券的比重, 就可以完全消除组合的非系统风险。
E(R) B D M 6.67 5 A
10
O
4
8
图9-3 两种证券的组合
从图9-3观察到MB线和MA线所代表的证券组合有
组合中证券的数量
图9-1证券组合投资的风险分散效应
二、证券投资组合期望收益与风险的计算 (一)单个证券的期望收益与风险的衡量
1. 期望收益
期望收益,也称为预期收益率、期望值,它是未来所有可能 获得的收益率的加权平均数。其计算公式为:
E R—期望收益率; Ri —第i种可能的收益率; Pi —收益率发生的概率; n—可能性的数目。
证券投资理论 (6学时)
知识目标
·掌握证券组合投资理论的基本原理; ·掌握资本资产定价理论模型; ·了解套利定价模型; ·掌握有效金融市场的概念及类型; ·了解行为金融学的主要内容
技能目标
·能够对单个证券的风险收益进行分析; ·能够根据证券市场线模型计算证券组合的 收益率。
证券投资组合理论
基准收益率计算公式

基准收益率计算公式基准收益率是金融领域中的重要指标,用于衡量投资组合的表现。
它是指某一特定投资组合所能达到的最低预期收益率。
基准收益率计算公式是根据投资组合中不同资产的权重和各资产的收益率进行加权平均得出的。
基准收益率计算公式如下:基准收益率 = (A1 * R1 + A2 * R2 + ... + An * Rn) / (A1 +A2 + ... + An)其中,A1、A2、...、An分别代表投资组合中第1个、第2个、...、第n个资产的权重;R1、R2、...、Rn分别代表第1个、第2个、...、第n个资产的收益率。
为了更好地理解基准收益率计算公式,我们将通过一个具体的例子进行解释。
假设某个投资组合中包含三个不同的资产,它们的权重分别为0.4、0.3和0.3,对应的收益率为0.05、0.02和0.03。
我们可以按照公式计算基准收益率。
基准收益率 = (0.4 * 0.05 + 0.3 * 0.02 + 0.3 * 0.03) /(0.4 + 0.3 + 0.3)经过计算,得出基准收益率为0.035,即3.5%。
基准收益率的计算公式反映了投资组合中各资产的权重对投资组合整体收益率的贡献程度。
权重越大的资产对基准收益率的影响越大。
因此,在选择和调整投资组合时,需要对各资产的收益率和权重进行综合考虑,以获得满足预期的基准收益率。
需要注意的是,基准收益率的计算公式只适用于合理分配权重的投资组合。
如果投资组合中存在非理性的权重分配,如权重之和不等于1或存在负权重,那么计算出的基准收益率将失去实际意义。
此外,基准收益率还有其他的计算方法,如等权重法和市值加权法。
等权重法将所有资产的权重设为相等,市值加权法则根据资产的市值确定其权重。
这些计算方法可以根据实际情况选择合适的方法来计算基准收益率。
总之,基准收益率是衡量投资组合表现的重要指标,通过加权平均资产收益率的方式计算得出。
准确计算基准收益率对于投资者了解投资组合的表现并作出相应的调整非常重要。
资本定价模型计算公式

资本定价模型计算公式资本定价模型(Capital Asset Pricing Model, 简称CAPM)是一种金融学理论,旨在预测股票投资的风险和收益。
它建立在假设之上,即投资者想要追求最大化回报,并且对市场变动性感到恐惧。
CAPM的核心思想是,投资者应该选择收益和风险之间的最佳平衡:该模型的结论是,如果一个投资者持有市场上所有股票,那么他的收益将达到最大化。
这就是CAPM主要用来说明的,即投资者应该在具有不同风险的投资中选择正确的权衡。
资本定价模型是通过一个简单的公式来计算的,公式如下:E (Ri) = Rf + βi [E (RM) - Rf]其中:E(Ri):预期证券i的收益率。
Rf:无风险利率,也称为基准利率。
βi:相对于市场(RM)的证券i风险系数。
E(RM):市场投资组合(Market Portfolio)的预期收益率。
从公式中可以看出,资本定价模型的计算主要依赖于三个变量:无风险利率、市场投资组合的预期收益率以及证券的风险系数。
无风险利率是指政府债券的收益率,它代表了一个高度信用的投资者可以获得的最低收益,而不会面临任何风险。
无风险利率的估计可以通过分析当前政府债券的收益率及市场上政府债券的购买行为来完成。
市场投资组合是指市场上所有股票的投资组合,它是一个综合性指标,代表了市场上所有股票的收益率。
市场投资组合的估计可以通过分析市场上所有股票的收益率及其购买行为来完成。
证券的风险系数(βi)是一种测量投资者面临的风险水平的指标,它表明了证券的波动程度,以及该投资者在市场上可能面临的变动程度。
一般来说,证券的风险系数越大,投资者就越可能面临较高的风险。
资本定价模型的计算公式可以用来预测投资者在不同市场条件下可能面临的收益和风险。
CAPM的公式可以帮助投资者判断其所投资的股票的预期收益率是否超过了市场的预期收益率。
资本定价模型的计算公式特别有用,它可以帮助投资者决定自己的投资策略,以及如何投资以获得最大化收益。
财务管理题目与解答
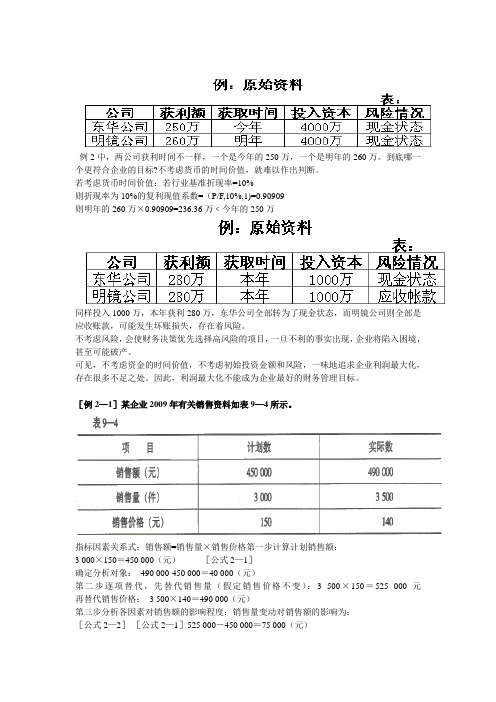
例2中,两公司获利时间不一样,一个是今年的250万,一个是明年的260万。
到底哪一个更符合企业的目标?不考虑货币的时间价值,就难以作出判断。
若考虑货币时间价值:若行业基准折现率=10%则折现率为10%的复利现值系数=(P/F,10%,1)=0.90909则明年的260万×0.90909=236.36万﹤今年的250万同样投入1000万,本年获利280万,东华公司全部转为了现金状态,而明镜公司则全部是应收账款,可能发生坏账损失,存在着风险。
不考虑风险,会使财务决策优先选择高风险的项目,一旦不利的事实出现,企业将陷入困境,甚至可能破产。
可见,不考虑资金的时间价值,不考虑初始投资金额和风险,一味地追求企业利润最大化,存在很多不足之处。
因此,利润最大化不能成为企业最好的财务管理目标。
[例2—1]某企业2009年有关销售资料如表9—4所示。
指标因素关系式:销售额=销售量×销售价格第一步计算计划销售额:3 000×150=450 000(元)[公式2—1]确定分析对象:490 000-450 000=40 000(元)第二步逐项替代,先替代销售量(假定销售价格不变):3 500×150=525 000元再替代销售价格:3 500×140=490 000(元)第三步分析各因素对销售额的影响程度:销售量变动对销售额的影响为:[公式2—2]-[公式2—1]525 000-450 000=75 000(元)销售价格变动对销售额的影响为:[公式2—3]-公式2—2]490 000-525 000=-35 000(元)第四步验证两个因素共同影响使销售额增加75 000-35 000=40 000(元)与分析对象吻合。
2、差额分析法这是直接用实际数与计划数之间的差额来计算各因素对指标变动影响程度的分析方法。
[例2—2]以上例资料为例,分析如下:由于销售量变动而影响的销售额:(3 500-3 000)×150=75 000(元)由于销售价格变动而影响的销售额:3 500×(140-150)=-35 000(元)两个因素共同影响,使销售额发生的差异为:75 000-35 000=40 000(元)1、某公司拟于5年后一次还清所欠债务100000元,假定银行利息率为10%,5年10%的年金终值系数为6.1051,5年10%的年金现值系数为3.7908,则应从现在起每年末等额存入银行的偿债基金为多少元?2、拟购买一只股票,预期公司最近两年不发股利,从第三年开始每年支付0.2元股利,若资金成本率为10%,则预期股利现值合计为多少?3、A公司拟构建一条新生产线,项目总投资800万元,建设期为2年,可以使用6年。
组合投资收益率的公式

组合投资收益率的公式【篇一:组合投资收益率的公式】()教授“the valuation of risk assets selection of risky investments in stock portfolio capital budget,” re s, 1965.[] 投资组合的基本理论马考维茨经过大量观察和分析,他认为若在具有相同回报率的两个证券之间进行选择的话,任何投资者都会选择风险小的。
这同时也表明投资者若要追求高回报必定要承担高风险。
同样,出于的原因,投资者通常持有多样化投资组合。
马考维茨从对回报和风险的定量出发,系统地研究了投资组合的特性,从数学上解释了投资者的避险行为,并提出了投资组合的。
一个投资组合是由组成的各证券及其权重所确定。
因此,投资组合的期望回报率是其成分证券期望回报率的加权平均。
除了确定期望回报率外,估计出投资组合相应的风险也是很重要的。
投资组合的风险是由其回报率的标准方差来定义的。
这些是描述回报率围绕其平均值变化的程度,如果变化剧烈则表明回报率有很大的不确定性,即风险较大。
从投资组合方差的数学展开式中可以看到投资组合的方差与各成分证券的方差、权重以及成分证券间的有关,而协方差与任意两证券的成正比。
相关系数越小,其协方差就越小,投资组合的总体风险也就越小。
因此,选择不相关的证券应是构建投资组合的目标。
另外,由投资组合方差的数学展开式可以得出:增加证券可以降低投资组合的风险。
基于回避风险的假设,马考维茨建立了一个投资组合的分析模型,其要点为:(1)投资组合的两个相关特征是期望回报率及其方差。
(2)投资将选择在给定风险水平下期望回报率最大的投资组合,或在给定期望回报率水平下风险最低的投资组合。
(3)对每种证券的期望回报率、方差和与其他证券的进行估计和挑选,并进行数学规划(mathematicalprogramming),以确定各证券在投资者资金中的比重。
[]投资组合理论的新发展(一)基于交易费用和流动性的投资组合理论如果市场是无效的和存在摩擦的,就会导致交易成本的存在,而的流动性直接与交易成本相关。
第0209讲 证券资产组合的预期收益率、方差

知识点:证券资产组合的收益与风险★★★(客、主)两个或两个以上资产所构成的集合,称为资产组合。
如果资产组合中的资产均为有价证券,该资产组合称为证券资产组合。
证券资产组合的收益与风险具有与单个资产不同的特征。
尽管收益率的方差、标准差、标准差率是衡量风险的有效工具,但当某项资产或证券成为投资组合的一部分时,这些指标就可能不再是衡量风险的有效工具。
一、证券资产组合的预期收益率证券资产组合的预期收益率是组成证券资产组合的各种资产收益率的加权平均数。
其权数为各种资产在组合中的价值比例。
E(R p)=∑[W i×E(R i)]其中:E(R p):证券组合的预期收益率W i:第i项资产所占比重E(R i):第i项资产预期收益率【提示】这意味着资产组合的收益率最低不会低于组合中收益率最低的那项资产的收益率,最高不会超过组合中收益率最高的那项资产的收益率。
换言之,在低收益率资产A的基础上加入高收益率资产B,组合AB的收益率将介于(A的收益率,B的收益率)之间。
【例题】某投资公司的一项投资组合中包含A、B和C三种股票,投资者共投资100万元,权重分别为30%、40%和30%,三种股票的预期收益率分别为15%、12%、10%。
要求计算该投资组合的预期收益率。
『正确答案』该投资组合的预期收益率E(R P)=30%×15%+40%×12%+30%×10%=12.3%或者:该投资组合的预期收益率=(100×30%×15%+100×40%×12%+100×30%×10%)/100=12.3%【例题·计算分析题】(2017年)资产组合M的期望收益率为18%,标准差为27.9%;资产组合N的期望收益率为13%,标准差率为1.2。
投资者张某和赵某决定将其个人资金投资于资产组合M和N中,张某期望的最低收益率为16%,赵某投资于资产组合M和N的资金比例分别为30%和70%。
财务管理题目与解答

例2中,两公司获利时间不一样,一个是今年的250万,一个是明年的260万。
到底哪一个更符合企业的目标?不考虑货币的时间价值,就难以作出判断。
若考虑货币时间价值:若行业基准折现率=10%则折现率为10%的复利现值系数=(P/F,10%,1)=0.90909则明年的260万×0.90909=236.36万﹤今年的250万同样投入1000万,本年获利280万,东华公司全部转为了现金状态,而明镜公司则全部是应收账款,可能发生坏账损失,存在着风险。
不考虑风险,会使财务决策优先选择高风险的项目,一旦不利的事实出现,企业将陷入困境,甚至可能破产。
可见,不考虑资金的时间价值,不考虑初始投资金额和风险,一味地追求企业利润最大化,存在很多不足之处。
因此,利润最大化不能成为企业最好的财务管理目标。
[例2—1]某企业2009年有关销售资料如表9—4所示。
指标因素关系式:销售额=销售量×销售价格第一步计算计划销售额:3 000×150=450 000(元)[公式2—1]确定分析对象:490 000-450 000=40 000(元)第二步逐项替代,先替代销售量(假定销售价格不变):3 500×150=525 000元再替代销售价格:3 500×140=490 000(元)第三步分析各因素对销售额的影响程度:销售量变动对销售额的影响为:[公式2—2]-[公式2—1]525 000-450 000=75 000(元)销售价格变动对销售额的影响为:[公式2—3]-公式2—2]490 000-525 000=-35 000(元)第四步验证两个因素共同影响使销售额增加75 000-35 000=40 000(元)与分析对象吻合。
2、差额分析法这是直接用实际数与计划数之间的差额来计算各因素对指标变动影响程度的分析方法。
[例2—2]以上例资料为例,分析如下:由于销售量变动而影响的销售额:(3 500-3 000)×150=75 000(元)由于销售价格变动而影响的销售额:3 500×(140-150)=-35 000(元)两个因素共同影响,使销售额发生的差异为:75 000-35 000=40 000(元)1、某公司拟于5年后一次还清所欠债务100000元,假定银行利息率为10%,5年10%的年金终值系数为6.1051,5年10%的年金现值系数为3.7908,则应从现在起每年末等额存入银行的偿债基金为多少元?2、拟购买一只股票,预期公司最近两年不发股利,从第三年开始每年支付0.2元股利,若资金成本率为10%,则预期股利现值合计为多少?3、A公司拟构建一条新生产线,项目总投资800万元,建设期为2年,可以使用6年。
收益率的概念

收益率的概念收益率是一种用于衡量投资回报率的指标。
它可以帮助投资者评估他们的投资表现以及做出合理的投资决策。
在金融领域,收益率通常指的是投资组合或资产在一定时间内所产生的盈利。
收益率是根据投资的成本和收益计算出来的。
收益率可以根据不同的计算方法和时间周期来衡量。
最常见的收益率计算方法是简单收益率和复合收益率。
简单收益率是根据资产价格的变化计算出来的。
它是在投资期间内资产价格变化的百分比。
简单收益率的计算公式为:(资产终值-资产初始值)/ 资产初始值。
复合收益率是基于资产连续复利计算出来的。
它考虑到了投资期间内的利息、股利、分红等回报。
复合收益率通常更准确地反映了投资者的实际回报率。
收益率可以用于评估各种类型的投资,包括股票、债券、基金、房地产等。
它可以帮助投资者比较不同投资之间的潜在回报,以及评估不同投资策略的风险和回报。
收益率的概念可以通过以下几个方面来理解和应用。
首先,收益率是投资回报的度量。
它可以帮助投资者了解他们的投资是否盈利,以及盈利的程度。
如果投资的收益率为正,则表示投资者获得了正向的回报;如果收益率为负,则表示投资者亏损。
通过计算投资的收益率,投资者可以更加准确地了解他们的投资表现,从而做出更好的投资决策。
其次,收益率可以帮助投资者进行风险评估。
通常情况下,高回报的投资往往伴随着高风险。
通过计算投资的收益率,投资者可以比较不同投资之间的风险和回报,并选择适合自己需求的投资策略。
例如,如果某个投资的收益率非常高,但伴随着非常高的风险,那么投资者可能需要权衡利益和风险,并决定是否进行投资。
第三,收益率可以帮助投资者进行资产配置和组合管理。
通过计算不同资产的收益率,投资者可以了解各种投资之间的相关性和差异,从而优化他们的资产配置。
在投资组合管理中,收益率是评估投资组合表现的重要指标之一。
投资者可以通过比较投资组合的收益率和风险,调整投资组合的权重和比例,以实现最优的投资组合。
最后,收益率可以帮助投资者评估投资者的长期目标和投资计划。
