信息论第6章有噪信道编码
合集下载
北工大信息论第六章 有噪信道编码14
0.8 0.2 [PY|X ] 0.1 0.9
转移矩阵各行元素乘以对应的输入概率，得联合概率矩阵
0.32 0.08 [PXY ] 0.06 0.54
译码规则F1对应的平均差错率为
s
Pe (F1) 1 P[F1(bj ), bj ] j 1 1 [P(a1b1) P(a1b2 )] 1 (0.32 0.08) 0.6
j 1
s
s
1 P(bj F (bj )) 1 P(bja*j )
j 1
j 1
Pe
P（aibj )
P（ai )P(bj | ai )
Y X a*
Y X a*
当输入等概:
上式可化为：
P[F(bj )] P a*j 1/ r
Pe
1 r
Y
P(bj | ai )
X a*
例6-1： 参见下图，假设P(a1)=0.4,分别求出4种译码规 则所对应的平均差错率。
最大后验概率条件可等价为最大联合概率条件,为什么呢?
P(a*j | bj ) P(ai | bj ) P(bj )P(a*j | bj ) P(bj )P(ai | bj ) P(a*jbj ) P(aibj )
则最佳译码规则又可表示为：
F：FP((ba*jjb)
j)
a*j A，bj P(aibj )
F1：FF（ （ 11 bb12
) )
a1 a1
F3：FF（ （ 33 bb21
) )
a1 a2
F2：FF（ （ 22 bb12
) )
a2 a2
F4：FF（ （ 44 bb12))
a2 a1
二.错误译码概率 “好”的译码规则的标准是：错误译码概率小
信息论基础课件第6章有噪信道编码
0
0
p p
1 p
p 0.01
1
p p 1
01
0p p
[P]
1
p
p
F (0) 0 F (1) 1
PE
PE m in
1 r
s j 1
i*
p(b j
/
ai
)
1 2
(
p
p) 102
➢ 重复发送可以使PE减小 但是：信息传输率降低
传输消息:
重复码
0, 0 00
1 1 11
校验元
若传000, 收到误传为100,010,001中的任一 种, 则认为是传的000，实现了纠错。
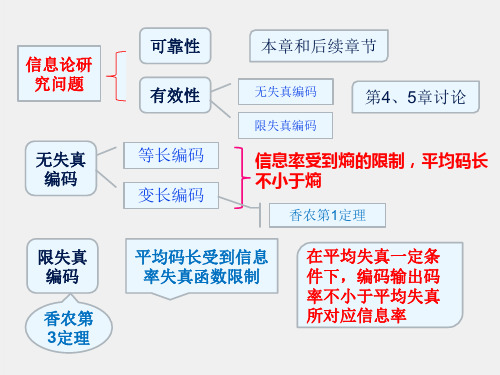
6.1 信道编码的概念
第5章结论：在无噪无损信道上，只要对信源 的输出进行恰当的编码，总能以信道容量C 无差错地传输信息。
实际信道都有噪声干扰，本章研究香农第二 定理，即通信的可靠性问题。包括：
1.怎么使有噪信道中消息传输错误达到最少? 2.在有噪信道中无错误传输的可达的最大信息
传输率是什么?
信道编码概述
0.57
2 编码方法
• 上一节结论： 消息通过有噪信道传输时会发生错误 错误概率与译码规则有关
• 噪声干扰：破坏了信号的内部结构－－产生畸变 而造成信息的损失。
• 提高信号抗噪声干扰能力：改造信号使其内部结 构具有更强的规律性或相关性，当信号的部分结 构被破坏时，仍能根据信号原有的内在规律和相 关性来发现甚至纠正错误，恢复原来的信息。
• 通信系统模型
消息集中 一个元素
信道波形 空间中的
一个点
失真后 的波形
恢复的 消息
信源 编码
信道 编码
信道
信道 译码
信息论第6章 有噪信道编码
2
6.1噪声信道的编码问1错误概率与译码规则
8
6.1.2译码规则
S个输出符号中的每一个都可以译成r个输入符号中的任何一个。
9
10
11
（X－X*）表示译码规则 之外对应的X
p( y j )
12
13
14
15
16
17
一般来说，后验概率是难以确定的，所有应用起来很不方便，这时引入极大似然译码规则
41
00－
01－
10－
11－
42
43
44
可见，汉明距离用来定量描述符号序列之间的“相似”程度， D越大，码字间相似性越小，反之，D越小，码字间相似性越大。
45
46
47
48
49
50
编码 选用M个消息所对应的码字间最 小距离dmin尽可能大的编码方法； 译码采用将接收序列bj译成与之距离 最近的那个码字ai的译码规则；
35
6.2.2消息符号个数
36
37
38
39
6.2.3（5，2）线性码
Ɩ（5，2）线性码：码长为5，码字的前2个码元是信息位，后3个码元是校验位。 一般来说，如果码长是N，信息位数目为K，那么校验位为（N－K）位， 这种码称为（N，K）分组码。
40
则四个消息分别为00，01，10， 11
51
52
53
54
55
56
关于香农第二定理的说明：
说明1：从上述定理可知，任何信道的信道容量 是一个明确的分界点，当取分界点以下的信息 传输率时，PE以指数趋于零；当取分界点以上 的信息传输率时、PE以指数趋于1。因此，在任 何信道中信道容量是可达的、最大的可靠信息 传输率。 说明2：香农第二定理只是一个存在定理，它只 说明错误概率趋于零的好码是存在的，但没有 给出令人满意的构码方法
信息论基础第6章有噪信道编码定理[103页]
![信息论基础第6章有噪信道编码定理[103页]](https://img.taocdn.com/s3/m/29f089d31ed9ad51f11df279.png)
6.5.2 线性分组码的译码
在二元域中，少 1 个方程导致 2 个解，少 2 个方程导致 22 个解，
以此类推，少 k 个方程导致 2k 个解，即每个伴随式对应的错误图样
有 2k 个解。究竟取哪一个作为错误图样的解呢？根据最小汉明距离
译码规则，应该取重量最小者作为 E 的估值。但是如果每接收一个码 字就要解一次线性方程，太麻烦。当 n-k 不大时，通常预先把不同 S 下的方程组解出来，把各种情况下的最小汉明距离译码输出列成一个 码表，称为标准阵列译码表。在实时译码时就不必解方程组，而只要 查标准阵列译码表就可以了。
《信息论基础》
第6章 有噪信道编码
本章内容
6.1 错误概率
6.7 卷积码
6.2 有噪信道编码定理
6.8 交织码
6.3 联合信源信道编码定理 6.9 级联码
6.4 信道编码的基本概念
6.10 Turbo码
6.5 线性分组码
6.11 LDPC码
6.6 循环码
《信息论基础》
6.1 错误概率
6.1.1 错误概率和译码规则
信道编码的实质就是通过牺牲有效性来换取可靠性的提高。在信
息码元中加入监督码元的多少，可以通过冗余度 来衡量。例如，每
3 个信息码元中加入 1 个监督码元，这时冗余度 1/ 4 。信道编码的
任务就.4.1 信道编码的分类
①
按照信道特性和设计的码字类型进行划分，信道编码可
标准阵列译码表为一个 2nk 行 2k 列的码表，用来存放接收码字
R rn1,rn2 ,,r1,r0 可能的 2n 种组合。
构造标准阵列译码表，一般可以采用以下几个步骤： ① 根据最小汉明距离译码规则，确定各伴随式对应的差错图样。
信息论与编码-第6章 有噪信道编码
p(e|bj)=1-p(ai|bj)=1-p[F(bj)|bj]
平均错误译码概率:
PE p(b j ) P(e | b j ) p(b j )[1 P(ai | b j )]
j 1 j 1
s
s
最小错误概率准则
问题: 如何选择p(ai|bj)? 使p(e|bj)最小, 就应选 择p[F(bj)|bj]为最大, 即选择译码函数
简单重复编码
根据这个规则计算得译码后的错误概率为
Y , X a
PE
p ( i ) p ( j | i ) p( j | i )
1 = M
Y , X a
1 3 2 2 2 2 2 2 3 ( p pp pp pp pp pp pp p ) 2 p 3 3 pp 2 3*104 ( p 0.01)
X a ,Y
p ( ai ) p (b j | ai ) p (ai ) pe( i )
X X Y
X a ,Y
p (b j | ai ) p (ai ) F (b j ) a
如果先验概率p(ai)相等, 则: 1 PE Pe( i ) r X
第6.1节 错误概率与译码规则
1 [(0.2 0.3) (0.3 0.3) (0.2 0.4)] 0.567 3
第6.1节 错误概率与译码规则
0.5 0.3 0.2 P 0.2 0.3 0.5 for A 0.3 0.3 0.4 若采用前述译码函数A, 则平均错误率为: 1 PE P(b | a ) 3 Y , X a*
p2 p pp 2
4
平均错误译码概率:
PE p(b j ) P(e | b j ) p(b j )[1 P(ai | b j )]
j 1 j 1
s
s
最小错误概率准则
问题: 如何选择p(ai|bj)? 使p(e|bj)最小, 就应选 择p[F(bj)|bj]为最大, 即选择译码函数
简单重复编码
根据这个规则计算得译码后的错误概率为
Y , X a
PE
p ( i ) p ( j | i ) p( j | i )
1 = M
Y , X a
1 3 2 2 2 2 2 2 3 ( p pp pp pp pp pp pp p ) 2 p 3 3 pp 2 3*104 ( p 0.01)
X a ,Y
p ( ai ) p (b j | ai ) p (ai ) pe( i )
X X Y
X a ,Y
p (b j | ai ) p (ai ) F (b j ) a
如果先验概率p(ai)相等, 则: 1 PE Pe( i ) r X
第6.1节 错误概率与译码规则
1 [(0.2 0.3) (0.3 0.3) (0.2 0.4)] 0.567 3
第6.1节 错误概率与译码规则
0.5 0.3 0.2 P 0.2 0.3 0.5 for A 0.3 0.3 0.4 若采用前述译码函数A, 则平均错误率为: 1 PE P(b | a ) 3 Y , X a*
p2 p pp 2
4
信息论课后习题答案
第六章 有噪信道编码6.1 R 为信息传输率，根据香农第二定理，当码长n->无穷大时，满足什么关系式，可使错误概率Pe->0。
答：Pe<exp{-nE(R)}->0，其中E(R)为可靠性函数，且在9<R<C 的范围为正。
信道容量C 是保证无差错传输时，信息传输率R 的权限值。
6.2 写出费诺不等式，其中哪一项表示是否判对的疑义度，log(k-1)又表示什么？答：H(X|Y)<=H2(Pe)+Pelog(k-1) ，H2(pe)是否判对的疑义度。
表示如果判决出错，错在k-1个符号中的一个，疑义度不会超过log(k-1)。
6.3 根据香农定理说明，（信息容量）是保证无差错传输时信息传输率R 的上限值，（平均错误概率）是信源可压缩信息的最低极限。
6.4 最大后验概率译码准则就是最小错误译码准则，对吗？错误。
()∑≠-==≠=k i k i k k e y x y xy x x y p )|(1)|()|(φφφ 这个公式可知最大后验概率与最小错误译码准则所得的最终结果是相等的。
但并非概念定义一致。
6.5 在信源等该分布时，则极大似然函数译码准则就是最小错误译码准则，对吗？ Proof: if ())|(|k k x y p x y p > m=1,2,……,MThen 信道等概率输入时，有),()(m k x q x q = 代入上式得)()|()()|(m m k k x q x y p x q x y p >So,it comes to )()(y x p y x p m k >所以说明全概率最大，对应最大联合概率译码准则。
1/2 1/6 1/36.6 离散无记忆信道DMC ，转移概率矩阵为 P= 1/3 1/2 1/61/6 1/3 1/2(1 )q(x1)=1/2 q(x2)=1/4 q(x3)=1/4. 求最佳判决译码及错误概率。
（2）若信源等概分布，求最佳判决译码及错误概率。
《信息论与编码》课件第6章 信道编码理论
X
信源编码
Y
差错控制 编码
Z
调制
信息错误
数据错 误一定
物理信道
条件：实
信宿
重建 符号
Xˆ
信源译码
Yˆ 差错控制 Zˆ
接收 信息
译码
接收 数据
解调
注
际信息传 输速率不 大于信道
容量，
意 1.信道一定，数据出现差错的概率一定，这是无
法改变的，与差错控制编码/译码方式无关
2.数据出现差错的概率不可改变，但是可以通过引 入差错控制编码/译码，降低信息传递中的错误
即如何选择 译码规则和 编码方法
减少信道传 输中的信息 差错
由于信道噪声或者干扰的存在， 会产生数据传输错误。
信道编码定理，也 称为香农第二定理
通信原理告诉我们，信噪声为例， 介绍虚警概率、漏报概率，以及 计算错误概率的过程和方法
原始
数
符号
信息
据
信源
(4) 纠正t个随机错误, ρ个删除,则要求码的最小距离满足 d0 ≥ ρ +2t+1
分组码的最小汉明距离满足下列关系
d0 n k 1
奇偶校验码是只有一个检验元的分组码 最小汉明距离为2，只能检测一个错误， 不能纠错。
是不等式， 不能用于计
算d0
差错 控制 译码 已知 条件
任务
6.3 译码规则
p( y)
p( y)
﹝ ❖ 考虑y的取值 两者之间比较
P(0 | y 0)
(1 pe ) p
p(1 pe ) (1 p) pe
P(1| y 0)
(1 p) pe
p(1 pe ) (1 p) pe
﹝ 两者之间比较
信源编码
Y
差错控制 编码
Z
调制
信息错误
数据错 误一定
物理信道
条件：实
信宿
重建 符号
Xˆ
信源译码
Yˆ 差错控制 Zˆ
接收 信息
译码
接收 数据
解调
注
际信息传 输速率不 大于信道
容量，
意 1.信道一定，数据出现差错的概率一定，这是无
法改变的，与差错控制编码/译码方式无关
2.数据出现差错的概率不可改变，但是可以通过引 入差错控制编码/译码，降低信息传递中的错误
即如何选择 译码规则和 编码方法
减少信道传 输中的信息 差错
由于信道噪声或者干扰的存在， 会产生数据传输错误。
信道编码定理，也 称为香农第二定理
通信原理告诉我们，信噪声为例， 介绍虚警概率、漏报概率，以及 计算错误概率的过程和方法
原始
数
符号
信息
据
信源
(4) 纠正t个随机错误, ρ个删除,则要求码的最小距离满足 d0 ≥ ρ +2t+1
分组码的最小汉明距离满足下列关系
d0 n k 1
奇偶校验码是只有一个检验元的分组码 最小汉明距离为2，只能检测一个错误， 不能纠错。
是不等式， 不能用于计
算d0
差错 控制 译码 已知 条件
任务
6.3 译码规则
p( y)
p( y)
﹝ ❖ 考虑y的取值 两者之间比较
P(0 | y 0)
(1 pe ) p
p(1 pe ) (1 p) pe
P(1| y 0)
(1 p) pe
p(1 pe ) (1 p) pe
﹝ 两者之间比较
第六章有噪信道编码
p( x i / y j ) = p( x i ) p( y j / x i ) p( y j ) p( x * ) p( y j / x )
p( 样，当信道输入符号集X的先验概率为等概时，根 这样，当信道输入符号集X的先验概率为等概时， 据最大后验概率译码准则， 据最大后验概率译码准则， p(x*)p(yj/x*)≥p(xi)p(yj/xi) (i=1,2,……n) 最大后验概率可以用最大信道转移概率来取代。 最大后验概率可以用最大信道转移概率来取代。
使用最大后验概率译码准则必须已知后验概率，一般 使用最大后验概率译码准则必须已知后验概率， 说来，后验概率很难确定， 说来，后验概率很难确定，但信道的统计特性描述总 是给出信道转移概率， 是给出信道转移概率，因此利用信道转移概率的译码 准则。 准则。 由概率中的贝叶斯定理可有： 由概率中的贝叶斯定理可有：
6.1.2译码准则 6.1.2译码准则
定义6.1.1 定义6.1.1 设信道 输入符号集X={x ,i=1,2,…,r}, 输入符号集X={xi,i=1,2, ,r}, 输符号集为Y={y ,j=1,2,…,s}, 输符号集为Y={yj,j=1,2, ,s}, 若对每一个输出符号y 若对每一个输出符号yj都有一个确定的函数 对应于惟一的一个输入符号x F(yj)，使yj对应于惟一的一个输入符号xi，则 这样的函数为译码规则。 这样的函数为译码规则。 F(yj)=xi (i=1,2,…r; j=1,2,…s) 对于有r个输入， 个输出的信道来说， 对于有r个输入，s个输出的信道来说，可以 rs个不同的译码准则 个不同的译码准则。 有rs个不同的译码准则。
消息集中 一个元素
信道波形 空间中的 一个点
失真后 的波形
恢复的 消息
信信 编编
p( 样，当信道输入符号集X的先验概率为等概时，根 这样，当信道输入符号集X的先验概率为等概时， 据最大后验概率译码准则， 据最大后验概率译码准则， p(x*)p(yj/x*)≥p(xi)p(yj/xi) (i=1,2,……n) 最大后验概率可以用最大信道转移概率来取代。 最大后验概率可以用最大信道转移概率来取代。
使用最大后验概率译码准则必须已知后验概率，一般 使用最大后验概率译码准则必须已知后验概率， 说来，后验概率很难确定， 说来，后验概率很难确定，但信道的统计特性描述总 是给出信道转移概率， 是给出信道转移概率，因此利用信道转移概率的译码 准则。 准则。 由概率中的贝叶斯定理可有： 由概率中的贝叶斯定理可有：
6.1.2译码准则 6.1.2译码准则
定义6.1.1 定义6.1.1 设信道 输入符号集X={x ,i=1,2,…,r}, 输入符号集X={xi,i=1,2, ,r}, 输符号集为Y={y ,j=1,2,…,s}, 输符号集为Y={yj,j=1,2, ,s}, 若对每一个输出符号y 若对每一个输出符号yj都有一个确定的函数 对应于惟一的一个输入符号x F(yj)，使yj对应于惟一的一个输入符号xi，则 这样的函数为译码规则。 这样的函数为译码规则。 F(yj)=xi (i=1,2,…r; j=1,2,…s) 对于有r个输入， 个输出的信道来说， 对于有r个输入，s个输出的信道来说，可以 rs个不同的译码准则 个不同的译码准则。 有rs个不同的译码准则。
消息集中 一个元素
信道波形 空间中的 一个点
失真后 的波形
恢复的 消息
信信 编编
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
可编辑ppt
定理
分组码最小汉明距离与检错和纠错能力的关系:
1）dmin e (t为纠错个数） 用于FEC
3）dmin e t 1（e>t） 用于HEC（又检又纠）
↑→ 检错和纠错能力↑
可编辑ppt
dmin e 1
可编辑ppt
可编辑ppt
4
差错控制方式
差错控制方式一般可以分为四种类型：
• 检错重发（ARQ） • 前向纠错（FEC） • 混合纠错检错（HEC） • 信息反馈（IRQ）
可编辑ppt
汉明距离与最大似然译码
• 定理 对于一个二进制对称信道，如果信道输 入码字为等概率分布，则其最大似然译码可以 等价于最小汉明距离译码。
8
dmin 2t 1
可编辑ppt
9
dmin e t 1
可编辑ppt
10
可编辑ppt
1
译码规则的选择依据: 使平均错误概率最小。
最小错误概率准则
选择译码函数F(bj)=a*并使之满足条件: p(a*|bj)≥p(ai|bj) （对所有ai≠a*）
极大似然译码准则
• 选择译码函数F(bj)=a*,使满足 p(bj|a*)p(a*)≥p(bj|ai)p(ai)，即p(a*bj)≥p(aibj)。
可编辑ppt
2
有噪信道编码定理 ——香农第二定理
定理1 设有一离散无记忆平稳信道，其信道容量为C，
只要待传送的信息传输率 R＜C，则存在一种编码， 当输入序列长度n足够大时，使译码错误概率任意小。 物理含义：
(1) 只要R＜C，就可以在有噪信道中以任意小 的错误概率(pE＜)传输信息；
(2) 当输入序列长度n足够大时，可以以任意接 近信道容量C的信息传输率传递信息。
第六章 有噪信道编码
错误概率与信道的统计特性有关, 但并不是唯一相 关的因素, 译码方法的选择也会影响错误率。
➢ 信道统计特性 信道统计特性用信道传递矩阵来描述, 该矩阵确 定了哪些是正确传递概率, 哪些是错误传递概率. ➢ 译码规则
通信过程并非到信道输出端就结束, 还要经过 译码过程(或判决过程)才到达消息的终端(收信者).
可编辑ppt
3
定理2 有噪信道编码定理的逆定理 设有一离散无记忆平稳信道，其信道容量为C，
对于任意>0，若要选用码字总数M=2n(C+ )，则无论
n取多大，也找不到一种编码，使译码错误概率任
意小。
物理含义： 在任何信道中，信道容量C是进行可靠传输的最大 信息传输率。要想使信息传输率大于信道容量而 又无错误地传输消息是不可能的。
定理
分组码最小汉明距离与检错和纠错能力的关系:
1）dmin e (t为纠错个数） 用于FEC
3）dmin e t 1（e>t） 用于HEC（又检又纠）
↑→ 检错和纠错能力↑
可编辑ppt
dmin e 1
可编辑ppt
可编辑ppt
4
差错控制方式
差错控制方式一般可以分为四种类型：
• 检错重发（ARQ） • 前向纠错（FEC） • 混合纠错检错（HEC） • 信息反馈（IRQ）
可编辑ppt
汉明距离与最大似然译码
• 定理 对于一个二进制对称信道，如果信道输 入码字为等概率分布，则其最大似然译码可以 等价于最小汉明距离译码。
8
dmin 2t 1
可编辑ppt
9
dmin e t 1
可编辑ppt
10
可编辑ppt
1
译码规则的选择依据: 使平均错误概率最小。
最小错误概率准则
选择译码函数F(bj)=a*并使之满足条件: p(a*|bj)≥p(ai|bj) （对所有ai≠a*）
极大似然译码准则
• 选择译码函数F(bj)=a*,使满足 p(bj|a*)p(a*)≥p(bj|ai)p(ai)，即p(a*bj)≥p(aibj)。
可编辑ppt
2
有噪信道编码定理 ——香农第二定理
定理1 设有一离散无记忆平稳信道，其信道容量为C，
只要待传送的信息传输率 R＜C，则存在一种编码， 当输入序列长度n足够大时，使译码错误概率任意小。 物理含义：
(1) 只要R＜C，就可以在有噪信道中以任意小 的错误概率(pE＜)传输信息；
(2) 当输入序列长度n足够大时，可以以任意接 近信道容量C的信息传输率传递信息。
第六章 有噪信道编码
错误概率与信道的统计特性有关, 但并不是唯一相 关的因素, 译码方法的选择也会影响错误率。
➢ 信道统计特性 信道统计特性用信道传递矩阵来描述, 该矩阵确 定了哪些是正确传递概率, 哪些是错误传递概率. ➢ 译码规则
通信过程并非到信道输出端就结束, 还要经过 译码过程(或判决过程)才到达消息的终端(收信者).
可编辑ppt
3
定理2 有噪信道编码定理的逆定理 设有一离散无记忆平稳信道，其信道容量为C，
对于任意>0，若要选用码字总数M=2n(C+ )，则无论
n取多大，也找不到一种编码，使译码错误概率任
意小。
物理含义： 在任何信道中，信道容量C是进行可靠传输的最大 信息传输率。要想使信息传输率大于信道容量而 又无错误地传输消息是不可能的。