数学八年级上册十字相乘法
数学人教版八年级上册十字相乘法分解因式

什么是因式分解? 把一个多项式分解成几个整式的积的形式,叫做 把这个多项式因式分解,也叫把这个多项式分解 因式.
前面我们都学习了哪些分解因式的方法? 提取公因式法、公式法
公式法中常用的乘法公式
平方差公式:a2-b2=(a+b)(a-b)
完全平方公式:a2±2ab+b2=(a±b)2
(1)X2-7x+12 (4)x2-11x-12 (2)x2-4x-12 (5)x2+13x+12 (3)x2+8x+12 (6)x2-x-12
对于x2+px+q (1)当q>0时,a、b﹍﹍,且a、b的符号与p的符号﹍﹍。
异号 a、b中绝对值较大的因数 (2)当q<0时,a、b﹍﹍,且﹍﹍﹍﹍﹍﹍﹍与 p的符号相同。 同号 相同
十字相乘法(借助十字交叉线分解因式的方法)
例一:分解因式
( x 7 )( x 1 )步骤: x 6 x 7
2
7 x 1 x 7 x 6 x
x
①竖分二次项与常数项 ②交叉相乘,和相加 ③检验确定,横写因式
顺口溜:
竖分常数交叉验,
横写因式不能乱。
将下列各式用十字相乘法进行因式分解
1、口答计算结果
(x+3)(x+4)= (x+3)(x- 4)= (x- 3)(x+4)= (x- 3)(x- 4)= x2+7x+12 x2-x-12 x2+x-12 x2-7x+12
2、提问:你有什么快速计算类似以 上多项式的方法吗?
两个一次二项式相乘的积
整式的乘法
一个二次三项式
人教版八年级数学上册《十字相乘法分解因式》课件

即:x 2+(p+q)x+pq=(x+p)(x+q)
实际在使用此公式时,需要把 一次项系数和常数项进行分拆,在 试算时,会带来一些困难。
下面介绍的方法,正好解决了 这个困难。
即:x 2+(p+q)x+pq=(x+p)(x+q)
=(2x +y)(x-2y)+3x+4y-2
=(2x +y-1)(x-2y+2)
2
1
(2x+y)
-1
1
-2 (x-2y)
2
-4+1=-3
2(2x+y) - (x- 2 y)=3x+4y
x
p
x
q
x2 px+qx=(p+q)x pq
十字相乘法:
对于二次三项式的分解因式,
借用一个十字叉帮助我们分解因式, 这种方法叫做十字相乘法。
例1 分解因式 x2-6x+8
解:x 2-6x+8
x
-2
=:分解因式 (x-y)2+(x-y) -6
对于一般地二次三项式ax+2 bx+c (a≠0) 此法依然好用。
• 8、普通的教师告诉学生做什么,称职的教师向学生解释怎么做,出色的教师示范给学生,最优秀的教师激励学生。下午6时56 分41秒下午6时56分18:56:4121.11.7
练习:将下列各式分解因式 1、 7x 2-13x+6 答案(7x+6)(x+1)
2、 -y 2-4y+12 答案- (y+6)(y-2)
例2 分解因式 3x2-10x+3
解:3x 2-10x+3
x
-3
=(x-3)(3x-1) 3x
-1
-9x-x=-10x
例3 分解因式 5x2-17x-12
十字相乘法(八年级数学精品课件)
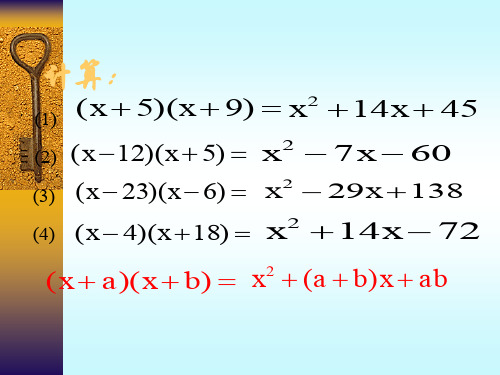
例2、把 y4-7y2-18 分 解因式
例3、把 x2-9xy+14y2 分解因式
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是:“头尾
十字相乘法
“十字相乘法”是乘法公式: (x+a)(x+b)=x2+(a+b)x+ab的反 向运算,它适用于分解二次三 项式。
例1、把 x2+6x-7分解因式
十字相乘法(借助十字交叉线分解因式的方法)
例一:
x2 6x 7 (x 7)(x 1)
x
7
x 1
x7x 6x
因式分解:
(1) x2 14x 45= (x 5)(x 9) (2) x2 7 x 60= (x 12)(x 5)
(3) x2 29x 138= (x 23)(x 6)
(4) x2 14x 72= (x 4)(x 18) x2 (a b)x ab = (x a)(x b)
分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
数学人教版八年级上册十字相乘法

(4)横写结论:x2+bx+c=(x+c1)(x+c2)
将下列多项式分解因式
(1)x2+7x+10 (2)x2-x-6 =(x+2)(x+5) =(x+2)(x-3)
(3)x2-7x+12 (4)x2-12x+20
=(x-3)(x-4) =(x-2)(x-10)
(5)x3+6x2-27x =x(x+9)(x-3)
则a+b=-5,ab=p
因为,满足a+!
将下列多项式分解因式
(1)x2-20xy+64y2 =(x-4y)(x-16y)
(2)5x2+6xy-8y2 =(x+2y)(5x-4y) =(2x-y)(3x-2y)
(3)6x2-7xy+2y2
拓展提高
1.要使二次三项式x2+px+5在整数范围内能进行因 6,-6 。 式分解,那么P的取值是______
2
3x 2 ( x 1)( x 2) 5 x 6 ( x 2)( x 3) 3x 4 ( x 1)( x 4) 5 x 6 ( x 2)( x 3)
归纳:x2+(p+q)x+pq= (x+p)(x+q)
• (2)x
2 2 2
2.用十字相乘法因式分解ax2+bx+c
例2:分解因式:12x2-5x-2
解: 12x2-5x-2
3x 4x
-2
+1
3x*1+4x*(-2)=-5x
12x2-5x-2=(3x-2)(4x+1)
人教版八年级数学上册 《十字相乘法》整式的乘法与因式分解PPT

归纳
用十字相乘法分解因式的步骤:
1
-2
1
-6
-2 + -6
1.分解首尾系数
2.交叉相乘
= -8
3.相加验证 4.横向写出因式
第十三页,共四十四页。
首一的十字相乘法
什么是十字相乘法?
如何用十字相乘法分解二次系数为1的二次三项式?
第十四页,共四十四页。
练习
用十字相乘法分解因式:
第十五页,共四十四页。
第八页,共四十四页。
12=1×12
归纳
试着把常数项分成两个整数的积
然后看这两个数之和是否等于一次项系数
是否
否
相等
是
写出分解结果
第九页,共四十四页。
思考 不难发现,如果常数项的因数比较多, 可能需要多次试数才能成功.
那有没有什么方法能让试数过程更直观呢?
十字相乘法就可以做到,下面我们来学习一下.
第十页,共四十四页。
其中p,q是不相等的正数. 三种方案哪种提价最多?
第四十四页,共四十四页。
练习
用十字相乘法分解因式:
第十六页,共四十四页。
练习
用十字相乘法分解因式:
第十七页,共四十四页。
练习
用十字相乘法分解因式:
第十八页,共四十四页。
思考
刚才我们分解的都是二次项系数为1的情况, 如果二次项系数不是1,也能用这个方法分解吗?
用十字相乘法分解因式:
1.分解首尾系数
3
2.交叉相乘
1
3.相加验证
人教版八年级数学上册 《十字相乘法》整式的乘法与因式分解PPT
科 目:数学 适用版本:人教版 适用范围:【教师教学】Fra bibliotek十字相乘法
十字相乘法 人教版八年级数学上册

解:(1) x4 - y4=(x2+y2)(x2-y2) = (x2+y2)(x+y)(x-y)
(2) (y2 + x2 )2 - 4x2y2 =(y2 + x2 +2xy) (y2 + x2 -2xy) =(x+y)2(x-y)2
(3) x4-8x2+16=(x2-4)2
=(x+2)2(x-2)2
=x2-3x+2
= x2+5x+6 = x2-x-6 = x2+x-6
= x2-5x+6
整式的乘法
两个一次二项式相乘的积
一个二次三项式
(x+a)(x+b)=x2+(a+b)x+ab
反过来,得
x2+(a+b)x+ab=(x+a)(x+b)
一个二次三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数q能 分解成两个因数a、b的积,即q=ab而且一次 项系数p又恰好是a、b的和,即p=a+b,那么 x2+px+q就可以进行如上的因式分解。
对于x2+px+q
(1)当q>0时,a、b﹍同﹍号,且a、b的符号与p的符号﹍相同﹍。 (2)当q<0时,a、b﹍异﹍号 ,且a、﹍b﹍中﹍绝对﹍值﹍较﹍大﹍的﹍因数﹍与p的符号相同。
例2:试将 x2 6x 16 分解因式
解: x2 6x 16
x2 6x 16
x 8x 2
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
我
行分解。
八年级数学上册分解因式之十字相乘法

1.十字相乘法分解因式的公式: x2+(a+b)x+ab=(x+a)(x+b) 2.能用十字相乘法来分解因式的二次三项式的系数的 特点:常数项能分解成两个数的积,且这两个数的和 恰好等于一次项的系数。 3.在用十字相乘法分解因式时,因为常数项的 分解因数有多种情况,所以通常要经过多次的 尝试才能确定采用哪组分解来进行分解因式。 4.十字相乘法的方法简单来讲就是: 十字左边相乘等于二次项系数, 右边相乘等于常数项,交叉相乘的和等于一次项系数。 其实就是运用乘法公式(x+a)(x+b)=x² +(a+b)x+ab 的逆运算来进行因式分解。
2 x +(a+b)x+ab=(x+a)(x+b)
因式分解
两个一次二项式相乘的积
一个二次三项式
反过来,得
一个二次三项式
如果二次三项式x2+px+q中的常数项系数q能分 解成两个因数a、b的积,而且一次项系数p又恰好 是a+b,那么x2+px+q就可以进行如上的因式分解。
试一试:把x2+3x+2分解因式
将下列多项式因式分解
(1)x2+3x-4 (7)(a+b)2-4(a+b)+3
(2)x2-3x-4
(3)x2+6xy-16y2
(8) x4-3x3 -28x2
(9) (10) 2x2-7x+3 5x2+6xy-8y2
(4)x2-11xy+24y2
(5)x2y2-7xy-18
(6)x4+13x2+36
(2) 常数项是负数时,它分解成两个异号因数, 其中绝对值较大的因数和一次项系数符号相同。
(完整版)初中数学十字相乘法因式分解

初中数学十字相乘法因式分解要点:一、2()x p q x pq +++型的因式分解特点是:(1)二次项的系数是1(2)常数项是两个数之积(3)一次项系数是常数的两个因数之和。
对这个式子先去括号,得到:pq x q p x +++)(2)()(22pq qx px x pq qx px x +++=+++=))(()()(q x p x p x q p x x ++=+++=1的二次三项式分解因式。
二、一般二次三项式2ax bx c ++的分解因式大家知道,2112212122112()()()a x c a x c a a x a c a c x c c ++=+++。
反过来,就可得到:2121221121122()()()a a x a c a c x c c a x c a x c +++=++我们发现,二次项系数a 分解成12a a ,常数项c 分解成12c c ,把1212,,,a a c c 写成1122a c a c ⨯,这里按斜线交叉相乘,再相加,就得到1221a c a c +,那么2ax bx c ++就可以分解成1122()()a x c a x c ++.这种借助画十字交叉线分解系数,从而将二次三项式分解因式的方法,叫做十字相乘法。
【典型例题】[例1] 把下列各式分解因式。
(1)232++x x (2)672+-x x 分析:(1)232++x x 的二次项的系数是1,常数项212⨯=,一次项系数213+=,这是一个pq x q p x +++)(2型式子。
(2)672+-x x 的二次项系数是1,常数项)6()1(6-⨯-=,一次项系数=-7)1(- )6(-+,这也是一个pq x q p x +++)(2型式子,因此可用公式pq x q p x +++)(2+=x ( ))(q x p +分解以上两式。
解:(1)因为212⨯=,并且213+=,所以)2)(1(232++=++x x x x(2)因为)6()1(6-⨯-=,并且)6()1(7-+-=-,所以)6)(1(672--=+-x x x x[例2] 把下列各式因式分解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学八年级上册十字相乘法1十字相乘法顺口溜
1.首尾分解,交叉相乘,求和凑中,平行书写。
竖分常数交叉验,横写因式不能乱。
2.竖分常数交叉验
(1)竖分二次项和常数项, 即把二次项和常数项的系数竖向写出来,
(2)交叉相乘, 和相加, 即斜向相乘然后相加,得出一次项系数,
(3)检验确定, 检验一次项系数是否正确。
3.横写因式不能乱,即把因式横向写,而不是交叉写, 这里不能搞乱。
2十字相乘法的注意事项
十字分解法的方法简单来讲就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数。
其实就是运用乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。
(1)用来解决两者之间的比例问题。
(2)得出的比例关系是基数的比例关系。
(3)总均值放中央,对角线上,大数减小数,结果放在对角线上。
