准滑动模态控制matlab仿真实例.
滑模变结构控制课件

Yoerger and Slotine (1985), Slotine and Li(1991), Healey and Lienard (1993) and Mc Gookin et al. (2000a, 2000b)
精品课件
滑模变结构控制的定义
有一控制系统状态方程为
超面 s(x) 0上,并选择这样的 s(x)使滑模面上运动是渐
近稳定的。 (2)滑动模态运动具有完全自适应性。
不受系统摄动和外界扰动的影响。滑模变结构控制 系统的最突出的优点,成为它受到重视的最主要原因。 (3)存在的问题—抖振。
不可避免的惯性等原因使得系统在光滑滑动模态上 叠加了一个自振,这是滑模变结构控制理论尚存在的一 精品课件些问题中最突出的问题。
选择控制律 u (x) :使正常运动段的品质得到提高。 选择切换函数 s(x): 使滑动模态运动段的品质改善。
精品课件
滑模变结构控制设计方法
设计滑模变结构控制器的基本步骤包括两个相对 独立的部分:
(1)设计切换函数 s(x),使它所确定的滑动模态渐近稳定且具有良 好的动态品质; ①线性: s(x) Cx,C Rn 主要适用于速度和精度要求都不高的非线性系统。
n1]v
1 Kˆ
wind
Kds
Ks
sgn(s)
1 s0
sgn(s)
0
s0
精品课件
1 s 0
Tˆ, Kˆ , nˆ3为T,K,n3的估
计值,目标求取Kd,Ks,
则控制律设计完成。
⑤通过控制律,保证系统渐近稳定-----V (s) 0 恒成立。
V (s) [n3r2 n1 Kd ]s2 Ks | s |
自动控制原理MATLAB仿真实验(于海春)

自动控制原理MATLAB仿真实验(于海春)实验一典型环节的MATLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB软件,在命令窗口栏“>>”提示符下键入imulink命令,按Enter键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个imulink仿真环境常规模板。
图1-1SIMULINK仿真界面图1-2系统方框图3.在imulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击imulink下的“Continuou”,再将右边窗口中“TranferFen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在imulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的imulink的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击imulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
5)选择输出方式。
滑模变结构控制方法

20世纪50年代: 前苏联学者Utkin和Emelyanov提出了变结构控制的概念,研究对象:二阶线性系统。 20世纪60年代: 研究对象:高阶线性单输入单输出系统。主要讨论高阶线性系统在线性切换函数下控制受限与不受限及二次型切换函数的情况。 1977年: Utkin发表一篇有关变结构控制方面的综述论文,系统提出变结构控制VSC和滑模控制SMC的方法。同时,在1992年详细讨论了滑模技术。
正常运动段:位于切换面之外, 如图的 段所示。
滑模变结构控制的整个控制过程由两部分组成:
滑模变结构控制的品质取决于这两段运动的品质。由于尚不能一次性地改善整个运动过程品质,因而要求选择控制律使正常运动段的品质得到提高。 选择切换函数使滑动模态运动段的品质改善。两段运动各自具有自己的高品质。 选择控制律 :使正常运动段的品质得到提高。 选择切换函数 : 使滑动模态运动段的品质改善。
滑模变结构控制发展历史
此后 各国学者开始研究多维滑模变结构控制系统,由规范空间扩展到了更一般的状态空间中。 我国学者贡献: 高为炳院士等首先提出趋近律的概念,首次提出了自由递阶的概念。 海洋运载器方面的应用: Yoerger and Slotine (1985), Slotine and Li(1991), Healey and Lienard (1993) and Mc Gookin et al. (2000a, 2000b)
定义1:系统结构 系统的一种结构为系统的一种模型,即由某一组数学方程描述的模型。系统有几种不同的结构,就是说它有几种(组)不同数学表达式表达的模型。 定义2 :滑动模态 人为设定一经过平衡点的相轨迹,通过适当设计,系统状态点沿着此相轨迹渐近稳定到平衡点,或形象地称为滑向平衡点的一种运动,滑动模态的”滑动“二字即来源于此。
MATLAB控制系统仿真-simulink

6 4 u 2 0
系统为一个两输入两输出系统 》A=[1 6 9 10; 3 12 6 8; 4 7 9 11; 5 12 13 14]; 》B=[4 6; 2 4; 2 2; 1 0]; 》C=[0 0 2 1; 8 0 2 2]; 》D=zeros(2,2);
第五节
一、模型的转换
• 举例应用: 1)exp3_2.m 系统1为:
0 x1 1 y 1 1
1 0 x1 u1 2 1 3 x 1 u 1
系统2为:
0 x2 1 y 2 1 1 0 x2 u2 3 1 4 x 2
0 . 25 i s 2i 2 s 1
2s 9s 1
3
k= 2
结果表达式: G ( s ) 2
0 . 25 i s 2i
第四节
状态空间描述
状态方程与输出方程的组合称为状态空间表达式,又称 为动态方程,经典控制理论用传递函数将输入—输出关 系表达出来,而现代控制理论则用状态方程和输出方程 来表达输入—输出关系,揭示了系统内部状态对系统性 能的影响。
零极点增益模型: G ( s ) 4 3 2 s 9 s 45 s 87 s 50 》num=[1,11,30,0]; 》den=[1,9,45,87,50]; [z,p,k]=tf2zp(num,den) 》 z= p= k= 0 -6 -5 -3.0000+4.0000i -3.0000-4.0000i -2.0000 1
用法举例: 0 1)已知系统状态空间模型为: x 1
y 1
1 0 x u 2 1 3 x u
》A=[0 1; -1 -2]; B=[0;1]; 》C=[1,3]; D=[1]; 》[num,den]=ss2tf(A,B,C,D,iu) %iu用来指定第n个输入,当只有一个输入时可忽略。 》num=1 5 2; den=1 2 1; 》[z,p,k]=ss2zp(A,B,C,D,iu) 》z= -4.5616 p= -1 k=1 -0.4384 -1
matlab的simulink仿真建模举例

matlab的simulink仿真建模举例Matlab的Simulink仿真建模举例Simulink是Matlab的一个工具包,用于建模、仿真和分析动态系统。
它提供了一个可视化的环境,允许用户通过拖放模块来构建系统模型,并通过连接和配置这些模块来定义模型的行为。
Simulink是一种功能强大的仿真平台,可以用于解决各种不同类型的问题,从控制系统设计到数字信号处理,甚至是嵌入式系统开发。
在本文中,我们将通过一个简单的例子来介绍Simulink的基本概念和工作流程。
我们将使用Simulink来建立一个简单的电机速度控制系统,并进行仿真和分析。
第一步:打开Simulink首先,我们需要打开Matlab并进入Simulink工作环境。
在Matlab命令窗口中输入"simulink",将会打开Simulink的拓扑编辑器界面。
第二步:创建模型在拓扑编辑器界面的左侧,你可以看到各种不同类型的模块。
我们将使用这些模块来构建我们的电机速度控制系统。
首先,我们添加一个连续模块,代表电机本身。
在模块库中选择Continuous中的Transfer Fcn,拖动到编辑器界面中。
接下来,我们添加一个用于控制电机速度的控制器模块。
在模块库中选择Discrete中的Transfer Fcn,拖动到编辑器界面中。
然后,我们需要添加一个用于输入参考速度的信号源模块。
在模块库中选择Sources中的Step,拖动到编辑器界面中。
最后,我们添加一个用于显示模拟结果的作用模块。
在模块库中选择Sinks 中的To Workspace,拖动到编辑器界面中。
第三步:连接模块现在,我们需要将这些模块连接起来以定义模型的行为。
首先,将Step模块的输出端口与Transfer Fcn模块的输入端口相连。
然后,将Transfer Fcn模块的输出端口与Transfer Fcn模块的输入端口相连。
接下来,将Transfer Fcn模块的输出端口与To Workspace模块的输入端口相连。
Matlab仿真实验-自动控制原理

实验一 典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB 中SIMULINK 是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK 功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB 软件,在命令窗口栏“>>”提示符下键入simulink 命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK 仿真环境下。
2.选择File 菜单下New 下的Model 命令,新建一个simulink 仿真环境常规模板。
3.在simulink 仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:图1-1 SIMULINK 仿真界面 图1-2 系统方框图1)进入线性系统模块库,构建传递函数。
点击simulink 下的“Continuous ”,再将右边窗口中“Transfer Fen ”的图标用左键拖至新建的“untitled ”窗口。
2)改变模块参数。
在simulink 仿真环境“untitled ”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK ,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink 的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math ”右边窗口“Gain ”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink 下的“Source ”,将右边窗口中“Step ”图标用左键拖至新建的“untitled ”窗口,形成一个阶跃函数输入模块。
MATLAB仿真实例(计算机仿真研究的步骤)
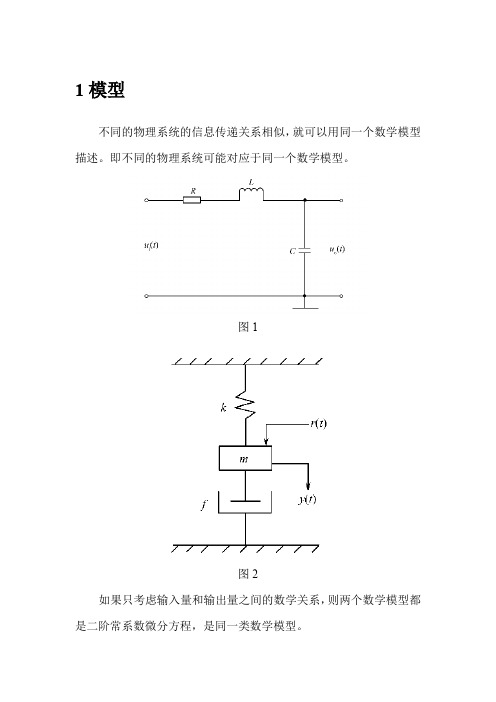
(1.1)
这是一个二阶常微分方程,为了后续步骤的需要,将它转换成状态方 程及输出方程
0 1 x k x 2 m 1 x1 0 f 1 r x m 2 m
当m1k4时分析系统在外力rt1t的作用下要使响应不发生振荡应在什么范围内取值其中f的取值约束为10建立系统的数学模型描述该系统输入输出关系的数学模型为11这是一个二阶常微分方程为了后续步骤的需要将它转换成状态方程及输出方程数学模型转换成仿真模型采用数值积分法中的欧拉公式可以得到离散状态方程及输出方编程和调试采用matlab语言进行编程文件名为exam20001m
【例 2.2】 利用 Simulink 对【例 2.1】中的质量-弹簧-阻尼器系统进 行仿真研究。 【解】 首先将描述该系统输入—输出关系的数学模型改写成传递 函数形式
G (s) Y (s) 1 2 R ( s ) ms fs k
(1.6)
从 Simulink 模块库的信号源子库(Sources)中,选择 Step 模块, 拖 入模型窗口,双击该模块,设置参数 Step time 为:0;从 Simulink 模 块库的连续模块子库(Continuous)中,选择 Tranfer Fcn 模块,拖入 模型窗口, 双击该模块,设置参数 Numerator 为:[1], Denominator [1 f 4] ; 为: 从 Simulink 模块库的接收器子库 (Sinks) 中, 选择 Scope 模块,拖入模型窗口。
% 置状态变量初值,其中 x(i)代表 xi(0) % Y 为 N×1 阵,记录输出 y,初始时为 1×1 阵,
% H 为 N×1 阵,记录时间 t,初始时为 1×1 阵 xs=x+(A*x+B)*T; % 计算离散状态方程
Matlab控制系统的仿真课件

(2)建立导数函数
function dy=cap(t,y) Vi=20; R=5; C=70e-6; dy=(Vi-y)/(R*C); (3)使用ode函数进行仿真,仿真时间0~0.006s,Vc 初始值为0V。
>> [t,y]=ode45('cap',[0,0.006],0); >> plot(t,y) >> axis([0 0.006 0 25]) >> title('Vc-Time') >> xlabel('Time/sec') >> ylabel('Vc/V')
例:根据传递函数求解零点、极点和增益,并判断该
系统是否稳定。
2 s2 3 s 4 H (s)3 s6 4 s5 5 s4 6 s3 7 s2 8 s 9
建立文件control2.m num=[2 3 4]; den=[3 4 5 6 7 8 9]; [z,p,k]=tf2zp(num,den); disp('zeros:'); z disp('poles:'); p disp('gain3:'); k
Q= -0.4605
7.2 微分方程模型
7.2.1 方法描述 微分方程模型是数学模型的一种主要形式。当采用
一阶微分方程的数值积分法进行数值计算时,应把高阶 微分方程变换成n个一阶微分方程形式。对于微分方程 而言,除了少数可以得到解析解外,大多数只能采用数 值解法。
在MATLAB中,使用ode函数建立微分方程模型。 7.2.2 范例分析 例:在RC低通滤波器电路中,电阻R=5Ω,理想电压 源为Vi=20V,电容C=70μF。分析电容元件的时域特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
准滑动模态控制 2.8.1准滑动模态控制 在滑动模态控制系统中,如果控制结构的切换具有理想的开关特性,则能在切换面上形成理想的滑动模态,这是一种光滑的运动,渐进趋近于原点。但在实际工程中,由于存在时间上的延迟和空间上的滞后等原因,使得滑动模态呈抖振形式,在光滑的滑动上叠加了抖振。理想的滑动模态是不存在的,现实中的滑动模态控制均伴随有抖振,抖振问题是影响滑动模态看控制广泛应用的主要障碍。 所谓准滑动模态,是指系统的运动轨迹被限制在理想滑动模态的某一领域内的模态。从相轨迹方面来说,具有理想滑动模态的控制是使一定范围内的状态点均被吸引至切换面。而准滑动模态控制则是使一定范围内的状态点均被吸引至切换面的某一领域内,通常称此领域为滑动模态切换面的边界层。 在边界层内,准滑动模态不要求满足滑动模态的存在条件,因此准滑动模态不要求在切换面上进行控制结构的切换。它可以在边界层上进行结构变换的控制系统,也可以根本不进行结构变换的连续状态反馈控制系统。准滑动模态控制在实现上的这种差别,使它从根本上避免或削弱了抖振,从而在实际中得到了广泛的应用。 在连续系统中,常用的准滑动模态控制有以下两种方法: (1) 用饱和函数()sats代替理想滑动模态中的符号函数sgn()s。 1()1ssatsksss
1k
(2.46)
其中称为“边界层”。饱和函数()sats如图2-26所示,饱和函数的本质为:在边界层外,采用切换控制;在边界之内,采用线性化反馈控制。 (2) 将继电特性连续化,用连续函数()s取代sgn()s。
()sss (2.47)
式中是很小的正常数。 2.8.2 仿真实例 对象为二阶传递函数: 2()pbGssas
其中25,133ab。 将传递函数描述为位置状态方程的形式: .xxu
其中010a, 0b。 设位置指令信号为r,则 ......[(1)](2)[(1)](2)scrxdrxscrxrxslaw
采用指数趋近律: sgn()slawsks
将(2)(2)xaxbu代入上式,得控制律为 ...1
[((2))(2)]ucrxrslawaxb
系统的初始状态为0.50。在仿真程序中,指令为正弦信号。1M
为指数趋近律,2M为采用饱和函数的指数趋近律,3M为采用继电特性的指数趋近律。取51C,15,30k,进行如下几种仿真: (1)采用指数趋近律。取1M,正弦跟踪结果如图所示。 00.511.522.533.544.55-0.8-0.6-0.4-0.200.20.40.6time(s)r,yout
正弦跟踪(M=1)
00.511.522.533.544.55-0.100.10.20.30.40.50.6
time(s)error
误差曲线(M=1) -0.100.10.20.30.40.50.6-3-2-101234ede
相轨迹(M=1)
00.511.522.533.544.55-10123456
time(s)s
切换函数s(M=1) 00.511.522.533.544.55-0.4-0.200.20.40.60.811.21.41.6time(s)u
控制器输出(M=1) (2)验证准滑动模态控制。2M为采用饱和函数的方法,取5.0,仿真结果如图所示。
00.511.522.533.544.55-0.8-0.6-0.4-0.200.20.40.6
time(s)r,yout
正弦信号跟踪(M=2) 00.511.522.533.544.55-0.100.10.20.30.40.50.6time(s)error
误差曲线(M=2)
-0.100.10.20.30.40.50.6-3-2-101234
ede
相轨迹(M=2) 00.511.522.533.544.55-10123456time(s)s
切换函数s(M=2)
00.511.522.533.544.55-1-0.500.511.52
time(s)u
控制器输出(M=2) (3)3M为采用继电特性的方法,取0.05,仿真结果如图所示 00.511.522.533.544.55-0.8-0.6-0.4-0.200.20.40.6time(s)r,yout
正弦信号跟踪(M=3)
00.511.522.533.544.55-0.100.10.20.30.40.50.6
time(s)error
误差曲线(M=3) -0.100.10.20.30.40.50.6-3-2-101234ede
相轨迹(M=3)
00.511.522.533.544.55-10123456
time(s)s
切换函数s(M=3) 00.511.522.533.544.55-1-0.500.511.52time(s)u
控制器输出(M=3) 仿真程序如下:
(1) 主程序:figure2_8.m clear all; close all; global a b c A F M ep k delta ts=0.001; T=5; TimeSet=[0:ts:T]; c=5.0; para=[]; [t,x]=ode45('figure2_8eq',TimeSet,[-0.5 0],[],para); x1=x(:,1); x2=x(:,2); r=A*sin(2*pi*F*t); dr=A*2*pi*F*cos(2*pi*F*t); ddr=-A*(2*pi*F)^2*sin(2*pi*F*t); s=c*(r-x(:,1))+dr-x(:,2); if M==1 slaw=-ep*sign(s)-k*s; %Exponential velocity trending law u=1/b*(c*(dr-x(2))+ddr-slaw+a*x(2)); elseif M==2 kk=1/delta; for i=1:1:T/ts+1; if s(i)>delta sats(i)=1; elseif abs(s(i))<=delta sats(i)=kk*s(i); elseif s(i)<-delta sats(i)=-1; end slaw(i)=-ep*sats(i)-k*s(i); u(i)=1/b*(c*(dr(i)-x2(i))+ddr(i)-slaw(i)+a*x2(i)); end elseif M==3 for i=1:1:T/ts+1; ths(i)=s(i)/(abs(s(i))+delta); slaw(i)=-ep*ths(i)-k*s(i); u(i)=1/b*(c*(dr(i)-x2(i))+ddr(i)-slaw(i)+a*x2(i)); end end
figure(1); plot(t,r,'r',t,x(:,1),'b'); xlabel('time(s)'); ylabel('r,yout'); figure(2); plot(t,r-x(:,1),'r'); xlabel('time(s)'); ylabel('error'); figure(3); plot(r-x(:,1),dr-x(:,2),'r',r-x(:,1),-c*(r-x(:,1)),'b'); %draw line (s=0) xlabel('e'); ylabel('de'); figure(4); plot(t,s,'r'); xlabel('time(s)'); ylabel('s'); figure(5); plot(t,u,'r'); xlabel('time(s)'); ylabel('u'); (2)控制子程序:figure2_8eq.m
function dx=DynamicModel(t,x,flag,para) global a b c A F M ep k delta
a=25;b=133; A=0.50;F=1.0;
