五年级奥数题精选 (1)
人教版【精选】小学五年级奥数题及答案(可直接打印) 图文百度文库

人教版【精选】小学五年级奥数题及答案(可直接打印) 图文百度文库一、拓展提优试题1.如图,在等腰直角三角形ABC中,斜边AB上有一点D,已知CD=5,BD 比AD长2,那么三角形ABC的面积是.2.如图,从A到B,有条不同的路线.(不能重复经过同一个点)3.数一数,图中有多少个正方形?4.鸡与兔共100只,鸡的脚比兔的脚多26只.那么,鸡有只.5.用0、1、2、3、4这五个数字可以组成个不同的三位数.6.(1)数一数图1中有个三角形.(2)数一数图2中有个正方形.7.如图,若每个小正方形的边长是2,则图中阴影部分的面积是.8.如图,若长方形S长方形ABCD=60平方米,S长方形XYZR=4平方米,则四边形S四边=平方米.形EFGH9.李双骑车以320米分钟的速度从A地驶向B地,途中因自行车故障推车继续向前步行5分钟到距B地1800米的某地修车,15分钟后以原来骑车速度的1.5倍继续向前驶向B地,到达B地时,比预计时间多用17分钟,则李双推车步行的速度是米/分钟.10.如图,将一个等腰三角形ABC沿EF对折,顶点A与底边的中点D重合,若△ABC的周长是16厘米,四边形BCEF的周长是10厘米,则BC=厘米.11.如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是.12.从1、2、3、4、5中任取3个组成一个三位数,其中不能被3整除的三位数有个.13.如图是一个正方体的平面展开图,若该正方体相对的两个面上的数值相等,则a﹣b×c的值是.14.(7分)如图,按此规律,图4中的小方块应为个.15.若2副网球拍和7个网球一共220元,且1副网球拍比1个网球贵83元.求网球的单价.【参考答案】一、拓展提优试题1.解:作CE⊥AB于E.∵CA=CB,CE⊥AB,∴CE=AE=BE,∵BD﹣AD=2,∴BE+DE﹣(AE﹣DE)=2,∴DE=1,在Rt△CDE中,CE2=CD2﹣DE2=24,=•AB•CE=CE2=24,∴S△ABC故答案为242.解:如图,因为,从A到B有5条直连线路,每条直连线路均有5种不同的路线可以到达B点,所以,共有不同线路:5×5=25(条),答:从A到B,有25条不同的路线,故答案为:25.3.解:通过有规律的数,得出:(1)边长为1的正方形有4×3=12(个);(2)边长为2的正方形有6个;(3)边长为3的正方形有2个.(4)以小正方形的对角线为边的正方形有8个;(5)以对角线的一半为边长的正方形是17个;(6)以3个对角线的一半为边长的正方形有1个.所以图中共有正方形:12+6+2+8+17+1=46(个).答:图中有46个正方形.4.解:设鸡有x只,则兔就有100﹣x只,根据题意可得方程:2x﹣4×(100﹣x)=26,2x﹣400+4x=26,6x=426,x=71,答:鸡有71只.故答案为:71.5.解:4×4×3,=16×3,=48(种);答:这五个数字可以组成 48个不同的三位数.故答案为:48.6.解:(1)三角形有:8+4+4=16(个);(2)正方形有:20+10+4+1=35(个),故答案为:16,35.7.解:根据分析,如图,将阴影部分进行剪切和拼接后得:此时,图中阴影部分的小正方形个数为:18个,每个小正方形的面积为:2×2=4,故阴影部分的面积=18×4=72.故答案是:72.8.解:根据分析,如下图所示:长方形S 长方形ABCD =S 长方形XYZR +△AEF +△EFR +△FBG +△FGX +△HCG +△HGY +△DHE +△HEZ=S 长方形XYZR +2×(a +b +c +d )⇒60=4+2×(a +b +c +d )⇒a +b +c +d =28四边形S 四边形EFGH =△EFR +△FGX +△HGY +△HEZ +S 长方形XYZR=a+b+c+d+S长方形XYZR=28+4=32(平方米).故答案是:32.9.解:1800÷320﹣1800÷(320×1.5)=5.625﹣3.75=1.875(分钟)320×[5﹣(17﹣15+1.875)]÷5=320×[5﹣3.875]÷5=320×1.125÷5=360÷5=72(米/分钟)答:李双推车步行的速度是72米/分钟.故答案为:72.10.解:△ABC的周长是16厘米,可得△AEF的周长为:16÷2=8 (厘米),△AEF和四边形BCEF周长和为:8+10=18(厘米),所以BC=18﹣16=2(厘米),答:BC=2厘米.故答案为:2.11.解:依题意可知:2个偶数中间间隔是2个奇数.发现只有数字10,11,9,12是符合条件的数字.乘积为10×12=120.故答案为:12012.解:1+2+3=6,1+2+4=7,1+2+5=8,2+3+4=9,2+3+5=10,3+4+5=12,其中不能被3整除的数的和是7、8、10,即有三组(1、2、4),(1、2、5)(2、3、5),每一组可以组成3×2×1=6个,三组共可以组成6×3=18个,即不能被3整除的数共有18个.故答案为:18.13.解:依题意可知:3a+2与17是对立面,3a+2=17,所以a=5;7b﹣4与10是对立面,7b﹣4=10,所以b=2;a+3b﹣2c与11的对立面,5+3×2﹣2c=11,所以c=0;所以a﹣b×c=5故答案为:514.解:因为图1中小方块的个数为1+2×3=7个,图2中小方块的个数为1+(1+2)+3×4=16个,图3中小方块的个数为1+(1+2)+(1+2+3)+4×5=30个,所以图4中小方块的个数为1+(1+2)+(1+2+3)+(1+2+3+4)+5×6=50个,故答案为:50.15.解:220﹣83×2=220﹣166=54(元)54÷(2+7)=54÷9=6(元)答:网球每个6元.。
五年级奥数试题(20套)

1、计算:(1)28×1111+9999×8= (2)36×1.09+1.2×67.3 =2、计算:(1)4.75-9.63+(8.25-1.37)= (2)2004×20032005=3、甲乙丙三个共存钱1620元,已知甲存的钱是丙的3倍,乙存的钱是丙的2倍,那么甲存钱()元,乙存了()元,丙存了()元。
4、一台彩电的价钱是一台冰箱价钱的3倍,买一台彩电比买一台冰箱多用2800元,那么一台彩电()元。
5、两个数的和是78,差是16,那么较大的一个数是(),较小的一个数是()。
6、今年小明和小刚年龄和是25岁,四年后,小刚比小明大3岁,那么四年后小刚()岁。
7、两个数的和是80,积是1456,这两个数分别是()和()。
8、已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?9、有红、黄、白三种颜色的球,红球和黄球一共有21个,黄球和白球一共有20个,红球和白球一共有19个。
三种球各有多少个?10、浓度为60%的酒精溶液200克,与浓度为30%的酒精溶液300克,混合后所得到的酒精溶液的浓度是多少?1、有10个同学握手话别,每两个同学握一次手,他们一共握了()次手。
2、有一列字母A C A A B A A C A A B A A C ……问:第74个字母是(),这前74个字母中一共有()个A。
3、 22只小鸡和小兔在一起,共有脚64只,那么其中有()只小鸡,有()只小兔。
4、两个数的和是374,大数去掉十位数字后和小数一样大,那么大数是()。
5、某化肥厂生产一批化肥,原计划每天生产60吨,实际每天比原计划多生产15吨,结果提前了6天完成任务,这批化肥有()吨。
6、甲、乙、丙三人的平均年龄17岁,加入丁,四人的平均年龄19岁,那么丁()岁。
7、如果某类自然数有四个不同的质因数,那么这样的自然数中最小的是()。
五年级奥数题练习题80道

五年级奥数题练习题五年级奥数题练习一1、晶晶每天早上步行上学,如果每分钟走60米,则要迟到5分钟,如果每分钟走75米,则可提前2分钟到校.求晶晶到校的路程?2、甲、乙、丙三人行路,甲每分钟走60米,乙每分钟走67.5米,丙每分钟走75米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙与乙相遇后,又经过2分钟与甲相遇,求东西两镇间的路程有多少米?3、A、B两辆汽车同时从甲、乙两站相对开出,两车第一次在距甲站32公里处相遇,相遇后两车继续行驶,各自到达乙、甲两站后,立即沿原路返回,第二次在距甲站64公里处相遇,甲、乙两站间相距多少公里?4、周长为400米的圆形跑道上,有相距100米的A、B两点,甲、乙两人分别从A、B两点同时相背而跑,两人相遇后,乙即转身与甲同向而跑,当甲跑到A时,乙恰好跑到B.如果以后甲、乙跑的速度和方向都不变,那么追上乙时,甲共跑了多少米(从出发时算起)?5、老王从甲城骑自行车到乙城去办事,每小时骑15千米,回来时改骑摩托车,每小时骑33千米,骑摩托车比骑自行车少用1.8小时,求甲、乙两城间的距离。
6、速度为快、中、慢的三辆汽车同时从同一地点出发,沿同一公路追赶前面一个骑车人,这三辆车分别用6分钟、10分钟、12分钟追上骑车人,现在知道快车每小时24公里,中速车每小时20公里,那么慢车每小时行多少公里?7、在环形跑道上,两人都按顺时针方向跑时,每12分钟相遇一次,如果两人速度不变,其中一人改成按逆时针方向跑,每隔4分钟相遇一次,问两人各跑一圈需要几分钟?五年级奥数题练习二1、小华在8点到9点之间开始解一道题,当时时针、分针正好成一直线,解完题时两针正好第一次重合.问:小明解这道题用了多长时间?2、甲、乙、丙三人行路,甲每分钟走60米,乙每分钟走50米,丙每分钟走40米.甲从A地,乙和丙从B地同时出发相向而行,甲和乙相遇后,过了15分钟又与丙相遇,求A、B两地间的距离。
3、甲、乙、丙是一条路上的三个车站,乙站到甲、丙两站的距离相等,小强和小明同时分别从甲、丙两站出发相向而行,小强经过乙站100米时与小明相遇,然后两人又继续前进,小强走到丙站立即返回,经过乙站300米时又追上小明,问:甲、乙两站的距离是多少米?4、甲、乙、丙三人进行200米赛跑,当甲到终点时,乙离终点还有20米,丙离终点还有25米,如果甲、乙、丙赛跑的速度都不变,那么当乙到达终点时,丙离终点还有多少米?5、甲、乙二人分别从A、B两地同时出发,如果两人同向而行,甲26分钟赶上乙;如果两人相向而行,6分钟可相遇,又已知乙每分钟行50米,求A、B两地的距离。
五年级下册数学奥数题(含答案) 小学五年级奥数题大全及答案(更新版)-通用版

五年级奥数题问题+答案1、一块草地,可供24匹马吃6天;20匹马吃10天。
多少马12天吃尽?2、一块草地,可供5只羊吃40天;6只羊吃30天。
如果4只羊吃30天后又增加2只羊一起吃,那么这块草地还可以再吃多少天?3、每小时有3000人到书店买书。
如果设一个售书口,每分钟可以让50人买完离开;如果设2个售书口,1小时后就没有人排队了。
那么如果设4个口,多长时间后就没有人排队了?4、一口井,用3部抽水机40分钟可以抽干;6部抽水机16分钟可以抽干。
那么5部同样的抽水机,多少分钟可以抽干?5、一个水池,池内除原有的水外,每天都流入同样多的水。
如果用池中的水每天浇50亩地,10天用完;如果每天浇45亩地,20天用完。
那么,用这些水浇多少亩地,正好可用25天?6、一个大水坑,每分钟从四周流掉一定数量的水。
如果用5台水泵,6小时抽干;用10台,4小时抽干。
现在要2小时抽干,要多少水泵?7、仓库装满水泥时,可用30天。
现在仓库是空的,用大车运水泥,除每天供工地使用外,要装5天才可装满;用小车,除每天供工地使用外,要装10天才可装满。
如果大车小车一起用,除每天供工地使用外,要装几天才可装满?8、甲、乙、丙、丁四人加工同样的零件,甲先加工了一段时间,然后乙、丙、丁三人一起参加加工,6小时后乙和甲加工的一样多;9小时后丙和甲加工的一样多,12小时后丁和甲加工的一样多。
又知乙每小时加工27个零件,丙每小时加工23个零件。
那么,丁每小时加工零件多少个?答案1、假设草地单位为“1”,所以24*6=144 20*10=200 (200-144)/4=14 因此每天草地长草14个单位“1” 200-14*10=60,因此草地原有草60个单位"1"。
60/12+14=19 19马12天吃尽2、同理,40*5=200 30*6=180 (200-180)/(40-30)=2[每天草地长草] 200-2*40=120[原有草] 120-(4-2)*30=60 60/(6-2)=15(天)3、30分钟{每分钟有100人来,3000/(200-100)}4、20分钟{3*40-6*16=24 24/24=1 120-40*1=80 80/4=20}5、44亩地{45*20-50*10=400 400/10=40 500-40*10=100100/25+40=44}8、21个 {9*23-6*27=45 45/3=15 162-15*6=72 72/12+15=21}五年级奥数题有关行程问题的答案一环行跑道周长为240米,甲乙同向,丙与他们背向,都从同地点出发,每秒钟甲跑8米,乙跑5米,丙跑7米,出发后三人第一次相遇时,丙跑了多少圈?解:由题得知:甲比乙快8-5=3米/秒,也就是240/3=80秒后,甲会比乙多跑1圈且追上乙第一次相遇;要使甲、乙、丙同时相遇,则三者所用的时间必须是80秒的位数。
小学五年级奥数题精选各类题型及答案
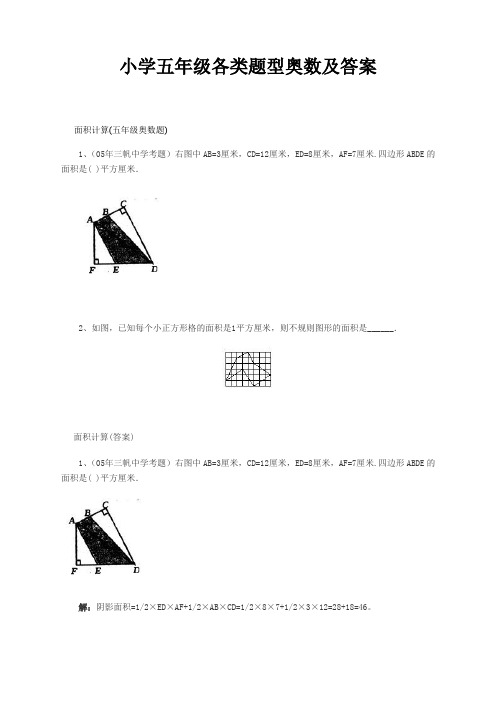
小学五年级各类题型奥数及答案面积计算(五年级奥数题)1、(05年三帆中学考题)右图中AB=3厘米,CD=12厘米,ED=8厘米,AF=7厘米.四边形ABDE的面积是( )平方厘米.2、如图,已知每个小正方形格的面积是1平方厘米,则不规则图形的面积是______.面积计算(答案)1、(05年三帆中学考题)右图中AB=3厘米,CD=12厘米,ED=8厘米,AF=7厘米.四边形ABDE的面积是( )平方厘米.解:阴影面积=1/2×ED×AF+1/2×AB×CD=1/2×8×7+1/2×3×12=28+18=46。
2、如图,已知每个小正方形格的面积是1平方厘米,则不规则图形的面积是______.解答:基本的格点面积的求解,可以用解答种这样的方法求解,当然也可以用格点面积公式来做,内部点有16个,周边点有8个,所以面积为16+8÷2-1=19图形面积(一)(五年级奥数题)1、(06年清华附中考题)如图,在三角形ABC中,D为BC的中点,E为AB上的一点,且BE=1 /3AB,已知四边形EDCA的面积是35,求三角形ABC的面积.2、正方形ABFD的面积为100平方厘米,直角三角形ABC的面积,比直角三角形(CDE的面积大30平方厘米,求DE的长是多少? 04.jpg图形面积(一)(答案)1、(06年清华附中考题)如图,在三角形ABC中,D为BC的中点,E为AB上的一点,且BE=1 /3AB,已知四边形EDCA的面积是35,求三角形ABC的面积.解答:根据定理:所以四边形ACDE的面积就是6-1=5份,这样三角形35÷5×6=42。
2、正方形ABFD的面积为100平方厘米,直角三角形ABC的面积,比直角三角形(CDE的面积大30平方厘米,求DE的长是多少?解:公共部分的运用,三角形ABC面积-三角形CDE的面积=30,两部分都加上公共部分(四边形BCDF),正方形ABFD-三角形BFE=30,所以三角形BFE的面积为70,所以FE的长为70×2÷10=14,所以DE=4。
五年级数学奥数题3篇

五年级数学奥数题
题目一:小学数学奥数题
小明的爷爷今年80岁,小明今年10岁。
请问小明的爷爷和小明出生相差了多少年?
解题思路:
小明的爷爷比小明大70年,因此他们出生相差了70年。
答案:70年
题目二:小学数学奥数题
小明有一个12厘米长,8厘米宽,5厘米高的长方体盒子,他想在盒子里装满小球,每个小球的直径是2厘米,问最多可以装几个小球?
解题思路:
先求出盒子的体积,即长×宽×高=12×8×5=480立方厘米。
再求出一个小球的体积,即πr³/6=π×1³=1.57立方厘米。
最后将盒子的体积除以一个小球的体积,得到可以装下的最多小球数为:480÷1.57≈305个。
答案:305个
题目三:小学数学奥数题
一根面积为64平方厘米的矩形板子,可以裁成4个面积相等的正方形,问每个正方形的边长是多少?
解题思路:
首先求出这个矩形板子的周长,即2(长+宽)=2(8+4)=24
厘米。
然后将周长等分成4份,即24÷4=6厘米,每个正方形的边长就等于6厘米。
答案:6厘米。
五年级具有代表性的奥数题1
宝典系列------思考版1、“△”表示一种运算,使下列等式成立:2△3=9,4△2=14,5△3=16,7△10=31 .按此规律:4△5 (宝1定义新运算)2、一个5层的中空方阵共有500人,最外层有多少人?最外层每边应站多少人?(宝2正方形队列)3、一次登山比赛中,小刚上山每分钟走50米,到达山顶沿原路下山,每分钟走75米,求小刚山下山平均每分钟走多少米?(宝3平均数应用题)4、3个足球和2个篮球共140元,同样的2个足球和3个篮球共135元,求1个足球和1个篮球各多少元?(消去法应用题)5、小李买5个足球和2个篮球应该是230元;到了商店,才想起应买2个足球和5个篮球,结果缺30元。
求每个单价。
6、竞赛共有12道题,每做对一道得10分,不做或做错都扣8分,小明得了66分,请问他得对了几道?(假设法解应用题)7、一个旅行团住宾馆,6人一间,多2个房间;若4人一间又少2个房间。
旅行团共有多少人?(盈亏问题)8、小李问老师年龄,老师说“当我像你这么大时,你4岁;当你像我这么大时,我61岁了。
”问老师今年多少岁?(年龄问题)9、甲比乙每天多加工10个零件,乙中途休息了15天。
40天后乙加工的正好是甲的一半。
甲乙各加工多少个?(一般应用题)10、超市里苹果的重量是橘子的4倍;如果每天卖出70公斤苹果,30公斤橘子,当橘子卖完时苹果还有400公斤,超市里原来有苹果橘子个多少公斤?(12讲列方程解应用题)11、在1到100的自然数中,既不是6的倍数也不是7的倍数的数有多少个?(容斥原理)12、甲乙两人同时从同一地点沿着长8千米的环形公路同方向前进,出发后20分钟,甲便从身后追上了乙,已知两人的速度和是1600米。
问甲乙速度分别是多少?(16讲行程问题)13、一排椅子只有35个座位,部分座位已有人就座,乐乐来后一看,他无论坐哪个座位,都将与已就做的人相邻。
在乐乐来之前就座的至少有多少人?(17讲最不利原则)14、玩具厂12个工人5天可以制作180个玩具,如果增加8个工人,16天可以制造多少个玩具?(18讲归总问题)15、用数字0、1、2、3、4、5可以组成多少个三位数?(19讲计数原理)16、计算图形面积。
小学五年级奥数题大全及答案(更新版)
小学五年级奥数题大全及答案五年级奥数1、小数的巧算2、数的整除性3、质数与合数4、约数与倍数5、带余数除法6、中国剩余定理7、奇数与偶数8、周期性问题9、图形的计数10、图形的切拼11、图形与面积12、观察与归纳13、数列的求和14、数列的分组15、相遇问题16、追及问题17、变换和操作18、逻辑推理19、逆推法20、分数问题1.1小数的巧算(一)年级班姓名得分一、填空题1、计算 1.135+3.346+5.557+7.768+9.979=_____.2、计算 1.996+19.97+199.8=_____.3、计算 9.8+99.8+999.8+9999.8+99999.8=_____.4、计算6.11+9.22+8.33+7.44+5.55+4.56+3.67+2.78 +1.89=_____.5、计算1.1+3.3+5.5+7.7+9.9+11.11+13.13+15.15+17.17+19.19=_____.6、计算 2.89⨯4.68+4.68⨯6.11+4.68=_____.7、计算 17.48⨯37-17.48⨯19+17.48⨯82=_____.8、计算 1.25⨯0.32⨯2.5=_____.9、计算 75⨯4.7+15.9⨯25=_____.10、计算 28.67⨯67+32⨯286.7+573.4⨯0.05=_____.二、解答题11、计算 172.4⨯6.2+2724⨯0.3812、计算 0.00...0181⨯0.00 (011)963个0 1028个013、计算12.34+23.45+34.56+45.67+56.78+67.89+78.91+89.12+91.2314、下面有两个小数:a=0.00...0105 b=0.00 (019)1994个0 1996个0求a+b,a-b,a⨯b,a÷b.1.2小数的巧算(二)年级班姓名得分一、真空题1、计算 4.75-9.64+8.25-1.36=_____.2、计算 3.17-2.74+4.7+5.29-0.26+6.3=_____.3、计算 (5.25+0.125+5.75)⨯8=_____.4、计算 34.5⨯8.23-34.5+2.77⨯34.5=_____.5、计算 6.25⨯0.16+264⨯0.0625+5.2⨯6.25+0.625⨯20=_____.6、计算 0.035⨯935+0.035+3⨯0.035+0.07⨯61⨯0.5=_____.7、计算 19.98⨯37-199.8⨯1.9+1998⨯0.82=_____.8、计算 13.5⨯9.9+6.5⨯10.1=_____.9、计算 0.125⨯0.25⨯0.5⨯64=_____.10、计算 11.8⨯43-860⨯0.09=_____.二、解答题11、计算32.14+64.28⨯0.5378⨯0.25+0.5378⨯64.28⨯0.75-8⨯64.28⨯0.125⨯0.537812、计算 0.888⨯125⨯73+999⨯313、计算 1998+199.8+19.98+1.99814、下面有两个小数:a=0.00...0125 b=0.00 (08)1996个0 2000个0试求a+b, a-b, a⨯b, a÷b.2.1数的整除性(一)年级班姓名得分一、填空题1、四位数“3AA1”是9的倍数,那么A=_____.2、在“25□79这个数的□内填上一个数字,使这个数能被11整除,方格内应填_____.3、能同时被2、3、5整除的最大三位数是_____.4、能同时被2、5、7整除的最大五位数是_____.5、1至100以内所有不能被3整除的数的和是_____.6、所有能被3整除的两位数的和是______.7、已知一个五位数□691□能被55整除,所有符合题意的五位数是_____.8、如果六位数1992□□能被105整除,那么它的最后两位数是_____.9、42□28□是99的倍数,这个数除以99所得的商是_____.10、从左向右编号为1至1991号的1991名同学排成一行,从左向右1至11报数,报数为11的同学原地不动,其余同学出列;然后留下的同学再从左向右1至11报数,报数为11的留下,其余同学出列;留下的同学第三次从左向右1至11报数,报到11的同学留下,其余同学出列,那么最后留下的同学中,从左边数第一个人的最初编号是_____号.二、解答题1、173□是个四位数字.数学老师说:“我在这个□中先后填入3个数字,所得到的3个四位数,依次可被9、11、6整除.”问:数学老师先后填入的3个数字的和是多少?12、在1992后面补上三个数字,组成一个七位数,使它们分别能被2、3、5、11整除,这个七位数最小值是多少?13、在“改革”村的黑市上,人们只要有心,总是可以把两张任意的食品票换成3张其他票券,也可以反过来交换.试问,合作社成员瓦夏能否将100张黄油票换成100张香肠票,并且在整个交换过程中刚好出手了1991张票券?14、试找出这样的最小自然数,它可被11整除,它的各位数字之和等于13.2.2数的整除性(二)年级班姓名得分一、填空题1、一个六位数23□56□是88的倍数,这个数除以88所得的商是_____或_____.2、123456789□□,这个十一位数能被36整除,那么这个数的个位上的数最小是_____.3、下面一个1983位数33…3□44…4中间漏写了一个数字(方框),已知这991个 991个个多位数被7整除,那么中间方框内的数字是_____.4、有三个连续的两位数,它们的和也是两位数,并且是11的倍数.这三个数是_____.5、有这样的两位数,它的两个数字之和能被4整除,而且比这个两位数大1的数,它的两个数字之和也能被4整除.所有这样的两位数的和是____.6、一个小于200的自然数,它的每位数字都是奇数,并且它是两个两位数的乘积,那么这个自然数是_____.7、任取一个四位数乘3456,用A表示其积的各位数字之和,用B表示A的各位数字之和,C表示B的各位数字之和,那么C是_____.8、有0、1、4、7、9五个数字,从中选出四个数字组成不同的四位数,如果把其中能被3整除的四位数从小到大排列起来,第五个数的末位数字是_____.9、从0、1、2、4、5、7中,选出四个数,排列成能被2、3、5整除的四位数,其中最大的是_____.10、所有数字都是2且能被66……6整除的最小自然数是_____位数.100个二、解答题11、找出四个互不相同的自然数,使得对于其中任何两个数,它们的和总可以被它们的差整除,如果要求这四个数中最大的数与最小的数的和尽可能的小,那么这四个数里中间两个数的和是多少?12、只修改21475的某一位数字,就可知使修改后的数能被225整除,怎样修改?13、500名士兵排成一列横队.第一次从左到右1、2、3、4、5(1至5)名报数;第二次反过来从右到左1、2、3、4、5、6(1至6)报数,既报1又报6的士兵有多少名?14、试问,能否将由1至100这100个自然数排列在圆周上,使得在任何5个相连的数中,都至少有两个数可被3整除?如果回答:“可以”,则只要举出一种排法;如果回答:“不能”,则需给出说明.3.1质数与合数(一)年级班姓名得分一、填空题1在一位的自然数中,既是奇数又是合数的有_____;既不是合数又不是质数的有_____;既是偶数又是质数的有_____.2、最小的质数与最接近100的质数的乘积是_____.3、两个自然数的和与差的积是41,那么这两个自然数的积是_____.4、在下式样□中分别填入三个质数,使等式成立.□+□+□=505、三个连续自然数的积是1716,这三个自然数是_____、_____、_____.6、找出1992所有的不同质因数,它们的和是_____.7、如果自然数有四个不同的质因数, 那么这样的自然数中最小的是_____.8、9216可写成两个自然数的积,这两个自然数的和最小可以达到_____.9、从一块正方形的木板上锯下宽为3分米的一个木条以后,剩下的面积是108平方分米.木条的面积是_____平方分米.10、今有10个质数:17,23,31,41,53,67,79,83,101,103.如果将它们分成两组,每组五个数,并且每组的五个数之和相等,那么把含有101的这组数从小到大排列,第二个数应是_____.二、解答题11、2,3,5,7,11,…都是质数,也就是说每个数只以1和它本身为约数.已知一个长方形的长和宽都是质数个单位,并且周长是36个单位.问这个长方形的面积至多是多少个平方单位?12、把7、14、20、21、28、30分成两组,每三个数相乘,使两组数的乘积相等.13、学生1430人参加团体操,分成人数相等的若干队,每队人数在100至200之间,问哪几种分法?14、四只同样的瓶子内分别装有一定数量的油,每瓶和其他各瓶分别合称一次,记录千克数如下:8、9、10、11、12、13.已知四只空瓶的重量之和以及油的重量之和均为质数,求最重的两瓶内有多少油?3.2质数与合数(二)年级班姓名得分一、填空题1、在1~100里最小的质数与最大的质数的和是_____.2、小明写了四个小于10的自然数,它们的积是360.已知这四个数中只有一个是合数.这四个数是____、____、____和____.3、把232323的全部质因数的和表示为AB,那么A⨯B⨯AB=_____.4、有三个学生,他们的年龄一个比一个大3岁,他们三个人年龄数的乘积是1620,这三个学生年龄的和是_____.5、两个数的和是107,它们的乘积是1992,这两个数分别是_____和_____.6、如果两个数之和是64,两数的积可以整除4875,那么这两数之差是_____.7、某一个数,与它自己相加、相减、相乘、相除,得到的和、差、积、商之和为256.这个数是_____.8、有10个数:21、22、34、39、44、45、65、76、133和153.把它们编成两组,每组5个数,要求这组5个数的乘积等于那组5个数的乘积.第一组数____________;第二组数是____________.9、有_____个两位数,在它的十位数字与个位数字之间写一个零,得到的三位数能被原两位数整除.10、主人对客人说:“院子里有三个小孩,他们的年龄之积等于72,年龄之和恰好是我家的楼号,楼号你是知道的,你能求出这些孩子的年龄吗?”客人想了一下说:“我还不能确定答案。
五年级奥数题100题(附答案)
五年级奥数题100题(附答案)1.765×213÷27+765×327÷27解:原式=765÷27×(213+327)= 765÷27×540=765×20=153002.(9999+9997+...+9001)-(1+3+ (999)解:原式=(9999-999)+(9997-997)+(9995-995)+……+(9001-1)=9000+9000+…….+9000(500个9000)=45000003.19981999×19991998-19981998×19991999解:(19981998+1)×19991998-19981998×19991999=19981998×19991998-19981998×19991999+19991998=19991998-19981998=100004.(873×477-198)÷(476×874+199)解:873×477-198=476×874+199因此原式=15.2000×1999-1999×1998+1998×1997-1997×1996+…+2×1解:原式=1999×(2000-1998)+1997×(1998-1996)+…+3×(4-2)+2×1=(1999+1997+…+3+1)×2=2000000。
6.297+293+289+…+209解:(209+297)*23/2=58197.计算:解:原式=(3/2)*(4/3)*(5/4)*…*(100/99)*(1/2)*(2/3)*(3/4)*…*(98/99)=50*(1/99)=50/998.解:原式=(1*2*3)/(2*3*4)=1/49.有7个数,它们的平均数是18。
小学五年级奥数题30道(附答案)
小学五年级奥数题30道(附答案)在小学五年级学习奥数的过程中,练习题是非常重要的。
通过解答奥数题,可以增强逻辑思维能力、提升解决问题的能力。
下面给大家分享30道小学五年级奥数题,并附上详细的解答,帮助大家更好地理解和掌握解题技巧。
题目1:小明有5块巧克力,小红有3块巧克力,他们一共有多少块巧克力?解答1:小明有5块,小红有3块,所以总共有5+3=8块巧克力。
题目2:5艘船将100个水桶分给海盗们,每艘船上都要有相同数量的水桶,问每艘船上装了多少个水桶?解答2:要将100个水桶平均分给5艘船,所以每艘船上装了100÷5=20个水桶。
题目3:有一辆公交车上有18个座位,现在已经有10个人上车了,还有多少个座位空着?解答3:公交车上一共有18个座位,已经有10个人上车了,空着的座位数为18-10=8个。
题目4:一年有365天,这些天分成几个星期和几天?解答4:一周有7天,所以365天可以分成52个星期和1天。
题目5:小明和小红共有50颗糖果,小明比小红多15颗,小红有多少颗糖果?解答5:小明比小红多15颗,小明和小红共有50颗,所以小红有50-15=35颗糖果。
题目6:一个矩形的长是5米,宽是3米,这个矩形的面积是多少平方米?解答6:矩形的面积可以通过长乘以宽计算,所以这个矩形的面积为5×3=15平方米。
题目7:一个正方形的边长是8厘米,这个正方形的周长是多少厘米?解答7:正方形的周长可以通过边长乘以4计算,所以这个正方形的周长为8×4=32厘米。
题目8:有40个苹果,每个篮子装8个苹果,问最多可以装多少个篮子?解答8:如果每个篮子装8个苹果,那么40个苹果可以装40÷8=5个篮子。
题目9:某商店的西瓜每公斤4元,小明买了3.5公斤的西瓜,他应该付多少钱?解答9:小明买了3.5公斤的西瓜,每公斤4元,所以他应该付3.5×4=14元。
题目10:一个三角形的底是6厘米,高是4厘米,这个三角形的面积是多少平方厘米?解答10:三角形的面积可以通过底乘以高再除以2计算,所以这个三角形的面积为6×4÷2=12平方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级奥数题精选
1.木块
数一数,每一堆各有多少小木块?
分析 同学们在数木块的时候,可以用各种不同的方法去思考如何数法,但根据图形中
的特征,我们可以移动某些小木块,将图形重新组合,然后利用乘法原理及加法原理解决立
方体问题。
解 (1)每一行 3个小木块,共有1+2+3+4=10行,因此共有小木块:3×10=30(块)
(2)如图中所示,将顶上一个移下来,一共有小木块3×7+5= 26(块)
答:第一堆小木块共有30块,第二堆小木块共有26块。
2.计算
分析与解答 这道题如直接计算显然很困难,先找一找上面算式中分数是按什么规律
来写的,发现这些分数都是用相邻的自然数的积作为分母,和作分子即。
3、钱数
某原材料收购站有一项定额收购款,计划以每吨1.2万元的价格收购一批原材料,由于
每吨原材料涨价0.3万元,实际比计划少收购了2吨,问这项定额收购款是多少万元?
分析与解答 要求这项定额收购款是多少万元,必须用计划每吨的收购价(1.2万元)乘
以计划收购吨数。已知实际比计划少收购2吨。假设按实际收购价再收购2吨,那么定额款
就必须增加(1.2+0.3)×2万元,产生这一差额的原因是因为现在每吨原材料比计划涨价了
0.3万元。用款数之差除以价格之差就可以算出计划收购的吨数。
解 1.2×[(1.2+0.3)×2÷0.3]
=1.2×10
=12(万元)
答:这项定额收购款是12万元。
4、网球
15个网球分成数量不同的4堆,数量最多的一堆至少有多少个球?
分析与解答 此题实际是求出15可分拆多少种4个互不相同的整数之和,而
15=1+2+3+9=1+2+4+8=1+2+
5+7=1+3+4+7=1+3+5+6=2+3+4+6,所以最多一堆的球数可能是9、8、7、6,其中至少有
6个。
5、追及问题
龟兔赛跑同时出发,全程7000米,乌龟以每分30米的速度爬行,兔子每分钟跑330 米,
兔子跑了10分钟就停下来睡觉,200分钟后醒来,立即以原速往前跑,当兔子追上乌龟时,
他们离终点的距离是多少千米?
6、完全平方数
在12=1 ,22=4 ,32=9 ,42=16 ,……中,1 4,9 ,16, ……叫做"完全平方数"。从
1到 500这 个整数中,去掉所有的"完全平方数",剩下的整数的和是( )。
7、 整除问题
有写着数字2、5、8的卡片各10张,现在从中任意抽出7张,这7张卡片的和可能等
于( )A.21 B.25 C.26 D.28
8、因数倍数 已知两个自然数的和为54,它们的最小公倍数与最大公约数的差为114,求
这两个自然数.
9、质数与合数
A,B ,C为 3个小于20 的质数,A+B+C=30 ,求这三个质数.
解答:因为三个质数之和为偶数,所以这三个质数必为两奇一偶,其中偶数只能是2 ,
另两个奇质数之和为 28,又因为这三个数都要小于20 ,所以只能为11 和 17,所以这三
个质数分别是2 ,11 ,17
10、在面前有一个长方体,它的正面和上面的面积之和是209 ,如果它的长、宽、高都
是质数,那么这个长方体的体积是多少?
11、
解答:
12. 整除
已知四十一位数55…5□99…9(其中5和9各有20个),能被7整除,那么方格内的
数字是多少?
解答:
13.数的整除
将所有的四位数用它的各位数字之和去除,可能得到的最大的商是______。
【答案】1000。
14.找规律、数学归纳
用火柴棒摆成"井"字型图案(见下图),按这种方式摆下去,当每边上摆999(即,n=999)
根时,需要的火柴棒总数是_____根。
【答案】5988。由图归纳得出,每边摆凡根火柴棒时,需要火柴棒总数是:
4n+(n一3)×2=6(n-1)。
所以当n=999时,需要火柴棒总数是
6×(999-1)=5988(根)
15、把下列各数写成质因数乘积的形式,并指出他们分别有多少个两位数的约数:
(1)126 (2)6435 (3)46200
解答:
(1)126=2×32×7有5个两位数的约数;
(2)6435=32×5×11×13有7个两位数的约数;
(3)46200=23×3×52×7×11有27个两位数的约数。
16.计算
把40、44、45、63、65、78、99、105这八个数平分成两组,使每组四个数的乘积相等。
解答:44,45,78,105和40,63,65,99。
17、 计算
写出十个连续的自然数,它们个个都是合数。
解答:从2312到2321十个连续自然数都是合数。
提示:2、3、…、10、11这十个数的最小公倍数为2310,将2310分别加上2、3、…、
10、11使得到十个连续的合数。利用这种方法可以构造出任意多个连续的合数。
18、.计算
有1、2、3、4、5、6、7、8、9九张牌,甲、乙、丙各拿了三张。甲说:"我的三张牌
的积是48",乙说:"我的三张牌的和是15",丙说:"我的三张牌的积是63"。
问:他们各拿了哪三张牌?
解答:甲拿了2、3、8;乙拿了4、5、6;丙拿了1、7、9。提示:先求出丙拿的牌。
19、1.计算
把下列各数写成质因数乘积的形式:
(1)3111 (2)1357 (3)1112111 (4)21112
解答:
(1)3111=3×17×61;(2)1357=23×59;
(3)1112111=7×112×13×101;
(4)21112=23×7×13×29。
20.计算
46305乘以一个自然数a,乘积是一个整数的平方。求最小的a和这个整数。
解答:a=3×5×7=105;46305×105=22052。
提示:完全平方数的所有质因数都是偶数次方。
21、1.乘积
小明的两个衣服口袋中各有13张卡片,每张卡片上分别写着1,2,3,…,13。如果从
这两个口袋中各拿出一张卡片来计算它们所写两数的乘积,可以得到许多不相等的乘积,其
中能被6整除的乘积共有多少个?
【答案】能被6整除的乘积一定有质因数2和3。
可能:
1×6=6 1×12=12 2×3=6 2×6=12 2×9=18 2×12=24
3×4=12 3×6=18 3×8=24 3×10=30 3×12=36 4×6=24 4×9=36
4×12=48 5×6=30 5×12=60 6×6=36 6×7=42 6×8=48 6×9=54
6×10=60 6×11=66 6×12=72 6×13=78 7×12=84 8×9=72 8×12=96
9×10=90 9×12=108 10×12=120 11×12=132 12×12=144 12×13=156
答:6、12、18、24、30、36、42、48、54、60、66、72、78、84、90、96、108、120、
132、144、156,共21种
22.平均数
老师在黑板上写了若干连续自然数:1、2、3、4、5......后擦掉其中一个数,计算出剩下
数的平均数保留两位小数后是12.52,问老师擦掉的数是多少?
【答案】最小的满足条件的等式为288/23≈12.52
猜测如果等式成功:
他们的和是288,有23个
(23+1)(1+23+1)/2=300
300-288=12
12<24
验证等式成功
老师擦掉的数是12
