2016年全国高中数学联赛山西赛区预赛

合集下载

2016年各省高中数学联赛预选赛试题及详解答案(最值部分)

2016年各省高中数学联赛预选赛试及详解答案（最值部分）1、为正数y x ，，且y x a y x +≤+，则a 的最小值为（2）解：∵0y x >, ∴y x y x +，，均为正数，所以0a >y x xy 21y x yx a y x a y x 22++=⎪⎪⎭⎫⎝⎛++≥⇔+≤+，而1xy 2xy 2y x xy 2=≤+，所以211a 2=+≥ ∴2a ≥2、设1x 0<<，b a ，大于零的常数，x1b x a 22-+则的最小值为（()2b a +）解：∵1x 0<< ∴0x 1>-，又b a ,大于零的常数由柯西不等式可知：()()2222b a x1x b a x 1b x a +=-++≥-+，当且仅当b a a x +=时，等号成立。

3、已知正实数b a ，满足36b a 9=+，则b1a 1+最小值时，=ab （27）解：∵0b a >,，由柯西不等式可知：()943616b a 913b 1a 99b 1a 12==++≥+=+，即当且仅当b 1a 93=，代入36b a 9=+计算，得⎩⎨⎧==9b 3a 时，等号成立。

∴2793ab =⨯=4、若正数y x ，满足xy 5y 3x =+，则y 4x 3+的最小值为（5）解：∵0y x >, ∴xy 为正数∴5x39y 445x 3y 15xy y 3xy x xy 5y 3x =+⇔=+⇔=+⇔=+ 由柯西不等式可知：()5y 4x 3x3y 432x 39y 4452≥+⇔++≥+=当且仅当x 33y 42=，代入xy 5y 3x =+计算，得⎪⎩⎪⎨⎧==21y 1x 时，等号成立。

5、 z y x ，，为正数时，222z y x yz xz 4+++的最大值为（217）。

解：思路：如果分母的最小值可以化为类似常数项×()yz xz 4+的形式，那么最大值就为此常数项的倒数。

2016年全国高中数学联赛A卷真题word版

2016年全国高中数学联赛A 卷一试一、填空题1. 设实数a 满足a a a a <-<1193，则a 的取值范围是__________.2. 设复数w z ,满足3=z ，()()i w z w z 47+=-+，其中i 是虚数单位，w z ,分别表示w z ,的共轭复数，则()()w z w z 22-+的模为__________.3. 正实数w v u ,,均不等于1，若5log log =+w vw v u ，3log log =+v u w v ，则u w log 的值为__________.4. 袋子A 中装有2张10元纸币和3张1元纸币，袋子B 中装有4张5元纸币和3张1元纸币.现随机从两个袋子中各取出两张纸币，则A 中剩下的纸币面值之和大于B 中剩下的纸币面值之和的概率为 .5. 设P 为一圆锥的顶点，C B A ,,是其底面圆周上的三点，满足︒=∠90ABC ，M 为AP 的中点.若2,2,1===AP AC AB ，则二面角A BC M --的大小为__________.6. 设函数()10cos 10sin 44kx kx x f +=，其中k 是一个正整数.若对任意实数a ，均有(){}(){}R x x f a x a x f ∈=+<<1，则k 的最小值为__________.7. 双曲线C 的方程为1322=-y x ，左、右焦点分别为1F 、2F .过点2F 作一直径与双曲线C 的右半支交于点Q P ,，使得︒=∠901PQ F ，则PQ F 1∆的内切圆半径是__________.8. 设4321,,,a a a a 是100,,2,1Λ中的四个互不相同的数，满足()()()2433221242322232221a a a a a a a a a a a a++=++++，则这样的有序数组()4321,,,a a a a 的个数为__________.二、解答题 9. 在ABC ∆中，已知⋅=⋅+⋅32.求C sin 的最大值.10. 已知()x f 是R 上的奇函数，()11=f ，且对任意0<x ，均有()x xf x x f =⎪⎭⎫ ⎝⎛-1. 求()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛511501981319912110011f f f f f f f f Λ的值.11. 如图所示，在平面直角坐标系xOy 中，F 是x 轴正半轴上的一个动点.以F 为焦点、O 为顶点作抛物线C .设P 是第一象限内C 上的一点，Q 是x 轴负半轴上一点，使得PQ 为C 的切线，且2=PQ .圆21,C C 均与直线OP 相切于点P ，且均与x 轴相切.求点F 的坐标，使圆1C 与2C 的面积之和取到最小值.2016年全国高中数学联赛A 卷二试一、设实数201621,,,a a a Λ满足21119+>i i a a ()2015,,2,1Λ=i .求()()()()212016220162015232221a a a a a a a a ----Λ的最大值.二、如图所示，在ABC ∆中，X 、Y 是直线BC 上的两点（X 、B 、C 、Y 顺次排列），使得AB CY AC BX ⋅=⋅. 设ACX ∆，ABY ∆的外心分别为21,O O ，直线21O O 与AB 、AC 分别交于点U 、V .证明：AUV ∆是等腰三角形.三、给定空间中10个点，其中任意四点不在一个平面上，将某些点之间用线段相连，若得到的图形中没有三角形也没有空间四边形，试确定所连线段数目的最大值.四、设p 与2+p 均是素数，3>p .数列{}n a 的定义为21=a ，⎥⎦⎤⎢⎣⎡+=--n pa a a n n n 11，Λ,3,2=n . 这里[]x 表示不小于实数x 的最小整数.证明：对1,,4,3-=p n Λ均有11+-n pa n 成立.。

全国高中数学联赛山西省预赛及参考答案5

全国高中数学联赛山西省预赛试题解答一、填空题（共8题，每题10分，计80分）1、在集合{}1,2,3,,2011A =中，末位数字为1的元素个数为．答案：202．解：将集合{}0001,0002,,2011A =中的每个数都截去其末位数字，都会得到集合{}000,001,,199,200,201B =中的数，而A 中形如1abc 的数，皆可看成由B 中的元素abc 后面添加数字1而得到；故A 中形如1abc 的元素个数，等于B 的元素个数，即202个． 2、椭圆2222153x y +=的焦点为12,F F ，如果椭圆上的一点P 使12PF PF ⊥，则12PF F ∆的面积为．答案：9．解：易知128F F =，1210PF PF +=，所以2212()10PF PF +=，在直角12PFF ∆中，222128PF PF +=，由以上两式得，1212192PF F S PF PF ∆=⋅=． 3、数列{}n a 满足：11a =，2212122,3,1k k k ka ak a a +-==≥；则其前100项的和为： 100S = ．答案：503(61)5-．解：212122222212122122126,6k k k k k k k k k k k ka a a a a aa a a a a a +++++--+=⋅==⋅=，121,2a a ==，所以， 112126,26k k k k a a ---==⋅，100123499100()()()S a a a a a a =++++++501501336(61)5k k -===-∑．4、若41,61n n ++都是完全平方数，则正整数n 的最小值是．答案：20．解：41,61n n ++都是奇平方数；设261(21)4(1)1n m m m +=+=++，则32(1)n m m =+，而(1)m m +为偶数，所以4n ，设4n k =，则41161n k +=+，61241n k +=+，当1,234k =时，41,61n n ++不同为平方数，而当5k =，即20n =时，4181,61121n n +=+=皆为平方数，因此正整数n 的最小值是20．5、函数25y x =-的最大值是．答案：6524．t =，则612304(113)14y x x =-+=--+223656546142244t t t ⎛⎫=-++=--+≤ ⎪⎝⎭，则6524y ≤，当34t =，即16748x =取得等号． 6、如图，单位正方体1111ABCD A BC D -中，,,E F G 分别是棱11111,,AA C D D A 的中点，则点1B 到EFG 所在平面的距离为．解一、补形法，如图，过,,E F G 的平面截正方体，所得截面是一个正六边形，易知该平面垂直平分正方体的对角线1B D，而1B D ，所以1B 到面EFG的距离h =．解二：等体积法，易知1111111113114488B FG B A G BC FD FG S S S S =---=---=，而点E 到平面1B FG 的距离012h =，所以11011316EB FG B FG V h S ==．又222222111111113()1442EF EA A F EA A D D F =+=++=++=，即EF =GF GE ==，2221cos 22GE GF EF EGF GE GF +-∠==-⋅，0120EGF ∠=，则01sin1202EGF S GE GF ∆=⋅=1B 到面EFG 的距离为h ，则 111163EB FG EGF V h S ∆==⋅=，所以h =． 7、2000sin 130sin 70cos80+= ．1A E答案：34．解：22sin 130sin 70cos80cos 40sin 70sin10+=+0000000001cos8011sin 70sin10(cos70cos10sin 70sin10)sin 70sin10222+=+=+-+0000011113(cos 70cos10sin 70sin10)cos 6022224=++=+=． 8、如果四位数abcd 的四个数码满足a b c d +=+，就称其为“好数”；例如2011就是一个“好数”．那么，“好数”的个数是．答案：615．解：由于19,0,,9a b c d ≤≤≤≤，记k a b c d =+=+，则118k ≤≤．当19k ≤≤，则上式中的a 可取{}1,,k 中的任意值，c 可取{}0,1,,k 中的任意值，而当,a c 取定后，,b d 便随之确定，因此满足k a b c d =+=+的四位数abcd 有(1)k k +个；从而满足9k ≤的四位数abcd 共有91(1)330k k k =+=∑个；当1018k ≤≤，由k a b c d =+=+知，,,,a b c d 皆不能为0，令1110,10a a b b =-=-，1110,10c c d d =-=-，则11111,,,9a b c d ≤≤，记11111k a b c d =+=+，则1210k ≤≤，且四位数abcd 与四位数1111a b c d 一一对应．上式中的1a 及1c 皆可取{}11,,1k -中的任意值，而当11,a c 取定后，11,b d 便随之确定，因此满足11111k a b c d =+=+的四位数1111a bc d 有21(1)k -个，从而满足1210k ≤≤的1111a bc d 共有110922121(1)k k k k ==-=∑∑个，即满足1018k ≤≤的四位数abcd 共有921285k k ==∑个．故“好数”的个数是330285615+=．二、解答题（共3题，合计70分）9、（20分）三角形ABC 三个内角的度数满足：13A B B C ==；求cos cos cos T A B C =++的值．解：设,3,9A B C θθθ===，由39θθθπ++=，得13πθ=．cos cos3cos9cos cos3cos 4T θθθθθθ=++=+-2222cos cos 22cos 212cos 22cos 211θθθθθ=-+>-+=．22222(cos cos3cos9)cos cos 3cos 92cos cos3T θθθθθθθθ=++=+++2cos cos92cos3cos9θθθθ++1cos 21cos 61cos8222θθθ+++=++ (cos 2cos 4)(cos8cos10)(cos6cos12)θθθθθθ++++++；而cos cos3cos9cos12cos10cos 4T θθθθθθ=++=---，所以22T T -=33(cos 2cos 4cos6cos8cos10cos12)θθθθθθ++++++，又令cos 2cos 4cos 6cos8cos10cos12P θθθθθθ=+++++，则2sin (sin3sin )(sin5sin3)(sin 7sin5)(sin9sin 7)P θθθθθθθθθ⋅=-+-+-+-(sin11sin9)(sin13sin11)sin θθθθθ+-++-=-，所以12P =-．从而2332322T T -=-=，即24230T T --=，由于1T >，解此方程得T =． 10、（25分）如图，,,D E F 分别是ABC ∆的边,,BC CA AB 上的点，且0DE AB F =，00,EFBC D FD CA E ==；证明：,,AD BE CF 三线共点，当且仅当000,,D E F 三点共线．证明：据梅尼劳斯定理，000,,D E F 三点共线，当且仅当0000001AE CD BF E C D B F A⋅⋅=；而据塞瓦定理，,,AD BE CF 三线共点，当且仅当1BD CE AFDC EA FB⋅⋅=．因直线0D EF 截ABC ∆，得到01BD CE AF EA FB D C ⋅⋅=，所以，00CD CE AF D B EA FB=⋅，同理，由直线0E DF 截ABC ∆得，00CE CD BFE A DB FA=⋅，由直线0F DE 截ABC ∆得，00BF BD CEF A DC EA=⋅．因此，2000000AE CD BF BD CE AF E C D B F A DC EA FB ⎛⎫⋅⋅=⋅⋅ ⎪⎝⎭；由于该等式中的一端取值为1当且仅当其另一端也取值为1，故结论得证．11、（25分）20个巫师孤岛聚会．在这期间,任何三个巫师都曾在一起诅咒过别的某些巫师；证明：其中必存在某个巫师，他至少受到过其余九个巫师的诅咒．证：20个巫师，共可作成320C 个“三巫组”，每个组至少诅咒过一人，故被诅咒过的巫师至少有320C 人次，设W 是受到诅咒最多的一个巫师，他被m 个“三巫组”诅咒过，则 3205720C m ≥=，若这m 个“三巫组”中，总共含有k 个巫师，这k 人共可作成3k C 个“三巫组”，因此，357k C m ≥≥，注意到，当3k ≥时，组合数3k C 严格递增；因为33895657,8457C C =<=>，由此得9k ≥．。

2016年全国高中数学联赛陕西赛区预赛真题(Word)

2.在平面直角坐标系中，不等式组

x
−
3y + 2≥0 表示的平面区域的面积为

y≥0
A. 3 2
B. 3
C. 2
（） D. 2 3
( ) ( ) 3.设 a,b,c 为同一平面内的三个单位向量，且 a ⊥ b .则 c − a c − b 的最大值为
A. 2 +1
B. 1− 2
C. 2 −1
的外接球 2
C. 3
D. 4
8.设非负实数 a、b、c 满足 ab + bc + ac = a + b + c 0.则 ab + bc + ac 的最小值为
（）
A. 2
B. 3
C. 3
D. 2 2
二、填空题（每题 8 分，共 4 小题，共 32 分）
9.在数列an中， a4 = 1, a11 = 9 ，且任意连续三项的和均为 15.则 a2016 = _____.
四、（本小题满分 30 分）
设函数
f
(x)
=
ln
x
+
a

1 x
−1(a R)，且
f
( x) 的最小值为
0.
（1）求 a 的值；
（2）若数列an满足 a1 =1, an+1 = f (an ) + 2(n Z+ ) ，记 Sn = a1 +a2 + + an ，m 表示不超过实数
10.设 m、n 均为正整数，且满足 24m = n4.则 m 的最小值为______.
11.设 f ( x)、g ( x) 分别是定义在 R 上的奇函数、偶函数，且 f ( x)+g ( x) = 2x. 若对 x 1, 2 ，不等式 af ( x) + g (2x)≥0恒成立，则实数 a 的取值范围为_______. 12.设 x R ，则函数 f ( x) = 2x −1 + 3x − 2 + 4x − 3 + 5x − 4 的最小值为________.

2012年全国高中数学联赛山西赛区预赛

# "./# 揣)-" s# n./.
20 13 年第 2 期
因此,所求集合个数为SC豫, 4c豫 .
二! 设抛物线方程为尹二 x ( "> 0 .则 4a )
顶点为 O (0 ,0 ) , 焦点为 F (a ,0 ).
现将 M 的
元素填人各个部分中, 由题
意, 知 x 处不能填数 , 而 / !0 !w 处必须填有数字, 且所填元素互不相同 (否则 , 相同元素将归人 x 区域中 ) ;a ! !"处可 b 以填或不填数字 , 不同的区域中不再填有相同元素( 否则 , 又将归人 u !"!! 中). 用云表示 / 处所填数字的个数 , 下同. 由对称性 , 不妨按云簇云毛而情形列举 ,则有四种情形 :
20 13 年第 2 期
201 年全国高中数学联赛山西赛区预赛 2
中图分类号 : 以2 .7 4 9 文献标识码 : A 文章编号 : 10 5 一 1 (20 13 0 一 3 一 0 4 6 6 ) 2 的2 3 0
一 ! 空题 ( 每小题 8 分 , 共 6 分 ) 填 4 1.a :, " , " , ,是一个等差数列 , 其中 2 3 a , > 0 , s " 示其前几项和. 如果 5 3 = s : , 在表 5 .,S :, 5 3, ,中最大数为 S*, 则 k =
若 t使方程有实数解二则 ,
v 二 , ( r一2 ) . 一 , t(t 一l ) ) o 4a 4a
幼 4 一3 t 弟0
4

山西省省际名校联考2016年高考数学押题卷(文科) Word

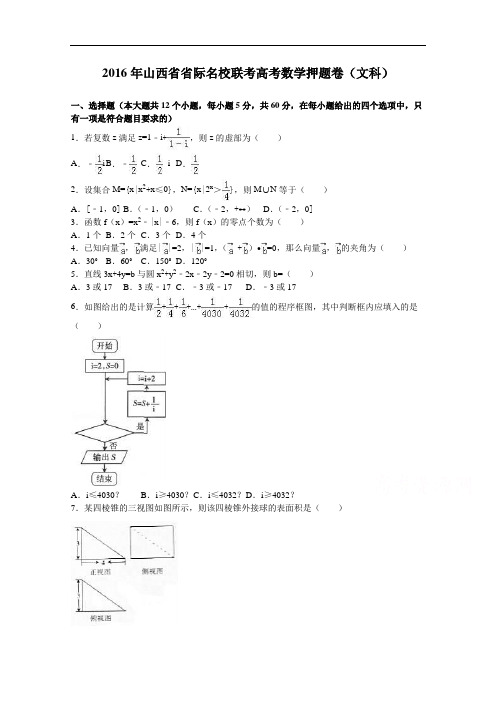
2016年山西省省际名校联考高考数学押题卷（文科）一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．若复数z满足z=1﹣i+，则z的虚部为（）A．﹣i B．﹣C．i D．2．设集合M={x|x2+x≤0}，N={x|2x＞}，则M∪N等于（）A．[﹣1，0] B．（﹣1，0）C．（﹣2，+∞）D．（﹣2，0]3．函数f（x）=x2﹣|x|﹣6，则f（x）的零点个数为（）A．1个B．2个C．3个D．4个4．已知向量，满足||=2，||=1，（ +）•=0，那么向量，的夹角为（）A．30°B．60°C．150°D．120°5．直线3x+4y=b与圆x2+y2﹣2x﹣2y﹣2=0相切，则b=（）A．3或17 B．3或﹣17 C．﹣3或﹣17 D．﹣3或176．如图给出的是计算+++…++的值的程序框图，其中判断框内应填入的是（）A．i≤4030？B．i≥4030？C．i≤4032？D．i≥4032？7．某四棱锥的三视图如图所示，则该四棱锥外接球的表面积是（）A．π B．34πC．π D．17π8．设a，b，c为三角形ABC三边长，a≠1，b＜c，若sinA+cosA=，且+=2，则B角大小为（）A．B．C．D．9．设抛物线C：y2=16x，斜率为k的直线l与C交于A，B两点，且OA⊥OB，O为坐标原点，则l恒过定点（）A．（8，0）B．（4，0）C．（16，0） D．（6，0）10．已知数列a n=lg，S n为{a n}的前n项和，若S n＜2，则项数n的最大值为（）A．98 B．99 C．100 D．10111．定义域为R的可导函数y=f（x）的导函数f′（x），满足f（x）＞f′（x），且f（0）=2，则不等式f（x）＜2e x的解集为（）A．（﹣∞，0）B．（﹣∞，2）C．（0，+∞）D．（2，+∞）12．设函数f（x）=，若f（f（））=8，则m=（）A．2 B．1 C．2或1 D．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上..13．设△ABC的内角A，B，C的对边分别为a，b，c，且a=2，b=3，cosC=，则sinA=．14．已知不等式组则z=的最大值为．15．正方体ABCD﹣A1B1C1D1的棱长为4，E、F分别是棱AB，BB1的中点，A1E与C1F所成的角的余弦值是．16．过双曲线﹣=1（a＞0，b＞0）的右焦点F作渐近线的垂线，设垂足为P（P为第一象限的点），延长FP交抛物线y2=2px（p＞0）于点Q，其中该双曲线与抛物线有一个共同的焦点，若=（+），则双曲线的离心率的平方为．三、解答题：本大题共5小题，满分60分，解答应写出文字说明、证明过程或演算步骤17．在△ABC中，a，b，c分别是角A，B，C的对边，=，且a+c=2．（1）求角B；（2）求边长b的最小值．（2）以十位为茎，个位数为叶，作出这30位志愿者年龄的茎叶图；（3）求这30位志愿者年龄的方差．19．在三棱锥D﹣ABC，AB=BC=CD=DA=9，∠ADC=∠ABC=120°，M、O分别为棱BC，AC的中点，DM=4．（1）求证：平面ABC⊥平面MDO；（2）求点M到平面ABD的距离．20．已知椭圆C： +=1（a＞b＞0），F1，F2分别是其左、右焦点，A是椭圆上一点，•=0，直线AF1的斜率为，长轴长为8．（1）求椭圆C的方程；（2）直线y=kx+（k≠0）交椭圆C于不同的点E，F，且E，F都在以B（0，﹣2）为圆心的圆上，求k的值．21．已知f（x）=x3﹣x2﹣2x+5．（1）求f（x）的单调区间；（2）过（0，a）可作y=f（x）的三条切线，求a的取值范围．[选修4-1几何证明选讲]22．BD是等腰直角三角形△ABC腰AC上的中线，AM⊥BD于点M，延长AM交BC于点N，AF⊥BC于点F，AF与BD交于点E．（1）求证；△ABE≌△ACN；（2）求证：∠ADB=∠CDN．[选修4-4坐标系与参数方程]23．在平面直角坐标系中，以坐标原点为极点，x轴非负半轴为极轴，建立极坐标系，已知曲线C的极坐标方程为：ρsin2θ﹣6cosθ=0，直线l的参数方程为：（t为参数），l与C交于P1，P2两点．（1）求曲线C的直角坐标方程及l的普通方程；（2）已知P0（3，0），求||P0P1|﹣|P0P2||的值．[选修4-5不等式选讲]24．函数f（x）=|x|﹣2|x+3|．（1）解不等式f（x）≥2；（2）若存在x∈R使不等式f（x）﹣|3t﹣2|≥0成立，求参数t的取值范围．2016年山西省省际名校联考高考数学押题卷（文科）参考答案与试题解析一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．若复数z满足z=1﹣i+，则z的虚部为（）A．﹣i B．﹣C．i D．【考点】复数代数形式的混合运算．【分析】化简z，从而求出z的虚部即可．【解答】解：∵z=1﹣i+=1﹣i+=﹣，则z的虚部是﹣，故选：B．2．设集合M={x|x2+x≤0}，N={x|2x＞}，则M∪N等于（）A．[﹣1，0] B．（﹣1，0）C．（﹣2，+∞）D．（﹣2，0]【考点】并集及其运算．【分析】化简集合M，N，然后求出它们的并集即可．【解答】解：由x2+x≤0，即x（x+1）≤0，解得﹣1≤x≤0，即M=[﹣1，0]，由2x＞=2﹣2，即x＞﹣2，即N=（﹣2，+∞），则M∪N=（﹣2，+∞）故选：C．3．函数f（x）=x2﹣|x|﹣6，则f（x）的零点个数为（）A．1个B．2个C．3个D．4个【考点】函数零点的判定定理．【分析】解方程，根据方程的根的个数，即可得出f（x）的零点个数．【解答】解：x＞0时，x2﹣x﹣6=0，解得x=﹣2或3，∴x=3；x＜0时，x2+x﹣6=0，解得x=2或﹣3，∴x=﹣3；∴f（x）的零点个数为2个．故选：B．4．已知向量，满足||=2，||=1，（ +）•=0，那么向量，的夹角为（）A．30°B．60°C．150°D．120°【考点】平面向量数量积的运算．【分析】展开（+）•=0，代入数量积公式即可求得向量，的夹角．【解答】解：设向量，的夹角为θ，由||=2，||=1，（ +）•=0，得，即2×1×cosθ=﹣1，∴cos．∵θ∈[0°，180°]，∴θ=120°．故选：D．5．直线3x+4y=b与圆x2+y2﹣2x﹣2y﹣2=0相切，则b=（）A．3或17 B．3或﹣17 C．﹣3或﹣17 D．﹣3或17【考点】直线与圆的位置关系．【分析】先求出圆x2+y2﹣2x﹣2y﹣2=0的圆心和半径，由直线3x+4y=b与圆x2+y2﹣2x﹣2y ﹣2=0相切，得到圆心到直线3x+4y=b的距离等于半径，由此能求出b．【解答】解：圆x2+y2﹣2x﹣2y﹣2=0的圆心（1，1），半径r==2，∵直线3x+4y=b与圆x2+y2﹣2x﹣2y﹣2=0相切，∴圆心（1，1）到直线3x+4y=b的距离d==2，解得b=﹣3或b=17．故选：D．6．如图给出的是计算+++…++的值的程序框图，其中判断框内应填入的是（）A．i≤4030？B．i≥4030？C．i≤4032？D．i≥4032？【考点】程序框图．【分析】程序的功能是求S=+++…++的值，且在循环体中，S=S+表示，每次累加的是的值，故当i≤4032应满足条件进入循环，进而得到答案．【解答】解：∵程序的功能是求S=+++…++的值，且在循环体中，S=S+表示，每次累加的是的值，故当i≤4032应满足条件进入循环，i＞4032时就不满足条件分析四个答案可得条件为：i≤4032，故选：C7．某四棱锥的三视图如图所示，则该四棱锥外接球的表面积是（）A．π B．34πC．π D．17π【考点】由三视图求面积、体积．【分析】由三视图知该几何体是一个四棱锥，并画出对应的长方体，由三视图求出几何元素的长度，由长方体求出外接球的半径，由球体的表面积公式求出该四棱锥外接球的表面积．【解答】解：根据三视图可知几何体是一个四棱锥P﹣ABCD，如图：且四棱锥P﹣ABCD是长方体的一部分，AP=4、AB=AD=3，∴该四棱锥和正方体的外接球相同，设外接球的半径是R，则2R==，R=，∴该四棱锥外接球的表面积S=4πR2=34π，故选：B．8．设a，b，c为三角形ABC三边长，a≠1，b＜c，若sinA+cosA=，且+=2，则B角大小为（）A．B．C．D．【考点】余弦定理．【分析】+=2，化为=2，可得c2=b2+a2，．由sinA+cosA=，可得2=，A∈，解得A．即可得出B．【解答】解：∵+=2，∴log a（c﹣b）+log a（c+b）==2，∴c2﹣b2=a2，即c2=b2+a2，∴．∵sinA+cosA=，∴2=，A∈，∴A+=，解得A=．则B==．故选：D．9．设抛物线C：y2=16x，斜率为k的直线l与C交于A，B两点，且OA⊥OB，O为坐标原点，则l恒过定点（）A．（8，0）B．（4，0）C．（16，0） D．（6，0）【考点】抛物线的简单性质．【分析】设直线l：x=my+b，代入抛物线y2=16x，利用韦达定理及向量数量积公式即可得到结论．【解答】解：设直线l：x=my+b，（b≠0），代入抛物线y2=16x，可得y2﹣16my﹣16b=0．设A（x1，y1），B（x2，y2），则y1+y2=16m，y1y2=﹣16b，∴x1x2=（my1+b）（my2+b）=b2，∵OA⊥OB，∴x1x2+y1y2=0，可得b2﹣16b=0，∵b≠0，∴b=16，∴直线l：x=my+16，∴直线l过定点（16，0）．故选：C．10．已知数列a n=lg，S n为{a n}的前n项和，若S n＜2，则项数n的最大值为（）A．98 B．99 C．100 D．101【考点】数列的求和．【分析】利用对数的运算性质展开a n，累加后求得S n，再由S n＜2求得项数n的最大值．【解答】解：由a n=lg=lg（n+1）﹣lgn，得S n=a1+a2+…+a n=（lg2﹣lg1）+（lg3﹣lg2）+（lg4﹣lg3）+…+[lg（n+1）﹣lgn]=lg（n+1）．由S n＜2，得lg（n+1）＜2，即n+1＜100，n＜99，∵n∈N*，∴n的最大值为98．故选：A．11．定义域为R的可导函数y=f（x）的导函数f′（x），满足f（x）＞f′（x），且f（0）=2，则不等式f（x）＜2e x的解集为（）A．（﹣∞，0）B．（﹣∞，2）C．（0，+∞）D．（2，+∞）【考点】函数的单调性与导数的关系．【分析】构造函数g（x）=，通过导函数判断函数的单调性，利用单调性得出x的范围．【解答】设g（x）=，则g'（x）=，∵f（x）＜f′（x），∴g'（x）＞0，即函数g（x）单调递增．∵f（0）=2，∴g（0）=f（0）=2，则不等式等价于g（x）＞g（0），∵函数g（x）单调递增．∴x＞0，∴不等式的解集为（0，+∞），故选：C．12．设函数f（x）=，若f（f（））=8，则m=（）A．2 B．1 C．2或1 D．【考点】分段函数的应用；函数的值；函数的零点；函数的零点与方程根的关系．【分析】直接利用分段函数以及函数的零点，求解即可．【解答】解：函数f（x）=，若f（f（））=8，可得f（4﹣m）=8，若4﹣m＜1，即3＜m，可得5（4﹣m）﹣m=8，解得m=2，舍去．若4﹣m≥1，即m≤3，可得24﹣m=8，解得m=1．故选：B．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上..13．设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且a=2，b=3，cosC=，则sinA= ．【考点】余弦定理；正弦定理．【分析】由余弦定理可得：解得c=3．△ABC 是等腰三角形．于是cosC==sin ，cos =．利用sinA=2sin cos 即可得出．【解答】解：由余弦定理可得：c 2=a 2+b 2﹣2abcosC=22+32﹣2×2×3×=9，解得c=3．∴△ABC 是等腰三角形．∴cosC==sin ，cos ==．∴sinA=2sin cos =，故答案为：．14．已知不等式组则z=的最大值为 3 ．【考点】简单线性规划．【分析】画出满足条件的平面区域，结合的几何意义求出z 的最大值即可．【解答】解：画出满足条件的平面区域，如图示：，的几何意义表示平面区域内的点与点A （﹣1，1）的直线的斜率，结合图象直线过AB 时，斜率最大，此时z==3，故答案为：3．15．正方体ABCD﹣A1B1C1D1的棱长为4，E、F分别是棱AB，BB1的中点，A1E与C1F所成的角的余弦值是．【考点】用空间向量求直线间的夹角、距离．【分析】先建立空间直角坐标系以D为坐标原点，DC为x轴，DA为y轴，DD1为z轴，规定棱长为1，再求出A1E与C1F直线所在的向量坐标，然后根据向量的夹角公式求出夹角的余弦值即可．【解答】解：以DC为x轴，DA为y轴，DD1为z轴；建立空间直角坐标系以D为坐标原点，棱长为1．∴A（0，1，0），B（1，1，0），B1（1，1，1），C1（1，0，1）．A1（0，1，1）∴E（，1，0），F（1，1，）可得=（），=（0，1，﹣）∴•=；||==，||==．则．故答案为：．16．过双曲线﹣=1（a＞0，b＞0）的右焦点F作渐近线的垂线，设垂足为P（P为第一象限的点），延长FP交抛物线y2=2px（p＞0）于点Q，其中该双曲线与抛物线有一个共同的焦点，若=（+），则双曲线的离心率的平方为．【考点】双曲线的简单性质．【分析】由=（+），可得P为FQ的中点，设F（c，0），一条渐近线方程和垂直的垂线方程，求得交点P的坐标，由中点坐标公式可得Q的坐标，代入抛物线的方程，结合离心率公式，解方程可得所求值．【解答】解：由=（+），可得P为FQ的中点，设F（c，0），由渐近线方程y=x，①可设直线FP的方程为y=﹣（x﹣c），②由①②解得P（，），由中点坐标公式可得Q（﹣c，），代入抛物线的方程可得=2p•（﹣c），③由题意可得c=，即2p=4c，③即有c4﹣a2c2﹣a4=0，由e=，可得e4﹣e2﹣1=0，解得e2=．故答案为：．三、解答题：本大题共5小题，满分60分，解答应写出文字说明、证明过程或演算步骤17．在△ABC中，a，b，c分别是角A，B，C的对边，=，且a+c=2．（1）求角B；（2）求边长b的最小值．【考点】余弦定理的应用；正弦定理．【分析】（1）利用正弦定理化简表达式，求角B；个两角和与差的三角函数化简求解即可．（2）利用余弦定理求边长b的最小值．推出b的表达式，利用基本不等式求解即可．【解答】解：（1）在△ABC中，由已知，即cosCsinB=（2sinA﹣sinC）cosB，sin（B+C）=2sinAcosB，sinA=2sinAcosB，…4分△ABC 中，sinA≠0，故．…6分．（2）a+c=2，由（1），因此b2=a2+c2﹣2accosB=a2+c2﹣ac …9分由已知b2=（a+c）2﹣3ac=4﹣3ac …10分…11分故b 的最小值为1．…12分（2）以十位为茎，个位数为叶，作出这30位志愿者年龄的茎叶图；（3）求这30位志愿者年龄的方差．【考点】极差、方差与标准差；频率分布表；茎叶图．【分析】（1）根据表格读出即可；（2）按要求作出茎叶图即可；（3）根据求平均数和方差的公式求出即可．【解答】解：（1）众数为19，极差为21．…2分，（2）茎叶图如图下：．…5分（3）年龄的平均数为：，…8分故这30位志愿者年龄的方差为：．…12分19．在三棱锥D﹣ABC，AB=BC=CD=DA=9，∠ADC=∠ABC=120°，M、O分别为棱BC，AC的中点，DM=4．（1）求证：平面ABC ⊥平面MDO ；（2）求点M 到平面ABD 的距离．【考点】点、线、面间的距离计算；平面与平面垂直的判定．【分析】（I ）证明OD ⊥OM ．OD ⊥AC ．推出OD ⊥平面ABC ，然后证明平面ABC ⊥平面MDO ．（Ⅱ）利用V M ﹣ABD =V D ﹣MAB ，求出相关几何体的底面面积，以及高，求解点M 到平面ABD 的距离．【解答】解：（I ）证明：由题意：OM=OD=4，∵，∴∠DOM=90°，即OD ⊥OM ．又∵在△ACD 中，AD=CD ，O 为AC 的中点，∴OD ⊥AC ． ∵OM ∩AC=O ，∴OD ⊥平面ABC ，又∵OD ⊂平面MDO ，∴平面ABC ⊥平面MDO ．… （Ⅱ）由（I ）知OD ⊥平面ABC ，OD=4△ABM 的面积为．又∵在Rt △BOD 中，OB=OD=4，得，AB=AD=8，∴．∵V M ﹣ABD =V D ﹣MAB ，即∴，∴点M 到平面ABD 的距离为．…20．已知椭圆C ：+=1（a ＞b ＞0），F 1，F 2分别是其左、右焦点，A 是椭圆上一点，•=0，直线AF 1的斜率为，长轴长为8．（1）求椭圆C 的方程；（2）直线y=kx +（k ≠0）交椭圆C 于不同的点E ，F ，且E ，F 都在以B （0，﹣2）为圆心的圆上，求k 的值．【考点】直线与圆锥曲线的综合问题；椭圆的标准方程．【分析】（1）利用直线的斜率，求出离心率，通过长轴长求解椭圆的几何量，然后求解椭圆的方程．（2）联立直线与椭圆方程，通过韦达定理求出D 的坐标，然后求解BD 的斜率，求解k 的值．【解答】解：（1）F 1，F 2分别是其左、右焦点，A 是椭圆上一点， •=0，A （c ，），直线AF1的斜率为，∴，，，，，，2a=8，∴a=4，，∴b2=4，∴．…（2），消去y，可得，（1+4k2）x2+12kx﹣7=0，，，中点，…由题意，∴，，，．…21．已知f（x）=x3﹣x2﹣2x+5．（1）求f（x）的单调区间；（2）过（0，a）可作y=f（x）的三条切线，求a的取值范围．【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．【分析】（1）求出函数的导数，解关于导函数的不等式，从而求出函数的单调区间；（2）设切点为（x0，f（x0）），表示出切线方程，求出a的表达式，通过求出求出a的范围即可．【解答】解：（1）f′（x）=3x2﹣x﹣2=（3x+2）（x﹣1），故，x∈（1，+∞），（﹣∞，﹣）时，f（x）单调递增，单调递减．…（Ⅱ）过（0，a）可作y=f（x）的切线，设切点为（x0，f（x0）），则切线的方程为：y﹣f（x0）=f′（x0）（x﹣x0），即，又（0，a）在切线上，故，即．…由已知得：y=a与有三个交点，y'=﹣6x2+x，令y'=0，得，…，，故a的取值范围为．…[选修4-1几何证明选讲]22．BD是等腰直角三角形△ABC腰AC上的中线，AM⊥BD于点M，延长AM交BC于点N，AF⊥BC于点F，AF与BD交于点E．（1）求证；△ABE≌△ACN；（2）求证：∠ADB=∠CDN．【考点】相似三角形的判定．【分析】（1）通过证明∠BAE=∠C，AB=AC，∠ABD=∠NAC，即可判定△ABE≌△ACN．（2）由AE=NC，AD=CD，∠EAD=∠C，可证明△ADE≌△CDN，利用全等三角形的性质即可证明∠ADB=∠CDN．【解答】（本题满分为10分）证明：（1）∠BAE=∠C=45°，AB=AC，∠ABD=∠NAC（∠ADB的余角），∴△ABE≌△ACN．…（2）由（1）可得AE=NC，AD=CD，∠EAD=∠C=45°，∴△ADE≌△CDN，∴∠ADB=∠CDN．…[选修4-4坐标系与参数方程]23．在平面直角坐标系中，以坐标原点为极点，x轴非负半轴为极轴，建立极坐标系，已知曲线C的极坐标方程为：ρsin2θ﹣6cosθ=0，直线l的参数方程为：（t为参数），l 与C交于P1，P2两点．（1）求曲线C的直角坐标方程及l的普通方程；（2）已知P0（3，0），求||P0P1|﹣|P0P2||的值．【考点】参数方程化成普通方程；简单曲线的极坐标方程．【分析】（1）根据极坐标和普通坐标之间的关系进行转化求解．（2）将直线的参数方程代入抛物线方程，利用参数方程的几何意义进行求解．【解答】解：（1）∵ρsin2θ﹣6cosθ=0，∴ρ2sin2θ﹣ρ6cosθ=0，由得y2=6x，即C的直角坐标方程，直线l消去参数t得x=3+（2y），整理得．（2）将l的参数方程代入y2=6x，得．设P1，P2对应参数分别为t1，t2，，t1•t2=﹣72，所求．[选修4-5不等式选讲]24．函数f（x）=|x|﹣2|x+3|．（1）解不等式f（x）≥2；（2）若存在x∈R使不等式f（x）﹣|3t﹣2|≥0成立，求参数t的取值范围．【考点】函数恒成立问题；绝对值不等式的解法．【分析】去掉绝对值符号，化简函数的解析式为分段函数，（I）不等式转化为或或，求出解集即可．（Ⅱ）求出f（x）max=3，转化不等式为f（x）max﹣|3t﹣2|≥0，然后求解参数t的取值范围．【解答】解：，…（I）或或，∴﹣4≤x＜﹣3或或ϕ．∴不等式f（x）≥2的解集为．…（Ⅱ）∵f（x）max=3∴只需f（x）max﹣|3t﹣2|≥0，即3﹣|3t﹣2|≥0，亦即|3t﹣2|≤3，解之得：，∴参数t的取值范围．…2016年9月6日。

2016年联赛预赛(答案)

2016年贵州省高中数学联赛预赛答案一. 选择题（每小题5分，共30分）： 1～6：,,,,,C D B A B D二. 填空题（每小题8分，共64分） 7. 27 ； 8.22564 ； 9. 15(,)()88k k k Z ++∈ ； 10.；11. 16π ； 12. 2π- ； 13. 267 ； 14. 2019 .三. 解答题（共56分）：15.（16分）在正项数列{}n a 中，14,a =其前n 项和n S 满足+12+ n n S S n =.令121(32)n n n b n a -+=-.证明：对于任意*n N ∈,均有215.12ni i b =<∑的值.16. （20分）已知实数,x y 满足112244x y x y +++=+.求88x y M =+的取值范围. (]8,1617. （20分）已知椭圆22:12x C y +=，M 是圆223x y +=上任一点，,MA MB 分别与曲线C 切于点,A B .求OAB ∆面积的最大值（O 为坐标原点）. 23⎡⎢⎣⎦参考答案一、选择题 1. 选C222222592AC AB BCAC AB BC AB BC BC BC =+∴=++⋅⇒=+-⇒=2. 选D42,1()2,13,24,3x x x x e x f x e x x e x ⎧-+<⎪=+≤≤⎨⎪-+>⎩所以1x ≥时，()f x 为增函数，又1x <时，()2x f x e '=-，由()0ln 2f x x '=⇒=，且ln 2x <时，()0f x '<，ln 21x <<时，()0f x '>。

所以()f x 在(],ln 2-∞上为减函数，在[)ln 2,+∞上为增函数. 因此，min ()(ln 2)42ln 226ln 4f x f ==-+=-.3. 选BMN 的最小值即异面直线AB 与CD 的距离.在四面体ABCD 中，设E 为CD 中点，连接,AE BE ,则,AE CD BE CD CD ABE ⊥⊥⇒⊥面，又在ABE ∆中，作EF AB ⊥于F ，则EF 即为异面直线AB 与CD 的距离.易求EF =4. 选A分别作点(34)A -，关于y 轴对称的点1(3,4)A 和直线0x y +=对称的点2(4,3)A -，连接12A A 分别交y 轴和直线0x y +=于点,B C ，则ABC ∆周长的最小值即为12A A的长5. 选B设正三角形ABC 三个顶点到平面α的距离分别为,,a b c ，由题意得222222()2()()3c a b a c b -+=-+=-+，令2222412,,3,,49,1,,, 2.x y x c a x y b a x z y z c b y z x z ⎧+=+=-=⎧⎧⎪⎪⎪=-⇒+=+⇒=⎨⎨⎨⎪⎪⎪=-+==⎩⎩⎩所以正三角形ABC6. 选D由222222220161009100710092016110071007C B A B C A A +=⇒-=, 令0,0C Bx y A A=>=>则2211007100720161009x y -=，显然双曲线2211007100720161009x y -=与直线1x y +=在第一象限的图像有交点，即1,1,1x y x y x y +>+=+<都有解，所以,,B C A B C A B C A +>+=+<都有可能，又A B C π++=，所以角A 取锐角、直角、钝角均有可能. 二、填空题7. 27.119119191043636363636369a b a b a b a b b a +⎛⎫+=+=+++≥+= ⎪⎝⎭. 当且仅当93636a bb a=时，上式取“=”，又由936a b +=，得3,927a b ab ==⇒=. 8.225.6433933331823212(1),(2),(3)886488648864p p p ξξξ⨯⨯+⨯⨯⨯=========⨯⨯⨯， 33923212224(4),(6),(9)886488648864p p p ξξξ⨯⨯⨯⨯=========⨯⨯⨯. 91812912422512346964646464646464E ξ∴=⨯+⨯+⨯+⨯+⨯+⨯=. . [][][][][][][]22221()0102x x x x x x x x x x x x x x ⎛⎫-+=-⇒+-=⇒+-=⇒== ⎪⎝⎭]x x ∴=，当[]1x =时，x =，满足题意，当[]2,3,4x =⋅⋅⋅时，[]1x x -≥，不合题意. 故12x +=10. 15(,)()88k k k Z ++∈()f x x x =在(,)-∞+∞上是增函数，由sin 2sin 2cos2cos2x x x x ππππ>得515sin 2cos 2222()4488x x k x k k x k k Z πππππππ>⇒+<<+⇒+<<+∈. 11. 16.π设ABC ∆外接圆半径为r ，则r =由题意知，四面体ABCD，而4ABC S ∆=,所以点D 到面ABC 的距离的最大值为3，易知，点D 即为与面ABC 垂直的球的直径的端点，由有关球的知识，得22222(3)3962=16r R R R R R R S π+-=⇒+-+=⇒=⇒球 12. 2.π-由2222221,1,(+y 1)(1)01, 1.x y x y x x y x y x y ⎧⎧+≥+≤⎪⎪-+-≤⇒⎨⎨+≤+≥⎪⎪⎩⎩或故点集对应的区域的面积为单位圆面积减去内接正方形的面积2π-.13.26.7{}{},n n a b 为等差数列，且前n 项和539n n A n B n -=+.所以设(53),(9)n n A kn n B kn n =-=+. 故665633236(563)5(553)52,263(39)2(29)14.7a A A k k k ab B B k k k b =-=⋅⋅⋅--⋅⋅⋅-==-=⋅⋅+-⋅⋅+=⇒=14. 2019.由()2017(2017)(12016)(1)2016f x f x f x f x +≤+=++≤++ 所以(1)() 1.............................(1)f x f x +≥+ 又()2016(2016)(20151)(2015)1(20141)1(2014)2(1)2015f x f x f x f x f x f x f x +≥+=++≥++=+++≥++≥⋅⋅⋅≥++所以(1)() 1........................(2)f x f x +≤+由（1）、（2）得120181(1)()11(20181)12019n n f x f x a a a a ++=+⇒-=⇒=+-⋅=. 三、解答题15. 解：112,21(2)n n n n S S n S S n n +-=+∴=+-≥，两式相减得：121(2)n n a a n +=+≥ 所以2111212(1)1(1)2221(2)n n n n n n n a a a a a n ---+-=-⇒-=-⋅=⇒=+≥.所以1,1,21, 2.32n n b n n ⎧=⎪⎪=⎨⎪≥⎪-⎩当1n =时，215412n b =<；当2n ≥时，221222111*********(34)(31)433431111111151154331432311233112nn n n i i i i i b i i i i i n n n ====⎛⎫⎛⎫=+<+=+- ⎪ ⎪-----⎝⎭⎝⎭⎛⎫⎛⎫=+=+-=-⋅< ⎪ ⎪---⎝⎭⎝⎭∑∑∑∑因此，对任意*n N ∈，均有21512ni i b =<∑. 16.解：由112244x y x y +++=+，得22(21)(21)2x y -+-=，令2,2x y a b ==，则22(1)(1)2a b -+-=，又令t a b =+，则(]2,4t ∈，且222t tab -=，33222321()()()()332M a b a b a ab b a b a b ab t t ⎡⎤=+=+-+=++-=-+⎣⎦ 所以2336(4)022M t t t t '=-+=--≥，即3212M t t =+（(]2,4t ∈）为增函数，所以(]8,16M ∈.17. 解：设001122(,),(,),(,)M x y A x y B x y ，则1212:1,:122x x x xMA y y MB y y +=+=，且22003x y +=.由001122(,),(,),(,)M x y A x y B x y ，得10100020201,2:121,2x x y y x x AB y y x x y y ⎧+=⎪⎪⇒+=⎨⎪+=⎪⎩. 将直线AB 的方程与椭圆C 的方程联立，得222000(3)4440y x x x y +--+=所以2200012122220004441),333x y y x x x x AB y y y -++==⇒=+++ 又原点O 到AB的距离d ==，所以0122OABS AB d ∆=⋅=，令[]2121,222223OAB t t S t t t∆⎡=⇒=⋅=⋅∈⎢+⎣⎦+。

2016年全国高中数学联赛陕西赛区预赛试卷

共3页第2页
五, (本题满分 30 分) 设 ��, ��, �� 为正实数, 且满足 �� = 1, 对任意整数 �� ≥ 2, 证明: �� + �� + �� ≥ 3 . √�� + �� √�� + �� √�� + �� √�� 2
A. ��
B.
3 2
��
C.
√6 4
��
D.
√6 8
��
7. 设函数 �� (��) = ��3 + ��2 + �� + ��(��, ��, �� 均为非零整数). 若 �� (��) = ��3, �� (��) = ��3, 则 �� 的值是 ( ).
均为非零实数,
且满足
��
sin
�� 5
��
cos
�� 5
+ �� cos − �� sin
�� 5 �� 5
=
t
an
9�� 20
(1)
求
��
的值;
(2)
在
△��
中,
若
tan ��
A. 2

2016年高中数学联赛预赛圆锥曲线部分汇编

高中数学联赛预赛解析几何高考链接1．设抛物线C：y2=4x的焦点为F，过点（–2，0）且斜率为23的直线与C交于M，N两点，则FM⋅FN=A．5B．6C．7D．82．已知双曲线C：x 23−y2=1，O为坐标原点，F为C的右焦点，过F的直线与C的两条渐近线的交点分别为M、N.若△OMN为直角三角形，则|MN|=A．32B．3C．23D．43．已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A、B两点，直线l2与C交于D、E两点，则|AB|+|DE|的最小值为A．16B．14C．12D．104．已知双曲线C：x 2a2−y2b2=1(a>0,b>0)的右顶点为A，以A为圆心，b为半径作圆A，圆A与双曲线C的一条渐近线于M、N两点，若∠MAN=60∘，则C的离心率为__________．5．设椭圆C:x 22+y2=1的右焦点为F，过F的直线l与C交于A,B两点，点M的坐标为(2,0).（1）当l与x轴垂直时，求直线AM的方程；（2）设O为坐标原点，证明：∠OMA=∠OMB.6．已知椭圆C：x 2a2+y2b2=1(a>b>0)，四点P1(1,1)，P2(0,1)，P3(–1，32)，P4(1，32)中恰有三点在椭圆C.（1）求C的方程；（2）设直线l不经过P2点且与C相交于A,B两点.若直线P2A 与直线P2B的斜率的和为–1，证明：l过定点.1D 2B 3A 4 233 5AM:y=−22(x−2) 6 x24+y2=1 (2,-1)焦点-准线统一定义1.（2016天津）若椭圆x2+ky2=1和双曲线x24−y25=1有相同的准线，则k等于_________2.（2016山西）若椭圆两准线之间的距离等于两焦点之间距离的两倍，则其离心率e=_________焦点三角形3.（2016辽宁）如图所示，在∆ABC中，cos C2=255,AH∙BC=0,AB∙ CA+CB=0，则过点C，以A、H为焦点的双曲线的离心率为_________4.（2016河南）已知双曲线x 2a2−y2b2=1(a>0,b>0)的左右焦点分别为F1、F2，过F1作圆x2+y2=a2的切线交双曲线的右支于点P，且∠F1PF2=45°，则双曲线的离心率为_______ 5.（2016四川）已知F1、F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且∠F1PF2=60°，则该椭圆与双曲线的离心率之积的最小值是________方程角度6.（2016山西）设直线y=x+2与椭圆x 2a2+y2b2=1(a>b>0)相交于M、N两点，且O M⊥ON（其中O为原点），若MN=6，求椭圆的方程。

2016年全国高中数学联赛广西赛区预赛试题及答案

2016年全国高中数学联赛赛区预赛试题及答案一、填空题（本大题共10个小题，每小题8分，共80分）1.函数()f x =的定义域是．答案：()10,100.解：()2lg 3lg 20,1lg 2,10100.x x x x -+-><<<<2.设实数,x y 满足62,1x y y x x ≤⎧⎪≤-⎨⎪≥⎩向量()()2,,1,1a x y m b =-=-，若//a b ，则实数m的最小值为．答案： 2.-解：因为()()2,,1,1a x y m b =-=-，所以211x y m-=-，2.m y x =- 在条件621x yy x x ≤⎧⎪≤-⎨⎪≥⎩下，求得2m y x =-的最小值为 2.-3.设a 、b 都为大于零的常数，01x <<，则221a b x x+-的最小值为．答案：()2.a b +解：设()()22,0,11a b f x x x x=+∈-，则 ()()()()()()()()()()22222222222222111111.1b x a x a b f x x x x x bx a x bx a x x x a b x a b a x a x x --'=-+=----+-⎡⎤⎡⎤⎣⎦⎣⎦=-+--+⎡⎤⎡⎤⎣⎦⎣⎦=-1）当a b ≠时，()()()()()22222222111.1a a a b x x a b a b f x x x a a b x x b a b a x x ⎛⎫⎛⎫--- ⎪⎪+-⎝⎭⎝⎭'=-⎛⎫ ⎪⎛⎫--- ⎪ ⎪+⎝⎭ ⎪-⎝⎭=-，因为,a b 都为正数，所以当0,a x ab ⎛⎫∈ ⎪+⎝⎭时，()0f x '<；当,1a x a b ⎛⎫∈ ⎪+⎝⎭时，()0.f x '>故函数()f x 在ax a b=+处取得最小值 ()222.1a a b f a b a a a b a b a b⎛⎫=+=+ ⎪+⎝⎭-++ 2）当a b =时，()221a a f x x x=+-，()()222122.1a x f x x x ⎛⎫- ⎪⎝⎭'=- 因为a 为正数，所以当10,2x ⎛⎫∈ ⎪⎝⎭时，()0f x '<；当1,12x ⎛⎫∈ ⎪⎝⎭时，()0f x '>．故函数()f x 在12x =处取得最小值 ()222214.112122aa f a a a ⎛⎫=+==+ ⎪⎝⎭- 综上所述，当01x <<时，221ab x x+-的最小值为()2.a b + 4.运行如图所示的程序框图，输出的结果S 的值为．答案：25.已知函数()3f x x =对应的曲线在点()(),k k a f a ()*k N ∈处的切线与x 轴的交点为()1,0k a +，若11a =，则(31010213ff fa +++=⎛⎫- ⎪⎝⎭．答案：3．6.已知点P 在曲线xy e =上，点Q 在曲线ln y x =上，则PQ 的最小值是．7.设*m N ∈，2log m 的整数部分用()F m 表示，则()()()121024F F F +++的值是．答案：8204.8.将一个四棱锥的每个顶点染上一种颜色，并使同一条棱的两的端点异色，若只有4种颜色可供使用，则不同的染色方法总数有种．答案：72.9.设函数()f x 的定义域为R ，若存在常数0ω>使()fx x ω≤对一切实数x 均成立，则称函数()f x 为“条件约束函数”．现给出下列函数：①()4f x x =；②()22f x x =+；③()2225xf x x x =-+；④()f x 是定义在实数集R 上的奇函数，且对一切12,x x 均有()()12124.f x f x x x -≤-其中是“条件约束函数”的序号是（写出符合条件的全部序号）．答案：①③④．10.已知线段AB 是半径为2的球O 的直径，C 、D 两点在球O 的球面上，2,CD AB CD =⊥，45135AOC ≤∠≤，则四面体ABCD 的体积的取值围是．答案：4.3⎡⎢⎣⎦二、解答题（本大题共3小题，共70分）11.（本小题满分20分）已知数列{}n a 中，1211,,4a a ==且 ()()112,3,4,.n nn a n n a +-==-（1）设()11n nb n a =-，球数列{}2n n b ≥的通项公式；（2）求证：对一切*n N ∈，有217.6nkk a =<∑ 解：（1）()()1111,2,3,4,,nn nn a a a n n a +-===-∴当2n ≥时，()()111.111n n n n n a n a n a n a n +-==---- 两边同时除以n ，得()()1111,11n n na n a n n +=--- 1111n n b b n n +⎛⎫∴-=-- ⎪-⎝⎭()12121111 111k n k n k k k k n b b -+-==⎛⎫⎛⎫-=-- ⎪ ⎪--⎝⎭⎝∴-⎭-=∑∑*2211321, 2.1,.111n n n b b n b b n N n n n -⎛⎫⎛⎫∴-=--≥∴=--+=∈ ⎪ ⎪---⎝⎭⎝⎭（2）证明：当2k ≥时，()()()2211111,34313343132k a k k k k k ⎛⎫=<=- ⎪----⎝⎭-∴当2n ≥时，22121111111113255834311111711.323166nnk k k k aa n n n ==⎡⎤⎛⎫⎛⎫⎛⎫=+<+-+-++- ⎪ ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫=+-<+= ⎪-⎝⎭∑∑又当1n =时，2171,6a =<∴对一切*n N∈，有217.6nk k a =<∑ 12.（本小题满分25分）如图，点H 为△ABC 的垂心，以AB 为直径的⊙1O 和△BCH 的外接圆⊙2O 相交于点D ，延长AD 交CH 于点P ，求证：点P 为CH 的中点．证明：如图，延长AP 交⊙2O 于点Q ，连接,,,,.AH BD QB QC QHAB 为⊙1O 的直径，90.ADB BDQ ∴∠=∠= BQ ∴为⊙2O 的直径．,.CQ BC BH HQ ∴⊥⊥点H 为△ABC 的垂心，,.AH BC BH AC ∴⊥⊥//,//AH CQ AC HQ ∴，四边形ACQH 为平行四边形．∴点P 为CH 的中点．13.（本小题满分25分）已知抛物线2:4C y x =，以()1,2M 为直角顶点作该抛物线的接直角三角形MAB ．（1）求证：动直线AB 过定点；（2）过点M 作AB 的垂线交AB 于点N ，求点N 的轨迹方程．解：（1）设直线AB 的方程为x my n =+，()()1122,,,.A x y B x y2,4,x my n y x =+⎧⎨=⎩得2440,y my n --= 12124,4y y m y y n ∴+==-．90,0,AMB MA MB ∠=∴⋅=即()()11221,21,20.x y x y --⋅--=()()()()121211220.x x y y ∴--+--=()()()()()()()()12122211211220,12140,my n my n y y m y y mn m y y n +-+-+--=++--++-+= ()()()221424250.mn mn m m n n +⋅-+--+-+=整理得()()22341,n m -=+()321n m ∴-=+或()321.n m -=-+当()321n m -=+，即25n m =+时，直线AB 的方程为()25x m y =++过定点()5,2P -；（2）由（1）知，点N 的轨迹是以PM 为直径的圆（除去点()1,2±），其方程为()()22381.x y x -+=≠。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ｎＤ
焦点为ｆ —ｃ０１３一＝．２０．２）一二Ｊｆ则ｃ～＝一，ＣＢ２．，０．
准线方程为：一２
，
２
：
，
Ｃ
２
ｃ
图３
两准线距离为２．，焦距为２ｃ．
ｋ＝Ｉ
故＝５（３ｓｉｎ。一４ｃ。ｓ）
＝５ｓｉｎ（ｘｏ一０） ≤５．
③
由式② 、 ③得
当一＝２＋詈时，上式等号成立，此时，
ｔａｎｘｏ＝ｔａｎ２ｋ＋詈＋）＝ｔａｎ（詈＋）
故ｃ。ｓ＝ √ ＤＥ＝：
Ｓ＆ＢＣＯ－・ＩＤＥ
．
项式．
６・一・
ＢＣ－８
．
设ｃ。ｓ＝３ｓｉｎ＝４（为锐角）
，
．
２０１７年第３期
１９
２７
ａｎ
＝
．
＝
（３一１）１Ｔ（３＋１）＝ …
２０１７年第３期
２０１６年全国高中数学联赛山西赛区预赛
中图分类号：Ｇ４２４．７９文献标识码：Ａ文章编号：１００５— ６４１６（２０１７）０３－００２５一ｏ４
一
、
填空题（每小题８分，共６４分）
—‘。。一 ● — ———…
Ｃ
口
Ｚ
８．３２￣￣－１
一
．
注意到，对于任何大于ｌ的数ｍ，均有
１
一一
ＧＢＭＡＮＤ ‘
１
一＝
２
—— — ： —— ——一
．
ｍ一１ｍ＋１ｍ — １ ‘
ＢＧ
—
＝
・
＝
ＡＮ１一ＣＮＩ
加得
＝一．
—
—
２（ＣＤＣＮ），’ ＮＤ ’ ‘
—
一
由于点Ｇ在中线ＢＤ上，从而，Ｇ为△ ＡＢＣ
②
的重心，即ＭＮ经过 △ ＡＢＣ的重心．
三、设点Ｍ（，Ｙ１），Ｎ（ｘ２，Ｙ：）．
又记Ｃ＝２。 × ２ ×… × ２＝２，
即Ｃｎｃ中最多只有一个元素，矛盾．
从而，ＩＣｎＣＩ ≤１（ｍ≠ｎ）．由容斥原理知
．
又令Ａ＝｛２，２， …，２加｝，
Ｂ＝｛２，２， …，２｝．
容易验证，若ｍ≠凡 ≠ ，则
ＧＤＭＡＮＤ
ＮＡ／ＮＤ
．
上式两边乘以２（
ＮＤ
－
＝２二
ＮＤ
３＋１＝３
一．一１３ “ 一１‘
①
一
—
— 。
在式① 中分别令ｋ＝０，１， …，９，然后相
将结论①代人上式得
ｏ２＋
ａ
其余ａｉ＝Ｏ（ｊ＃ｒ）．
显然，（，．＋１）＜ｎ＋１．
ｂ２
一２０＋ｂ２
。
。
若１ ≤ｎ ≤１０一１，记ｎ，的各位数字中
⑦
２＋ｂ＝０。ｂ
．
如图１，设平面ＡＡ。Ｐ与棱ＢＣ、ＢＣ１分别交于点Ｅ、Ｅ．
记＾ｓ＝ ∑ｎ．于是，２０１６＝Ｓｄ．
欲使ｄ最大，应使ｓ取最小．
由于ａ１，ａ２， …，口ｌ２互异，则
．
／
Ｄ
／
２。 ×３。 × … ×１０。 ≤ ｎ＋１．
５．记“ ∑” 表示轮换对称和．若ｎ、ｂ、ｃ为
给定的互不相同的实数，则
ｆ（ｘ）＝ ∑ 警
０
．
并确定使等号成立的条件．
＝３２０一ｌ２０：２Ｏ０．
＝
ｂ，０厶ｂ，
Ｓ≥ １＋２＋… ＋１２＝７８．
Ｃ：
注意到，Ｓ１２０１６，且７８不为２０１６的因数
Ａ
蘑跫Ｅ＼
如图２，在矩形ＡＥＥＡ中，易知，
又２０１６＝２ × ３ × ７，其大于７８的最小
记
刚
注意到，ｆ（）为二次多项式，且当分
１ＡＰ＝ＡＥＤ＝０．
ＡｌＰ＝
＝．
别取口、６、ｃ三个不同的值时，均有．厂（）＝。因此，．厂（）＝为恒等式．
【注】本题实际上就是拉格朗日插值多
２ｎ＋１＝３（２ｋ一１）
ｎ＜＿＝一＜ｎ＋１．
４３— — １
＝＝３ｋ一２，ｍ＝３ｋ２ — ３ｋ＋１（ｋ＝１，２， …）．故ｎ＝凡（＋１）＝３ｍ —ｌ＝９ｋ一９ｋ＋２．
，，
７．若椭圆两准线之间的距离为两焦点之
间距离的两倍，则其离心率ｅ＝ — — ．
ｏｋ
序排成一个数列｛口｝，则数列｛０｝的通项公
— —
ｔ
８．设口＝
Ｊ
（ ∈ Ｎ），令
Ｔ１
口
— — —
２．已知正三棱柱ＡＢＣ— ＡＢ１ｃ１的高为
含有ａ１个１，ａ２个２， …，口，个ｒ， …，ａ９个９．
于是，结论①为
一
则ｎ的各位数字中，含有ａ，＋１个，．、ａｉ个ＩＬ ③
（１ ≤９， ≠ｒ）．
由ＭＮ＝ √ ６，得（１一２）。＋（Ｙｌ一）＝６．
的两根，所以，
”
假设当正整数不超过ｋ位，即ｎ＜１０时，结论皆成立．
ｔ忆ｚ筹ｚ
Ｘ，１２＋Ｙ１Ｙ２０
由ＯＭ上ＯＮ
现考虑ｎ为ｋ＋ｌ位数，即ｌＯ ≤ｎ＜１０． ‘ ① 时的情形．设ｎ的首位数字为，．则
一ｃｏｔ一
／Ｊ２Ｂ — ２３一１八２』
－
一
１
：
一
０２１１八／３２
—
＇￣
１
｝．
３一１
１
丁
一 ‘
Ａ
７．２．
二、如图３，取ＡＣ的中点Ｄ．
设椭圆方程为＋＝１（ｎ＞ｂ＞０），
故ｎ＝［】＝４（［］表示不超过实数
的最大整数）．
４．２４．
“ ８ ’
堡
设最大公约数为ｄ，１２个数分别为ｄ，
ａ２ｄ， …， Ⅱ １２ｄ（（ａｌ，ａ２， …，ａ１２）＝１）．
１６
．
ｃｎＣｎ＝｛２＋２｝，ｃｎｃｎＣ＝．
因此，ｌＡ＋Ｉ＝２００．
１Ａ＋日Ｉ－－Ｕ１ＣＩ
１６
≥∑ ＪＪ一 ∑ ＪＣｔ３Ｃ．Ｊ
综上，ｌ＋曰Ｉ的最小值为２００．
Ｃ
由于ＣＮ＜１＝
，
则点 Ⅳ在线段ｃＤ内．
＝４ｃｅ＝ｃ＝４Ｙ据条件知２・２
。
故线段ＢＤ与ＭＮ相交，设交点为Ｇ．下面证明：Ｇ即为△ ＡＢＣ的重心．对ＭＮ和ＡＡＢＤ应用梅涅劳斯定理得
ＤＧＢＭＡＮ
经化简后得到一
１．设集合Ａ＝｛（１１，＋１）Ｉ＝１，２， …｝，Ｂ＝｛３ｍ一１Ｊｍ＝１，２， …｝．若将集合ＡｆｑＢ的元素按自小到大的顺
６．若函数Ｙ＝３ｓｉｎ一４ｃｏｓ在０处取得最大值，则ｔａｎ。的值为一
将Ｙ＝＋代人椭圆方程并消去Ｙ得
２
Ｄ＝ Ⅱ（３＋１）
＝
＋
－１
ａ‘
ｂ ‘
１（３一１） Ⅱ（３＋１）
（０＋６）＋２０＋０（２一ｂ）＝０．
２８
中等数学
因为点、 Ⅳ在椭圆上，即、为方程
Ｂ＝｛２，５，８，１１，１４，１７，２０， …｝．
若ｎ（ｎ＋１）＝３ｍ一１
（２ｎ＋１）＝３（４ｍ～１）．
ｊ＜一－＜
于是，４ｍ一１为某个奇平方数的３倍．
设４ｍ一１＝３（２ｋ一１）．则