运筹学(胡运权)第五版课后答案,运筹作业
清华大学运筹学教程胡运权主编课后习题答案
8 10
x1 , x2 0
目标函数最优值(下界)为:6.4
17
第18页/共66页
l.7 分别用单纯形法中的大M法和两阶 段法求解下列线性规划问题,并指出属哪—
类解。
max Z 3x1 x2 2x3
x1 x2 x3 6
(1)
st
2x1 2x2
x3 x3
0
2
x j 0(, j 1,,3)
所以最优解为X*=(1,3/2,0,0)T
第11页/共66页
0点
A1点 A2点
max Z 2x1 x2 3x1 5x2 15
(2) st.6x1 2x2 24 x1, x2 0
11
第12页/共66页
第13页/共66页
第14页/共66页
d
x
2
,
l.5 讨论c
,
上题(1)中,若目标函数变为max Z = d的值如何变化,使该问题可行域的每个
8
第9页/共66页
1.4 分别用图解法和单纯形法求解下述 线性规划问题,并对照指出单纯形表中的各 基可行解对应图解法中可行域的哪一顶点。
max Z 10x1 5x2
(1)
st.35xx11
4 x2 2 x2
9 8
x1, x2 0
9
第10页/共66页
cj
10
5 00
CB
xB
b
x1
x2
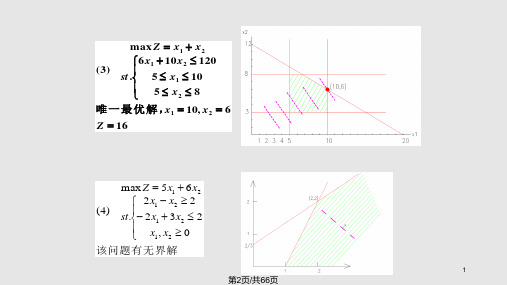
max Z x1 x2
(3)
st
6 .
x1 10x2 5 x1
120 10
5 x2 8
唯 一 最 优 解 ,x1 10, x2 6
Z 16
max Z 5x1 6x2 2x1 x2 2
清华大学《运筹学教程》胡运权主编课后习题答案

st2x1x1 22x2x23xx33
4x4 2x4
7 3
xj 0,( j 1, 4)
maxZ 3x1 x2 2x3
12x1 3x2 6x3 3x4 9
(1)
st
8x1 3x1
x2 x6
4x3 0
2x5
10
xj 0( , j 1, ,6)
x1
x2
x3
(x1,x2,x3)
x1 0, x2 0, x3无约束
解 : 令W Z , x11 x1 , x31 x32 x3 同 时 引 入 松 弛 变 量x4, 则 标 准 形 式 为 :
maxW 2x112x2 3x313x32
st2x1x111x2x2 x3x131x3x232
4 x4
6
x11, x2, x31, x32, x4 0
第一章习题解答
1.1 用图解法求解下列线性规划问题。 并指出问题具有惟一最优解、无穷多最优解、 无界解还是无可行解。
min Z 2 x1 3 x2
(1)
st
.
4 3
x1 x1
6 x2 2 x2
6 4
x1 , x2 0
max Z 3x1 2x2
(2)
st
.32xx11
x2 2 4x2 12
0
0
0 -M -M
i
x2
x3
x4
x5
x6
0 1/5 0 3/5 -1/5
1 -3/5 0 -4/5 -3/5
0 [1] 1
0
0
0
1 -1
-1 -1
该模型最优解为X=(3/5,6/5,0,1,0,0)T, 其基变量不含人工变量,说明原问题的一个基可行解为 X=( 3/5,6/5,0,1 )T,转入第二阶段。
胡运权《运筹学教程》(第5版)配套题库-考研真题精选及课后习题(第一~三章)【圣才出品】

2.μ是关于可行流 f 的一条增广链,则在μ上有:对一切(i,j)∈μ-,有 fij>0。( ) [暨南大学 2019 研]
【答案】√ 【解析】由增广链定义可知,当边(i,j)属于μ的反向边集时,该条边的流量大于 0。
3.事件 j 的最早时间 TE(j)是指以事件 j 为开工事件的工序最迟必须开工时间。( ) [暨南大学 2019 研]
零元素的最少直线数目的集合。结果如下:
4 / 113
圣才电子书 十万种考研考证电子书、题库视频学习平台
(4)在未被覆盖的元素中找最小元素,未被覆盖的行分别减去该最小元素,在出现负
数的列上整列加上最小元素,得到新矩阵 C′:
0 2 6 1 0 0 4
表 1-1-1
解:(1)先对各行减去本行的最小元素,再对各列减去本列最小元素,得到矩阵 C 如
下:
0 2 6 9
C 1 4 4 0 1 0 0 3 2 3 6 0
(2)确定独立零元素,对 C 加圈,得到
◎ 2 6 9
C
1
1
4 ◎
4
◎ 3
2
3
6
(3)由于只有 3 个独立零元素,少于系数矩阵阶数 n=4,故需要确定能够覆盖所有
A.没有无穷多最优解 B.没有最优解 C.有无界解 D.有最优解 【答案】B 【解析】有最优解的前提是有可行解,该题无可行解,则也无最优解。
2.如果某种资源的影子价格大于其市场价格,则说明( )。[暨南大学 2019 研] A.该资源稀缺 B.该资源过剩 C.企业应尽快处理该资源 D.企业应充分利用该资源,开辟新的生产途径 【答案】A 【解析】当资源的影子价格不为 0 时,表明该种资源在生产中已耗费完毕;且若影子 价格大于其市场价格,说明企业应买进该种资源,该种资源稀缺。
运筹学(胡运权)第五版课后答案-运筹作业

运筹学(胡运权)第五版课后答案-运筹作业47页1.1b用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解47页1.1d无界解1 2 3 454321-1-6 -5 -4 -3 -2X2X12x1--2x1+3x1 2 3 44321X12x1+x2=23x1+4x2=X1.2(b)约束方程的系数矩阵A= 1 2 3 42 1 1 2P1 P2 P3 P4基基解是否可行解目标函数值X1 X2 X3 X4P1 P2 -4 11/2 0 0 否P1 P3 2/5 0 11/5 0 是43/5 P1 P4 -1/3 0 0 11/6 否P2 P3 0 1/2 2 0 是 5 P2 P4 0 -1/2 0 2 否P3 P4 0 0 1 1 是 5最优解A=(0 1/2 2 0)T和(0 0 1 1)T49页13题设Xij为第i月租j个月的面积minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x1 3 +6000x23+7300x14s.t.x11+x12+x13+x14≥15x12+x13+x14+x21+x22+x23≥10x13+x14+x22+x23+x31+x32≥20x14+x23+x32+x41≥12Xij≥0用excel求解为:( )用LINDO求解:LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION V ALUE1) 118400.0V ARIABLE V ALUE REDUCED COSTZ 0.000000 1.000000X11 3.000000 0.000000X21 0.000000 2800.000000X31 8.000000 0.000000X41 0.000000 1100.000000X12 0.000000 1700.000000X22 0.000000 1700.000000X32 0.000000 0.000000X13 0.000000 400.000000X23 0.0000001500.000000X14 12.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 -2800.0000003) 2.000000 0.0000004) 0.000000 -2800.0000005) 0.000000 -1700.000000NO. ITERATIONS= 3答若使所费租借费用最小,需第一个月租一个月租期300平方米,租四个月租期1200平方米,第三个月租一个月租期800平方米,50页14题设a1,a2,a3, a4, a5分别为在A1, A2, B1, B2, B3加工的Ⅰ产品数量,b1,b2,b3分别为在A1, A2, B1加工的Ⅱ产品数量,c1为在A2,B2上加工的Ⅲ产品数量。
清华大学《运筹学教程》胡运权主编课后习题答案

3 x1 x2 x5 3
st
4 x1 3 x2 x3 x6
x1
2 x2
x4
4
6
x j 0(, j 1,,4)
cj
CB
xB
b
-M x5 3
-M
x6
6
0
x4
4
cj zj
-4 x1 1
-M x6 2
0
x4
3
cj zj
-4
-1 0
x1
x2
x3
3
1
0
4
3 -1
1
20
7M-4 4M-1 -M
小于0 ,因此已经得到唯一最优解,最优解为:
X * 2 5 ,9 / 5,1,0T
max Z 10x1 15x2 12x3
5x1 3x2 x3 9
(4)
st
5x1 2x1
6x2 x2 x3
15x3 5
15
x j 0(, j 1,,3)
39
1.8 已知某线性规划问题的初始单纯形
表和用单纯形法迭代后得到下面表格,试求括
弧中未知数a∼l值。
项目
X1 X2 X3 X4 X5
X4 6 (b) (c) (d) 1 0
X5 1 -1 3 (e) 0 1
Cj-Zj
a -1 2 0 0
X1 (f) (g) 2 -1 1/2 0
X5 4 (h) (i) 1 1/2 1
Cj-Zj
0 -7 (j) (k) (l)
6 4
x1 , x2 0
无穷多最优解
(蓝 色 线 段 上 的 点 都 是 最优 解 )
x1
6 5
,
x2
运筹学(第五版) 习题答案

当所有非基变量为负数,人工变量 =0.5,所以原问题无可行解。
两阶段法(略)
(4)解法一:大M法
单纯形法,(表略)非基变量 的检验数大于零,此线性规划问题有无界解。
两阶段法略
1.7求下述线性规划问题目标函数z的上界和下界;
Max z= +
其中: , , , , , , ,
解:
求Z的上界
班次时间所需人数16点到10点60210点到14点70314点到18点60418点到22点50522点到2点2062点到6点30设司机和乘务人员分别在各时间区段一开始时上班并连续上班8小时问该公交线路至少配备多少司机和乘务人员
运筹学习题答案
第一章(39页)
1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
以( , )为基,基解 =(0,0,1,1 是 =-3;
最大值为 =43/5;最优解为 =(2/5,0,11/5,0 。
1.4分别用图解法和单纯形法求解下列线性规划问题,并指出单纯形迭代每一步相当于图形的哪一点。
(1)max z=2 +
3 +5 15
6 +2 24
, 0
(2)max z=2 +5
4
2 12
1
0
0
0
14
-M
2
-2
[3]
-1
2
-2
0
-1
1
0
2/3
-
4M
3-6M
4M-4
2-3M
3M-5
5-3M
0
-M
0
0
(2)解:加入人工变量 , , ,… ,得:
运筹学胡运权第五版第三章

➢ 课后题答案
3.1 表3-35 最终表如下:
销地 产地
A1 A2 A3
销量
B1
B2 B3 B4 产 量
15 5 16 10 15
12 10 15 4
25
5 5 50
5
5 15 15 10 45
注:黑色数字表最优解,红色表示对应非基变量的 检验数。即:最优值Z*=335. 亦或是:
➢ 课后题答案
习题讲解
课程:运筹学 内容:第三章课后习题解
LOGO
表上作业法的步骤
1.将运输问题化为产销平衡的问题 ✓供过于求:增加假设销地; ✓供不应求:增加假设产地; 2.确定初始调运方案 ✓(最小元素法,西北角法,vogel法) 3.最优性检验(闭回路法,位势法) 若所有非基变量的检验数都有σij ≥0,则得最优方案,结 束计算。否则,转4; 4.调整方案(闭回路法),转3。
第1年 第2年 第3年 多余 产量
期初贮存 第1年正常生产数 第1年加班生产数 第2年正常生产数 第2年加班生产数 第3年正常生产数 第3年加班生产数 需要量
40
80 120 0
2
500 540 580 0
2
570 610 650 0
3
M 600 640 0
4
M 670 710 0
2
M
M 550 0
33.4 答案: (a) 最优方案不变,最优值z'=z+kar (b) 最优方案不变,最优值z'=z+kbp,同理与(a) (c) 最优方案不变,最优值z'=kz
➢ 课后题答案
3.5 答案:
(a)Δc22∈[-4,3] 即:c22∈[3,10]
胡运权《运筹学教程》习题答案(第一章)[1]
![胡运权《运筹学教程》习题答案(第一章)[1]](https://img.taocdn.com/s3/m/5266ca4b767f5acfa1c7cd73.png)
第一章习题解答1.1 用图解法求解下列线性规划问题。
并指出问题具有惟一最优解、无穷多最优解、无界解还是无可行解。
+=32min 21x x Z +=23max 21x x Z ⎪⎩⎪⎨⎧≥≥+≥+0,422664.)1(212121x x x x x x st ⎪⎩⎪⎨⎧≥≥+≤+0,124322.)2(212121x x x x x x st ⎪⎩⎪⎨⎧≤≤≤≤≤++=85105120106.max )3(212121x x x x st x x Z ⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答无穷多最优解,,422664.32min )1(21212121⎪⎩⎪⎨⎧≥≥+≥++=x x x x x x st x x Z 是一个最优解3,31,121===Z x x 该问题无解⎪⎩⎪⎨⎧≥≥+≤++=0,124322.23max )2(21212121x x x x x x st x x Z 第一章习题解答85105120106.max )3(212121⎪⎩⎪⎨⎧≤≤≤≤≤++=x x x x st x x Z 唯最优解16,6,1021===Z x x 唯一最优解,该问题有无界解⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答1.2 将下述线性规划问题化成标准形式。
1422245243min )1(432143214321⎪⎪⎧≤+−+−=−+−+−+−=x x x x x x x x x x x x Z .,0,,23243214321⎪⎪⎩⎨≥≥−++−无约束x x x x x x x x st ⎪⎩⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min )2(x x x x x x x x x st x x x Z 第一章习题解答.2321422245243min )1(4321432143214321⎪⎪⎪⎨⎧≥−++−≤+−+−=−+−+−+−=x x x x x x x x x x x x st x x x x Z ,0,,4321⎪⎩≥无约束x x x x ⎪⎪⎩⎪⎪⎨⎧≥=−+−++−=+−+−+=−+−+−+−+−=0,,,,,232142222455243max 64241321642413215424132142413214241321x x x x x x x x x x x x x x x x x x x x x x x st x x x x x Z 第一章习题解答⎪⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min)2(x x x x x x x x x st x x x Z ⎩⎪⎩⎪⎨⎧≥=++−+=−++−+−+=0,,,,6243322max 43231214323121323121323121x x x x x x x x x x x x x x st x x x x Z第一章习题解答634334max )3(3212121⎪⎪⎧=−+=++=x x x x x st x x Z 517,0,1,59,524,,1,0424321421=====⎪⎪⎩⎨=≥=++Z x x x x j x x x x j 该题是唯一最优解:)("第一章习题解答⎪⎧≤++−≤++++=151565935121510max 321321x x x x x x x x x Z 该题无可行解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
47页1.1b用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解47页1.1d无界解1.2(b)约束方程的系数矩阵A= 1 2 3 4( )2 1 1 2P1 P2 P3 P4最优解A=(0 1/2 2 0)T和(0 0 1 1)T49页13题设Xij为第i月租j个月的面积minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13+6000x23+7300x14s.t.x11+x12+x13+x14≥15x12+x13+x14+x21+x22+x23≥10x13+x14+x22+x23+x31+x32≥20x14+x23+x32+x41≥12Xij≥0用excel求解为:用LINDO求解:LP OPTIMUM FOUND A T STEP 3OBJECTIVE FUNCTION V ALUE1) 118400.0VARIABLE V ALUE REDUCED COST Z 0.000000 1.000000X11 3.000000 0.000000X21 0.000000 2800.000000X31 8.000000 0.000000X41 0.000000 1100.000000X12 0.000000 1700.000000X22 0.000000 1700.000000X32 0.000000 0.000000X13 0.000000 400.000000X23 0.000000 1500.000000X14 12.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 -2800.0000003) 2.000000 0.0000004) 0.000000 -2800.0000005) 0.000000 -1700.000000NO. ITERATIONS= 3答若使所费租借费用最小,需第一个月租一个月租期300平方米,租四个月租期1200平方米,第三个月租一个月租期800平方米,50页14题设a1,a2,a3, a4, a5分别为在A1, A2, B1, B2, B3加工的Ⅰ产品数量,b1,b2,b3分别为在A1, A2, B1加工的Ⅱ产品数量,c1为在A2,B2上加工的Ⅲ产品数量。
则目标函数为‘maxz= (1.25-0.25)( a1+a2+a3)+( 2-0.35) b3+( 2.8-0.5)c1 -0.05 (a1+b1)-0.03 (a2+b2+c1)- 0.06 (a3+b3)-0.11(a4+c1)-0.05a5=0. 95a1+0. 97a2+0. 94a3+1.5b3+2.1c1-0.05b1-0.11a4-0.05a5s.t.5a1+10b1≤60007a2+b2+12c1≤100006a3+8a3≤40004a4+11c1≤70007a5≤4000a1+a2-a3-a4-a5=0b1+b2-b3=0a1,a2,a3, a4, a5, b1,b2,b3, c1≥0用lindo求解得:LP OPTIMUM FOUND AT STEP 6OBJECTIVE FUNCTION V ALUE1) 16342.29V ARIABLE V ALUE REDUCED COSTA1 1200.000000 0.000000A2 0.000000 9.640000A3 285.714294 0.000000B3 10000.000000 0.000000C1 0.000000 15.900000B1 0.000000 0.230000A4 342.857147 0.000000A5 571.428589 0.000000B2 10000.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 0.1680003) 0.000000 1.5000004) 0.000000 0.0750005) 5628.571289 0.0000006) 0.000000 0.0085717) 0.000000 0.1100008) 0.000000 -1.500000NO. ITERATIONS= 6计算lindo截屏2.1a:对偶问题为:maxz=2y1+3y2+5y3s.t.y1+2y2+y3≤23y3+y2+4y3≤24y1+3y2+3y3=4y1≥0, y 2≤0,y3无约束因为原问题的对偶问题的对偶问题仍是原问题,因此本问题的对偶问题的对偶问题为:minz=2x1+2x2+4x3s.t.x1+3x2+4x3≥22x1+x2+3x3≤3x1+4x2+3x3=5x1,x2≥0,x3无约束81页2.12a)设x1,x2,x3分别为A,B,C产品数量maxz=3x1+x2+4x3s.t.6x1+3x2+5x3≤453x1+4x2+5x3≤30x1,x2,x3≥0用lomdo求解为LP OPTIMUM FOUND AT STEP 2OBJECTIVE FUNCTION V ALUE1) 27.00000V ARIABLE V ALUE REDUCED COST X1 5.000000 0.000000X2 0.000000 2.000000X3 3.000000 0.000000 X1,X2,X3 0.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 0.2000003) 0.000000 0.6000004) 0.000000 0.000000NO. ITERATIONS= 2最大生产计划为A生产5个单位,C生产3个单位b)LP OPTIMUM FOUND AT STEP 2OBJECTIVE FUNCTION V ALUE1) 27.00000V ARIABLE V ALUE REDUCED COSTX1 5.000000 0.000000X2 0.000000 2.000000X3 3.000000 0.000000X1,X2,X3 0.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 0.2000003) 0.000000 0.6000004) 0.000000 0.000000NO. ITERATIONS= 2RANGES IN WHICH THE BASIS IS UNCHANGED:OBJ COEFFICIENT RANGES V ARIABLE CURRENT ALLOWABLE ALLOWABLECOEF INCREASE DECREASEX1 3.000000 1.800000 0.600000X2 1.000000 2.000000 INFINITYX3 4.000000 1.000000 1.500000 X1,X2,X3 0.000000 0.000000 INFINITYRIGHTHAND SIDE RANGESROW CURRENT ALLOWABLE ALLOWABLERHS INCREASE DECREASE2 45.000000 15.000000 15.0000003 30.000000 15.000000 7.5000004 0.000000 0.000000 INFINITY可知A产品的利润变化范围【6. 8,2.4】,上述计划不变。
c)设x4为产品D的数量maxz=3x1+x2+4x3+3x4s.t.6x1+3x2+5x3+8x4≤453x1+4x2+5x3+2x4≤30x1,x2,x3 ,x4≥0用lomdo求解为LP OPTIMUM FOUND AT STEP 0OBJECTIVE FUNCTION V ALUE1) 27.50000V ARIABLE V ALUE REDUCED COSTX1 0.000000 0.100000X2 0.000000 1.966667X3 5.000000 0.000000X4 2.500000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 0.2333333) 0.000000 0.566667NO. ITERATIONS= 0安排生产D有利,新最有生产计划为x1=x2=0,x3=5,x4=2.5,利润为27.5 d)maxz=3x1+x2+4x3-0.4ys.t.6x1+3x2+5x3≤453x1+4x2+5x3-y≤30x1,x2,x3,y≥0用lomdo求解为LP OPTIMUM FOUND AT STEP 0OBJECTIVE FUNCTION V ALUE1) 30.00000V ARIABLE V ALUE REDUCED COST X1 0.000000 0.600000X2 0.000000 1.800000X3 9.000000 0.000000Y 15.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 0.4000003) 0.000000 0.400000NO. ITERATIONS= 0可知购进原材料15个单位为宜。
4.1a)设yi= 1 第i组条件起作用0 第i组条件不起作用x1+x2≤2-(1-y1)M M —充分大正数2x1+3x2≥5+(1-y2)My1+y2=1y1,y2=0或1b)设yi= 1 第i 组条件起作用0 第i 组条件不起作用x=0y1 x=3y2 x=5y2 x=7y4y1+y2+y3+y4=1 y1,y2,y3,y4=0或1c) 设yi= 1 为假定取值≥500 为假定取值x=0x=0y1x ≥50--(1-y2)M y1+y2=1 y1,y2=0或1d) 设yi= 1 第i 组条件起作用0 第i 组条件不起作用 i=1,2 则x1≤2+(1-y1)M x2≥1-(1-y1)M x2≤4+(1-y2)M y1+y2=1 y1,y2=0或1e) 设yi= 1 第i 组条件起作用0 第i 组条件不起作用 i=1,2 则x1+x2≤5-(1-y1)Mx1≤2-(1-y2)M x3≥2+(1-y3)M x3+x4≥6+(1-y4)M y1+y2+y3+y4≥2 y1,y2,y3,y4=1或04.2minz =∑cjxj 10j=1 ∑xj 10j=1=5 x1+x8=1 x7+x8=1 s.t. x3+x5≤1x4+x5≤1x5+x6+x7+x8≤2xj= 1 选择钻探第sj 井位 0 否4.5设xij 为第i 种泳姿用第名运动员minz=∑∑ai 5j=1jxij 4i=1s.t.x11+x12+x13+x14+x15=1x21+x22+x23+x24+x25=1 x31+x32+x33+x34+x35=1 x41+x42+x43+x44+x45=1 x11+x21+x22+x23=1 x12+x22+x32+x42=1 x13+x23+x33+x43=1 x14+x24+x34+x44=1 x15+x25+x35+x45=1xij=1或0(i=1,2,3,4 j=1,2,3,4,5)由excel 计算得出;张游仰泳,王游蛙泳,赵游自由泳,预期总成绩为126.2s.因为使mind1-,故在x1+x2=40的右侧,若使mind4+,则在x1+x2=50的左侧,即阴影区域,因为在阴影部分无法使2d2-+d3-最小,故比较E(20,30),F(24,26),E点:d2-=4,d3-=0 min2d2-+d3-=8,F点:d2-=0,d3-=4, min2d2-+d3-=4,故选F 点程序法6.4a破圈法避圈法6最小部分树166.4b10 1210 12 最小部分树32172页6.112.9红色曲线为使用一年卖出蓝色曲线为使用两年卖出绿色曲线为使用三年卖出紫色曲线为使用四年卖出最短路程为3.7万元,路径为v0-v1-v4或v0-v2-v4或v0-v1-v2-v4三种方案分别为:第一年年初买新车,年末卖掉再买新车,一直用到第四年年末卖掉;第一年出买新车,用两年后于第二年末卖掉再买新车,用两年于第四年末卖掉;第一年出买新车,年末卖掉后再买新车,第二年末卖掉再买新车,再用两年于第四年年末卖掉。
