高三数学 直线的交点坐标与距离公式复习 文
直线的交点坐标与距离公式最新版

【例3】 设直线l的方程为(a+1)x+y+2-a =0(a∈R).
(1)若l在两坐标轴的截距相等,求l的方 程;
(2)若l不经过第二象限,求实数a的取值 范围.
(2)由(a+1)x+y+2-a=0得a(x-1)+(x+y +2)=0.
无论a取何值,直线l过A(1,-3)点, 则直线l的斜率k≥0,即-(a+1)≥0.解得a≤-
1.可通过解方程组
求得,
若方程组有唯一解,则l1与l2相
交;若方程组无解,则直线l ∥l ;若方
【例1】直线l被两条直线l1:4x+y+3=0 和l2:3x-5y-5=0截得的线段的中点为 P(-1,2),求直线l的方程.
解 答 : 解 法 一 : 设 直 线 l 与 l1 的 交 点 为 A(x0,y0),由已知条件,则直线l与l2的交 点为B(-2-3,0),直线l2经过点B(0,4), 且l1∥l2,用d表示l1,l2间的距离,则( )
A.d≥5 B.3≤d≤5 C . 0≤d≤5 D.0<d≤5
答案:D 4.直线l过点(2,1),且原点到l的距离是1,
直线l1:A1x+B1y+C1=0与直线l2:A2x+ B2y+C2=0的交点:
当E与D重合时,E点坐标为(0,1),由①式 得k=-1.
当F与B重合时,F点坐标为(2,0),由①式 得k=-2+
当k∈[-2+
,0]时,f(k)递减,f(k)的最
大值为f(-2+ )=32-16 ;
当k∈[-1,-2+ - ]上递减;
)时,可证f(k)在[-1,
在[-
,-2+
)上递增,f(-1)=
2<f(-2+ )=32-16 .
高考总复习一轮数学精品课件 第九章 平面解析几何 第二节 两条直线的位置关系

与距离有关的问题
典例突破
例4.(1)若两条平行直线l1:x-2y+m=0(m>0)与l2:x+ny-3=0之间的距离是√5 ,
则m+n=(
)
A.0
C.-2
B.1
D.-1
(2)已知点P(4,a)到直线4x-3y-1=0的距离不大于3,则实数a的取值范围
为
.
答案 (1)A
解析
(2)[0,10]
1
(1)由两直线平行,得1
)
记 P 的轨迹为 E,则(
A.E 是一个半径为√5的圆
B.E 是一条与 l 相交的直线
C.E 上的点到 l 的距离均为√5
D.E 是两条平行直线
答案 (1)C
(2) C
解析(1)因为直线 x-y-m=0 与直线 mx+y-4=0 平行,所以
m≠0,且 1
=
1
-1
≠
-4
,解
-
得 m=-1,即两直线为直线 x-y+1=0 与直线 x-y+4=0,所以它们之间的距离为
式.
2 -1
提示
· = -1,
2 -1
1 +2
2
=
1 +2
·
+ .
2
常用结论
1.两种求直线方程的设法
(1)与直线Ax+By+C=0(A2+B2≠0)垂直的直线可设为Bx-Ay+m=0.
(2)与直线Ax+By+C=0(A2+B2≠0)平行的直线可设为Ax+By+n=0.
2.六种常见的对称点
(1)点(x,y)关于原点(0,0)的对称点为(-x,-y).
两直线的交点坐标和距离公式

利用求交点坐标的方法,能否判断两条 直线的位置关系?
将两条直线的方程联立 A1 x B1 y C1 0
A2 x B2 y C2 0
方程组有唯一解 方程组无解 方程组有无数解
两条直线相交
两条直线平行
两条直线重合
例1:判断下列直线的位置关系。 如果相交,求出交点的坐标
两点间距离公式
y
y2
P2(x2, y2)
| P2Q || y2 y1 |
y1 P1(x1,y1) x1 Q(x2,y1) x2
O
x
| PQ 1 || x2 x1 |
两点间距离公式
y
| PQ 1 || x2 x1 |
P2(x2,y2)
| P2Q || y2 y1 |
P1(x1,y1) O
x=3 x+2y-1=0, 得 y= -1 2x-y-7=0 ∴这两条直线的交点坐标为(3,-1)
又∵直线x+2y-5=0的斜率是-1/3 ∴所求直线的斜率是3 所求直线方程为y+1=3(x-3)即 3x-y-10=0
解法二:所求直线在直线系2x-y-7+λ(x+2y-1)=0中 经整理,可得(2+λ)x+(2λ-1)y-λ-7=0 2+λ ∴ - ———— =3 解得 λ= 1/7 2λ-1 因此,所求直线方程为3x-y-10=0
3x 4 y 4 0 l2 : 6 x 2 y 1 0
b1 b2
3 k1 k2 4
所以l1//l2
另一方面
3x 4 y 4 0 6x 2 y 1 0
所以l1//l2
无解 直线l1与l2的无交点
直线的交点坐标与距离公式

13.3.1直线的交点坐标第二课时 交点线系【学习目标】1、理解交点线系2、交点线系的应用 【重难点】 1、交点线系 2、交点线系的应用 【学习过程】 复习引入:1、两直线的位置关系如何判定?2、怎样求两直线的交点坐标?3、解下列方程组 (1)⎩⎨⎧=++=-+0220243y x y x (2)⎩⎨⎧=++-=-+0)22(0243y x y x (3)⎩⎨⎧=++=-+0)22(20243y x y x4、由此我们猜想:当λ 变化时,方程()022243=+++-+y x y x λ表示什么图形?图形有何特点?表示直线,都经过同一点M你能找出M 点的坐标吗?()2,2- 该点坐标如何求? 解方程组知识点一:交点线系一般地,方程 ()0222111=+++++C y B x A C y B x A λ表示经过直线0:1111=++C y B x A l 和直线0:2222=++C y B x A l 交点(不含2l )的直线的集合——直线束(简称交点线系)于是,过两条相交直线0:1111=++C y B x A l ,0:2222=++C y B x A l 交点的直线方程可设为()0222111=+++++C y B x A C y B x A λ(不含2l ),反之形如()0222111=+++++C y B x A C y B x A λ的方程表示的直线过定点,定点即为1l 与2l 的交点。
例题1:(新课程导学P44例1改编)求经过两条直线042:1=+-y x l ,02:2=-+y x l 交点P ,且满足下列条件的直线l :的方程:(1)l 过点(2,1); (2)l 与直线0543=+-y x 垂直; (3)l 与直线0543=+-y x 平行;巩固练习1:(课本P109习题3.3第5题)求满足下列条件的直线方程:(1)经过两直线024301032=-+=+-y x y x 和的交点,且垂直于直线0423=+-y x ; (2)经过两直线012082=+-=-+y x y x 和的交点,且平行于直线07-34=-y x ; 知识点二:含参直线过定点例2:两条直线y=kx+2k+1和x+2y-4=0,则y=kx+2k+1恒过点_____;若两直线的交点在第四象限,则k 的取值范围是__________巩固练习2:两条直线()23-+=x k y 和044=-+y x 的交点在第四象限,则k 的取值范围是__________ 【课堂检测】1、(新课程导学P44跟踪训练1-1(2))求经过两条直线02010-32=++=-y x y x 和交点,且与直线013=-+y x 平行的直线方程;2、(新课程导学P45达标检测第4题)当a 取不同值时,直线()()0312=+-++a y a x a 恒过一个定点,这个定点的坐标为 ________【拓展训练】【课堂小结】本节课我们主要学习了交点线系及其应用 【课后作业】作业与检测P88第3、6、7、11题 【课后反思】。
两直线的交点坐标及两点间距离公式

例2.k为何值时,直线l1:y=kx+3k-2,与直线l2:x+
4y-4=0的交点在第一象限?
例3 已知直线l:5ax-5y-a+3=0.
(1)求证:不论a为何值,直线l总经过第一象限; (2)为使直线不经过第二象限,求a的取值范围.
思维拓展
当变化时,方程3x+4y-2+(2x+y+2)=0表示什么
(1) 求 | AB | 的值; (2) 在x轴上求一点P,使 | PA || PB | , 并求 | PA | 的值.
例2.求在x轴上与点A(5, 12)的距离为13的点的坐标. 例3.求函数 y
x 8 x 20 x 1 的最小值.
2 2
两直线的交点坐标
复习引入
:两直线交点与方程组的解之间有什么关系?
讲授新课
1. 讨论:直线上的点与其方程Ax+By+C=0的解有 什么样的关系? 2. 完成P.102的表格
几何元素及关系 代数表示 点A A(a, b) 直线l l: Ax+By+C=0 A∈ l 点A在直线l上 直线l1与l2的交点是A l1∩ l2=A
A1 x B1 y C 1 0 A2 x B2 y C 2 0
(1) 若方程组无解, 则l1// l2;
(2) 若方程组有且只有一个解, 则l1与l2相交; (3) 若方程组有无数解, 则l1与l2重合.
例1. 判断下列各对直线的位置关系,如果相交,求出交 点坐标. (1) l1: x-y=0,l2: 3x+3y-10=0; (2) l1: 3x-y+4=0,l2: 6x-2y-1=0; (3) l1: 3x+4y-5=0,l2: 6x+8y-10=0.
图形?图形有什么特点?
两点间的距离公式
2024年高考数学总复习第九章《平面解析几何》两条直线的位置关系

2024年高考数学总复习第九章《平面解析几何》§9.2两条直线的位置关系最新考纲1.能根据斜率判定两条直线平行或垂直.2.能用解方程组的方法求两直线的交点坐标.3.探索并掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离.1.两条直线的位置关系(1)两条直线平行与垂直①两条直线平行:(ⅰ)对于两条不重合的直线l 1,l 2,若其斜率分别为k 1,k 2,则有l 1∥l 2⇔k 1=k 2.(ⅱ)当直线l 1,l 2不重合且斜率都不存在时,l 1∥l 2.②两条直线垂直:(ⅰ)如果两条直线l 1,l 2的斜率存在,设为k 1,k 2,则有l 1⊥l 2⇔k 1·k 2=-1.(ⅱ)当其中一条直线的斜率不存在,而另一条的斜率为0时,l 1⊥l 2.(2)两条直线的交点直线l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0,则l 1与l 2的交点坐标就是方程组1x +B 1y +C 1=0,2x +B 2y +C 2=0的解.2.几种距离(1)两点P 1(x 1,y 1),P 2(x 2,y 2)之间的距离|P 1P 2|=(x 2-x 1)2+(y 2-y 1)2.(2)点P 0(x 0,y 0)到直线l :Ax +By +C =0的距离d =|Ax 0+By 0+C |A 2+B 2.(3)两条平行线Ax +By +C 1=0与Ax +By +C 2=0(其中C 1≠C 2)间的距离d =|C 1-C 2|A 2+B2.概念方法微思考1.若两条直线l 1与l 2垂直,则它们的斜率有什么关系?提示当两条直线l 1与l 2的斜率都存在时,12l l k k ⋅=-1;当两条直线中一条直线的斜率为0,另一条直线的斜率不存在时,l 1与l 2也垂直.2.应用点到直线的距离公式和两平行线间的距离公式时应注意什么?提示(1)将方程化为最简的一般形式.(2)利用两平行线之间的距离公式时,应使两平行线方程中x ,y 的系数分别对应相等.题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)当直线l 1和l 2斜率都存在时,一定有k 1=k 2⇒l 1∥l 2.(×)(2)已知直线l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0(A 1,B 1,C 1,A 2,B 2,C 2为常数),若直线l 1⊥l 2,则A 1A 2+B 1B 2=0.(√)(3)点P (x 0,y 0)到直线y =kx +b 的距离为|kx 0+b |1+k2.(×)(4)直线外一点与直线上一点的距离的最小值就是点到直线的距离.(√)(5)若点A ,B 关于直线l :y =kx +b (k ≠0)对称,则直线AB 的斜率等于-1k ,且线段AB 的中点在直线l 上.(√)题组二教材改编2.已知点(a,2)(a >0)到直线l :x -y +3=0的距离为1,则a 等于()A.2B .2-2 C.2-1D.2+1答案C 解析由题意得|a -2+3|1+1=1.解得a =-1+2或a =-1- 2.∵a >0,∴a =-1+ 2.3.已知P (-2,m ),Q (m,4),且直线PQ 垂直于直线x +y +1=0,则m =________.答案1解析由题意知m -4-2-m=1,所以m -4=-2-m ,所以m =1.4.若三条直线y =2x ,x +y =3,mx +2y +5=0相交于同一点,则m 的值为________.答案-9解析=2x ,+y =3,=1,=2.所以点(1,2)满足方程mx +2y +5=0,即m ×1+2×2+5=0,所以m =-9.题组三易错自纠5.直线2x +(m +1)y +4=0与直线mx +3y -2=0平行,则m 等于()A .2B .-3C .2或-3D .-2或-3答案C解析直线2x +(m +1)y +4=0与直线mx +3y -2=0平行,则有2m =m +13≠4-2m =2或-3.故选C.6.直线2x +2y +1=0,x +y +2=0之间的距离是______.答案324解析先将2x +2y +1=0化为x +y +12=0,则两平行线间的距离为d =|2-12|2=324.7.若直线(3a +2)x +(1-4a )y +8=0与(5a -2)x +(a +4)y -7=0垂直,则a =________.答案0或1解析由两直线垂直的充要条件,得(3a +2)(5a -2)+(1-4a )(a +4)=0,解得a =0或a =1.题型一两条直线的平行与垂直例1已知直线l 1:ax +2y +6=0和直线l 2:x +(a -1)y +a 2-1=0.(1)试判断l 1与l 2是否平行;(2)当l 1⊥l 2时,求a 的值.解(1)方法一当a =1时,l 1:x +2y +6=0,l 2:x =0,l 1不平行于l 2;当a =0时,l 1:y =-3,l 2:x -y -1=0,l 1不平行于l 2;当a ≠1且a ≠0时,两直线可化为l 1:y =-a2x -3,l 2:y =11-ax -(a +1),l 1∥l 2-a2=11-a ,3≠-(a +1),解得a =-1,综上可知,当a=-1时,l1∥l2,a≠-1时,l1与l2不平行.方法二由A1B2-A2B1=0,得a(a-1)-1×2=0,由A1C2-A2C1≠0,得a(a2-1)-1×6≠0,∴l1∥l2(a-1)-1×2=0,(a2-1)-1×6≠0,2-a-2=0,(a2-1)≠6,可得a=-1,故当a=-1时,l1∥l2.a≠-1时,l1与l2不平行.(2)方法一当a=1时,l1:x+2y+6=0,l2:x=0,l1与l2不垂直,故a=1不成立;当a=0时,l1:y=-3,l2:x-y-1=0,l1不垂直于l2,故a=0不成立;当a≠1且a≠0时,l1:y=-a2x-3,l2:y=11-ax-(a+1),·11-a=-1,得a=23.方法二由A1A2+B1B2=0,得a+2(a-1)=0,可得a=23.思维升华(1)当直线方程中存在字母参数时,不仅要考虑到斜率存在的一般情况,也要考虑到斜率不存在的特殊情况.同时还要注意x,y的系数不能同时为零这一隐含条件.(2)在判断两直线平行、垂直时,也可直接利用直线方程的系数间的关系得出结论.跟踪训练1(1)(2018·潍坊模拟)直线l1:(3+m)x+4y=5-3m,l2:2x+(5+m)y=8,则“m=-1或m=-7”是“l1∥l2”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案B解析由题意,当直线l1∥l2时,满足3+m2=45+m≠5-3m8,解得m=-7,所以“m=-1或m=-7”是“l1∥l2”的必要不充分条件,故选B.(2)(2018·青岛模拟)已知两条直线l1:ax-by+4=0和l2:(a-1)x+y+b=0,求满足下列条件的a,b的值.①l1⊥l2,且直线l1过点(-3,-1);②l 1∥l 2,且坐标原点到这两条直线的距离相等.解①∵l 1⊥l 2,∴a (a -1)-b =0,又∵直线l 1过点(-3,-1),∴-3a +b +4=0.故a =2,b =2.②∵直线l 2的斜率存在,l 1∥l 2,∴直线l 1的斜率存在.∴k 1=k 2,即ab=1-a .又∵坐标原点到这两条直线的距离相等,∴l 1,l 2在y 轴上的截距互为相反数,即4b=b .故a =2,b =-2或a =23,b =2.题型二两直线的交点与距离问题1.(2018·西宁调研)若直线l 与两直线y =1,x -y -7=0分别交于M ,N 两点,且MN 的中点是P (1,-1),则直线l 的斜率是()A .-23 B.23C .-32D.32答案A解析由题意,设直线l 的方程为y =k (x -1)-1,分别与y =1,x -y -7=0联立解得1,又因为MN 的中点是P (1,-1),所以由中点坐标公式得k =-23.2.若P ,Q 分别为直线3x +4y -12=0与6x +8y +5=0上任意一点,则|PQ |的最小值为()A.95B.185C.2910D.295答案C解析因为36=48≠-125,所以两直线平行,将直线3x +4y -12=0化为6x +8y -24=0,由题意可知|PQ |的最小值为这两条平行直线间的距离,即|-24-5|62+82=2910,所以|PQ |的最小值为2910.3.已知直线y =kx +2k +1与直线y =-12x +2的交点位于第一象限,则实数k 的取值范围是________.答案-16,解析方法一=kx +2k +1,=-12x +2,=2-4k 2k +1,=6k +12k +1.(若2k +1=0,即k =-12,则两直线平行)∴又∵交点位于第一象限,,,解得-16<k <12.方法二如图,已知直线y =-12x +2与x 轴、y 轴分别交于点A (4,0),B (0,2).而直线方程y =kx +2k +1可变形为y -1=k (x +2),表示这是一条过定点P (-2,1),斜率为k 的动直线.∵两直线的交点在第一象限,∴两直线的交点必在线段AB 上(不包括端点),∴动直线的斜率k 需满足k P A <k <k PB .∵k P A =-16,k PB =12.∴-16<k <12.4.已知A (4,-3),B (2,-1)和直线l :4x +3y -2=0,若在坐标平面内存在一点P ,使|PA |=|PB |,且点P 到直线l 的距离为2,则P点坐标为________________.答案(1,-4)解析设点P 的坐标为(a ,b ).∵A (4,-3),B (2,-1),∴线段AB 的中点M 的坐标为(3,-2).而AB 的斜率k AB =-3+14-2=-1,∴线段AB 的垂直平分线方程为y +2=x -3,即x -y -5=0.∵点P (a ,b )在直线x -y -5=0上,∴a -b -5=0.①又点P (a ,b )到直线l :4x +3y -2=0的距离为2,∴|4a +3b -2|42+32=2,即4a +3b -2=±10,②由①②a =1,b =-4a =277,b =-87.∴所求点P 的坐标为(1,-4)277,-87思维升华(1)求过两直线交点的直线方程的方法先求出两直线的交点坐标,再结合其他条件写出直线方程.(2)利用距离公式应注意:①点P (x 0,y 0)到直线x =a 的距离d =|x 0-a |,到直线y =b 的距离d =|y 0-b |;②两平行线间的距离公式要把两直线方程中x ,y 的系数化为相等.题型三对称问题命题点1点关于点中心对称例2过点P (0,1)作直线l ,使它被直线l 1:2x +y -8=0和l 2:x -3y +10=0截得的线段被点P 平分,则直线l 的方程为________________.答案x +4y -4=0解析设l 1与l 的交点为A (a,8-2a ),则由题意知,点A 关于点P 的对称点B (-a,2a -6)在l 2上,代入l 2的方程得-a -3(2a -6)+10=0,解得a =4,即点A (4,0)在直线l 上,所以直线l 的方程为x +4y -4=0.命题点2点关于直线对称例3如图,已知A (4,0),B(0,4),从点P (2,0)射出的光线经直线AB 反射后再射到直线OB 上,最后经直线OB 反射后又回到P 点,则光线所经过的路程是()A .33B .6C .210D .25答案C解析直线AB 的方程为x +y =4,点P (2,0)关于直线AB 的对称点为D (4,2),关于y 轴的对称点为C (-2,0),则光线经过的路程为|CD |=62+22=210.命题点3直线关于直线的对称问题例4直线2x -y +3=0关于直线x -y +2=0对称的直线方程是______________.答案x -2y +3=0解析设所求直线上任意一点P (x ,y ),则P 关于x -y +2=0的对称点为P ′(x 0,y 0),-y +y 02+2=0,(y -y 0),0=y -2,0=x +2,由点P ′(x 0,y 0)在直线2x -y +3=0上,∴2(y -2)-(x +2)+3=0,即x -2y +3=0.思维升华解决对称问题的方法(1)中心对称①点P (x ,y )关于Q (a ,b )的对称点P ′(x ′,y ′)′=2a -x ,′=2b -y .②直线关于点的对称可转化为点关于点的对称问题来解决.(2)轴对称①点A (a ,b )关于直线Ax +By +C =0(B ≠0)的对称点A ′(m ,n ),则有1,B ·b +n 2+C =0.②直线关于直线的对称可转化为点关于直线的对称问题来解决.跟踪训练2已知直线l :3x -y +3=0,求:(1)点P (4,5)关于l 的对称点;(2)直线x -y -2=0关于直线l 对称的直线方程;(3)直线l 关于(1,2)的对称直线.解(1)设P (x ,y )关于直线l :3x -y +3=0的对称点为P ′(x ′,y ′),∵k PP ′·k l =-1,即y ′-yx ′-x×3=-1.①又PP ′的中点在直线3x -y +3=0上,∴3×x ′+x 2-y ′+y 2+3=0.②由①②′=-4x +3y -95,③′=3x +4y +35.④把x =4,y =5代入③④得x ′=-2,y ′=7,∴点P (4,5)关于直线l 的对称点P ′的坐标为(-2,7).(2)用③④分别代换x -y -2=0中的x ,y ,得关于l 对称的直线方程为-4x +3y -95-3x +4y +35-2=0,化简得7x +y +22=0.(3)在直线l :3x -y +3=0上取点M (0,3),关于(1,2)的对称点M ′(x ′,y ′),∴x ′+02=1,x ′=2,y ′+32=2,y ′=1,∴M ′(2,1).l 关于(1,2)的对称直线平行于l ,∴k =3,∴对称直线方程为y -1=3×(x -2),即3x -y -5=0.妙用直线系求直线方程在求解直线方程的题目中,可采用设直线系方程的方式简化运算,常见的直线系有平行直线系,垂直直线系和过直线交点的直线系.一、平行直线系例1求与直线3x +4y +1=0平行且过点(1,2)的直线l 的方程.解由题意,设所求直线方程为3x +4y +c =0(c ≠1),又因为直线过点(1,2),所以3×1+4×2+c =0,解得c =-11.因此,所求直线方程为3x +4y -11=0.二、垂直直线系例2求经过A (2,1),且与直线2x +y -10=0垂直的直线l 的方程.解因为所求直线与直线2x +y -10=0垂直,所以设该直线方程为x -2y +C =0,又直线过点A (2,1),所以有2-2×1+C =0,解得C =0,即所求直线方程为x -2y =0.三、过直线交点的直线系例3求经过两直线l 1:x -2y +4=0和l 2:x +y -2=0的交点P ,且与直线l 3:3x -4y +5=0垂直的直线l 的方程.解方法一-2y +4=0,+y -2=0,得P (0,2).∵l 3的斜率为34,且l ⊥l 3,∴直线l 的斜率为-43,由斜截式可知l 的方程为y =-43x +2,即4x +3y -6=0.方法二设直线l 的方程为x -2y +4+λ(x +y -2)=0,即(1+λ)x +(λ-2)y +4-2λ=0.又∵l ⊥l 3,∴3×(1+λ)+(-4)×(λ-2)=0,解得λ=11.∴直线l 的方程为4x +3y -6=0.1.直线2x +y +m =0和x +2y +n =0的位置关系是()A .平行B .垂直C .相交但不垂直D .不能确定答案C解析直线2x +y +m =0的斜率k 1=-2,直线x +2y +n =0的斜率k 2=-12,则k 1≠k 2,且k 1k 2≠-1.故选C.2.已知直线l 1:x +my +7=0和l 2:(m -2)x +3y +2m =0互相平行,则实数m 等于()A .-1或3B .-1C .-3D .1或-3答案A解析当m =0时,显然不符合题意;当m ≠0时,由题意得,m -21=3m ≠2m7,解得m =-1或m =3,故选A.3.已知过点A (-2,m )和B (m,4)的直线为l 1,直线2x +y -1=0为l 2,直线x +ny +1=0为l 3.若l 1∥l 2,l 2⊥l 3,则实数m +n 的值为()A .-10B .-2C .0D .8答案A解析因为l 1∥l 2,所以k AB =4-mm +2=-2.解得m =-8.又因为l 2⊥l 3,所以-1n ×(-2)=-1,解得n =-2,所以m +n =-10.4.过点M (-3,2),且与直线x +2y -9=0平行的直线方程是()A .2x -y +8=0B .x -2y +7=0C .x +2y +4=0D .x +2y -1=0答案D 解析方法一因为直线x +2y -9=0的斜率为-12,所以与直线x +2y -9=0平行的直线的斜率为-12,又所求直线过M (-3,2),所以所求直线的点斜式方程为y -2=-12(x +3),化为一般式得x +2y -1=0.故选D.方法二由题意,设所求直线方程为x +2y +c =0,将M (-3,2)代入,解得c =-1,所以所求直线为x +2y -1=0.故选D.5.若直线l 1:x +ay +6=0与l 2:(a -2)x +3y +2a =0平行,则l 1与l 2之间的距离为()A.423B .42 C.823D .22答案C解析∵l 1∥l 2,∴a ≠2且a ≠0,∴1a -2=a 3≠62a,解得a =-1,∴l 1与l 2的方程分别为l 1:x -y +6=0,l 2:x -y +23=0,∴l 1与l 2的距离d =|6-23|2=823.6.已知直线l1:y=2x+3,直线l2与l1关于直线y=-x对称,则直线l2的斜率为()A.1 2B.-12C.2D.-2答案A解析直线y=2x+3与y=-x的交点为A(-1,1),而直线y=2x+3上的点(0,3)关于y=-x的对称点为B(-3,0),而A,B两点都在l2上,所以kl2=1-0-1-(-3)=12.7.已知直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,若l1⊥l2,则a=________,此时点P的坐标为________.答案1(3,3)解析∵直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,且l1⊥l2,∴a×1+1×(a-2)=0,即a=1+y-6=0,-y=0,易得x=3,y=3,∴P(3,3).8.将一张坐标纸折叠一次,使得点(0,2)与点(4,0)重合,点(7,3)与点(m,n)重合,则m+n=________.答案34 5解析由题意可知,纸的折痕应是点(0,2)与点(4,0)连线的中垂线,即直线y=2x-3,它也是点(7,3)与点(m,n)连线的中垂线,2×7+m2-3,=-12,=35,=315,故m+n=34 5 .9.直线l1:y=2x+3关于直线l:y=x+1对称的直线l2的方程为______________.答案x-2y=0解析=2x+3,=x+1,解得直线l1与l的交点坐标为(-2,-1),所以可设直线l2的方程为y+1=k(x+2),即kx-y+2k-1=0.在直线l上任取一点(1,2),由题设知点(1,2)到直线l1,l2的距离相等,由点到直线的距离公式得|k -2+2k -1|k 2+1=|2-2+3|22+1,解得k =12(k =2舍去),所以直线l 2的方程为x -2y =0.10.已知入射光线经过点M (-3,4),被直线l :x -y +3=0反射,反射光线经过点N (2,6),则反射光线所在直线的方程为______________.答案6x -y -6=0解析设点M (-3,4)关于直线l :x -y +3=0的对称点为M ′(a ,b ),则反射光线所在直线过点M ′,=-1,-b +42+3=0,解得a =1,b =0.又反射光线经过点N (2,6),所以所求直线的方程为y -06-0=x -12-1,即6x -y -6=0.11.已知方程(2+λ)x -(1+λ)y -2(3+2λ)=0与点P (-2,2).(1)证明:对任意的实数λ,该方程都表示直线,且这些直线都经过同一定点,并求出这一定点的坐标;(2)证明:该方程表示的直线与点P 的距离d 小于42.(1)解显然2+λ与-(1+λ)不可能同时为零,故对任意的实数λ,该方程都表示直线.∵方程可变形为2x -y -6+λ(x -y -4)=0,x -y -6=0,-y -4=0,=2,=-2,故直线经过的定点为M (2,-2).(2)证明过P 作直线的垂线段PQ ,由垂线段小于斜线段知|PQ |≤|PM |,当且仅当Q 与M 重合时,|PQ |=|PM |,此时对应的直线方程是y +2=x -2,即x -y -4=0.但直线系方程唯独不能表示直线x -y -4=0,∴M 与Q 不可能重合,而|PM |=42,∴|PQ |<42,故所证成立.12.已知三条直线:l 1:2x -y +a =0(a >0);l 2:-4x +2y +1=0;l 3:x +y -1=0,且l 1与l 2间的距离是7510.(1)求a 的值;(2)能否找到一点P ,使P 同时满足下列三个条件:①点P 在第一象限;②点P 到l 1的距离是点P 到l 2的距离的12;③点P 到l 1的距离与点P 到l 3的距离之比是2∶5.若能,求点P 的坐标;若不能,说明理由.解(1)直线l 2:2x -y -12=0,所以两条平行线l 1与l 2间的距离为d =7510,所以|a +12|5=7510,即|a +12|=72,又a >0,解得a =3.(2)假设存在点P ,设点P (x 0,y 0).若P 点满足条件②,则P 点在与l 1,l 2平行的直线l ′:2x -y +c =0上,且|c -3|5=12|c +12|5,即c =132或116,所以2x 0-y 0+132=0或2x 0-y 0+116=0;若P 点满足条件③,由点到直线的距离公式,有|2x 0-y 0+3|5=25|x 0+y 0-1|2,即|2x 0-y 0+3|=|x 0+y 0-1|,所以x 0-2y 0+4=0或3x 0+2=0;由于点P 在第一象限,所以3x 0+2=0不可能.联立方程2x 0-y 0+132=0和x 0-2y 0+4=0,0=-3,0=12,(舍去)联立方程2x 0-y 0+116=0和x 0-2y 0+4=0,=19,0=3718.所以存在点P 13.已知直线y =2x 是△ABC 中∠C 的平分线所在的直线,若点A ,B 的坐标分别是(-4,2),(3,1),则点C的坐标为()A.(-2,4)B.(-2,-4) C.(2,4)D.(2,-4)答案C解析设A(-4,2)关于直线y=2x的对称点为(x,y),则2=-1,2×-4+x2,解得=4,=-2,∴BC所在直线方程为y-1=-2-14-3(x-3),即3x+y-10=0.同理可得点B(3,1)关于直线y=2x的对称点为(-1,3),∴AC所在直线方程为y-2=3-2-1-(-4)(x+4),即x-3y+10=0.x+y-10=0,-3y+10=0,=2,=4,则C(2,4).故选C.14.若三条直线y=2x,x+y=3,mx+ny+5=0相交于同一点,则点(m,n)到原点的距离的最小值为()A.5B.6C.23D.25答案A解析=2x,+y=3,解得x=1,y=2.把(1,2)代入mx+ny+5=0可得,m+2n+5=0.∴m=-5-2n.∴点(m,n)到原点的距离d=m2+n2=(5+2n)2+n2=5(n+2)2+5≥5,当n=-2,m=-1时取等号.∴点(m,n)到原点的距离的最小值为 5.15.数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半.这条直线被后人称为三角形的欧拉线.已知△ABC的顶点A (1,0),B (0,2),且AC =BC ,则△ABC 的欧拉线的方程为()A .4x +2y +3=0B .2x -4y +3=0C .x -2y +3=0D .2x -y +3=0答案B解析因为AC =BC ,所以欧拉线为AB 的中垂线,又A (1,0),B (0,2),故AB k AB =-2,故AB 的中垂线方程为y -1即2x -4y +3=0.16.在平面直角坐标系xOy 中,将直线l 沿x 轴正方向平移3个单位长度,沿y 轴正方向平移5个单位长度,得到直线l 1.再将直线l 1沿x 轴正方向平移1个单位长度,沿y 轴负方向平移2个单位长度,又与直线l 重合.若直线l 与直线l 1关于点(2,4)对称,求直线l 的方程.解由题意知直线l 的斜率存在,设直线l 的方程为y =kx +b ,将直线l 沿x 轴正方向平移3个单位长度,沿y 轴正方向平移5个单位长度,得到直线l 1:y =k (x -3)+5+b ,将直线l 1沿x 轴正方向平移1个单位长度,沿y 轴负方向平移2个单位长度,则平移后的直线方程为y =k (x -3-1)+b +5-2,即y =kx +3-4k +b ,∴b =3-4k +b ,解得k =34,∴直线l 的方程为y =34x +b ,直线l 1为y =34x +114+b ,取直线l 上的一点,b P 关于点(2,4)-m ,8-b ∴8-b -3m 4=34(4-m )+b +114,解得b =98.∴直线l 的方程是y =34x +98,即6x -8y +9=0.。
高三数学直线的交点坐标与距离公式

• 当 F 与 B 重合时, F 点坐标为 (2,0) ,由①式
得k=-2+
• 当k∈[-2+ 大值为f(-2+
,0]时,f(k)递减,f(k)的最 )=32-16 ;
• 当k∈[-1,-2+
- • 在 [- 2<f(-2+ ]上递减; ,-2+
• 2.点到直线距离公式
• 点P(x0,y0)到直线l:Ax+By+C=0的距离
为: • 3.两平行线间的距离公式 • 已知两条平行线直线l1和l2的一般式方程为l1:
• 1.过点A(4,a)和点B(5,b)的直线与直线y =x+m平行,则|AB|的值为( )
•
A. 6 D.不能确定
B.
C.2
•
)时,可证f(k)在[-1,
)上递增,f(-1)= .
)=32-16
【分析点评】
• 本题对直线方程,两点间的距离公式和分段 函数问题进行了综合考查,在考查
• 直线方程时是以折叠为背景,实质是考查对 称问题.
• (1)点与点关于点对称,图形与图形关于点对 称,主要利用中点坐标公式解决. • (2)图形与图形对称问题可转化为点与点对称 解决,对于点与点关于直线x=0,
B2y+C2=0的交点:
• 1.可通过解方程组 若方程组有唯一解,则l1与l2相 • 交;若方程组无解,则直线 l ∥l ;若方 求得,
• 【例 1】 直线 l 被两条直线 l1 : 4x + y + 3 = 0
和 l2 : 3x - 5y - 5 = 0 截得的线段的中点为
P(-1,2),求直线l的方程. • 解 答 : 解 法 一 : 设 直 线 l 与 l1 的 交点为 A(x0 , y0) ,由已知条件,则直线 l 与 l2 的交
2025高二上数学专题第7讲 直线的交点坐标与距离公式(解析版)
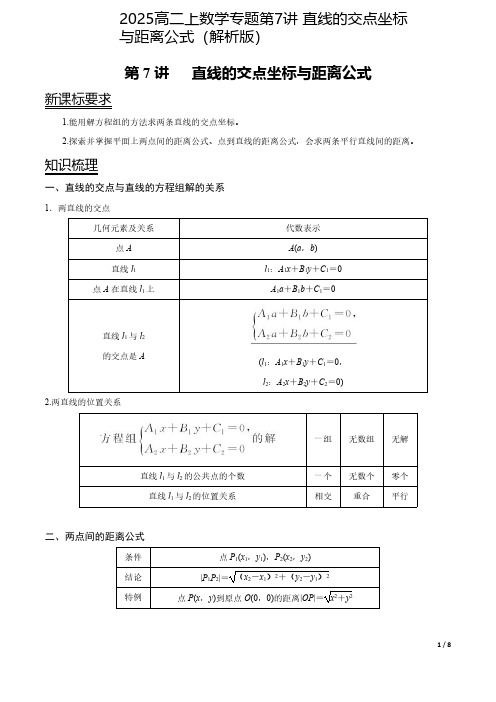
第7讲直线的交点坐标与距离公式新课标要求1.能用解方程组的方法求两条直线的交点坐标。
2.探索并掌握平面上两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离。
知识梳理一、直线的交点与直线的方程组解的关系1.两直线的交点几何元素及关系代数表示点A A (a ,b )直线l 1l 1:A 1x +B 1y +C 1=0点A 在直线l 1上A 1a +B 1b +C 1=0直线l 1与l 2的交点是A(l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0)2.两直线的位置关系一组无数组无解直线l 1与l 2的公共点的个数一个无数个零个直线l 1与l 2的位置关系相交重合平行二、两点间的距离公式条件点P 1(x 1,y 1),P 2(x 2,y 2)结论|P 1P 2|=(x 2-x 1)2+(y 2-y 1)2特例点P (x ,y )到原点O (0,0)的距离|OP |=x 2+y 22025高二上数学专题第7讲 直线的交点坐标与距离公式(解析版)三、点到直线的距离1.概念:过一点向直线作垂线,则该点与垂足之间的距离,就是该点到直线的距离.2.公式:点P (x 0,y 0)到直线l :Ax +By +C =0的距离d =|Ax 0+By 0+C |A 2+B 2.四、两平行直线间的距离1.概念:夹在两条平行直线间的公垂线段的长度就是两条平行直线间的距离.2.公式:两条平行直线l 1:Ax +By +C 1=0与l 2:Ax +By +C 2=0之间的距离d =|C 1-C 2|A 2+B 2.名师导学知识点1两直线的交点问题【例1-1】(宜昌期末)已知两直线1:3420l x y +-=,2:220l x y ++=,则1l 与2l 的交点坐标为.【例1-2】(雅安期末)过直线1:240l x y -+=与直线2:10l x y ++=的交点,且过原点的直线方程为()A .20x y -=B .20x y +=C .20x y -=D .20x y +=【例1-3】(芜湖期末)若三条直线2380x y ++=,10x y --=和0x ky +=交于一点,则k 的值为()A .2-B .12-C .2D .12【变式训练1-1】(阎良区期末)直线5y x =-+与直线1y x =+的交点坐标是()A .(1,2)B .(2,3)C .(3,2)D .(2,1)【变式训练1-2】((安庆期末)直线210x y ++=与直线20x y -+=的交点在()A .第一象限B .第二象限C .第三象限D .第四象限【变式训练1-3】((庐江县期中)直线230x y k +-=和直线120x ky -+=的交点在x 轴上,则k 的值为()A .24-B .24C .6D .6±知识点2直线过定点问题【例2-1】(宿迁期末)设直线2(3)260x k y k +--+=过定点P ,则点P 的坐标为()A .(3,0)B .(0,2)C .(0,3)D .(2,0)【例2-2】(江阴市期中)直线:1(2)l y k x -=+必过定点()A .(2,1)-B .(0,0)C .(1,2)-D .(2,1)--【变式训练2-1】(黄浦区期末)已知a R ∈,若不论a 为何值时,直线:(12)(32)0l a x a y a -++-=总经过一个定点,则这个定点的坐标是()A .(2,1)-B .(1,0)-C .21(,)77-D .12(,)77-【变式训练2-2】(慈溪市期末)直线1(y kx k k =++为常数)经过定点()A .(1,1)B .(1,1)-C .(1,1)-D .(1,1)--知识点3两点间距离公式的应用【例3-1】(南充期末)已知点(1A ,0,2)与点B (1,3-,1),则||(AB =)A .2B C .3D【例3-2】(临川区校级一模)已知ABC ∆的三个顶点的坐标分别为(3,4)A ,(5,2)B ,(1,4)C --,则这个三角形是()A .锐角三角形B .直角三角形C .钝角三角形D .等腰直角三角形【变式训练3-1】(琼山区校级期末)已知ABC ∆的顶点坐标为(7,8)A ,(10,4)B ,(2,4)C -,则BC 边上的中线AM 的长为()A .8B .13C .D 【变式训练3-2】(雁江区校级月考)如图,已知等腰梯形ABCD ,用坐标法证明:AC BD =.知识点4点到直线的距离【例4-1】(金凤区校级期末)已知点(2,1)P -.(1)若一条直线经过点P ,且原点到直线的距离为2,求该直线的一般式方程;(2)求过点P 且与原点距离最大的直线的一般式方程,并求出最大距离是多少?【例4-2】(韶关期末)已知点(1,3)A 和点(5,2)B 到直线l 的距离相等,且l 过点(3,1)-,则直线l 的方程为()A .410x y ++=或3x =B .410x y +-=或3x =C .410x y ++=D .410x y +-=【变式训练4-1】(保山期末)若直线l 过点,倾斜角为120︒,则点(1,到直线l 的距离为()A .32B C .332D .532【变式训练4-2】(新课标Ⅲ)点(0,1)-到直线(1)y k x =+距离的最大值为()A .1BC D .2知识点5两平行线间距离公式及其应用【例5-1】(张家界期末)直线3430x y +-=与直线690x my ++=平行,则它们的距离为()A .65B .32C .125D .2【例5-2】(广州期末)若两平行直线20(0)x y m m ++=>与30x ny --=之间的距离是,则(m n +=)A .0B .1C .1-D .2-【变式训练5-1】(靖远县期末)已知直线240x y +-=与直线230x my m +++=平行,则它们之间的距离为()A B C .352D .3102【变式训练5-2】(连云港期末)两条平行直线6450x y -+=与32y x =的距离是()A .13B .26C .13D .26【变式训练5-3】(广东期末)已知直线1:(1)2l x m y m ++=-与2:24160l mx y ++=,若12//l l ,则实数m 的值为()A .2或1-B .1C .1或2-D .2-【变式训练5-4】(崇左期末)已知直线1:20l x y n ++=,2:440l x my +-=互相平行,且1l ,2l 之间的距离(m n +=)A .3-或3B .2-或4C .1-或5D .2-或2知识点6运用距离公式解决最值问题【例6-1】(北碚区校级期末)已知ABC ∆的三个顶点(1,2)A ,(2,1)B ,(3,3)C ,若ABC ∆夹在两条斜率为1的平行直线之间,则这两条平行直线的距离的最小值是()A .355B C .322D 【例6-2】(鼓楼区校级期中)已知直线1:4270l x y +-=和2:210l x y +-=,直线m 分别与1l ,2l 交于A ,B 两点,则线段AB 长度的最小值为.【变式训练6-1】(闵行区校级模拟)过点(1,2)-且与原点的距离最大的直线方程是.【变式训练6-2】(和平区校级期末)已知点(2,5)A 和点(4,7)B ,点P 在y 轴上,若||||PA PB +的值最小,则点P 的坐标为.名师导练A 组-[应知应会]1.(辽源期末)点(3,1)到直线3420x y -+=的距离是()A .45B .75C .425D .2542.(宁波期末)直线6820x y +-=与6830x y +-=间的距离为()A .1B .3C .110D .253.(内江期末)已知点(1,3)M 到直线:10l mx y +-=的距离等于1,则实数m 等于()A .34B .43C .43-D .34-4.(兴庆区校级期末)设有直线(3)1y k x =-+,当k 变动时,所有直线都经过定点()A .(0,0)B .(0,1)C .(3,1)D .(2,1)5.(沙坪坝区校级期中)已知直线1:10l x ay +-=与2:210l x y -+=平行,则1l 与2l 的距离为()A .15B .55C .35D .3556.(包头期末)点(,)P x y 在直线20x y +-=上,O 是坐标原点,则||OP 的最小值是()A .1B C .2D .7.(河池期末)点2(2,)P m m 到直线70x y ++=的距离的最小值为()A .4B .C .D .8.(江阴市期中)直线l 过(1,2)P ,且(2,3)A ,(4,5)B -到l 的距离相等,则直线l 的方程是()A .460x y +-=B .460x y +-=C .2370x y +-=或460x y +-=D .3270x y +-=或460x y +-=9.(平顶山期末)已知(1,2)P -,(2,4)Q ,直线:3l y kx =+.若P 点到直线l 的距离等于Q 点到直线l 的距离,则(k =)A .2.3或6B .23C ..0D ..0或2310.(昆山市期中)已知(2,3)M -,(6,2)N ,点P 在x 轴上,且使得PM PN +取最小值,则点P 的坐标为()A .(2,0)-B .12(5,0)C .14(5,0)D .(6,0)11.(宝安区校级模拟)已知0x <<,0y <<M =则M 的最小值为()A .B .C .2D .12.(多选)(江阴市期中)若两条平行直线1:20l x y m -+=与2:260l x ny +-=之间的距离是则m n +的可能值为()A .3B .17-C .3-D .1713.(多选)(山东模拟)若三条直线1:10l ax y ++=,2:10l x ay ++=,3:0l x y a ++=不能围成三角形,则a 的取值为()A .1a =B .1a =-C .2a =-D .2a =14.(田家庵区校级期末)原点(0,0)到直线:20l x y -+=的距离是.15.(尖山区校级期末)两条平行直线110l y -+=与2:230l ax y +-=之间的距离为.16.(嘉兴期末)直线1:0l x y m --=与直线2:30l mx y -+=平行,则m =;1l 与2l 之间的距离为.17.(金华期末)已知直线:(1)2l x m y m ++=-,则当0m =时,直线l 的倾斜角为;当m 变化时,直线l 过定点.18.(镇江期末)已知直线1:0l x y a ++=与直线2:0l x y +=a 的值为.19.(珠海期末)已知平面直角坐标系xOy 中,点(4,1)A ,点(0,4)B ,直线:31l y x =-,则直线AB 与直线l 的交点坐标为.20.(苏州期末)已知A ,B 两点分别在两条互相垂直的直线20x y -=和5x ay +=上,且线段AB 的中点为(0,5)P ,则||AB =.21.(昆山市期中)在平面直角坐标xOy 中,已知(4,3)A ,(5,2)B ,(1,0)C ,平面内的点P 满足PA PB PC ==,则点P 的坐标为.22.(新余期末)已知直线:2(2)l y ax a =+-过一、三、四象限,其中a Z ∈,则点(1,3)A -到直线l 的距离为.23.(乐山期末)已知两条直线1:420l mx y +-=和2:10l x my ++=.(1)当12//l l 时,求m 的值;(2)在(1)的条件下,求1l 、2l 间的距离.24.(宁德期末)已知直线:260l x y --=与x 轴的交点为A ,且点A 在直线m 上.(1)若m l ⊥,求直线m 的方程;(2)若点(1,1)B 到直线m 的距离等于2,求直线m 的方程.25.(新都区期末)已知ABC ∆的三个顶点坐标为(3,1)A -,(3,3)B -,(1,7)C .(1)求BC 边的中线所在直线方程的一般式方程;(2)求ABC ∆的面积.26.(沭阳县期中)已知直线:(12)(1)720l m x m y m ++-++=.(1)求证:不论m 为何实数,直线l 恒过一定点M ;(2)过定点M 作一条直线1l ,使夹在两坐标轴之间的线段被M 点平分,求直线1l 的方程.27.(宁城县期末)已知点ABC ∆三顶点坐标分别是(1,0)A -,(1,0)B ,(0,2)C ,(1)求A 到BC 边的距离d ;(2)求证AB 边上任意一点P 到直线AC ,BC 的距离之和等于d .B 组-[素养提升]1.(尖山区校级期末)已知在ABC ∆中,顶点(4,2)A ,点B 在直线:20l x y -+=上,点C 在x 轴上,则ABC ∆的周长的最小值.2.(兰州期末)已知点(2,1)P -.(1)求过P 点与原点距离最大的直线l 的方程,最大距离是多少?(2)是否存在过P 点与原点距离为6的直线?若存在,求出方程;若不存在,请说明理由.第7讲直线的交点坐标与距离公式新课标要求1.能用解方程组的方法求两条直线的交点坐标。
