平均数-中位数-众数PPT课件
合集下载
§4 4.1 平均数、中位数、众数、极差、方差 4.2 标准差

在上一节中,从甲、乙两个城市随机抽取的16 16台自动 例2 在上一节中,从甲、乙两个城市随机抽取的16台自动 售货机的销售额可以用茎叶图表示,如图所示: 售货机的销售额可以用茎叶图表示,如图所示: (1)甲、乙两组数据的中位数、众数、极差分别是多少? 乙两组数据的中位数、众数、极差分别是多少? (2)你能从图中分别比较甲、乙两组数据的平均数和方差 你能从图中分别比较甲、 的大小吗? 的大小吗? 观察茎叶图, 解:(1) 观察茎叶图,我们不难 看出: 看出:甲城市销售额的中位数为 20,众数为10,18,30,极差为53;乙 20,众数为10,18,30,极差为53;乙 众数为10,18,30,极差为53; 城市销售额的中位数为29,众数为 城市销售额的中位数为29,众数为 29, 23,34,极差为38. 23,34,极差为38.
5. 方 差 是 样 本 数 据 到 平 均 数 的 平 均 距 离 , 一 般 用 s 2 表 示 , 通 常 用 公 式
1 s 2 = [( x1 − x ) 2 + ( x2 − x ) 2 + L + ( xn − x ) 2 ] 来计算.反映了数据的离散程度.方差越大,数据的离散程度越 来计算.反映了数据的离散程度.方差越大, n
(2)从茎叶图中我们不难看出:甲城市销售额分布主要在 从茎叶图中我们不难看出: 茎叶图的上方且相对较散, 茎叶图的上方且相对较散,而乙城市的销售额分布则相对 集中在茎叶图的中部.由此,我们可以估计:甲城市销售额 集中在茎叶图的中部.由此,我们可以估计: 的平均数比乙城市的小,而方差比乙城市的大. 的平均数比乙城市的小,而方差比乙城市的大.
对数据数字特征内容的评价, 对数据数字特征内容的评价,应当更多地关注对其本 身意义的理解和在新情境中的应用, 身意义的理解和在新情境中的应用,而不是记忆和使用的 熟练程度. 熟练程度.
平均数、中位数、众数、极差、方差标准差的概念讲解

【解析】1.选A.中位数为 1 (91+92)=91.5;
2
平均数为 1 (87+89+90+91+92+93+94+96)=91.5.
8
2. x甲=1 (65+82+80+85)=78,
4
x乙=1 (75+65+70+90)=75,
4
知识点2 对方差与标准差的理解 标准差、方差的作用 (1)标准差、方差描述了一组数据围绕着平均数波动的大小, 标准差、方差越大,数据的离散程度越大;标准差、方差越小, 数据的离散程度越小. (2)标准差、方差为0时,表明样本数据全相等,数据没有波动 幅度和离散性.
(2)据报道,某公司的33名职工的月工资(以元为单位)如下:
职务
人数 工资
董事 长
副董 事长
董事
总经 理
经理
管理 员
职员
1
1
2
1
5
3 20
5 500 5 000 3 500 3 000 2 500 2 000 1 500
①求该公司职工月工资的平均数、中位数、众数. ②假设副董事长的工资从5000元提升到20000元,董事长的工资 从5500元提升到30000元,那么新的平均数、中位数、众数又是 什么?(精确到元) ③你认为哪个统计量更能反映这个公司员工的工资水平?结合 此问题谈一谈你的看法.
【即时练】
1.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,
则这组数据的中位数和平均数分别是
()
A.91.5和91.5
B.91.5和92
C.91和91.5
D.92和92
众数、中位数、平均数与样本频率分布直方图和关系47页PPT

23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!ห้องสมุดไป่ตู้
众数、中位数、平均数与样本频率分布直 方图和关系
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!ห้องสมุดไป่ตู้
众数、中位数、平均数与样本频率分布直 方图和关系
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
右偏分布众数 ,中位数,平均数
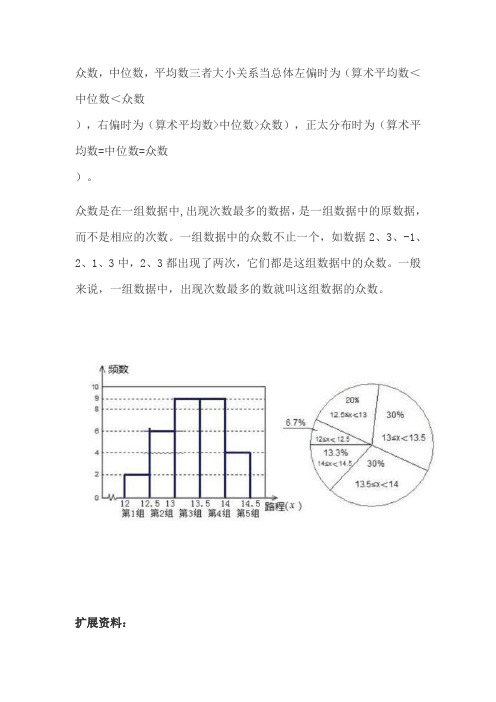
众数,中位数,平均数三者大小关系当总体左偏时为(算术平均数<中位数<众数
),右偏时为(算术平均数>中位数>众数),正太分布时为(算术平均数=中位数=众数
)。
众数是在一组数据中,出现次数最多的数据,是一组数据中的原数据,而不是相应的次数。
一组数据中的众数不止一个,如数据2、3、-1、2、1、3中,2、3都出现了两次,它们都是这组数据中的众数。
一般来说,一组数据中,出现次数最多的数就叫这组数据的众数。
扩展资料:
对于有限的数集,可以通过把所有观察值高低排序后找出正中间的一个作为中位数。
如果观察值有偶数个,通常取最中间的两个数值的平均数作为中位数。
一个数集中最多有一半的数值小于中位数,也最多有一半的数值大于中位数。
如果大于和小于中位数的数值个数均少于一半,那么数集中必有若干值等同于中位数。
高中数学必修三 18-19 第1章 §4 4.1 平均数、中位数、众数、极差、方差 4.2 标准差

难
(6)样本的标准差和方差都是正数.( )
返 首 页
[解析] (1)×,根据平均数的定义可知错误.
自
当
主 预
(2)×,根据众数定义知众数可以一个,也可以多个.
堂 达
习
标
•
(3)×,由中位数的定义可知错误.
•
探
固
新 知
(4)√,极差与标准差都反映了样本数据的波动性和离散程度.
双 基
(5)×,平均数与数据的波动性无关.
究 •
(4)算出(3)中 n 个平方数的平均数,即为样本方差.
攻
重 难
(5)算出(4)中方差的算术平方根,即为样本标准差.
课 时 分 层 作 业
返 首 页
自
当
主
堂
预
达
习 •
2.标准差(方差)的两个作用:
标 •
探
固
新
(1)标准差(方差)越大,数据的离散程度越大;标准差(方差)越小,数据的 双
知
基
离散程度越小.
达 标
•
•
探
A.茎叶图
B.频率分布直方图
固
新
双
知
C.频率折线图
D.频率分布表
基
合
作
探 究
B [当收集到的数据量很大时,一般用频率分布直方图.]
攻
重 难
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
课 时 分 层 作 业
返 首 页
[解] (1) x 甲=16(99+100+98+100+100+103)=100,
自 主
x 乙=16(99+100+102+99+100+100)=100.
20.2 第2课时 华东师大版数学八年级下册课件(共15张PPT)

答:上述问题中最关心的数据为众数,最不关心的数据为中位数.
1.检验某厂生产的手表质量时,检查人员随机抽取了10只手表,在下表中记下 了每只手表的走时误差(正数表示比标准时间快,负数表示比标准时间 慢),你认为用这10只手表误差的平均数来衡量这10只手表的精度合适吗?
手表序号 1 2 3 4 5 6 7 8 9 10 日走时误差 -2 0 1 -3 -1 0 2 4 -3 2 (秒)
4.某餐厅共有10名员工,所有员工工资的情况如下表:
请解答下列问题: (1)餐厅所有员工的平均工资是多少? (2)所有员工工资的中位数是多少? 解:(1)平均工资为 4350 元.(2)工资的中位数为 2000 元.
(3)用平均数还是中位数描述该餐厅员工工资的一般水平比较恰当? (4)去掉经理和厨师甲的工资后,其他员工的平均工资是多少?它是否能 反映餐厅员工工资的一般水平?
解:不合适,虽然这10只手表误差的平均数是0,但从测得的数据看, 10只手表中只有2只不快不慢,显然不能认为这些手表有很高的精度.
1.根据实际情况填写(填平均数、中位数、众数) ①老板进货时关注卖出商品的众数 . ②评委给选手综合得分时关注平均数. ③被招聘的员工关注公司员工工资的 中位数. 2. 校有 25 名同学参加某比赛,预赛成绩各不相同,取前 13 名 参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛, 只需要再知道这 25 名同学成绩的( B ) A.最高分 B.中位数 C.方差 D.平均数
3.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄 如下:(单位:岁) 甲群:13、13、14、15、15、15、16、17、17. 乙群:3、4、4、5、5、6、6、54、57.
(1)甲群游客的平均年龄是 15 岁,中位数是 15 岁,众数是 15 岁,其中
1.检验某厂生产的手表质量时,检查人员随机抽取了10只手表,在下表中记下 了每只手表的走时误差(正数表示比标准时间快,负数表示比标准时间 慢),你认为用这10只手表误差的平均数来衡量这10只手表的精度合适吗?
手表序号 1 2 3 4 5 6 7 8 9 10 日走时误差 -2 0 1 -3 -1 0 2 4 -3 2 (秒)
4.某餐厅共有10名员工,所有员工工资的情况如下表:
请解答下列问题: (1)餐厅所有员工的平均工资是多少? (2)所有员工工资的中位数是多少? 解:(1)平均工资为 4350 元.(2)工资的中位数为 2000 元.
(3)用平均数还是中位数描述该餐厅员工工资的一般水平比较恰当? (4)去掉经理和厨师甲的工资后,其他员工的平均工资是多少?它是否能 反映餐厅员工工资的一般水平?
解:不合适,虽然这10只手表误差的平均数是0,但从测得的数据看, 10只手表中只有2只不快不慢,显然不能认为这些手表有很高的精度.
1.根据实际情况填写(填平均数、中位数、众数) ①老板进货时关注卖出商品的众数 . ②评委给选手综合得分时关注平均数. ③被招聘的员工关注公司员工工资的 中位数. 2. 校有 25 名同学参加某比赛,预赛成绩各不相同,取前 13 名 参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛, 只需要再知道这 25 名同学成绩的( B ) A.最高分 B.中位数 C.方差 D.平均数
3.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄 如下:(单位:岁) 甲群:13、13、14、15、15、15、16、17、17. 乙群:3、4、4、5、5、6、6、54、57.
(1)甲群游客的平均年龄是 15 岁,中位数是 15 岁,众数是 15 岁,其中
《中位数和众数》精品课件22人教版

3.(5分)(凉山州中考)某班40名同学一周参加体育锻炼时间统计如表所示:
人数(人) 时间(小时)
3 17 13 7 7 8 9 10
那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( D ) A.17,8.5 B.17,9 C.8,9 D.8,8.5 4.(5分)(攀枝花中考)一组数据1,2,x,5,8的平均数是5,则该组数据的中位数是 __5__.
合作探究
新知 平均数、众数和中位数的应用
有6 户家庭的年收入分别为(单位:万元):4,5, 5,6,7,50.你认为这6户家庭的年收入水平大概是多少? 如果把数据50改成9,结果又会怎样?
(1)用平均数估计: x = 4+5+5+6+7+50 12.83 (万元);
6
(2)用中位数估计:中位数= 5+6 =5.5(万元);
(3)如果想让一半左右的营业员都能达到销售目标,你认为月
销售额定为多少合适?说明理由.
销售额/万 元
13
22
23
24
26
28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
解:(3)月销售额可以定为每月__1_8_万元(中位数).因为从
样本情况看,月销售额在_1_8__万元以上(含18万元)的有16人,
销售额/万 元
13
14
15
16
17
18
19
22
23
24
26
28 30
32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
解:(1)样本数据的众数是__1_5__,中位数是__1_8__,利用计算
平均数、众数、中位数、方差

九年级(上册)
平均数、中位数、众数 方差
初中数学
定义1
x1,xC2,ONT,ENxTn,S
x x1 x2 n
“x”
xn
01 02 03 04
那么
读作
“x 拔”.
一般地,如果有n 个数 ○ 通常,平均数可以用来表示一组数据的“平均水平”. ○ 叫做这 n 个数的算术平均数,简称平均数,
定义2
某商店有220升,215升,185升,182升 四种型号的某种名牌电冰箱,在一周内 分别销售了6台,30台,14台,8台.在研究 电冰箱销售情况时,商店经理关心的应 是哪些数据?哪些数据对于进货最有参 考价值?
定义4
极差=最大值-最小值.
在一组数据 x1 ,x2 ,…,xn 中,各2,(x2 x )2, ,(xn x )2, 我们用它们的平均数,即
一般地,设 x1,x2, xn 为n 个数据, w1,w2, wn 依次为这 n 个数据的权数,
则称 x1w1 x2w2 xnwn 为这组数 w1 w2 wn
据的加权平均数.
将一组数据按大小顺序排列,如果数 据
的个数是奇数,那么处于中间位置的 数叫做
这组数据的中位数;如果数据的个数 是偶数,
s2
1 n
( x1
x )2
( x2
x )2
(xn x )2
来表示这组数据的离散程度,并把它们叫做这组数据
的方差.
方差越小,离散程度越小,说明数据越稳定.
归纳
即
数据的标准差.
s
1 n
( x1
x
)2
( x2
x
)2
(xn x )2
在有些情况下, 需要用方差的算 术平方根,
平均数、中位数、众数 方差
初中数学
定义1
x1,xC2,ONT,ENxTn,S
x x1 x2 n
“x”
xn
01 02 03 04
那么
读作
“x 拔”.
一般地,如果有n 个数 ○ 通常,平均数可以用来表示一组数据的“平均水平”. ○ 叫做这 n 个数的算术平均数,简称平均数,
定义2
某商店有220升,215升,185升,182升 四种型号的某种名牌电冰箱,在一周内 分别销售了6台,30台,14台,8台.在研究 电冰箱销售情况时,商店经理关心的应 是哪些数据?哪些数据对于进货最有参 考价值?
定义4
极差=最大值-最小值.
在一组数据 x1 ,x2 ,…,xn 中,各2,(x2 x )2, ,(xn x )2, 我们用它们的平均数,即
一般地,设 x1,x2, xn 为n 个数据, w1,w2, wn 依次为这 n 个数据的权数,
则称 x1w1 x2w2 xnwn 为这组数 w1 w2 wn
据的加权平均数.
将一组数据按大小顺序排列,如果数 据
的个数是奇数,那么处于中间位置的 数叫做
这组数据的中位数;如果数据的个数 是偶数,
s2
1 n
( x1
x )2
( x2
x )2
(xn x )2
来表示这组数据的离散程度,并把它们叫做这组数据
的方差.
方差越小,离散程度越小,说明数据越稳定.
归纳
即
数据的标准差.
s
1 n
( x1
x
)2
( x2
x
)2
(xn x )2
在有些情况下, 需要用方差的算 术平方根,
