北京邮电大学数学物理方法1
北京邮电大学学术型硕士研究生培养方案(2016)

2031101036 信息网络安全技术
3111100007 宽带通信网
3111100014 高等通信原理
3111100034 IP/WDM 网络基础理论
选
3111100035 IPv6 与移动计算技术
修
第 6 组至少修 6 学分
3111100036 计算机视觉模型学习与推理
课
(专业方向选修课)
程
3111100042 L硕士研究生培养方案 4、掌握至少一门外国语,能较为熟练地阅读本专业的外文资料,具有一定的
写作能力并具备一定的国际学术交流能力,掌握至少一种计算机语言及编程方法, 熟练运用计算机操作系统和文献检索工具查询技术文献。
四、 学制 3年
五、 课程设置与学分
硕士研究生课程主要划分为学位课、非学位选修课、必修环节三大部分。 硕士研究生应在导师指导下制定个人培养计划和具体选课,应修满不少于 30
二、 研究方向 1、 信息理论与信息处理 2、信息通信网络 3、多媒体与网络大数据 4、无线和移动通信 5、光通信 6、网络服务、管理与安全
三、 培养目标 1、掌握马克思主义的基本理论,树立科学的世界观,坚持四项基本原则,热
爱祖国,遵纪守法,品行端正,学风严谨,团结协作,具有强烈的事业心和献身 精神,积极为社会主义现代化服务,身心健康。
2031100965 工程计算方法
3111100091 电磁场理论
3111100571 现代数字通信
第 4 组, 至少选 1 门 (专业基础课-基础专业
课)
3111100606 3111100941 3111101116
信息论基础 模式识别与机器学习 通信网理论(硕)
3111101119 统计信号处理基础
数学物理方法第一章

(或微商),以 f '(z) 或 df/dz 表示
讨论:
1、从形式上看,复变函数导数的定义与实变函数的定义相同,
因而实变函数论中关于导数的规则和公式往往可以适用于实变 函数。
则
x cos y sin
z (cos i sin )
z e
i
指数式
讨论:i)复数的辐角不能唯一地确定。如果 0 是其中一个辐角, 则
0 2k (k 0,1,2,) 也是其辐角,把属于 [0,2 ) 的辐角称为主值辐角,记为arg z .
存在,且连续,并
且满足柯西-黎曼条件。 证明:由于这些偏导数连续,二元函数 u 和 v 的增量可分别写为
各 个
,于是有
根据柯西-黎曼条件,上式即
这一极限是与 z 0 无关的有限值。证毕。
讨论:复变函数与实变函数的导数有本质上的差别,复变函数 可微,不但要求复变函数的实部与虚部可微,而且还要求其实 部与虚部满足柯西-黎曼条件。
单连通区域:在区域 B 做任何简单的闭曲线,曲线包围 的点全属于 B。否则为多连通区域。
三、复变函数例
多项式
a0 a1 z a2 z an z
2
n
n 为正整数
有理分式
a0 a1 z a2 z 2 an z n b0 b1 z b2 z 2 bm z m
ii)当 1时,z cos i sin ei 称为单位复数。
iii)复数 z 的共轭复数
z x iy (cos isin ) e
数学物理方法(第四版)高等教育出版社第一章1

-2
(x,y)
x
(0,-1)
(3) Im(i+ z) = 4
Im[i + (x −iy)] = Im[x + i(1− y)] = 4
1− y = 4
表示y= 的直线 表示 -3的直线
y=-3
5、复平面与复数球之关系
例3 设 z =
z1 7 1 ( )=− + i z2 5 5
−1 3i 求 − , Re( z ), Im(z ) 与 zz i 1− i
−1 3i 3i(1+ i) 3 3 3 1 z= − =i − =i − i+ = − i i 1− i (1− i)(1+ i) 2 2 2 2
3 ∴Re(z) = 2
2 x 2
3、复数的三种表示: 、复数的三种表示
1). 代数式 2). 三角式
z = x + iy
z =ρ
x = ρ cosθ
y = ρ sinθ
z = ρ (cos θ + i sin θ )
3). 指数式
e = cosθ + i sin θ
iθ
欧拉公式
z = ρe
iθ
θ = Argz
4、复数的运算
A
S
•作业:P6 作业: 作业
•1(2)( )( ) ( )( )(5) )(3)( •2(1)( )( )( ) ( )( )(5)( )(4)( )(6) •3(1)( ) ( )( )(4)
§1.2
复变函数
复变函数的定义与定义域: 一、复变函数的定义与定义域: 复变函数定义: 1、复变函数定义: 复数平面上存在一个点集E, 复数平面上存在一个点集 , 对于E的每一点( 每一个 值 ) , 对于 的每一点(每一个z值 的每一点 按照一定的规律, 按照一定的规律 , 有一个或多 ω 与之相对应, 个复数值 与之相对应 , 则称 为z的函数 的函数——复变函数,z称为 复变函数, 称为 的函数 复变函数
数学物理方法1-137页PPT文档

u u(x,t) u
T'
采用微元法来建立位移u满足的方程:
M'
'
把弦上点的运动先看成小弧段的运动,然 后再考虑小弧段趋于零的极限情况。
ds
M
gds
在弦上任取一弧段 M M ,' 其长度为ds, T
弧段两端所受张力为 T 和 T '
N
N'
O
x
x dx
x
是弦的线密度
由于假定弦是柔软的,所以在任意点处张力的方向总是沿着弦在该点的 切线方向。
13
现在考虑弧段 M M ' 在t时刻的受力和运动情况。
根据牛顿第二定律,作用于弧段上任一方向上力的总和等于这段弧的
质量乘以该方向上的运动加速度。
u
T'
在x方向弧段 M M ' 受力总和为
M'
'
TcosT'cos'
ds
M
由于弦只做横向运动,所以
gds
T
T c o s T 'c o s' 0 O
1
教材与参考书
教材:《数学物理方法——理论、历史与计算机》,郭玉 翠,大连理工大学出版社
《数学物理方法》第二版,谷超豪、李大潜、陈恕行等, 高教出版社,2019年
《实用偏微分方程》英文版第四版,(美)理查德.哈伯 曼,机械工业出版社,2019年
学时
32学时
2
对大家的要求
按时上课 课上记笔记,做标记 独立完成作业
4
主要内容
第一章 数学物理方程及其定解条件 §1.1 基本方程的建立 §1.2 定解条件 §1.3 定解问题的提法 §1.4 二阶线性偏微分方程的分类与化简
数学物理方法第四版课后答案

数学物理方法第四版课后答案《数学物理方法第四版课后答案》第一章:复变函数1.1 复数与复平面题目1:将以下复数写成极坐标形式:a) z = 3 + 4ib) z = -2 - 5ic) z = 5i解答:a) r = √(3^2 + 4^2) = 5, θ = arctan(4/3)∴ z = 5(cos(arctan(4/3)) + i*sin(arctan(4/3)))b) r = √((-2)^2 + (-5)^2) = √(4 + 25) = √29, θ = arctan((-5)/(-2)) = arctan(5/2)∴ z = -√29(cos(arctan(5/2)) + i*sin(arctan(5/2)))c) r = √(0^2 + 5^2) = 5, θ = arctan(0/5) = 0∴ z = 5(cos(0) + i*sin(0)) = 5i题目2:计算以下复数的共轭:a) z = 3 + 4ib) z = -2 - 5ic) z = 5i解答:a) z* = 3 - 4ib) z* = -2 + 5ic) z* = -5i...第二章:常微分方程2.1 一阶微分方程题目1:求解以下一阶线性非齐次微分方程:a) \\frac{dy}{dx} + 2y = e^xb) \\frac{dy}{dx} - y = 3x^2解答:a) 首先求齐次方程的解,即 \\frac{dy}{dx} + 2y = 0观察到该方程的解为 y = Ce^{-2x},其中 C 为任意常数然后考虑非齐次方程的解,即 \\frac{dy}{dx} + 2y = e^x令 y = A e^{-2x},其中 A 为待定常数\\frac{dy}{dx} = -2A e^{-2x},代入方程得到 -2A e^{-2x} + 2A e^{-2x} = e^x解得 A = -\\frac{1}{4}∴ 非齐次方程的解为 y = -\\frac{1}{4} e^{-2x},加上齐次方程的解得到最终解 y = Ce^{-2x} - \\frac{1}{4} e^{-2x}b) 首先求齐次方程的解,即 \\frac{dy}{dx} - y = 0观察到该方程的解为 y = Ce^x,其中 C 为任意常数然后考虑非齐次方程的解,即 \\frac{dy}{dx} - y = 3x^2令 y = A e^x + B,其中 A、B 为待定常数\\frac{dy}{dx} = A e^x,代入方程得到 A e^x - (A e^x + B) = 3x^2解得 B = -3x^2∴ 非齐次方程的解为 y = A e^x - 3x^2,加上齐次方程的解得到最终解 y = Ce^x - 3x^2...通过以上两个例题,可以看出在解一阶线性非齐次微分方程时,首先解齐次方程得到通解,然后根据非齐次项的形式确定待定系数,最后将通解与待定解相加得到最终解。
育明考博-北京邮电大学理学院电子科学与技术专业考试大纲报录比参考书复习方法
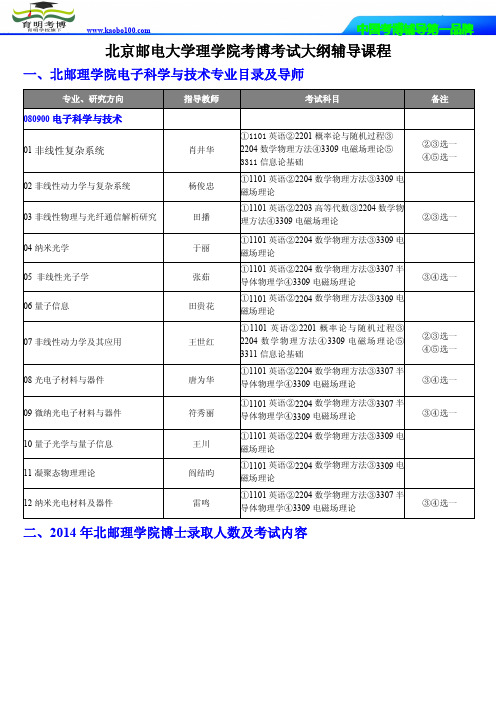
09 微纳光电子材料与器件
符秀丽
①1101 英语②2204 数学物理方法③3307 半 导体物理学④3309 电磁场理论
10 量子光学与量子信息 11 凝聚态物理理论 12 纳米光电材料及器件
王川 阎结昀
雷鸣
①1101 英语②2204 数学物理方法③3309 电 磁场理论
2
1、10 分 2、15 分
①1101 英语②2204 数学物理方法③3309 电 磁场理论
①1101 英语②2204 数学物理方法③3307 半 导体物理学④3309 电磁场理论
二、2014 年北邮理学院博士录取人数及考试内容
备注 ②③选一 ④⑤选一
②③选一
③④选一
②③选一 ④⑤选一 ③④选一 ③④选一
③④选一
中国考博辅导第一品牌
售各院校真题)
四、2014 年公开招考博士生初试合格标准
1、单科不低于 35 分,总分不限。 2、初试成绩有一科或两科成绩低于 35 分,低于部分累计不超过 10 分(含),复试 成绩优异且获得省部级(含)以上科研学术奖励;或作为第一作者发表的论文被 SCI、EI、 CSSCI 收录;或获得发明专利以及其它反映考生科研创新能力的获奖证明等。 符合第 2 条考生须经拟录取导师推荐,学院招生领导小组审议通过后提交学校研究生 招生委员会讨论。
2204 数学物理方法
2、《数学物理方法学习指导》(第 1 版)郭玉翠编着,清华大学出版社,2006 年 2 月。 3、《数学物理方法》(第 2 版)梁昆淼编,高等教育出版社,1978 年 7 月。
4、《矢量分析与场论》(第二版)谢树艺编,高等教育出版社,1985 年 3 月。
北邮考博辅导班:2019北京邮电大学系统科学考博难度解析及经验分享

北邮考博辅导班:2019北京邮电大学系统科学考博难度解析及经验分享下面是启道考博辅导班整理的关于北京邮电大学系统科学考博相关内容。
一、专业介绍系统科学是研究系统的结构与功能关系、演化和调控规律的科学,是一门新兴的综合性、交叉性学科。
它以不同领域的复杂系统为研究对象,从系统和整体的角度,探讨复杂系统的性质和演化规律,目的是揭示各种系统的共性以及演化过程中所遵循的共同规律,发展优化和调控系统的方法,并进而为系统科学在科学技术、社会、经济、军事、生物等领域的应用提供理论依据。
系统科学是在数学、物理、生物、化学等学科基础上,结合运筹、控制、信息科学等技术科学发展起来的,并在工程、社会、经济、军事、生命、生态、管理等领域得到发展与应用。
·系统是由相互联系、相互作用的要素(部分)组成的具有一定结构和功能的有机整体。
北京邮电大学理学院的系统科学专业在博士招生方面,划分为16究方向071100系统科学研究方向:01 复分析和复动力系统02 非线性偏微分方程03 微分动力系统04 非线性动力学及其在神经系统中的应用05 智能信息处理与最优化方法06 群体智能与演化系统07 应用概率与服务管理08 最优控制问题及其科学计算09 非线性复杂系统、统计物理与生物物理10 复杂系统与量子光学11 复杂系统与非线性动力学12 非线性动力学与复杂系统13 新型光纤通信等领域中计算机符号计算与分析14 智能信息系统15 光纤非线性基础理论及其应用16 量子密码与量子信息理论考试科目:①1101英语②2203高等代数③2204数学物理方法二、申请材料1) 《北京邮电大学“申请-审核”制招收博士生申请表》。
2) 英语水平成绩证明复印件。
3) 两名与申请学科相关的具有副高职(含)以上职称专家的推荐书各一份(网上报名时下载)。
4) 已取得的科研成果(含专利、公开发表的学术性论文、专著等)复印件。
5) 获奖证书或其他可以证明申请人科研能力和学术水平的证明材料。
大学物理(第三版)北京邮电大学 教学PPT 绪论与第一章-质点运动学

消去t,得轨道方程
x 2 y 2 R2
22
二、位移r
1、定义 :由起始位臵指向终了位臵的有向线段;△t时间 内位臵矢量的增量
Z
S
A
A
B
r
r1
X
r
r2
r1
Y
r1
B
r2
r r2 r2 r1
r r2 r1 r | r2 | | r1 | 直角坐标系中 r xi yj zk
vA
v
o
vB
v a t
2 v dv d r a lim 2 t 0 t dt dt
28
2、加速度在直角坐标系中
dv dv x dv y dvz a i j k dt dt dt dt
d 2 x d 2 y d 2z 2 i 2 j 2 k dt dt dt
5
绪
论
物理学是关于自然界最基本形态的科学。它研究物质的结 构,相互作用以及物质的运动。
一、物理学的研究对象
1、研究物质的两种形态
实物和场是物质的两种基本形态 ▲关于实物物质结构
实物包括微观粒子和宏观物体,它的范围是从基本粒子的亚 核世界到整个宇宙。
▲关于场物质结构 例如:电磁场、引力场、各种介子场。
7
三、物理学的发展历程
经典物理、近代物理、现代物理
四、物理学的意义
1、物理学是一切自然科学的基础; 2、物理学推动技术革命和社会文明。
8
大学物理
第一篇 第二篇 第三篇 第四篇 第五篇 力学基础 热 学 电 磁 学 波动光学 量子物理
9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 2 u ( x, t ) 2 u ( x, t ) a 2 t x 2 2 2u ( x, t ) 2 u ( x, t ) a f ( x, t ) t 2 x 2
( *) (**)
方程(*)和方程(**)的差别在于方程( ** )的右端多了一个与未 知函数u无关的项f(x,t),这个项称为自由项。
x
P ( x, t ) A' u ( x, t )
P( x x, t ) B' u ( x x, t )
2u ( , t ) S x ( x x, t ) S ( x, t ) S F ( x 2 x, t ) S x 2 t x x
所以式(*)变为
或
2 u x, t 2 u x, t g dx dx T 2 2 x t
2 2 T u x, t u x , t g 2 2 x t
u 2 ( x, t ) 一般来说,张力较大时弦振动的速度变化很快,即 要比g大得多, t 2 所以可以把g略去。
则方程组
T cos T ' cos ' 0
重复以上的推导过程,可得有外力作用时弦的振动方程为:
2 2u ( x, t ) 2 u ( x, t ) a f ( x, t ) t 2 x 2
(**)
其中, f ( x, t ) F ( x, t ) / ,表示t时刻单位质量的弦在x点所受的外力。 式(**)称为弦的受迫振动方程。
'
ds
M
gds
T
N
弦是均匀的,设其线密度为 ;
O
x
N' x dx
x
13
设弦上具有横坐标为x的点,在时刻t的位置为M,其位移MN记为u。
显然,在振动过程中,位移u是变量x和t的函数,即
u u ( x, t )
采用微元法来建立位移u满足的方程:
u
T'
M'
'
把弦上点的运动先看成小弧段的运动,然 后再考虑小弧段趋于零的极限情况。
2 u x, t T sin T ' sin ' gds ds t 2 应该变为: T cos T ' cos ' 0 2 u x, t ' ' Fds T sin T sin gds ds t 2
12
§1.1.1 波动方程
1.
均匀弦的微小横振动
设有一根均匀柔软的细弦,平衡时沿直线拉紧,而且除了受不随时间变 化的张力及弦本身的重力外,不受其他外力的作用。 下面研究弦作微小横振动的规律。
u
T'
M'
所谓“横向”是指全部运动出现在一个 平面内,而且弦上的点沿垂直于x轴的方 向运动。
所谓“微小”是指运动的幅度及弦在任 意位置处切线的倾角都很小,以致它们 的高于一次方的项可以忽略不计。
,横截面为S(常数),长度为 x
A B
P( x x, t ) B' u ( x x, t )
外力密度为F(x,t),
x点在t时刻的纵向位移为u(x,t) 。 弹性模量E:杆伸长单位长度所需的 力
x
P ( x, t ) A' u ( x, t )
应力 :杆在伸缩过程中各点相互之间单位截面上的作用力 ( x, t ) :杆上x点在t时刻的应力。 应变:杆的相对伸长
x
T sin T ' sin ' gds,
' 其中, gds 是 MM 的重力。
16
当
0, ' 0
时,
2u ( x, t ) 小弧段在时刻t沿u方向的加速度近似为 , 2 t 小弧段的质量为 ds
u x, t sin tan , 2 x 1 tan u x dx, t ' ' sin tan , x 2 u x, t ds 1 dx dx. O x tan
可得:
2 2 u ( x, t ) 2 u ( x, t ) a t 2 x 2
其中, a 2 T /
这就是均匀弦的横振动所满足的泛定方程。它是一种波动方程。由于在 18 空间上是一维的,故称一维波动方程。
受迫振动
如果均匀弦上沿位移方向还经受外力场作用,单位长度弦上所受之力, 即力密度为F(x,t)。则在方程左端还应加上一项外力 F ( x, t )dx 。
由牛顿第二定律,可得[x,x+△x]段的运动方程为:
2u ( , t ) S x ( x x, t ) S ( x, t ) S F ( x 2 x, t ) S x 2 t x x 22
1
u ( x x, t ) u ( x, t ) u ( x, t ) lim x 0 x x
9
教学基本要求
掌握波动方程、热传导方程、Laplace方程的 物理背景及其定解问题的提法; 熟练掌握三类方程定解问题的解法:分离变量 法,行波法、积分变换法等; 熟悉Bessel函数和Legendre函数的性质及其 应用。
学习方法
物理过程 数学模型 数学解 物理解 物理现象
第1章 数学物理方程及其 定解条件
ds
M
gds
T
N
在弦上任取一弧段
MM
' ,其长度为 ds,
'
弧段两端所受张力为 T 和 T
O
x
N' x dx
x
是弦的线密度
由于假定弦是柔软的,所以在任意点处张力的方向总是沿着弦在该点的 切线方向。
14
现在考虑弧段
MM ' 在t时刻的受力和运动情况。
根据牛顿第二定律,作用于弧段上任一方向上力的总和等于这段弧的 质量乘以该方向上的运动加速度。
与初等函数相对; 初等函数:常函数、指数函数、对数函数、幂函数、 三角函数和反三角函数
5
主要内容
第一章 §1.1 §1.2 §1.3 §1.4
数学物理方程及其定解条件 基本方程的建立 定解条件 定解问题的提法 二阶线性偏微分方程的分类与化简
第二章 分离变量法 §2.1 (1+1)维齐次方程的分离变量法 §2.2 二维Laplace方程的定解问题 §2.3 非齐次方程的解法 §2.4 非齐次边界条件的处理
21
如图,AB段的相对伸长是: x点的应变为:
A B AB
——
—— ' '
——
AB
u ( x x, t ) u ( x, t ) x
A B
由于振动是微小的,可认为不超过杆的弹性限度
虎克(Hooke)定律:应力=弹性模量*应变
u ( x, t ) ( x, t ) E x
u
在x方向弧段
MM ' 受力总和为
' '
M
T'
M'
'
T cos T cos
由于弦只做横向运动,所以
' '
ds
gds
T
N
T cos T cos 0
O
x
N' x dx
x
按照弦作微小振动的假设,可知在振动过程中,弦上M和M’点处切线 的倾角都很小,即:
0, ' 0
17
2 u x, t u x dx, t u x, t T dx(*) gdx 2 x x t
上式左端方括号的部分是由于x产生 的改变量,可以用微分近似代替:
dx
u ( x, t ) 的变化引起的 x
u x dx, t u x, t u x, t 2u x , t dx dx 2 x x x x x
6
第三章 二阶常微分方程的级数解法 本征值问题 §3.1 二阶常微分方程的级数解法 §3.2 Legendre(勒让德)方程的级数解 §3.3 Bessel(贝塞尔)方程的级数解 §3.4 Sturm-Liouville(斯特姆--刘维尔)本征值问题 第四章 Bessel函数的性质及其应用 §4.1 Bessel方程的引出 §4.2 Bessel函数的性质 §4.3 Bessel函数的应用 *§4.4 修正Bessel函数 *§4.5 可化为Bessel方程的方程
u
T'
M'
'
ds
M
gds
T
N
x
N' x dx
x
2 u x, t ' ' 由牛顿第二定律有 T sin T sin gds ds t 2
2 u x dx , t u x , t u x, t 将近似式代入,T dx gdx 2 x x t
包括有非零自由项的方程称为非齐次方程。
自由项恒等于零的方程称为齐次方程。
方程(*)为一维齐次波动方程,
方程(**)为一维非齐次波动方程。
20
2.
均匀弹性杆的微小纵振动
一根弹性杆中任意小段受外界影响发生纵振动,必使其相邻部分发生伸 长或缩短。最终,杆上任意小段的纵振动必然传播到整根杆。这种振动 的传播就是波。 杆的质量密度为
