2015年历年华东师大版初三数学中考总复习二十四命题与证明精练精析2及答案
华师大版九年级上册数学第24章 解直角三角形含答案(历年考试题)

华师大版九年级上册数学第24章解直角三角形含答案一、单选题(共15题,共计45分)1、如图,在正方形中,是等边三角形,,的延长线分别交于点,,连接,,与相交于点.有下列结论:① ;② ;③ ;④.其中正确的个数是()A.1B.2C.3D.42、如图,一艘船由港沿北偏东65°方向航行至港,然后再沿北偏西40°方向航行至港,港在港北偏东20°方向,则,两港之间的距离为().A. B. C. D.3、如图,中,,,,若,则的长为()A.6B.C.7.5D.104、如图,⊙O直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足M,OM:OD=3:5,则AB 的长是()A. cmB. cmC. cmD. cm5、等腰三角形两边长分别为4和8,则这个等腰三角形的周长为( )A.16B.18C.20D.16或206、△ABC中,∠B=90°,AC=,tan∠C=,则BC边的长为()A.2B.2C.D.47、以长为8cm、6cm、10cm、4cm的四条线段中的三条线段为边,可以画出三角形的个数为()A.1个B.2个C.3个D.4个8、如图,小明站在某广场一看台C处,测得广场中心F的俯角为21°,若小明身高CD=1.7米,BC=1.9米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10.5米,则看台底端A点距离广场中心F点的距离约为()米.(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)A.8.9B.9.7C.10.8D.11.99、如图,在直角坐标系中,四边形 OABC 为菱形,对角线 OB、AC 相交于 D 点,已知 A点的坐标为(10,0),双曲线 y= ( x>0 )经过 D 点,交BC 的延长线于 E 点,且OB•AC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=(x>0);②E 点的坐标是(4,6);③sin∠CO A= ;④EC= ;⑤AC+OB=8 .其中正确的结论有()A.4 个B.3 个C.2 个D.1 个10、如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是()A. B. C. D.11、如图,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD、DE、BE,则下列结论:①∠ECA=165°,②BE=BC;③AD=BE;④CD=BD.其中正确的是()A.①②③B.①②④C.①③④D.①②③④12、两根木棒分别长5cm、7cm,第三根木棒与这两根木棒首尾依次相接构成三角形.如果第三根木棒的长是偶数(单位:cm),则一共可以构成不同的三角形有()A.4个B.5个C.8个D.10个13、三角形两条边分别为3和7,则第三边可以为()A.9B.3C.2D.1014、下列长度的各组线段中可组成三角形的是( )A.1,2,3B.2,3,5C.3,3,6D. ,,15、以长为3cm,5cm,7cm,10cm的四条线段中的三条线段为边可以画出三角形的个数为( )A.1B.2C.3D.4二、填空题(共10题,共计30分)16、如图,直线y=﹣x+4与两坐标轴交A、B两点,点P为线段OA上的动点,连接BP,过点A作AM垂直于直线BP,垂足为M,当点P从点O运动到点A 时,则点M运动路径的长为________.17、如图,在平面直角坐标系中,点A的坐标(﹣2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为________.18、如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为________米.19、如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为________米.20、如图△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若cos∠BDC= ,则BC的长为________.21、已知三角形的两边长是3和4,周长是偶数,则这样的三角形的第三边是________.22、如图,当太阳光与地面成角时,直立于地面的玲玲测得自己的影长为1.25m,则玲玲的身高约为________ m.(精确到0. 01m)(参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.428).23、将一张长方形纸片ABCD如图所示折叠,使顶点C落在点,已知,,则折痕DE的长为________(用含a的式子表示).24、如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上。
华师大版九年级数学上 第24章 解直角三角形《练闯考》2015年秋章末检测(含答案)
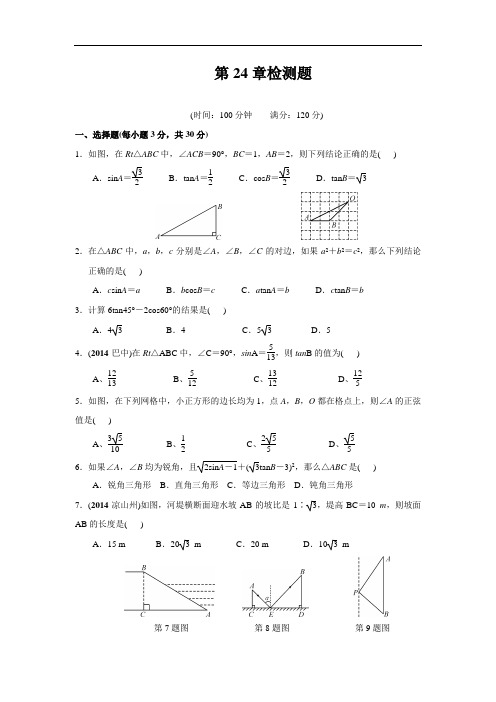
第24章检测题(时间:100分钟 满分:120分)一、选择题(每小题3分,共30分)1.如图,在Rt △ABC 中,∠ACB =90°,BC =1,AB =2,则下列结论正确的是( )A .sin A =32 B .tan A =12 C .cos B =32D .tan B =32.在△ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的对边,如果a 2+b 2=c 2,那么下列结论正确的是( )A .c sin A =aB .b cos B =cC .a tan A =bD .c tan B =b 3.计算6tan45°-2cos60°的结果是( )A .4 3B .4C .5 3D .5 4.(2014·巴中)在Rt △ABC 中,∠C =90°,sin A =513,则tan B 的值为( )A 、1213B 、512C 、1312D 、1255.如图,在下列网格中,小正方形的边长均为1,点A ,B ,O 都在格点上,则∠A 的正弦值是( )A 、3510B 、12C 、255D 、556.如果∠A ,∠B 均为锐角,且2sin A -1+(3tan B -3)2,那么△ABC 是( )A .锐角三角形B .直角三角形C .等边三角形D .钝角三角形7.(2014·凉山州)如图,河堤横断面迎水坡AB 的坡比是1∶3,堤高BC =10 m ,则坡面AB 的长度是( )A .15 mB .20 3 mC .20 mD .10 3 m第7题图 第8题图 第9题图8.如图,CD 是平面镜,光线从A 点射出,经CD 上点E 反射后照射到B 点,若入射角为α,AC ⊥CD ,BD ⊥CD ,垂足分别为C ,D ,且AC =3,BD =6,CD =11,则tan α的值为( )A 、113B 、311C 、911D 、1199.(2014·绵阳)如图,一艘海轮位于灯塔P 的北偏东30°方向,距离灯塔80海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45°方向上的B 处,这时,海轮所在的B 处与灯塔P 的距离为( )A .40 2 海里B .40 3 海里C .80海里D .40 6 海里10.如图,在两建筑物之间有一旗杆,高15米,从A 点经过旗杆顶点恰好看到矮建筑物的墙角C 点,且俯角α为60°,又从A 点测得D 点的俯角β为30°,若旗杆底点G 为BC 的中点,则矮建筑物的高CD 为( )A .20米B .10 3 米C .15 3 米D .5 6 米 二、填空题(每小题3分,共24分)11.(2014·锦州)计算:tan 45°-13(3-1)0=____.12.如图,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD =2,AC =3,则sinA 的值是____.13.如图,某山坡的坡面AB =200米,坡角∠BAC =30°,则该山坡的高BC 的长为____米.第12题图 第13题图 第14题图14.如图,在菱形ABCD 中,DE ⊥AB ,垂足为E ,DE =6 cm ,sinA =35,则菱形ABCD 的面积是____cm 2、15.将一副三角尺如图所示叠放在一起,则BEEC的值是____.16.如图,△ABC 的顶点A ,C 的坐标分别是(0,4),(3,0),且∠ACB =90°,∠B =30°,则顶点B 的坐标是_____________.第15题图 第16题图 第18题图17.△ABC 中,AB =4,BC =3,∠BAC =30°,则△ABC 的面积为. 18.(2014·宁波)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5 米,宽2、2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出____个这样的停车位.(2≈1、4)三、解答题(共66分) 19.(8分)计算:(1)(-2)2+|-3|+2sin 60°-12; (2)6tan 230°-3cos 30°-2sin 45°、20.(8分)(2014·重庆)如图,△ABC 中,AD ⊥BC ,垂足是D ,若BC =14,AD =12,tan ∠BAD =34,求sinC 的值.21.(8分)如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A,B,C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.22.(10分)(2014·乐山)如图,在梯形ABCD中,AD∥BC,∠ADC=90°,∠B=30°,CE⊥AB,垂足为点E,若AD=1,AB=23,求CE的长.23、(10分)如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0、01米;参考数据:sin62°≈0、88,cos62°≈0、47,tan50°≈1、20)24.(10分)(2014·泰州)图①,②分别是某型号跑步机的实物图与示意图,已知踏板CD 长为1、6 m,CD与地面DE的夹角∠CDE为12°,支架AC长为0、8 m,∠ACD为80°,求跑步机手柄的一端A的高度h、(精确到0、1 m;参考数据:sin12°=cos78°≈0、21,sin68°=cos22°≈0、93,tan68°≈2、48)25.(12分)如图,已知斜坡AB长602米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE、(1)若修建的斜坡BE的坡比为3∶1,求休闲平台DE的长是多少米?(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°,点B,C,A,G,H在同一个平面内,点C,A,G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?参考答案一、选择题(每小题3分,共30分)1.如图,在Rt △ABC 中,∠ACB =90°,BC =1,AB =2,则下列结论正确的是( D )A .sin A =32 B .tan A =12 C .cos B =32D .tan B =32.在△ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的对边,如果a 2+b 2=c 2,那么下列结论正确的是( A )A .c sin A =aB .b cos B =cC .a tan A =bD .c tan B =b 3.计算6tan45°-2cos60°的结果是( D )A .4 3B .4C .5 3D .5 4.(2014·巴中)在Rt △ABC 中,∠C =90°,sin A =513,则tan B 的值为( D )A 、1213B 、512C 、1312D 、1255.如图,在下列网格中,小正方形的边长均为1,点A ,B ,O 都在格点上,则∠A 的正弦值是( D )A 、3510B 、12C 、255D 、556.如果∠A ,∠B 均为锐角,且2sin A -1+(3tan B -3)2,那么△ABC 是( B )A .锐角三角形B .直角三角形C .等边三角形D .钝角三角形7.(2014·凉山州)如图,河堤横断面迎水坡AB 的坡比是1∶3,堤高BC =10 m ,则坡面AB 的长度是( C )A .15 mB .20 3 mC .20 mD .10 3 m第7题图 第8题图 第9题图8.如图,CD 是平面镜,光线从A 点射出,经CD 上点E 反射后照射到B 点,若入射角为α,AC ⊥CD ,BD ⊥CD ,垂足分别为C ,D ,且AC =3,BD =6,CD =11,则tan α的值为( D )A 、113B 、311C 、911D 、1199.(2014·绵阳)如图,一艘海轮位于灯塔P 的北偏东30°方向,距离灯塔80海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45°方向上的B 处,这时,海轮所在的B 处与灯塔P 的距离为( A )A .40 2 海里B .40 3 海里C .80海里D .40 6 海里10.如图,在两建筑物之间有一旗杆,高15米,从A 点经过旗杆顶点恰好看到矮建筑物的墙角C 点,且俯角α为60°,又从A 点测得D 点的俯角β为30°,若旗杆底点G 为BC 的中点,则矮建筑物的高CD 为( A )A .20米B .10 3 米C .15 3 米D .5 6 米 二、填空题(每小题3分,共24分)11.(2014·锦州)计算:tan 45°-13(3-1)0=__23__.12.如图,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD =2,AC =3,则sinA 的值是4. 13.如图,某山坡的坡面AB =200米,坡角∠BAC =30°,则该山坡的高BC 的长为__100__米.第12题图 第13题图 第14题图14.如图,在菱形ABCD 中,DE ⊥AB ,垂足为E ,DE =6 cm ,sinA =35,则菱形ABCD 的面积是__60__cm 2、15.将一副三角尺如图所示叠放在一起,则BE EC 的值是3.16.如图,△ABC 的顶点A ,C 的坐标分别是(0,4),(3,0),且∠ACB =90°,∠B =30°,则顶点B 的坐标是.第15题图 第16题图 第18题图17.△ABC 中,AB =4,BC =3,∠BAC =30°,则△ABC 的面积为. 18.(2014·宁波)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5 米,宽2、2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出__17__个这样的停车位.(2≈1、4)点拨:如图,BC =2、2×sin 45°≈1、54,CE =5×sin 45°≈3、5,BE =BC +CE ≈5、04,EF =2、2÷sin 45°≈3、14,(56-5、04)÷3、14+1≈16+1=17(个),故这个路段最多可以划出17个这样的停车位 三、解答题(共66分) 19.(8分)计算:(1)(-2)2+|-3|+2sin 60°-12; 解:4(2)6tan 230°-3cos 30°-2sin 45°、 解:12-220.(8分)(2014·重庆)如图,△ABC 中,AD ⊥BC ,垂足是D ,若BC =14,AD =12,tan ∠BAD =34,求sinC 的值.解:121321.(8分)如图,湖中的小岛上有一标志性建筑物,其底部为A ,某人在岸边的B 处测得A 在B 的北偏东30°的方向上,然后沿岸边直行4公里到达C 处,再次测得A 在C 的北偏西45°的方向上(其中A ,B ,C 在同一平面上).求这个标志性建筑物底部A 到岸边BC 的最短距离.解:过A 作AD ⊥BC 于点D ,则AD 的长度就是A 到岸边BC 的最短距离.在Rt △ACD 中,∠ACD =45°,设AD =x ,则CD =AD =x ,在Rt △ABD 中,∠ABD =60°,BD =xtan60°=33x ,又BC =4,即BD +CD =4,所以33x +x =4,解得x =6-23,则这个标志性建筑物底部A 到岸边BC 的最短距离为(6-23)公里22.(10分)(2014·乐山)如图,在梯形ABCD 中,AD ∥BC ,∠ADC =90°,∠B =30°,CE ⊥AB ,垂足为点E ,若AD =1,AB =23,求CE 的长.解:过点A 作AH ⊥BC 于点H ,则AD =HC =1,在△ABH 中,BH =AB ·cos 30°=3,∴BC =BH +BC =4,∵CE ⊥AB ,∴CE =BC ·sin 30°=223、(10分)如图,一堤坝的坡角∠ABC =62°,坡面长度AB =25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB =50°,则此时应将坝底向外拓宽多少米?(结果保留到0、01米;参考数据:sin 62°≈0、88,cos 62°≈0、47,tan 50°≈1、20)解:过A 点作AE ⊥CD 于点E ,在Rt △ABE 中,AE =AB ·sin 62°≈22,BE =AB ·cos 62°≈11、75,在Rt △ADE 中,DE =AE tan50°≈18、33,∴DB =DC -BE ≈6、58,故此时应将坝底向外拓宽大约6、58米24.(10分)(2014·泰州)图①,②分别是某型号跑步机的实物图与示意图,已知踏板CD 长为1、6 m ,CD 与地面DE 的夹角∠CDE 为12°,支架AC 长为0、8 m ,∠ACD 为80°,求跑步机手柄的一端A 的高度h 、(精确到0、1 m ;参考数据:sin 12°=cos 78°≈0、21,sin 68°=cos 22°≈0、93,tan 68°≈2、48)解:过C 点作FG ⊥AB 于点F ,交DE 于点G 、∵CD 与地面DE 的夹角∠CDE 为12°,∠ACD 为80°,∴∠ACF =90°+12°-80°=22°,∴∠CAF =68°,在Rt △ACF 中,CF =AC ·sin ∠CAF ≈0、744,在Rt △CDG 中,CG =CD ·sin ∠CDE ≈0、336,∴FG =FC +CG ≈1、1,故跑步机手柄的一端A 的高度约为1、1 m25.(12分)如图,已知斜坡AB 长602米,坡角(即∠BAC )为45°,BC ⊥AC ,现计划在斜坡中点D 处挖去部分斜坡,修建一个平行于水平线CA 的休闲平台DE 和一条新的斜坡BE 、(1)若修建的斜坡BE 的坡比为3∶1,求休闲平台DE 的长是多少米?(2)一座建筑物GH 距离A 点33米远(即AG =33米),小亮在D 点测得建筑物顶部H 的仰角(即∠HDM )为30°,点B ,C ,A ,G ,H 在同一个平面内,点C ,A ,G 在同一条直线上,且HG ⊥CG ,问建筑物GH 高为多少米?解:(1)∵FM ∥CG ,∴∠BDF =∠BAC =45°,∵斜坡AB 长602,D 是AB 的中点,∴BD =302,∴DF =BD ·cos ∠BDF =30,BF =DF =30,∵斜坡BE 的坡比为3∶1,∴BF EF =31,∴EF =103,∴DE =DF -EF =30-103,即休闲平台DE 的长是(30-103)米 (2)设GH =x 米,则MH =GH -GM =x -30,DM =AG +AP =33+30=63,在Rt △DMH 中,tan 30°=MH DM ,即x -3063=33,解得x =30+213,则建筑物GH 的高为(30+213)米。
华师大版九年级(上) 中考题单元试卷:第24章 图形的相似(15)

华师大版九年级(上)中考题单元试卷:第24章图形的相似(15)一、选择题(共11小题)1.如图,△ABC中,DE∥BC,DE=1,AD=2,DB=3,则BC的长是()A.B.C.D.2.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CE交AD 于E,点F是AB的中点,则S△AEF:S四边形BDEF为()A.3:4B.1:2C.2:3D.1:33.如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,CD=3cm,则AF的长为()A.5cm B.6cm C.7cm D.8cm4.如图,AB∥CD,=,则△AOB的周长与△DOC的周长比是()A.B.C.D.5.如图,在△ABC中,点D,E分别在边AB,AC上,且,则S△ADE:S四边形BCED的值为()A.1:B.1:2C.1:3D.1:46.如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,AD=1,BC=4,则△AOD 与△BOC的面积比等于()A.B.C.D.7.如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF;②△ABE∽△ACD;③BE+DC>DE;④BE2+DC2=DE2,其中正确的有()个.A.1B.2C.3D.48.如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S=4:25,则DE:EC=()△ABFA.2:5B.2:3C.3:5D.3:29.如图,边长为2的正方形ABCD中,P是CD的中点,连接AP并延长,交BC的延长线于点F,作△CPF的外接圆⊙O,连接BP并延长交⊙O于点E,连接EF,则EF的长为()A.B.C.D.10.如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2,则MF的长是()A.B.C.1D.11.如图,△ABC中,D、E两点分别在BC、AD上,且AD为∠BAC的角平分线.若∠ABE =∠C,AE:ED=2:1,则△BDE与△ABC的面积比为何?()A.1:6B.1:9C.2:13D.2:15二、填空题(共6小题)12.如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC=.13.△ABC中,D、E分别是边AB与AC的中点,BC=4,下面四个结论:①DE=2;②△ADE∽△ABC;③△ADE的面积与△ABC的面积之比为1:4;④△ADE的周长与△ABC的周长之比为1:4;其中正确的有.(只填序号)14.如图,在△ABC中,点D,点E分别是边AB,AC的中点,则△ADE和△ABC的周长之比等于.15.如图,在△ABC中,EF∥BC,=,S四边形BCFE=15,则S△ABC=.16.如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,O n和点E4,E5,…,E n.则O n E n=AC.(用含n的代数式表示)17.如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则的值为.三、解答题(共13小题)18.如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.(1)求证:△APB≌△APD;(2)已知DF:F A=1:2,设线段DP的长为x,线段PF的长为y.①求y与x的函数关系式;②当x=6时,求线段FG的长.19.如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点E.若AE=4,CE=8,DE=3,梯形ABCD的高是,面积是54.求证:AC⊥BD.20.如图,在等腰梯形ABCD中,DC∥AB,E是DC延长线上的点,连接AE,交BC于点F.(1)求证:△ABF∽△ECF;(2)如果AD=5cm,AB=8cm,CF=2cm,求CE的长.21.如图所示,AB是半圆O的直径,AB=8,以AB为一直角边的直角三角形ABC中,∠CAB=30°,AC与半圆交于点D,过点D作BC的垂线DE,垂足为E.(1)求DE的长;(2)过点C作AB的平行线l,l与BD的延长线交于点F,求的值.22.如图,在Rt△ABC中,∠B=90°,AC=60,AB=30.D是AC上的动点,过D作DF ⊥BC于F,过F作FE∥AC,交AB于E.设CD=x,DF=y.(1)求y与x的函数关系式;(2)当四边形AEFD为菱形时,求x的值;(3)当△DEF是直角三角形时,求x的值.23.如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.(1)求证:四边形BMNP是平行四边形;(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.24.阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图2).请回答:∠ACE的度数为,AC的长为.参考小腾思考问题的方法,解决问题:如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD 交于点E,AE=2,BE=2ED,求BC的长.25.如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM 交BD于点N,且ON=1.(1)求BD的长;(2)若△DCN的面积为2,求四边形ABNM的面积.26.如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.(1)求证:AP=AO;(2)求证:PE⊥AO;(3)当AE=AC,AB=10时,求线段BO的长度.27.如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.(1)求线段PQ的长;(2)问:点P在何处时,△PFD∽△BFP,并说明理由.28.如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:=.29.如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN 平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.(1)判断△BMN的形状,并证明你的结论;(2)判断△MFN与△BDC之间的关系,并说明理由.30.如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.(1)求证:△ABC∽△BCD;(2)求x的值;(3)求cos36°﹣cos72°的值.华师大版九年级(上)中考题单元试卷:第24章图形的相似(15)参考答案一、选择题(共11小题)1.C;2.D;3.B;4.D;5.C;6.D;7.C;8.B;9.D;10.D;11.D;二、填空题(共6小题)12.6;13.①②③;14.1:2;15.16;16.;17.;三、解答题(共13小题)18.;19.;20.;21.;22.;23.;24.75°;3;25.;26.;27.;28.;29.;30.;。
中考数学总复习 二十四 命题与证明精练精析2 华东师大版

图形的性质——命题与证明2一.选择题(共9小题)1.下列命题中,假命题是()A.对顶角相等B.三角形两边的和小于第三边C.菱形的四条边都相等D.多边形的外角和等于360°2.下列命题中,不正确的是()A.n边形的内角和等于(n﹣2)•180°B.两组对边分别相等的四边形是矩形C.垂直于弦的直径平分弦所对的两条弧D.直角三角形斜边上的中线等于斜边的一半3.下列命题中,错误的是()A.平行四边形的对角线互相平分B.菱形的对角线互相垂直平分C.矩形的对角线相等且互相垂直平分D.角平分线上的点到角两边的距离相等4.下列四个命题中,真命题是()A.对角线互相垂直平分的四边形是正方形B.对角线垂直相等的四边形是菱形C.对角线相等且互相平分的四边形是矩形D.四边都相等的四边形是正方形5.下列命题:①对角线相等且垂直的四边形是正方形;②平分弦的直径必垂直于弦;③相等的圆心角所对的弧一定相等;④买彩票中奖概率是,则买4张彩票一定一张会中奖;⑤真命题的逆命题一定是真命题,其中正确的命题个数是()A.0个B.1个C.2个D.3个6.说明命题“如果a,b,c是△ABC的三边,那么长为a﹣1,b﹣1,c﹣1的三条线段能构成三角形”是假命题的反例可以是()A.a=2,b=2,c=3 B.a=2,b=2,c=2 C.a=3,b=3,c=4 D.a=3,b=4,c=57.已知下列命题:①若a>0,b>0,则a+b>0;②若a=b,则a2=b2;③角的平分线上的点到角的两边的距离相等;④矩形的对角线相等.其中原命题与逆命题均为真命题的个数是()A.1个B.2个C.3个D.4个8下列命题是真命题的是()①若ac>bc,则a>b;②抛物线y=x2﹣2x﹣3与坐标轴有2个不同交点;③对角线相等的菱形是正方形;④过三点可以作一个圆.A.①②③B.②③ C.③D.③④9.已知下列命题:①若a>0,b>0,则ab>0;②直径是弦;③若,则a>0;④线段垂直平分线上的点到这条线段两个端点的距离相等.其中原命题与逆命题均为真命题的个数是()A.4 B.3 C.2 D.1二.填空题(共7小题)10.已知三条不同的直线a、b、c在同一平面内,下列四条命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.其中真命题的是_________ .(填写所有真命题的序号)11.写出定理“直角三角形斜边上的中线等于斜边的一半”的逆命题:_________ .12.把命题“如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2”的逆命题改写成“如果…,那么…”的形式:_________ .13.下列命题中,其逆命题成立的是_________ .(只填写序号)①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.14.下列命题①不相交的直线是平行线;②同位角相等;③矩形的对角线相等且互相平分;④平行四边形既是中心对称图形又是轴对称图形;⑤同圆中同弦所对的圆周角相等.其中错误的序号是_________ .15.在命题“同位角相等,两直线平行”中,题设是:_________ .16.已知命题“如果一个平行四边形的两条对角线互相垂直,那么这个平行四边形是菱形”,写出它的逆命题:_________ .三.解答题(共5小题)17.如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.(1)你构造的是哪几个命题?(2)你构造的命题是真命题还是假命题?请加以证明.18.如图,在△ADF与△CBE中,点A,E,F,C在同一直线上,现给出下列四个论断:①AE=CF;②AD=CB;③∠B=∠D;④AD∥BC.请你选择其中三个作为条件,余下的一个作为结论,构成一个命题.请问:(1)在所有构成的命题中有假命题吗?若有,请写出它的条件和结论(用序号表示);若没有,请说明理由;(2)在所有构成的真命题中,任意选择一个加以证明.19.把命题改写成”如果…那么…”的形式.(1)对顶角相等.(2)两直线平行,同位角相等.(3)等角的余角相等.20.对于同一平面的三条直线,给出下列5个论断,①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c.以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题.解:已知:_________ ;结论_________ ;理由:_________ .21.将下列命题改写成“如果…,那么…”的形式.(1)能被2整除的数也能被4整除;(2)相等的两个角是对顶角;(3)若xy=0,则x=0;(4)角平分线上的点到这个角两边的距离相等.图形的性质——命题与证明2参考答案与试题解析一.选择题(共9小题)1.下列命题中,假命题是()A.对顶角相等 B.三角形两边的和小于第三边C.菱形的四条边都相等 D.多边形的外角和等于360°考点:命题与定理.分析:分别利用对顶角的性质、三角形的三边关系、菱形的性质及多边形的外角和对四个选项分别判断后即可确定正确的选项.解答:解:A、对顶角相等,正确,是真命题;B、三角形的两边之和大于第三边,错误,是假命题;C、菱形的四条边都相等,正确,是真命题;D、多边形的外角和为360°,正确,为真命题,故选:B.点评:本题考查了命题与定理的知识,解题的关键是熟知对顶角的性质、三角形的三边关系、菱形的性质及多边形的外角和定理,属于基础知识,难度较小.2.下列命题中,不正确的是()A.n边形的内角和等于(n﹣2)•180°B.两组对边分别相等的四边形是矩形C.垂直于弦的直径平分弦所对的两条弧D.直角三角形斜边上的中线等于斜边的一半考点:命题与定理.分析:利用多边形的内角和定理、矩形的判定、垂径定理及直角三角形的性质逐一判断后即可确定正确的选项.解答:解:A、n边形的内角和等于(n﹣2)•180°,故A选项正确;B、两组对边分别相等的四边形是平行四边形,故B选项错误;C、垂直于弦的直径平分弦所对的两条弧,故C选项正确;D、直角三角形斜边上的中线等于斜边的一半,故D选项正确,故选B.点评:本题考查了命题与定理的知识,解题的关键是了解多边形的内角和定理、矩形的判定、垂径定理及直角三角形的性质,难度不大.3.下列命题中,错误的是()A.平行四边形的对角线互相平分B.菱形的对角线互相垂直平分C.矩形的对角线相等且互相垂直平分D.角平分线上的点到角两边的距离相等考点:命题与定理.分析:根据平行四边形的性质对A进行判断;根据菱形的性质对B进行判断;根据矩形的性质对C进行判断;根据角平分线的性质对D进行判断.解答:解:A、平行四边形的对角线互相平分,所以A选项的说法正确;B、菱形的对角线互相垂直平分,所以B选项的说法正确;C、矩形的对角线相等且互相平分,所以C选项的说法错误;D、角平分线上的点到角两边的距离相等,所以D选项的说法正确.故选:C.点评:本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.4.下列四个命题中,真命题是()A.对角线互相垂直平分的四边形是正方形B.对角线垂直相等的四边形是菱形C.对角线相等且互相平分的四边形是矩形D.四边都相等的四边形是正方形考点:命题与定理.分析:根据菱形、矩形、等腰梯形的判定与性质分别判断得出即可.解答:解:A、根据菱形的判定方法,对角线互相垂直平分的四边形是菱形,故此选项错误;B、两条对角线相等且互相垂直的四边形有可能是等腰梯形,故此选项错误;C、根据对角线相等且互相平分的四边形是矩形,故此选项正确;D、根据四边都相等的四边形是菱形,故此选项错误.故选:C.点评:此题主要考查了菱形、矩形的判定等知识,熟练掌握其性质是解题关键.5.下列命题:①对角线相等且垂直的四边形是正方形;②平分弦的直径必垂直于弦;③相等的圆心角所对的弧一定相等;④买彩票中奖概率是,则买4张彩票一定一张会中奖;⑤真命题的逆命题一定是真命题,其中正确的命题个数是()A.0个B.1个C.2个D.3个考点:命题与定理.专题:常规题型.分析:根据正方形的判定方法对①进行判断;根据垂径定理对②进行判断;根据圆心角、弦和弧的关系对③进行判断;根据概率的意义对④进行判断;利用反例对⑤进行判断.解答:解:对角线互相平分、相等且垂直的四边形是正方形,所以①错误;平分弦(非直径)的直径必垂直于弦,所以②错误;在同圆或等圆中,相等的圆心角所对的弧一定相等,所以③错误;买彩票中奖概率是,则中奖的机会为,但不是买4张彩票一定一张会中奖,所以④错误;真命题的逆命题不一定是真命题,如对顶角相等,所以⑤错误.故选A.点评:本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.6.说明命题“如果a,b,c是△ABC的三边,那么长为a﹣1,b﹣1,c﹣1的三条线段能构成三角形”是假命题的反例可以是()A.a=2,b=2,c=3 B.a=2,b=2,c=2 C.a=3,b=3,c=4 D. a=3,b=4,c=5考点:命题与定理;三角形三边关系.分析:举例能使得两边之和小于或等于第三边即可得到反例.解答:解:当a=2,b=2,c=3时,a﹣1=1,b﹣1=1,c﹣1=2,此时:1+1=2,所以不能构成三角形,故选A.点评:本题考查了命题与定理及三角形的三边关系,举反例是判定命题为假命题的一个方法.7.已知下列命题:①若a>0,b>0,则a+b>0;②若a=b,则a2=b2;③角的平分线上的点到角的两边的距离相等;④矩形的对角线相等.其中原命题与逆命题均为真命题的个数是()A.1个B.2个C.3个D.4个考点:命题与定理.分析:分别利用不等式的性质以及角平分线的性质和矩形的判定和性质分析得出即可.解答:解:①若a>0,b>0,则a+b>0,原命题正确,逆命题:如果a+b>0,那么a>0,b>0不一定正确,故不合题意;②若a=b,则a2=b2,原命题正确,逆命题:如果a2=b2,那么a=b不一定正确,故不合题意;③角的平分线上的点到角的两边的距离相等,原命题正确,逆命题也正确,符合题意;④矩形的对角线相等,原命题正确,逆命题不正确,故不合题意.其中原命题与逆命题均为真命题的个数有1个.故选:A.点评:此题主要考查了命题与定理,熟练掌握相关定理与判定方法是解题关键.8.下列命题是真命题的是()①若ac>bc,则a>b;②抛物线y=x2﹣2x﹣3与坐标轴有2个不同交点;③对角线相等的菱形是正方形;④过三点可以作一个圆.A.①②③B.②③C.③D.③④考点:命题与定理.分析:根据不等式的性质对①进行判断;根据抛物线与x轴的交点问题对②进行判断;根据正方形的判定方法对③进行判断;根据确定圆的条件对④进行判断.解答:解:若ac>bc,c>0,则a>b,所以①错误;由于△=4﹣4×(﹣3)>0,则抛物线y=x2﹣2x﹣3与坐标轴有2个不同交点,所以②正确;对角线相等的菱形是正方形,所以③正确;过不共线的三点可以作一个圆,所以④错误.故选B.点评:本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.也考查了逆命题.9.已知下列命题:①若a>0,b>0,则ab>0;②直径是弦;③若,则a>0;④线段垂直平分线上的点到这条线段两个端点的距离相等.其中原命题与逆命题均为真命题的个数是()A. 4 B.3 C.2 D.1考点:命题与定理.分析:利用等式的性质、弦的定义、绝对值的意义及线段垂直平分线的性质分别判断后即可确定正确的选项.解答:解:①若a>0,b>0,则ab>0中原命题正确,逆命题错误;②直径是弦,原命题正确,逆命题错误;③若,则a>0,原命题与逆命题均错误;④线段垂直平分线上的点到这条线段两个端点的距离相等,原命题与逆命题均正确.故选D.点评:本题考查了命题与定理的知识,解题的关键是能够写出该命题的逆命题并判断真假.二.填空题(共7小题)10.已知三条不同的直线a、b、c在同一平面内,下列四条命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.其中真命题的是①②④.(填写所有真命题的序号)考点:命题与定理;平行线的判定与性质.专题:推理填空题.分析:分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.解答:解:①如果a∥b,a⊥c,那么b⊥c是真命题,故①正确;②如果b∥a,c∥a,那么b∥c是真命题,故②正确;③如果b⊥a,c⊥a,那么b⊥c是假命题,故③错误;④如果b⊥a,c⊥a,那么b∥c是真命题,故④正确.故答案为:①②④.点评:本题主要考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题,难度适中.11.写出定理“直角三角形斜边上的中线等于斜边的一半”的逆命题:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.考点:命题与定理.分析:把一个命题的条件和结论互换就得到它的逆命题.命题“直角三角形斜边上的中线等于斜边的一半”的条件是直角三角形,结论是斜边上的中线等于斜边的一半,故其逆命题:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.解答:解:定理“直角三角形斜边上的中线等于斜边的一半”的逆命题:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.点评:本题考查了互逆命题的知识及命题的真假判断,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.12.把命题“如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2”的逆命题改写成“如果…,那么…”的形式:如果三角形三边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形.考点:命题与定理;勾股定理.分析:命题都能写成“如果…,那么…”的形式,如果后面是题设,那么后面是结论,题设和结论互换后就是原命题的逆命题.解答:解:逆命题为:三角形三边长a,b,c,满足a2+b2=c2,这个三角形是直角三角形,逆命题改写成“如果…,那么…”的形式:如果三角形三边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形,故答案为:如果三角形三边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形.点评:本题考查把命题写成“如果…,那么…”的形式以及逆命题的概念,难度适中.13.下列命题中,其逆命题成立的是①④.(只填写序号)①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.考点:命题与定理;实数的运算;角的概念;平行线的判定与性质;勾股定理;勾股定理的逆定理.专题:推理填空题.分析:把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.解答:解:①两直线平行,同旁内角互补,正确;②如果两个角相等,那么它们是直角,错误;③如果两个实数的平方相等,那么这两个实数相等,错误;④如果一个三角形是直角三角形,c为斜边,则a2+b2=c2,正确.故答案为①④.点评:本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题,难度适中.14.下列命题①不相交的直线是平行线;②同位角相等;③矩形的对角线相等且互相平分;④平行四边形既是中心对称图形又是轴对称图形;⑤同圆中同弦所对的圆周角相等.其中错误的序号是①②④⑤.考点:命题与定理;同位角、内错角、同旁内角;平行线;平行四边形的性质;矩形的性质;圆周角定理;轴对称图形;中心对称图形.专题:应用题.分析:根据平行的性质,矩形的性质,平行四边形的性质,圆周角的性质来判断所给选项是否正确即可.解答:解:①在同一平面内,不相交的直线是平行线,故本选项错误,②两直线平行,同位角相等,故本选项错误,③矩形的对角线相等且互相平分,故本选项正确,④平行四边形是中心对称图形不是轴对称图形,故本选项错误,⑤同弦对应的圆周角中,在弦的同侧时,两圆周角相等,在两侧时两圆周角互补,故本选项错误,故答案为①②④⑤.点评:本题主要考查了综合利用相关性质和判定,难度适中.15.在命题“同位角相等,两直线平行”中,题设是:同位角相等.考点:命题与定理.专题:应用题.分析:由命题的题设的定义进行解答.命题由题设和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项.解答:解:命题中,已知的事项是“同位角相等”,所以“同位角相等”是命题的题设部分.故答案为同位角相等.点评:本题主要考查命题的基本概念与组成,比较简单.注意命题写成“如果…,那么…”的形式,这时,“如果”后面接的部分是题设,“那么”后面解的部分是结论.16.已知命题“如果一个平行四边形的两条对角线互相垂直,那么这个平行四边形是菱形”,写出它的逆命题:如果一个平行四边形是菱形,那么这个平行四边形的两条对角线互相垂直.考点:命题与定理.专题:压轴题.分析:把一个命题的条件和结论互换就得到它的逆命题.解答:解:命题“如果一个平行四边形的两条对角线互相垂直,那么这个平行四边形是菱形”的逆命题是“如果一个平行四边形是菱形,那么这个平行四边形的两条对角线互相垂直”.点评:本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.三.解答题(共5小题)17.如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.(1)你构造的是哪几个命题?(2)你构造的命题是真命题还是假命题?请加以证明.考点:命题与定理;平行线的判定与性质.专题:常规题型.分析:(1)分别以其中2句话为条件,第三句话为结论可写出3个命题;(2)根据平行线的判定与性质对3个命题分别进行证明,判断它们的真假.解答:解:(1)由①②得到③;由①③得到②;由②③得到①;(2)∵AB∥CD,∴∠B=∠CDF,∵∠B=∠C,∴∠C=∠CDF,∴CE∥BF,∴∠E=∠F,所以由①②得到③为真命题;∵AB∥CD,∴∠B=∠CDF,∵∠E=∠F,∴CE∥BF,∴∠C=∠CDF,∴∠B=∠C,所以由①③得到②为真命题;∵∠E=∠F,∴CE∥BF,∴∠C=∠CDF,∵∠B=∠C,∴∠B=∠CDF,∴AB∥CD,所以由②③得到①为真命题.点评:本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.18.如图,在△ADF与△CBE中,点A,E,F,C在同一直线上,现给出下列四个论断:①AE=CF;②AD=CB;③∠B=∠D;④AD∥BC.请你选择其中三个作为条件,余下的一个作为结论,构成一个命题.请问:(1)在所有构成的命题中有假命题吗?若有,请写出它的条件和结论(用序号表示);若没有,请说明理由;(2)在所有构成的真命题中,任意选择一个加以证明.考点:命题与定理.专题:证明题;开放型.分析:(1)结合题意和图形,可知构成的命题中有假命题;(2)本题答案不唯一,可以用条件①③④作为已知;②作为结论,构造命题,再结合图形进行证明.解答:解:(1)假命题为:条件①②③;结论④.(2)(答案不唯一)已知条件①③④;结论②已知AE=CF,∠B=∠D,AD∥BC.求证:AD=CB证明:∵AE=CF,∴AE+EF=CF+EF.∴AF=EC.∵AD∥BC,∴∠A=∠C.又∵∠B=∠D,∴△ADF≌△EBC(AAS).∴AD=CB.点评:主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.19.把命题改写成”如果…那么…”的形式.(1)对顶角相等.(2)两直线平行,同位角相等.(3)等角的余角相等.考点:命题与定理.分析:找出原命题的条件和结论即可得出答案.解答:解:(1)如果两个角是对顶角,那么这两个角相等;(2)如果两直线平行,那么同位角相等;(3)如果两个角同为等角的余角,那么这两个角相等.点评:本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单.20.对于同一平面的三条直线,给出下列5个论断,①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c.以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题.解:已知:①②;结论④;理由:平行于同一条直线的两直线平行.考点:命题与定理;垂线;平行线的判定与性质.分析:利用平行线的判定方法可由①②得到④组成一个真命题.解答:解:若a∥b,b∥c,则a∥c.理由为平行于同一条直线的两直线平行.故答案为①②,④,平行于同一条直线的两直线平行.点评:本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式;有些命题的正确性是用推理证实的,这样的真命题叫做定理.21.将下列命题改写成“如果…,那么…”的形式.(1)能被2整除的数也能被4整除;(2)相等的两个角是对顶角;(3)若xy=0,则x=0;(4)角平分线上的点到这个角两边的距离相等.考点:命题与定理.分析:把命题的题设写在如果的后面,把命题的结论部分写在那么的后面即可.解答:解:(1)如果一个数能被2整除,那么这个数也能被4整除;(2)如果两个角相等,那么这两个角是对顶角;(3)如果xy=0,那么x=0;(4)如果一个点在角平分线上,那么它到角两边的距离相等..点评:本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.。
华师大版数学九年级上册课件:24章小结与复习题(1)

一、四个定义式
二、三个角的Biblioteka 角函数值三、二个性质1、直角三角形的性质 性质1:两个锐角互余; 性质2:两直角边的平方和等于斜边的平方; 性质3:斜边上的中线等于斜边的一半; 性质4:30°所对的直角边等于斜边的一半;
四、一个方法:解直角三角形的方 法
• 解直角三角形,只有两种情况: • 一是已知两条边; • 二是已知一条边和一个锐角;
A
D E
B
C
A
D E
B
C
A
B
D
C
例3、如图,为了测量某建筑物MN的高度,在平地上 A处测得建筑物顶端M的仰角为30°,向N点方向前进 16m到达B处,在B处测得建筑物顶端M的仰角为45°, 则建筑物MN的高度等于( )
M
A B
N
四个定义式
小结
三个角的函数值
二个性质
一类方法
例1、(2016•绵阳)如图,△ABC中 AB=AC=4,∠C=72°,D是AB中点,点E在AC 上,DE⊥AB,则cosA的值为( )
解:∵△ABC中,AB=AC=4, ∠C=72°, ∴∠ABC=∠C=72°,∠A=36°, ∵D是AB中点,DE⊥AB, ∴AE=BE, ∴∠ABE=∠A=36°, ∴∠EBC=∠ABC﹣∠ABE=36°, ∠BEC=180°﹣∠EBC﹣∠C=72°, ∴∠BEC=∠C=72°, ∴BE=BC, ∴AE=BE=BC. 设AE=x,则BE=BC=x,EC=4﹣x.
(华师大版)初中数学九年级上册 第24章综合测试试卷03及答案

第24章综合测试一、选择题(共10小题)1.如图,Rt ACB △中,90ACB Ð=°,ABC Ð的平分线BE 和BAC Ð的外角平分线AD 相交于点P ,分别交AC 和BC 的延长线于E ,D .过P 作PF AD ⊥交AC 的延长线于点H ,交BC 的延长线于点F ,连接AF 交DH 于点G .则下列结论:①45APB Ð=°;②PF PA =;③BD AH AB -=;④DG AP GH =+.其中正确的是( )A .①②③B .①②④C .②③④D .①②③④2.下列说法正确的有( )①如果A B C Ð+Ð=Ð,那么ABC △是直角三角形;②如果::1:2:3A B C ÐÐÐ=,则三角形是直角三角形;③如果三角形的三边长分别为4、4、6,那么这个三角形不是直角三角形;④有一个角是直角的三角形是直角三角形.A .1个B .2个C .3个D .4个3.下列说法中,正确的是( )A .直角三角形中,已知两边长为3和4,则第三边长为5B .三角形是直角三角形,三角形的三边为a ,b ,c 则满足222a b c -=C .以三个连续自然数为三边长不可能构成直角三角形D .ABC △中,若::1:5:6A B C ÐÐÐ=,则ABC △是直角三角形4.如图,BD 平分ABC Ð,CD BD ⊥,D 为垂足,55C Ð=°,则ABC Ð的度数是( )A .35°B .55°C .60°D .70°5.若一个三角形的三条高线交点恰好是此三角形的一个顶点,则此三角形一定是( )A .等腰三角形B .等边三角形C .等腰直角三角形D .直角三角形6.如图,在Rt ABC △中,90ACB Ð=°,CD AB ⊥于点D ,如果3AC =,6AB =,那么AD 的值为( )A .32B .92C D .7.如图,ABC △中,点D 在线段BC 上,且BAD C Ð=Ð,则下列结论一定正确的是( )A .2AB AC BD=×B .AB AD BD BC ×=×C .2AB BC BD=×D .AB AD BD CD ×=×8.Rt ABC △中,90C Ð=°,3cos 5A =, 6 cm AC =,那么BC 等于( )A .8 cmB .24 cm 5C .18 cm 5D .6 cm 59.如果A Ð为锐角,1sin 4A =,那么( )A .030A °Ð°<<B .3045A °Ð°<<C .4560A °Ð°<<D .6090A °Ð°<<10.Rt ABC △中,90C Ð=°,已知3cos 5A =,那么tan A 等于( )A .43B .34C .45D .54二、填空题(共8小题)11.在Rt ABC △中,锐角35A Ð=°,则另一个锐角B Ð=________.12.直角三角形中,两锐角平分线相交所成的角的度数是________.13.如图ABC △中,:1:2A B ÐÐ=,DE AB ⊥于E ,且75FCD Ð=°,则D Ð=________.14.Rt ABC △中,90C Ð=°,2B A Ð=Ð, 3 cm BC =,AB =________cm .15.如图,在Rt ABC △中,90C Ð=°,CD AB ⊥,垂足为D ,8AD =,2DB =,则CD 的长为________.16.如图,若CD 是Rt ABC △斜边上的高,3AD =,4CD =,则BC =________.17.如图,在84´的矩形网格中,每格小正方形的边长都是1,若ABC △的三个顶点在图中相应的格点上,则tan ACB Ð的值为________.18.已知A Ð为锐角,且1cos 2A £,那么A Ð的范围是________.三、解答题(共8小题)19.如图,在Rt ABC △中,90B Ð=°,60 cm AC =,60A Ð=°,点D 从点C 出发沿CA 方向以4 cm 秒的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以2 cm 秒的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D 、E 运动的时间是t 秒(015t £<).过点D 作DF BC ⊥于点F ,连接DE ,EF .(1)求证:AE DF =;(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值,如果不能,说明理由;(3)当t 为何值时,DEF △为直角三角形?请说明理由.20.如图,在ABC △中,CE ,BF 是两条高,若70A Ð=°,30BCE Ð=°,求EBF Ð与FBC Ð的度数.21.如图,在ACB △中,90ACB Ð=°,CD AB ⊥于D .(1)求证:ACD B Ð=Ð;(2)若AF 平分CAB Ð分别交CD 、BC 于E 、F ,求证:CEF CFE Ð=Ð.22.如图所示,在ABC △中,已知AD BC ⊥,64B Ð=°,56C Ð=°,(1)求BAD Ð和DAC Ð的度数;(2)若DE 平分ADB Ð,求AED Ð的度数.23.如图,定义:在直角三角形ABC 中,锐角a 的邻边与对边的比叫做角a 的余切,记作tan c a ,即tan AC c BCa a a ==角的邻边角的对边,根据上述角的余切定义,解下列问题:(1)tan30c °=________;(2)如图,已知3tan 4A =,其中A Ð为锐角,试求tan c A 的值.24.下列关系式是否成立(090a °<<),请说明理由.(1)sin cos 1a a +£;(2)sin 22sin a a =.25.小明在某次作业中得到如下结果:2222sin 7sin 830.120.990.9945°+°»+=,2222sin 22sin 680.370.93 1.0018°+°»+=,2222sin 29sin 610.480.870.9873°+°»+=,2222sin 37sin 53 1.0000°+°»+=,2222sin 45sin 451°+°=+=.据此,小明猜想:对于任意锐角a ,均有()22sin sin 901a a +°-=.(Ⅰ)当30a =°时,验证()22sin sin 901a a +°-=是否成立;(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.26.计算:224sin 60tan 458cos 30°+°-°.第24章综合测试答案解析一、1.【答案】A【解析】解:①ABC Ð∵的角平分线BE 和BAC Ð的外角平分线,12ABP ABC Ð=Ð∴,()11904522CAP ABC ABC Ð=°+Ð=°+Ð,在ABP △中,18011 180******** 18045902245APB BAP ABPABC ABC ABC ABC ABC ABC Ð=°-Ð-Ðæö=°-°+Ð+°-Ð-Ðç÷èø=°-°-Ð-°+Ð-Ð=°,故本小题正确;②45PF AD APB Ð=°∵⊥,(已证),45APB FPB Ð=Ð=°∴,PB ∵为ABC Ð的角平分线,ABP FBP Ð=Ð∴,在ABP △和FBP △中,APB FPB PB PBABP FBP Ð=Ðìï=íïÐ=Ðî,()ABP FBP ASA ∴△≌△,AB BF AP PF ==∴,;故②正确;③90ACB PF AD Ð=°∵,⊥,9090FDP HAP AHP HAP Ð+Ð=°Ð+Ð=°∴,,AHP FDP Ð=Ð∴,PF AD ∵⊥,90APH FPD Ð=Ð=°∴,在AHP △与FDP △中,90AHP FDP APH FPD AP PF Ð=ìïÐ=Ð=°íï=î,()AHP FDP AAS ∴△≌△,DF AH =∴,BD DF BF =+∵,BD AH AB =+∴,BD AH AB -=∴,故③小题正确;④AP PF PF AD =∵,⊥,45PAF Ð=°∴,45ADG DAG Ð=Ð=°∴,DG AG =∴,45PAF AG DH Ð=°∵,⊥,ADG ∴△与FGH △都是等腰直角三角形,DG AG GH GF ==∴,,DG GH AF =+∴,AF AP ∵>,DG AP GH =+∴不成立,故本小题错误,综上所述①②③正确.故选:A .【考点】直角三角形的性质,全等三角形的判定,以及等腰直角三角形的判定与性质2.【答案】D【解析】解:①A B C Ð+Ð=Ð∵,且180A B C Ð+Ð+Ð=°,得90C Ð=°,ABC ∴△是直角三角形,故①正确;②设A x Ð=,2B x Ð=,3C x Ð=,则A B C Ð+Ð=Ð,由①知,该三角形是直角三角形,故②正确;③2416=,2636=,显然22446+¹,不符合勾股定理的逆定理,该三角形不是直角三角形,故③正确;④符合直角三角形的判定方法,故④正确;所以4个结论都正确,故选D .【考点】直角三角形的判定方法3.【答案】D【解析】解:A 、应为“直角三角形中,已知两直角边的边长为3和4,则斜边的边长为5”,故错误;B 、应为“三角形是直角三角形,三角形的直角边分别为a ,b ,斜边为c 则满足222a b c +=”,故错误;C 、比如:边长分别为3,4,5,有22234255+==,能构成直角三角形,故错误;D 、根据三角形内角和定理可求出三个角分别为15°,75°,90°,因而是直角三角形,故正确.故选:D .【考点】直角三角形的性质和判定4.【答案】D【解析】解:55CD BD C Ð=°∵⊥,,905535CBD Ð=°-°=°∴,BD ∵平分ABC Ð,223570ABC CBD Ð=Ð=´°=°∴.故选:D .【考点】直角三角形两锐角互余的性质,角平分线的定义5.【答案】D【解析】解:A 、等腰三角形,三条高线交点在三角形内或外或某一顶点处,故A 错误;B 、等边三角形,三条高线交点在三角形内,故B 错误;C 、因为已知无法确定其两腰相等,而只要是直角三角形就行了,不一定非得是等腰直角三角形,故C 错误;D 、因为直角三角形的直角所在的顶点正好是三条高线的交点,所以可以得出这个三角形是直角三角形,故D 正确.故选:D .【考点】直角三角形的性质6.【答案】A【解析】解:如图,∵在Rt ABC △中,90ACB Ð=°,CD AB ⊥,2AC AD AB =×∴,又36AC AB ==∵,,236AD =∴,则32AD =.故选:A .【考点】射影定理7.【答案】C【解析】解:BAD C Ð=Ð∵,而ABD CBA Ð=Ð,BAD BCA ∴△∽△,::AB BC BD AB =∴,2AB BC BD =×∴.故选:C .【考点】射影定理8.【答案】A【解析】解:∵在Rt ABC △中,90C Ð=°,3cos 5AC A AB ==, 6 cm AC =,10 cm AB =∴,8 cm BC ==∴.故选:A .【考点】锐角三角函数的定义9.【答案】A 【解析】解:111sin 300242°=∵,<,030A °Ð°∴<<.故选:A .10.【答案】A 【解析】解:3cos 5A =∵知,设3b x =,则5c x =,根据222a b c +=得4a x =.44tan 33a x Ab x ===∴.故选:A .二、11.【答案】55°【解析】解:∵在Rt ABC △中,锐角35A Ð=°,∴另一个锐角903555B Ð=°-°=°,故答案为:55°.【考点】直角三角形的性质12.【答案】45°或135°【解析】解:如图,90ABC BAC Ð+Ð=°,AD ∵、BE 分别是BAC Ð和ABC Ð的角平分线,()1452OAB OBA ABC BAC Ð+Ð=Ð+Ð=°∴,45AOE OAB OBA Ð=Ð+Ð=°∴,135AOB Ð=°∴∴两锐角的平分线的夹角是45°或135°,故答案为:45°或135°.【考点】直角三角形两锐角互余的性质,角平分线的定义13.【答案】40°【解析】解:75FCD Ð=°∵,75A B Ð+Ð=°∴,:1:2A B ÐÐ=∵,175253A Ð=´°=°∴,DE AB ∵⊥于E ,90902565AFE A Ð=°-Ð=°-°=°∴,65CFD AFE Ð=Ð=°∴,75FCD Ð=°∵,180180657540D CFD FCD Ð=°-Ð-Ð=°-°-°=°∴.故答案为:40°.【考点】直角三角形的性质,垂直定义,三角形内角和定理,三角形外角性质的应用14.【答案】6【解析】解:如图:Rt ABC ∵△中,90C Ð=°,2B AÐ=Ð90A B Ð+Ð=°∴3060A B Ð=°Ð=°∴,12BC AB =∴,3 cm BC =∵,23 6 cm AB =´=∴.故答案为:6.15.【答案】4【解析】解:∵在Rt ABC △中,90C Ð=°,CD AB ⊥,垂足为D ,8AD =,2DB =,282CD AD BD =×=´∴,则4CD =.故答案是:4.【考点】射影定理16.【答案】203【解析】解:∵若CD 是Rt ABC △斜边上的高,3AD =,4CD =2CD AD BD =´∴,即243BD =´解得:163BD =在Rt BCD △中,222BC CD BD =+∵,203BC ===∴.故答案为:203.【考点】三角形的性质及对勾股定理的应用17.【答案】13【解析】解:由图形知:21tan 63ACB Ð==,故答案为:13.【考点】锐角三角函数的定义18.【答案】6090A °£Ð°<【解析】解:1cos602°=∵,余弦函数值随角增大而减小,∴当1cos 2A £时,60A г°.又A Ð∵是锐角,6090A °£Ð°∴<.故答案为:6090A °£Ð°<.【考点】锐角三角函数的增减性三、19.【答案】(1)证明:∵直角ABC △中,9030C A Ð=°-Ð=°.42CD t AE t ==∵,,又∵在直角CDF △中,30C Ð=°,122DF CD t ==∴,DF AE =∴;解:(2)DF AB DF AE =∵∥,,∴四边形AEFD 是平行四边形,当AD AE =时,四边形AEFD 是菱形,即6042t t -=,解得:10t =,即当10t =时,AEFD Y 是菱形;(3)当152t =时DEF △是直角三角形(90EDF Ð=°);当12t =时,DEF △是直角三角形(90DEF Ð=°).理由如下:当90EDF Ð=°时,DE BC ∥.2AD AE=∴4CD t =∵,2DF t AE ==∴,4AD t =∴,4460t t +=∴,152t =∴时,90EDF Ð=°.当90DEF Ð=°时,DE EF ⊥,∵四边形AEFD 是平行四边形,AD EF ∴∥,DE AD ∴⊥,ADE ∴△是直角三角形,90ADE Ð=°,60A Ð=°∵,30DEA Ð=°∴,12AD AE =∴,604AD AC CD t =-=-,122AE DF CD t ===,604t t -=∴,解得12t =.综上所述,当152t =时DEF △是直角三角形(90EDF Ð=°);当12t =时,DEF △是直角三角形(90DEF Ð=°).【考点】直角三角形的性质,菱形的判定与性质20.【答案】解:在Rt ABF △中,70A Ð=°,CE ,BF 是两条高,2020EBF ECA Ð=°Ð=°∴,,又30BCE Ð=°∵,50ACB Ð=°∴,∴在Rt BCF △中40FBC Ð=°.【考点】直角三角形的性质,三角形内角和定理21.【答案】证明:(1)90ACB Ð=°∵,CD AB ⊥于D ,9090ACD BCD B BCD Ð+Ð=°Ð+Ð=°∴,,ACD B Ð=Ð∴;(2)在Rt AFC △中,90CFA CAF Ð=°-Ð,同理在Rt AED △中,90AED DAE Ð=°-Ð.又AF ∵平分CAB Ð,AED CFE Ð=Ð∴,又CEF AED Ð=Ð∵,CEF CFE Ð=Ð∴.【考点】直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质22.【答案】解:(1)AD BC ∵⊥,①∴在Rt BAD △中,90BAD B Ð+Ð=°,又64B Ð=°∵,26BAD Ð=°∴;②∴在Rt BAD △中,90DAC C Ð+Ð=°,又56C Ð=°∵,34DAC Ð=°∴;(2)AD BC ∵⊥,DE 平分ADB Ð,45BDE Ð=°∴;在BED △中,64B Ð=°,109B BDE Ð+Ð=°∴;AED B BDE Ð=Ð+Ð∵,109AED Ð=°∴.【考点】直角三角形的两个锐角互余的性质,角平分线的定义以及外角定理23.【答案】解:(1)Rt ABC ∵△中,30a =°,12BC AB =∴,AC AB ==∴,tan 30AC c BC °==∴.;(2)3tan 4A =∵,∴设3BC x =,4AC x =,44tan 33AC x c A BC x ===∴.【考点】锐角三角函数的定义及直角三角形的性质24.【答案】解:(1)该不等式不成立,理由如下:如图,在ABC △中,90B Ð=°,C a Ð=.则sin cos 1AB BC AC BC AC AC ACa a ++=+=,故sin cos 1a a +£不成立;(2)该等式不成立,理由如下:假设30a =°,则sin 2sin 60a =°=,12sin 2sin 30212a =°=´=,1¹,sin 22sin a a ¹∴,即sin 22sin a a =不成立.【考点】同角三角函数的关系25.【答案】解:(1)当30a =°时,()222222113sin sin 90sin 30sin 601244a a æö+°-=°+°=+=+=ç÷èø;(2)小明的猜想成立,证明如下:如图,在ABC △中,90C Ð=°,设A a Ð=,则90B a Ð=°-,()222222222sin sin 901BC AC BC AC AB AB AB AB AB a a +æöæö+°-=+===ç÷ç÷èøèø∴.26.【答案】解:原式2233418418316244=´+-´=´+-´=+-=-.【考点】特殊角的三角函数值。
【VIP专享】【详解版】2015届九年级中考总复习(华师大版)精练精析:二十四、命题与证明1(11页,考点+分析+点
11.以下四个命题: ①每一条对角线都平分一组对角的平行四边形是菱形.
②当 m>0 时,y=﹣mx+1 与 y= 两个函数都是 y 随着 x 的增大而减小.
③已知正方形的对称中心在坐标原点,顶点 A,B,C,D 按逆时针依次排列,若 A 点坐
标为(1,
1,2,3,4 的四个完全相同的小球,从袋中随机摸
取一个然后放回,再从袋中随机地摸取一个,则两次取到的小球标号的和等于 4 的概率
为.
其中正确的命题有 _________ (只需填正确命题的序号)
12.命题“对顶角相等”的逆命题为 _________ .
13.命题“对顶角相等”的题设是 _________ ,结论是 _________ .
【详解版】2015届九年级中考总复习(华师大版)精练精析:四、整式2(10页,考点+分析+点评)
数与式——整式2一.选择题(共9小题)1.计算(2a2)3•a正确的结果是()A.3a7B.4a7C.a7D.4a62.若□×3xy=3x2y,则□内应填的单项式是()A.xy B.3xy C.x D.3x3.若2x3﹣ax2﹣5x+5=(2x2+ax﹣1)(x﹣b)+3,其中a、b为整数,则a+b之值为何?()A.﹣4 B.﹣2 C.0 D.44.下列运算正确的是()A.(a2)3=a5 B.(a﹣b)2=a2﹣b2C.﹣=3 D.=﹣35.下列运算正确的是()A.(m+n)2=m2+n2B.(x3)2=x5C.5x﹣2x=3 D.(a+b)(a﹣b)=a2﹣b26.如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为()A.a2+4 B.2a2+4a C.3a2﹣4a﹣4 D.4a2﹣a﹣27.请你计算:(1﹣x)(1+x),(1﹣x)(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+x n)的结果是()A.1﹣x n+1B.1+x n+1C.1﹣x n D.1+x n8.若a+b=2,ab=2,则a2+b2的值为()A.6 B.4 C.3D.29.如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF 的面积为()A.4 B.C. D.2二.填空题(共8小题)10.=_________.11.已知a+b=3,ab=2,则代数式(a﹣2)(b﹣2)的值是_________.12.计算:=_________.13.若a m=6,a n=3,则a m﹣n=_________.14.计算(﹣a)10÷(﹣a)3的结果等于_________.15.(2×102)2×(3×10﹣2)=_________(结果用科学记数法表示)16.已知(x+5)(x+n)=x2+mx﹣5,则m+n=_________.17.已知x﹣=1,则x2+=_________.三.解答题(共8小题)18.已知2x+y=0,求代数式x(x+2y)﹣(x+y)(x﹣y)+2的值.19.已知2x+y=4,求[(x﹣y)2﹣(x+y)2+y(2x﹣y)]÷(﹣2y)的值.20.先化简,再求值:(a+2)(a﹣2)﹣(a﹣3)2,其中.21.先化简,再求值:(2x+y)(2x﹣y)﹣4x(x﹣y),其中x=,y=﹣1.22.已知3x2+2x﹣1=0,求代数式3x(x+2)+(x﹣2)2﹣(x﹣1)(x+1)的值.23.先化简,再求值:(m+n)2﹣(m+n)(m﹣n)﹣2n2,其中m=1,n=﹣2.24.已知2x﹣y=0,求代数式x(x﹣2y)﹣(x+y)(x﹣y)的值.25.先化简,再求值:a(1﹣a)+(a+2)(a﹣2),其中.数与式——整式2参考答案与试题解析一.选择题(共9小题)1.计算(2a2)3•a正确的结果是()A.3a7 B 4a7 C a7D.4a6考点:单项式乘单项式;幂的乘方与积的乘方.专题:计算题.分析:根据幂的乘方与积的乘方、单项式与单项式相乘及同底数幂的乘法法则进行计算即可.解答:解:原式==4a7,故选:B.点评:本题考查了同底数幂的乘法法则,同底数幂相乘,底数不变指数相加;幂的乘方的法则,幂的乘方,底数不变,指数相乘.2.若□×3xy=3x2y,则□内应填的单项式是()A.xy B.3xy C.x D.3x考点:单项式乘单项式.专题:计算题.分析:根据题意列出算式,计算即可得到结果.解答:解:根据题意得:3x2y÷3xy=x,故选:C点评:此题考查了单项式乘单项式,熟练掌握运算法则是解本题的关键.3.若2x3﹣ax2﹣5x+5=(2x2+ax﹣1)(x﹣b)+3,其中a、b为整数,则a+b之值为何?()A.﹣4 B.﹣2 C.0 D. 4考点:多项式乘多项式.分析:先把等式右边整理,在根据对应相等得出a,b的值,代入即可.解答:解:∵2x3﹣ax2﹣5x+5=(2x2+ax﹣1)(x﹣b)+3,∴2x3﹣ax2﹣5x+5=2x3+(a﹣2b)x2﹣(ab+1)x+b+3,∴﹣a=a﹣2b,ab+1=5,b+3=5,解得b=2,a=2,∴a+b=2+2=4.故选D.点评:本题考查了多项式乘以多项式,让第一个多项式的每一项乘以第二个多项式的每一项,再把所得的积相加.4.下列运算正确的是()A.(a2)3=a5B.(a﹣b)2=a2﹣b2C.﹣=3 D.=﹣3考点:完全平方公式;实数的运算;幂的乘方与积的乘方.专题:计算题.分析:A、原式利用幂的乘方运算法则计算得到结果,即可作出判断;B、原式利用完全平方公式展开得到结果,即可作出判断;C、原式不能合并,错误;D、原式利用立方根定义化简得到结果,即可做出判断.解答:解:A、原式=a6,错误;B、原式=a2﹣2ab+b2,错误;C、原式不能合并,错误;D、原式=﹣3,正确,故选:D点评:此题考查了完全平方公式,合并同类项,同底数幂的乘法,以及平方差公式,熟练掌握公式是解本题的关键.5.下列运算正确的是()A.(m+n)2=m2+n2B.(x3)2=x5C.5x﹣2x=3 D.(a+b)(a﹣b)=a2﹣b2考点:完全平方公式;合并同类项;幂的乘方与积的乘方;平方差公式.分析:根据完全平方公式,幂的乘方,合并同类项法则,平方差公式分别求出每个式子的值,再判断即可.解答:解:A、(m+n)2=m2+2mn+n2,故本选项错误;B、(x3)2=x6,故本选项错误;C、5x﹣2x=3x,故本选项错误;D、(a+b)(a﹣b)=a2﹣b2,故本选项正确;故选:D.点评:本题考查了对完全平方公式,幂的乘方,合并同类项法则,平方差公式的应用,注意:完全平方公式有(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,题目比较好,难度适中.6.如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为()A.a2+4 B.2a2+4a C.3a2﹣4a﹣4 D.4a2﹣a﹣2考点:平方差公式的几何背景.专题:几何图形问题.分析:根据拼成的平行四边形的面积等于大正方形的面积减去小正方形的面积,列式整理即可得解.解答:解:(2a)2﹣(a+2)2=4a2﹣a2﹣4a﹣4=3a2﹣4a﹣4,故选:C.点评:本题考查了平方差公式的几何背景,根据拼接前后的图形的面积相等列式是解题的关键.7.请你计算:(1﹣x)(1+x),(1﹣x)(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+x n)的结果是()A.1﹣x n+1B.1+x n+1C.1﹣x n D.1+x n考点:平方差公式;多项式乘多项式.专题:规律型.分析:已知各项利用多项式乘以多项式法则计算,归纳总结得到一般性规律,即可得到结果.解答:解:(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1+x+x2﹣x﹣x2﹣x3=1﹣x3,…,依此类推(1﹣x)(1+x+x2+…+x n)=1﹣x n+1,故选:A点评:此题考查了平方差公式,多项式乘多项式,找出规律是解本题的关键.8.若a+b=2,ab=2,则a2+b2的值为()A. 6 B.4 C.3D.2考点:完全平方公式.分析:利用a2+b2=(a+b)2﹣2ab代入数值求解.解答:解:a2+b2=(a+b)2﹣2ab=8﹣4=4,故选:B.点评:本题主要考查了完全平方公式的应用,解题的关键是牢记完全平方公式,灵活运用它的变化式.9.如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF 的面积为()A. 4 B.C.D. 2考点:整式的混合运算.专题:计算题.分析:设正方形CEFH边长为a,根据图形表示出阴影部分面积,去括号合并即可得到结果.解答:解:设正方形CEFH的边长为a,根据题意得:S△BDF=4+a2﹣×4﹣a(a﹣2)﹣a(a+2)=2+a2﹣a2+a﹣a2﹣a=2.故选:D.点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.二.填空题(共8小题)10.=.考点:整式的混合运算.专题:计算题.分析:先把(x+)提,再把4x2﹣1分解,然后约分即可.解答:解:原式=(2x+1)(2x﹣1)÷[(2x﹣1)(2x+1)]=.故答案为:.点评:本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.11.已知a+b=3,ab=2,则代数式(a﹣2)(b﹣2)的值是0.考点:整式的混合运算—化简求值.专题:计算题.分析:原式利用多项式乘以多项式法则计算,将已知等式代入计算即可求出值.解答:解:原式=ab﹣2a﹣2b+4=ab﹣2(a+b)+4,当a+b=3,ab=2时,原式=2﹣6+4=0.故答案为:0点评:此题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解本题的关键.12.计算:=﹣a3b6.考点:幂的乘方与积的乘方.专题:计算题.分析:利用积的乘方以及幂的乘方法则即可求解.解答:解;原式=﹣a3b6.故答案是:﹣a3b6.点评:本题考查了积的乘方,幂的乘方,理清指数的变化是解题的关键.13.若a m=6,a n=3,则a m﹣n=2.考点:同底数幂的除法.分析:根据同底数幂的除法法则求解.解答:解:a m﹣n==2.故答案为:2.点评:本题考查了同底数幂的除法,解答本题的关键是掌握同底数幂的除法法则:底数不变,指数相减.14.计算(﹣a)10÷(﹣a)3的结果等于﹣a7.考点:同底数幂的除法;幂的乘方与积的乘方.分析:运用同底数幂的除法,底数不变,指数相减.解答:解:(﹣a)10÷(﹣a)3=﹣a7故答案为:﹣a7.点评:本题主要考查了同底数幂的除法,熟记法则是解题的关键.15.(2×102)2×(3×10﹣2)= 1.2×103(结果用科学记数法表示)考点:单项式乘单项式;幂的乘方与积的乘方;负整数指数幂.分析:根据积得乘方等于每个因式分别乘方,再把所得的幂相乘,可得幂,根据有理数的乘法运算律,可简便运算,根据科学记数法的表示方法,可得答案.解答:解:原式=4×104×3×10﹣2=12×(104×10﹣2)=1.2×103,故答案为:1.2×103.点评:本题考查了单项式乘单项式,先算积的乘方,再算有理数的乘法.16.已知(x+5)(x+n)=x2+mx﹣5,则m+n=3.考点:多项式乘多项式.专题:计算题.分析:把式子展开,根据对应项系数相等,列式求解即可得到m、n的值.解答:解:展开(x+5)(x+n)=x2+(5+n)x+5n∵(x+5)(x+n)=x2+mx﹣5,∴5+n=m,5n=﹣5,∴n=﹣1,m=4.∴m+n=4﹣1=3.故答案为:3点评:此题主要考查了多项式乘多项式,根据对应项系数相等求解是解本题的关键.17.已知x﹣=1,则x2+=3.考点:完全平方公式.专题:计算题.分析:首先将x﹣=1的两边分别平方,可得(x﹣)2=1,然后利用完全平方公式展开,变形后即可求得x2+的值.或者首先把x2+凑成完全平方式x2+=(x﹣)2+2,然后将x﹣=1代入,即可求得x2+的值.解答:解:方法一:∵x﹣=1,∴(x﹣)2=1,即x2+﹣2=1,∴x2+=3.方法二:∵x﹣=1,∴x2+=(x﹣)2+2,=12+2,=3.故答案为:3.点评:本题主要考查完全平方公式,利用了(x﹣)2的展开式中乘积项是个常数是解题的关键.三.解答题(共8小题)18.已知2x+y=0,求代数式x(x+2y)﹣(x+y)(x﹣y)+2的值.考点:整式的混合运算—化简求值.分析:先算乘法,再合并同类项,变形后代入求出即可.解答:解:x(x+2y)﹣(x+y)(x﹣y)+2=x2+2xy﹣(x2﹣y2)+2=x2+2xy﹣x2+y2+2=y2+2xy+2=y(y+2x)+2,∵2x+y=0∴原式=2点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算能力和化简能力,题目比较好,难度适中.19.已知2x+y=4,求[(x﹣y)2﹣(x+y)2+y(2x﹣y)]÷(﹣2y)的值.考点:整式的混合运算—化简求值.分析:先求出x+y的值,再算乘法,合并同类项,最后整体代入求出即可.解答:解:∵2x+y=4,∴x+y=2,∴原式=[x2﹣2xy+y2﹣x2﹣2xy﹣y2+2xy﹣y2]÷(﹣2y)=(﹣2xy﹣y2)÷(﹣2y)=x+y=2.点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算能力,用了整体代入思想,题目比较好,难度适中.20.先化简,再求值:(a+2)(a﹣2)﹣(a﹣3)2,其中.考点:整式的混合运算—化简求值.分析:先算乘法,再合并同类项,最后代入求出即可.解答:解:原式=a2﹣4﹣(a2﹣6a+9)=a2﹣4﹣a2+6a﹣9=6a﹣13,当时,原式==﹣17.点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算能力和化简能力,题目比较好,难度适中.21.先化简,再求值:(2x+y)(2x﹣y)﹣4x(x﹣y),其中x=,y=﹣1.考点:整式的混合运算—化简求值.分析:先算乘法,再合并同类项,变形后代入求出即可.解答:解:(2x+y)(2x﹣y)﹣4x(x﹣y)=4x2﹣y2﹣4x2+4xy=﹣y2+4xy,当x=,y=﹣1时,原式=﹣(﹣1)2+4××(﹣1)=﹣3.点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算能力和化简能力,题目比较好,难度适中.22.已知3x2+2x﹣1=0,求代数式3x(x+2)+(x﹣2)2﹣(x﹣1)(x+1)的值.考点:整式的混合运算—化简求值.分析:先算乘法,再合并同类项,最后代入求出即可.解答:解:3x(x+2)+(x﹣2)2﹣(x﹣1)(x+1)=3x2+6x+x2﹣4x+4﹣x2+1=3x2+2x+5,∵3x2+2x﹣1=0,∴3x2+2x=1,∴原式=1+5=6.点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算和化简能力,用了整体代入思想.23.先化简,再求值:(m+n)2﹣(m+n)(m﹣n)﹣2n2,其中m=1,n=﹣2.考点:整式的混合运算—化简求值.分析:先算乘法,再合并同类项,最后代入求出即可.解答:解:原式=m2+2mn+n2﹣(m2﹣n2)﹣2n2=m2+2mn+n2﹣m2+n2﹣2n2=2mn,当m=1,n=﹣2时,则原式=﹣4.点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算能力,题目比较好,难度适中.24.已知2x﹣y=0,求代数式x(x﹣2y)﹣(x+y)(x﹣y )的值.考点:整式的混合运算—化简求值.分析:先算乘法,再喝吧同类项,最后整体代入求出即可.解答:解:x(x﹣2y)﹣(x+y)(x﹣y)=x2﹣2xy﹣(x2﹣y2)=x2﹣2xy﹣x2+y2=﹣2xy+y2∵2x﹣y=0,∴原式=﹣y(2x﹣y)=0.点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算和化简能力,题目是一道中等题,难度适中,用了整体代入思想.25.先化简,再求值:a(1﹣a)+(a+2)(a﹣2),其中.考点:整式的混合运算—化简求值.分析:先算乘法,再合并同类项,最后代入求出即可.解答:解:原式=a﹣a2+a2﹣4=a ﹣4,当时,原式==.点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算能力,题目比较好,难度适中.。
华师大版九年级上册数学第24章 解直角三角形含答案(考点梳理)
华师大版九年级上册数学第24章解直角三角形含答案一、单选题(共15题,共计45分)1、由一些大小相等的小正方体组成的几何体的主视图与左视图相同如图所示,设组成这个几何体的小正方体个数最少为m,最多为n,若以m,n的值分别为某个等腰三角形的两条边长,则该等腰三角形的周长为( )A.11或13B.13或14C.13D.12或13或14或152、如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于()A. B. C. D.3、如图,∠DAE=∠ADE=15°,DE∥AB,DF⊥AB.若AE=10,则DF等于()A.5B.4C.3D.24、在Rt△ABC中,∠C=90°,sinA=,则tanA的值为()A. B. C. D.5、把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值()A.不变B.缩小为原来的C.扩大为原来的3倍D.不能确定6、如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC-BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=3AD,其中正确的个数有()A.4个B.3个C.2个D.1个7、等腰三角形的周长为,其中一边长为,则该等腰三角形的底边长为()A. 或B. 或C.D.8、如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若,则次斜坡的水平距离AC为()A.75mB.50mC.30mD.12m9、如图,以等边三角形ABC的BC边为直径画半圆,分别交AB,AC于点E,D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为()A.4B.C.6D.10、如图.在坡角为a的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为()A.5cosaB.C.5sinaD.11、如图,△ABC的顶点是正方形网格的格点,则cos∠C=()A. B. C. D.12、用计算器求sin24°37′18″的值,以下按键顺序正确的是()A. B.C.D.13、如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高()A.5mB.6mC.7mD.8m14、在Rt△ABC中,∠C=90°,AB=5,AC=3,则下列等式正确的是( )A.sinA=B.cosA=C.tanA=D.cosA=15、如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα= ,则小车上升的高度是()A.5米B.6米C.6.5米D.12米二、填空题(共10题,共计30分)16、如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,则BD:AB________.17、将一副三角尺按图所示叠放在一起,若AB=6cm ,则阴影部分的面积是________ .18、如图∠AOP=∠BOP=15°,PC∥OA ,PD⊥OA ,若PC=6,则PD等于________.19、荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为________米(≈1.73,结果精确到0.1).20、边长为8,一个内角为120°的菱形的面积为________ .21、一个三边都是整数的三角形,其中两边长分别为1和2,第三边长是________22、如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是________.23、已知sinA=0.2675,则∠A=________24、如图,小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为30°,侧倾器到旗杆底部的距离AD为12米,侧倾器的高度AB 为1.6米,那么旗杆的高度CD为________ 米(保留根号)25、在△ABC中,AC=6 ,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为,并且CD⊥AC,则BC的长为________.三、解答题(共5题,共计25分)26、计算:﹣﹣()﹣1+4cos30°27、如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB 的长度.28、某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼五楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知CD=12米,求旗杆AB的高度.29、位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)30、如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D,E,F,G,已知∠CGD=42°(1)求∠CEF的度数;(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示,点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)参考答案一、单选题(共15题,共计45分)1、B2、B3、A4、D6、B7、A8、A9、B10、B11、D12、A13、D14、B15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题,共计25分)26、27、28、29、。
中考数学总复习二十四命题与证明精练精析2华东师大版
图形的性质——命题与证明2一.选择题(共9小题)1.下列命题中,假命题是()A.对顶角相等B.三角形两边的和小于第三边C.菱形的四条边都相等D.多边形的外角和等于360°2.下列命题中,不正确的是()A.n边形的内角和等于(n﹣2)•180°B.两组对边分别相等的四边形是矩形C.垂直于弦的直径平分弦所对的两条弧D.直角三角形斜边上的中线等于斜边的一半3.下列命题中,错误的是()A.平行四边形的对角线互相平分B.菱形的对角线互相垂直平分C.矩形的对角线相等且互相垂直平分D.角平分线上的点到角两边的距离相等4.下列四个命题中,真命题是()A.对角线互相垂直平分的四边形是正方形B.对角线垂直相等的四边形是菱形C.对角线相等且互相平分的四边形是矩形D.四边都相等的四边形是正方形5.下列命题:①对角线相等且垂直的四边形是正方形;②平分弦的直径必垂直于弦;③相等的圆心角所对的弧一定相等;④买彩票中奖概率是,则买4张彩票一定一张会中奖;⑤真命题的逆命题一定是真命题,其中正确的命题个数是()A.0个B.1个C.2个D.3个6.说明命题“如果a,b,c是△ABC的三边,那么长为a﹣1,b﹣1,c﹣1的三条线段能构成三角形”是假命题的反例可以是()A.a=2,b=2,c=3B.a=2,b=2,c=2C.a=3,b=3,c=4D.a=3,b=4,c=57.已知下列命题:①若a>0,b>0,则a+b>0;②若a=b,则a2=b2;③角的平分线上的点到角的两边的距离相等;④矩形的对角线相等.其中原命题与逆命题均为真命题的个数是()A.1个B.2个C.3个D.4个8下列命题是真命题的是()①若ac>bc,则a>b;②抛物线y=x2﹣2x﹣3与坐标轴有2个不同交点;③对角线相等的菱形是正方形;④过三点可以作一个圆.A.①②③B.②③C.③D.③④9.已知下列命题:①若a>0,b>0,则ab>0;②直径是弦;③若,则a>0;④线段垂直平分线上的点到这条线段两个端点的距离相等.其中原命题与逆命题均为真命题的个数是()A.4B.3C.2D.1二.填空题(共7小题)10.已知三条不同的直线a、b、c在同一平面内,下列四条命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.其中真命题的是_________.(填写所有真命题的序号)11.写出定理“直角三角形斜边上的中线等于斜边的一半”的逆命题:_________.12.把命题“如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2”的逆命题改写成“如果…,那么…”的形式:_________.13.下列命题中,其逆命题成立的是_________.(只填写序号)①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.14.下列命题①不相交的直线是平行线;②同位角相等;③矩形的对角线相等且互相平分;④平行四边形既是中心对称图形又是轴对称图形;⑤同圆中同弦所对的圆周角相等.其中错误的序号是_________.15.在命题“同位角相等,两直线平行”中,题设是:_________.16.已知命题“如果一个平行四边形的两条对角线互相垂直,那么这个平行四边形是菱形”,写出它的逆命题:_________.三.解答题(共5小题)17.如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.(1)你构造的是哪几个命题?(2)你构造的命题是真命题还是假命题?请加以证明.。
