如何用调和常数推算潮汐
航海学(下)重点知识

航海学(下)易错点总结7潮汐与潮流7.1潮汐7.1.1潮汐不等现象周日不等:在同一太阳日所发生的两次高潮或两次低潮的潮高以及相邻的高、低潮的时间间隔不相等。
成因:月赤纬≠0°且地理纬度ψ≠0°。
赤纬越大周日不等越明显。
分点潮无周日不等,回归潮周日不等最显著。
现象:一天一次高潮与一次低潮的条件ψ≥90°-Dec半月不等成因:月引潮力与太阳引潮力合力的变化;日、月与地球相互位置关系不同;月相不同。
现象:大潮和小潮潮汐半月变化规律:潮差的变化是以半个太阴月为周期(约14.5天)。
太阳的赤纬不等于0时,也会发生潮汐的周日不等现象。
视差不等:由地球和月球距离变化(注意:不是相对位置的变化)而产生的潮汐不等的现象。
周期:一个恒星月(约27.3天)太阳潮中也存在视差不等现象。
周期:一个回归年(约365.24日)简言之,视差不等是由于日、月、地三者空间距离的变化。
7.1.2潮汐类型半日潮型:一个太阴日内出现两次高潮和两次低潮,前一次高潮和低潮的潮差与后一次高潮和低潮的潮差大致相同,涨潮过程和落潮过程的时间也几乎相等(6小时12.5分)。
我国渤海、东海、黄海的多数地点为半日潮型,如大沽、青岛、厦门等。
全日潮型:一个太阴日内只有一次高潮和一次低潮。
如南海汕头、渤海秦皇岛等。
南海的北部湾是世界上典型的全日潮海区。
混合潮型:一月内有些日子出现两次高潮和两次低潮,但两次高潮和低潮的潮差相差较大,涨潮过程和落潮过程的时间也不等;而另一些日子则出现一次高潮和一次低潮。
我国南海多数地点属混合潮型。
如榆林港,十五天出现全日潮,其余日子为不规则的半日潮,潮差较大。
从各地的潮汐观测曲线可以看出,无论是涨、落潮时,还是潮高、潮差都呈现出周期性的变化,根据潮汐涨落的周期和潮差的情况,可以把潮汐大体分为如下的4种类型:正规半日潮:在一个太阴日(约24时50分)内,有两次高潮和两次低潮,从高潮到低潮和从低潮到高潮的潮差几乎相等,这类潮汐就叫做正规半日潮。
7.5_潮汐调和分析

大摩擦力; 海水粘滞性、惯性影响。
潮差及潮汐的改变 沿岸海区水深变化大、海底地形复杂、岸
形曲折,尤其是浅滩、狭窄海湾的存在。
7.5 潮汐调和分析
潮汐分析
根据潮汐静力学理论,海洋潮汐是许多 分潮迭加的,实际观测记录是各分潮迭加的 结果;
潮汐调和分析的目的,是依据实测潮汐 资料求得各地点各分潮实际的平均振幅以及 各分潮实际与理论相角的差值(它们称之为 调和常数),从而达到掌握特定地区的潮汐 特征状况幵达到潮汐预报的目的。
ij
(i j)
sin( i j ) T 2 ( i j ) T 2
sin( i j ) T 2 ( i j ) T 2
7.5 潮汐调和分析
潮汐最小二乘法分析
11B1 21B1
12B2 22B2
7.5 潮汐调和分析
分潮的调和常数
由平衡潮理论导出的分潮表达式为:
式中 表示分潮潮高,f为分潮的交点因数,H’为分潮
的平均系数,V0 u 表示理论分潮表达式的初相。
7.5 潮汐调和分析
式中的H为分潮的实际平均振幅,如果t 是区时, (V0+u)是区栺林威治时的理
论初相,那么g是区时迟角。
7.5 潮汐调和分析
潮汐最小二乘法分析
D
A0
2
T/2
T
/
2
(t
)
A0
m
( Aj
j 1
cos
jt
Bj
sin jt)dt
潮汐调和分析

潮汐调和常数计算方式及其应用梁国亭李文学张晨霞(黄委员黄河水利科学研究院郑州450003)(黄委会黄河水利技术学院475001)摘要在潮位预测中最大体的工作,第一就是计算潮汐调和常数。
本文在前人研究的基础上,开发了短时刻观测资料和30天观测资料的潮汐调和常数计算及潮汐预测模型,为深切研究黄河口的治理计划提供重要工具。
关键词潮汐分潮调和常数潮位预测1前言潮汐是河口最重要的海洋动力之一。
由于它周而复始的作用于河口、海岸的冲淤转变和入海泥沙等物质的扩散运移,直接影响着河口防洪安全、河口航运事业进展和人们的日常生活。
关于定点潮汐现象的预测研究,主如果按如实测资料通过调和分析,把复杂的潮汐曲线分解成许多调和项,即许多分潮,然后再按照调和常数和天文要素的转变推算潮汐。
所以调和常数是潮汐推算和进行潮波散布数值计算不可缺少的数据[1][2]。
河口泥沙数学模型除具有一般泥沙数学模型的特点外,还必需解决数学模型的下边界条件,即河口开边界的潮位进程线。
因此,研究潮汐调和常数的计算方式是研制河口泥沙数学模型的一项基础性研究工作。
2潮汐调和常数潮汐转变取决于地球、月球和太阳相对位置的转变。
按照万有引力定律,潮高的表达式,通过度解可取得月球平衡潮如下形式:ζ月=34(ME) (aD)3 a [(12-32Sin2ϕ) (23-2Sin2δ)+Sin2ϕSin2δCosT1+Cos2ϕCos2δCos2T1 ](1) 式中,M、E别离为月球和地球的质量,a~地球平均半径,D~地、月中心距,ϕ~地理纬度,δ~月球赤纬,T1~月球时角。
对(1)式中的变量,赤纬用经度、月球时角用太阳时替换,并引进辅助春分点,展开后略去4次方项,取得许多主要的调和项,即称分潮。
由于系数决定着潮差,相角决定着分潮周期。
在实际的海洋中,由于水流运动存在惯性、摩擦等缘故,天体在天顶时刻潮位并非发生最高,往往要掉队一段时刻才出现高潮,因此,通过对式(1)进行简化,可得:ζ=fHCos(σt+v0+u-K) (2) 式中的H为平均振幅,K为地方迟角。
潮汐与及潮汐推算

4 潮汐预报精度:正常情况下,我国沿岸潮时误差在20-30min, 潮高误差在20-30cm
中版《潮汐表》使用注意事项
实际中应注意下列情况: 寒潮、台风及其他天气剧烈变化时,潮汐预报值和实际值出入 较大,寒潮会引起减水,台风会造成增水,个别情况预报和实 际值相差1m以上。 有些日潮混合潮港,高低潮常常有较长时间的平潮时间,预报 的潮时与实际有时相差1小时以上,但潮高与实际较相符。 在江河口预报点,在汛期洪水下泄时,水位急涨。 一般利用差比关系推算的潮汐精度较低。 我国沿岸潮流预报分为两种:往复流和回转流,而第4册潮流大 多数为往复流。 还须注意,潮流预报仅仅是实际流中的潮流部分,但有些情况下, 表层海流受实际风影响较大,实际流与预报值相差较大。
由于月引潮力的存在,使地球表面 上的海水形成月潮椭圆体。 特点:长轴方向位于月地连线上,
短轴方向位于月地垂线上。
A
如4图,设是月球赤纬为零
的月潮椭圆体,此时椭圆
体长轴与地轴垂直,PN为
地理北极,A1、A2、A3、
M
A 1
PA4分别为A在地球A自3转一周
中的四个位置。
在A1点,月球处于上中天,该地海面上升A到最高位置形成高潮;
❖ 第二册:中国东海沿岸,从长江口至台湾。
❖ 第三册:中国南海沿岸及诸岛,包括广东、广西和 南海诸岛。
❖ 第四册:太平洋及邻近海域。
❖ 第五册:印度洋沿岸(含地中海)及欧洲水域。 。
❖ 第六册:大西洋沿岸及非洲东海岸。
中版《潮汐表》主要内容
主港(Standard Port):《潮汐表》中刊载了高、低潮的 潮汐资料的港口。
附港(Secondary Port):利用和主港的差比关系和主港的 潮汐资料来推算潮汐的港口。
海洋要素计算(潮汐)
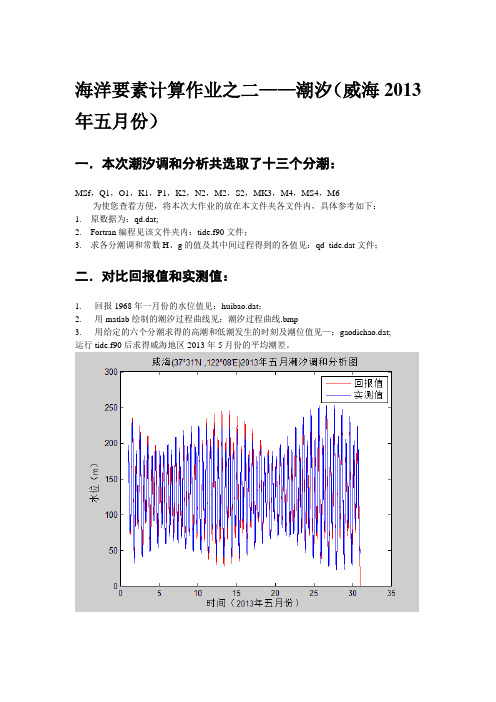
海洋要素计算作业之二——潮汐(威海2013年五月份)一.本次潮汐调和分析共选取了十三个分潮:MSf,Q1,O1,K1,P1,K2,N2,M2,S2,MK3,M4,MS4,M6为使您查看方便,将本次大作业的放在本文件夹各文件内,具体参考如下:1.原数据为:qd.dat;2.Fortran编程见该文件夹内:tide.f90文件;3.求各分潮调和常数H、g的值及其中间过程得到的各值见:qd_tide.dat文件;二.对比回报值和实测值:1. 回报1968年一月份的水位值见:huibao.dat;2. 用matlab绘制的潮汐过程曲线见:潮汐过程曲线.bmp3. 用给定的六个分潮求得的高潮和低潮发生的时刻及潮位值见—:gaodichao.dat;运行tide.f90后求得威海地区2013年5月份的平均潮差。
由图可知:由于只计算了一个月的潮汐数据,所以回报值和实测值相符的不是很好,如果计算一年的数据,应该会取得比较良好的结果。
三.程序%% 潮汐过程曲线图clear,clc%%huibao=load('G:\chaoxi\huibao.dat');% huibao=fread(fhuibao);shice=load('G:\chaoxi\qd.dat');% shice=fread(fshice);%huibao_y=zeros(1,12*62);%shice_y=zeros(1,12*62);huibao=double(huibao');huibao_y=double(huibao(:));%shice_y=reshape(shice',1,[])%for i=1:12;% for j=1:62% huibao_y(i)=huibao(i,j)% shice_y(i)=shice(i,j)%end%endshice=double(shice');shice_y=double(shice(:));x=linspace(1,31,length(huibao_y));plot(x,huibao_y,'r-')hold onplot(x,shice_y,'b-')title('威海(37°31′N ,122°08′E)2013年五月潮汐调和分析图') legend('回报值','实测值')xlabel('时间(2013年五月份)')ylabel('水位(m)')。
潮汐推算1

潮 汐计 算一 求任意时间的潮高和任意潮高的潮时(1)公式法1)求任意时间的潮高A )以高潮为基准高、低潮时分别为T HW 、T LW ,高、低潮高分别为H HW 、H LW ,潮差R=H HW -H LW 。
θ为相位角。
△h 称为潮高改正数任意时潮高H t : h H H HW t ∆-=而 )cos 1(2cos 22θθ-=-=∆RR R h︒⨯--=180HWLW HWT T T T θ所以,任意时潮高H t : )cos 1(2θ--=RH H HW t )]180cos(1[2︒⨯----=HWLW HWHW T T T TRHT H T TH HT .D .BR △h△h′R () /2/2R H 求任意时潮高高潮面任意时水面平均海面低潮面潮高基准面B )以低潮为基准(对应图中的θ'与h '∆),任意时刻T 的潮高H t 可由下式求得:h H H LW t'∆+=而 )cos 1(2θ'-='∆R h 所以,任意时潮高H t : )cos 1(2θ'--=R H H LW t )]180cos(1[2︒⨯---+=LWHW LW LW T T T T R H 例:求1992年2月8日铜沙T=1200的潮高H t 。
已知铜沙该日潮汐为0428 108;0959 418;1737 101;2219 350。
解:因为 6.471805909371759090012180︒=︒⨯--=︒⨯--=mh m h mh m h HW LW HW T T T T θ )(317101418cm H H R LW H W =-=-=)cos 1(2θ-=∆R h =)(5.51)6.47cos 1()2/317(cm =︒-⨯所以 )(36652418cm h H H H W t =-=∆-=以低潮为基准计算H t :4.1321805909371700123717180︒=︒⨯--=︒⨯--=mh m h mh m h HW LW LW T T T T θ )cos 1(2θ'-=∆R h )(4.265)4.132cos 1(2317cm =︒-= )(366265101cm H H LW t =+==两种方法的计算结果完全一致。
中期水位资料对潮汐进行调和分析

!利用1996年7月厦门站的潮汐观测数据计算调和常数,并利用主要分潮和浅水分潮进行潮汐预报program workimplicit nonecharacter*80::a1character(len=5),dimension(62,16)::aainteger::bb(62,12),c(62,2),caita(-371:371),i,i1,i2,j,t1real::N0,n(13,6),a(0:13,0:13),b(1:13,1:13),s,s0,s1,s2,s3,sa,hh !n代表Doodson代码;a,b为系数矩阵real::xiaoa(0:13),xiaob(13),gg1,gg2,pjchaocha,t,ma,mi!计算法方程所需的参数real,dimension(1:13)::w,u,f,V0,f1(0:13),f2!f1和f2为法方程右边系数real,dimension(13)::sita,h,g,r,h0(13),g0(13),h1(13),g1(13)!调和常数参数real,dimension(-371:371)::caita1,caita3,caita4,caita8,caita9,caita5,caita11 !主分潮、浅水分潮的潮高数值real,dimension(:),allocatable::hightide,lowtide,chaocha!高低潮数值integer,dimension(:),allocatable::hightrq,lowtrq,hight,hightt,lowt,lowtt!读取数据,把潮位数据赋值给bb,把年月份数据赋值给copen(unit=2,file='XM_July1996.dat')read(2,'(a)')a1print*,'数据文件的第一行信息:',a1do i=1,62read(2,'(16a5)')aa(i,:)end dodo i=1,62read(aa(i,5:16),*)bb(i,:)read(aa(i,3:4),*)c(i,:)end dodo i=1,62c(i,2)=int(real(c(i,2))/10.0)end doclose(2)!计算分潮角速率ww=(/0.002822,0.037219,0.038731,0.041781,0.163845,0.241534,0.078999 ,&&0.080511,0.083333,0.122292,0.161023,0.041553,0.083561/)w=360*wprint*print*,'角速率w:',w!计算N0 (middle time:1996-7-16 ; data sum:744, middle number:372 ) N0=259.157-19.32818*(1996-1900)-0.05295*(31*3+30*2+29+15+int((9 5.0)/4.0)) !初始升交点平均黄经N0=-(0.00220641*3+N0)print*!转换成格林威治时间print*,'N0:',N0!数字序号对应选取的分潮,但将5、6(P1、K2)分别与12、13(MS4、M6)对调,其中P1、K2为随从分潮!计算交点订正角uu(3)=10.8*sind(N0)-1.34*sind(2*N0)+0.19*sind(3*N0)u(4)=-8.86*sind(N0)+0.68*sind(2*N0)-0.07*sind(3*N0)u(8)=-2.14*sind(N0)u(13)=-17.74*sind(N0)+0.68*sind(2*N0)-0.04*sind(3*N0)u(1)=-u(8)u(2)=u(3)u(7)=u(8)u(9)=0u(10)=u(8)+u(4)u(11)=2*u(8)u(5)=u(8)u(6)=3*u(8)u(12)=0 !print*print*,'交点订正角u:',u!计算交点因子ff(3)=1.0089+0.1871*cosd(N0)-0.147*cosd(2*N0)+0.0014*cosd(3*N0) f(4)=1.006+0.115*cosd(N0)-0.0088*cosd(2*N0)+0.0006*cosd(3*N0) f(8)=1.0004-0.0373*cosd(N0)+0.0003*cosd(2*N0)f(13)=1.0241+0.2863*cosd(N0)+0.0083*cosd(2*N0)-0.0015*cosd(3*N0 )f(1)=f(8)f(2)=f(3)f(7)=f(8)f(9)=1f(10)=f(8)*f(4)f(11)=f(8)**2f(5)=f(8)**2f(6)=f(8)**3f(12)=1 !print*print*,'交点因子f:',f!查表得到的Doodson代码n(1,:)=(/0,2,-2,0,0,0/)n(2,:)=(/1,-2,0,1,0,0/)n(3,:)=(/1,-1,0,0,0,0/)n(4,:)=(/1,1,0,0,0,0/)n(5,:)=(/4,2,-2,0,0,0/)n(6,:)=(/6,0,0,0,0,0/)n(7,:)=(/2,-1,0,1,0,0/)n(8,:)=(/2,0,0,0,0,0/)n(9,:)=(/2,2,-2,0,0,0/)n(10,:)=(/3,1,0,0,0,0/)n(11,:)=(/4,0,0,0,0,0/)n(12,:)=(/1,1,-2,0,0,0/)n(13,:)=(/2,2,0,0,0,0/)!计算V0do i=1,13V0(i)=(14.49205212*3+180)*n(i,1)+(0.54901653*3+277.025+129.3848 *96+13.1764*(220))*n(i,2)+&&(0.04106864*3+280.190-0.23872*96+0.98565*(220))*n(i,3)+(0.00464 183*3+334.385+40.66249*96+&&0.11140*(220))*n(i,4)-(0.00220641*3+259.157-19.32818*96-0.05295* (220))*n(i,5)+&&(0.00000196*3+281.221+0.01718*96+0.000047*(220))*n(i,6) end doprint*print*,'初始幅角V0:',V0!设caita为潮高数据do i=1,61j=-371+(i-1)*12caita(j:j+11)=bb(i,:)end docaita(361:371)=bb(62,1:11)!计算法方程等式右边的数据,相邻数据时间间隔为1小时f1(0)=sum(caita)!f1为A阵中除第一行外的等式右边一维数据f1(1:13)=0do i=1,13do j=-371,371f1(i)=f1(i)+caita(j)*cosd(j*w(i))end doend do!f2为B阵中等式右边的一维数据f2=0do i=1,13do j=-371,371f2(i)=f2(i)+caita(j)*sind(j*w(i))end doend do!计算A阵中的系数矩阵Aa(0,0)=743do j=1,13a(0,j)=sind(743.0/2*w(j))/sind(0.5*w(j))a(j,0)=a(0,j)end dodo j=1,13a(j,j)=0.5*(743+sind(743.0*w(j))/sind(w(j)))end dodo i=1,13do j=i+1,13a(i,j)=0.5*(sind(743.0/2*(w(i)-w(j)))/sind(0.5*(w(i)-w(j)))+& & sind(743.0/2*(w(i)+w(j)))/sind(0.5*(w(i)+w(j)))) a(j,i)=a(i,j)end doend doprint*print*,'系数矩阵A:',a!计算B阵中的系数矩阵Bdo j=1,13b(j,j)=0.5*(743-sind(743.0*w(j))/sind(w(j)))end dodo i=1,13do j=i+1,13b(i,j)=0.5*((sind(743.0/2*(w(i)-w(j)))/sind(0.5*(w(i)-w(j)))-&& sind(743.0/2*(w(i)+w(j)))/sind(0.5*(w(i)+w(j))))) b(j,i)=b(i,j)end doend doprint*print*,'系数矩阵B:',b!Guass-Seidel迭代法求解方程组h=0;g=0;i1=0doh0=hg0=g!A阵do i=0,11s1=0do j=0,11s1=s1+xiaoa(j)*a(i,j)end doxiaoa(i)=-s1/a(i,i)+f1(i)/a(i,i)+xiaoa(i)-xiaoa(12)*a(i,12)/a(i,i)-xiaoa(13)* a(i,13)/a(i,i)end do!B阵do i=1,11s1=0do j=1,11s1=s1+xiaob(j)*b(i,j)end doxiaob(i)=-s1/b(i,i)+f2(i)/b(i,i)+xiaob(i)-xiaob(12)*b(i,12)/b(i,i)-xiaob(13) *b(i,13)/b(i,i)end do!计算调和常数h,gdo j=1,11sita(j)=atand(xiaob(j)/xiaoa(j))+180r(j)=sqrt(xiaoa(j)**2+xiaob(j)**2)g(j)=V0(j)+u(j)+sita(j)h(j)=r(j)/f(j)end dodo i=1,11do while(g(i)>360.or.g(i)<0)if(g(i)>360)thendog(i)=g(i)-360if(g(i)>0.and.g(i)<360)exitend doelseend ifif(g(i)<0)thendog(i)=g(i)+360if(g(i)>0.and.g(i)<360)exitend doelseend ifend doend dogg1=g(4)-g(3)gg2=g(9)-g(8)do while(gg1>230.or.gg1<-130)if(gg1>230)thendogg1=gg1-360if(gg1<230.and.gg1>-130)exitend doelseend ifif(gg1<-130)thendogg1=gg1+360if(gg1>-130.and.gg1<230)exitend doelseend ifend dodo while(gg2>230.or.gg2<-130)if(gg2>230)thendogg2=gg2-360if(gg2<230.and.gg2>-130)exitend doelseend ifif(gg2<-130)thendogg2=gg2+360if(gg2>-130.and.gg2<230)exitend doelseend ifend dog(12)=g(4)-0.075*(g(4)-g(3))g(13)=g(9)+0.081*(g(9)-g(8)) sita(12)=-(u(12)+V0(12)-g(12)) sita(13)=-(u(13)+V0(13)-g(13)) h(12)=h(4)*0.324h(13)=h(9)*0.282do j=12,13r(j)=h(j)*f(j)xiaoa(j)=r(j)*cosd(sita(j))xiaob(j)=r(j)*sind(sita(j)) end dog1=g-g0h1=h-h0i1=i1+1if(all(abs(h1)<10.0).and.all(abs(g1)<2.0))exit !退出循环条件end doprint*print*,'系数a:',xiaoaprint*print*,'系数b:',xiaobprint*print*,'迭代循环次数:',i1print*print*,'调和常数h:',hprint*print*,'调和常数g:',g!计算平均水位s0=xiaoa(0)print*print*,'平均水位s0:',s0!向文件中输入数据!将各分潮的调和常数写入'hg.txt'open(unit=2,file='hg.txt')do i=1,13write(2,*)h(i),g(i)end doclose(2)!将所有潮汐数据写入'tides.txt'open(unit=2,file='tides.txt')do i=1,62write(2,'(12i5)')bb(i,:)end doclose(2)!将所有主要分潮(3,4,8,9)、浅水分潮(5,11)数据按随时间的变化情况写入向量中do j=-371,371caita3(j)=s0+f(3)*h(3)*cosd(w(3)*j-sita(3))caita4(j)=s0+f(4)*h(4)*cosd(w(4)*j-sita(4))caita8(j)=s0+f(8)*h(8)*cosd(w(8)*j-sita(8))caita9(j)=s0+f(9)*h(9)*cosd(w(9)*j-sita(9))caita5(j)=s0+f(5)*h(5)*cosd(w(5)*j-sita(5))caita11(j)=s0+f(11)*h(11)*cosd(w(11)*j-sita(11))caita1(j)=caita3(j)+caita4(j)+caita8(j)+caita9(j)+caita5(j)+caita11(j)-5*s0 end do!计算高低潮个数i1=0;i2=0do j=-370,370if(caita(j)>caita(j-1).and.caita(j)>caita(j+1))theni1=i1+1 !高潮个数end ifif(caita(j)<caita(j-1).and.caita(j)<caita(j+1))theni2=i2+1 !低潮个数end ifend doprint*print*,'高潮个数:',i1print*,'低潮个数:',i2if(allocated(hightide))deallocate(hightide)if(allocated(lowtide))deallocate(lowtide)if(allocated(hight))deallocate(hight)allocate(hightide(1:i1),lowtide(1:i2))!将观测时的高潮写入文件open(unit=2,file='realh.txt')do i=1,size(hightide)write(2,*)hightide(i)end doclose(2)!将观测时的低潮写入文件open(unit=2,file='reall.txt')do i=1,size(lowtide)write(2,*)lowtide(i)end doclose(2)!潮汐预报部分!计算高低潮对应的潮位及时刻if(allocated(hightide))deallocate(hightide) if(allocated(lowtide))deallocate(lowtide) if(allocated(hight))deallocate(hight)if(allocated(lowtrq))deallocate(lowtrq)if(allocated(hightrq))deallocate(hightrq)i=min(i1,i2)allocate(hightide(1:i1),lowtide(1:i2),hightrq(i1),lowtrq(i2),hight(i1),hightt (i1),lowtt(i2),lowt(i2),chaocha(i))i1=0;i2=0do j=-370,370!高潮潮位及时刻if(caita1(j)>caita1(j-1).and.caita1(j)>caita1(j+1))theni1=i1+1do t=j-1,j+1,0.01s=s0+f(3)*h(3)*cosd(w(3)*(t)+V0(3)+u(3)-g(3))+&f(4)*h(4)*cosd(w(4)*(t)+V0(4)+u(4)-g(4))+&f(5)*h(5)*cosd(w(5)*(t)+V0(5)+u(5)-g(5))+&f(8)*h(8)*cosd(w(8)*(t)+V0(8)+u(8)-g(8))+&f(9)*h(9)*cosd(w(9)*(t)+V0(9)+u(9)-g(9))+&f(11)*h(11)*cosd(w(11)*(t)+V0(11)+u(11)-g(11)) sa=s0+f(3)*h(3)*cosd(w(3)*((t+1/60.0))+V0(3)+u(3)-g(3))+& f(4)*h(4)*cosd(w(4)*((t+1/60.0))+V0(4)+u(4)-g(4))+&f(5)*h(5)*cosd(w(5)*((t+1/60.0))+V0(5)+u(5)-g(5))+&f(8)*h(8)*cosd(w(8)*((t+1/60.0))+V0(8)+u(8)-g(8))+&f(9)*h(9)*cosd(w(9)*((t+1/60.0))+V0(9)+u(9)-g(9))+&f(11)*h(11)*cosd(w(11)*((t+1/60.0))+V0(11)+u(11)-g(11)) if(s<sa)thenma=sahightt(i1)=int((t-floor(t))*60)hight(i1)=floor(t)+371end ifend dohightide(i1)=maelseend if!低潮潮位及时刻if(caita1(j)<caita1(j-1).and.caita1(j)<caita1(j+1))theni2=i2+1do t=j-1,j+1,0.01s=s0+f(3)*h(3)*cosd(w(3)*(t)+V0(3)+u(3)-g(3))+&f(4)*h(4)*cosd(w(4)*(t)+V0(4)+u(4)-g(4))+&f(5)*h(5)*cosd(w(5)*(t)+V0(5)+u(5)-g(5))+&f(8)*h(8)*cosd(w(8)*(t)+V0(8)+u(8)-g(8))+&f(9)*h(9)*cosd(w(9)*(t)+V0(9)+u(9)-g(9))+&f(11)*h(11)*cosd(w(11)*(t)+V0(11)+u(11)-g(11)) sa=s0+f(3)*h(3)*cosd(w(3)*((t+1/60.0))+V0(3)+u(3)-g(3))+& f(4)*h(4)*cosd(w(4)*((t+1/60.0))+V0(4)+u(4)-g(4))+&f(5)*h(5)*cosd(w(5)*((t+1/60.0))+V0(5)+u(5)-g(5))+&f(8)*h(8)*cosd(w(8)*((t+1/60.0))+V0(8)+u(8)-g(8))+&f(9)*h(9)*cosd(w(9)*((t+1/60.0))+V0(9)+u(9)-g(9))+&f(11)*h(11)*cosd(w(11)*((t+1/60.0))+V0(11)+u(11)-g(11)) if(s>sa)thenmi=salowtt(i2)=int((t-floor(t))*60)lowt(i2)=floor(t)+371end ifend dolowtide(i2)=mielseend ifend do!将高潮位写入'hightide.txt',第1列为潮位,第2、3列为时刻open(unit=2,file='hightide.txt')do i=1,i1write(2,*)hightide(i),hight(i),hightt(i)end doclose(2)do i=1,i1j=1if(hight(i)<=23)thenhightrq(i)=1end ifdo while(hight(i)>23)hight(i)=hight(i)-24j=j+1hightrq(i)=jend doend doopen(unit=2,file='hightidexiu.xls')do i=1,i1hightide(i)=int(hightide(i)+0.5)*1.0write(2,*)hightide(i),hightrq(i),hight(i),hightt(i) !将高潮位及时刻写入'hightidexiu.xls',第1列为潮位,第2、3、4列为天数、小时、分钟end doclose(2)!将低潮位写入'lowtide.txt',第1列为潮位,第2、3列为时刻open(unit=2,file='lowtide.txt')do i=1,i2write(2,*)lowtide(i),lowt(i),lowtt(i)end doclose(2)do i=1,i2j=1if(lowt(i)<=23)thenlowtrq(i)=1endifdo while(lowt(i)>23)lowt(i)=lowt(i)-24j=j+1lowtrq(i)=jend doend doopen(unit=2,file='lowtidexiu.xls')do i=1,i2write(2,*)lowtide(i),lowtrq(i),lowt(i),lowtt(i) !将低潮位及时刻写入'lowtidexiu.xls',第1列为潮位,第2、3、4列为天数、小时、分钟end do!将四大主分潮潮位数据写入'zhuyaotides.txt'中,第1列为O1,第2列为K1,第3列为M2,第4列为S2open(unit=2,file='zhuyaotides.txt')do i=-371,371write(2,'(4f7.1)')caita3(i),caita4(i),caita8(i),caita9(i)end doclose(2)!将浅水分潮潮位数据写入'qianshuitides.txt'中,第1列为MS4,第2列为M4open(unit=2,file='qianshuitides.txt')do i=-371,371write(2,'(2f7.1)')caita5(i),caita11(i)end doclose(2)!计算平均潮差s=0do i=1,size(chaocha)s=s+(hightide(i)-lowtide(i))pjchaocha=s/size(chaocha)print*print*,'平均潮差:',pjchaochaprint*deallocate(hightide,lowtide,hight,lowt,chaocha,hightrq,lowtrq) !释放掉潮位数据!判断XM站潮汐类型hh=(h(3)+h(4))/h(8)if(hh<0.5)thenprint*,'潮型数:',hh,'所以XM站潮汐类型为半日潮'else if(hh>=0.5.and.hh<2.0)thenprint*,'潮型数:',hh,'所以XM站潮汐类型为不规则半日潮混合潮' else if(hh>=2.0.and.hh<=4.0)thenprint*,'潮型数:',hh,'所以XM站潮汐类型为不规则日潮混合潮' else if(hh>=4.0)thenprint*,'潮型数:',hh,'所以XM站潮汐类型为全日潮'elseprint*,'error'end ifend program work。
江苏省燕尾港天文潮的推算

江苏省燕尾港天文潮的推算戴荣,梁忠民河海大学水文水资源学院,南京(210098)E-mail :dairong@摘 要:本文首先对燕尾港潮位站的实测资料进行潮汐调和分析,以求得潮汐各分潮的调和常数。
接着根据所得到的调和常数,进行潮汐推算。
计算结果表明该法具有精度高、速度快、简便实用等优点,很适合于燕尾港天文潮的推算。
关键词:潮汐调和分析,调和常数,潮汐推算,天文潮1 前言燕尾港位于灌云县的灌河口。
东临黄海,南濒灌河,与响水县相望。
由于来自太平洋通过东海,进入黄海的前进波在台风等气象因素的作用下,该海区经常受到风暴潮袭击,造成海堤损坏、海岸坍淤、部分地段的港槽摆动不定,不利于沿海地区的进一步开发,因而风暴潮灾害十分严重。
因为天文潮是风暴潮的主部,所以准确地预报出天文潮是提高风暴潮预报精度的关键之一。
虽说,国家每年都刊登下一年各潮位站的潮汐表,但由于人工将潮汐表中的数据输入到计算机中,耗费时间长,且易出现输入错误等缺点,因此本文利用燕尾港潮位站的资料,开发了自己的燕尾港天文潮推算程序。
2 天文潮的分析及预报计算天文潮预报方法通常可分为调和法和非调和法两类。
本文拟采用调和法进行江苏省燕尾港的天文潮预报。
调和法以潮汐静力学理论为基础,经过潮汐动力学理论的补充与完善。
根据调和法的计算过程,将其分为以下两步:前一步为调和分析,后一步为潮汐预报。
2.1 潮汐调和分析2.1.1 潮高公式海洋中的潮汐是在地球、月球和太阳三个天体相对运动中,由月球和太阳对地球的引潮力引起的[1],将其按球面三角函数处理,并进一步用级数公式展开,可得出如下潮高公式: ])(cos[)(100∑=−+++=Q j j j j j j p g u t H fx t h νσ (2.1)式中,)(t h p 为t 时刻的潮位;0x 为平均潮位;H ,g 为调和常数;f ,u 为交点因子和订正角;σ为分潮的角速率;0v 为0=t 时刻的天文相角;Q 为分潮数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 096 006 - 090 - 144 058 - 086
2. 332 0. 027 0. 063 D43 Cosd4 0 3. 561 0. 011 0. 039 D63 Cosd6 0. 003
40
4. 125
计算过程详细说明 : A 部分 : (1)完成 A 部分开头表格中的内容 :根据所要
A1 ( Tab Ⅶ) A2 ( Tab Ⅶ)
M2
S2
K1
O1
216
343
031
165
243
343
030
192
06
A1 - A2
- 027 000 - 001 - 027
07
360°3 n
720° 720° 360° 360°
08 P = (A1 - A2) + 360°3 n 693° 720° 359° 333°
(4)依据英版潮汐表 (A. T. T. )的附表 Ⅶ ( Tab Ⅶ) ,查出如下各值 :
( a)查当日 (2001年 11月 10日 )该港的四个分 潮 ( M2 S2 K1 O1 ) 的 天 文 相 角 ( A1 ) : 分 别 是 216 (M2 ) 、343 ( S2 ) 、031 ( K1 ) 、165 (O1 ) ,并将上述值分 别填入序号为 04栏和 10栏 。
1. 13 1. 13 1. 11 1. 20
27 F1 + P’/24 3 T = Ft 28 H ( Part Ⅲ)
1. 13 1. 13 1. 11 1. 20 1. 84 0. 54 0. 34 0. 28
29 H3 Ft 30 (H 3 Ft) Sinθ 31 (H 3 Ft) Coθs
2. 079 - 1. 638 + 1. 281
(2)依据厦门港编号 7163 查英版潮汐表的第 三部分 ( Part Ⅲ - HARMON IC CONSTANTS)查出该 港的平均海面值 : Z0 3. 28m; 季节改正 ( SEASONAL CHANGES IN M EAN LEVEL ) + 0. 2。并将上述值分 别填入序号为 01栏和 02栏中 ;并将 01 栏和 02 栏 的值进行求和 ( Sum ) ,并填入 03栏 。
0. 610 + 0. 548 - 0. 267
0. 377 #
0. 336 - 0. 377 + 0. 005
32 R Sin r R Cos r
- 1. 135 1. 014
1. 014
33 r R
- 048 1. 527 ML (L INE 3) 3. 48
34 2 r R2 35 f4 ( Part Ⅲ) F4 ( Part Ⅲ) 36 2 r + f4 = d4 R23 F4 37 3 r R3 38 F6 ( Part Ⅲ) F6 ( Part Ⅲ) 39 3 r + F6 = d6 R33 F6
Xiamen Gang( 7163) NP204 - 01 2001. 11. 10 - 0800
序号 01 02 03
Mean Level Z0 ( Part Ⅲ) or ( Tab V I) Seasonal Corr. ( Part ⅢP)
Sum =ML
3. 28 + 0. 2 3. 48
序号 04 05
(3)对浅水改正和季节改正修正 : 利用每卷英 版潮汐表的附表 6提供的浅水改正和季节改正数据 进行修正 ,会使得潮汐推算的精度将达到利用 36个 分潮进行推算的精度 。
举例 :推算厦门港 ( Xiamen Gang) 2001年 11月 10日 0900潮汐 。 A 部分
Port A. T. T. NO. D a te Time Zone
( b)查次日 (2001年 11月 11日 )该港的四个分
如何用调和常数推算潮汐 李维利
7
潮 ( M2 S2 K1 O1 ) 的 天 文 相 角 (A2 ) : 分 别 是 243 (M2 ) 、343 ( S2 ) 、030 ( K1 ) 、192 (O1 ) ,并将上述值填 入序号为 05栏 。
推算的港口和时间“推算厦门港 2001年 11月 10日 0900潮汐 ”。使 用 英 版 潮 汐 表 (A. T. T. ) 第 四 卷 (NP204 - 01) ,首先利用地理索引 ( Geographical In2 dex)查取厦门港的编号为 7163。并依据编号查英 版潮汐表的第三部分 ( Part Ⅲ - HARMON IC CON2 STANTS)得到厦门港的“Tim e Zone”为 - 0800。
牛顿之后的 1个世纪 ,法国天文学家拉普拉斯 建立了潮汐动力学理论 。他认为 :引潮力除了使海 水发生“潮峰 ”之外 ,还造成周期与引潮力相同的潮 汐波 。潮汐波由强制波和自由波组成 。强制波以月 球在天空沿视轨道运动的速度为传播速度在地球表 面移动 ,而自由波则在引潮力因某种原因突然中断 时 ,失去平衡的水团在其惯性作用下继续进行涨落 运动 ,直至所有波能消耗殆尽 。故此 ,分析潮汐时不 仅要考虑到引潮力造成的“潮峰 ”,还要考虑到潮汐 波的存在 ,同时还要考虑到地形 、地球自转力和摩擦 力等因素的影响 。这种潮汐动力学理论要比牛顿的 潮汐静力学理论完善得多 。
(3)依据厦门港编号 7163 查英版潮汐表的第 三部分 ( Part Ⅲ - HARMON IC CONSTANTS)查出该 港的四个 分 潮 (M2 S2 K1 O1 ) 的 迟 角 值 ( g°) : 352 (M2 ) 、043 ( S2 ) 、281 ( K1 ) 、283 (O1 ) ,并将上述值分 别填入序号为 11栏 。
关键词 : 英版潮汐表 调和常数 潮汐推算
根据牛顿的潮汐静力学理论 ,潮汐的成因是因 天体的引潮力形成的 ,即天体的引力和地球与天体 相对运动所需的惯性离心力的向量和 。其中主要是 月球的引潮力 ,其次是太阳的引潮力 。而潮汐周日 不等现象是因月球赤纬不等于零时的潮汐椭圆体造 成的 ;潮汐的半月不等现象是因月球 、太阳和地球在 空间周期性地改变着它们的相对位置 ,从而产生了 潮汐半月不等现象 。牛顿的潮汐静力学理论是在理 想的假设条件下进行的 ,事实上 ,高潮并不发生在月 上 (下 )中天之时 ,而是滞后一个高潮间隙 ; 大潮也 不发生在朔 、望之日 ,而是滞后 1~3天 (潮龄 ) 。且 各地的潮差也不相等 ,甚至相距很近的两个地区却 发生性质不同的潮汐现象 。所有这些是用牛顿的潮 汐静力学理论无法解释的 。
M2 28. 88° 260° 568°
0900
S2
K1
O1
30° 14. 96° 13. 88°
270° 135° 125°
386° 312° 403°
21 (A1 + g°) - (P /243 T) =θ 308° 116° 177° 278°
22 Sinθ
- 0. 788 + 0. 899
23 Coθs
目前运用潮汐静力学理论的计算和潮汐动力学
收稿日期 : 2007 - 03 - 02 作者简介 :李维利 ( 1965 - ) ,男 ,天津人 ,讲师 ,主要从事航
海教学 。
理论的分析来推算潮汐比较精确 ,我们将这种方法 称为潮汐调和分析法 。其中最为关键的是运用了波 动合成原理 ,即将几个同时作用在潮汐上的作用力 归结为若干正规的分潮力 ,然后按照简谐振荡的形 式分别地计算出来 ,并对这些分潮进行总和 。每个 分潮形成的曲线由两个因素确定 :分潮振幅 H 和分 潮迟角 g°一般分潮振幅 H 为潮差的一半 ;分潮迟角 g°是假象天体上中天到该地分潮高潮的时间间隔 。
6
天津航海 2007年第 2期
利用调和常数法进行潮汐推算主要需进行以下 三方面的调和修正 :
(1)对平均海面和四个主要分潮的修正 : 利用 每卷英版潮汐表的第三部分即“调和常数 ”部分提
供了平均海面和四个主要分潮 (M2 S2 K1 O1 )的调和 常数 (H 和 g°。)进行修正 ;
( 2 )对四个主要分潮的节点因素和天文相角修 正 :利用每卷英版潮汐表 (A. T. T. )的附表 Ⅶ ( Tab Ⅶ)提供 的 该 四 个 主 要 分 潮 的 节 点 因 素 和 天 文 相 角 ,并相对于其它分潮进行修正 ,使得利用四个主要 分潮求得的潮汐的精度得到极大提高 。
(5)将 A1 - A2的值求出填入序号为 06栏 。 (6)将天文相角的每天天文值变化率 ( 360°1n) 填入序号为 07栏 :近似计算形成的这些天文值是这 样形成的 : M2 和 S2 天文相角的每小时天文值变化 率为 30°/ h, 所以 07 栏的 M2 和 S2 为 30°3 24 = 720°; K1 和 O1 天文相角每小时的天文值变化率为 15°/ h,所以 07栏的 K1 和 01 为 15°3 24 = 360°; ( 7 )将该地区的天文相角的每天天文值变化率 P填入序号为 08栏 : P = (A1 - A2) + 360°1n ( 8 )将该地区的天文相角的小时天文值变化率 P /24填入序号为 09栏 : P /24 (9)将第 10栏当日 ( 2001 年 11 月 10 日 )该港 的四个分潮 ( M2 S2 K1 O1 )的天文相角 (A1)值和第 11栏的各迟角值相加 (A1 + g)并填入第 12栏 ; (10)将第 13栏的次日 (2001年 11月 11日 )该 港的四个分潮 (M2 S2 K1 O1 ) 的节点因素即系数值 ( F2)减去第 14栏当日 (2001年 11月 10日 )该港的 四个分潮 (M2 S2 K1 O1 )的节点因素即系数值 ( F1) : 求出每天的节点因素变化值 : F2 - F1 = P’ (11)求出每小时的节点因素变化值填入第 16 栏 : P’/24 B 部分 :完成任意时的潮汐预报 (12)将时间填入第 17 栏 ,如果你的计算器不 能进行小时 /分钟 /秒以及小数点之后的换算 ,应该 将小时精确到小数点后 1位 。如 : 1812 = 18. 2 (13 ) 查 英版 潮汐表 (ATT) 的第 三 部 分 ( Part Ⅲ) : 将各分潮 (M2 S2 K1 O1 )的振幅 H 值填入第 28 栏。
