机械制图-点线面的投影(第四章)
机械制图第四章

(2)圆头棱柱体,在对称面上开圆孔
(3)开孔扁圆柱
分析各基本体的相对位置以及两形体的表面之 间的连接关系,想象出整体的形状。
归纳整理
2.线面分析法:视图上的一个封闭线框,一般
情况下代表一个面的投影,不同线框之间的关系, 反映了物体表面的变化。
由长方体被 截后形成的
物体的 三视图
S为正
垂面 s'
(2)视图上相套两封闭线框里面的小线框是 通孔或凸台。
3.从反映形状和位置特征最明显的视图入手
(1)形状特征:主视图最能反映组合体的形体
特征,故应从主视图入手。
每个视图中又能反映
物体的一部分形状特征.
(2)位置特征
从主、俯两个视图看,则 物体上的凸出或凹下部分无 法确定。
从主、左两个视图看,则 只能唯一的判定一个物体。
首先看主视图 左上部缺口,可看 成是切去一个棱体。
俯视图右半部分, 可看成切去一个四棱柱
左半部分的缺口可 看成是切去一个四棱柱
左视图上部中间有一 缺口,可以看成是切去 一个小长方体。
整理加深,完成图形
4.5 组合体视图的尺寸标注
视图只能表达物体的形状,物体的真实大小是根据图样 上所注的尺寸来确定的。加工时也是按照图样上的尺寸来制 定的。组合体的尺寸标注要做到:正确、完整、清晰、合理。
2.分解形体对投影
分解形体,利用“三等”关系,找出每一部分的三 个投影,以确定每一部分形体的形状。。
3.综合起来想整体
分析它们之间的组合方式相对位置关系,从而想象 出整体的形状。
看图的一般顺序是“先整体后细部”、“先主要后次要” 大致形状心中有数后,再作细部分析;当然也要掌握 “先易后难”的原则。
(1)四棱柱,在对称面上开圆孔,下方开通槽
第四章 点直线和平面的投影资料

§1 点的投影1.1 点的三个投影1.1.1 三个投影之间的位置关系a点A的水平投影a'点A的正面投影a"点A的侧面投影规定:空间点用大写字母表示,点的三个投影都用同一个小写字母表示,其中:H 投影不加撇,V 投影加一撇,W 投影加两撇将投影面展开得点的正投影图1.1.2 点的投影和坐标的关系点的每个投影反映两个坐标:V 投影反映高标和横标,H 投影反映纵标和横标,W 投影反映高标和纵标。
小结:点的投影规律1)V、H 两投影都反映横标,且投影连线垂直X 轴;2)V、W两投影都反映高标,且投影连线垂直Z 轴;3)H、W两投影都反映纵标,投影连线是一条折线。
例:已知点A(30,20,40),求作三投影。
●a "●a a x 作图步骤O X Z Y HY W a z 304020●a '1.2 两点的相对位置和重影点1.2.1 两点的相对位置根据两点相对于投影面的距离(坐标)不同,即可确定两点的相对位置。
图中A 点的横标小于B 点的横标,点A 在点B 的右方。
同样,可以判断点A 在点B上方;点A 在点B 前方(规定距V 面远为前,距V 面近为后)。
[例1]如图,已知点A 的三投影,另一点B 在点A上方8mm,左方12mm,前方10mm处,求点B的三个投影。
作图步骤:1)在a′左方12mm,上方8mm处确定b′;2)作b′b⊥OX,且在a前10mm处确定b;3)按投影关系求得b″。
[例2]试比较如图所示三棱锥四个顶点S、A、B、C的相对位置。
1.2.2 重影点当空间两点位于对投影面的同一条投影线上时,这两点在该投影面上的投影重合,称这两点为对该投影面的重影点。
点A、B 称为对H面的重影点。
而点C、D 则称为对V 面的重影点。
1.3 各种位置点的投影1.3.1 四分角中的点二一三四第一分角中的点A;第二分角中的点B;第三分角中的点C;第四分角中的点D;一般位置点:空间点的三个坐标值X、Y、Z均不为零,称该点为一般位置点。
机械制图课件第四章

4.1 平面立体的视图画法
• 3、棱锥画法步骤 下面以正六棱锥为例来讲解棱锥的三视图画 法。 ①:(4-5-1)先画能反映特征形状的俯视图。 确定好中心线、基准线及轴线位置后在俯视 图位置上画出正六棱锥的俯视图正六边形。 ②:(4-5-2)根据投影对齐关系画底面在主 视图和左视图上的投影。 因为底面是水平面,所以它在主视图图和左 视图上均积聚投影成线。直接根据俯视图 的正六边形最左端和最右端引线来确定主 视图投影的左右端;再根据宽度来确定左 视图投影的前后端。 同时做引线确定六边形顶点在主视图和左视 图上的投影位置,再根据棱锥的高度来确 定顶点S的投影点s′、s”位置。
4.1 平面立体的视图画法
例:如图4-4-1,已知棱柱表面上点A、B、C的 投影a′、b、c′′,求这三点在其他表面 的投影点并标明可见性。 分析:棱柱找点的关键是先判断该点所在 的是哪个面。因为棱柱所有的面都有积聚性 投影,所以可以根据这个积聚投影线来确定 该点的第二个投影点。找出了第二个投影点 就能根据投影关系确定第三个投影点。 侧棱面在俯视图积聚,水平面在主视图、 左视图积聚。
4.1 平面立体的视图画法
• 2、棱柱投影分析 • 以下图的正六棱柱为例,因为其顶面、底面均为水平 面,而所有的侧面均为铅垂面,根据水平面与铅垂面 的投影特性,该棱柱在水平面上的投影将是其特征面 形状正六边形;而正平面与侧平面上的投影则为矩形
4.1 平面立体的视图画法
• 3、棱柱画法步骤 下面以4-3正六棱柱为例讲解棱柱的三视图画法。 ①:(4-3-1)根据需要在相 应位置画中心线、基准线及 轴线等。目的是先确定三个 视图的位置关系,保证视图 符合上下对正、左右平齐关 系。
工程上常见的曲面立体是回转体,所以本节要介绍的是基本回转 体圆柱、圆锥、圆球的视图画法。 由直线或曲线绕指定轴回转而成的曲面称为回转面,如图4-8所 示,该圆柱表面是由一条直母线AB绕圆柱中心轴旋转一周而成。再由 回转面或回转面与平面一起所围而成的立体就称作回转体。 因为回转面是光滑曲面,所以其投影视图仅需画出对 应投影面可见与不可见部分的分界线即可,这种分界线称为 视图的轮廓线。
机械制图第4章 截交线与相贯线

4.1 截交线
4.1.2. 回转体的截交线
1. 圆柱体的截交线
上一页
下一页
例1 求圆柱截交线
a' e'(f ') c'(d') g'(h') d" a"
解题步骤 1.分析 截平面为正垂面, 截交线的侧面投影为圆,水 平投影为椭圆; 2.求出截交线上的特殊点A、 B、 C、D;
1 .相贯线一般是封闭的空间折线或曲线。并随相交两立体表面的形状、 大小及相互位置不同而形状各异。 2.相贯线是两立体表面的分界线、共有线,是两立体表面共有点的集 合。求相贯线,也就是求两相交立体表面的共有点。
第4章 截交线和相贯线 上一页 下一页
4.2.1 平面立体与回转体的相贯线 4.2.2 回转体的相贯线 4.2.3 组合相贯线 4.2.1 平面立体与回转体的相贯线
2. 圆锥的截交线
上一页
下一页
截平面倾斜于轴线(θ =ψ),截交线为抛物线。
投影图
ψ θ
虚拟 与母线 平行切圆锥
4.1 截交线
4.1.2. 回转体的截交线
2. 圆锥的截交线
上一页
下一页
截平面倾斜于轴线(θ <ψ), 或 平行于轴线(θ =0°), 截交线为双曲线。
投影图
ψ
θ
虚拟 与轴线 倾斜 2 切圆锥
求截交线上一般位置的点方法通常采用纬圆法:在圆锥 表面上取若干个纬圆,并求出这些纬圆与截平面的交点。
4.1 截交线
4.1.2. 回转体的截交线
2. 圆锥的截交线
上一页
机械制图 点、直线、平面的投影共89页

1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
机械制图 点、直线、平面的投影
56、极端的法规,就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要,人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益, 而是为 了公共 的利益 ;一部 分靠有 害的强 制,一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ,那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
机械制图第四章 第2节 相贯线
两圆柱的轴线由垂直相交逐渐分开时,相贯线由两 条封闭的空间曲线变为一条封闭的空间曲线。即当两圆 柱部分相交时,相贯线是一条封闭的空间曲线。
相 贯 线 变 化 过 程
两圆柱内、外表面的相贯线画法
外相贯线
圆柱上开圆孔
内相贯线
两圆柱内外表面相贯线画法实例
外相贯线
圆圆柱柱开上圆开孔方孔
内相贯线
二、辅助平面法
间曲线2。)其求投一影般可位利置用点圆,柱用表“面表投面
求影点的法积”聚作性出,。用表面求点法求出。
画法相:3贯)以线判图的别中H可大、见圆W性柱面,的投整半影理径,外(分形D别轮/2)
为廓与半线两径。圆画柱弧表即面得的。积聚性投影重合, 实故质只:需以4要)圆求连弧出线代相,替贯完非线成圆的作曲正图线面。。投影。
用一辅助平面同时切割两相交体,则得两组截交线,两组截 交线的交点即为相贯线上的点。这种求相贯线投影的方法,称 为辅助平面法。
选择辅助平面的原则是:
选取特殊位置平面(一般为投影 面平行面),使其切得的截交线简单、 易画,即为直线或圆。
例10 圆柱与圆锥台相交,求其相贯线的投影。
分作析图
由图看出,圆锥台的轴线
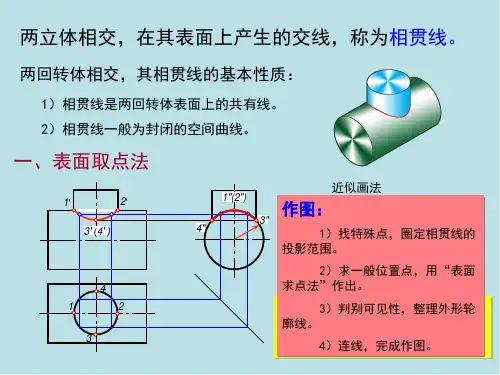
两立体相交,在其表面上产生的交线,称为相贯线。
两回转体相交,其相贯线的基本性质:
1)相贯线是两回转体表面上的共有线。 2)相贯线一般为封闭的空间曲线。
一、表面取点法
1'
2'
3' (4' )
4
1
2
3
1"(2")
近似画法
作图:
4"
3" 分析1:)找特殊点,D/圈2 定相贯线的
D
机械制图第二版第四章第4章
O A
3′
O1 A1
1″
3″
4′
2″
4″
3(4)
(4) 圆柱面上取点
利用投影的积聚性
(a)
a b
( b)
a b
×
2.圆锥体
⑴ 圆锥体的组成 由圆锥面和底面组成。
圆锥面是由直线SA绕与它相 交的轴线OO1旋转而成。 S称为锥顶,直线SA称为 母线。圆锥面上过锥顶的任一 直线称为圆锥面的素线。
圆柱面轮廓素线
③ 回转面轮廓素线 的投影 交线
平面
⒉ 利用线框,分析体表面的相对位置关系。
视图中一个封闭线框一般情况下表示一个面的 投影,线框套线框,通常是两个面凹凸不平或者是 具有打通的孔。
两个线框相邻,表示两个面高低不平或相交。
⒊ 利用虚、实线区分各部分的相对位置关系。
⒋ 几个视图对照分析以确定物体的形状
a
b
2.棱锥
⑴ 棱锥的组成
由一个底面和若干侧棱面组成。侧 棱线交于有限远的一点——锥顶。
S
C
A
B
⑵ 棱锥的三视图
棱锥处于图示位置时,其底面 ABC是水平面,在俯视图上反映实 形,正面投影和侧面投影积聚成水 平直线段 。
棱面SAC为 侧垂面,侧面投 影积聚成直线段, 正面投影和水平 a′ 投影为类似形。 另两个棱面 (SAB,SBC)为一 般位置平面,三 投影均不反映实 形。
k
k
圆的半径?
k
重点掌握:
⒈ ⒉ ⒊ ⒋
小
结
一、基本体的三视图画法及面上找点的方法。
平面体表面找点,利用平面上找点的方法。 圆柱体表面找点,利用投影的积聚性。 圆锥体表面找点,用辅助线法和辅助圆法。 球体表面找点,用辅助圆法。
机械制图第四章教案
教师教学实施方案(教案 2011~2012 学年第二学期院(系名称:教研室名称:课程名称:主讲教师:职称:教研室主任签字:教学过程:一、复习旧课1、截交线的两个基本性质。
2、订正作业,复习求曲面立体截交线的方法和步骤。
二、引入新课题上次课学习了平面立体的截交线,本次课继续学习曲面立体的截交线。
平面与曲面立体相交产生的截交线一般是封闭的平面曲线,也可能是由曲线与直线围成的平面图形,其形状取决于截平面与曲面立体的相对位置。
三、教学内容曲面立体的截交线,就是求截平面与曲面立体表面的共有点的投影,然后把各点的同名投影依次光滑连接起来。
当截平面或曲面立体的表面垂直于某一投影面时,则截交线在该投影面上的投影具有积聚性,可直接利用面上取点的方法作图。
(一圆柱的截交线1、基本类型平面截切圆柱时,根据截平面与圆柱轴线的相对位置不同,其截交线有三种不同的形状。
对照表3-1分析讲解。
2、讲解例题(1例一(例3-3如图3-15(a所示,求圆柱被正垂面截切后的截交线。
分析:截平面与圆柱的轴线倾斜,故截交线为椭圆。
此椭圆的正面投影积聚为一直线。
由于圆柱面的水平投影积聚为圆,而椭圆位于圆柱面上,故椭圆的水平投影与圆柱面水平投影重合。
椭圆的侧面投影是它的类似形,仍为椭圆。
可根据投影规律由正面投影和水平投影求出侧面投影。
边画图边讲解作图方法与步骤。
(2例二(例3-4如图3-16(a所示,完成被截切圆柱的正面投影和水平投影。
分析:该圆柱左端的开槽是由两个平行于圆柱轴线的对称的正平面和一个垂直于轴线的侧平面切割而成。
圆柱右端的切口是由两个平行于圆柱轴线的水平面和两个侧平面切割而成。
图3-16补全带切口圆柱的投影教学过程:一、复习旧课1、截交线的两个基本性质。
2、订正作业,复习求曲面立体截交线的方法和步骤。
二、导入新课上次课学习了圆柱的截交线,回转体除了圆柱意外,常用的还有圆锥、圆球。
本次课我们学习圆锥、圆球的截交线。
三、教学内容(一圆锥的截交线1、基本类型平面截切圆锥时,根据截平面与圆锥轴线的相对位置不同,其截交线有五种不同的情况。
机械制图_点线面解析
a
cb H
a’ c’ b’
X b
ac
例1 已知C在AB上,根据c求c、c。
Z
b’
b”
c’ a’
X
c’’
a”
O
YW
a c
b YH
例2 已知C在AB上使AC:CB=1:2。
a’ c’ b’
X
c
b
a
1 23
四、直线上的点的投影特性(二)
例3 判断点K是否在直线AB上。1.利用从属性
a’
k’
b’ X
XV
ax
H
a
XV H
X1
V a’
H1 ax1
A
aH1
ax
X
a
H
V b’
bx X
b’
V
bV1 V1
b’ B
bx
bx1
X
b
X1
H
H2 V1
X2
b2 b1 B
b H X1
bX
bH1
b’
X2 H1ຫໍສະໝຸດ bH1bX1V1
b H XV1 1
V X
bX
H
bX2
bX1
bH1
b
H V1 X1
五、点的相对位置
1. 判断方法 规定: X坐标大为左,小为右; Y坐标大为前,小为后; Z坐标大为上,小为下。
定理:空间两直线垂直(包括垂直相交、 交叉相交),如其中一条平行于某 一投影面,则两直线在该投影面上 的投影也垂直。
例1:BC为水平线及 A点的投影a’、 a。过A点作一 直线与BC垂直 相交。
1.直角三角形法——作图方法一般有两种:
V
a’ A X
机械制图-点线面关系
例:求一般位置直线AB和迹线平面Q的交点 如图所示,作图过程与前述完全一样。
15
3. 直线与平面垂直
直线垂直(包括交错垂直)于平面上的两条相交 直线,则该直线垂直于平面。 如图,直线AB垂直于平面P上的相交直线L1、L2 (或交错垂直于直线l1、l2),则AB垂直于P。 反之,若直线垂直于平面,则直线必垂直于该平 面上的所有直线。
38
三. 综合举例
39
常见综合几何问题有距离、角度的度 量和轨迹作图等。 距离的度量有一般位置直线的实长( 两点之距)、点线、线线、两平行平面 之间的距离等。 角度的度量有直线、平面对投影面的 倾角,两直线(相交或交错)的夹角, 线面、面面夹角等。
40
轨迹作图可使许多几何问题迎刃而解。 部分常见轨迹有:
分析:由于铅垂线EF的水平 投影积聚成一点,利用其积 聚性,它与平面的交点K的水 平投影可直接得到,然后就 可求得其他投影。 可见性判别:求出交点后, 为了使图形清晰,还需在线、 面投影的重叠部分判别其可 见性,并把被平面图形遮住 的部分画成虚线。 66
11
3) 线、面均是一般位置 例 直线AB与三角形DEF均为一般位置, 求AB与三角形CDE的交点K,并判别可见性。
44
拟定作图方法
根据以上分析,作图方法可拟定为: (1)过点D作三角形ABC的垂线,垂足M; (2)延长DM到F,并取DM=FM; (3)连接EF,作出EF与三角形ABC的交点即所 求点G。
45
具体作图
如图所示,采用一 次辅投影将三角形ABC 转化为投影面的垂直 面,在一次辅投影中 完成上述作图步骤, 求作出点G的一次辅投 影g1。返回求作g、 g′,应注意利用点G 在EF上且df//X1。如 果不用辅投影,采用 直接作垂线、求垂足, 再求EF与三角形ABC的 交点G,则作图较繁。
