电路分析基础(第四版)ppt

电路分析基础第四版

Rjk:互电阻
+ : 流过互阻两个网孔电流方向相同 - : 流过互阻两个网孔电流方向相反
特例：不含受控源的线性网络 Rjk=Rkj , 系数矩阵为对称阵。（平面电路， Rjk均为负(当网孔电流均取顺(或逆)时针方向))
网孔分析法
网孔电流法的一般步骤：
(1) 选定m=b-(n-1)个网孔，确定其绕行方向； (2) 对m个网孔，以网孔电流为变量，列写
i2 i3

G2uN 2 G3 (u N 2
u N 3 )
i4 G4uN3

i5 G5 (u N1 u N 3 )
(G1 G5 )uN1 G1uN 2 G5uN3 iS

G1uN1
(G1
G2
G3 )uN 2
G3uN3

0

量，列写其KCL方程； (3) 求解上述方程，得到n-1个节点电压； (4) 求各支路电流(用节点电压表示)； (5) 其它分析。
节点分析法
仅含有电流源、电阻的电路
节点分析法
节点分析法
含有电压源、电阻的电路
节点分析法
例试列写下图含理想电压源电路的节点电压方程。
选择合适的参考点（方程简洁）
+ Us
网孔电压升的代数和
网孔分析法
一般情况，对于具有 m=b-(n-1) 个网孔的电路，有
R11iM1+R12iM2+ …+R1m iMm=uS11
R21iM1+R22iM2+ …+R2m iMm=uS22 …
其中
Rm1iM1+Rm2iM2+ …+Rmm iMm=uSmm

电路分析(第四版)(章 (2)

R1R2
R2 R3
R3R1
R12 R23 R31 R12 R23 R31
(2-22)
第2章电路的等效变换
将式(2-22)分别除以式(2-20)、 (2-18)和式(2-19)，可得
R12
R1
R2
R1R2 R3
(2-23)
R23
R2
R3
R3R2 R1
(2-24)
R31
R3
R1
R3R1 R2
(2-25)
电源作用下，通过各电阻的电流都相同，则称此连接方式为电阻的串联。图2.1(a)所示为三个电阻串联。
设电压和电流的参考方向如图2.1(a)中所示，则根据KVL，有
U＝U1+U2+U3
(2 - 1)
第2章电路的等效变换
又由欧姆定律，可得
U1=R1I
U2=R2I
(2-2)
U3=R3I 由式(2-1)及式(2-2)可得
G2 G
I
I3
G3U
G3 G
I
(2-11)
第2章电路的等效变换
式(2-11)为并联电导的分流公式，由此可得
I１∶I２∶I３=G１∶G２∶G３上式说明，并联电导中电流的分配与电导大小成正比，即与电阻成反比。若给式(2-6)两边各乘以电压U，则得
UI=UI１+UI２+UI３
即
P=P１+P２+P３
可得
I=(G１+G２+G３)U
(2-8)
第2章电路的等效变换
若用一个电导
G=G１+G２+G３
(2-9)
来替代图2.3(a)中三个电导并联之和，如图2.3(b)所示，则在对

电子课件-《电子电路基础(第四版)》-A05-2999电子电路基础(第四版)第四章

第四章集成运算放大器的应用
二、集成运放的理想化
（1）开环差模电压放大倍数 Aud→∞。
（2）开环差模输入电阻ri→∞。（3）开环输出电阻ro→0。（4）共模抑制比KCMR→∞。（5）没有失调现象，即当输入信号为零时，输出信号也为零。
集成运放等效电路
第四章集成运算放大器的应用
三、理想集成运放工作于线性状态的特点
若将反相放大器中的反馈电阻 Rf 用电容C代替，便构成积分运算电路，如图所示。
积分运算电路
第四章集成运算放大器的应用
设电容C上初始电压为零，当输入阶跃信号时输出电压波形如图 a所示，当输入方波信号时输出电压波形如b所示。
积分运算电路输入、输出波形ห้องสมุดไป่ตู้
a)输入阶跃信号 b)输入方波信号 c)输入、输出信号实测波形
减法运算电路
第四章集成运算放大器的应用
ui1与ui2共同作用时的输出电压为当R1=R2，且Rf =R3时，上式可化简为
第四章集成运算放大器的应用
三、积分运算电路
在图所示电路中，当输入脉冲电压上升时，电容C充电，输出电压 uo(即uC)随时间增大而逐渐增大，当电荷量充足后，输出电压便不会再增大。但如果脉冲宽度较小，在输出达到稳定值之前，脉冲电压已变为零，则电容转为放电，而最终电压也变为零。电容充放电速度的快慢，
又因为理想集成运放输入电阻ri→∞,所以两个输入端输入电流也均为零,即iP = iN = 0，这一特性称为“虚断”。
第四章集成运算放大器的应用
四、集成运放组成的两种基本放大器
1. 反相放大器 (反相比例运算放大器)
反相放大器
第四章集成运算放大器的应用
放大器的电压放大倍数为式中，负号表示uo与ui反相，故称为反相放大器。又由于uo与ui 成比例关系，故又称反相比例运算放大器。若取Rf = R1 = R，则比例系数为–1，电路便成为反相器。

电路课件第一章(第四版邱关源高等教育出版社)

U
A
UAB
B
3. 关联参考方向
元件或支路的u，i 采用相同的参考方向称之为关联参考方向。反之，称为非关联参考方向。
i + U
关联参考方向
i +
U
非关联参考方向
例
i
＋
A U B
电压电流参考方向如图中所标，问：对A 、B两部分电路电压电流参考方向关联否？
答： A 电压、电流参考方向非关联；
B 电压、电流参考方向关联。
解得电流
t0 0 t 1s 1 t 2s t 2s t0 0 t 1s 1 t 2s t 2s
0 1
电源波形
i/A
1
2 t /s
-1
1
2 t /s
p( t ) u( t )i ( t ) 0 2t 2t 4 0 t0 0 t 1s 1 t 2s t 2s
0 -2
2
p/W
吸收功率
例
3. 集总参数电路
由集总元件构成的电路集总元件集总条件假定发生的电磁过程都集中在元件内部进行
d
1.2 电流和电压的参考方向
(reference direction)
电路中的主要物理量有电压、电流、电荷、磁链、能量、电功率等。在线性电路分析中人们主要关心的物理量是电流、电压和功率。
t 若u ( ) 0
t

1 2 1 2 Cu ( t ) q (t ) 0 2 2C
从t0到 t 电容储能的变化量：
1 1 1 2 1 2 2 2 WC Cu ( t ) Cu ( t 0 ) q (t ) q (t 0 ) 2 2 2C 2C

电路分析基础PPT课件

i Cdu1064105 0.4A dt
编辑版ppt
11
解答
从0.75ms到1.25ms期间
du 200 4 105 dt 0.5
i C du dt
106 4 105 0.4 A
编辑版ppt
12
例5-2
设电容与一电流源相接，电流波形如图(b)中所示，试求电
容电压。设u(0)=0。
编辑版ppt
6
❖ 把两块金属极板用介质隔开就可构成一个简单的电容器。
❖ 理想介质是不导电的，在外电源作用下，两块极板上能分别存储等量的异性电荷。
❖ 外电源撤走后，电荷依靠电场力的作用互相吸引，由于介质绝缘不能中和，极板上的电荷能长久地存储下去。因此，电容器是一种能存储电荷的器件。
❖ 电容元件定义如下：一个二端元件，如果在任一时
(2)当信号变化很快时，一些实际器件已不能再用电阻模型来表示，必须考虑到磁场变化及电场变化的现象，在模型中需要增添电感、电容等动态元件。
❖ 至少包含一个动态元件的电路称为动态电路。
❖ 基尔霍夫定律施加于电路的约束关系只取决于电路的连接方式，与构成电路的元件性质无关。
编辑版ppt
3
§5-1 电容元件
• 电容元件是一种反映电路及其附近存在电场而可以储存电能的理想电路元件。
• 电容效应是广泛存在的，任何两块金属导体，中间用绝缘材料隔开，就形成一个电容器。工程实际中使用的电容器虽然种类繁多、外形各不相同，但它们的基本结构是一致的，都是用具有一定间隙、中间充满介质（如云母、涤纶薄膜、陶瓷等）的金属极板（或箔、膜）、再从极板上引出电极构成。这样设计、制造出来的电容器，体积小、电容效应大，因为电场局限在两个极板之间，不宜受其它因素影响，因此具有固定的量值。如果忽略这些器件的介质损耗和漏电流，电容器可以用电容元件作为它们的电路模型。

电路分析基础完整ppt课件

可否短路？
恒压源特性中不变的是：__ __U_S________
恒压源特性中变化的是：_____I________
___外__电__路__的__改__变____ 会引起 I 的变化。
I 的变化可能是 _大__小____ 的变化，
或者是__方__向___ 的变化。
22.04.2020
.
24
电工基础教学部
电路的基本分析方法。
22.04.2020
.
电工基础教学部
4
目录
电工电子技术
1.1 电路元件
1.1.1 电路及电路模型
电路——电流流通的路径。
1.电路的组成和作用
电路是由若干电路元件或设备组成的，能够传输能量、转换能量；能够采集电信号、传递和处理电信号的有机整体。
①电路的组成：
电源信号源
中间环节
目录
电工电子技术
②理想电流源（恒流源): RO= 时的电流源.
Ia
Uab
外
Is
U RL
特
I性
b
o
IS
特点：（1）输出电流 I 不变，即 I IS （2）输出电压U由外电路决定。
22.04.2020
.
电工基础教学部
25
目录
电工电子技术
（3）恒流源的电流 IS为零时，恒流源视为开路。
IS=0
（4）与恒流源串联的元件对外电路而言为可视为短路。
E
+ _
R2
Is
a
R1 b
Is
a R1
b
例设: IS=1 A
则: R=1 时， U =1 V Is R=10 时， U =10 V
I UR

电路分析基础 739页PPT文档

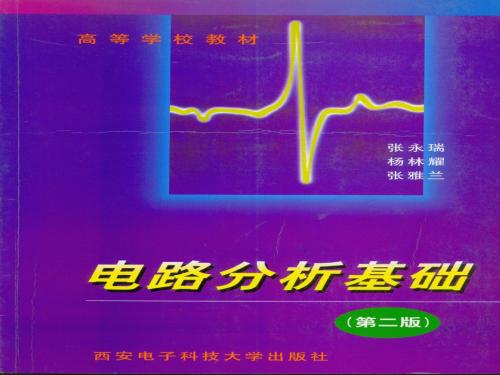
1 kA 10 3 A
1 mA 10 3 A
1 uA 10 6 A
电流不但有大小，而且有方向。规定正电荷运动的方向为电流的实际方向。在一些很简单的电路中，如图 1.1-4，电流的实际方向是显而易见的，它是从电源正极流出，流向电源负极的。但在一些稍复杂的电路里，如图 1.2-3 所示桥形电路中，R5上的电流实际方向就不是一看便知的。不过，R5 上电流的实际方向只有 3 种可能：(1) 从a流向b; (2) 从b流向a; (3) 既不从a 流向b, 又不从b流向a(R5上电流为零)。所以说，对电流这个物理现象可以用代数量来描述它。简言之，电流是代数量，当然可以像研究其它代数量问题一样选择正方向，即参考方向。假定正电荷运动的方向为电流的参考方向，用箭头标在电路图上。今后若无特殊说明，就认为电路图上所标箭头是电流的参考方向。对电路中电流设参考方向还有另一方面的原因，那就是在交流电路中电流的实际方向在不断地改变，因此很难在这样的电路中标明电流的实际方向，而引入电流的参考方向也就解决了这一难题。在对电路中电流设出参考方向以后，若经计算得出电流为正值，说明所设参考方向与实际方向一致；若经计算得出电流为负值，说明所设参考方向与实际方向相反。电流值的正与负在设定参考方向的前提下才有意义。
电流的参考方向设成从a流向b, 电压的参考方向设成a 为高电位端，b为低电位端，这样所设的电流电压参考方向称为参考方向关联。设在dt时间内在电场力作用下由a点移动到b点的正电荷量为dq, a点至b点电压u意味着单位正电荷从a移动到b点电场力所做的功，那么移动dq正电荷电场力做的功为dw=udq。电场力做功说明电能损耗，损耗的这部分电能被ab这段电路所吸收。
例1.2-1 如图 1.2-7(a)所示电路，若已知2s内有4C正电荷均匀的由a点经b点移动至c点，且知由a点移动至b点电场力做功8J，由b点移动到c点电场力做功为12J。

电路分析基础第4章课件.ppt

4.1 正弦量
大小和方向都按正弦规律变化的电压和电流称为正弦电压或正弦电流，常称为正弦量。其相应的波形称为正弦波。
正弦电流 i I m cos(t i ) 的波形如图所示。
4.1.1 正弦量的三要素
1．频率、周期和角频率
要完全描述一个正弦量，必须知道正弦量的 I m、、i
这三个物理量称为正弦量的三要素。
N
、
i
eL
i
u
eL L
u
磁链匝数
磁通
电感系数 L NΦ
ii
单位：亨（H，mH)
N
由电磁感应定律和楞次定律，感应电动势与磁链之间的关系为
eL
d
dt
N d dt
L di dt
则
u
eL
L di dt
2.电压与电流的关系设电压、电流的参考方向关联，有
u L di dt
设 i 2I cost ,代入上式有
2
f 314 50Hz u(0) 100cos 100cos30 86.6V
2
6
该正弦电压的波形如图所示。若
u 100 cos(314 t 30 )V
波形如何？
【例4.2】已知同频率正弦电流分别为
i1
20 c os (314t
)A 3
i2
10sin(314t
)A 4
试求（1）画出波形图、求相位差；（2）若以 t 0.005s
2
2U cos(t u )
（3）有效值
感抗
令 X L L 单位（Ω）
则 U I XL
容抗 X L L 是频率的函数，表示电感在电路
中因感抗随着频率变化而起的作用而不同。

电路分析基础(第四版)ppt