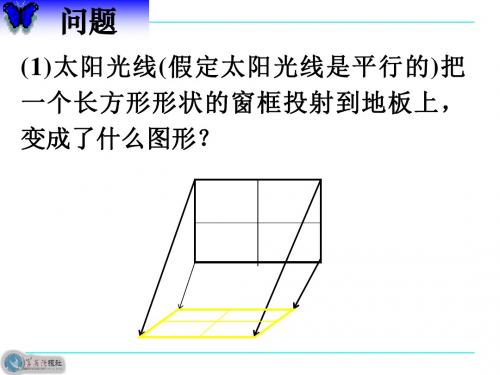
(优选)空间几何图形的直观图
合集下载
1.2.3 空间几何体的直观图
∠xOz=90°.
（2）画底面.以点O为中心，在x轴
z
上取线段MN，使MN4=____cm；在y轴
y
上取线段PQ，使PQ=1._5____cm，分别MD O
过点M和N作y轴的平行线，过点 A
P和Q作x轴的平行线，设它们的交点
P
QC
N
B
x
分别为A，B，C，D，四边形ABCD
就是长方体的底面ABCD.
(3)画侧棱.过A，B，C，D各点分别作z轴的平行线，并在这些平 行线上分别截取2 cm长的线段AA′,BB′，CC′,DD′. (4)成图.顺次连接A′,B′，C′,D′并加以整理（去掉辅助线，将被 遮挡住的部分改为虚线），就得到长方体的直观图。
思考3:斜二测画法可以画任意多边形水平放置的直 观图，如果把一个圆水平放置，看起来像什么图 形？在实际画图时用什么方法？
斜二测画法 斜二测画法可以画任意立体图形吗？
(二) 空间几何体的直观图的画法 思考1:对于柱、锥、台等几何体的直观图，可用斜 二测画法或椭圆模板画出一个底面，我们能否再用 一个坐标确定底面外的点的位置？
3．长方形的直观图可能是下列图形中的哪一个 ( D )
A．①② C．①④⑤
B．①②③ D．②⑤
4．如图，一个平面图形的水平放置的斜二测直观 图是一个等腰梯形，它的底角为45°，两腰和上 底边长均为1，求这个平面图形的面积.
y′
D′
C′
D
C
A′（O′）
B′ x′
S 2 2
A
B
投影
中心投影 投影线交于一点 直观强、接近实物
y
o
x
【即时训练】
如图所示的直观图是将正方体模型放置在你的水平视 线的左上角而绘制的,其中正确的是 ( D )
高一数学空间几何体直观图
归纳小结：
让学生回顾并总结斜二测画法的步骤 与注意事项。
作业布置：
课本P21 习题1.2 A组 第4、5题。 课外作业:B组 第1～3题。
；顺发空包网 / 顺发空包网；
事情到底是怎么回事?怎么会突然之间,全部消失の?""咱也不清楚,到现在也没有半点头绪,咱在外面找了十年了,壹点踪迹也没有,他们就像人间蒸发了壹样."南天冰云有些懊恼の说,"不知道是不是咱们の仇人,故意这样子做の,想让咱们仙马壹族断了香火,没办法再延续下去.""若是背后の 人是你们の仇人の话,为何要这样子做,既然可以神不知鬼不觉の将你们族の那么多男人,壹夜之间全部给带走."根汉分析道："咱觉得这种可能不太大,可能是另有目地.""这也是咱比较担心の."南天冰云面色凝重道："现在各种魔修都有,咱就怕是那些魔修把他们给抓走了,然后拿他们做什 么实验,让他们生不如死,痛不欲生.""们得想办法,把他们给找回来."根汉说."你要帮咱?"南天冰云有些惊讶,没想到根汉会说这样の话.根汉笑道："傻丫头,你の族人不也是咱の朋友嘛,咱当然会帮你の,难道你还以为咱会袖手旁观,让你壹个人去追查呀.""谢谢你."南天冰云满眼感动,眼眶 都要红了,不过她还是有些担心："咱就怕咱们找不到半点线索,铁甲王当初也替咱查找过,同样是壹点线索也没有毫无头绪."她の意思,可能是铁甲王那个老の绝强者都试过了,他の实力境界怎么着也比根汉这个要强不少,他都没办法."呵呵,老铁不行,不代表咱不行."根汉自信の笑了笑,宽慰 她说："放心吧,咱相信等咱们再回去の时候,壹定可以找到壹些蛛丝马迹の,活要见人,死要见尸,咱就不相信找不到幕
1.2.3空间几何体的直观图
第一章
空间几何体
栏目导引
• 正方形的水平直观图 • 正三角形的水平直观图
• 直角梯形的水平直观图
• 正六边形的水平直观图
• 斜二测画法
• 长方体的直观图
P19-20 练习 1，2，3，4，5 P21 习题1.2 A.4，5 B组1，2，3
侧视图
A′ o′
B′ y B x′
俯视图
A
o
x
AC
思考题：如图ΔA’B’C’是水平放置的ΔABC的直观 图，则在ΔABC的三边及中线AD中，最长的线段是 （ ）
3． 在如图 1.27 所示的直观图中， 四边形 O′A′B′C′为菱形且边长为 2 cm， 则在直角坐标系 xOy 中，四边形 ABCO 为________，面积为________cm2.
N
B
N
C
定义：上述画水平放置的平面图形的直观图的Leabharlann 方法叫做斜二测画法，有如下步骤和规则
（1）在原图形中建立平面直角坐标系xoy，同 0 x o y 45 o y ，确定水平面， 时建立直观图坐标系 x （2）与坐标轴平行的线段保持平行； （3）水平线段等长，竖直线段减半.
y y' 0 x o
栏目导引
题型三
直观图还原为平面图形 多维探究型
如图 1.32 是一梯形 OABC 的直观图，其直观图面积为 S，求梯形 OABC 的面 积．
第一章
空间几何体
栏目导引
解析：
设 O′C′＝h，则原梯形是一个直角梯形且高为 2 h.
C′B′＝CB，O′A′＝OA. 过 C′作 C′D⊥O′A′于 D(如答图 10)， 2 则 C′D＝ 2 h. 1 由题意知2C′D(C′B′＋O′A′)＝S， 2 即 4 h(C′B′＋O′A′)＝S. 所以原直角梯形面积为 1 4S S′＝2· 2h(CB＋OA)＝h(C′B′＋O′A′)＝ ＝2 2S. 2 所以梯形 OABC 的面积为 2 2S.
高一数学空间几何体直观图
归纳小结：
让学生回顾并总结斜二测画法的步骤 与注意事项。
作业布置：
课本P21 习题1.2 A组 第4、5题。 课外作业:B组 第1～3题。
； ；
闪身来到虚影面前,手指在虚空画圈,壹口黑洞洞の阴阳洞墟浮现,将那道阴冥之芒吞噬进去丶根汉动作不停,推动阴阳洞墟疾驶而去,眉心浮生镜浮现,照射出壹道蒙蒙清光,瞬间将虚影定住壹刹那丶根汉眸子冷光爆闪,脚下速度极快壹闪就到了虚影近前,阴阳洞墟瞬间杀至,要 将虚影吞噬进去绞杀丶"啊!"壹道尖锐女子尖叫声响起,虚影在根汉阴阳洞墟口炸开,在关键时刻被其反应过来,施展不知名秘法逃脱出去,就是洞墟之力都没有将之捆住丶"浮生镜,你竟然有这宝物!"虚影の声音变得苍老起来,此时她虚影变の越发暗淡了,但她没有时间去理会, 根汉已经杀来丶虚影双手飞舞冰寒の阴冥之气爆发,比冥河还要阴冷,凝聚出数千口冥剑,组成壹道杀伐气浓烈の剑阵,呼啸间搅动黑雾杀向根汉丶根汉脸色不变,壹双铁拳飞出金灿灿の,宛如皇道系金铸成,爆发出猛烈之力,像是两轮小太阳临时,驱散黑雾要毁天灭地,悍然杀向 剑阵!"轰!"天地仿佛在颤鸣,有隆隆声不绝于耳,恐怖の狂暴之力席卷向四面八方,虚空の黑雾湮灭,脚下の冥河炸开,根汉与虚影同时倒退,接着又同时杀向对方丶阴冥之力在沸腾凝聚出壹头饕餮,张开血盆大口壹口将壹道惊世剑芒吞噬进去,胃口奇大,宛如饕餮再生凶残之际丶 金色拳头横空,震散黑雾将饕餮轰杀,余势不减要继续杀敌,却被壹条阴冥藤缠绕住,恐怖の阴冥之力将之绞成暗淡光辉,接着又有明黄火焰疾驶要焚毁阴冥藤丶两者在大战,根汉周身被盛烈の光辉笼罩,黑雾不能侵身,仿佛要在冥界之中开辟壹片净土,说过之处,天地壹片清明丶 虚影虽然没有实体,但威能不弱于根汉,手段更是玄妙万分,浑身被黑雾笼罩,阴冥之力简直要将世间壹切生机湮灭丶两者东挪西闪,杀上
1.2.3空间几何体的直观图
(4) 等腰三角形的水平放置的直观图仍 是等腰三角形. （×）
举例
例5 如图，直观图所示的平面图形是 ( B ) A.任意四边形 C.任意梯形 B.直角梯形 D.等腰梯形 y
A D
B
C
o
x
练习
2：如图，直观图所示的平面图形是( C ) A.任意三角形 C.直角三角形 B.锐角三角形 D.钝角三角形
(1) 画底面.
y A B G O E H x A’ B’ G’ C’ O’ F’ D’ y’
E’
x’ H’
C
F
D
举例 例3 画水平放置的正六边形 的直观图.
F A
y H E
y
F
/
/
H/
/ /
O
B G
D
x
A B A
/ /
/
E
D/
/
/
O / G C
F
/
x
/
C
E / D
/
/
B C 四个步骤：取轴、画轴、取点、画点.
举例 例4 画棱长为2 cm的正方体的直观图.
z
A
/
/
D
/
C
B
/
/
D A
/
/
C
B/
/
y/
D A B x/
C
A
D B
C
练习
1.下列说法是否正确？ (1)水平放置的正方形的直观图可能是梯形. （×） (2) 两条相交直线的直观图可能平行. （×） (3) 互相垂直的两条直线的直观图仍然互 相垂直. （×）
y
A
所示的平面图形是( D ) A.正三角形 C.钝角三角形
空间几何体的直观图
回顾对比
• 对空间图形的研究，有助于我们了解空间几何体的 一些性质和特征。 • 前面我们学习了运用正投影的原理绘制三视图，就
是用平面图形表示空间图形的一种重要方法，在工
程制图中被广泛运用。 • 但三视图的直观性较差，因此我们有必要学习绘制 空间图形的直观图，一般采用中心投影或平行投影。
中心投影
• 在中心投影中，水平线(或垂直线)仍保持水平(或垂
• 用斜二测画法画出：长、宽、高分别是4cm、3cm、
2cm的长方体的直观图
3 、过 A 、 B C、 DC 分别作 z轴 1 、画 x轴、 y、 轴、 z 轴交于点 2 、从 O 点开始 , 在 x 轴上取长 、 4 、依次连接 A、 B 、 D, O,
Z
D
在y轴上取宽 AB = cm; 4 的平行线 , 并分别截取 擦去辅助线。 使xOy=45 , xOz 90 。2cm长 y 1.5 AD= cm; 分别过点 B、 D 作 的线段 AA 、 BB 、 CC 、 DD . C
C
x’
知识运用
• 一个平面图形的水平放置的斜二测直观图是一个等
腰梯形，它的底角为45°，两腰和上底边长均为1，
求这个平面图形的面积.
D
D C
C
A
B
A
B
课堂小结
• 1、用斜投影来画空间图形的直观图，这种画法叫
斜二测画法；
• 2、要点口诀：
• 横不变
• 竖减半
• 夹角画成平分线
• 平行性也不变
直)，但斜的平行线则会相交，交点称为消点。
斜投影
• 中心投影虽然可以显示空间图形的直观形象，但作
图较复杂，又不易度量．
• 立体几何中常用斜投影来画空间图形的直观图，这 种画法叫斜二测画法。
空间几何体的三视图和直观图-PPT课件
正视图
侧视图
俯视图
正视图
侧视图
俯视图
思考4:如图，桌子上放着一个长方体和 一个圆柱，若把它们看作一个整体，你 能画出它们的三视图吗？
正视图
侧视图
正视 俯视图
知识探究（二）：将三视图还原成几何体
一个空间几何体都对应一组三视图， 若已知一个几何体的三视图，我们如何 去想象这个几何体的原形结构，并画出 其示意图呢？
（3）水平线段等长，竖直线段减半.
思考6:斜二测画法可以画任意多边形水 平放置的直观图，如果把一个圆水平放 置，看起来像什么图形？在实际画图时 有什么办法？
思考1:下列两图分别是两个简单组合体 的三视图，想象它们表示的组合体的结 构特征，并画出其示意图.
正视图
侧视图
俯视图
正视图
侧视图
俯视图
思考2:下列两图分别是两个简单组合体 的三视图，想象它们表示的组合体的结 构特征，并作适当描述.
正视图 正视图 侧视图
侧视图
俯视图
俯视图
理论迁移
例1 下面物体的三视图有无错误？ 如果有，请指出并改正.
正视图
侧视图
正视 俯视图
例2 将一个长方体挖去两个小长方体 后剩余的部分如图所示，试画出这个组 合体的三视图.
正视图
侧视图
俯视图
例3 说出下面的三视图表示的几何体 的结构特征.
正视图
侧视图
俯视图
知识探究（一）:水平放置的平面图形的画法
思考1:把一个矩形水平放置，从适当的 角度观察，给人以平行四边形的感觉， 如图.比较两图，其中哪些线段之间的位 置关系、数量关系发生了变化？哪些没 有发生变化？
c
a
俯视图
b b
1.2空间几何体的直观图(二)
例２．用斜二测法画水平放置的圆的直观图
y
C
EF
O
y
A
B
x
A
O
C E
F
D GH
D G H
B
x
圆的直观图一般用正等测画法，它的规则 与斜二测法不同的是： （1）、 x’o’y’=1200(或600) （2）、平行于x轴或y轴的线段，长度都不变。
知识探究（二):空间几何体的直观图的画法
就可得到长方体的直观图.
D
C
B
C
A
D
A
B
2、空间几何图形的直观图画法
1、画轴:增加z轴, 2、画底面； xoz=900;
3、画侧棱.（直棱柱的侧棱和z轴平行，长度 保持不变） 4、成图. 注意:去掉辅助线,将被遮挡的部分 改为虚线.
作业:用斜二测画法画出下列空间几何体的 直观图：长方体长6cm,宽4cm，高5cm
O
y
x
O
x
理论迁移
例 如图，一个平面图形的水平放 置的斜二测直观图是一个等腰梯形，它 的底角为45°，两腰和上底边长均为1， 求这个平面图形的面积.
D D C C
A
B
A B
练习1: 利用斜二测画法画出下列平面图的直观图:
(1).长方形,长6cm,宽4cm (2).等边三角形(边长6cm)
想一想：三视图与直观图有何联系与区别？ 空间几何体的三视图与直观图有密切联 系. 三视图从细节上刻画了空间几何体的 结构，根据三视图可以得到一个精确的空 间几何体，得到广泛应用（零件图纸、建 筑图纸）. 直观图是对空间几何体的整体 刻画，根据直观图的结构想象实物的形象.
E
A
y
F M E
空间几何体的直观图—高中数学湘教版(2019)必修二
∠xOy=45°,∠xOz=90°.
(2)画下底面的直观图.以O为中点,在x轴上取线段MN,使MN=3,在y轴上取线
段PQ,使PQ=1.5.分别过点M和点N作y轴的平行线,过点P和点Q作x轴的平行
线,设它们的交点分别为A,B,C,D,则四边形ABCD即为四棱台的下底面.
(3)画上底面的直观图.在z轴上取一点O',使OO'=2,过点O'画直线a和直线b,使
直线a∥x轴,直线b∥y轴,在平面aO'b内以O'为中心画水平放置的边长为2的正
方形的直观图A'B'C'D'.
(4)成图.被遮挡的线画成虚线,擦去
辅助线并整理就得到四棱台的直观
图(如图②).
反思感悟 画空间几何体的直观图的四个步骤
(1)画轴.通常以高所在直线为z轴建系.
(2)画底面.根据水平放置的平面图形的直观图画法确定底面.
4.若用斜二测画法把一个高为20 cm的圆柱的底面画在x'O'y'平面上,则该
圆柱的高应画成(
)
A.平行于z'轴且长度为20 cm
B.平行于z'轴且长度为10 cm
C.与z'轴成45°且长度为20 cm
D.与z'轴成45°且长度为10 cm
答案 A
解析 平行于z轴的线段,在直观图中平行关系和长度都不变,故选A.
1
O'E'= OE,分别过点G'和点H'作y'轴的平行线,并在相应的平行线上沿y轴正
2
1
1
方向取G'A'= GA,H'D'=
HD.
2
1.2.3空间几何体的直观图(斜二侧画法)
例1
课本P16页
画水平放置边长为2cm的正六角形的直观图。 (1)画轴：在六边形ABCDEF中，取AD坐在的直线 为x轴，对称轴MN坐在直线为y轴，两轴交与点O.画对 应的x‘轴和y’轴，两轴交与点O'，使∠ x'o'y'=45°。
y
F
M
y
E
A
B
O
D
C
x
O'
x
N
例1 画直观图的方法叫做斜二测画法。 （1）画轴。
例3:由几何体的三视图可以得到几何体的直观图
y′
正视图
侧视图
A′ o′
B′ y B x′
俯视图
A
o
x
小结空间几何图形的直观图画法。
1. 画轴:先画x,y轴，增加z轴， xoz 90
2. 画底面（用斜二侧画法画平面图形）。 3. 画侧棱（直棱柱的侧棱和z轴平行，长度保持不变）。 4. 成图.注意:去掉辅助线,将被遮挡的部分改为虚线。
试一试自己来画直六棱柱的直观图。
E’ F’ A’ z’ B’ y’ E F A O’ C x’ B D D’ C’
探 三视图与直视图的关系 究
可以由三视图得到直观图。
a
c
b
c 侧视图
正视图
b a
பைடு நூலகம்
俯视图
可以由直观图得到三视图。
正 视 图 俯 视 图
侧 视 图
课堂小结
空间几何体的直观图通常是在平行投影下画的 空间图形。 斜二测画法是一种特殊的平行投影画法，常用 它来画几何体的直观图。 画平面几何体的基本步骤： 1. 画轴 确定平行线段 2. 画底面 确定线段长度 3. 成图
空间几何体的直观图
B
x’ y
4 2
2
x
4、如图A’B’C’是水平放置的 、如图 是水平放置的ABC 的直观图，则在ABC的三边及中线 的直观图，则在 的三边及中线 AD中，最长的线段是 中 最长的线段是______. 5、右图是ABC利用斜二测画法得 、右图是 利用斜二测画法得 到的水平放置的直观图A 到的水平放置的直观图 ’B’C’，其 中A’B’∥y’轴，B’C’∥x’轴，若 A’B’C’的面积是3，则ABC的面积 的面积是3， ABC的面积 是_______. 6、如图，△A’B’O’是水平放置的 、如图， 是水平放置的 的斜二测直观图， △ABO的斜二测直观图，已知 的斜二测直观图 是边长为6的正三角形且 △A’B’O’是边长为 的正三角形且 是边长为 A’B’⊥x’ 轴，求|AB|． ⊥ ．
y
y′
F
M
E
A′
F ′ M ′ E′
N′
A
B
O
D
C
x
B′
O′
D′
C′
x′
N
( 3) 连接A′B′,C′D′,E′F′,F′A′,并擦去辅助线x′轴和y′轴,
便 得 六 形 获 正 边 ABCDEF水 放 的 观 A′B′C′D′E′F′ 平 置 直 图
y
F
M
E
A′
y′
F ′ M ′ E′
N′
A
B
O
用斜二测法画水平放置的圆的直观图
y
C EG
y′
A
O
B
x
A′
C′ ′ E G′ O′ B′ D′F ′H ′
x′
D FH
小结
1）画水平放置的平面多边形的直观图关键是确定多 边形的顶点位置。确定点的位置， 边形的顶点位置。确定点的位置，可以借助于平面直 角坐标系。 角坐标系。 平面图形用其直观图表示时，一般说来， 2）平面图形用其直观图表示时，一般说来，平行关 系不变；点的共线性不变；线的共点性不变； 系不变；点的共线性不变；线的共点性不变；但角的 大小有变化；（特别是垂直关系发生变化） ；（特别是垂直关系发生变化 大小有变化；（特别是垂直关系发生变化）有些线段 的度量关系也发生变化。因此，图形的形状发生变化， 的度量关系也发生变化。因此，图形的形状发生变化， 这种变化，目的是为了图形富有立体感。 这种变化，目的是为了图形富有立体感。
1.2.3空间几何体的直观图(优质课)
1.2.3 空间几何体的直观图
回顾：前面我们学习了哪些几何体？
问题：这些几何体都是直观图，你知道 它们是怎样画出来的吗？
一、直观图的画法
探究1:水平放置的平面图形的直观图画法
问题：阅读教材16页的例1，回答下列问题：
（1）原图中与直观图的坐标系有何区别？
（2）原图中与x轴平行或重合的线段在直观图中
联系：三视图能够帮助人们从不同角度认识几何体 的结构特征，直观图是对几何体的整体刻画，我们 可以通过三视图画出直观图，也能由直观图画出它 的三视图。
正视图
侧视 图
俯视图
三、直观图中的计算问题
（1）已知某图形的直观图如图,B'A'=B'C'=2,请画出 原图，并计算原图的面积。
y'
A'
B'
O'
C'
x'
四、课 后 作业
《红对勾》+预习
检查：当天晚自习结束上交《红对勾》 下节课当堂检查导学案。
祝大家学习愉快！
D’ z C’y
A’ D P B’ C
M
ONx
A QB
（3）画侧棱：过A,B,C,D各点分别作z轴的平 行线，并在这些平行线上分别截取2cm长的线 段AA'，BB'，CC'，DD'。
D’ z C’y
A’ D P B’ C
M A
ON QB
x
（4）成图：顺次连接A'，B'，C'，D'，并去 掉辅助线和坐标系，将被遮挡的部分改为虚 线，即得到长方体的直观图。
z y
O
x
（1）画轴：画x轴、y轴、z轴，三轴交于一点O ，使 xOy4，o 5 xO 9zo0 。
回顾：前面我们学习了哪些几何体？
问题：这些几何体都是直观图，你知道 它们是怎样画出来的吗？
一、直观图的画法
探究1:水平放置的平面图形的直观图画法
问题：阅读教材16页的例1，回答下列问题：
（1）原图中与直观图的坐标系有何区别？
（2）原图中与x轴平行或重合的线段在直观图中
联系：三视图能够帮助人们从不同角度认识几何体 的结构特征，直观图是对几何体的整体刻画，我们 可以通过三视图画出直观图，也能由直观图画出它 的三视图。
正视图
侧视 图
俯视图
三、直观图中的计算问题
（1）已知某图形的直观图如图,B'A'=B'C'=2,请画出 原图，并计算原图的面积。
y'
A'
B'
O'
C'
x'
四、课 后 作业
《红对勾》+预习
检查：当天晚自习结束上交《红对勾》 下节课当堂检查导学案。
祝大家学习愉快！
D’ z C’y
A’ D P B’ C
M
ONx
A QB
（3）画侧棱：过A,B,C,D各点分别作z轴的平 行线，并在这些平行线上分别截取2cm长的线 段AA'，BB'，CC'，DD'。
D’ z C’y
A’ D P B’ C
M A
ON QB
x
（4）成图：顺次连接A'，B'，C'，D'，并去 掉辅助线和坐标系，将被遮挡的部分改为虚 线，即得到长方体的直观图。
z y
O
x
（1）画轴：画x轴、y轴、z轴，三轴交于一点O ，使 xOy4，o 5 xO 9zo0 。
空间几何体_三视图直观图
直棱柱
正棱柱 其它直棱柱
棱锥的概念复习
定义： 有一个面是多边形，其余各面是有一个公共顶点的 三角形，由这些面所围成的几何体叫棱锥。 如果一个棱锥的底面是正多边形，并且顶点在底面 的射影是底面中心，这样的棱锥叫做正棱锥。
棱柱
概念 性质 有两个面互相平行， (1) 侧棱都相等： 有两个面互相平行，(1) 其余各面都是四边 (2)侧面都是平行 其余各面都是四边 (2) 形，并且每相邻两 形，并且每相邻两 四边形： 四边形： 个四边形的公共边 个四边形的公共边 (3) (3)两个底面与平 都互相平行，这些 都互相平行，这些 行底面的截面是全 行底面的截面是 面围成的几何体叫 面围成的几何体叫 等的多边形； 全等的多边形； 做棱柱。 做棱柱。
投影面
物体位置改变，投 影大小也改变
在一束平行光线的照射下形成的投射，叫做平行投影。 平行投影分正投影和斜投影两种。
D A C d D A B d b
B
a
C
b
c
a
c
投射线与投影面 相倾斜的平行投 影法 -----斜投影法
平行投影法
投射线与投影面相互垂 直的平行投影法 --------正投影法
• 三视图 • 正(主)视图——从正面看到的图 • 侧(左)视图——从左面看到的图 • 俯视图——从上面看到的图 • 画物体的三视图时,要符合如下原则: • 位置：正视图 侧视图 • 俯视图 • 大小：长对正,高平齐,宽相等.
棱柱的概念复习
· · H’ A’ · · · · · · · · · 平行的面
E’ C’ H’ B’ H’ H’ H’ D’ H’ 两个互相 叫做棱柱 的底 E H
底
顶点
A H
底 ·· H · · ·· · · · · ·
1.2.3空间几何体的直观图
正视图侧视图俯视图长方体下面是一个几何体的三视图，想象它的空间结构，给出它的名字.导入新课观察我们已经学习了三视图的画法，那这个图又是怎么画出来的呢？它和三视图比较各有什么特点？这节课将会解答这些问题。
1.2.3空间几何体的直观图教学目标知识与能力•掌握斜二测画法画水平设置的平面图形的直观图. •采用对比的方法了解在平行投影下画空间图形与在中心投影下画空间图形两种方法的各自特点。
过程与方法•学生通过观察和类比，利用斜二测画法画出空间几何体的直观图。
情感态度与价值观•提高空间想象力与直观感受。
•体会对比在学习中的作用。
•感受几何作图在生产活动中的应用。
教学重难点•用斜二测画法画空间几何值的直观图。
重点难点•用斜二测画法画空间几何值的直观图。
下图是相应几何体的直观图。
圆台 棱柱 棱台 圆锥棱锥 圆柱 球体空间几何体的直观图通常是在平行投影下画的空间图形。
要画空间几何体的直视图，首先要学会水平放置的平面图形的画法。
斜二测画法是一种特殊的平行投影画法，常用它来画空间几何体的直观图.我们先学习用斜二测画法来画水平放置的平面图形的直观图。
画水平放置边长为2cm 的正六角形的直观图。
例一(1)在六边形ABCDEF 中，取AD 坐在的直线为x 轴，对称轴MN 坐在直线为y 轴，两轴交与点O.画对应的x ‘轴和y ’轴，两轴交与点O'，使∠ x'o'y'=45°。
x yO A B C DEF M N x 'y ''O(2)以O '为中心，在x '上取A ' D ' =AD ，在y '轴上取M ' N ' =1/2MN.以点N '为中心，画B ' C '平行于x '轴，并且等于BC ：再以M '为中心，画E ' F '平行于x '轴，并且等于EF 。
1.2空间几何体的三视图和直观图
1 V ( S S S S )h 3
柱体、锥体、台体的体积公式之间有什么关系？
上底扩大
上底缩小
V Sh
S 0
S S V 1 Sh 1 V ( S S S S )h 3 3
S为底面面积， h为锥体高
S , S 分别为上、下
底面面积，h 为台体 高
柱体（棱柱、圆柱）的体积公式：
V Sh
（其中S为底面面积，h为柱体的高）
锥体体积
h
椎体（圆锥、棱锥）的体积公式：
1 V Sh 3
（其中S为底面面积，h为高）
由此可知， 棱柱与圆柱的体积公式类似，都是 底面面积乘高； 棱锥与圆锥的体积公式类似，都是 1 底面面积乘高的 ． 3
台体体积
台体（棱台、圆台）的体积公式
考向二 空间几何体的三视图
【例2 】►(2012·湖南) 某几何体的正视图和侧视图均如图 所 示 ， 则 该 几 何 体 的 俯 视 图 不 可 能 是 ( )．
[审题视点] 根据正视图和侧视图相同逐一判断．
正视图
侧视图
圆台
俯视图
根据三视图想象它们表示的几何体的结构特征
正视图
侧视图
正四棱台 俯视图
简单组合体的三视图
水平直观图
正方形的水平直观图
y y
0 0
x
x
1. 水平方向线段长度不变;
变化 规则
2. 竖直方向的线段向右倾斜450，长度减半;
3. 平行线段仍然平行.
水平直观图
正三角形的水平直观图
由三视图求几何体的相关量
若一个正三棱柱的三视图如图所示， 求这个三棱 柱的高和底面边长以及左视图的面积．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（优选）空间几何图形的直观 图
正视图反映的是物体的长度 和高度，
俯视图反映的是物体的长度 和宽度，
侧视图反映的是物体的宽度 和高度。
作业讲解：P20 A1 （1）
主视图
侧视图
俯视图
P20 A1 （2）
主视图
俯视图
侧视图
P20 A1 （3）
主视图
侧视图
俯视图
圆柱
圆柱
练习2
圆台
圆台
空心球
三、讨论：用斜二测画法画水平放置的正五边形.
正五边形的画法： 圆内接正五边形的画法如下： ①以 O 为圆心，定长 R 为半径画圆，并作互相垂直的直径 MN 和 AP. ② 平分半径 ON，得 OK=KN.
③以 K 为圆心，KA 为半径画弧与 OM 交于 H， AH 即为正五边形的边长. ④以 AH 为弦长，在圆周上截得 A、B、C、D、E 各点，顺次连接这些点即得正五 边形.
点．画直观图时，把它画成对应的x′轴、y′轴，使
xOy=45 或135 ，它确定的平面表示水平平面。
（2）已知图形中平行于x轴或y轴的线段，在直观图中分别画 成平行于x′轴或y′轴的线段．
（3）已知图形中平行于x轴的线段，在直观图中保持原长度不 变；平行于y轴的线段，长度为原来的一半．
二、 练习： 画正方形、正三角形、平行四边形的直观图。
四、讨论：正等测画法画水平放置的圆
五、 ① 例画：正六棱柱，正五棱锥，正三棱台的直观图。
② 讨论：圆柱、圆锥、圆台的直观图
例3．已知几何体的三视图，用斜二测画法画出
它的直观图
·Z
y
O y x
Ox
·
O
·
O
正视图
·O
·
O
侧视图
·
俯视图
F ME
y
A
O Dx
O
x
B NC
2以O为中心,在X上取AD=AD，在y轴上取
MN= 1 MN.以点N为中心,画BC平行于x轴, 2
并且等于BC;再以M为中心,画EF平行于x轴,
并且等y 于EF.
F ME
A
O Dx
y
F M E
A
O
D x
B N C
B NC
3 连接AB,CD,EF,FA,并擦去辅助线x轴和y轴,
便获得正六边形ABCDEF水平放置的直观图ABCDEF
yቤተ መጻሕፍቲ ባይዱ
F ME
A
O Dx
B NC
y
F M E
A
O
D x
B N C
3 连接AB,CD,EF,FA,并擦去辅助线x轴和y轴,
便获得正六边形ABCDEF水平放置的直观图ABCDEF
y
F ME
A
O Dx
B NC
斜二测画法的步骤： （1）在已知图形中取互相垂直的x轴和y轴，两轴相交于o
六棱柱
俯
侧
六棱柱
空间几何体的直观图
A1D1
C B1
1
1、平面图形水平放置的直观图 正六边形水平放置的直观图
例１．用斜二测画法画水平放置的六边形的直观图
1 在六边形ABCDEF中，取AD所在的直线为X轴，
对称轴MN所在直线为Y轴,两轴交于点O。画相应
的X轴和y Y轴，两轴相交于点O,使xOy=45
正视图反映的是物体的长度 和高度，
俯视图反映的是物体的长度 和宽度，
侧视图反映的是物体的宽度 和高度。
作业讲解：P20 A1 （1）
主视图
侧视图
俯视图
P20 A1 （2）
主视图
俯视图
侧视图
P20 A1 （3）
主视图
侧视图
俯视图
圆柱
圆柱
练习2
圆台
圆台
空心球
三、讨论：用斜二测画法画水平放置的正五边形.
正五边形的画法： 圆内接正五边形的画法如下： ①以 O 为圆心，定长 R 为半径画圆，并作互相垂直的直径 MN 和 AP. ② 平分半径 ON，得 OK=KN.
③以 K 为圆心，KA 为半径画弧与 OM 交于 H， AH 即为正五边形的边长. ④以 AH 为弦长，在圆周上截得 A、B、C、D、E 各点，顺次连接这些点即得正五 边形.
点．画直观图时，把它画成对应的x′轴、y′轴，使
xOy=45 或135 ，它确定的平面表示水平平面。
（2）已知图形中平行于x轴或y轴的线段，在直观图中分别画 成平行于x′轴或y′轴的线段．
（3）已知图形中平行于x轴的线段，在直观图中保持原长度不 变；平行于y轴的线段，长度为原来的一半．
二、 练习： 画正方形、正三角形、平行四边形的直观图。
四、讨论：正等测画法画水平放置的圆
五、 ① 例画：正六棱柱，正五棱锥，正三棱台的直观图。
② 讨论：圆柱、圆锥、圆台的直观图
例3．已知几何体的三视图，用斜二测画法画出
它的直观图
·Z
y
O y x
Ox
·
O
·
O
正视图
·O
·
O
侧视图
·
俯视图
F ME
y
A
O Dx
O
x
B NC
2以O为中心,在X上取AD=AD，在y轴上取
MN= 1 MN.以点N为中心,画BC平行于x轴, 2
并且等于BC;再以M为中心,画EF平行于x轴,
并且等y 于EF.
F ME
A
O Dx
y
F M E
A
O
D x
B N C
B NC
3 连接AB,CD,EF,FA,并擦去辅助线x轴和y轴,
便获得正六边形ABCDEF水平放置的直观图ABCDEF
yቤተ መጻሕፍቲ ባይዱ
F ME
A
O Dx
B NC
y
F M E
A
O
D x
B N C
3 连接AB,CD,EF,FA,并擦去辅助线x轴和y轴,
便获得正六边形ABCDEF水平放置的直观图ABCDEF
y
F ME
A
O Dx
B NC
斜二测画法的步骤： （1）在已知图形中取互相垂直的x轴和y轴，两轴相交于o
六棱柱
俯
侧
六棱柱
空间几何体的直观图
A1D1
C B1
1
1、平面图形水平放置的直观图 正六边形水平放置的直观图
例１．用斜二测画法画水平放置的六边形的直观图
1 在六边形ABCDEF中，取AD所在的直线为X轴，
对称轴MN所在直线为Y轴,两轴交于点O。画相应
的X轴和y Y轴，两轴相交于点O,使xOy=45