角的比较与运算ppt课件
合集下载
七年级数学角的比较与运算

两个角的另一边落在重合一边的同侧;
由两个角的另一边的位置确定两个角的大小.
探究新知
角的比较(叠合法)
∠AOB >∠A′O′B′
∠AOB < ∠A′O′B′
∠AOB =∠A′O′B′
探究新知
估计图中∠1与∠2的大小关系,
(1)
(2)
并用适当的方法检验.
巩固练习
观察与思考
角的大小与角的两边画出的长短有关吗?
原式=101°41′25″
原式=63°38′45″
原式=164°
原式=18.75°
巩固练习
1.角的大小比较方法(度量法、叠合法).
2.角的和差关系.
3.角的平分线的性质.
4.角的和、差、积、商运算.
总结提升
布置作业
P139~140 习题4.3第3,5,6,10题
谢谢!
已知∠AOB=80°,∠AOC=40°,求∠BOC的度数.
角的比较与运算
如图,已知线段AB,CD,你能比较它们的长短吗?你有几种方法?
2.叠合法
1.度量法
知识回顾
怎样比较下列两个角的大小?
新课引入
类比线段长短的比较,你认为该如何比较两个角的大小?试着画图来解决.
1.度量法
∠ABC >∠DEF
B
C
A
70°
30°
探rpp究新知
2.叠合法
步骤: 将两个角的顶点及一边叠合在一起;
解:因为射线OC可能在∠AOB的内部,如图①,可得到∠BOC=∠AOB-∠AOC=80°-40°=40°.而射线OC也可能在∠AOB的外部,如图②,可得到∠BOC=∠AOB+∠AOC=80°+40°=120°.
由两个角的另一边的位置确定两个角的大小.
探究新知
角的比较(叠合法)
∠AOB >∠A′O′B′
∠AOB < ∠A′O′B′
∠AOB =∠A′O′B′
探究新知
估计图中∠1与∠2的大小关系,
(1)
(2)
并用适当的方法检验.
巩固练习
观察与思考
角的大小与角的两边画出的长短有关吗?
原式=101°41′25″
原式=63°38′45″
原式=164°
原式=18.75°
巩固练习
1.角的大小比较方法(度量法、叠合法).
2.角的和差关系.
3.角的平分线的性质.
4.角的和、差、积、商运算.
总结提升
布置作业
P139~140 习题4.3第3,5,6,10题
谢谢!
已知∠AOB=80°,∠AOC=40°,求∠BOC的度数.
角的比较与运算
如图,已知线段AB,CD,你能比较它们的长短吗?你有几种方法?
2.叠合法
1.度量法
知识回顾
怎样比较下列两个角的大小?
新课引入
类比线段长短的比较,你认为该如何比较两个角的大小?试着画图来解决.
1.度量法
∠ABC >∠DEF
B
C
A
70°
30°
探rpp究新知
2.叠合法
步骤: 将两个角的顶点及一边叠合在一起;
解:因为射线OC可能在∠AOB的内部,如图①,可得到∠BOC=∠AOB-∠AOC=80°-40°=40°.而射线OC也可能在∠AOB的外部,如图②,可得到∠BOC=∠AOB+∠AOC=80°+40°=120°.
角的比较和运算
方法二:测量法
小学我们学过用量角器测量一个角, 角的大小也可以按其度数比较,度数大的 角则大,度数小的则小.反之,角大度 数大,角小度数小. 注意:使用量角器应注意的问题.即三点: 对中;重合;读数.
如: A 45, P 60 P A
.
.
;https:// 新视觉
①EF与BC重合,∠DEF等于∠ABC,记作 ∠DEF=∠ABC. ②EF落在∠ABC的内部,∠DEF小于 ∠ABC,记作∠DEF<∠ABC. ③EF落在∠ABC的外部,∠DEF大于 ∠ABC,记作∠DEF>∠ABC
注意:角的大小只与开口大小有关,与边的长短 无关,以及角的符号与小于号、大于号书写时的 区别.
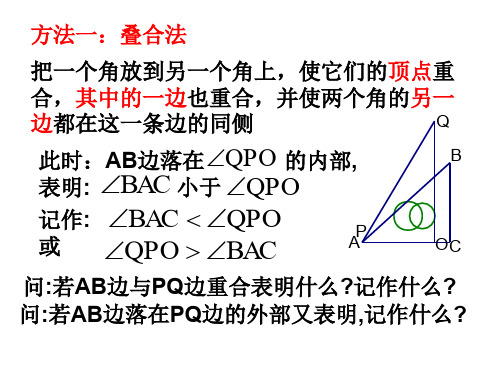
方法一:叠合法
把一个角放到另一个角上,使它们的顶点重
合,其中的一边也重合,并使两个角的另一
边都在这一条边的同侧
Q
此时:AB边落在QPO 的内部,
B
表明: BAC 小于 QPO
记作: BAC QPO 或 QPO BAC
AP
OC
问:若AB边与PQ边重合表明什么?记作什么? 问:若AB边落在PQ边的外部又表明,记作什么?
子长县第二中学七年级数学上册第四章几何图形初步4.3角4.3.2角的比较与运算教学课件新版新人教版3

105°、120°、135°、150°、 165 °180°
75°
15°
观察思考 , 探究新知
动手做一做 : 在纸上画∠AOC , 然后将其剪下来 , 将其沿经过顶点的线対折 , 使边OA与OC重合.将角展开 , 折痕上任取一点记作点B.类比线段中点的定义 , 填 空:
C
∠AOB=∠BOC= 1 ∠AOC ;
即 a + b - c = a + b + ( -c )
➢ 把加减混合运算的算式转化为加法运算后 , 为书写 简单 , 可以省略算式中的括号及它前面的加号.
8 + 3 +〔-5〕+〔-7〕可以写成 : 8 + 3–5 + 7
计算 : (-21)+30-15-(-17).
解 (-21)+ 30-15-(-17) = (-21)+ 30 +(-15)+ 17 = (-21)+ (-15)+ 30 + 17 = -36 + 47 = 11
2
E
D
C
B
O
A
(2) 如果∠AOB=40° , ∠DOE=30° , 那么∠BOD
是多少度 ? 解 : 因为 OB 平分∠AOC ,
E
D
C
B
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE ,
所以∠COD=∠DOE = 30° ,
O
A
所以 ∠BOD =∠BOC+∠COD = 40°+30°= 70°.
数的
〔-2〕× 3 = -6
发现 : 两数相乘 , 把一个因数换成它的相反数 , 所得的积是原来积的相反数.
75°
15°
观察思考 , 探究新知
动手做一做 : 在纸上画∠AOC , 然后将其剪下来 , 将其沿经过顶点的线対折 , 使边OA与OC重合.将角展开 , 折痕上任取一点记作点B.类比线段中点的定义 , 填 空:
C
∠AOB=∠BOC= 1 ∠AOC ;
即 a + b - c = a + b + ( -c )
➢ 把加减混合运算的算式转化为加法运算后 , 为书写 简单 , 可以省略算式中的括号及它前面的加号.
8 + 3 +〔-5〕+〔-7〕可以写成 : 8 + 3–5 + 7
计算 : (-21)+30-15-(-17).
解 (-21)+ 30-15-(-17) = (-21)+ 30 +(-15)+ 17 = (-21)+ (-15)+ 30 + 17 = -36 + 47 = 11
2
E
D
C
B
O
A
(2) 如果∠AOB=40° , ∠DOE=30° , 那么∠BOD
是多少度 ? 解 : 因为 OB 平分∠AOC ,
E
D
C
B
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE ,
所以∠COD=∠DOE = 30° ,
O
A
所以 ∠BOD =∠BOC+∠COD = 40°+30°= 70°.
数的
〔-2〕× 3 = -6
发现 : 两数相乘 , 把一个因数换成它的相反数 , 所得的积是原来积的相反数.
角的比较与运算-角的比较

观察另一条边的位置关系,判断两个 角的大小。
03
角的性质与定理
角的性质
角的大小与边的长短 无关,只与两条边叉 开的大小有关。
角可以参与运算,如 角的和、差、倍、分 等。
角的大小可以度量, 可以比较。
角平分线的性质
角平分线将一个角平分为两个 相等的角。
角平分线上的点到这个角的两 边的距离相等。
在角的内部到角的两边距离相 等的点在这个角的平分线上。
一个角的互补角。
互余角
两个角的度数之和等于 180度,其中一个角是 另一个角的互余角。
02
角的比较方法
重合法比较
两个角的顶点和两条边分别重合,则 这两个角相等。
通过观察或测量验证两个角是否重合 。
量角器测量法
使用量角器分别测量两个角的度数。 比较两个角的度数,确定它们的大小关系。
叠合法比较
把两个角叠合在一起,使它们的顶点 和一条边重合。
在摄影中,摄影师需要掌握角度的知识,通过调整相机的角度和位置,拍摄出更具 艺术感和视觉冲击力的照片。
在体育比赛中,角度的比较和运算也经常被用到。例如,在足球比赛中,球员需要 根据球的位置和对方的防守角度,选择合适的进攻路线和射门角度。
THANKS
感谢观看
角的减法运算
同向角的减法
同向角相减时,被减数减 去减数,差取正值。
异向角的减法
异向角相减时,被减数加 上减数,差取负值。
带正负号的角相减
同向角相减时,被减数减 去减数,差取正值;异向 角相减时,被减数加上减 数,差取负值。
角的乘法与除法运算
角的乘法
特殊角的乘法与除法
角度乘以一个正数时,角度的大小不 变,方向也不变;角度乘以一个负数 时,角度的大小不变,方向相反。
03
角的性质与定理
角的性质
角的大小与边的长短 无关,只与两条边叉 开的大小有关。
角可以参与运算,如 角的和、差、倍、分 等。
角的大小可以度量, 可以比较。
角平分线的性质
角平分线将一个角平分为两个 相等的角。
角平分线上的点到这个角的两 边的距离相等。
在角的内部到角的两边距离相 等的点在这个角的平分线上。
一个角的互补角。
互余角
两个角的度数之和等于 180度,其中一个角是 另一个角的互余角。
02
角的比较方法
重合法比较
两个角的顶点和两条边分别重合,则 这两个角相等。
通过观察或测量验证两个角是否重合 。
量角器测量法
使用量角器分别测量两个角的度数。 比较两个角的度数,确定它们的大小关系。
叠合法比较
把两个角叠合在一起,使它们的顶点 和一条边重合。
在摄影中,摄影师需要掌握角度的知识,通过调整相机的角度和位置,拍摄出更具 艺术感和视觉冲击力的照片。
在体育比赛中,角度的比较和运算也经常被用到。例如,在足球比赛中,球员需要 根据球的位置和对方的防守角度,选择合适的进攻路线和射门角度。
THANKS
感谢观看
角的减法运算
同向角的减法
同向角相减时,被减数减 去减数,差取正值。
异向角的减法
异向角相减时,被减数加 上减数,差取负值。
带正负号的角相减
同向角相减时,被减数减 去减数,差取正值;异向 角相减时,被减数加上减 数,差取负值。
角的乘法与除法运算
角的乘法
特殊角的乘法与除法
角度乘以一个正数时,角度的大小不 变,方向也不变;角度乘以一个负数 时,角度的大小不变,方向相反。
角的比较与运算

O
A
∠AOB =2∠AOC =2∠BOC
(角的二等分线)
从一个角的顶点出发,把这个角分成相等的两 个角的射线叫做这个角的角平分线。
角的三等分线αα Nhomakorabeaα
角的四等分线
α
α
α α
练习:已知 OB是∠AOC的平分线,OD是∠COE 平 分线。
(1)如果∠AOB=40度,∠DOE=30度, 那么 ∠BOD是多少度?
B (E) (F) A D C
C B (E) (F)
∠ABC>∠DEF
图中共有几个角? 它们之间有什么关系? 二、角的和与差:
C
B O
C D
A
B
O
A
(1) 如图,∠AOC和∠BOD都是直角。
若∠DOC=28°,说出∠AOB的度数。
D A
C
B O
探究:
利用三角尺 还可以画出哪 些度数的角?
75°
15°
30°、45°、60°、90°、15°、 75°、105°、120°、135°、 150°、 180°
计算 (1) 153°39′44″+ 26°40′28″ (2) 51°37′-32°5′31″ (3) 53°25′28″×5 (4) 157°43′÷5
B
C
∵OC是∠AOB的平分线
1 ∴∠AOC =∠BOC = ∠ AOB 2
怎样比较∠ABC和∠DEF的大小?
你的方法有:
A
1. 度量法比较 2.叠合法比较
D
B
C
E
F
1、度量法比较
90
A
90
D
0 180 0
180 O
B
C
高中数学必修四:1.1.1《任意角》 PPT课件 图文
精讲领学
例题1 写出与下列各角终边相同的角的集合S,并把S中在 360~720范围的角写出来.
( 1 ) 6 0 ;( 2 ) 2 1 ;( 3 ) 3 6 3 1 4
解: ( 1 ) S {| k 3 6 0 6 0 , k Z }300,60,420
( 2 ) S {| k 3 6 0 2 1 , k Z }21,339,699
2、下列角中终边与330°相同的角是( ) A.30° B.-30° C.630° D.-630°
3、把-1485°转化为α+k·360° (0°≤α<360°, k∈Z)的形式是( ) A.45°-4×360° B.-45°-4×360° C.-45°-5×360° D.315°-5×360°
反馈固学
1.1.1 任意角
第一课时
(1)推广角的概念;理解并掌握正角、负角、零角的定义; (2)理解任意角以及象限角的概念; (3)掌握所有与角终边相同的角(包括角)的表示方法; (4)树立运动变化观点,深刻理解推广后的角的概念;
思考:那么工人在拧紧或拧松螺丝时,转动的角度 如何表示才比较合适?
逆时 针
4、下列结论中正确的是( ) A.小于90°的角是锐角 B.第二象限的角是钝角 C.相等的角终边一定相同 D.终边相同的角一定相等
5:任意两个角的数量大小可以相加、相减.
例如50°+80°=130°, 50°-80°=-30°, 你能解释一下这两个式子的几何意义吗?
130°是以50°角的终边为始边,逆时针旋转80°所成的角. -30°是以50°角的终边为始边,顺时针旋转80°所成的角.
注3:(1) 为任意角 (2) k Z这一条件必不可少;
(3) 终边相同的角不一定相等, 终边相等的角有无数多个,它们相差3600的整数倍.
角的比较与运算
C ∠BOD = ∠COD+ ∠ BOC __ D ∠AOC= ∠AOD-∠ COD __ O ∠BOD= ∠ AOD -∠AOB __ __ A
B
学以致用…
利用三角尺 还可以画出哪 些度数的角?
30°、45°、60°、90°、15°、75°、 105°、120°、135°、150°、 180°
角平分线
1 2
C B
BOC ∠AOB = ∠ __ = ∠ AOC __
(2)若OB是∠AOC的平分线,OC是∠BOD的平分线, 你能从中找出哪些相等的角? D ∠AOB= ∠BOC= ∠COD ∠AOC= ∠BOD O C B A
这节课你有哪些收获? 1、角的比较 2、角的运算
3、角平分线
作业:
必做题:课本P138 第1-4题 选做题:P147 第8题
(A′) A
O(O′)
B (B′)
O (O′)
A (A′)
角的运算
图中共有几个角,它们之间的大小有什么关系? ∠AOC = ∠AOB + ∠AOC-∠ BOC __ AOC AOB ∠BOC = ∠__ -∠ __
O
A
学而时习 之…
∠AOC =∠AOB + ∠ BOC __
将你手中的角对折,使其两边重合,折痕把 这个角分成的两部分是什么图形,你发现它们的大 小有什么关系?
折痕与这个角的两边组成两个角
它们的大小相等 ∠1 =∠2
从一个角的顶点出发,把这个 角分成相等的两个角的射线, 叫做这个角的平分线
1 2
角平分线
(1)若OC是∠AOB的平分线,那么 BOC ∠AOB =∠ __ ∠AOC =2∠AOB =2∠ BOC __ O A
B
学以致用…
利用三角尺 还可以画出哪 些度数的角?
30°、45°、60°、90°、15°、75°、 105°、120°、135°、150°、 180°
角平分线
1 2
C B
BOC ∠AOB = ∠ __ = ∠ AOC __
(2)若OB是∠AOC的平分线,OC是∠BOD的平分线, 你能从中找出哪些相等的角? D ∠AOB= ∠BOC= ∠COD ∠AOC= ∠BOD O C B A
这节课你有哪些收获? 1、角的比较 2、角的运算
3、角平分线
作业:
必做题:课本P138 第1-4题 选做题:P147 第8题
(A′) A
O(O′)
B (B′)
O (O′)
A (A′)
角的运算
图中共有几个角,它们之间的大小有什么关系? ∠AOC = ∠AOB + ∠AOC-∠ BOC __ AOC AOB ∠BOC = ∠__ -∠ __
O
A
学而时习 之…
∠AOC =∠AOB + ∠ BOC __
将你手中的角对折,使其两边重合,折痕把 这个角分成的两部分是什么图形,你发现它们的大 小有什么关系?
折痕与这个角的两边组成两个角
它们的大小相等 ∠1 =∠2
从一个角的顶点出发,把这个 角分成相等的两个角的射线, 叫做这个角的平分线
1 2
角平分线
(1)若OC是∠AOB的平分线,那么 BOC ∠AOB =∠ __ ∠AOC =2∠AOB =2∠ BOC __ O A
8.2.1角的比较与运算
解: 由图形可以看出, ∠ AOC是
∠AOB与∠BOC的和,即 ∠ AOC= ∠AOB+∠BOC; 同样的,∠ BOD= ∠BOC+∠COD;
当∠ AOB= ∠ COD时,
∠ AOC= ∠ BOD.
通过这堂课的学习,你有什么收获?
1、比较两个角大小的方法
2、角的和、差、倍、分 关系 3、角平分线
A D B ( ) ( ) C
E
F
ED落在∠ABC的内部,则∠DEF < ∠ABC
D A A D A D BE C F
BE
C F B
E
C F
∠DEF >∠ABC
∠DEF =∠ABC
∠DEF < ∠ABC
思考:下图中共有几个角?它们 A 有什么关系?
C
O 完成下列问题: ∠ AOB ∠AOC ∠BOC 3 1、图中共有__个角,它们分别是 ______________ ∠AOC ∠BOC 2、∠AOB=____ +_____ ∠AOB ∠BOC 3、∠AOC=____-_____
利用一副三角板,我们能 画出哪些度数的角?
180 º
150 º
135 º
120 º
105 º
75 º
60 º
15 º
45 º
30 º
角的平分线:
A
C
O
B
从一个角的顶点出发,把这个角分成相 等的两个角的射线,叫做这个角的平分线。
问题:
已知射线OC是∠AOB的角平分线, 你能写出图中各角的关系吗?
黄岗中学数学组
A
读数为45
45°
o
D
B
60°
E
F
所以:∠AOB<∠DEF
七年级数学上册《角的比较与运算》
15°,30°,45°,60°,75°,90°,105°,120°, 135°,150°,165°.
如何进行角的运算
和或差
加减
※ 一个角可以用其他角的 来表示.
※ 角之间可以进行 运算.
共11个
15。的倍数
解决问题
A
B
C
O
∠COB=∠AOB -∠AOC ,
解决问题
解:360°÷7
3. 如图,把一个蛋糕等分成7份,每份中的角 是多少度(精确到分)?
注意:度、分、秒是60进制的,要把剩余的度数化成分.
5
35
7
3
1
10
=51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份中的角约是51°26′.
图案设计:
.
图案设计:
小于
<
探究新知
(2)如果BC与EF重合,[来源:学*科*网]
B
A
C
E
D
F
如何比较两角的大小
等于
那么∠ABC ∠ DEF,记作∠ABC ∠DEF.
=
探究新知
(3)如果BC落在∠DEF的外部,
E
D
F
如何比较两角的大小
大于
>
那么∠ABC ∠ DEF,记作∠ABC ∠DEF.
B
A
C
E
D
F
如何比较两角的大小
1.请拿出你手里的角与同桌比一比看谁的角大?
[来源:学*科*网]
[来源:学*科*网]
探究新知
(1)如果BC落在∠DEF的内部,
B
A
C
E
D
F
人教版七年级数学上册《角的计算》课件
4.3 角
4.3.2 角的比较与运算(2课时)
第2课时 角的计算
会进行度、分、秒间的单位互化及角的和、差、倍、分 计算.
重点 角的度分秒之间的换算与计算. 难点 借助几何图形进行角的计算.
一、创设情境,导入新课 练习:比较大小. 1.36.5°与36°28′. 2.0.15°与15′. 3.用度分秒表示30.24°. 学生独立完成,然后同学间交流.
解答略,教师应当关注第2个题,一是问题的分析, 二是解答过程的叙述,不必强求过程叙述的完美,但 至少要让学生叙述清楚.
四、小结与作业 小结:谈谈本节课你的收获. 作业:习题4.3第3,5,10,11题.
在本节课教学中,始终坚持以学生为主体,教师为主导, 致力启发学生已掌握的知识,充分调动学生的学习兴趣和 积极性,使他们最大限度地参与到课堂中,使每个学生都 学有所得,真正实现“人人学有价值的数学,人人都能获得 必需的数学,不同的人在数学上得到不同的发展,人人都 得到良好的数学”教育的最终目标.
谢谢观赏
You made my d 教师注意规范的书写过程. 点评:观察图形,发现各角之间的关系是解决问题的关 键. 教师出示例2 把一个周角7等分,每一份是多少度的角(精确到分)? 解:略. 点评:教师要注意方法过程,要详细地把计算过程讲解给 学生,学生刚开始对60进制不太熟练,所以要注意放慢速 度.
三、综合运用 练习:教材练习第2,3题. 补充例题(教师投影展示) 1.如果一个角是另一个角的3倍,且这两个角的和是 90°,求这两个角的度数. 2.如图,O是直线AB上一点,OD平分∠AOC,OE平 分∠BOC,求∠DOE的度数.
二、探索新知 教师出示教材例1. 例 1 : 如 图 , O 是 直 线 上 AB 一 点 , ∠AOC = 53°17′ , 求 ∠BOC的度数.
4.3.2 角的比较与运算(2课时)
第2课时 角的计算
会进行度、分、秒间的单位互化及角的和、差、倍、分 计算.
重点 角的度分秒之间的换算与计算. 难点 借助几何图形进行角的计算.
一、创设情境,导入新课 练习:比较大小. 1.36.5°与36°28′. 2.0.15°与15′. 3.用度分秒表示30.24°. 学生独立完成,然后同学间交流.
解答略,教师应当关注第2个题,一是问题的分析, 二是解答过程的叙述,不必强求过程叙述的完美,但 至少要让学生叙述清楚.
四、小结与作业 小结:谈谈本节课你的收获. 作业:习题4.3第3,5,10,11题.
在本节课教学中,始终坚持以学生为主体,教师为主导, 致力启发学生已掌握的知识,充分调动学生的学习兴趣和 积极性,使他们最大限度地参与到课堂中,使每个学生都 学有所得,真正实现“人人学有价值的数学,人人都能获得 必需的数学,不同的人在数学上得到不同的发展,人人都 得到良好的数学”教育的最终目标.
谢谢观赏
You made my d 教师注意规范的书写过程. 点评:观察图形,发现各角之间的关系是解决问题的关 键. 教师出示例2 把一个周角7等分,每一份是多少度的角(精确到分)? 解:略. 点评:教师要注意方法过程,要详细地把计算过程讲解给 学生,学生刚开始对60进制不太熟练,所以要注意放慢速 度.
三、综合运用 练习:教材练习第2,3题. 补充例题(教师投影展示) 1.如果一个角是另一个角的3倍,且这两个角的和是 90°,求这两个角的度数. 2.如图,O是直线AB上一点,OD平分∠AOC,OE平 分∠BOC,求∠DOE的度数.
二、探索新知 教师出示教材例1. 例 1 : 如 图 , O 是 直 线 上 AB 一 点 , ∠AOC = 53°17′ , 求 ∠BOC的度数.
