统计作业计算
统计学作业汇总

统计学作业汇总第1—3章复习题1. 1. 简答题(1)什么是统计学?怎样理解统计学与统计数据的关系?答:统计学是⼀门收集,整理和分析统计数据的⽅法论科学,其⽬的是探索数据内在的规律性,已达到对客观事物的科学认识。
统计学和统计数据之间有着密不可分的关系。
统计学是由⼀套收集和处理统计数据的⽅法所组成,这些⽅法来源于对统计数据的研究,⽬的也在于对统计数据的研究。
统计数据不⽤统计⽅法去分析也仅仅是⼀堆数据⽽已,⽆法得出任何有益的结论。
(2)简述统计调查⽅案的基本内容答:调查⽅案是调查⼯作的计划性⽂件,是对整个调查⼯作的事先安排。
调查内容不同,调查⽅案有⼀定的差异,但⼀般都包括以下⼏个⽅⾯的内容:即调查⽬的、调查对象和调查单位、调查内容(调查项⽬)、调查⽅式与⽅法、调查⼯作的组织与实施计划等。
(3)最常⽤的统计调查⽅式是什么?他有什么特点?答:统计调查⽅式是指搜集数据时所采⽤的组织形式。
在实际中应⽤最⼴泛的调查⽅式是抽样调查。
抽样调查是从调查对象中随机抽取⼀部分单位作为样本进⾏调查,并根据样本调查结果来推断总体数量特征的⼀种⾮全⾯调查⽅法。
与其它调查⽅式相⽐,抽样调查具有经济性、时效性强、适应⾯⼴、准确性⾼等特点。
(4)最常⽤的搜集统计资料的⽅法是什么?答:搜集统计资料的⽅法是指搜集数据所采⽤的具体办法,其主要有访问法、观察法和实验法,其中访问法最为常⽤。
(5)简述组距式分组的步骤。
答:第⼀步,确定全距,以了解数据的变动范围,为确定组距提供依据;第⼆步,确定组数,确定组数的基本原则是确保组内的同质性、组间的差异性,同时能反映数据的分布特征,具体可参考经验公式确定;第三步,确定组距,等组距时,组距=全局/组数;第四步,确定组限,注意组限的表⽰⽅式;第五步,分组并编制次数分布表,会制次数分布图。
2. 2. 填空题(1)⼀个完整的统计⼯作过程,包括统计设计、统计调查、统计整理、统计分析和统计资料的管理与提供。
(2)统计⼀词有三种含义,即统计⼯作、统计资料、统计学。
统计学练习与作业(内)2013
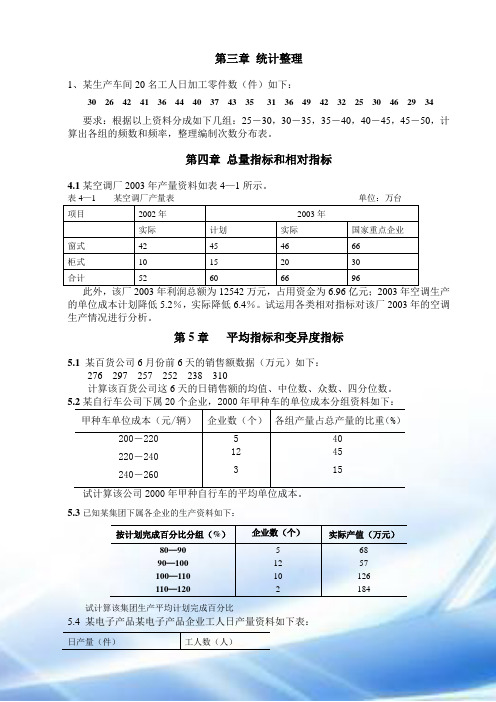
第三章统计整理1、某生产车间20名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 43 35 31 36 49 42 32 25 30 46 29 34要求:根据以上资料分成如下几组:25-30,30-35,35-40,40-45,45-50,计算出各组的频数和频率,整理编制次数分布表。
第四章总量指标和相对指标4.1某空调厂2003年产量资料如表4—1所示。
项目2002年2003年实际计划实际国家重点企业窗式42 45 46 66柜式10 15 20 30合计52 60 66 96的单位成本计划降低5.2%,实际降低6.4%。
试运用各类相对指标对该厂2003年的空调生产情况进行分析。
第5章平均指标和变异度指标5.1某百货公司6月份前6天的销售额数据(万元)如下:276 297 257 252 238 310计算该百货公司这6天的日销售额的均值、中位数、众数、四分位数。
5.2某自行车公司下属20个企业,2000年甲种车的单位成本分组资料如下:甲种车单位成本(元/辆)企业数(个)各组产量占总产量的比重(%)200-220 220-240 240-26051234045155.3已知某集团下属各企业的生产资料如下:按计划完成百分比分组(%)企业数(个)实际产值(万元)80—90 90—100 100—110 110—120 5121026857126184试计算该集团生产平均计划完成百分比5.4 某电子产品某电子产品企业工人日产量资料如下表:日产量(件)工人数(人)试根据表中资料计算工人日产量的平均数、中位数和众数,并判断该分布数列的分布状态。
5.5一位投资者持有一种股票,2001-2004年的收益率分别为 4.5%,2.1%,25.5%和1.9%。
要求计算该投资者在这4年内的平均收益率。
5.6 一种产品需要人工组装,现有两种可供选择的组装方法。
为检验哪种方法更好,随机抽取6名工人,让他们分别用两种方法组装,测试在相同的时间内组装的产品数量。
概率统计作业题

概率统计作业题《概率统计》习题(⼀)⼀、填空题1.设 A 、B 、C 是三个随机事件。
试⽤ A 、B 、C 分别表⽰事件 1)A 、B 、C ⾄少有⼀个发⽣ 2)A 、B 、C 中恰有⼀个发⽣3)A 、B 、C 不多于⼀个发⽣2.设 A 、B 为随机事件, P (A)=0.5,P(B)=0.6,P(B A)=0.8。
则P(B )A = 3.若事件A 和事件B 相互独⽴, P()=,AαP(B)=0.3,P(A B)=0.7, 则α= 4. 将C,C,E,E,I,N,S 等7个字母随机的排成⼀⾏,那末恰好排成英⽂单词SCIENCE 的概率为5. 甲、⼄两⼈独⽴的对同⼀⽬标射击⼀次,其命中率分别为0.6和0.5,现已知⽬标被命中,则它是甲射中的概率为⼆、选择题1. 设A,B 为两随机事件,且B A ?,则下列式⼦正确的是(A )P (A+B) = P (A); (B )()P(A);P AB = (C )(|A)P(B);P B =(D )(A)P B -=()P(A)P B -2. 以A 表⽰事件“甲种产品畅销,⼄种产品滞销”,则其对⽴事件A 为(A )“甲种产品滞销,⼄种产品畅销”;(B )“甲、⼄两种产品均畅销” (C )“甲种产品滞销”;(D )“甲种产品滞销或⼄种产品畅销”。
3. 袋中有50个乒乓球,其中20个黄的,30个⽩的,现在两个⼈不放回地依次从袋中随机各取⼀球。
则第⼆⼈取到黄球的概率是(A )1/5 (B )2/5 (C )3/5 (D )4/5 4. 对于事件A ,B ,下列命题正确的是(A )若A ,B 互不相容,则A 与B 也互不相容。
(B )若A ,B 相容,那么A 与B 也相容。
(C )若A ,B 互不相容,且概率都⼤于零,则A ,B 也相互独⽴。
(D )若A ,B 相互独⽴,那么A 与B 也相互独⽴。
5.若()1P B A =,那么下列命题中正确的是(A )A B ? (B )B A ? (C )A B -=? (D )()0P A B -=三、计算题1. 10把钥匙中有3把能打开门,今任意取两把,求能打开门的概率。
统计学作业——精选推荐

统计学作业Homework 11.下⾯是⼀种⾦属零件重量的误差数据:61.4 46.8 65.1 61.7 77.463.9 54.6 71.1 60.5 52.773.4 87.8 32.5 27.3 47.557.3 60.5 52.9 40.1 47.954.8 60.1 19.9 30.4 58.656.8 46.8 32.7 81.6 60.276.4 54.9 37.4 71.6 48.232.1 39.1 19.1 48.9 38.153.3 26.4 53.3 55.1 58.127.3 67.9 74.1 55.6 32.5 要求:(1)以10为组距编制零件重量的频数分布。
(2)绘制直⽅图,说明零件重量误差分布的特征。
解:(1)(2)26.某公司所属三个企业⽣产同种产品,2007年实际产量、计划完成情况及产品优质品率资料如下,要求计算:(1)该公司产量计划完成百分⽐;(2)该公司实际的优质品率。
企业实际产量(万件)完成计划(%)实际优质品率(%)甲⼄丙100 150 250120 110 8095 96 98解:(1)产量计划完成百分⽐:%95.9320.5325008.02501.11502.1100250150100==++++==∑∑x m m x(2)实际优质品率:%8.9650048425015010098.025096.015095.0100==++?+?+?==∑∑fxf x7.⼀种产品需要⼈⼯组装,现有三种可供选择的组装⽅法。
为检验那种⽅法更好,随机抽取了15个⼯⼈,让他们分别⽤三种⽅法组装。
下⾯是15个⼯⼈分别⽤三种⽅法在相同的时间内组装的产品数量:⽅法A ⽅法B ⽅法C 164 129 125 167 130 126 168 129 126 165 130 127 126 170 131 165 130 128 164 129 127 168 127 126 164 128 127 162 128 127 163 127 125 166 128 126 167 128 116 166 125 126 165132125要求:(1)采⽤合适的⽅法来评价组装⽅法的优劣。
统计学期末大作业题目及答案

统计学实践作业参数估计练习题1. 某大学为了解学生每天上网的时间,在全校7500名学生中采取不重复抽样方法随机抽取36人,调查他们每天上网的时间(单位:小时),得到的数据见表。
求该校大学生平均上网时间的置信区间,置信水平分别为90%、95%和99%。
平均标准误差中位数众数标准差方差峰度偏度区域最小值最大值求和观测数36最大(1)最小(1)置信度%)置信区间平均标准误差中位数众数标准差方差峰度偏度区域最小值最大值求和观测数36最大(1)最小(1)置信度%)置信区间平均标准误差中位数众数标准差方差峰度偏度区域最小值最大值求和观测数36最大(1)最小(1)置信度%)置信区间 2.2.某机器生产的袋茶重量(g)的数据见。
构造其平均重量的置信水平为90%、95%和99%的置信区间。
平均 3.标准误差中位数众数标准差方差峰度偏度区域最小值最大值求和观测数21最大(1)最小(1)置信度%)置信区间平均 3.标准误差中位数众数标准差方差峰度偏度区域最小值最大值求和观测数21最大(1)最小(1)置信度%)置信区间 3.平均 3.标准误差中位数众数标准差方差峰度偏度区域最小值最大值求和观测数21最大(1)最小(1)置信度%)置信区间3. 某机器生产的袋茶重量(g)的数据见。
构造其平均重量的置信水平为90%、95%和99%的置信区间。
平均标准误差中位数众数标准差方差峰度偏度区域最小值最大值求和观测数35最大(1)最小(1)置信度%)置信区间平均标准误差中位数众数标准差方差峰度偏度区域最小值最大值求和观测数35最大(1)最小(1)置信度%)置信区间平均标准误差中位数众数标准差方差峰度偏度区域最小值最大值求和观测数35最大(1)最小(1)置信度%)置信区间资料整理练习题1. 为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C.一般;D.差;E.较差。
调查结果见表。
应用数理统计作业

<应用数理统计>实验习题二1.某切割机在正常工作时,切割每段金属棒的平均长度为10.5cm.今从一批产品中随机地抽取15段,测得其长度(单位:cm)如下10.4 10.6 10.1 10.4 10.5 10.3 10.3 10.2 10.9 10.6 10.8 10.5 10.7 10.2 10.7设金属棒长度服从正态分布,且标准差没有变化,(04.02=σ),试问(1)该机工作是否正常(05.0=α)?(2)上题中假定切割的长度服从正态分布,问该机切割的金属棒的平均长度有无显著变化(05.0=α)?(3)如果只假定切割的长度服从正态分布,问该机切割的金属棒长度的标准差有无显著变化(05.0=α)?>> clear all>>x=[10.4,10.6,10.1,10.4,10.5,10.3,10.3,10.2,10.9,10.6,10.8,10.5,10.7,10.2,10.7];>> [h,p,ci,u]=ztest(x,10.5,0.2,0.05,1)h =p =0.650710.3951 Infu =-0.3873一>> [h,p,ci,u]=ztest(x,10.5,0.2,0.05,0)h =p =0.6985ci =10.3788 10.5812-0.3873二[h,sig]=ztest(x,10.5,0.2,0.05,0)h =sig =0.6985三x=[10.4,10.6,10.1,10.4,10.5,10.3,10.3,10.2,10.9,10.6,10.8,10.5,10.7,1 0.2,10.7];>> [p,sig]=xtest(x,0.2,0.05,0)p =1sig =2.下表列出了18个5~8岁儿童的重量和体积.(1) 画出散点图;(2) 求y 关于x 的线性回归方程,ˆˆˆx b a y+=并作回归分析;。
统计学(本)作业
1.一个企业产品销售收入计划增长8%,实际增长20%,则计划超额完成程度为( C ) A 、12% B 、150% C 、111.11% D 、11.11% 2.时点指标的数值( A )A 、与其时间间隔长短无关B 、通常连续登记C 、时间间隔越长,指标数值越大D 、具有可加性3.总体各部分指标数值与总体数值计算求得的结构相对数之和( C ) A 、大于100% B 、小于100% C 、等于100% D 、无法确定 4.统计分组的核心问题是( B )A 、划分各组界限B 、选择分组标志C 、确定组数D 、确定组距 5.平均指标反映了( A )A 、总体次数分布的集中趋势B 、总体分布的特征C 、总体单位的集中趋势D 、总体次数分布的离中趋势 6.抽样调查和重点调查的主要区别是( A )A 、选取调查单位的方式不同B 、调查的目的不同C 、调查的单位不同D 、两种调查没有本质区别 7. 已知环比增长速度为9.2%、8.6%、7.1%、7.5%,则定基增长速度为( D ) A 、9.2%×8.6%×7.1%×7.5% B 、(9.2%×8.6%×7.1%×7.5%)-100% C 、109.2%×108.6%×107.1%×107.5%D 、(109.2%×108.6%×107.1%×107.5%)-100%8.累计增长量与其相应的各个逐期增长量的关系表现为( B ) A 、累计增长量等于相应的各个逐期增长量之积 B 、累计增长量等于相应的各个逐期增长量之和 C 、累计增长量等于相应的各个逐期增长量之差 D 、以上都不对9.设p 表示商品的价格,q 表示商品的销售量,1011q p q p ∑∑说明了( B )A 、在基期销售量条件下,价格综合变动的程度B 、在报告期销售量条件下,价格综合变动的程度C 、在基期价格水平下,销售量综合变动的程度D 、在报告期价格水平下,销售量综合变动的程度10.在回归方程y ˆ=a+bx 中,回归系数b 表示( D )A 、当x =0时y 的期望值B 、x 变动一个单位时y 的变动总额C 、y 变动一个单位时x 的平均变动量D 、x 变动一个单位时y 的平均变动量11.下面属于连续变量的是( C )A 、职工人数B 、机器台数C 、工业总产值D 、车间数12.人均收入,人口密度,平均寿命,人口净增数,这四个指标中属于质量指标的有( C )。
统计学练习与作业(内)2013
第三章统计整理1、某生产车间20名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 43 35 31 36 49 42 32 25 30 46 29 34要求:根据以上资料分成如下几组:25-30,30-35,35-40,40-45,45-50,计算出各组的频数和频率,整理编制次数分布表。
第四章总量指标与相对指标4.1某空调厂2003年产量资料如表4—1所示。
表4—1 某空调厂产量表单位:万台的单位成本计划降低5.2%,实际降低6.4%。
试运用各类相对指标对该厂2003年的空调生产情况进行分析。
第5章平均指标与变异度指标5.1某百货公司6月份前6天的销售额数据(万元)如下:276 297 257 252 238 310计算该百货公司这6天的日销售额的均值、中位数、众数、四分位数。
5.3已知某集团下属各企业的生产资料如下:试计算该集团生产平均计划完成百分比5.4 某电子产品某电子产品企业工人日产量资料如下表:试根据表中资料计算工人日产量的平均数、中位数和众数,并判断该分布数列的分布状态。
5.5一位投资者持有一种股票,2001-2004年的收益率分别为4.5%,2.1%,25.5%和1.9%。
要求计算该投资者在这4年内的平均收益率。
5.6 一种产品需要人工组装,现有两种可供选择的组装方法。
为检验哪种方法更好,随机抽取6名工人,让他们分别用两种方法组装,测试在相同的时间内组装的产品数量。
得到第一种组装方式组装的产品平均数量是127件,标准差为5件。
第二种组装方式组装的产品数量(单位:件)如下:129,130,131,127,128,129。
要求:1) 计算第二种组装方式组装产品的平均数和标准差。
2)如果让你选择一种组装方式,你会选择哪种?5.7一家公司在招收职员时,首先要通过两项能力测试。
在A项测试中,其平均分数是100分,标准差是15分;在B项测试中,其平均分数是400分,标准差是50分。
概率论与数理统计作业B
目录第二章随机变量及其分布与数字特征 (1)习题A(作业题) (1)习题B(练习题) (4)一、填空题 (4)二、选择题 (5)三、计算题 (8)第六章统计量和抽样分布 (17)习题A(作业题) (17)习题B(练习题) (19)一、填空题 (19)二、选择题 (20)三、计算题 (23)第八章假设检验 (28)习题A(作业题) (28)习题B(练习题) (29)一、填空题 (29)二、选择题 (30)三、计算题 (33)第二章 随机变量及其分布与数字特征习题A(作业题)1求()⎪⎭⎫ ⎝⎛≤≤⎪⎭⎫ ⎝⎛≤2523;252;1X p X p x F )()()(.DX EX ,2.一批产品20个, 其中有5个次品, 从这批产品中随意抽取4个, 求(1)这4个中的次品数X 的分布列;(2))1(<X p3. 连续型随机变量X 的分布函数为)0(,1,arcsin ,0)(>⎪⎩⎪⎨⎧≥<<-+-≤=a a x a x a a x B A a x x F试求:(1)系数A 、B ;(2)求2(a X p <);(3)X 的分布密度函数。
4.服从拉普拉斯分布的随机变量X 的概率密度xAex f -=)( , 求(1)系数A ; (2))11(<<-X p ,(3)分布函数)(x F .5. 已知随机变量X ),(~2σμN ,975.0)9(=<X p ,062.0)2(=<X p ,利用标准正态分布表求)6(>X p 和)3(>X p 。
6.某保险公司对顾客进行人身保险,如果在一年内投保人死亡,保险公司赔偿10000元,若投保人受伤,保险公司赔偿5000元,已知一年内投保人死亡的概率为0.002,受伤的概率为0.005,为使保险公司的期望收益不低于保费的10%,该公司应该要求顾客至少交多少保险费?习题B(练习题)一、填空题1.用随机变量X 来描述掷一枚硬币的试验结果(正面为1,反面为0). 则X 的分布函数为 。
数学人教版3年级下册第3单元统计分层作业(提升版)
数学人教版3年级下册第3单元《统计》分层作业(提升版)一、选择题1.下面是希望小学三年级兴趣小组活动人数的信息:一班:航模18人、书法7人、踢球16人;二班:航模20人、书法9人、美术16人;三班:航模12人、书法9人、踢球23人。
可以把()的兴趣小组人数合并在一张统计表里。
A.一班和二班B.二班和三班C.一班和三班2.从复式统计表中可以看出()。
A.草莓味酸奶销售的最好B.一月份比二月份销售情况好C.两个月销售情况呈上升趋势3.四个小朋友都在读《一千零一夜》,读书情况如下表。
平均每天阅读的页数最多的是()。
A.张林B.王芳C.李月D.赵玲4.学校的图书室要购买一些新书,想知道大多数学生最喜欢看什么类型的书,下列收集数据的方法中合理的是()。
A.找一个班统计每名学生一年读多少本书B.找一个班统计每名学生最喜欢看什么类型的书C.找每个年级的一部分学生统计他们最喜欢看什么类型的书D.随便问一名学生最喜欢看什么类型的书5.下表列出了一支气温计液柱高度与气温的关系,表中“?”处应填入()。
A.119B.120C.122D.1236.杨树再种()棵就和柳树同样多。
A.4B.6C.87.某班统计数学考试成绩,平均成绩是86.5分,后来发现小刚的成绩是96分,被错记为69分,重新计算后,平均成绩是87.1分,那么这个班有()名学生.A.47B.45C.43D.42二、填空题8.小刚在体育课上记录了本小组12名同学1分钟跳绳的次数。
《国家学生体质健康测试标准》对三年级学生1分钟跳绳的成绩规定如下:(1)请你根据上面的标准帮小刚把他们组的跳绳成绩整理在下表中。
(2)这个组一共有()名学生达到优秀。
(3)男生和女生比较,这个组()生的跳绳成绩更好。
9.观察统计表填空。
A、B两种酸奶第一季度销量统计表(1)A种酸奶( )月销售量最多,是( )箱;B种酸奶( )月销售量最少,是( )箱。
(2)第一季度,( )种酸奶销售量多。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.按照某市城市社会发展十年规划,该市人均绿化面积要在2000年的人均4平
方米的基础上十年后翻一番。试问:
1)若在2010年达到翻一番的目标,每年的平均发展速度是多少?
2)若在2008年就达到翻一番的目标,每年的平均增长速度是多少?
3).若2001年和2002年的平均发展速度都为110%,那么后8年应该以怎样的
平均发展速度才能实现这一目标?
4)假设2007年的人均绿化面积为人均6.6平方米,以2000年为基期,那么其
平均年增长量是多少?
1. 210=107.18%
2. 28-1=9.05%
3. 84∗110%∗110%8=106.48%
4. 6.6/47-1=7.42%
第一季度 第二季度 第三季度 第四季度
2002 13 18
2003 5 8 14 18
2004 6 10 16 22
2005 8 12 19 25
2006 15 17
季平均数 8.5 11.75 15.5 20.75
季节比率(%) 60.18 83.19 109.73 146.90
年份 季度 销售量 移动平均 季节指数
2002 3 13
4 18
2003 1 5 11.125 0.499
2 8 11.25 0.711
3 14 11.375 1.231
4 18 11.75 1.532
2004 1 6 12.25 0.490
2 10 13 0.769
3 16 13.75 1.164
4 22 14.25 1.544
2005 1 8 14.875 0.538
2 12 15.625 0.768
3 19 16.875 1.126
4 25 18.375 1.361
2006 1 15
2 17
年份 一季度 二季度 三季度 四季度
2003 0.449 0.711 1.231 1.532
2004 0.490 0.769 1.164 1.544
2005 0.538 0.768 1.126 1.361
各季平均 0.492 0.749 1.174 1.479
季节比率% 50.54 76.94 120.60 151.93
