九上数学二次函数提高题常考题型抛物线压轴题(含解析)
二次函数多结论压轴小题精选30道(必考点分类集训)(解析版)—2024-2025学年九年级数学上册

二次函数多结论压轴小题精选30道1.(2024春•岳麓区校级期末)已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中,正确的有( )①abc>0;②b2>4ac;③a﹣b+c<0;④2a﹣b>0;⑤a+c<1.A.1个B.2个C.3个D.4个【分析】根据图上给的信息,结合二次函数的性质去判断对错即可.【解答】解:①如图所示,图象开口向上,∴a>0,∵图象与y轴的交点在x轴下方∴c<0,∵图象的对称轴在y轴的左边,且a>0,∴b>0,∴abc<0,故①错误;②根据图象可知,抛物线与x轴有两个交点,∴b2﹣4ac>0,即b2>4ac,故②正确;③由图可得,当x=﹣1时,y<0,∴a﹣b+c<0,故③正确;④由图可得,―b2a>―1,∵a>0,∴2a>b,∴2a﹣b>0,故④正确;⑤当x=1时,a+b+c=2,∴a+c=2﹣b,∵a﹣b+c<0,∴2﹣b﹣b<0,解得:b>1,∴2﹣b<1,∴a+c<1,故⑤正确;综上所述,共有4个是正确的;故选:D.2.(2024•宝安区校级模拟)已知抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列结论①abc<0,②a+b+c=2,③a>12④0<b<1中正确的有( )A.①②B.①②③C.①②④D.①②③④【分析】根据抛物线开口方向,对称轴的位置,与y轴的交点的位置,可以得出a、b、c的符号,进而确定abc的符号,对①做出判断;把(1,2)代入可对②做出判断;而无法判断③④一定正确,综合得出答案.【解答】解:因为抛物线开口向上,可知a>0,对称轴在y轴的左侧,a、b同号.故b>0,抛物线与y轴的交点在负半轴,因此c<0,∴abc<0,故①正确;把(1,2)代入得a+b+c=2,故②正确;当x=﹣1时,y=a﹣b+c<0,又∵a+b+c=2,∴2b>2,即:b>1,因此④不正确,因为对称轴x=―b2a介在﹣1与0之间,因此―b2a>―1,得2a>b,而b>1,∴a>12,因此③正确.故选:B.3.(2024•凤凰县模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数).其中正确结论个数有( )A.4个B.3个C.2个D.1个【分析】根据抛物线的开口方向、对称轴、与y轴的交点判定系数符号,及运用一些特殊点解答问题.【解答】解:开口向下,a<0;对称轴在y轴的右侧,a、b异号,则b>0;抛物线与y轴的交点在x轴的上方,c>0,∴abc<0,所以①正确,符合题意;当x=﹣1时图象在x轴下方,则y=a﹣b+c<0,即a+c<b,所以②不正确,不符合题意;对称轴为直线x=1,则x=2时图象在x轴上方,则y=4a+2b+c>0,所以③正确,符合题意;x=―b2a=1,则a=―12b,而a﹣b+c<0,则―12b―b+c<0,2c<3b,所以④正确,符合题意;开口向下,当x=1,y有最大值a+b+c;当x=m(m≠1)时,y=am2+bm+c,则a+b+c>am2+bm+c,即a+b>m(am+b)(m≠1),所以⑤错误,不符合题意.故①③④正确,故选:B.4.(2024•汝阳县一模)图形结合法既可以由数解决形的问题,也可以由形解决数的问题.如图所示,已知二次函数y=ax2+bx+c的图象如图所示.下列结论:①ab>0;②4a﹣2b+c<0;③2a﹣b<0;④|a+c|<|b|.其中正确的个数有( )A.1B.2C.3D.4【分析】根据所给函数图象,可得出a,b,c的正负,再根据抛物线的对称性和增减性对四个结论依次进行判断即可.【解答】解:由所给函数图象可知,a<0,b<0,所以ab>0.故①正确.抛物线上横坐标为﹣2的点在x轴下方,所以4a﹣2b+c<0.故②正确.因为抛物线的对称轴在直线x=﹣1和y轴之间,所以―b2a>―1,则2a﹣b<0.故③正确.当x=1时,函数值小于零,则a+b+c<0;当x=﹣1时,函数值大于零,则a﹣b+c>0;所以(a+b+c)(a﹣b+c)<0,即(a+c)2﹣b2<0,所以(a+c)2<b2,所以|a+c|<|b|.故④正确.故选:D.5.(2024•斗门区校级模拟)二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②3a+c>0;③(a+c)2﹣b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的为( )A.①④B.②③④C.①②④D.①②③④【分析】由抛物线开口方向,对称轴位置,抛物线与y轴交点位置判断①,由a与b的关系及x=﹣1时y<0可判断②,利用(a+c)2﹣b2=(a+b+c)(a﹣b+c),根据x=﹣1时y>0,x=1时y<0可判断③,由x=1时y取最小值可判断④.【解答】解:∵抛物线开口向上,∴a>0,∵抛物线对称轴为直线x=―b2a=1>0∴b=﹣2a<0,∵抛物线与y轴交点在x轴下方,∴c<0∴abc>0,故①正确.∵x=﹣1时,y=a﹣b+c=3a+c=0,故②不正确.∵(a+c)2﹣b2=(a+b+c)(a﹣b+c),且a+b+c<0,a﹣b+c=0,∴(a+c)2﹣b2=0,故③不正确.∵x=1时,y=a+b+c为最小值,∴a+b≤m(am+b),故④正确.故选:A.6.(2024•岚山区二模)已知二次函数y=ax2+bx+c(a≠0)与x轴的一个交点为(4,0),其对称轴为直线x=1,其部分图象如图所示,有下列5个结论:①abc<0;②b2﹣4ac<0;③8a+c=0;④若关于x 的方程ax2+bx+c=﹣1有两个实数根x1x2,且满足x1<x2,则x1<﹣2,x2>4;⑤直线y=kx﹣4k(k≠0)经过点(0,c),则关于x的不等式ax2+(b﹣k)x+c+4k>0的解集是0<x<4.其中正确结论的个数为( )A.5B.4C.3D.2【分析】根据抛物线与方程、不等式的关系及二次函数的性质求解.【解答】解:由图象得:a<0,c>0,b=﹣2a>0,∴abc<0,故①是正确的;∵抛物线与x轴有两个交点,∴0=ax2+bx+c有两个不相等的实数根,∴b2﹣4ac>0,故②是错误的;根据抛物线的对称性,抛物线与x轴的交点的横坐标分别为:﹣2,4,∴当x=﹣2时,4a﹣2b+c=8a+c=0,故③是正确的;由图象得:抛物线与y=﹣1的交点的横坐标分别位于﹣2的左边,4的右边,∴x1<﹣2,x2>4;故④是正确的;∵直线y=kx﹣4k(k≠0)经过点(0,c)和(4,0),∴于x的不等式ax2+(b﹣k)x+c+4k>0即:ax2+bx+c>kx﹣4k的解集是0<x<4,故⑤是正确的;故选:B.7.(2024•旺苍县三模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b2<4ac;③2c<3b;④a+b>m(am+b)(m≠1);⑤若方程|ax2+bx+c|=1有四个根,则这四个根的和为2.其中正确的结论有( )A.2个B.3个C.4个D.5个【分析】①由二次函数图象性质知,开口向下,则a<0.再结合对称轴―b2a>0,得b>0.据二次函数图象与y轴正半轴相交得c>0;②由于二次函数图象与x轴交于不同两点,则b2﹣4ac>0,即b2>4ac;③由―b2a=1,得b=﹣2a,当x=﹣1时,y<0,即a﹣b+c<0,所以2a﹣2b+2c<0,把b替换成a计算;④x=1时函数有最大值,所以当x=1时的y值大于当x=m(m≠1)时的y值,即a+b+c>m(am+b)+c,所以a+b>m(am+b)(m≠1)成立;⑤将x轴下方二次函数图象翻折到x轴上方,则与直线y=1有四个交点即可,由二次函数图象的轴对称性知:关于对称轴对称的两个根的和为2,四个根的和为4.【解答】解:∵图象开口向下,∴a<0,∵对称轴在y轴的右侧,a与b异号,∴b>0,∵与y轴交于正半轴,∴c>0,∴abc<0,故①错误;∵二次函数图象与x轴交于不同两点,则Δ=b2﹣4ac>0.∴b2>4ac.故②错误;∵―b2a=1,∴b=﹣2a.又∵当x=﹣1时,y<0.即a﹣b+c<0.∴2a﹣2b+2c<0.∴﹣3b+2c<0.∴2c<3b.故③正确;∵x=1时函数有最大值,∴当x=1时的y值大于当x=m(m≠1)时的y值,即a+b+c>m(am+b)+c∴a+b>m(am+b)(m≠1)成立,故④正确.将x轴下方二次函数图象翻折到x轴上方,则与直线y=1有四个交点即可,由二次函数图象的轴对称性知:关于对称轴对称的两个根的和为2,四个根的和为4,故⑤错误.综上:③④正确,8.(2023秋•龙港区期中)函数y =ax 2+bx +c 与y =kx 的图象如图所示,下列结论:①b 2﹣4ac >0;②a +b +c =0;③x =﹣2时,函数y =﹣ax 2+(k ﹣b )x ﹣c 有最大值;④关于x 的方程ax 2+(b ﹣k )x +c =0的根是x 1=﹣1,x 2=﹣3,其中正确的个数是( )A .1B .2C .3D .4【分析】根据抛物线与x 轴交点个数与Δ=b 2﹣4ac 的关系即可判断①;由x =1时,二次函数的函数值即可判断②;由抛物线与直线的两个交点的横坐标为﹣3,﹣1得到9a ―3b +c =―3k①a ―b +c =―k②,解得k ﹣b =﹣4a ,代入y =﹣ax 2+(k ﹣b )x ﹣c 得到y =﹣ax 2+(k ﹣b )x ﹣c =﹣ax 2﹣4ax ﹣c =﹣a (x +2)2+4a ﹣c ,根据二次函数的性质即可判断③;抛物线与直线的交点的坐标与函数解析式的关系即可判断④.【解答】解:∵抛物线与x ∴Δ=b 2﹣4ac <0,故选项①错误;由图象可知,当x =1时,y =a +b +c >0,故选项②错误;∵抛物线与直线的两个交点的横坐标为﹣3,﹣1,∴9a ―3b +c =―3k①a ―b +c =―k②,②﹣①得﹣8a +2b =2k ,即k ﹣b =﹣4a ,∴y =﹣ax 2+(k ﹣b )x ﹣c =﹣ax 2﹣4ax ﹣c =﹣a (x +2)2+4a ﹣c ,∵﹣a <0.∴x =﹣2时,函数y =﹣ax 2+(k ﹣b )x ﹣c 有最大值,故选项③正确;∵抛物线与直线的两个交点的横坐标为﹣3,﹣1,∴方程ax 2+bx +c 与y =kx 的解为x 1=﹣1,x 2=﹣3,∴关于x 的方程ax 2+(b ﹣k )x +c =0的根是x 1=﹣1,x 2=﹣3,故选项④正确.9.(2023•石城县模拟)二次函数y=ax2+bx+c(a≠0)的图象如图所示.下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax21+bx1=ax22+bx2且x1≠x2,则x1+x2=2.其中正确的有( )A.①④B.③④C.②⑤D.②③⑤【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.【解答】解:①抛物线开口方向向下,则a<0.抛物线对称轴位于y轴右侧,则a、b异号,即ab<0.抛物线与y轴交于正半轴,则c>0.所以abc<0.故①错误.②∵抛物线对称轴为直线x=b2a=1,∴b=﹣2a,即2a+b=0,故②正确;③∵抛物线对称轴为直线x=1,∴函数的最大值为:y=a+b+c;∴a+b+c≥am2+bm+c,即a+b≥am2+bm,故③错误;④∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,∴抛物线与x轴的另一个交点在(﹣1,0)的右侧,∴当x=﹣1时,y<0,∴a﹣b+c<0,故④错误;⑤∵ax21+bx1=ax22+bx2,∴ax21+bx1―ax22―bx2=0,∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,∴(x1﹣x2)[a(x1+x2)+b]=0,而x1≠x2,∴a(x1+x2)+b=0,即x1+x2=―b a ,∵b=﹣2a,∴x1+x2=2,故⑤正确.综上所述,正确的有②⑤.故选:C.10.(2024•苍溪县模拟)如图,已知二次函数y=ax2+bx+c(a,b,c是常数)的图象关于直线x=﹣1对称,则下列五个结论:①abc>0;②2a﹣b=0;③9a﹣3b+c<0;④a(m2﹣1)+b(m+1)≤0(m为任意实数);⑤3a+c<0.其中结论正确的个数为( )A.2个B.3个C.4个D.5个【分析】根据所给函数图象可得出a,b,c的正负,再结合抛物线的对称性及增减性,利用数形结合的思想对所给结论依次进行判断即可.【解答】解:由函数图象可知,a<0,b<0,c>0,所以abc>0.故①正确.因为抛物线的对称轴为直线x=﹣1,所以―b2a=―1,即2a﹣b=0.因为抛物线的对称轴为直线x =﹣1,且x =1时,函数值小于零,所以x =﹣3时,函数值小于零,则9a ﹣3b +c <0.故③正确.因为抛物线的对称轴为直线x =﹣1,且开口向下,所以当x =m 时,am 2+bm +c ≤a ﹣b +c ,即am 2﹣a +bm +b ≤0,所以a (m 2﹣1)+b (m +1)≤0.故④正确.由函数图象可知,当x =1时,函数值小于零,则a +b +c <0,又因为b =2a ,所以3a +c <0.故⑤正确.故选:D .11.(2024•y =ax 2+bx +c 的图象中,观察得出了下面五条信息:①c <0;②abc >0;③a ﹣b +c >0;④2a ﹣3b =0;⑤c ﹣4b >0,你认为其中正确信息的个数有( )A .2个B .3个C .4个D .5个【分析】观察图象易得a >0,―b 2a =13>0,所以b <0,2a ﹣3b >0,因此abc >0,由此可以判定①②是正确的,而④是错误的;当x =﹣1,y =a ﹣b +c ,由点(﹣1,a ﹣b +c )在第二象限可以判定a ﹣b +c >0③是正确的;当x =2时,y =4a +2b +c =2×(﹣3b )+2b +c =c ﹣4b ,由点(2,c ﹣4b )在第一象限可以判定c ﹣4b >0⑤【解答】解:∵抛物线开口方向向上,∴a>0,∵与y轴交点在x轴的下方,∴c<0,∵―b2a=13>0,∵a>0,∴b<0,2a﹣3b>0,∴abc>0,∴①②是正确的,④对称轴x=―b2a=13,∴3b=﹣2a,∴2a+3b=0,∴④是错误的;当x=﹣1,y=a﹣b+c,而点(﹣1,a﹣b+c)在第二象限,∴a﹣b+c>0是正确的;当x=2时,y=4a+2b+c=2×(﹣3b)+2b+c=c﹣4b,而点(2,c﹣4b)在第一象限,∴c﹣4b>0.故选:C.12.(2024•沂源县一模)已知二次函数y=ax2+bx+c(a≠0)的图象的一部分如图所示,其中对称轴为:x =1,下列结论:①abc>0;②a+c>0;③2a+3b>0;④a+b>am2+bm(m≠1);上述结论中正确结论的个数为( )A.1个B.2个C.3个D.4个【分析】由抛物线的开口方向可判定a的符号;结合抛物线的对称轴b的符号可判断①;通过x=﹣1和x=3的对称性判断②;将不等式的两边加上c,进而判断出③;将b=﹣2a,a﹣b+c=0可推出④.【解答】解:∵抛物线的开口向下,∴a<0,∵对称轴为:x=―b2a=1,∴b=﹣2a>0,∵抛物线与y轴交于y轴的正半轴,∴c>0,∴abc<0,故①不正确;∵2×1﹣3=﹣1,当x=3时,y>0,∴当x=﹣1时,a﹣b+c>0,∴a+c>b,∵b=﹣2a>0,∴a+c>0,故②正确;∵b=﹣2a,∴2a+3b=2a﹣6a=﹣4a>0,故③正确,∵当x=1时,y=a+b+c,a<0,∴函数的最大值为:a+b+c,∴a+b+c>am2+bm+c(m≠0),∴a+b>am2+bm,∴②③④正确,故选:C.13.(2024•桃江县一模)抛物线y=ax2+bx+c的顶点坐标为(2,﹣a)(如图所示),则下列说法:①abc <0;②(a+b)2≥c;③关于x的方程ax2+bx=0有两个不相等的实数根;④﹣1≤a≤0.则正确的结论有( )A.1个B.2个C.3个D.4个【分析】由二次函数图象的性质及二次函数图象与系数的关系逐一判定即可.【解答】解:∵抛物线开口向下,∴a<0,∵抛物线的顶点坐标为(2,﹣a),∴―b2a=2,∴b=﹣4a>0,∵抛物线交y轴的负半轴,∴c<0,∴abc>0,故①错误;∵抛物线的顶点坐标为(2,﹣a),∴4a+2b+c=﹣a,∵b=﹣4a,∴4a﹣8a+c=﹣a,即c=3a,∴(a+b)2﹣c=9a2﹣3a=3a(3a﹣1),∴3a (3a ﹣1)>0,∴(a +b )2﹣c >0,∴(a +b )2>c ,故②错误;由图可知抛物线与直线y =c 有两个交点,∴关于x 的方程ax 2+bx +c =c ,即ax 2+bx =0有两个不相等的实数根,故③正确;∵a 为抛物线二次项系数,∴a ≠0,故④错误.故选:A .14.(2023秋•中山市校级期末)二次函数y =ax 2+bx +c (a ≠0)的图象如图所示.下列结论:①2a +b =0;②3a +c >0;③m 为任意实数,则a +b >am 2+bm ;④若A (x 1,0),B (x 2,0),则x 1+x 2=2,其中正确的有( )A .①②B .①③C .①④D .②④【分析】根据对称轴为直线x =x =1时取得最大值,即可判断①③,根据x =3时,y <0,即可判断②,根据对称性即可判断④.【解答】解:∵抛物线对称轴为直线x =―b 2a=1,∴b =﹣2a ,即2a +b =0,所以①正确;∵x =3时,y =9a +3b +c <0,即9a +3×(﹣2a )+c <0,∴3a +c <0,故②不正确;抛物线对称轴为直线x =1,开口向下,∴函数的最大值为a +b +c ,∴a +b +c ≥am 2+bm +c (m 为任意实数),即a +b ≥am 2+bm ,故③不正确;∵A (x 1,0),B (x 2,0),对称轴为直线x =1,则x 1+x 2=2,故④正确,15.(2023秋•西城区校级月考)已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①a<0;②9a+3b+c>0;③c>0;④﹣3<―b2a<0其中正确的有( )A.4个B.3个C.2个D.1个【分析】根据开口方向判断a的符号,当x=3时,判断9a+3b+c>0;根据抛物线与y轴的交点位置判断c的符号;根据抛物线对称轴的位置判断④.【解答】解:∵抛物线开口向下,∴a<0,故①正确;由图可以看出,对称轴﹣3<x=―b2a<0,故④正确;设抛物线与x1,由题意得,对称轴x=x1―32<0,解得x1<3,∴当x=3时,y=9a+3b+c<0,故②错误;∵抛物线与y轴交于正半轴,∴c>0,故③正确.综上所述,①③④正确.故选:B.16.(2023•东港区校级三模)函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c=0;③2b+c+3=0;④当1<x<3时,x2+(b﹣1)x+c<0其中正确的有( )个.A.4B.3C.2D.1【分析】①根据开口方向判定a的符号,根据对称轴判断b的符号,根据抛物线与y轴的交点判断c的符号,根据抛物线与x轴的交点情况判断b2﹣4ac的符号;②当x=1时,y=1,判断b+c+1的符号,由b+c+1=1,可得b+c=0;③根据对称轴求b的值,由b+c=0,代入可作判定;④由抛物线和直线所处的位置判断x2+bx+c<x,得出x2+(b﹣1)x+c<0.【解答】解:①∵函数y=x2+bx+c与x轴没交点,∴Δ=b2﹣4ac<0,∵a=1,∴Δ=b2﹣4c<0,故①错误;②∵函数y=x2+bx+c与y=x的交点的横坐标为1,∴交点为:(1,1),(3,3),∴b+c+1=1,∴b+c=0;故②正确;③由图象得:抛物线的对称轴是:x=32,且a=1,∴―b2=32,∴b=﹣3,∴2b+c+3=b+0+3=0,故③正确;④由图象可知:当1<x<3时,抛物线在直线的下方,∴x2+bx+c<x,∴x2+(b﹣1)x+c<0,故选:B.17.(2023•双台子区校级一模)二次函数y=ax2+bx+c的图象如图所示,给出四个结论:①abc>0;②4a﹣2b+c>0;③对于任意实数m,有am2+bm+c<a﹣b+c;④ca>―3,其中正确的有( )A.①②B.①④C.②③D.③④【分析】二次函数y=ax2+bx+c的系数确定了抛物线开口方向、对称轴、与y轴的交点等.对于①,先根据二次函数图象的性质判断a,b,c的正负,进而得出答案;对于②,令x=﹣2求出y值,判断即可;对于③,先求出当x=﹣1时,求初最大值,再比较即可;对于④,根据对称轴求出a,b的关系,再将x=1,y=0代入关系式,即可判断.【解答】解:①∵对称轴位于x轴的左侧,∴―b2a<0,∴即ab>0.∵与y轴交于正半轴,∴c>0,∴abc>0.故①正确;②∵x=﹣2时,y>0,∴4a﹣2b+c>0,故②正确;③当x=﹣1时,y最大=a﹣b+c,当x=m时,y=am2+bm+c,∴有am2+bm+c≤a﹣b+c,故③错误;④∵抛物线的对称轴为直线x=―b2a=―1,∵x=1时,y=0,∴a+b+c=0,∴c=﹣3a,∴ca=―3aa=―3,故④错误;正确的结论有:①②,故选:A.18.(2023•遂溪县模拟)如图是二次函数y=ax2+bx+c的图象,对称轴是直线l,则以下说法:①a﹣b+c=0;②4a+b=0;③abc>0;④16a+5b+2c>0,其中正确的个数是( )A.1B.2C.3D.4【分析】先由抛物线与x5,0),对称轴为x=2,可以得到抛物线与x轴的另一交点为(﹣1,0)可以判断①;利用抛物线的对称轴为x=2,判断出结论②;先由抛物线的开口方向判断出a>0,进而判断出b<0,再用抛物线与y轴的交点的位置判断出c>0,判断出结论③;先求出b=﹣4a,c=﹣5a,然后代入16a+5b+2c即可判断.【解答】解:有图象知,抛物线过点(5,0),对称轴为直线x=2,∴抛物线过点(﹣1,0),∴a﹣b+c=0,故①正确;∵抛物线的对称轴为直线x=2,∴―b2a=2,∴4a+b=0,故②正确;由图象知,抛物线开口向上,∴a>0,∵4a+b=0,∴b<0,而抛物线与y轴的交点在y轴的负半轴上,∴c<0,∴abc>0,故③正确;∵4a+b=0,∴b=﹣4a,∵a﹣b+c=0,∴c=﹣5a,∴16a+5b+2c=16a﹣20a﹣10a=﹣14a<0,故④错误.故选:C.19.(2023秋•义乌市期中)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc >0;②b2>4ac;③a(m2﹣1)+b(m﹣1)<0(m≠1);④关于x的方程|ax2+bx+c|=1有四个根,且这四个根的和为4A.①②③B.②③④C.①④D.②③【分析】由抛物线开口方向,对称轴位置,抛物线与y轴交点位置可判断①,由抛物线与x轴有两个交点可判断②,由当x=1时函数取最大值可判断③,由函数最大值大于1且抛物线开口向下可判断④.【解答】解:∵抛物线开口向下,∴a<0,∵抛物线对称轴为直线x=1,∴―b2a=1,∴b=﹣2a>0,∵抛物线与y轴交点在x轴上方,∴c>0,∴abc<0,①错误;∵抛物线与x轴有2个交点,∴b2﹣4ac>0,∴b2>4ac,②正确;∵x=1时函数取最大值,∴am2+bm+c<a+b+c(m≠1),∴am2﹣a+bm﹣b<0,即a(m2﹣1)+b(m﹣1)<0(m≠1),③正确.∴由图象可得函数最大值大于2,∴ax2+bx+c=1有两个不相等的实数根x1,x2,ax2+bx+c=﹣1有两个不相等的实数根x3,x4,∵图象对称轴为直线x=1,∴x1+x2=2,x3+x4=2.∴x1+x2+x3+x4=4,∴④正确.故选:B.20.(2023秋•铜梁区校级期中)二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②2a+b<0;③若﹣1<m<n<1,则m+n<―b a ;④3|a|+|c|<2|b|.其中正确的结论有( )A.1个B.2个C.3个D.4个【分析】分别根据二次函数开口方向以及对称轴位置和图象与y轴交点得出a,b,c的符号,再利用特殊值法分析得出各选项.【解答】解:∵抛物线开口向下,∴a<0,∴2a<0,∵对称轴x=―b2a>1,b>0,∵抛物线与y轴交于负半轴,∴c<0,∴abc>0,故选项①正确;对称轴x=―b2a>1,又a<0,则﹣b<2a,则2a+b>0,故②错误;∵﹣1<m<n<1,则﹣2<m+n<2,∴抛物线对称轴为:x=―b2a>1,―ba>2,m+n<―ba,故选项③正确;当x=1时,a+b+c>0,2a+b>0,则3a+2b+c>0,∴3a+c>﹣2b,∴﹣3a﹣c<2b,∵a<0,b>0,c<0(图象与y轴交于负半轴),∴3|a|+|c|=﹣3a﹣c<2b=2|b|④选项正确.故选:C.21.(2023•仁怀市模拟)如图,根据二次函数y=ax2+bx+c的图象得到如下结论:①abc>0 ②2a﹣b=0 ③a+b+c=0 ④3a+c<0 ⑤当x>﹣2时,y随x的增大而增大⑥一定存在实数x0,使得ax20+bx0>a﹣b 成立.上述结论,正确的是( )A.①②⑤B.②③④C.②③⑥D.③④⑤【分析】由开口方向、对称轴及抛物线与y轴的交点位置可判断结论①;由对称轴为直线x=﹣1即可得到,2a﹣b=0,即可判断②;由抛物线的对称性即可判断③④;由抛物线的增减性可判断结论⑤;函数的最值即可判断结论⑥.【解答】解:∵抛物线开口向上、顶点在y轴左侧、抛物线与y轴交于负半轴,∴a>0,b>0,c<0,∴abc<0,故①错误;∵―b2a=―1,∴b=2a,∴2a﹣b=0,故②正确;∵抛物线过点(﹣3,0),对称轴为直线x=﹣1,∴抛物线过点(1,0),∴a+b+c=0,故③正确;∴b=2a,a+b+c=0,∴3a+c=0,故④错误;∵抛物线开口向上,对称轴是直线x=﹣1,∴当x>﹣1时,y随x的增大而增大;故⑤错误;∵函数最小值为a﹣b+c,∴当x0≠﹣1时,则ax20+bx0c a﹣b+c,即ax20+bx0>a﹣b,∴一定存在实数x0,使得ax20+bx0>a﹣b成立,故⑥正确;故选:C.22.(2023•广东模拟)二次函数y=ax2+bx+c的图象如图所示,有如下结论:①abc<0;②2a﹣b+c≤0;③3b﹣2c<0;④对任意实数m,都有2am2+2bm﹣b≥0.其中正确的有( )A.①②B.②③C.②④D.③④【分析】由抛物线开口方向,对称轴位置,抛物线与y轴的交点位置可判断①;由x=﹣1时y>0及a>0,可判断②;由x=﹣1时y>0及a与b的数量关系可判断③,由x=1时函数取最小值可判断④.【解答】解:∵抛物线开口向上,∴a>0,∵抛物线对称轴为直线x=1,∴―b2a=1,∴b=﹣2a<0,∵抛物线与y轴交点在x轴下方,∴c<0,∴abc>0,故①错误;∵x=﹣1时,y>0,∴a﹣b+c>0,∵a>0,∴2a﹣b+c>0,故②错误;∵b=﹣2a,∴a=―b 2,由图象可得x=﹣1时,y=a﹣b+c=―32b+c>0,∴3b﹣2c<0,故③正确;由x=1时函数取最小值可得am2+bm+c≥a+b+c,∴am2+bm≥a+b,∵a=―b 2,∴am2+bm≥b 2,∴2am2+2bm﹣b≥0,故④正确.故选:D.23.(2023•凤凰县模拟)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论①abc<0;②3a+b>―13c;③2c<3b;④(k+1)(ak+a+b)≤a+b,其中正确的是( )A.①③④B.①②④C.①④D.②③④【分析】根据二次函数图象与性质,先判断a<0,b=﹣2a,即b>0,c>0,即可判断①正确;根据图象得出x=3时y<0,即可得出9a+3b+c<0,通过变形可判断②错误;根据9a+3b+c<0结合b=﹣2a 可以判断③正确;根据x=1时,y=a+b+c是函数的最大值,可以判断④正确.【解答】解:∵抛物线开口向下,∴a<0,∵对称轴是直线x=1,∴―b2a=1,即b=﹣2a,∴b>0,∵抛物线与y轴交点在正半轴,∴c>0,∴abc<0,故①正确;由图象可知,抛物线与x轴左侧的交点在(﹣1,0)的右侧,∵抛物线的对称轴为x=1,∴抛物线与x轴右侧的交点在(3,0)的左侧,∴当x=3时,y<0,∴9a+3b+c<0,∴3a+b<―13 c,故②错误;∵9a+3b+c<0,b=﹣2a,∴―92b+3b+c<0,∴2c<3b,故③正确;当x=1时,y=a+b+c是函数的最大值,∴a(k+1)2+b(k+1)+c≤a+b+c,∴a(k+1)2+b(k+1)≤a+b,∴(k+1)(ak+a+b)≤a+b,故④正确;∴正确的有①③④,故选:A.24.(2024•黄石模拟)已知抛物线y=ax2+bx+c(a<0)与x轴交于点(x1,0),(2,0),其中﹣1<x1<0.下列四个结论:①abc<0;②a﹣b+c>0;③2b﹣c<0;④不等式ax2+bx+c>―c2x+c的解集为0<x<2.其中正确结论的序号为( )A.①②B.①③C.②③D.①④【分析】根据题意画出函数图象,得到a、b异号,c>0,可判断①结论;根据当x=﹣1时,y<0,可判断②结论;根据抛物线y=ax2+bx+c(a<0)过点(2,0),得到a=―12b―14c,可判断③结论;令y1=―c2x+c,画出一次函数图象,利用图象可判断④结论.【解答】解:根据题意画出函数图象如下:∵抛物线y=ax2+bx+c(a<0x轴交于点(x1,0),(2,0),其中﹣1<x1<0,∴抛物线开口向下,对称轴在12~1之间,与y轴交点在正半轴,∴a、b异号,c>0,∴abc<0,①结论正确;由图象可知,当x=﹣1时,y<0,∴a﹣b+c<0,②结论错误;∵抛物线y=ax2+bx+c(a<0)过点(2,0),∴4a+2b+c=0,∴a=―2b+c4=―12b―14c,∴a―b+c=―12b―14c―b+c=―32b+34c=―34(2b―c)<0,∴2b﹣c>0,③结论错误;令y1=―c2x+c,当x=0时,y=c;当y=0,x=2,函数图象如下:由图象可知,当0<x<2时,抛物线y=ax2+bx+c图象在一次函数y1=―c2x+c的上方,∴不等式ax2+bx+c>―c2x+c的解集为0<x<2,④结论正确,故选:D.25.(2024•殷都区模拟)如图,在平面直角坐标系中,直线y1=mx+n与抛物线y2=ax2+bx―3相交于点A,B.结合图象,判断下列结论:①当﹣3<x<2时,y1>y2;②x=﹣3是方程ax2+bx﹣3=0的一个解;③若(﹣4,t1),(1,t2t1>t2;④对于抛物线y2=ax2+bx―3,当﹣3<x<2时,y2的取值范围是0<y2<5.其中正确结论的个数是( )A.4个B.3个C.2个D.1个【分析】根据函数图象即可判断①②④;求出对称轴,再由开口向上得到离对称轴越远函数值越大,即可判断③.【解答】解:由函数图象可知,当一次函数图象在二次函数图象上方时,自变量的取值范围为﹣3<x<2,∴当﹣3<x<2时,y1>y2,故①正确;∵二次函数与x轴的一个交点坐标为当(﹣3,0),∴x=﹣3是方程ax2+bx﹣3=0的一个解,故②正确;∵抛物线经过(2,5),(﹣3,0)∴4a+2b﹣3=5,9a﹣3b﹣3=0,∴a=1,b=2,∴抛物线对称轴为直线x=b―2a=―1,∵函数开口向上,∴离对称轴越远,函数值越大,∵﹣1﹣(﹣4)=3>1﹣(﹣1)=2,∴t1>t2,故③正确;由函数图象可知,当﹣3<x<2时,y2的取值范围是不是0<y2<5,故④错误,故选:B.26.(2024•东港区校级一模)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)和(0,3)两点之间(包含端点).下列结论中正确的是( )①不等式ax2+c<﹣bx的解集为x<﹣1或x>3;②9a2﹣b2<0;③一元二次方程cx2+bx+a=0的两个根分别为x1=13,x2=﹣1;④6≤3n﹣2≤10.A.①②③B.①②④C.②③④D.①③④【分析】由已知求出b=﹣2a,c=﹣3a,由抛物线的对称性可求抛物线与x轴的另一个的交点为(3,0),则不等式ax2+c<﹣bx的解集为x<﹣1或x>3;再将b=﹣2a,c=﹣3a,代入9a2﹣b2,即可判断②;将一元二次方程cx2+bx+a=0化为﹣3ax2﹣ax+a=0,即可求方程的根;由已知可得2≤c≤3,再由抛物线的顶点坐标可求n=﹣4a,从而进一步可求n的范围为83≤n≤4,即可求出6≤3n﹣2≤10.【解答】解:∵顶点坐标为(1,n),∴b=﹣2a,∵与x轴交于点A(﹣1,0),∴a﹣b+c=0,∴c=﹣3a,∵对称轴为直线x=1,经过点(﹣1,0),∴抛物线与x轴的另一个的交点为(3,0),∵抛物线开口向下,∴不等式ax2++bx+c<0的解集为x<﹣1或x>3,即不等式ax2+c<﹣bx的解集为x<﹣1或x>3,故①正确;∵9a2﹣b2=9a2﹣(﹣2a)2=5a2>0,故②不正确;∵一元二次方程cx2+bx+a=0可化为﹣3ax2﹣2ax+a=0,即3x2+2x﹣1=0,∴方程的根为x1=13,x2=﹣1,故③正确;∵抛物线与y轴的交点在(0,2)和(0,3)两点之间,∴2≤c≤3,∵顶点坐标为(1,n),∴n=﹣4a,∵c=﹣3a,∴n=43 c,∴83≤n≤4,∴6≤3n﹣2≤10;故④正确;故选:D.27.(2024•射洪市一模)二次函数y =ax 2+bx +c (a ≠0)的大致图象如图所示(1<x =h <2,0<x A <1).下列结论:①abc <0;②2a +b >0;③若OC =2OA ,则2b ﹣ac =4;④3a ﹣c <0.其中正确的有 ②③④ .(只填写序号)【分析】①根据抛物线的开口向下即可得出a <0,再根据抛物线的对称轴在x =1和x =2之间即可得出b >﹣2a ,②正确;②由b >﹣2a 可得出b >0,再根据抛物线与y 轴交于y 轴负半轴可得出c <0,由此即可得出abc >0,①错误;③将A(―c 2,0)代入抛物线解析式中,整理后可得出2b ﹣ac =4,③正确;④根据抛物线的对称轴1<―b 2a<2可得出﹣2a <b <﹣4a ,再由当x =1时y >0即可得出a +b +c >0,进而即可得出3a ﹣c <0,④正确.综上即可得出结论.【解答】解:∵抛物线的开口向下,∴a <0.∵抛物线的对称轴―b 2a>1,∴b >﹣2a ,即2a +b >0,②成立;∵b >﹣2a ,a <0,∴b >0,∵抛物线与y 轴的交点在y 轴的负半轴,∴c <0,∴abc >0,①错误;∵OC =2OA ,∴A(―c 2,0),∴14ac 2―14bc +c =0,整理得:2b ﹣ac =4,③成立;∵抛物线的对称轴1<―b 2a<2,∴﹣2a <b <﹣4a ,∵当x =1时,y =a +b +c >0,∴a ﹣4a +c >0,即3a ﹣c <0,④正确.综上可知正确的结论为②③④.故答案为:②③④.28.(2023秋•太康县期末)已知二次函数y =ax 2+bx +c (a ≠0,a 、b 、c 为常数)的图象如图所示.下列4个结论:①b >0;②b <a +c ;③c <4b ;④a +b <k 2a +kb (k 为常数,且k ≠1).其中正确的结论序号是 ①③ .【分析】由抛物线的开口方向判断a 的符号,然后根据对称轴及抛物线与x 轴交点情况进行推理,进而对所得结论进行判断.【解答】解:由图象可知,a <0,―b 2a=1,∴b =﹣2a ,∴b >0,故①正确;由图象可知,当x =﹣1时,y <0,即a ﹣b +c <0,∴b >a +c ,故②错误;∵二次函数y =ax 2+bx +c 图象的对称轴为直线x =1,∴当x =3时,函数值小于0,y =9a +3b +c <0,且b =﹣2a ,即a =―b 2,代入得9(―b 2)+3b +c <0,得c <32b ,∵b >0,∴c <4b ,故③正确;当x=1时,y的值最大.此时,y=a+b+c,而当x=k时,y=ak2+bk+c,∵k为常数,且k≠1,所以a+b+c>ak2+bk+c,故a+b>ak2+bk,故④错误.故①③正确.故答案为:①③.29.(2023秋•青山区期末)已知抛物线y=ax2+bx+c经过点(2,c),且满足a﹣b+c=0.下列四个结论:①抛物线的对称轴是直线x=1;②b与c同号;③若a+2b+4c>0,则不等式ax2+bx+c<﹣2ax﹣a﹣b的解集﹣2<x<2;④抛物线上的两个点M(m﹣1,y1),N(m+2,y2),当c<0,且y1>y2时,m<1 2.其中一定正确的是 .(填写序号)【分析】根据二次函数的性质及抛物线与不等式的关系求解.【解答】解:由题意得:4a+2b+c=c,∴b=﹣2a∴―b2a=1,故①是正确的;又∵a﹣b+c=0,∴c=﹣3a,∴a、c异号,a、b异号,∴b、c同号,故②是正确的;∵a+2b+4c>0,∴a﹣4a﹣12a=﹣15a>0,∴a<0,∴不等式化为:x2﹣4>0,解得:﹣2<x <2,故③是正确的;∵c <0,∴a >0,抛物线开口向上,∵m ﹣1<m +2,y 1>y 2,∴m +2≤1,或1﹣(m ﹣1)>m +2﹣1解得:m ≤﹣1或m <12,故④是错误的;故答案为:①②③.30.(2023秋•城厢区校级月考)如图,是抛物线y 1=ax 2+bx +c (a ≠0)图象的一部分,抛物线的顶点坐标为A (1,3),与x 轴的一个交点为B (4,0),点A 和点B 均在直线y 2=mx +n (m ≠0)上.①2a +b =0;②abc >0;③抛物线与x 轴的另一个交点是(﹣4,0);④方程ax 2+bx +c =﹣3有两个不相等的实数根;⑤a ﹣b +c <4m +n ;⑥不等式mx +n >ax 2+bx +c 的解集为1<x <4.其中正确的是 .【分析】利用抛物线的对称轴方程得到―b 2a=1,则可对①进行判断;由抛物线开口向下得到a <0,则b >0,由抛物线与y 轴的交点在x 轴上方得到c >0,则可对②进行判断;利用抛物线的对称性得到抛物线与x 轴的一个交点为(﹣2,0),则可对③进行判断;利用抛物线与直线y =﹣3只有一个交点可对④进行判断;利用x =﹣1时,y 1>0,即a ﹣b +c >0,x =4时,y 2=0,即4m +n =0,则可对⑤进行判断;结合函数图象可对⑥进行判断.【解答】解:∵抛物线的对称轴为直线x =―b 2a=1,∴b=﹣2a,即2a+b=0,所以①正确;∵抛物线开口向下,∴a<0,∴b=﹣2a>0,∵抛物线与y轴的交点在x轴下方,∴c>0,∴abc<0,所以②错误;∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点为B(4,0),∴抛物线与x轴的一个交点为(﹣2,0),所以③错误;∵抛物线的顶点坐标为(1,3),∴抛物线与直线y=﹣3有两个交点,∴方程ax2+bx+c=﹣3有两个不相等的实数根,所以④正确;∵x=﹣1时,y1>0,即a﹣b+c>0,而x=4时,y2=0,即4m+n=0,∴a﹣b+c>4m+n;所以⑤错误;∵当1<x<4时,y2<y1,∴不等式mx+n>ax2+bx+c的解集为x<1或x>4.所以⑥错误.故答案为:①④.。
人教版九年级上册数学期末二次函数压轴题(最值问题)专题训练(含解析)

人教版九年级上册数学期末二次函数压轴题(最值问题)专题训练(1)求三个点,,的坐标;(2)当点运动至抛物线的顶点时,求此时(3)设点的横坐标为,的长度为范围;是否存在最值,如有写出最值.(1)求二次函数的解析式;(2)当x 为何值时,函数有最大值还是最小值?并求出最值;(3)在抛物线上是否存在点,若存在,请求出点A B C N N t MN L 8AOP S =△(1)求抛物线的表达式和点D 的坐标.(2)连接AD ,交y 轴于点E ,P 是抛物线上的一个动点.Q 是抛物线对称轴上一个点,是否存在以B ,E ,P ,Q 为顶点的四边形为平行四边形,若存在,求出存在,请说明理由.(3)如图,点P 在第四象限的抛物线上,连接AP 、BE 交于点G ,设(1)求二次函数解析式;(2)设的面积为,试判断PCD ∆S S请说明理由;(3)在上是否存在点,使为直角三角形?若存在,请写出点的坐标若不存在,请说明理由.5.如图,抛物线与轴相交于两点(点位于点的左侧),与轴相交于点,是抛物线的顶点,直线是抛物线的对称轴,且点的坐标为.(1)求抛物线的解析式.(2)已知为线段上一个动点,过点作轴于点.若的面积为.①求与之间的函数关系式,并写出自变量的取值范围;②当取得最值时,求点的坐标.(3)在(2)的条件下,在线段上是否存在点,使为等腰三角形?如果存在,请求出点的坐标;如果不存在,请说明理由.6.如图,已知二次函数,回答下列问题:(1)求出此抛物线的对称轴和顶点坐标;MB P PCD ∆P 2y x bx c =-++x ,A B A B y C M 1x =C (0,3)P MB P PD x ⊥D ,PD m PCD =∆S S m m S P MB P PCD ∆P 243y x x =++(2)写出抛物线与轴交点、的坐标,与轴的交点的坐标;(3)写出函数的最值和增减性;(4)取何值时,①,②.7.如图,抛物线y =﹣x 2+bx +c 与x 轴相交于A 、B 两点,与y 轴相交于点C ,且点B 与点C 的坐标分别为B (3,0),C (0,3),点M 是抛物线的顶点.(1)求二次函数的关系式;(2)点P 为线段MB 上一个动点,过点P 作PD ⊥x 轴于点D .若OD =m ,△PCD 的面积为S ,①求S 与m 的函数关系式,写出自变量m 的取值范围.②当S 取得最值时,求点P 的坐标;(3)在MB 上是否存在点P ,使△PCD 为直角三角形?如果存在,请直接写出点P 的坐标;如果不存在,请说明理由.8.已知抛物线y =x 2﹣2ax+m .(1)当a =2,m =﹣5时,求抛物线的最值;(2)当a =2时,若该抛物线与坐标轴有两个交点,把它沿y 轴向上平移k 个单位长度后,得到新的抛物线与x 轴没有交点,请判断k 的取值情况,并说明理由;(3)当m =0时,平行于y 轴的直线l 分别与直线y =x ﹣(a ﹣1)和该抛物线交于P ,Q 两点.若平移直线l ,可以使点P ,Q 都在x 轴的下方,求a 的取值范围.9.如图,Rt △OAB 如图所示放置在平面直角坐标系中,直角边OA 与x 轴重合,∠OAB=90°,OA=4,AB=2,把Rt △OAB 绕点O 逆时针旋转90°,点B 旋转到点C 的位置,一条抛物线正好经过点O ,C ,A 三点.x A B y C x 0y <0y >(1)填空:点B 的坐标为 ,点D 的坐标为 .(2)如图1,连结,P 为x 轴上的动点,当以O ,D ,P 为顶点的三角形是等腰三角形时,求点P 的坐标;(3)如图2,M 是点B 关于抛物线对称轴的对称点,Q 是抛物线上的动点,m ,连结,,与直线交于点E .设别为和,设己,试求t 关于m 的函数解析式并求出OD (05)m <<MQ BQ MQ OB 1S 2S 12S t S =(1)求抛物线的解析式;(2)如图1,点P为直线CB上方抛物线上一点,过P作PE∥y轴交BC于点E,连接CP,PD,DE,求四边形CPDE面积的最值及点P的坐标;(3)如图2,将抛物线沿射线CB方向平移得新抛物线y=a1x2+b1x+c1(a1≠0),是否在新抛物线上存在点M,在平面内存在点N,使得以A,C,M,N为顶点的四边形为正方形?若存在,直接写出此时新抛物线的顶点坐标,若不存在,请说明理由.13.如图1,抛物线y=ax2+bx+c(a≠0),与x轴交于A(4,0)、O两点,点D(2,-2)为抛物线的顶点.(1)求该抛物线的解析式;(2)点E为AO的中点,以点E为圆心、以1为半径作⊙E交x轴于B、C两点,点M 为⊙E上一点.①射线BM交抛物线于点P,设点P的横坐标为m,当tan∠MBC=2时,求m的值;②如图2,连接OM,取OM的中点N,连接DN,则线段DN的长度是否存在最大值或最小值?若存在,请求出DN的最值;若不存在,请说明理由.14.在平面直角坐标系xOy中,已知抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y 轴交于C点,D为抛物线顶点.连接AD,交y轴于点E,P是抛物线上的一个动点.参考答案:∴β=1,∴A(-1,0),B (3,0),∴,解得:,∴抛物线的表达式为,当x =1时,y =1-2-3=-4,∴点D 的坐标为(1,4);(2)解:∵A (-1,0),B (3,0),D (1,4),设直线AD 的表达式为y =kx +c ,∴,解得,∴直线AD 的表达式为y =-2x -2,当x =0时,y =-2,∴点E 的坐标为(0,-2),∵P 是抛物线上的一个动点,Q 是抛物线对称轴上一个点,∴设P (m ,),Q (1,t ),①当BE 为边时,PQ BE 且PQ =BE ,当E 对应Q ,由(0,-2)变为(1,t ),要向右平移1个单位,则当B (3,0)对应P (m ,),也要向右平移1个单位,即m =3+1=4,∴=5,∴P (4,5);309330a b a b --=⎧⎨+-=⎩12a b =⎧⎨=-⎩2=23y x x --04k c k c -+=⎧⎨+=⎩22k c =-⎧⎨=-⎩223m m --∥223m m --223m m --∵∠OBC=45°,∵轴∴时,轴∴,即,解得:,∴此时;②时,如图②,PD x ⊥90CDP ∠=︒//CP x 3c p y y ==263m -+=32m =3,32P ⎛⎫ ⎪⎝⎭90P CD ''∠=︒∵轴,∴,∴,又∵,∴,即,∵,,,P D x ''⊥//P D OC ''12∠=∠90P CD D OC '''∠=∠=︒P CD D OC '''∆∆∽OC CD CD P D '='''(0,3)C (,0)D m (,26)P m m -+【点睛】本题考查了二次函数的动点问题,掌握二次函数的性质以及解二次函数的方法是解题的关键.8.(1)-9;(2)当m=0时,k>4或当m=4时,k>0时,得到新的抛物线与x轴没有交点;(3)a>1或a<﹣1【分析】(1)把a=2,m=﹣5代入抛物线解析式即可求抛物线的最值;(2)把a=2代入,当该抛物线与坐标轴有两个交点,分抛物线与x轴、y轴分别有一个交点和抛物线与x轴、y轴交于原点,分别求出m的值,把它沿y轴向上平移k个单位长度,得到新的抛物线与x轴没有交点,列出不等式,即可判断k的取值;(3)根据题意,分a大于0和a小于0两种情况讨论即可得a的取值范围.【详解】解:(1)当a=2,m=﹣5时,y=x2﹣4x﹣5=(x﹣2)2﹣9所以抛物线的最小值为﹣9.(2)当a=2时,y=x2﹣4x+m因为该抛物线与坐标轴有两个交点,①该抛物线与x轴、y轴分别有一个交点∴△=16-4m=0,∴m=4,∴y=x2﹣4x+4=(x-2)2沿y轴向上平移k个单位长度后,得到新的抛物线与x轴没有交点,则k>0;②该抛物线与x轴、y轴交于原点,即m=0,∴y=x2﹣4x∵把它沿y轴向上平移k个单位长度后,得到新的抛物线与x轴没有交点,∴y=x2﹣4x+k此时△<0,即16﹣4k<0解得k>4;综上,当m=0时,k>4或当m=4时,k>0时,得到新的抛物线与x轴没有交点;(3)当m=0时,y=x2﹣2ax抛物线开口向上,与x轴交点坐标为(0,0)(2a,0),a≠0.直线l分别与直线y=x﹣(a﹣1)和该抛物线交于P,Q两点,平移直线l,可以使点P,Q都在x轴的下方,①当a>0时,如图1所示,此时,当x=0时,0﹣a+1<0,解得a>1;②当a<0时,如图2所示,此时,当x=2a时,2a﹣a+1<0,解得a<﹣1.综上:a>1或a<﹣1.【点睛】本题主要考查的是二次函数的综合应用,掌握二次函数的最值问题和根据题意进行分类讨论是解本题的关键.9.(1)、y=﹣x2+4x;(2)、10;(3)、N1(2+2,﹣4),N2(2﹣2,﹣4)【详解】试题分析:(1)、根据旋转的性质可求出C的坐标和A的坐标,又因为抛物线经过原点,故设y=ax2+bx把(2,4),(4,0)代入,求出a和b的值即可求出该抛物线的解析式;(2)、四边形PEFM的周长有最大值,设点P的坐标为P(a,﹣a2+4a)则由抛物线的对称性知OE=AF,所以EF=PM=4﹣2a,PE=MF=﹣a2+4a,则矩形PEFM的周长L=2[4﹣2a+(﹣a2+4a)]=﹣2(a﹣1)2+10,利用函数的性质即可求出四边形PEFM的周长的最大值;(3)、在抛物线上存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形,由(1)可求出抛物线的顶点坐标,过点C作x轴的平行线,与x轴没有其它交点,过y=﹣4作x轴的平行线,与抛物线有两个交点,这两个交点为所求的N点坐标所以有﹣x2+4x=﹣4,解方程即可求出交点坐标.试题解析:(1)、因为OA=4,AB=2,把△AOB绕点O逆时针旋转90°,可以确定点C的坐标为(2,4);由图可知点A的坐标为(4,0),又因为抛物线经过原点,故设y=ax2+bx把(2,4),(4,0)代入,得,解得所以抛物线的解析式为y=﹣x2+4x;(2)、四边形PEFM的周长有最大值,理由如下:由题意,如图所示,设点P的坐标为P(a,﹣a2+4a)则由抛物线的对称性知OE=AF,∴EF=PM=4﹣2a,PE=MF=﹣a2+4a,则矩形PEFM的周长L=2[4﹣2a+(﹣a2+4a)]=﹣2(a﹣1)2+10,∴当a=1时,矩形PEFM的周长有最大值,L max=10;=2+,﹣2+,﹣,,点Q 的横坐标为m ()1,16N MN ∴--=, (,Q m m ∴,()2245KQ m m m m m ∴=--=-+()121122B E S QK x x S MN =-= ,()21S 115QK m m ∴==--=-【点睛】本题主要考查二次函数的性质,熟练掌握二次函数的性质,最值,是解题的关键.13.(1);(2)①m=2或4+2和.【分析】(1)用抛物线顶点式表达式得:y=a 2122y x x =-50.5-50.5+(2)∵点P在第四象限的抛物线上,设直线AP的解析式为代入,∵,∴,y=(1,0)A-2(,2P m m-03m<<10m+≠∵点C 与点关于对称轴对称∴设直线的解析式为解得:∴直线的解析式为:C '1x =()2,3C '-AC 'y kx b =+13432k b ⎧=-⎪⎪⎨⎪=-⎪⎩AC '3y =-设点在中,当时,在中,由勾股定理知:即:化简得:解得:(舍),233,384R k k k ⎛⎫-- ⎪⎝⎭Rt OBC 222BC OC OB =+190BCR ∠= 1Rt BCR ()222334384k k k k ⎛⎫-+--= ⎪⎝⎭29+140k k =()9+14=0k k 0k =14k =-。
2023年中考数学复习《二次函数综合压轴题》培优提升专题训练(含解析)

2023年春九年级数学中考复习《二次函数综合压轴题》培优提升专题训练(附答案)1.已知:抛物线y=x2+x+m交x轴于A,B两点,交y轴于点C,其中点B在点A的右侧,且AB=7.(1)如图1,求抛物线的解析式;(2)如图2,点D在第一象限内抛物线上,连接CD,AD,AD交y轴于点E.设点D 的横坐标为d,△CDE的面积为S,求S与d之间的函数关系式(不要求写出自变量d的取值范围);(3)如图3,在(2)的条件下,过点D作DH⊥CE于点H,点P在DH上,连接CP,若∠OCP=2∠DAB,且HE:CP=3:5,求点D的坐标及相应S的值.2.如图,在平面直角坐标系中,矩形ABCD的顶点B,C,D的坐标分别(1,0),(3,0),(3,4),以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,以每秒个单位的速度沿线段AD向点D匀速运动,过点P作PE⊥x轴,交对角线AC于点N.设点P运动的时间为t(秒).(1)求抛物线的解析式;(2)若PN分△ACD的面积为1:2的两部分,求t的值;(3)若动点P从A出发的同时,点Q从C出发,以每秒1个单位的速度沿线段CD向点D匀速运动,点H为线段PE上一点.若以C,Q,N,H为顶点的四边形为菱形,求t的值.3.如图1,过原点的抛物线与x轴交于另一点A,抛物线顶点C的坐标为,其对称轴交x轴于点B.(1)求抛物线的解析式;(2)如图2,点D为抛物线上位于第一象限内且在对称轴右侧的一个动点,求使△ACD 面积最大时点D的坐标;(3)在对称轴上是否存在点P,使得点A关于直线OP的对称点A'满足以点O、A、C、A'为顶点的四边形为菱形.若存在,请求出点P的坐标;若不存在,请说明理由.4.综合与探究如图,已知抛物线y=ax2﹣2x+c与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,对称轴为直线l,顶点为D.(1)求抛物线的解析式及点D坐标;(2)在直线l上是否存在一点M,使点M到点B的距离与到点C的距离之和最小?若存在,求出点M的坐标;若不存在,请说明理由.(3)在x轴上取一动点P(m,0),﹣3<m<﹣1,过点P作x轴的垂线,分别交抛物线,AD,AC于点E,F,G.①判断线段FP与FG的数量关系,并说明理由②连接EA,ED,CD,当m为何值时,四边形AEDC的面积最大?最大值为多少?5.如图,抛物线y=ax2+bx(a>0)与双曲线y=相交于点A、B,已知点A坐标(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).(1)求实数a、b、k的值;(2)在该抛物线的对称轴上是否存在点P使得△POB为等腰三角形?若存在请求出所有的P点的坐标,若不存在请说明理由.(3)在坐标系内有一个点M,恰使得MA=MB=MO,现要求在y轴上找出点Q使得△BQM的周长最小,请求出M的坐标和△BQM周长的最小值.6.如图,已知,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,过点A的直线y=kx+k与该抛物线交于点C,点P是该抛物线上不与A,B重合的动点,过点P作PD⊥x轴于D,交直线AC于点E.(1)求抛物线的解析式;(2)若k=﹣1,当PE=2DE时,求点P坐标;(3)当(2)中直线PD为x=1时,是否存在实数k,使△ADE与△PCE相似?若存在请求出k的值;若不存在,请说明你的理由.7.如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;(3)一动点M从点D出发,以每秒1个单位的速度沿平行于y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?8.如图,已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.(1)求抛物线的解析式;(2)点P是第一象限抛物线上一动点,过点P作x轴的垂线l,交BC于点H.当点P 运动到何处时满足PC=CH?求出此时点P的坐标;(3)若m≤x≤m+1时,二次函数y=ax2+bx+3的最大值为m,求m的值.9.综合与探究如图,在平面直角坐标系中,点A,B的坐标分别为(﹣4,0),(2,0),点C在y轴上,其坐标为(0,﹣3),抛物线经过点A,B,C.P为第三象限内抛物线上一动点.(1)求该抛物线的解析式.(2)连接AC,过点P作PD⊥AC,PE∥y轴交AC于点E,当△PDE的周长最大时,求P点的坐标和△PDE周长的最大值.(3)若点M为x轴上一动点,点F为平面直角坐标系内一点.当点M,B,C,F构成菱形时,请直接写出点F的坐标.10.已知:如图,在Rt△ABC中,∠ACB=90°,BC=3,CA=4,将∠ABC对折,使点C 的对应点H恰好落在直线AB上,折痕交AC于点O,以点O为坐标原点,AC所在直线为x轴建立平面直角坐标系.(1)求过A,B,O三点的抛物线解析式;(2)若在线段AB上有一动点P,过点P作x轴的垂线,交抛物线于M,连接MB,MA,求△MAB的面积的最大值;(3)若点E在抛物线上,点F在对称轴上,且以O,A,E,F为顶点的四边形为平行四边形,求点E的坐标.11.如图,矩形AOBC放置在平面直角坐标系xOy中,边OA在y轴的正半轴上,边OB在x轴的正半轴上,抛物线的顶点为F,对称轴交AC于点E,且抛物线经过点A(0,2),点C,点D(3,0).∠AOB的平分线是OE,交抛物线对称轴左侧于点H,连接HF.(1)求该抛物线的解析式;(2)在x轴上有动点M,线段BC上有动点N,求四边形EAMN的周长的最小值;(3)该抛物线上是否存在点P,使得四边形EHFP为平行四边形?如果存在,求出点P 的坐标;如果不存在,请说明理由.12.如图抛物线y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),C(0,3).(1)求抛物线的解析式,并指出抛物线的顶点坐标.(2)在抛物线的对称轴上是否存在一点P,使得△P AC的周长最小,若存在,请求出点P的坐标及△P AC的周长;若不存在,请说明理由.(3)在(2)的条件下,在抛物线上是否存在点M(不与C点重合),使得S△P AM=S△P AC,若存在,请求出点M的坐标;若不存在,请说明理由.13.已知:抛物线y=ax2﹣3(a﹣1)x+2a﹣6(a>0).(1)求证:抛物线与x轴有两个交点.(2)设抛物线与x轴的两个交点的横坐标分别为x1,x2(其中x1>x2).若t是关于a的函数、且t=ax2﹣x1,求这个函数的表达式;(3)若a=1,将抛物线向上平移一个单位后与x轴交于点A、B.平移后如图所示,过A作直线AC,分别交y的正半轴于点P和抛物线于点C,且OP=1.M是线段AC上一动点,求2MB+MC的最小值.14.如图,在平面直角坐标系中,一次函数y=x﹣2的图象分别交x、y轴于点A、B,抛物线y=x2+bx+c经过点A、B,点P为第四象限内抛物线上的一个动点.(1)求此抛物线对应的函数表达式;(2)如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;(3)如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.15.如图,已知直线y=﹣x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+3经过B、C两点并与x轴的另一个交点为A,且OC=3OA.(1)求抛物线的解析式;(2)点R为直线BC上方对称轴右侧抛物线上一点,当△RBC的面积为时,求R点的坐标;(3)在(2)的条件下,连接CR,作RH⊥x轴于H,连接CH、AC,点P为线段CR上一点,点Q为线段CH上一点,满足QH=CP,过点P作PE∥AC交x轴于点E,连接EQ,当∠PEQ=45°时,求CP的长.16.综合与探究如图,在平面直角坐标系中,直线y=x﹣4分别与x轴,y轴交于点A和点C,抛物线y =ax2﹣3x+c经过A,C两点,并且与x轴交于另一点B.点D为第四象限抛物线上一动点(不与点A,C重合),过点D作DF⊥x轴,垂足为F,交直线AC于点E,连接BE.设点D的横坐标为m.(1)求抛物线的解析式;(2)当∠ECD=∠EDC时,求出此时m的值;(3)点D在运动的过程中,△EBF的周长是否存在最小值?若存在,求出此时m的值;若不存在,请说明理由.17.如图,抛物线y=ax2+bx+3经过点A(1,0),B(4,0).(1)求抛物线的表达式;(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形P AOC的周长最小?若存在,求出四边形P AOC的周长最小值;若不存在,请说明理由;(3)如图②,点Q是OB上的一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM是直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.18.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的顶点A(﹣3,0),与y轴交于点B(0,4),在第一象限内有一点P(m,n),且满足4m+3n=12.(1)求二次函数解析式.(2)若以点P为圆心的圆与直线AB、x轴相切,求点P的坐标.(3)若点A关于y轴的对称点为点A′,点C在对称轴上,且2∠CBA+∠P A′O=90◦.求点C的坐标.19.如图,在直角坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A(﹣3,0)、B(1,0),与y轴交于点C.(1)求抛物线的函数表达式.(2)在抛物线上是否存在点D,使得△ABD的面积等于△ABC的面积的倍?若存在,求出点D的坐标;若不存在,请说明理由.(3)若点E是以点C为圆心且1为半径的圆上的动点,点F是AE的中点,请直接写出线段OF的最大值和最小值.20.如图,抛物线y=ax2+6x﹣5交x轴于A,B两点,交y轴于C点,点B的坐标为(5,0),直线y=x﹣5经过点B,C.(1)求抛物线的函数表达式;(2)点P是直线BC上方抛物线上的一动点,求△BCP面积S的最大值并求出此时点P 的坐标;(3)过点A的直线交直线BC于点M,连接AC当直线AM与直线BC的一个夹角等于∠ACB的3倍时,请直接写出点M的坐标.21.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.(1)求这个二次函数的解析式,并直接写出当x满足什么值时y<0?(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP面积最大?若存在,求出点P的坐标;若不存在,请说明理由;(3)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.22.如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).(1)求该抛物线的表达式及顶点坐标;(2)点P为抛物线上一点(不与点A重合),连接PC.当∠PCB=∠ACB时,求点P的坐标;(3)在(2)的条件下,将抛物线沿平行于y轴的方向向下平移,平移后的抛物线的顶点为点D,点P的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.23.如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(2,﹣3)和点B(5,0),顶点为C.(1)求这条抛物线的表达式和顶点C的坐标;(2)点A关于抛物线对称轴的对应点为点D,联结OD、BD,求∠ODB的正切值;(3)将抛物线y=x2+bx+c向上平移t(t>0)个单位,使顶点C落在点E处,点B落在点F处,如果BE=BF,求t的值.24.如图,直线y=﹣x+1与x轴,y轴分别交于A,B两点,抛物线y=ax2+bx+c过点B,并且顶点D的坐标为(﹣2,﹣1).(1)求该抛物线的解析式;(2)若抛物线与直线AB的另一个交点为F,点C是线段BF的中点,过点C作BF的垂线交抛物线于点P,Q,求线段PQ的长度;(3)在(2)的条件下,点M是直线AB上一点,点N是线段PQ的中点,若PQ=2MN,直接写出点M的坐标.25.如图,直线y=﹣x+m与抛物线y=ax2+bx都经过点A(6,0),点B,过B作BH垂直x轴于H,OA=3OH.直线OC与抛物线AB段交于点C.(1)求抛物线的解析式;(2)当点C的纵坐标是时,求直线OC与直线AB的交点D的坐标;(3)在(2)的条件下将△OBH沿BA方向平移到△MPN,顶点P始终在线段AB上,求△MPN与△OAC公共部分面积的最大值.26.在平面直角坐标系xOy中(如图),已知抛物线y=ax2+(a+)x+c(a≠0)经过点A (﹣3,﹣2),与y轴交于点B(0,﹣2),抛物线的顶点为点C,对称轴与x轴交于点D.(1)求抛物线的表达式及点C的坐标;(2)点E是x轴正半轴上的一点,如果∠AED=∠BCD,求点E的坐标;(3)在(2)的条件下,点P是位于y轴左侧抛物线上的一点,如果△P AE是以AE为直角边的直角三角形,求点P的坐标.27.如图1,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、C(3,0),点B为抛物线顶点,直线BD为抛物线的对称轴,点D在x轴上,连接AB、BC,∠ABC=90°,AB与y轴交于点E,连接CE.(1)求顶点B的坐标并求出这条抛物线的解析式;(2)点P为第一象限抛物线上一个动点,设△PEC的面积为S,点P的横坐标为m,求S关于m的函数关系式,并求出S的最大值;(3)如图2,连接OB,抛物线上是否存在点Q,使直线QC与直线BC所夹锐角等于∠OBD,若存在请直接写出点Q的坐标;若不存在,说明理由.28.如图,直线y=﹣x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.点G是抛物线y =ax2+bx+c位于直线y=﹣x+3下方的任意一点,连接PB、GB、GC、AC.(1)求该抛物线的解析式;(2)求△GBC面积的最大值;(3)连接AC,在x轴上是否存在一点Q,使得以点P,B,Q为顶点的三角形与△ABC 相似?若存在,求出点Q的坐标;若不存在,请说明理由.参考答案1.(1)由y=x2+x+m,令y=0,则(x+2)(x﹣m)=0,∴AO=2,BO=m,∴A(﹣2,0),B(m,0),∵AB=7,∴m﹣(﹣2)=7,m=5,∴y=;(2)过点D作DK⊥x轴于点K,设∠DAB=α,则D(d,﹣),∴=.∴EO=AO•tanα=5﹣d,CE=5﹣(5﹣d)=d,∴;(3)过点E作CE的垂线,过C作∠OCP的平分线交DE于点J,交CE的垂线于点F,过点F作ED的平行线交HD于点N.∴∠ECF=∠HDE=α,HE=3k,CP=5k,CE=HD=d,∵CE=HD,∠CEF=∠CHD=90°,∴△CEF≌△DHE(ASA),∵EF∥DN,NF∥DE,∴四边形EDNF为平行四边形,∴EF=HE=DN=3k,CF=DE=FN,∴△CFN为等腰直角三角形,∴∠PCN=∠FNC=45°,∴∠PCN=∠PNC=45°﹣α,∴PC=PN=5k,∴PD=2k,∴CH=d﹣3k,PH=d﹣2k,∴(d﹣3k)2+(d﹣2k)2=(5k)2,∴(d﹣6k)(d+k)=0,∴d=6k,∴在Rt△DHE中,tan,由(2)知,∴.∴d=4,∴D(4,3),∴==8.2.解:(1)∵四边形ABCD为矩形,且B(1,0),C(3,0),D(3,4),∴A(1,4),设抛物线的解析式为y=a(x﹣1)2+4,将C(3,0)代入y=a(x﹣1)2+4,得0=4a+4,解得a=﹣1,∴抛物线的解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3;(2)∵PE⊥x轴,DC⊥x轴,∴PE∥DC,∴△APN∽△ADC,∵PN分△ACD的面积为1:2的两部分,∴=或,当=时,==,∵AD=2,∴AP=,∴t的值为×2=;当=时,==,∵AD=2,∴AP=,∴t的值为×2=,综上所述,t的值为或;(3)如图2﹣1,当CN为菱形的对角线时,点P,N的横坐标均为,设直线AC的解析式为y=kx+b,将A(1,4),C(3,0)代入y=kx+b,得,解得,∴直线AC的表达式为y=﹣2x+6,将点N的横坐标代入y=﹣2x+6,得,即EN=4﹣t,由菱形CQNH可得,CQ=NH=t=CH,可得EH=(4﹣t)﹣t=4﹣2t,∵,∴,在Rt△CHE中,∵CE2+EH2=CH2,∴,解得,t1=,t2=4(舍);如图2﹣2,当CN为菱形的边时,由菱形CQHN可得,CQ=CN=t,在Rt△CNE中,∵NE2+CE2=CN2,∴(4﹣t)2+(2﹣t)2=t2,解得,t1=20﹣8,t2=20+8(舍);综上所述,t的值为或.3.解:(1)设抛物线解析式为y=a(x﹣h)2+k,(a≠0)∵顶点,∴,又∵图象过原点,∴,解出:,∴,即;(2)令y=0,即,解得:x1=0,x2=4,∴A(4,0),设直线AC的解析式为y=kx+b,将点A(4,0),代入,得,解得,∴直线AC的解析式为y=﹣x+4,过点D作DF∥y轴交AC于点F,设,则,∴,∴=,∴当m=3时,S△ACD有最大值,当m=3时,,∴;(3)∵∠CBO=∠CBA=90°,OB=AB=2,,∴,∴OA=OC=AC=4,∴△AOC为等边三角形,①如图3﹣1,当点P在C时,OA=AC=CA'=OA',∴四边形ACA'O是菱形,∴;②作点C关于x轴的对称点C',当点A'与点C'重合时,OC=AC=AA'=OA',∴四边形OCAA'是菱形,∴点P是∠AOA'的角平分线与对称轴的交点,记为P2,∴,∵∠OBP2=90°,OB=2,∴OP2=2BP2,设BP2=x,∴OP2=2x,又∵,∴(2x)2=22+x2,解得或,∴;综上所述,点P的坐标为或.4.解:(1)由抛物线y=ax2﹣2x+c与x轴交于A(﹣3,0),B(1,0)两点,得,解得,∴抛物线解析式为y=﹣x2﹣2x+3;由y=﹣x2﹣2x+3=﹣(x+1)2+4,得,点D坐标为(﹣1,4);(2)在直线l上存在一点M,到点B的距离与到点C的距离之和最小,根据抛物线对称性MA=MB,∴MB+MC=MA+MC,∴使MB+MC的值最小的点M应为直线AC与对称轴l:x=﹣1的交点,当x=0时,y=3,∴C(0,3),设直线AC解析式为直线y=kx+b,把A(﹣3,0)、C(0,3)分别代入y=kx+b,得,,解得,,∴直线AC解析式为y=x+3,把x=﹣1代入y=x+3得,y=2,∴M(﹣1,2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2);(3)①PF=2FG,理由如下,设直线AD解析式为y=k'x+b',把A(﹣3,0)、D(﹣1,4)分别代入直线y=k'x+b',得,,解得,∴直线AD解析式为y=2x+6,则点F的坐标为(m,2m+6),同理G的坐标为(m,m+3),则FG=(2m+6)﹣(m+3)=m+3,FP=2m+6=2(m+3),∴FP=2FG;②根据题意得点E的坐标为(m,﹣m2﹣2m+3),设直线l与x轴交于点N,EF=(﹣m2﹣2m+3)﹣(2m+6)=﹣m2﹣4m﹣3=﹣(m+2)2+1∴S△AED=S△AEF+S△EFD==,∴当m为﹣2时,S△AED的最大值为1,如图,过点D作DH∥x轴,交y轴于点H,在△DHC中,∠DHC=180°﹣∠AOB=90°,,在Rt△AOC中,,在Rt△ADN中,,∵,∴DC2+AC2=AD2,∴∠ACD=90°,∴,∴,∴当m为﹣2时,四边形AEDC的面积最大,最大值为4.5.解:(1)将A(1,4)代入y=,得,k=4,∴双曲线解析式为y=,设B(m,)(m<0),连接AB,交x轴于点C,设直线AB的解析式为y=kx+b,将点A(1,4),B(m,)代入,得,解得,,∴直线AB的解析式为y=﹣x+,当y=0时,x=m+1,∴C(m+1,0),OC=﹣m﹣1,∴S△AOB=OC•(y A﹣y B)=(﹣m﹣1)(4﹣),∵△AOB的面积为3,∴(﹣m﹣1)(4﹣)=3,整理,得2m2+3m﹣2=0,解得,m1=(舍去),m2=﹣2,∴B(﹣2,﹣2),将A(1,4),B(﹣2,﹣2)代入y=ax2+bx,得,,解得,,∴抛物线的解析式为y=x2+3x,∴a=1,b=3,k=4;(2)在抛物线y=x2+3x中,对称轴为x=﹣,设P(﹣,y),∵O(0,0),B(﹣2,﹣2),∴PO2=+y2,OB2=8,PB2=+(y+2)2,∵△POB为等腰三角形,∴①PO2=OB2时,+y2=8,解得,y=±,∴P1(﹣,﹣),P2(﹣,);②PB2=OB2时,+(y+2)2=8,解得,y=﹣2±,∴P3(﹣,﹣2﹣),P4(﹣,﹣2+);③PB2=OP2时,+(y+2)2=+y2,解得,y=﹣,∴P5(﹣,﹣);综上所述,点P的坐标为P1(﹣,﹣),P2(﹣,),P3(﹣,﹣2﹣),P4(﹣,﹣2+),P5(﹣,﹣);(3)设M(x,y),∵A(1,4),B(﹣2,﹣2),O(0,0),∴MO2=x2+y2,MA2=(x﹣1)2+(y﹣4)2,MB2=(x+2)2+(y+2)2,又∵MO=MA=MB,∴,解得,,∴M(﹣,),作B关于y轴的对称点B'(2,﹣2),连接B'M交y轴于Q,则此时MQ+BQ的值最小,理由是两点之间,线段最短,又∵MB的长度为定值,∴此时△BQM的周长最小,C△BQM=MB+MQ+BQ=MB+MB'==,∴M的坐标为(﹣,),△BQM周长的最小值为.6.解:(1)将点A(﹣1,0),B(4,0)代入y=x2+bx+c,得,,解得,,∴抛物线的解析式为y=x2﹣3x﹣4;(2)当k=﹣1时,直线AC的解析式为y=﹣x﹣1,设P(x,x2﹣3x﹣4),则E(x,﹣x﹣1),D(x,0),则PE=|x2﹣3x﹣4﹣(﹣x﹣1)|=|x2﹣2x﹣3|,DE=|x+1|,∵PE=2ED,∴|x2﹣2x﹣3|=2|x+1|,当x2﹣2x﹣3=2(x+1)时,解得,x1=﹣1(舍去),x2=5,∴P(5,6);当x2﹣2x﹣3=﹣2(x+1)时,解得,x1=﹣1(舍去),x2=1,∴P(1,﹣6);综上所述,点P的坐标为(5,6)或(1,﹣6);(3)存在,理由如下;∵∠AED=∠PEC,∴要使△ADE与△PCE相似,必有∠EPC=∠ADE=90°或∠ECP=∠ADE=90°,①当∠EPC=∠ADE=90°时,如图1,CP∥x轴,∵P(1,﹣6),根据对称性可得C(2,﹣6),将C(2,﹣6),代入直线AC解析式中,得2k+k=﹣6,解得,k=﹣2;②当∠ECP=∠ADE=90°时,如图2,过C点作CF⊥PD于点F,则有∠FCP=∠PEC=∠AED,则△PCF∽△AED,∴=,在直线y=kx+k上,当x=1时,y=2k,∴E(1,2k),∴DE=﹣2k,由,得或,∴C(k+4,k2+5k),∴F(1,k2+5k),∴CF=k+3,FP=k2+5k+6,∴=,解得,k1=k2=﹣1,k3=﹣3(此时C与P重合,舍去),综上,当k=﹣2或﹣1时,△ADE与△PCE相似.7.(1)∵抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0),B(3,0)两点,∴,∴,∴抛物线解析式为;(2)如图1,过点A作AH∥y轴交BC于H,交BE于G,由(1),C(0,﹣2),将B(3,0),C(0,﹣2)代入y=kx+b,得,,解得,,∴直线BC的解析式为,∵H(1,y)在直线BC上,∴,∴,将点B(3,0),E(0,﹣1)代入y=kx+b,得,,解得,,∴直线BE的解析式为y=x﹣1,∴G(1,﹣),∴GH=,∵直线BE:y=x﹣1与抛物线y=﹣x2+x﹣2相交于F,B,∴F(,﹣),∴S△FHB=GH×(x B﹣x F)=××(3﹣)=;(3)如图2,由(1)y=﹣x2+x﹣2=﹣(x﹣2)2+,∴顶点D(2,),∵动点M从点D出发,以每秒1个单位的速度沿平行于y轴方向向上运动,∴设M(2,m),m>,∴OM2=m2+4,BM2=m2+1,OB2=9,∵∠OMB=90°,∴OM2+BM2=OB2,∴m2+4+m2+1=9,∴m1=,m2=﹣(舍),∴M(2,),∴MD=﹣,∴,∴当时,∠OMB=90°.8.解:(1)将点A(﹣1,0),B(3,0)代入y=ax2+bx+3,得,解得,,∴抛物线的解析式为y=﹣x2+2x+3;(2)设直线BC的解析式为y=kx+3,将点B(3,0)代入y=kx+3,得,k=﹣1,∴直线BC的解析式为y=﹣x+3,设点P(x,﹣x2+2x+3),则点H(x,﹣x+3),过点C作CM⊥PH于点M,则CM=x,PH=﹣x2+3x,当CP=CH时,PM=MH,∠MCH=∠MCP,∵OB=OC,∴∠OBC=45°,∵CM∥OB,∴∠MCH=∠OBC=45°,∴∠PCH=90°,∴MC=PH=(﹣x2+3x),即x=(﹣x2+3x),解得,x1=0(舍去),x2=1,∴P(1,4);(3)在y=﹣x2+2x+3中,对称轴为x=1,若m+1≤1,即m≤0时,当x=m+1时,函数有最大值m,∴﹣(m+1)2+2(m+1)+3=m,解得,m1=(舍去),m2=;若m<1<m+1,即0<m<1时,当x=1时,函数有最大值为m=4(舍);若m>1,当x=m时,函数有最大值为m,∴﹣m2+2m+3=m,解得,m1=(舍去),m2=,综上所述,m的值为或.9.解:(1)∵抛物线经过点A,B,它们的坐标分别为(﹣4,0)、(2,0),∴设其解析式为y=a(x+4)(x﹣2),将点C(0,﹣3)代入y=a(x+4)(x﹣2),解得,,∴抛物线的解析式为;(2)∵OA=4,OC=3,∠AOC=90°,∴AC==5,∵PD⊥AC,∠PDE=∠AOC=90°,又∵PE∥y轴,∴∠PED=∠ACO,∴△PDE∽△AOC,∴PD:AO=DE:OC=PE:AC,即PD:4=DE:3=PE:5,∴,∴△PDE的周长=,则要使△PDE周长最大,PE取最大值即可,设直线AC的解析式为y=kx﹣3,将点A(﹣4,0)代入y=kx﹣3,得,k=﹣,∴直线AC的解析式为,设点,则,∴当a=﹣2时,取得最PE大值,最大值为,则,∴P(﹣2,﹣3),△PDE周长的最大值为;(3)如右图,①当BM为对角线时,显然,点F在y轴上,根据对称性得到点F的坐标为(0,3);②当BM为边时,∵,则有以下几种情况:(I)BC为边时,BM=BC=,点M在x轴负半轴上时,点M是点B向左平移个单位长度得到的,∴M(2﹣,0),∴点C(0,﹣3)向左平移个单位长度得到点F;点M在x轴正半轴上时,点M是点B向平右移个单位长度得到的,∴M(2+,0),∴点C(0,﹣3)向右平移个单位长度得到点F;(II)BC为对角线时,设OM=x,在直角三角形OMC中,由勾股定理可得OM2+OC2=MC2,即x2+32=(x+2)2,解得,x=,∴菱形的边长为2+=,∴CF=,∴F(,﹣3),综上所述,点F的坐标为(0,3)或或或.10.解:(1)在Rt△ABC中,AB===5,由翻折知,△BCO≌△BHO,∴BH=BC=3,∴AH=AB﹣BH=2,∵∠HAO=∠CAB,∠OHA=∠BCA=90°,∴△AHO∽△ACB,∴=,即=,∴AO=,∴A(,0),B(﹣,3),∵抛物线经过原点O,∴可设抛物线的解析式为y=ax2+bx,将点A(,0),B(﹣,3)代入,得,解得,,∴过A,B,O三点的抛物线解析式为y=x2﹣x;(2)设直线AB的解析式为y=kx+b,将点A(,0),B(﹣,3)代入,得,解得∴直线AB的解析式为y=﹣x+,∴可设P(x,﹣x+),则M(x,x2﹣x),∴PM=﹣x+﹣(x2﹣x)=﹣x2+x+,∴S△MAB=PM(x A﹣x B)=(﹣x2+x+)×4=﹣x2+x+=﹣(x﹣)2+4,∴当x=时,△MAB的面积取最大值4;(3)在y=x2﹣x中,对称轴为x=,①如图3﹣1,当OA为平行四边形的一边时,OA平行且等于EF,∵OA=,∴EF=,∵x F=,∴x E=±=或﹣,当x E=或﹣,时y E=,∴点E的坐标为(,)或(﹣,);②如图3﹣2,当OA为平行四边形的对角线时,OA与EF互相平分,则点E在抛物线顶点处,∵当x=时,y=﹣,∴点E的坐标为(,﹣),综上所述,点E的坐标为(,)或(﹣,)或(,﹣).11.解:(1)∵AE∥x轴,OE平分∠AOB,∴∠AEO=∠EOB=∠AOE,∴AO=AE,∵A(0,2),∴E(2,2),∴点C(4,2),设二次函数解析式为y=ax2+bx+2,∵C(4,2)和D(3,0)在该函数图象上,∴,得,∴该抛物线的解析式为y=x2﹣x+2;(2)作点A关于x轴的对称点A1,作点E关于直线BC的对称点E1,连接A1E1,交x 轴于点M,交线段BC于点N.根据对称与最短路径原理,此时,四边形AMNE周长最小.易知A1(0,﹣2),E1(6,2).设直线A1E1的解析式为y=kx+b,,得,∴直线A1E1的解析式为.当y=0时,x=3,∴点M的坐标为(3,0).∴由勾股定理得AM=,ME1=,∴四边形EAMN周长的最小值为AM+MN+NE+AE=AM+ME1+AE=;(3)不存在.理由:过点F作EH的平行线,交抛物线于点P.易得直线OE的解析式为y=x,∵抛物线的解析式为y=x2﹣x+2=,∴抛物线的顶点F的坐标为(2,﹣),设直线FP的解析式为y=x+b,将点F代入,得,∴直线FP的解析式为.,解得或,∴点P的坐标为(,),FP=×(﹣2)=,,解得,或,∵点H是直线y=x与抛物线左侧的交点,∴点H的坐标为(,),∴OH=×=,易得,OE=2,EH=OE﹣OH=2﹣=,∵EH≠FP,∴点P不符合要求,∴不存在点P,使得四边形EHFP为平行四边形.12.解:(1)∵抛物线y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),C(0,3),∴,得,∴y=﹣x2+2x+3=﹣(x﹣1)2+4,∴该抛物线的顶点坐标为(1,4),即该抛物线的解析式为y=﹣x2+2x+3,顶点坐标为(1,4);(2)点A关于对称轴的对称点是点B,连接CB与对称轴的交点为P,此时点P即为所求,设过点B(3,0),点C(0,3)的直线解析式为y=kx+m,,得,∴直线BC的解析式为y=﹣x+3,当x=1时,y=﹣1+3=2,∴点P的坐标为(1,2),∵点A(﹣1,0),点C(0,3),点B(3,0),∴AC=,BC=3,∴△P AC的周长是:AC+CP+P A=AC+CB=,即点P的坐标为(1,2),△P AC的周长是;(3)存在点M(不与C点重合),使得S△P AM=S△P AC,∵S△P AM=S△P AC,∴当以P A为底边时,只要两个三角形等高即可,即点M和点C到P A的距离相等,当点M在点C的上方时,则CM∥P A时,点M和点C到P A的距离相等,设过点A(﹣1,0),点P(1,2)的直线l1解析式为:y=kx+m,,得,∴直线AP的解析式为y=x+1,∴直线CM的解析式为y=x+3,由得,,,∴点M的坐标为(1,4);当点M在点C的下方时,则点M所在的直线l2与AP平行,且直线l2与直线AP之间的距离与直线l1与直线AP 之间的距离相等,∴直线l2的的解析式为y=x﹣1,由得,,,∴M的坐标为(,)或(,);由上可得,点M的坐标为(1,4),(,)或(,).13.(1)证明:△=b2﹣4ac=[﹣3(a﹣1)]2﹣4a(2a﹣6)=a2+6a+9=(a+3)2,∵a>0,∴(a+3)2>0,∴抛物线与x轴有两个交点;(2)解:令y=0,则ax2﹣3(a﹣1)x+2a﹣6=0,∴或,∵a>0,∴且x1>x2,∴x1=2,,∴,∴t=a﹣5;(3)解:当a=1时,则y=x2﹣4,向上平移一个单位得y=x2﹣3,令y=0,则x2﹣3=0,得,∴,,∵OP=1,∴直线,联立:,解得,,,即,,∴AO=,在Rt△AOP中,AP==2,过C作CN⊥y轴,过M作MG⊥CN于G,过C作CH⊥x轴于H,∵CN∥x轴,∴∠GCM=∠P AO,又∵∠AOP=∠CGM=90°,∴△AOP∽△CGM,∴==,∴,∵B到CN最小距离为CH,∴MB+GM的最小值为CH的长度,∴2MB+MC的最小值为.14.解:(1)令x=0,得y=x﹣2=﹣2,则B(0,﹣2),令y=0,得0=x﹣2,解得x=4,则A(4,0),把A(4,0),B(0,﹣2)代入y=x2+bx+c(a≠0)中,得:,解得:,∴抛物线的解析式为:y=x2﹣x﹣2;(2)∵PM∥y轴,∴∠ADC=90°,∵∠ACD=∠BCP,∴以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,存在两种情况:①当∠CBP=90°时,如图1,过P作PN⊥y轴于N,设P(x,x2﹣x﹣2),则C(x,x﹣2),∵∠ABO+∠PBN=∠ABO+∠OAB=90°,∴∠PBN=∠OAB,∵∠AOB=∠BNP=90°,∴△AOB∽△BNP,∴,即=,解得:x1=0(舍),x2=,∴P(,﹣5);②当∠CPB=90°时,如图2,则B和P是对称点,当y=﹣2时,x2﹣x﹣2=﹣2,∴x1=0(舍),x2=,∴P(,﹣2);综上,点P的坐标是(,﹣5)或(,﹣2);(3)∵OA=4,OB=2,∠AOB=90°,∴∠BOA≠45°,∴∠BQP≠2∠BOA,∴分两种情况:①当∠PBQ=2∠OAB时,如图3,取AB的中点E,连接OE,过P作PG⊥x轴于G,交直线AB于H,∴OE=AE,∴∠OAB=∠AOE,∴∠OEB=2∠OAB=∠PBQ,∵OB∥PG,∴∠OBE=∠PHB,∴△BOE∽△HPB,∴,由勾股定理得:AB==2,∴BE=,∵GH∥OB,∴,即,∴BH=x,设P(x,x2﹣x﹣2),则H(x,x﹣2),∴PH=x﹣2﹣(x2﹣x﹣2)=﹣x2+4x,∴,解得:x1=0,x2=3,∴点P的横坐标是3;②当∠BPQ=2∠OAB时,如图4,取AB的中点E,连接OE,过P作PG⊥x轴于G,交直线AB于H,过O作OF⊥AB于F,连接AP,则∠BPQ=∠OEF,设点P(t,t2﹣t﹣2),则H(t,t﹣2),∴PH=t﹣2﹣(t2﹣t﹣2)=﹣t2+4t,∵OB=2,OA=4,∴AB=2,∴OE=BE=AE=,OF===,∴EF===,S△ABP==,∴2PQ=4(﹣t2+4t),PQ=,∵∠OFE=∠PQB=90°,∴△PBQ∽△EOF,∴,即,∴BQ=,∵BQ2+PQ2=PB2,∴=,化简得,44t2﹣388t+803=0,即:(2t﹣11)(22t﹣73)=0,解得:t1=5.5(舍),t2=;综上,存在点P,使得△PBQ中有某个角的度数等于∠OAB度数的2倍时,其P点的横坐标为3或.15.解:(1)在直线y=﹣x+3中,当x=0时,y=3;当y=0时,x=4,∴C(0,3),B(4,0),∴OC=3,∵OC=3OA,∴OA=1,∴A(﹣1,0),把A(﹣1,0),B(4,0)代入y=ax2+bx+3,得,,解得,a=﹣,b=,∴抛物线的解析式为y=﹣x2+x+3;(2)如图1,连接RO,RC,RB,设R(t,﹣t2+t+3),则S△RBC=S△OCR+S△OBR﹣S△OBC=×3t+×4(﹣t2+t+3)﹣×3×4=﹣t2+6t,∵S△RBC=,∴﹣t2+6t=,解得,t1=1,t2=3,∵点R为直线BC上方对称轴右侧,∴R(3,3);(3)如图2﹣1,在RH上截取RM=OA,连接CM、AM,AM交PE于G,作QF⊥OB 于H,∵CR=CO,∠CRM=∠COA,∴△CRM≌△COA(SAS),∴CM=CA,∠RCM=∠OCA,∴∠ACM=∠OCR=90°,∴∠CAM=∠CMA=45°,∵AC∥PE,∴∠CAM=∠AGE=45°,∴∠PEQ=45°,∴∠AGE=∠PEQ,∴AM∥QE,∴∠MAH=∠QEF,∵∠QFE=MHA=90°,∴△QEF∽△MAH,∴=,∴EF=2QF,设CP=m,∴QH=CP=m,∵OC=OH,∴∠OHC=45°,∴QF=FH=m,∴EF=2m,∴EH=3m,∵四边形ACPE为平行四边形,∴AE=CP=m,∵EH=AH﹣AE=4﹣m,∴3m=4﹣m,∴m=1,∴CP=1;如图2﹣2,在RH上截取RM=OA,连接CM、AM,AM交PE于G,交QE于N,作QF ⊥OB于H,∵CR=CO,∠CRM=∠COA,∴△CRM≌△COA(SAS),∴CM=CA,∠RCM=∠OCA,∴∠ACM=∠OCR=90°,∴∠CAM=∠CMA=45°,∵AC∥PE,∴∠CAM=∠AGE=45°,∴∠PEQ=45°,∴∠AGE=∠PEQ=45°,∴∠ENG=∠ENA=90°,∵∠EQF+∠QEF=90°,∠EAN+∠QEF=90°,∴∠EQF=∠MAB,∵∠QFE=∠AHM=90°,∴△QEF∽△AMH,∴=,∴QF=2EF,设CP=m,∴QH=CP=m,∵OC=OH,∴∠OHC=45°,∴QF=FH=m,∴EF=m,∴EH=m,∵四边形ACPE为平行四边形,∴AE=CP=m,∵EH=AH﹣AE=4﹣m,∴4﹣m=m,∴m=,∴CP=,综上所述,CP的长度为1或.16.解:(1)在y=x﹣4中,当x=0时,y=﹣4;当y=0时,x=4.∴A(4,0),C(0,﹣4)把A(4,0),C(0,﹣4)代入y=ax2﹣3x+c中,得,解得,∴抛物线的解析式是y=x2﹣3x﹣4.(2)如图1,过点E作EH⊥y轴,垂足为H.∵OA=OC=4,∴∠OAC=∠ACO=45°,∴∠HEC=∠HCE=45°.∵点D(m,m2﹣3m﹣4),E(m,m﹣4),∴EH=HC=m,ED=(m﹣4)﹣(m2﹣3m﹣4)=﹣m2+4m.∴,∴当∠ECD=∠EDC时,EC=ED.∴,解得m=0(舍去)或;(3)存在.∴点D为第四象限抛物线上一动点(不与点A,C重合),∴0<m<4,在抛物线y=x2﹣3x﹣4中,当y=0时,x2﹣3x﹣4=0,解得x1=﹣1,x2=4,∴点B坐标为(﹣1,0).∵∠F AE=∠FEA=45°,∴EF=AF.设△BFE的周长为n,则n=BF+FE+BE=BF+AF+BE=AB+BE,∵AB的值不变,∴当BE最小,即BE⊥AC时,△BFE的周长最小.∵当BE⊥AC时,∠EBA=∠BAE=45°,∴BE=AE,∴BF=AF=2.5.∴m=4﹣2.5=1.5时,△BEF的周长最小.17.解:(1)∵抛物线y=ax2+bx+3经过点A(1,0)、B(4,0),∴,解得,∴该抛物线的解析式:y=x+3;(2)∵抛物线y=ax2+bx+3经过点A(1,0),B(4,0),∴A、B关于对称轴对称,。
人教版数学九年级上学期期末压轴备考练习题:《二次函数》(含答案)

人教版数学九年级上学期期末压轴备考练习题:《二次函数》(含答案)1.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点c的距离之和最小,求出点M的坐标:(3)在抛物线上存在点P,使得△APB的面积与△ACB的面积相等,求点P的坐标.解:(1)且抛物线经过A(1,0),x=﹣1,故点B(﹣3,0),则抛物线的表达式为:y=a(x﹣1)(x+3)=a(x2+2x﹣3),故﹣3a=3,解得:a=﹣1;故抛物线的表达式为:y=﹣x2﹣2x+3;(2)点A关于抛物线对称轴的对称点为点B(﹣3,0),直线BC交函数对称轴于点M,则点M为所求,将点A、C的坐标代入一次函数表达式并解得:直线BC的表达式为:y=x+3,当x=﹣1时,y=2,故点M(﹣1,2);(3)△APB的面积与△ACB的面积相等,则|y P|=y C=3,即﹣x2﹣2x+3=±3,解得:x=0(舍去)﹣2或1±,故点P的坐标为:(﹣2,2)或(1,﹣2)或(﹣1﹣,﹣2).2.如图1,已知抛物线;C1:y=﹣(x+2)(x﹣m)(m>0)与x轴交于点B、C(点B 在点C的左侧),与y轴交于点E.(1)求点B、点C的坐标;(2)当△BCE的面积为6时,若点G的坐标为(0,b),在抛物线C1的对称轴上是否存在点H,使得△BGH的周长最小,若存在,则求点H的坐标(用含b的式子表示);若不存在,则请说明理由;(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.解:(1)y=﹣(x+2)(x﹣m)(m>0),令y=0,则x=﹣2或m,故点B、C的坐标分别为:(﹣2,0)、(m,0);(2)存在,理由:y=﹣(x+2)(x﹣m),令x=0,则y=2,故点E(0,2),△BCE的面积=×BC×OE=(m+2)×2=6,解得:m=4,则抛物线的对称轴为:x=(﹣2+4)=1,点B关于函数对称轴的对称点为点C(m,0),连接CE交对称轴于点H,则点H为所求,将点C、E的坐标代入一次函数表达式并解得:直线CE的表达式为:y=﹣bx+b,当x=1时,y=b,故点H(1,b);(3)∵OE=OB=2,故∠EBO=45°,过点F作FT⊥x轴于点F;①当△BEC∽△BCF时,则BC2=BE•BF,∠FBO=EBO=45°,则直线BF的函数表达式为:y=﹣x﹣2,故点F(x,﹣x﹣2);将点F的坐标代入抛物线表达式得:﹣x﹣2=﹣(x+2)(x﹣m),解得:x=﹣2(舍去)或2m,故点F(2m,﹣2m﹣2),则BF=2(m+1),BE=2,∵BC2=BE•BF,则(m+2)2=22(m+1),解得:m=2±2(舍去负值),故m=2+2;②当△BEC∽△FCB时,则BC2=BF•EC,∠CBF=∠ECO,则△BFT∽△COE,则,则点F[x,﹣(x+2)],将点F的坐标代入抛物线表达式得:﹣(x+2)=﹣(x+2)(x﹣m),解得:x=﹣2(舍去)或m+2;则点F[m+2,﹣(m+4)]BC2=BF•EC,则(m+2)2=,化简得:m3+4m2+4m=m3+4m2+4m+16,此方程无解;综上,m=2.3.四边形的一条对角线将这个四边形分成两个三角形,如果这两个三角形相似(不全等),那么我们将这条对角线叫做这个四边形的相似对角线.(1)如图1,四边形ABCD中,∠DAB=100°,∠DCB=130°,对角线AC平分∠DAB,求证:AC是四边形ABCD的相似对角线;(2)如图2,直线y=﹣x+分别与x,y轴相交于A,B两点,P为反比例函数y=(k<0)上的点,若AO是四边形ABOP的相似对角线,求反比例函数的解析式;(3)如图3,AC是四边形ABCD的相似对角线,点C的坐标为(3,1),AC∥x轴,∠BCA=∠DCA=30°,连接BD,△BCD的面积为.过A,C两点的抛物线y=ax2+bx+c (a<0)与x轴交于E,F两点,记|m|=AC+1,若直线y=mx与抛物线恰好有3个交点,求实数a的值.解:(1)如图1,设∠ACD=α,则∠ACB=130°﹣α,∴∠B=180°﹣∠BAC﹣∠ACB=180°﹣50°﹣(130°﹣α)=α,在△ABC和△ACD中,∠B=∠ACD,∠BAC=∠CAD,∴△ABC∽△ACD,∴AC是四边形ABCD的相似对角线;(2)①当∠APO为直角时,当∠OAP=30°时,过点P作PH⊥x轴于点H,设OH=x,则HP=x,HA=3x,则x+3x=4,解得:x=1,故点P(1,﹣),故k=﹣;当∠AOP=30°时,同理可得:k=﹣3;②当∠OAP为直角时,当∠OP A=30°时,点P(4,﹣4),k=﹣16;当∠AOP=30°时,同理可得:k=﹣;综上,反比例函数的表达式为:y=﹣或y=﹣或y=﹣或y=﹣;(3)如图3,过点B作BH⊥CD于点H,则∠CBH=60°﹣∠BCD=30°,故CH=BC,则BH=BC,△BCD的面积=CD•BH=CD×HB=,故CD•BC=4而△BAC∽△ACD,故CD2=BC•CD=4,故CD=2,则点A(1,1),而点C(3,1),将点A、C的坐标代入抛物线表达式并解得:抛物线的表达式为:y=ax2+(4a+3)x+3a+1,AC=1,则m=±3,故直线的表达式为:y=±3x,直线y=﹣3x与抛物线有两个交点,而直线y=mx与抛物线恰好有3个交点,则直线y=3x与抛物线有一个交点,联立直线y=3x于抛物线的表达式并整理得:ax2﹣(4a+3)x+3a+1=0,△=(4a+3)2﹣4a(3a+1)=0,解得:a=﹣或﹣.4.如图,已知一次函数y=﹣x与二次函数y=﹣x2+bx+c的图象相交于原点O和另一点A (4,﹣4).(1)求二次函数表达式;(2)直线x=m和x=m+2分别交线段AO于C、D,交二次函数y=﹣x2+bx+c的图象于点E、F,当m为何值时,四边形CEFD是平行四边形;(3)在第(2)题的条件下,设CE与x轴的交点为M,将△COM绕点O逆时针旋转得到△C′OM′,当C′、M′、F三点第一次共线时,请画出图形并直接写出点C′的纵坐标.解:(1)把(0,0),A(4,4)代入y=x2+bx+c得,解得:,故抛物线的表达式为:y=x2﹣3x;(2)设C(m,m),D(m+2,m+2),则E(m,m2﹣3m),F[m+2,(m+2)2﹣3(m+2)],即F(m+2,m2+m﹣2),∵CE∥DF,∴当CE=DF时,四边形CEFD为平行四边形,即m+2﹣(m2﹣3m)=m+2﹣(m2+m ﹣2),解得m=1,即当m为1时,四边形CEFD是平行四边形;(3)画图如下,作C′H⊥x轴于H,当m=1时,C(1,1),D(3,3),F(3,0),即F点为抛物线与x轴的一个交点,∴OM=CM=1,OC=,∵△COM绕点O逆时针旋转得到△C′OM′,∴OM′=C′M′=1,∠OM′C′=∠OMC=90°,在Rt△OM′F中,FM′==2,∴FC′=2﹣1,∵∠C′FH=OFM′,∴△FHC′∽△FM′O,∴,即=∴FH =,C ′H =,∴OH =OF ﹣FH =,∴C ′(,).5.二次函数y =﹣x 2+bx +c 的图象与直线y =﹣x +1相交于A 、B 两点(如图),A 点在y 轴上,过点B 作BC ⊥x 轴,垂足为C (﹣3,0).(1)填空:b = ﹣ ,c = 1 ;(2)点N 是二次函数图象上一点(点N 在AB 上方),过N 作NP ⊥x 轴,垂足为点P ,交AB 于点M ,求MN 的最大值;(3)在(2)的条件下,点N 在何位置时,BM 与NC 相互垂直平分?并求出所有满足条件的N 点的坐标.解:(1)由直线y =﹣x +1得到:A (0,1),把x =﹣3代入y =﹣x +1得到:y =﹣×(﹣3)+1=.故B (﹣3,).将A 、B 的坐标分别代入y =﹣x 2+bx +c ,得.解得b =﹣,c =1;(2)设N (m ,﹣m 2﹣m +1)则,M,P点的坐标分别是(m,﹣m+1),(m,0)∴MN=(﹣m2﹣m+1)﹣(﹣m2+1)=﹣m2﹣m=﹣(m+)2+∴当m=﹣时,MN的最大值为;(3)连接MN,BN,由BM与NC互相垂直平分∴四边形BCMN是菱形由BC∥MN∴MN=BC,且BC=MC而BC=﹣×(﹣3)+1=即:﹣m2﹣m=且(﹣m+1)2+(m+3)2=.解得:m=﹣1故当N(﹣1,4)时,BM与NC互相垂直平分.6.综合与探究如图,抛物线y=﹣x2﹣x+与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线l经过B、C两点,点M从点A出发以每秒1个单位长度的速度向终点B运动,连接CM,将线段MC绕点M顺时针旋转90°得到线段MD,连接CD、BD.设点M运动的时间为t(t>0),请解答下列问题:(1)求点A的坐标与直线l的表达式;(2)①请直接写出点D的坐标(用含t的式子表示),并求点D落在直线l上时t的值;②求点M运动的过程中线段CD长度的最小值.解:(1)当y=0时,,解得x1=1,x2=﹣3,∵点A在点B的左侧,∴A(﹣3,0),B(1,0),当x=0时,y=,即C(0,),设直线l的表达式为y=kx+b,将B,C两点坐标代入得,,解得,,则直线l的表达式为y=﹣x+;(2)①如图1,当点M在AO上运动时,过点D作DN⊥x轴于N,由题意可知,AM=t,OM=3﹣t,MC⊥MD,则∠DMN+∠CMO=90°,∠CMO+∠MCO=90°,∴∠MCO=∠DMN,在△MCO与△DMN中,,∴△MCO≌△DMN(AAS),∴MN=OC=,DN=OM=3﹣t,∴D(t﹣3+,t﹣3);同理,如图2,当点M在OB上运动时,点D的坐标为:D(﹣3+t+,t﹣3)将D点坐标代入直线BC的解析式y=﹣x+得,t﹣3=﹣×(﹣3+t+)+,t=6﹣2,即点D落在直线l上时,t=6﹣2;②∵△COD是等腰直角三角形,∴CM=MD,∴线段CM最小时,线段CD长度的最小,∵M在AB上运动,∴当CM⊥AB时,CM最短,CD最短,即CM=CO=,根据勾股定理得,CD的最小值为.7.如图,△OAP是等腰直角三角形,∠OAP=90°,点A在第四象限,点P坐标为(8,0),抛物线y=ax2+bx+c经过原点O和A、P两点.(1)求抛物线的函数关系式.(2)点B是y轴正半轴上一点,连接AB,过点B作AB的垂线交抛物线于C、D两点,且BC=AB,求点B坐标;(3)在(2)的条件下,点M是线段BC上一点过点M作x轴的垂线交抛物线于点N,求△CBN面积的最大值.解:(1)△OAP是等腰直角三角形,∠OAP=90°,点P坐标为(8,0),则点A在抛物线的对称轴上,故点A(4,﹣4),故抛物线的表达式为:y=a(x﹣4)2﹣4…①,将点P的坐标代入上式并解得:a=,故抛物线的表达式为:y=x2﹣2x;(2)设点B(0,m),过点C作CH⊥y轴于点H,过点A作AQ⊥y轴于点Q,∵∠BAQ+∠QBA=90°,∠QBA+∠HBC=90°,∴∠HBC=∠BAQ,BC=AB,∠CHB=∠BQA=90°,∴△CHB≌△BQA(AAS),∴AQ=BH=4,CH=BQ=4+m,故点C(m+4,m+4),将点C的坐标代入①式并解得:m=8,故点B(0,8);(3)点B(0,8),点C(12,12),将点B、C的坐标代入一次函数表达式并解得:直线BC的表达式为:y=x+4,设点M(x,x2﹣2x),则点N(x,x+4),△CBN面积S=×MN×CH=12×(x+4﹣x2+2x)=﹣x2+14x+24,∵﹣<0,故S有最大值.8.如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和B(3,0),与y轴交于点C.(1)求b和c的值;(2)求直线AC的解析式.解:(1)抛物线解析式为y=(x﹣1)(x﹣3),即y=x2﹣4x+3,∴b=﹣4,c=3;(2)当x=0时,y=x2﹣4x+3=3,则C(0,3),设直线AC的解析式为y=mx+n,把A(1,0),C(0,3)代入得,解得,∴直线AC的解析式为y=﹣3x+3.9.如图,抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),交y轴于点C;(1)求抛物线的解析式;(2)点D为y轴右侧抛物线上一点,是否存在点D,使S△ABC =S△ABD?若存在,请求出点D坐标:若不存在,请说明理由.解:(1)∵抛物线y =ax 2+bx +2经过点A (﹣1,0),B (4,0),∴,解得,∴抛物线解析式为y =﹣x 2+x +2; (2)存在点D ,使S △ABC =S △ABD .当x =0时,y =﹣x 2+x +2=2,则C (0,2),设D (x ,﹣x 2+x +2)(x >0),×(4+1)×|﹣x 2+x +2|=×(4+1)×2,当﹣x 2+x +2=2时,解得x 1=0(舍去),x 2=3,此时D (3,2);当﹣x 2+x +2=﹣2时,解得x 1=(舍去),x 2=,此时D (,2).10.如图1,点A 在x 轴的负半轴上,点B 的坐标为(﹣2,﹣4),抛物线y =ax 2+bx 的对称轴为x =﹣5,该抛物线经过点A 、B ,点E 是AB 与对称轴x =﹣5的交点.(1)如图1,点P 为直线AB 下方的抛物线上的任意一点,在对称轴x =﹣5上有一动点M ,当△ABP 的面积最大时,求|PM ﹣OM |的最大值以及点P 的坐标.(2)如图2,把△ABO 沿射线BA 方向平移,得到△CDF ,其中点C 、D 、F 分别是点A 、B 、O 的对应点,且点F 与点O 不重合,平移过程中,是否存在这样的点F ,使得以点A 、E 、F 为顶点的三角形为等腰三角形?若存在,直接写出点F 的坐标,若不存在,请说明理由.【解答】解:(1)函数的对称轴为x =﹣5,则点A (﹣10,0),则函数表达式为:y=ax(x+10),将点B的坐标代入上式并解得:a=,故抛物线的表达式为:y=x2+x,将点A、B的坐标代入一次函数表达式并解得:直线AB的表达式为:y=﹣x﹣5,过点P作x轴的垂线交AB于点H,设点P(x,x2+x)、点H(x,﹣x﹣5),△ABP的面积S=×PH×(x B﹣x A)=(﹣x﹣5﹣x2﹣x)×(10﹣2)=﹣x2﹣12x﹣20,∵﹣1<0,故当x=﹣6时,S有最大值,此时点P(﹣6,﹣6),点P关于抛物线对称轴的对称点Q(﹣4,﹣6),连接OQ交函数对称轴于点M,则点M 为所求,同理:直线OQ的表达式为:y=x,当x=﹣5时,y=﹣,即点M(﹣5,﹣);|PM﹣OM|的最大值=OQ==2;(2)直线AB的表达式为:y=﹣x﹣5,当x=﹣5时,y=﹣,即点E(﹣5,﹣),则设图线向上平移m个单位,则向左平移2m个单位,故点F(﹣2m,m),而点A(﹣10,0),则AF2=(10﹣2m)2+m2,EF2=(2m﹣5)2+(m+)2,AE2=25+;①当AF=EF时,则(10﹣2m)2+m2=(2m﹣5)2+(m+)2,解得:m=;②当AF=AE时,同理可得:m=﹣5或﹣11;③当EF=AE时,同理可得:m=0(舍去)或7;综上点F 的坐标为:(﹣,)或(﹣5,)或(﹣11,)或(﹣14,7).11.如图,已知抛物线y 1=﹣2x 2+2与直线y 2=2x +2交于A ,B 两点, (1)求A ,B 两点的坐标. (2)求△ABO 的面积.解:(1)联立,解得:或,所以A 、B 两点的坐标分别是(﹣1,0),(0,2); (2)∵A 、B 两点的坐标分别是(﹣1,0),(0,2), ∴OA =1,OB =2,∴S △OAB =OA •OB ==112.如图所示,已知抛物线经过点A (﹣2,0)、B (4,0)、C (0,﹣8),抛物线y =ax 2+bx +c (a ≠0)与直线y =x ﹣4交于B 、D 两点.(1)求抛物线的解析式及顶点的坐标; (2)求D 点坐标;(3)点P 为抛物线上的一个动点,且在直线BD 下方,试求出△BDP 面积的最大值及此时点P 的坐标.解:(1)抛物线的表达式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),故﹣8a=﹣8,解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣8;(2)联立y=x﹣4和y=x2﹣2x﹣8并解得:x=4或﹣1(舍去4),故点D(﹣1,﹣5);(3)过点P作y轴的平行线交BD于点H,设点P(x,x2﹣2x﹣8),则点H(x,x﹣4)△BDP面积=PH×(x B﹣x D)=×(x﹣4﹣x2+2x+8)×(4+1)=(﹣x2+3x+4),∵0,故面积有最大值为:;此时,x=,即点P(,﹣).13.如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0),B(0,﹣3),点P 是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.(1)分别求出直线AB和这条抛物线的解析式.(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.解:(1)设直线AB的解析式为y=kx+b,把A(3,0),B(0,﹣3)代入y=kx+b得,解得,∴直线AB的解析式为y=x﹣3;把A(3,0),B(0,﹣3)代入y=x2+mx+n得,解得,∴抛物线解析式为y=x2﹣2x﹣3;(2)设P(t,t﹣3)(0<t<3),则M(t,t2﹣2t﹣3),∴PM=t﹣3﹣(t2﹣2t﹣3)=﹣t2+3t=﹣(t﹣)2+,当t=时,线段PM最长,最长为,此时△ABM的面积=×3×=.14.如图,抛物线y=﹣x2+bx+c交x轴于A,B两点,交y轴于点C直线y=﹣x+2经过点B,C.(1)求抛物线的解析式;(2)点P是直线BC上方抛物线上一动点,设点P的横坐标为m.①求△PBC面积最大值和此时m的值;②Q是直线BC上一动点,是否存在点P,使以A、B、P、Q为顶点的四边形是平行四边形,若存在,直接写出点P的坐标.解:(1)直线y=﹣x+2经过点B,C,则点B、C的坐标分别为:(4,0)、(0,2),将点B、C的坐标代入抛物线表达式并解得:b=,c=2,故抛物线的表达式为:y=﹣x2+x+2;(2)①过点P作y轴的平行线交直线BC于点H,则点P(m,﹣m2+m+2),点H(m,﹣m+2),△PBC面积=×PH×OB=×4×(﹣m2+m+2+m﹣2)=﹣2m2+8m,∵﹣2<0,∴面积存在最大值为8,此时,m=2;②设P(m,﹣m2+m+2),点Q(n,﹣n+2),当AB是平行四边形的边时,点A向右平移个单位得到B,同样点P(Q)向右平移个单位得到Q(P),则m=n,﹣m2+m+2=﹣n+2,解得:m=﹣(舍去)或(舍去)或;当AB是平行四边形的对角线时,由中点公式得:m+n=,﹣m2+m+2﹣n+2=0,解得:m=﹣或(重复,舍去);综上点P的坐标为:(,)或(,).15.抛物线y=ax2﹣1交x轴于A,B(A左B右),交y轴于C,且AB=4OC.(1)求a的值;(2)过抛物线上的点P(不与点B重合)作y轴的平行线交直线CB与点M,交x轴于点N,当PM=2MN时,求点P的坐标.解:(1)点C(0,﹣1),则OA=OB=2,故点A、B的坐标分别为:(﹣2,0)、(2,0),点B的坐标代入函数表达式并解得:a=;(2)将点B、C的坐标代入一次函数表达式并解得:直线BC的表达式为:y=x﹣1,设点P(x,x2﹣1),点M(x,x﹣1),PM=2MN,即|x2﹣1﹣x+1|=2|x﹣1|,解得:x=2(舍去)或4或﹣4,故点P的坐标为:(4,3)或(﹣4,3).。
2023年九年级数学中考专题:二次函数综合压轴题(含简单答案)
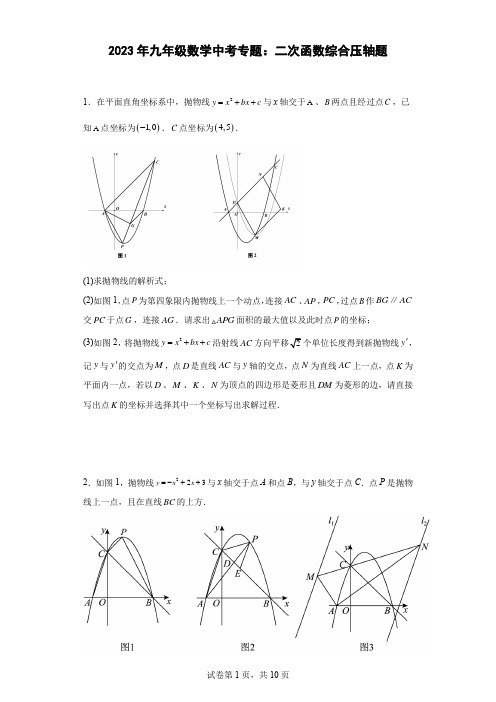
2023年九年级数学中考专题:二次函数综合压轴题1.在平面直角坐标系中,抛物线2y x bx c =++与x 轴交于A 、B 两点且经过点C ,已知A 点坐标为()1,0-.C 点坐标为()4,5.(1)求抛物线的解析式;(2)如图1,点P 为第四象限内抛物线上一个动点,连接AC 、AP ,PC ,过点B 作BG AC ∥交PC 于点G ,连接AG .请求出APG 面积的最大值以及此时点P 的坐标;(3)如图2,将抛物线2y x bx c =++沿射线AC y ',记y 与y '的交点为M ,点D 是直线AC 与y 轴的交点,点N 为直线AC 上一点,点K 为平面内一点,若以D 、M 、K 、N 为顶点的四边形是菱形且DM 为菱形的边,请直接写出点K 的坐标并选择其中一个坐标写出求解过程.2.如图1,抛物线223y x x =-++与x 轴交于点A 和点B ,与y 轴交于点C .点P 是抛物线上一点,且在直线BC 的上方.(1)直接写出点A 的坐标为 ,点B 的坐标为 ; (2)当点P 的坐标为()1,4时,求四边形BOCP 的面积;(3)如图2,AP 交BC 于点D .PE AC ∥交BC 于点E ,记,,DEP CPD CDA 的面积分别为123,,S S S ,判断1223S S S S +是否存在最大值.若存在,求出最大值;若不存在,请说明理由.(4)如图3,点C 在线段MN 上,满足90MAN ∠=︒,2CN CM =,直线1l 过点M ,直线2l 过点N ,且12l AC l ∥∥,求直线1l 与2l 之间的最大距离.3.如图,抛物线212y x bx c =-++与x 轴交于点A ,点B ,与y 轴交于点C .抛物线的对称轴为直线1x=-,点C 坐标为()04,.(1)求抛物线表达式;(2)在抛物线上是否存在点P ,使ABP BCO ∠=∠,如果存在,求出点P 坐标;如果不存在,请说明理由;(3)在(2)的条件下,若点P 在x 轴上方,点M 是直线BP 上方抛物线上的一个动点,求点M 到直线BP 的最大距离.4.如图1,在平面直角坐标系xOy 中,抛物线223y x x =-++与x 轴分别交于点A 和点B ,与y 轴交于点C ,连接BC .(1)求点B 和点C 的坐标;(2)如图2,点P 是该抛物线上一个动点,并沿抛物线从点B 运动至点A ,连接PO 、PB ,并以PO 、PB 为边作POQB .①当POQB 的面积为9时,求点P 的坐标;①在整个运动过程中,求点Q 与线段BC 的最大距离.5.如图,已知抛物线2=++30y ax bx a ≠()经过点10A (),和点30B (),,与y 轴相交于点C .(1)求此抛物线的解析式.(2)若点P 是直线BC 下方的抛物线上一动点(不与点B 、C 重合),过点P 作y 轴的平行线交直线BC 于点D ,设点P 的横坐标为m . ①用含有m 的代数式表示线段PD 的长;①连接PB ,PC ,求PBC 的面积最大时点P 的坐标.6.如图,抛物线212y x bx c =++与x 轴交于点()1,0A -和点B ,与y 轴交于点()0,2C -,(1)求抛物线的解析式;(2)点P 在第四象限的抛物线上,设ABC 的面积为1S ,PBC 的面积为2S ,当2S =451S 时,求点P 的坐标;(3)点M 在抛物线上,当2MAB ACO ∠∠=时,求点M 的横坐标.7.如图,已知抛物线2y ax c =+交x 轴于点()10A -,和点B ,交y 轴于点()01C -,.(1)求此抛物线的解析式.(2)过点A 作AP CB ∥交抛物线于点P ,求四边形ACBP 的面积.(3)在x 轴上方的抛物线上是否存在一点M ,过M 作MG x ⊥轴于点G ,使以A 、M 、G 三点为顶点的三角形与ACP △相似.若存在,请求出M 点的坐标;否则,请说明理由.8.如图1,直线25y x =-+与x 轴、y 轴分别交于点A 、点B ,抛物线2L y x bx c =-++:(1)①点A 的坐标为__________,点B 的坐标为__________;①求L 的解析式; (2)当点P 到AB 距离最大时,求出点P 的坐标;(3)尺规作图:在图2中作出经过C 、D 两点且圆心在抛物线对称轴上的圆,并结合图像直接写出该圆与抛物线的交点P 的坐标.9.在平面直角坐标系中,抛物线(1)(3)y a x x =+-(0)a ≠与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点(0,3)C ,点D 为抛物线的顶点,点P 是抛物线的对称轴上一点.(1)求抛物线的解析式及点D 的坐标;(2)如图①连接PB ,PD ,求PB 的最小值; (3)如图①,连接CP ,PB ,BC ,若135CPB ∠=︒,求点P 的坐标.的左边),与y 轴交于点C .点P ,Q 为抛物线上两动点.(1)若点P 坐标为(1,3),求抛物线的表达式;(2)如图①,连接BC ,在(1)的条件下,是否存在点Q ,使得BCQ ABC ∠=∠.若存在,请求出点Q 的坐标,若不存在,请说明理由;(3)若点P 为抛物线顶点,连接OP ,当a 的值从3-变化到1-的过程中,求线段OP 扫过的面积.11.如图,已知二次函数2y ax 2x c =++的图象经过点()0,3C ,与x 轴分别交于点()1,0A -和点B ,点P 是直线BC 上方的抛物线上一动点.(1)求二次函数的表达式; (2)求BC 所在直线的函数解析式;(3)过点P 作PM y ∥轴交直线BC 于点M ,求线段PM 长度的最大值.12.如图,在平面直角坐标系中,点O 为坐标原点,抛物线22y ax x c =-+与x 轴交于点A (1,0),点B (﹣3,0),与y 轴交于点C ,连接BC ,点P 在第二象限的抛物线上,连接PC 、PO ,线段PO 交线段BC 于点E .(1)求抛物线的表达式;(2)设:PCE 的面积为1S ,OCP △的面积为2S ,当1225S S =时,求点P 的坐标; (3)设:点C 关于抛物线对称轴的对称点为点N ,连接BN ,点H 在x 轴上,当HCB NBC ∠=∠时,①直接写出所有满足条件的所有点H 的坐标;①当点H 在线段AB 上时,点Q 是线段BH 外一点,1QH =,连接AQ ,将线段AQ 绕着点Q 逆时针旋转90︒得到线段QM ,连接MH ,直接写出线段MH 的取值范围.13.如图,直线1112y x =+与抛物线221482y x x =-+交于B 、C 两点(B 在C 的左侧)(1)求B 、C 两点的坐标;(2)直接写出12y y <时,x 的取值范围; (3)抛物线的顶点为A ,求ABC 的面积.14.如图,二次函数2y ax bx c =++的图象交x 轴于()1,0A -,()2,0B ,交y 轴于()0,2C -.(1)求二次函数的解析式;(2)点P 在该二次函数图象的对称轴上,且使PB PC -最大,求点P 的坐标; (3)若点M 为该二次函数图象在第四象限内一个动点,当点M 运动到何处时,四边形ACMB 的面积最大?求出此时点M 的坐标及四边形ACMB 面积的最大值.15.如图,直线1112y x =+与抛物线221482y x x =-+交于B 、C 两点(B 在C 的左侧).(1)求B 、C 两点的坐标;(2)直接写出12y y <时,x 的取值范围; (3)抛物线的顶点为A ,求ABC 的面积.16.如图,在平面直角坐标系中,二次函数2y x bx c =++的图像与x 轴交于()1,0A -,(1)求这个二次函数的解析式;(2)是否存在点P ,使POC △是以OC 为底边的等腰三角形?若存在,求出P 点坐标;若不存在,请说明理由;(3)动点P 运动到什么位置时,PBC 面积最大,求出此时P 点坐标和PBC 的最大面积.17.如图1,在平面直角坐标系中,抛物线212y x bx c =-++的顶点为()2,8D ,与x 轴交于两点A ,B (A 在B 的左侧),与y 轴交于点C .(1)求抛物线的函数表达式;(2)如图2,连接AD BC ,,点P 是线段BC 上方抛物线上的一个动点,过点P 作PQ AD ∥交CB 于点Q ,求PQ 的最大值及此时点P 的坐标;(3)将该抛物线关于直线1x =对称得到新抛物线1y ,点E 是原抛物线y 和新抛物线1y 的交点,F 是原抛物线对称轴上一点,G 为新抛物线上一点,若以E 、F 、A 、G 为顶点的四边形是是平行四边形,请直接写出点F 的坐标.18.如图,在平面直角坐标系xOy 中,抛物线22y ax bx =++与x 轴相交于()()4010A C -,,,两点,于y 轴相交于点B .(1)求抛物线的解析式;(2)若P 为线段AB 的中点,连接OP ,求三角形PAO 的面积;(3)在(2)的条件下,点M 是抛物线第二象限上一点,若2APM ABO ∠∠=,求点M 的横坐标.参考答案:1.(1)2=23y x x --(2)当32t =时,APG 面积的最大,最大值为458;点P 的坐标为31524⎛⎫ ⎪⎝⎭,-(3)(23-或(23-.2.(1)()1,0-;()3,0 (2)152(3)存在,983.(1)2142y x x =--+ (2)532P ⎛⎫- ⎪⎝⎭,或752P ⎛⎫-- ⎪⎝⎭,(3)MN4.(1)(3,0)B ;(0,3)C(2)点P 的坐标为(0,3)或(2,3);点Q 与线段BC .5.(1)2=4+3y x x -(2)①2+3m m -;①3122⎛⎫- ⎪⎝⎭,6.(1)213222y x x =-- (2)P 的坐标为()2,3-(3)点M 的横坐标为203或437.(1)21y x =-(2)4(3)存在点M ,使以A 、M 、G 三点为顶点的三角形与PCA 相似,M 点的坐标为()23-,,4739⎛⎫ ⎪⎝⎭,,()415,8.(1)①5,02⎛⎫ ⎪⎝⎭,()0,5;①23522y x x =-++ (2)733416P ⎛⎫ ⎪⎝⎭, (3)39,44P ⎛⎫ ⎪⎝⎭9.(1)223y x x =-++,(1,4)D(2)(3)P 或(1,3P10.(1)233322y x x =-++; (2)存在;()1,3Q ;339(,)525Q -; (3)3411.(1)223y x x =-++(2)3y x =-+ (3)9412.(1)223y x x =--+;(2)()1,4-或()2,3-;(3)①()1,0-或()9,0-;①22MH ≤≤13.(1)()2,2B ,97,2C ⎛⎫ ⎪⎝⎭(2)2x <或7x > (3)15214.(1)2y x x 2=-- (2)1,32⎛⎫- ⎪⎝⎭(3)1,2,415.(1)(2,2)B ,9(7,)2C ; (2)7x >或2x <; (3)152.16.(1)234y x x =--(2)2-) (3)当P 点坐标为()26-,时,PBC 的最大面积为817.(1)21262y x x =-++(2)PQ =153,2P ⎛⎫ ⎪⎝⎭ (3)()2,4或()2,15或()2,12-.18.(1)213222y x x =--+ (2)2(3)7-。
二次函数(10大题型)(50道压轴题专练)(原卷版)—2024-2025学年九年级数学上册(沪教版)

二次函数(10大题型)(50道压轴题专练)压轴题型一 二次函数的图象与性质压轴题1.已知抛物线2(0)y ax bx c a =++>的对称轴为直线1x =,与x 轴的一个交点为(1,0)-.若关于x 的一元二次方程2(0)ax bx c p p ++=<有整数根,则p 的值有( )A .1个B .2个C .3个D .5个2.已知抛物线221(0)y x bx b b =-++->,当46x ££时,y 的值恒大于等于9.则b 的取值范围为 .3.在平面直角坐标系中,抛物线2221y x mx m =-++存在两点()11,A m y -,()22,B m y +.(1)请比较1y 与2y 的大小,并说明理由;(2)记抛物线在A ,B 之间的部分为图象F (包括A ,B 两点);y 轴上一动点()0,C a ,过点C 作垂直于y 轴的直线l 与F 有且仅有一个交点,求a 的取值范围;(3)若点()32,M y 也是抛物线上的点,记抛物线在A ,M 之间的部分为图象G (包括M ,A 两点),记图形G 上任意一点的纵坐标的最大值与最小值的差为t ,若21t y y ³-,求m 的取值范围.4.问题:已知抛物线L :22y x x =-,抛物线W 的顶点在抛物线L 上(非抛物线L 的顶点)且经过抛物线L 的顶点.请求出一个满足条件的抛物线W 的表达式.(1)解这个问题的思路如下:先在抛物线L 上任取一点(非顶点),你所取的点是 ① ;再将该点作为抛物线W 的顶点,可设抛物线W 的表达式是 ② ;然后求出抛物线L 的顶点是 ③ ;再将抛物线L 的顶点代入所设抛物线W 的表达式,求得其中待定系数的值为 ④ ;最后写出抛物线W 的表达式是 ⑤ .(2)用同样的方法,你还可以获得其他满足条件的抛物线W ,请再写出一个抛物线W 的表达式.(3)如果问题中抛物线L 和W 在x 轴上所截得的线段长相等,求抛物线W 的表达式.5.如图,在平面直角坐标系xOy 中,抛物线23y x bx =+-的图象与x 轴交于A 、B 两点,与y 轴交于点C ,顶点为E .点D CD x ∥轴,2CD =.(1)求这条抛物线的函数解析式及顶点E 的坐标;(2)在x 轴上有一点F ,若以点F 、B 、C 为顶点的三角形与BCD △相似,求点F 坐标;(3)点Q 是二次函数图象上一点,过点Q 向抛物线的对称轴作垂线,垂足为H ,若3HE HQ =,求点Q 的坐标.压轴题型二 二次函数的最值问题1.如图,在平面直角坐标系中,E 、F 、C 三点的坐标分别为1(4,1)、(3,1)、(3,0),点A 为线段EF 上的一个动点,连接AC ,过点A 作AB AC ^交y 轴于点B ,点A 从E 运动到F 时,点B 随之运动.设点B 的坐标为(0,)b ,则b 的最小值为( )A .94-B .94C .54-D .542.如图,在ABC V 中,AB AC ==4BC =,D 为边AB 上一动点(不与点B 重合),以CD 为边作正方形CDEF ,连接BE ,则当BDE V 的面积最大时,AD 的长为 .3.已知抛物线2421y x mx m =-++,m 为实数.(1)如果该抛物线经过点()4,3,求此抛物线的顶点坐标.(2)如果当2321m x m -+≤≤时,y 的最大值为4,求m 的值.(3)点()0,0O ,点()1,0A ,如果该抛物线与线段OA (不含端点)恰有一个交点,求m 的取值范围.4.如图,在平面直角坐标系中,抛物线2y x bx c =++(b ,c 是常数)经过点()1,0A ,()3,0B ,动点P 在抛物线上,其横坐标为m .(1)求抛物线的解析式;(2)若点P 到y 轴的距离小于3,求点P 的纵坐标的取值范围;(3)若抛物线位于点P 右侧(包含点P )部分的函数值最小为2m -,求m 的值.5.如图,抛物线2y x bx c =-++与x 轴交于,A B 两点(点A 在点B 的左侧),其中()()1,0,3,0A B -,与y 轴相交于点C ,抛物线的对称轴与x 轴交于点E .点P 是抛物线上的一个动点.(1)求抛物线的解析式;(2)如图所示,点P 是抛物线上位于第一象限内的一个动点,过点P 作PF CE ^,求PF 的最大值.压轴题型三 二次函数的平移问题1.如图,抛物线21445y x x =-+与x 轴交于点A 、B ,把抛物线在x 轴及其下方的部分记作1C ,将1C 向左平移得到2C ,2C 与x 轴交于点B 、D ,若直线y x k =+与1C 、2C 共有3个不同的交点,则k 的取值范围是( )A .2554k -<<-B .51k -£<-C .95k -£<-D .2954k -<<-2.二次函数223y x x =--的图象与x 轴交于点,A B (A 在B 的左侧),将该函数图象向右平移()0m m >个单位后与x 轴交于点,C D (C 在D 的左侧),平移前后的函数图象相交于点E ,若90AED Ð=°,则m 的值为 .3.已知抛物线L 的解析式为22y x mx n =-++(m ,n 为常数).(1)若抛物线L 的顶点在第四象限,且221n m m =-+-,求m 的取值范围;(2)若抛物线L 经过点()1,1P ,将抛物线L 经过平移后得到抛物线S ,点P 的对应点为点()1,2Q t m -,其中1t ³.抛物线仍然经过点P ,求m 的最小值.4.已知抛物线213:4L y x bx c =-++与y 轴交于点C ,与x 轴交于(4,0)(1,0)A B -,两点.(1)求抛物线1L 的函数解析式及点C 的坐标;(2)平移抛物线1L 得到抛物线2L ,抛物线2L 经过点C ,且与x 轴交于()3,0M N ,两点,连接CB ,CN .点P 是抛物线2L 上的点,连接PN ,若PNC BCN Ð=Ð,请求出所有符合条件的点P 的坐标.5.综合与探究:如图,在平面直角坐标系中,抛物线22y ax x c =-+与x 轴交于点()3,0A -和点C ,与y 轴交于点B (0,3),点P 是抛物线上点A 与点C 之间的动点(不包括点A ,点C ). 备用图(1)求抛物线的解析式;(2)动点P 在抛物线上,且在直线AB 上方,求ABP V 面积的最大值及此时点P 的坐标;(3)在(2)的条件下,将该抛物线向右平移2.5个单位,点F 为点P 的对应点,平移后的抛物线与y 轴交于点E ,Q 为平移后的抛物线的对称轴上任意一点,若QFE △是以QE 为腰的等腰三角形,求出所有符合条件的点Q 的坐标.压轴题型四 二次函数的翻折问题1.函数()220,40y ax bx c a b ac =++>->的图象是由函数()220,40y ax bx c a b ac =++>->的图象x 轴上方部分不变,下方部分沿x 轴向上翻折而成,如图所示,则下列结论正确的是( )①20a b += ;②3c =; ③0abc >;④将图象向上平移1个单位后与直线5y =有3个交点.A .①②B .①③C .②③④D .①③④2.函数()220,40y ax bx c a b ac =++>->的图象是由函数()220,40y ax bx c a b ac =++>->的图象轴上方部分不变,x 轴下方部分沿x 轴向上翻折而成,如图所示,则下列结论正确的是①20a b +=;②3c =;③0abc >; ④30a c +=;⑤将图象向上平移1个单位后与直线5y =有3个交点.3.已知二次函数图像的对称轴为y 轴,且经过点()1,5和111,24æö-ç÷èø.(1)求此二次函数的解析式;(2)若将该二次函数图像先向下平移4个单位,再沿x 轴翻折后与x 轴交于A ,B 两点,设顶点为P ,求AOP V 的面积.4.如图,二次函数2y x bx c =++的图象过点(3520())A B ,-,-,.(1)求这个二次函数的解析式;(2)将一次函数21y x =+的图象向下平移a 个单位长度,与二次函数的图象总有交点,求a 的取值范围;(3)过点()0N m ,作y 轴的垂线EF ,以EF 为对称轴将二次函数的图象位于EF 下方的部分翻折,若翻折后所得部分与x 轴有交点,且交点都位于x 轴的正半轴,直接写出m 的取值范围.5.如图,函数()()21130y a x x =-++£的图象过原点,将其沿y 轴翻折,得到函数2y 的图象,把函数1y 与2y的图象合并后称为函数L 的图象.(1)a 的值为__________;函数2y 的解析式为_______________(注明x 的取值范围);(2)对于函数L ,当函数值y 随x 的增大而减小时,x 的取值范围是_____________;(3)当直线y x b =+与函数L 的图象有3个公共点时,求b 的值.压轴题型五 二次函数与方程、不等式压轴题1.函数2y x bx c =++与y x =的图象如图所示,有以下结论:①240b c ->;②1b c +=-;③360b c ++=;④当13x <<时,()210x b x c +-+<,其中正确的个数是( )A .1B .2C .3D .42.已知二次函数22y x x =-++,当3a x a ££+对应的函数值y 随x 的增大而增大,且对应的图象与直线4y =-有公共点时,a 的取值范围为 .3.二次函数2y x bx c =++的图象经过点()1,0A ,B (0,3),点C 与点B 关于该二次函数图象的对称轴对称,已知一次函数y mx n =+的图象经过A ,C 两点.(1)求二次函数解析式;(2)根据图象,写出满足不等式2x bx c mx n ++<+的解集_____;(3)二次函数2y x bx c =++,当13x ££时,对应的函数值y 的取值范围为_____.4.在平面直角坐标系中,设二函数1()(2)y x m x m =-++,其中0m ¹.(1)求证:函数1y 与x 轴有交点;(2)若函数2y mx n =+经过函数1y 的顶点,求实数n 的最大值;(3)已知点()1(3,),,P a Q x b -在函数1y 的图象上,若a b ³,求1x 的取值范围.5.在平面直角坐标系中,抛物线23y ax bx =++(a b 、为常数)的对称轴为直线1x =,且经过点()1,0-.(1)当132x -££时,二次函数的最大值是_____,最小值是______;(2)当1t x t -££时,若二次函数的最大值和最小值的差为3,求t 的值;(3)现有一点P 在抛物线上,横坐标为m ,过点P 作直线PQ 平行于x 轴,交抛物线于另一点Q .抛物线上另有两点M N 、,横坐标分别为1-和4,M N 、两点之间的部分(不包括M N 、两点)记作图象G .若图象G 上恰好有三个点到直线PQ 的距离为2,求出m 的取值范围.压轴题型六 二次函数的销售问题(含参问题)1.某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.A .50B .90C .80D .702.某快餐店销售A 、B 两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A 种快餐的利润,同时提高每份B 种快餐的利润.售卖时发现,在一定范围内,每份A 种快餐利润每降1元可多卖2份,每份B 种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.3.为助推乡村经济发展,解决茶农卖茶难问题,某地政府在新茶上市30天内,帮助“幸福村”茶农合作社集中销售茶叶,设第x 天(x 为整数)的售价为y (元/斤),日销售额为w (元).据销售记录知:①第1天销量为42斤,以后每天比前一天多卖2斤;②前10天的价格一直为500元/斤,后20天价格每天比前一天跌10元,(1)当1130x ££时,写出y 与x 的关系式;(2)当x 为何值时日销售额w 最大,最大为多少?(3)若日销售额不低于31680元时可以获得较大利润,当天合作社将向希望小学捐款m 元,用于捐资助学,若“幸福村”茶农合作社计划帮助希望小学购买10800元的图书,求m 的最小整数值.4.电商小李在抖音平台上对一款成本单价为10元的商品进行直播销售,规定销售单价不低于成本价,且不高于成本价的3倍.通过前几天的销售发现,当销售定价为15元时,每天可售出700件,销售单价每上涨10元,每天销售量就减少200件,设此商品销售单价为x (元),每天的销售量为y (件).(1)求y 关于x 之间的函数关系式,并写出x 的取值范围;(2)若销售该商品每天的利润为7500元,求该商品的销售单价;(3)小李热心公益事业,决定每销售一件该商品就捐款m 元(m >0)给希望工程,当每天销售最大利润为6000元时,求m 的值.5.某商品的进价为每件40元,当售价为每件50元,每月可卖出200件,如果售价每上涨1元,则每月少卖10件(每件售价不能高于65元);如果售价每下降1元,则每月多卖12件(每件售价不低于48元).设每件商品的售价为x 元(x 为正整数),每月的销售量为y 件.(1)①当售价上涨时,y 与x 的函数关系为______,自变量x 的取值范围是______;②当售价下降时,y 与x 的函数关系为______,自变量x 的取值范围是______;(2)每件商品的售价x 定为多少元时,每月可获得最大利润?最大的月利润是多少元?(3)商家发现:在售价上涨的情况下,每件商品还有()0a a >元的其他费用需要扣除,当售价每件不低于60元时,每月的利润随x 的增大而减小,请直接写出a 的取值范围______.压轴题型七 二次函数的存在性问题1.对于平面直角坐标系xOy 中的点P 和图形G ,给出如下定义:在图形G 上若存在两点M ,N ,使PMN V 为正三角形,则称图形G 为点P 的T 型线,点P 为图形G 的T 型点,PMN V 为图形G 关于点P 的T 型三角形.若()0,2H -是抛物线2y x n =+的T 型点,则n 的取值范围是( )A .1n ³-B .1n £-C .54n £-D .54n ³-2.如图,已知二次函数2(1)y x a x a =-++-的图像与x 轴交于A 、B 两点(点A 位于点B 的左侧),与y 轴交于点C .已知BAC V 的面积是6,若在抛物线上存在一点P (与点C 不重合),使ABP ABC S S =△△,则点P 的坐标为 .3.如图所示,已知以M 为顶点的抛物线2y x bx c =-++交x 轴于A ,B 两点,交y 轴于点C ,直线BC 的表达式为3y x =-+.(1)求抛物线的表达式.(2)连接AC ,在x 轴上方的抛物线上有一点D ,若ABD ACO Ð=Ð,求点D 的坐标;(3)若点P 为抛物线位于第一象限图象上一动点,过P 作PQ BC ^,求PQ 的最大值;(4)在x 轴上是否存在一点N ,使得以A ,C ,N 为顶点的三角形与BCM V 相似?若存在,请求出点N 的坐标;若不存在,请说明理由.4.如图1,抛物线()240y ax bx a =++¹与x 轴,y 轴分别交于()1,0A -,B (4,0),C 三点.(1)试求抛物线的解析式;(2)若P 点在第一象限的抛物线上,连接PC PB 、,当PCB V 的面积最大时,求点P 的坐标.(3)点()3,D m 在第一象限的抛物线上,连接,BC BD .试问,在对称轴左侧的抛物线上是否存在一点P ,满足PBC DBC Ð=Ð?如果存在,请求出点P 的坐标;如果不存在,请说明理由.5.综合与探究如图,在平面直角坐标系中,抛物线22y ax bx =+-经过()()1,0,4,0A B -两点,与y 轴交于点C ,P 是抛物线上一动点,设点P 的横坐标为302m m æö<<ç÷èø,连接AC CP BC BP ,,,.(1)求抛物线的函数表达式及点C 的坐标.(2)当BCP V 的面积等于ABC V 的面积的35时,求m 的值.(3)在(2)的条件下,若M 为x 轴上一动点,N 是抛物线上一动点,是否存在以点C ,P ,M ,N 为顶点的平行四边形?若存在,直接写出点M 的坐标;若不存在,请说明理由.压轴题型八 二次函数的角度问题1.已知抛物线 ²30y ax bx a =++<()与x 轴交于()1,0A ,()3,0B - 两点, 与y 轴交于点C .若点P 在抛物线的对称轴上,线段PA 绕点P 逆时针旋转90°后,点A 的对应点A ¢恰好也落在此抛物线上,则点P 的坐标为( )A .()1,1-B .()1,1--C .()1,1- 或()1,2--D .()1,1-- 或()1,2-2.如图,抛物线213222y x x =+-与x 轴交于点A 和点B 两点,与y 轴交于点C ,D 点为抛物线上第三象限内一动点,当2180ACD ABC ÐÐ=°+时,点D 的坐标为 .3.抛物线23y ax bx =++与x 轴交于A (―2,0),()60B ,两点,与y 轴交于点C ,点D 在抛物线上.(1)求抛物线的解析式;(2)如图,点D 在BC 上方的抛物线上,当BCD △的面积最大时,求点D 的坐标;(3)是否存在点D ,使得BCD ABC Ð=Ð?若存在,求出点D 的坐标;若存在,请说明理由.4.抛物线22y x x c =-+经过点115,24P æö-ç÷èø,与x 轴交于A ,B 两点(A 在B 的左侧),与y 轴交于点C .(1)直接写出c 的值及点A ,B ,C 的坐标;(2)如图1,连接,AC BC ,点F 在抛物线上,满足FCB ACO Ð=Ð,求点F 的坐标;(3)如图2,向上平移直线BC 交抛物线于M ,N 两点,直线,MP NP 分别交y 轴的负半轴于D ,E 两点,求证:PD PE =.5.如图,抛物线212y x bx c =-++与x 轴交于点()1,0A -和点B ,交y 轴于点C ,连接AC ,BC ,点()2,3D 在抛物线上.(1)求抛物线的表达式;(2)判断ABC V 的形状,并说明理由;(3)连接CD ,点M 在抛物线上,ACM BCD Ð=Ð,求点M 的坐标.压轴题型九 二次函数铅垂高、水平宽求面积最大值1.如图,抛物线2y ax bx c =++与x 轴交于点()()2,0,4,0A B -,交y 轴的正半轴于点C ,对称轴交抛物线于点D ,交x 轴于点E ,则下列结论:①20a b +=;②0abc >;③2a b am bm +>+(m 为任意实数);④若点(),Q m n 是抛物线上第一象限上的动点,当QBC △的面积最大时,1,m n a b c ==++,其中正确的有( )A .1个B .2个C .3个D .4个2.如图,已知抛物线2y x =和直线21y x =+相交与点A ,B .点P 是抛物线上一点,且在直线AB 的下方,连接AP ,BP ,当ABP V 的面积最大时,则点P 的坐标是 .3.如图,在直角坐标系中,二次函数212y x bx c =++的图象与x 轴相交于点A (―2,0)和点()6,0B ,与y 轴交于点C .(1)求b 、c 的值;(2)若点P 是抛物线BC 段上的一点,当PBC △的面积最大时求出点P 的坐标,并求出PBC △面积的最大值.4.如图,在平面直角坐标系中,二次函数2y x bx c =-++的图象与x 轴交于A ,B 两点,与y 轴交于点()0,3C ,点A 在原点的左侧,点B 的坐标为()3,0,点P 是抛物线上一个动点.(1)求这个二次函数的解析式;(2)在抛物线上是否存在点P ,使得ABP V 的面积等于10.若存在,请求出点P 的坐标,若不存在,请说明理由.(3)若点P 在直线BC 的上方,当点P 运动到什么位置时,BPC V 的面积最大?请求出点P 的坐标.5.如图,在平面直角坐标系中,直线1y ax =+与抛物线23y x bx =+-交于点A 和点()4,5B .(1)求a 和b 的值;(2)求点A 的坐标,并结合图象写出不等式231x bx ax +->+的解集;(3)点P 是直线AB 下方的抛物线上的一动点(不与点A ,B 重合),请直接写出当PAB V 的面积最大时,点P 的坐标.压轴题型十 二次函数与相似相关压轴题1.抛物线()230y ax ax b a =++<,设该抛物线与x 轴的交点为()5,0A -和B ,与y 轴的交点为C ,若ACO CBO D D ∽,则tan CAB Ð的值为 ( )A B C D 2.在同一平面内,直线1y kx =+与抛物线 214y x =交于A 、B 两点,设 ()()1122,,A x y B x y ,.(1) 12x x = ;(2)若点()01N -,,且AN 与BN 不垂直,则k 的取值范围是: .3.如图1,平面直角坐标系中,抛物线2y ax bx c =++交x 轴于()1,0A ,()3,0B -两点,交y 轴于点()0,3C ,点M 是线段OB 上一个动点,过点M 作x 轴的垂线,交直线BC 于点F ,交抛物线于点E .(1)求抛物线的解析式;(2)当BCE V 面积最大时,求M 点的坐标;(3)如图2,是否存在以点C 、E 、F 为顶点的三角形与ABC V 相似,若存在,求点M 的坐标;若不存在,请说明理由.4.如图,在平面直角坐标系内,点(20)A -,,点(40)B ,,点4(0)C ,.连接AC BC ,.(1)求经过点A 、B 、C 三点的抛物线的表达式;(2)点D 在x 轴正半轴上,当以点D 、O 、C 为顶点的三角形与AOC △相似时,求点D 的坐标.(3)在(1)的抛物线上找一点E ,使得BE CE -的值最小并求点E 的坐标.5.如图,在平面直角坐标系中,抛物线()240y ax bx a =++¹与x 轴交于()1,0A -、()4,0C 两点,与y 轴交于点B .(1)求该抛物线的解析式以及顶点坐标;(2)若点D 是抛物线上的一个动点,满足ABD △与BCD △的面积相等.求出点D 的坐标;(3)若点E 在第一象限内抛物线上,过点E 作EF x ^轴于点F ,交BC 于点P ,且满足BFP △与CEP △相似,求出点E 的横坐标.。
人教版九年级数学上册期末备考训练:二次函数压轴(含答案)

期末备考训练:二次函数压轴1.如图,在平面直角坐标系中,已知点B的坐标为(﹣1,0),且OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点.(1)求A,C两点的坐标;(2)求抛物线的解析式;(3)若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.2.如图1,抛物线y=ax2+bx﹣3经过点A,B,C,已知点A(﹣1,0),点B(3,0)(1)求抛物线的解析式(2)点D为抛物线的顶点,DE⊥x轴于点E,点N是线段DE上一动点①当点N在何处时,△CAN的周长最小?②若点M(m,0)是x轴上一个动点,且∠MNC=90°,求m的取值范围.3.如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.(1)求抛物线的函数表达式;(2)设D为抛物线的顶点,连接DA、DB,试判断△ABD的形状,并说明理由;(3)设P为对称轴上一动点,要使PC﹣PB的值最大,求出P点的坐标.4.如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点(A在B的左侧),与y轴正半轴交于点C,对称轴为直线x=1,且OB=OC,(1)求抛物线的表达式;(2)D是直线BC上方抛物线上一点,DE⊥BC于E,若CE=3DE,求点D的坐标;(3)将抛物线向左平移,使顶点P落在y轴上,直线l与抛物线相交于M、N两点(点M,N都不与点P重合),若以MN为直径的圆恰好经过O,P两点,求直线l的表达式.5.如图,抛物线y=﹣x2﹣x+c与x轴交于A,B两点,且点B的坐标为(3,0),与y 轴交于点C,连接AC,BC,点P是抛物线上在第二象限内的一个动点,点P的横坐标为a,过点P作x轴的垂线,交AC于点Q.(1)求A,C两点的坐标.(2)请用含a的代数式表示线段PQ的长,并求出a为何值时PQ取得最大值.(3)试探究在点P运动的过程中,是否存在这样的点Q,使得以B,C,Q为顶点的三角形是等腰三角形?若存在,请写出此时点Q的坐标;若不存在,请说明理由.6.【概念认识】城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系xOy,对两点A(x1,y1)和B(x2,y2),用以下方式定义两点间距离:d(A,B)=|x1﹣x2|+|y1﹣y2|.【数学理解】(1)①已知点A(﹣2,1),则d(O,A)=.②函数y=﹣2x+4(0≤x≤2)的图象如图①所示,B是图象上一点,d(O,B)=3,则点B的坐标是.(2)函数y=(x>0)的图象如图②所示.求证:该函数的图象上不存在点C,使d (O,C)=3.(3)函数y=x2﹣5x+7(x≥0)的图象如图③所示,D是图象上一点,求d(O,D)的最小值及对应的点D的坐标.【问题解决】(4)某市要修建一条通往景观湖的道路,如图④,道路以M为起点,先沿MN方向到某处,再在该处拐一次直角弯沿直线到湖边,如何修建能使道路最短?(要求:建立适当的平面直角坐标系,画出示意图并简要说明理由)7.如图,直线y=x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=x2+bx+c 经过点B,C,与x轴的另一个交点为点A.(1)求抛物线的解析式;(2)点P是直线BC下方的抛物线上一动点,求四边形ACPB的面积最大时点P的坐标;(3)若点M是抛物线上一点,请直接写出使∠MBC=∠ABC的点M的坐标.且过点D(2,﹣3).点P、Q是抛物线y=ax2+bx+c上的动点.(1)求抛物线的解析式;(2)当点P在直线OD下方时,求△POD面积的最大值.(3)直线OQ与线段BC相交于点E,当△OBE与△ABC相似时,求点Q的坐标.9.如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣2,3),过点A作AB⊥y轴,垂足为B,连结OA,抛物线y=﹣x2﹣2x+c经过点A,与x轴正半轴交于点C.(1)求c的值;(2)将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围;(3)连结BC,设点E在x轴上,点F在抛物线上,如果B、C、E、F构成平行四边形,请求出点E的坐标.(1)求抛物线的解析式;(2)连接BC,若点P为线段BC上的一个动点(不与点B、点C重合),过点P作直线PN⊥x轴于点N,交抛物线于点M,当△BCM面积最大时,求△BPN的周长.(3)在(2)的条件下,当△BCM面积最大时,在抛物线的对称轴上是否存在点Q,使△CNQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.11.如图,点A,B,C都在抛物线y=ax2﹣2amx+am2﹣9(其中a>0)上,AB∥x轴,点P是抛物线的顶点,tan∠PBA=2,∠BAC=45°(1)填空:抛物线的顶点P的坐标为(用含m的代数式表示);(2)求△ABC的面积(用含a的代数式表示);(3)若△ABC的面积为10,当2m﹣3≤x≤2m+5时,y的最小值为5,求m的值.12.如图,在平面直角坐标系xOy中,已知抛物线y=ax2﹣2x+c与直线y=kx+b都经过A (0,﹣3)、B(3,0)两点,该抛物线的顶点为C.(1)求此抛物线和直线AB的解析式;(2)设直线AB与该抛物线的对称轴交于点E,在射线EB上是否存在一点M,过M作x轴的垂线交抛物线于点N,使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;(3)设点P是直线AB下方抛物线上的一动点,当△P AB面积最大时,求点P的坐标,并求△P AB面积的最大值.13.如图,二次函数y=x2+bx﹣3的图象l交x轴于点A(﹣3,0)、B(1,0),交y轴于点C,将图象l沿坐标轴翻折得到新的图象,与图象l开口方向相同的新的图象l1交x轴于点A1(在x轴的正半轴上)(1)求出b的值,并写出点A1的坐标以及新的图象所对应的函数解析式;(2)若P为y轴上的一个动点,E为直线A1C上的一个动点,请找出点P,使得PB+PE 最小,并求出最小值;(3)在y轴的正半轴上有一点M,使得∠MA1O=k∠OCB,直线A1M交图象l1于点D (点D在第二象限).①若k=2,试求点D的坐标;②若k=3,请直接写出OM的长.14.如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO =3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.15.如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.点D是直线BC上方抛物线上一动点.(1)求抛物线的解析式;(2)如图1,连接BD、CD,设点D的横坐标为m,△BCD的面积为s.试求出s与m的函数关系式,并求出s的最大值;(3)如图2,设AB的中点为E,作DF⊥BC,垂足为F,连接CD、CE,是否存在点D,使得以C、D,F三点为顶点的三角形与△CEO相似?若存在,请直接写出点D的坐标;若不存在,请说明理由.16.已知,如图在平面直角坐标系中,直线y=﹣x与抛物线y=﹣x2﹣x交于点A,抛物线与x轴的一个交点为B,以A为圆心,AB的长为半径的圆与y轴的正半轴交于点C,过点B作BD⊥x轴交圆于点D,连接CD交直线y=﹣x于点E.(1)请直接写出点A、B、C、D的坐标;(2)在抛物线上是否存在一点P,使得△AEP的面积等于△ACE的面积;若存在求出点P坐标;(3)若点M是直线y=﹣x上一个动点,点N抛物线上一个动点,若以点B、C、M、N 为顶点的四边形是平行四边形,求此时抛物线上点N的坐标.参考答案1.解:(1)OA=OC=4OB=4,故点A、C的坐标分别为(4,0)、(0,﹣4);(2)抛物线的表达式为:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),即﹣4a=﹣4,解得:a=1,故抛物线的表达式为:y=x2﹣3x﹣4;(3)直线CA过点C,设其函数表达式为:y=kx﹣4,将点A坐标代入上式并解得:k=1,故直线CA的表达式为:y=x﹣4,过点P作y轴的平行线交AC于点H,∵OA=OC=4,∴∠OAC=∠OCA=45°,∵PH∥y轴,∴∠PHD=∠OCA=45°,设点P(x,x2﹣3x﹣4),则点H(x,x﹣4),PD=HP sin∠PFD=(x﹣4﹣x2+3x+4)=﹣x2+2x,∵<0,∴PD有最大值,当x=2时,其最大值为2,此时点P(2,﹣6).2.解:(1)函数的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),故﹣3a=﹣3,解得:a=1,故函数的表达式为:y=x2﹣2x﹣3;(2)①过点C作x轴的平行线交抛物线于点C′(2,﹣3),连接AC′交DE于点N,则此时△CAN的周长最小,将点A、C′的坐标代入一次函数表达式:y=kx+b得:,解得:,故直线AC′的表达式为:y=﹣x﹣1,当x=1时,y=﹣2,故点N(1,﹣2);②如图2,过点C作CG⊥ED于点G,设NG=n,则NE=3﹣n,∵∠CNG+∠GCN=90°,∠CNG+∠MNE=90°,∴∠NCG=∠MNE,则tan∠NCG=n=tan∠MNE=,故ME=﹣n2+3n,∴﹣1<0,故ME有最大值,当n=时,ME=,则m的最小值为:﹣;如下图所示,当点N与点D处时,m取得最大值,同理可得:m=5;故:﹣≤m≤5.3.解:(1)如图,∵AB=2,对称轴为直线x=2.∴点A的坐标是(1,0),点B的坐标是(3,0).∵抛物线y=x2+bx+c与x轴交于点A,B,∴1、3是关于x的一元二次方程x2+bx+c=0的两根.由韦达定理,1+3=﹣b,1×3=c,∴b=﹣4,c=3,∴抛物线的函数表达式为y=x2﹣4x+3;(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,∴D(2,﹣1),∴AD2+BD2=(2﹣1)2+(﹣1)2+(2﹣3)2+(﹣1)2=4,∵AB2=22=4,∴AD2+BD2=AB2,∴△ADB是直角三角形,由对称性有AD=BD,∴△ADB是等腰直角三角形;(3)连接CA,延长CA与直线x=2交于点P,连接BP,如图2,∵A、B两点关于直线x=2对称,∴PB=P A,∴PC﹣PB=PC﹣P A=AC其值最大(∵另取一点P′,有P′C﹣P′B=P′C﹣P′A<AC),A令x=0,得y=x2﹣4x+3=3,∴C(0,3),∵A(1,0),∴易求直线AC的解析式为:y=﹣3x+3,当x=2时,y=﹣3x+3=﹣3,∴P(2,﹣3).4.解:(1)x=﹣,则b=2,设点C(0,c),则点B(c,0),将点B的坐标代入二次函数表达式并解得:c=3,故函数的表达式为:y=﹣x2+2x+3,函数的顶点为(1,4);(2)过点D作y轴的平行线交直线BC与点H,过点C作x轴的平行线交DH于点R,将点C、B的坐标代入一次函数表达式得:直线BC的表达式为:y=﹣x+3,设点D(m,﹣m2+2m+3),则点H(m,3﹣m),∵OB=OB=3,∴∠OCB=∠OBC=45°,∴CR=CH=m,DH=﹣m2+2m+3﹣3+m=﹣m2+3m,3DE=3×DH,CE=CH﹣EH=m﹣DH,∵CE=3DE,即RH=2DH,则m=2(﹣m2+3m),解得:m=,则点D(,);(3)平移前函数的顶点为(1,4),则平移后函数的表达式为:y=﹣x2+4,如图所示,以MN为直径的圆恰好经过O,P两点,则∠MON=∠MPN=90°,在点O处,过点M、N分别作x轴的垂线交于点G、H,∵∠GOM+∠NOH=90°,∠NOH+∠ONH=90°,∴∠MOG=∠ONH=α,设点M、N的坐标分别为(m,4﹣m2)、(n,4﹣n2),(m<n,m<0),则tan∠MOG=tan∠ONH=α,即:…①,在点P处,同理可得:…②,联立①②并整理得:m2+n2=4,mn=﹣1,解得:m=±,n=,将点M、N的坐标代入一次函数表达式:y=kx+b并解得:k=,b=3,故直线l的表达式:y=x+3.5.解:(1)把点B的坐标(3,0)代入抛物线解析式得,,解得:c=4,令y=0,则,解得x1=3,x2=﹣4,∴A(﹣4,0),C(0,4);(2)∵A(﹣4,0),C(0,4),设直线AC的解析式为y=kx+b,∴,∴,∴直线AC的解析式y=x+4,点P的横坐标为a,P(a,),则点Q(a,a+4),∴PQ==,∵,∴a=﹣2时,PQ有最大值;(3)存在,理由:点A、B、C的坐标分别为(﹣4,0)、(3,0)、(0,4),则BC=5,AB=7,AC=4,∠OAC=∠OCA=45°,将点B、C的坐标代入一次函数表达式:y=mx+n并解得:,∴直线BC的解析式为y=﹣x+4,设BC的中点为H,由中点坐标公式可得H(),∴过BC的中点H且与直线BC垂直直线的表达式为:y=,①当BC=BQ时,如图1,∴BC=BQ=5,设:QM=AM=n,则BM=7﹣n,由勾股定理得:(7﹣n)2+n2=25,解得:n=3或4(舍去4),故点Q1(﹣1,3);②当BC=CQ时,如图1,∴CQ=5,则AQ=AC﹣CQ=4,∴,∴,③当CQ=BQ时,联立直线AC解析式y=x+4和y=,解得x=﹣(不合题意,舍去),综合以上可得点Q的坐标为:Q(﹣1,3)或().6.解:(1)①由题意得:d(O,A)=|0+2|+|0﹣1|=2+1=3;②设B(x,y),由定义两点间的距离可得:|0﹣x|+|0﹣y|=3,∵0≤x≤2,∴x+y=3,∴,解得:,∴B(1,2),故答案为:3,(1,2);(2)假设函数的图象上存在点C(x,y)使d(O,C)=3,根据题意,得,∵x>0,∴,,∴,∴x2+4=3x,∴x2﹣3x+4=0,∴△=b2﹣4ac=﹣7<0,∴方程x2﹣3x+4=0没有实数根,∴该函数的图象上不存在点C,使d(O,C)=3.(3)设D(x,y),根据题意得,d(O,D)=|x﹣0|+|x2﹣5x+7﹣0|=|x|+|x2﹣5x+7|,∵,又x≥0,∴d(O,D)=|x|+|x2﹣5x+7|=x+x2﹣5x+7=x2﹣4x+7=(x﹣2)2+3,∴当x=2时,d(O,D)有最小值3,此时点D的坐标是(2,1).(4)如图,以M为原点,MN所在的直线为x轴建立平面直角坐标系xOy,将函数y=﹣x的图象沿y轴正方向平移,直到与景观湖边界所在曲线有交点时停止,设交点为E,过点E作EH⊥MN,垂足为H,修建方案是:先沿MN方向修建到H处,再沿HE方向修建到E处.理由:设过点E的直线l1与x轴相交于点F.在景观湖边界所在曲线上任取一点P,过点P作直线l2∥l1,l2与x轴相交于点G.∵∠EFH=45°,∴EH=HF,d(O,E)=OH+EH=OF,同理d(O,P)=OG,∵OG≥OF,∴d(O,P)≥d(O,E),∴上述方案修建的道路最短.7.解:(1)将点B坐标代入y=x+c并解得:c=﹣3,故抛物线的表达式为:y=x2+bx﹣3,将点B坐标代入上式并解得:b=﹣,故抛物线的表达式为:y=x2﹣x﹣3;(2)过点P作PH∥y轴交BC于点H,设点P(x,x2﹣x﹣3),则点H(x,x﹣3),S 四边形ACPB =S △AOC +S △PCB ,∵S △AOC 是常数,故四边形面积最大,只需要S △PCB 最大即可,S △PCB =×OB ×PH =×2(x ﹣3﹣x 2+x +3)=﹣x 2+3x ,∵﹣<0,∴S △PCB 有最大值,此时,点P (2,﹣);(3)过点B 作∠ABC 的角平分线交y 轴于点G ,设∠MBC =∠ABC =2α,过点B 分别在x 轴之上和BC 之下作角度数为α的两个角,分别交y 轴于点N 交抛物线于点M ′,交抛物线于点M ,过点G 作GK ⊥BC 交BC 于点K ,延长GK 交BM 于点H ,则GH =GN ,BC 是GH 的中垂线,OB =4,OC =3,则BC =5,设:OG =GK =m ,则CK =CB ﹣HB =5﹣4=1,由勾股定理得:(3﹣m )2=m 2+1,解得:m =,则OG =ON =,GH =GN =2OG =,点G (0,﹣),在Rt △GCK 中,GK =OG =,GC =OC ﹣OG =3﹣=,则cos ∠CGK ==,sin ∠CGK =,则点K(,﹣),点K是点GH的中点,则点H(,﹣),则直线BH的表达式为:y=x﹣…②,同理直线BN的表达式为:y=﹣x+…③联立①②并整理得:27x2﹣135x+100=0,解得:x=1或4(舍去4),则点M(1,﹣);联立①③并解得:x=﹣,故点M′(﹣,);故点M(1,﹣)或(﹣,).8.解:(1)函数的表达式为:y=a(x+1)(x﹣3),将点D坐标代入上式并解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣3…①;(2)设直线PD与y轴交于点G,设点P(m,m2﹣2m﹣3),将点P、D的坐标代入一次函数表达式:y=sx+t并解得:直线PD的表达式为:y=mx﹣3﹣2m,则OG=3+2m,S=×OG(x D﹣x P)=(3+2m)(2﹣m)=﹣m2+m+3,△POD有最大值,当m=时,其最大值为;∵﹣1<0,故S△POD(3)∵OB=OC=3,∴∠OCB=∠OBC=45°,∵∠ABC=∠OBE,故△OBE与△ABC相似时,分为两种情况:①当∠ACB=∠BOQ时,AB=4,BC=3,AC=,过点A作AH⊥BC于点H,S=×AH×BC=AB×OC,解得:AH=2,△ABC则sin∠ACB==,则tan∠ACB=2,则直线OQ的表达式为:y=﹣2x…②,联立①②并解得:x=,故点Q1(,﹣2),Q2(﹣,2),②∠BAC=∠BOQ时,tan∠BAC==3=tan∠BOQ,则点Q(n,3n),则直线OQ的表达式为:y=﹣3x…③,联立①③并解得:x=,故点Q3(,),Q4(,);综上,当△OBE与△ABC相似时,Q的坐标为:(,﹣2)或(,)或(﹣,2)或(,).9.解:(1)将点A的坐标代入抛物线表达式得:﹣4+4+c=3,解得:c=3;(2)则抛物线的表达式为:y=﹣x2﹣2x+3=﹣(x+1)2+4,抛物线的对称轴是:x=﹣1,点A(﹣2,3),则直线AO的函数表达式为:y=﹣x,当x=﹣1时,y=,∵平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),∴4﹣3<m<4﹣,即1<m<;(3)设点F(m,n),n=﹣m2﹣2m+3,点E(s,0),①当BC是平行四边形的一条边时,则点B向右平移一个单位、向下平移3个单位得到C,同样:点F(E)向右平移一个单位、向下平移3个单位得到E(F),故:m+1=s,n﹣3=0,或m﹣1=s,n﹣3=0;解得:m=0或﹣2(舍去0)或m=﹣1,故点E的坐标为(﹣1,0)或(﹣2+,0)或(﹣﹣2,0);②当BC是平行四边形的对角线时,则由中点的性质得:1=m+s,3=n,解得:m=0或﹣2(舍去0),故点E(3,0);综上,点E的坐标为:(﹣1,0)或(﹣2+,0)、(﹣﹣2,0)或(3,0).10.解:(1)由题意可得:,解得,∴抛物线解析式为y=﹣x2+2x+3;(2)设直线BC的解析式为:y=kx+b,则有:,解得:,∴直线BC的解析式为:y=﹣x+3.设P(x,﹣x+3),则M(x,﹣x2+2x+3),∴PM=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x.∴S△BCM =S△PMC+S△PMB=(x B﹣x C)=,∴S△BCM==,∴当x=时,△BCM的面积最大.此时P(),∴PN=ON=,∴BN=OB﹣ON=3﹣=,在Rt△BPN中,由勾股定理得:PB=,C△BCN=BN+PN+PB=3+,∴当△BCM的面积最大时,△BPN的周长为3+;(3)由(2)知P点坐标为(),∴,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴抛物线的对称轴为x=1,设Q(1,a),∵C(0,3),N(),∴CQ2=12+(3﹣a)2,,,若△CNQ为等腰三角形,可分三种情况:当CQ=QN时,1+,解得:a=,∴点Q的坐标为(1,),当CQ=CN时,1+,解得:a=3,∴点Q的坐标为(1,3﹣),(1,3+),当QN=CN时,,解得:a=,∴点Q的坐标为(1,),(1﹣),综合以上可得点Q的坐标为(1,)或(1,3﹣)或(1,3+)或(1,)或(1,﹣).11.解:(1)∵y=ax2﹣2amx+am2﹣9=a(x﹣m)2﹣9∴顶点P的坐标为(m,﹣9)故答案为:(m,﹣9).(2)过点P作PD⊥AB于点D,过点C作CE⊥AB于点E∵AB∥x轴,且点A、B在抛物线上∴P A=PB∴AD=BD∵tan∠PBA==2∴PD=2BD=AB设AD=BD=n(n>0),则PD=AB=2n∴A(m﹣n,﹣9+2n)把A的坐标代入抛物线解析式得:a(m﹣n﹣m)2﹣9=﹣9+2n整理得:n=∴AB=,A(m﹣,﹣9+)∵∠AE C=90°,∠BAC=45°∴AE=CE设AE=CE=t(t>0),则C(m﹣+t,﹣9++t)把C的坐标代入抛物线解析式得:a(m﹣+t﹣m)2﹣9=﹣9++t整理得:t=∴CE==AB•CE=∴S△ABC(3)∵S==10,a>0△ABC∴a=1∴抛物线解析式为:y=(x﹣m)2﹣9∴抛物线最小值y=﹣9<5∴当2m﹣3≤x≤2m+5时,不包含有对称轴x=m①若2m+5<m,即m<﹣5时,x=2m+5对应最小值y=5∴(2m+5﹣m)2﹣9=5解得:m1=﹣5+(舍去),m2=﹣5﹣②若2m﹣3>m,即m>3时,x=2m﹣3对应最小值y=5∴(2m﹣3﹣m)2﹣9=5解得:m1=3+,m2=3﹣(舍去)综上所述,m的值为﹣5﹣或3+.12.解:(1)∵抛物线y=ax2﹣2x+c经过A(0,﹣3)、B(3,0)两点,∴,∴,∴抛物线的解析式为y=x2﹣2x﹣3,∵直线y=kx+b经过A(0,﹣3)、B(3,0)两点,∴,解得:,∴直线AB的解析式为y=x﹣3,(2)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的顶点C的坐标为(1,﹣4),∵CE∥y轴,∴E(1,﹣2),∴CE=2,①如图,若点M在x轴下方,四边形CEMN为平行四边形,则CE=MN,设M(a,a﹣3),则N(a,a2﹣2a﹣3),∴MN=a﹣3﹣(a2﹣2a﹣3)=﹣a2+3a,∴﹣a2+3a=2,解得:a=2,a=1(舍去),∴M(2,﹣1),②如图,若点M在x轴上方,四边形CENM为平行四边形,则CE=MN,设M(a,a﹣3),则N(a,a2﹣2a﹣3),∴MN=a2﹣2a﹣3﹣(a﹣3)=a2﹣3a,∴a2﹣3a=2,解得:a=,a=(舍去),∴M(,),综合可得M点的坐标为(2,﹣1)或().(3)如图,作PG∥y轴交直线AB于点G,设P(m,m2﹣2m﹣3),则G(m,m﹣3),∴PG=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,∴S△P AB =S△PGA+S△PGB===﹣,∴当m=时,△P AB面积的最大值是,此时P点坐标为().13.解:(1)函数l的表达式为:y=a(x+3)(x﹣1)=a(x2+2x﹣3),即﹣3a=﹣3,解得:a=1,故函数l的表达式为:y=x2+2x﹣3,b=2,点A、A1关于y轴对称,故点A1(3,0);(2)点B′是点B关于y轴的对称点,过点B′作B′E⊥A1C交于点E,B′E交y轴于点P,则此时,PB+PE最小,最小值为B′E,∵OA1=OC=3,故直线A1C的表达式为:y=x﹣3…①,B′E⊥A1C,则B′E的函数表达式为:y=﹣x+s,将点B′坐标代入上式并解得:直线B′E的表达式为:y=﹣x﹣1…②,联立①②并解得:x=1,故点E(1,﹣2),则PB+PE的最小值B′E=2;(3)将图象A、B、C区域放大为图2,连接OB′,则∠BCB′=2OCB=2α,在点B右侧作∠BCB″=α,交x轴于点B″,则∠B′CB″=3α,则tan∠OCB===tanα,B′C=BC=,设∠CB′B=β,则tanβ=3,则sinβ=当k=2时,即∠MA1O=2∠OCB=2α,故点B作BH⊥CB′,BH=B′B sinβ=2×=,tan∠HCB=tan2α==,当k=3时,同理tan∠MA1O=tan3α=;①当k=2时,tan∠MA1O=tan2α=,则直线A1M的表达式为:y=﹣x+b,将点A1(3,0)的坐标代入上式并解得:直线A1M的表达式为:y=﹣x+,将A1M表达式与l的表达式联立并解得:x=﹣(正值也舍去),故点D(﹣,),②k=3时,tan∠MA1O=tan3α=;则OM=OA1tan∠MA1O=×3=.14.解:(1)在Rt△AOB中,OA=1,tan∠BAO==3,∴OB=3OA=3∵△DOC是由△AOB绕点O逆时针旋转90°而得到的,∴△DOC≌△AOB,∴OC=OB=3,OD=OA=1.∴A,B,C的坐标分别为(1,0),(0,3),(﹣3,0),代入解析式为,解得,抛物线的解析式为y=﹣x2﹣2x+3;(2)∵抛物线的解析式为y=﹣x2﹣2x+3,∴对称轴为l=﹣=﹣1,∴E点坐标为(﹣1,0),如图,①当∠CEF=90°时,△CEF∽△COD,此时点P在对称轴上,即点P为抛物线的顶点,P(﹣1,4);②当∠CFE=90°时,△CFE∽△COD,过点P作PM⊥x轴于M点,△EFC∽△EMP,∴===∴MP=3ME,∵点P的横坐标为t,∴P(t,﹣t2﹣2t+3),∵P在第二象限,∴PM=﹣t2﹣2t+3,ME=﹣1﹣t,∴﹣t2﹣2t+3=3(﹣1﹣t),解得t1=﹣2,t2=3,(与P在二象限,横坐标小于0矛盾,舍去),当t=﹣2时,y=﹣(﹣2)2﹣2×(﹣2)+3=3∴P(﹣2,3),∴当△CEF与△COD相似时,P点的坐标为(﹣1,4)或(﹣2,3).15.解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0)∴y=﹣(x+1)(x﹣3)=﹣x2+2x+3∴抛物线解析式为y=﹣x2+2x+3(2)过点D作DM∥y轴,交BC于点M∵当x=0时,y=﹣x2+2x+3=3∴C(0,3)∴直线BC解析式为y=﹣x+3∵点D的横坐标为m(0<m<3)∴D(m,﹣m2+2m+3),M(m,﹣m+3)∴DM=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m∴s=OB•DM=(﹣m2+3m)=﹣m2+m=﹣(m﹣)2+∴s与m的函数关系式为s=﹣m2+m,s的最大值为.(3)存在点D,使得以C、D,F三点为顶点的三角形与△CEO相似如图2,连接BD∵点E为AB中点,A(﹣1,0),B(3,0),C(0,3)∴E(1,0),OE=1,OC=3,CD2=m2+(﹣m2+2m+3﹣3)2∴CE=∴sin∠OCE=,cos∠OCE=∵BC=,DF⊥BC∴s=BC•DF=﹣m2+m∴DF=∵以C、D,F三点为顶点的三角形与△CEO相似,∠CFD=∠COE=90°∴△CFD∽△COE或△CFD∽△EOC①若△CFD∽△COE,则∠FCD=∠OCE∴sin∠FCD=∴10DF2=CD2∴10()2=m2+(﹣m2+2m)2解得:m1=4(舍去),m2=∴﹣m2+2m+3=﹣+5+3=∴D(,)②若△CFD∽△EOC,则∠FDC=∠OCE∴cos∠FDC=∴10DF2=9CD2∴10()2=9[m2+(﹣m2+2m)2]解得:m1=0(舍去),m2=∴﹣m2+2m+3=﹣+3+3=∴D(,)∴点D的坐标为(,)或(,).16.解:(1)∵直线y=﹣x与抛物线y=﹣x2﹣x交于点A,∴﹣x=﹣x2﹣x,∴x1=0,x2=﹣1,∴点A(﹣1,1),令﹣x2﹣x=0,解得x1=﹣3,x2=0,∴B(﹣3,0),AB==,设点C的坐标为(0,c),∴AC==,解得c=3,∴C(0,3),设点D的坐标为(﹣3,n),∴AD==,解得n=2,∴D(﹣3,2).∴A(﹣1,1)、B(﹣3,0)、C(0,3)、D(﹣3,2).(2)过点C作OA的平行线,则解析式为y=﹣x+3,将y=﹣x+3向下平移6个单位后与抛物线的交点就是所求的点P,令﹣x﹣3=﹣x2﹣x,解得,,∴点P的坐标为(2,﹣5)或(﹣3,0).(3)①当BC为对角线时,点O即为点N,∴N1(0,0).②当BC为边时,过N作y轴的平行线交直线OA于点Q,∵OA⊥BC,BC∥MN,∴∠QMN=90°,又∵BC=OB=3,∴MN=3,∵∠MQN=45°,∴NQ=MN=6,设N(a,﹣a2﹣a),则点Q(a,﹣a),∴﹣a﹣(﹣a2﹣a)=6,解得a1=3,a2=﹣4,∴N2(3,﹣9),N3(﹣4,﹣2).综上所述,点N的坐标为(0,0)、(3,﹣9)、(﹣4,﹣2).。
2023年九年级数学中考专题:二次函数综合压轴题附答案附答案

2023年九年级数学中考专题:二次函数综合压轴题附答案1.如图,已知抛物线2y x bx c =++(b ,c 是常数)与x 轴交于()1,0A ,()3,0B -两点,顶点为C ,点P 为线段AB 上的动点(不与A 、B 重合),过P 作PQ BC ∥交抛物线于点Q ,交AC 于点D .(1)求该抛物线的表达式;(2)求CPD △面积的最大值;(3)连接CQ ,当CQ PQ ⊥时,求点Q 的坐标;(4)点P 在运动过程中,是否存在以A 、O 、D 为顶点的三角形是等腰三角形?若存在,求出所有点P 的坐标;若不存在,请说明理由2.在平面直角坐标系中,抛物线24y x x c =--+与x 轴交于点A ,B (点A 在点B 的左侧),与y 轴交于点C ,且点A 的坐标为()5,0-.(1)求点C 的坐标;(2)如图1,若点P 是第二象限内抛物线上一动点,求点P 到直线AC 距离的最大值,并求出此时点P 的坐标;(3)如图2,若点M 是抛物线上一点,点N 是抛物线对称轴上一点,是否存在点M 使以A ,C ,M ,N 为顶点的四边形是平行四边形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.3.已知:如图,抛物线()2430y mx mx m =++>交x 轴于E 、F 两点,交y 轴于A 点,直线AE :y x b =+交x 轴于E 点,交y 轴于A 点.(1)求抛物线的解析式;(2)若Q 为抛物线上一点,连接,QE QA ,设点Q 的横坐标为()3t t <-,QAE 的面积为S ,求S 与t 函数关系式;(不要求写出自变量t 的取值范围)(3)在(2)的条件下,点M 在线段QA 上,点N 是位于Q 、E 两点之间的抛物线上一点,15S =,QMN AEM ∠=∠,且MN EM =,求点N 的坐标.4.如图,抛物线22y ax ax c =++经过()()1003B C ,,,两点,与x 轴交于另一点A ,点D 是抛物线的顶点.(1)求抛物线的解析式及点D 的坐标;(2)如图1,连接AC ,点E 在直线AC 上方的抛物线上,连接EA EC ,,当EAC 面积最大时,求点E 坐标;(3)如图2,连接AC BC 、,在抛物线上是否存在点M ,使ACM BCO ∠=∠,若存在,求出M 点的坐标;若不存在,请说明理由.5.抛物线21164y ax x =+-与x 轴交于(,0),(8,0)A t B 两点,与y 轴交于点C ,直线6y kx =-经过点B .点P 在抛物线上,设点P 的横坐标为m .(1)求二次函数与一次函数的解析式;(2)如图1,连接AC ,AP ,PC ,若APC △是以CP 为斜边的直角三角形,求点P 的坐标;(3)如图2,若点P 在直线BC 上方的抛物线上,过点P 作PQ BC ⊥,垂足为Q ,求12CQ PQ +的最大值.6.在平面直角坐标系中,抛物线223y x x =-++与x 轴交于点A 、B (A 在B 左侧),与y 轴交于点C ,顶点为D ,对称轴为直线l ,点P 是抛物线上位于点B 、C 之间的动点.(1)求ABC ∠的度数;(2)若PBC ACO ∠=∠,求点P 的坐标;(3)已知点(),P p n ,若点(),Q q n 在抛物线上,且p q >;①仅用无刻度的直尺在图2中画出点Q ;②若2PQ t =,求232022p tq t +-+的值.7.如图,在平面直角坐标系中,抛物线2y x bx c =-++经过()0,1A ,()4,1B -.直线AB 交x 轴于点C ,P 是直线AB 上方且在对称轴右侧的一个动点,过P 作PD AB ⊥,垂足为D ,E 为点P 关于抛物线的对称轴的对应点.(1)求抛物线的函数表达式;(2)PE +的最大值时,求此时点P PE +的最大值;(3)将抛物线y 关于直线3x =作对称后得新抛物线y ',新抛物线与原抛物线相交于点F ,M 是新抛物线对称轴上一点,N 是平面中任意一点,是否存在点N ,使得以C ,F ,M ,N 为顶点的四边形是菱形,写出所有符合条件的点N 的坐标,并写出求解点N 的坐标的其中一种情况的过程.8.如图所示,在平面直角坐标系中,直线3y x =-+交坐标轴于B 、C 两点,抛物线23y ax bx =++经过B 、C 两点,且交x 轴于另一点()1,0A -.点D 为抛物线在第一象限内的一点,过点D 作DQ CO ∥,DQ 交BC 于点P ,交x 轴于点Q .(1)求抛物线的解析式;(2)设点P 的横坐标为m ,在点D 的移动过程中,存在DCP DPC ∠=∠,求出m 值;(3)在抛物线上取点E ,在平面直角坐标系内取点F ,问是否存在以C 、B 、E 、F 为顶点且以CB 为边的矩形?如果存在,请求出点F 的坐标;如果不存在,请说明理由.9.在平面直角坐标系中,抛物线2y ax bx c =++与x 轴交于点()1,0A -和点B ,与y 轴交于点C ,顶点D 的坐标为()1,4-.(1)求出抛物线的解析式;(2)如图1,若点P 在抛物线上且满足PCB CBD ∠=∠,求点P 的坐标;(3)如图2,M 是线段CB 上一个动点,过点M 作MN x ⊥轴交抛物线于点N ,Q 是直线AC 上一个动点,当QMN 为等腰直角三角形时,直接写出此时点M 的坐标.10.二次函数2y ax bx c =++交x 轴于点()10A -,和点()30B -,,交y 轴于点()03C -,.(1)求二次函数的解析式;(2)如图1,点E 为抛物线的顶点,点()0T t ,为y 轴负半轴上的一点,将抛物线绕点T 旋转180︒,得到新的抛物线,其中B ,E 旋转后的对应点分别记为B E '',,当四边形BEB E ''的面积为12时,求t 的值;(3)如图2,过点C 作CD x ∥轴,交抛物线于另一点D .点M 是直线CD 上的一个动点,过点M 作x 轴的垂线,交抛物线于点P .是否存在点M 使PBC 为直角三角形,若存在,请直接写出点M 的坐标,若不存在,请说明理由.11.如图,已知抛物线2y ax 2x c =++交x 轴于点()10A -,和点()30B ,,交y 轴于点C ,点D 与点C 关于抛物线的对称轴对称.(1)求该抛物线的表达式,并求出点D 的坐标;(2)若点E 为该抛物线上的点,点F 为直线AD 上的点,若EF x ∥轴,且1EF =(点E 在点F 左侧),求点E 的坐标;(3)若点P 是该抛物线对称轴上的一个动点,是否存在点P ,使得APD △为直角三角形?若不存在,请说明理由;若存在,直接写出点P 坐标.12.在平面直角坐标系中,O 为坐标原点,直线3y x =-+与x 轴、y 轴分别交于B 、C 两点,抛物线2y x bx c =-++经过B 、C 两点,与x 轴的另一个交点为A .(1)如图1,求b 、c 的值;(2)如图2,点P 是第一象限抛物线2y x bx c =-++上一点,直线AP 交y 轴于点D ,设点P 的横坐标为t ,ADC △的面积为S ,求S 与t 的函数关系式;(3)如图3,在(2)的条件下,E 是直线BC 上一点,45EPD ∠=︒,ADC △的面积S 为54,求E 点坐标.13.抛物线24y ax =-经过A 、B 两点,且OA OB =,直线EC 过点()41E -,,()03C -,,点D 是线段OA (不含端点)上的动点,过D 作PD x ⊥轴交抛物线于点P ,连接PC 、PE .(1)求抛物线与直线CE 的解析式;(2)求证:PC PD +为定值;(3)在第四象限内是否存在一点Q ,使得以C 、P 、E 、Q 为顶点的平行四边形面积最大,若存在,求出Q 点坐标;若不存在,请说明理由.14.如图,已知抛物线()230y ax bx a =++≠与x 轴交于()1,0A 、()4,0B 两点,与y 轴交于点C ,点D 为抛物线的顶点.(1)求抛物线的函数表达式及点D 的坐标;(2)若四边形BCEF 为矩形,3CE =.点M 以每秒1个单位的速度从点C 沿CE 向点E 运动,同时点N 以每秒2个单位的速度从点E 沿EF 向点F 运动,一点到达终点,另一点随之停止.当以M 、E 、N 为顶点的三角形与BOC 相似时,求运动时间t 的值;(3)抛物线的对称轴与x 轴交于点P ,点G 是点P 关于点D 的对称点,点Q 是x 轴下方抛物线上的动点.若过点Q 的直线l :94y kx m k ⎛⎫=+< ⎪⎝⎭与抛物线只有一个公共点,且分别与线段GA 、GB 相交于点H 、K ,求证:GH GK +为定值.15.在平面直角坐标系中,已知抛物线2y ax bx =+经过(40)(13)A B ,,,两点.P 是抛物线上一点,且在直线AB的上方.(1)求抛物线的表达式;(2)若OAB 面积是PAB 面积的2倍,求点P 的坐标;(3)如图,OP 交AB 于点C ,PD BO ∥交AB 于点D .记CPB △,BCO 的面积分别为12S S ,,判断12S S 是否存在最大值.若存在,求出最大值;若不存在,请说明理由.16.已知抛物线212y x bx c =-++(b 、c 是常数)的顶点B 坐标为()1,2-,抛物线的对称轴为直线l ,点A 为抛物线与x 轴的右交点,作直线AB .点P 是抛物线上的任意一点,其横坐标为m ,过点P 作x 轴的垂线交直线AB 于点Q ,过点P 作PN l ⊥于点N ,以PQ PN 、为边作矩形PQMN .(1)b =___________,c =___________.(2)当点Q 在线段AB 上(点Q 不与A 、B 重合)时,求PQ 的长度d 与m 的函数关系式,并直接写出d 的最大值.(3)当抛物线被矩形PQMN 截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2时,求点P 的坐标.(4)矩形PQMN 的任意两个顶点到直线AB 的距离相等时,直接写出m 的值.17.如图1.在平面直角坐标系中,抛物线2(0)y ax bx c a =++≠与x 轴交于点()2,0A -,点()4,0B ,与y 轴交于点()0,2C .(2)点P 是第一象限内的抛物线上一点.过点P 作PH x ⊥轴于点H ,交直线BC 于点Q ,求PQ 的最大值,并求出此时点P 的坐标;(3)如图2.将地物线沿射线BC()2111110y a x b x c a =++≠,新抛物线与原抛物线交于点G ,点M 是x 轴上一点,点N 是新抛物线上一点,若以点C 、G 、M 、N 为顶点的四边形是平行四边形时,请直接写出点N 的坐标.18.如图,抛物线()20y ax bx c a =++≠与x 轴交于A 、B 两点,与y 轴交于点()0,6C ,顶点为D ,且()1,8D .(1)求抛物线的解析式;(2)若在线段BC 上存在一点M ,过点O 作OH OM ⊥交BC 的延长线于H ,且MO HO =,求点M 的坐标;(3)点P 是y 轴上一动点,点Q 是在对称轴上一动点,是否存在点P ,Q ,使得以点P ,Q ,C ,D 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.参考答案:1.(1)223y x x =+-(2)2(3)11524Q ⎛⎫-- ⎪⎝⎭(4)1,05⎛⎫- ⎪ ⎪⎝⎭或()0,0或1,05⎛⎫ ⎪⎝⎭2.(1)()0,5(2)点P 到直线AC 距离为8,此时535,24P ⎛⎫- ⎪⎝⎭(3)点M 的坐标为()3,8-或()7,16--或()3,16-3.(1)243y x x =++(2)23922S t t =+(3)()2N -4.(1)223y x x =--+,()14D -,(2)E 的坐标为31524⎛⎫- ⎪⎝⎭,(3)存在,()45M --,或5724⎛⎫- ⎪⎝⎭,5.(1)2111644y x x =-+-;364y x =-(2)710,2P ⎛⎫- ⎪⎝⎭(3)169166.(1)45︒(2)(1,4)P(3)①见解析;②20237.(1)2712y x x =-++PE +的最大值为1,此时点P 的坐标为961,416⎛⎫ ⎪⎝⎭(3)存在点N ,使以C ,F ,M ,N 为顶点的四边形是菱形,此时点N 的坐标为215,424N ⎛+ ⎝⎭或215,424⎛- ⎝⎭或13,544N ⎛⎫+ ⎪ ⎪⎝⎭或13,544N ⎛- ⎝⎭或299,204N ⎛⎫ ⎪⎝⎭8.(1)223y x x =-++(2)2m =(3)存在,此时点F 的坐标为()4,1或()5,2--9.(1)2=23y x x --(2)满足PCB CBD ∠=∠,点P 的坐标为(4,5)或(2,2)-(3)M 点的坐标为(1,2)-或(2,5)--或924,55⎛⎫-- ⎪⎝⎭10.(1)243y x x =---(2)3t =-(3)存在,532⎛⎫-- ⎪ ⎪⎝⎭或532⎛⎫-- ⎪ ⎪⎝⎭或(23)--,或(53)--,11.(1)223y x x =-++,()23D ,(2)11024E ++⎝⎭,或1124E --+⎝⎭,(3)存在点P ,使得APD △为直角三角形,此时点P 的坐标为312⎛⎫+ ⎪⎝⎭,或312⎛ ⎝⎭,或()12-,或()14,12.(1)2b =,3c =(2)12S t =(3)3513,1616⎛⎫ ⎪⎝⎭13.(1)2144y x =-;132y x =-(2)见解析(3)存在,754Q ⎛⎫- ⎪⎝⎭,14.(1)2315344y x x =-+,527,216D ⎛⎫- ⎪⎝⎭(2)当911t =或65t =时(3)见解析15.(1)24y x x=-+(2)(24)P ,或(3,3)(3)见解析16.(1)1-,32(2)21122d m =-+()11m -<<,d 最大值为12(3)()3,0-或1--(4)3-或0或317.(1)211242y x x =-++;(2)5PQ +最大值为94,此时点5(3,4P ;(3)(1-,14-或(1-,1)4-或(1-+1)4或(1--1)4.18.(1)2246y x x =-++(2)129,55⎛⎫ ⎪⎝⎭(3)(1,8或(1,8或271,4⎛⎫ ⎪⎝⎭。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数常考题型与解析一.选择题(共12小题)1.若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为()A.x1=0,x2=6 B.x1=1,x2=7 C.x1=1,x2=﹣7 D.x1=﹣1,x2=72.点P1(﹣1,y1),P2(3,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是()A.y3>y2>y1B.y3>y1=y2C.y1>y2>y3D.y1=y2>y33.抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为()A.B.C.D.4.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:下列说法正确的是()A.抛物线的开口向下B.当x>﹣3时,y随x的增大而增大C.二次函数的最小值是﹣2D.抛物线的对称轴是x=﹣5.已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是()A.当a=1时,函数图象过点(﹣1,1)B.当a=﹣2时,函数图象与x轴没有交点C.若a>0,则当x≥1时,y随x的增大而减小D.若a<0,则当x≤1时,y随x的增大而增大6.如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0②4a+2b+c>0③4ac﹣b2<8a④<a<⑤b>c.其中含所有正确结论的选项是()A.①③B.①③④C.②④⑤D.①③④⑤7.抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是()A.4 B.6 C.8 D.108.已知二次函数y=ax2﹣bx﹣2(a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为()A.或1 B.或1 C.或D.或9.已知二次函数y=ax2+bx+c(a>0)的图象经过点A(﹣1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是()A.c<3 B.m≤C.n≤2 D.b<110.已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()A.只能是x=﹣1B.可能是y轴C.可能在y轴右侧且在直线x=2的左侧D.可能在y轴左侧且在直线x=﹣2的右侧11.如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中所示的方法从这些边角料上截取矩形(阴影部分)片备用,当截取的矩形面积最大时,矩形两边长x、y应分别为()A.x=10,y=14 B.x=14,y=10 C.x=12,y=15 D.x=15,y=1212.如图,反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点(﹣,m)(m>0),则有()A.a=b+2k B.a=b﹣2k C.k<b<0 D.a<k<0二.填空题(共9小题)13.已知点P(m,n)在抛物线y=ax2﹣x﹣a上,当m≥﹣1时,总有n≤1成立,则a的取值范围是.14.a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是b c(用“>”或“<”号填空)15.二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b﹣2c|,Q=|2a﹣b|﹣|3b+2c|,则P,Q的大小关系是.16.如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为.17.如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为.18.二次函数y=x2﹣2x﹣3的图象如图所示,若线段AB在x轴上,且AB为2个单位长度,以AB为边作等边△ABC,使点C落在该函数y轴右侧的图象上,则点C的坐标为.19.直线y=kx+b与抛物线y=x2交于A(x1,y1)、B(x2,y2)两点,当OA⊥OB 时,直线AB恒过一个定点,该定点坐标为.20.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C 的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为.21.抛物线y=﹣x2+4ax+b(a>0)与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.(1)a=时,求抛物线的解析式和BC的长;(2)如图a>1时,若AP⊥PC,求a的值.三.解答题(共12小题)22.已知二次函数y=x2+bx+c的图象与y轴交于点C(0,﹣6),与x轴的一个交点坐标是A(﹣2,0).(1)求二次函数的解析式,并写出顶点D的坐标;(2)将二次函数的图象沿x轴向左平移个单位长度,当y<0时,求x的取值范围.23.已知二次函数y=ax2﹣2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3(1)求A、B两点的坐标;(2)若tan∠PDB=,求这个二次函数的关系式.24.已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0,),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为.(1)求a的值;(2)当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;(3)当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF.25.如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.(1)当抛物线F经过点C时,求它的表达式;(2)设点P的纵坐标为y P,求y P的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.26.如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).(1)求a,b的值;(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.27.在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D,求△BCD的面积;(3)若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.28.如图,顶点为A(,1)的抛物线经过坐标原点O,与x轴交于点B.(1)求抛物线对应的二次函数的表达式;(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.29.如图1(注:与图2完全相同),二次函数y=x2+bx+c的图象与x轴交于A (3,0),B(﹣1,0)两点,与y轴交于点C.(1)求该二次函数的解析式;(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC 边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).30.已知抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.(1)写出点C的坐标并求出此抛物线的解析式;(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;(3)是否存在实数k使得△ABC的面积为?若存在,求出k的值;若不存在,请说明理由.31.在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点D在AB的延长线上.(1)已知a=1,点B的纵坐标为2.①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.②如图2,若BD=AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.(2)如图3,若BD=AB,过O,B,D三点的抛物线L3,顶点为P,对应函数的二次项系数为a3,过点P作PE∥x轴,交抛物线L于E,F两点,求的值,并直接写出的值.32.小明的爸爸和妈妈分别驾车从家同时出发去上班,爸爸行驶到甲处时,看到前面路口时红灯,他立即刹车减速并在乙处停车等待,爸爸驾车从家到乙处的过程中,速度v(m/s)与时间t(s)的关系如图1中的实线所示,行驶路程s(m)与时间t(s)的关系如图2所示,在加速过程中,s与t满足表达式s=at2(1)根据图中的信息,写出小明家到乙处的路程,并求a的值;(2)求图2中A点的纵坐标h,并说明它的实际意义;(3)爸爸在乙处等待7秒后绿灯亮起继续前行,为了节约能源,减少刹车,妈妈驾车从家出发的行驶过程中,速度v(m/s)与时间t(s)的关系如图1中的折线O﹣B﹣C所示,加速过程中行驶路程s(m)与时间t(s)的关系也满足s=at2,当她行驶到甲处时,前方的绿灯刚好亮起,求此时妈妈驾车的行驶速度.33.科技馆是少年儿童节假日游玩的乐园.如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y=,10:00之后来的游客较少可忽略不计.(1)请写出图中曲线对应的函数解析式;(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?20XX年03月20日初中数学3的初中数学组卷参考答案与试题解析一.选择题(共12小题)1.(2016•荆门)若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为()A.x1=0,x2=6 B.x1=1,x2=7 C.x1=1,x2=﹣7 D.x1=﹣1,x2=7【分析】先根据二次函数y=x2+mx的对称轴是x=3求出m的值,再把m的值代入方程x2+mx=7,求出x的值即可.【解答】解:∵二次函数y=x2+mx的对称轴是x=3,∴﹣=3,解得m=﹣6,∴关于x的方程x2+mx=7可化为x2﹣6x﹣7=0,即(x+1)(x﹣7)=0,解得x1=﹣1,x2=7.故选D.【点评】本题考查的是二次函数的性质,熟知二次函数的对称轴方程是解答此题的关键.2.(2016•兰州)点P1(﹣1,y1),P2(3,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是()A.y3>y2>y1B.y3>y1=y2C.y1>y2>y3D.y1=y2>y3【分析】根据函数解析式的特点,其对称轴为x=1,图象开口向下,在对称轴的右侧,y随x的增大而减小,据二次函数图象的对称性可知,P1(﹣1,y1)与(3,y1)关于对称轴对称,可判断y1=y2>y3.【解答】解:∵y=﹣x2+2x+c,∴对称轴为x=1,P2(3,y2),P3(5,y3)在对称轴的右侧,y随x的增大而减小,∵3<5,∴y2>y3,根据二次函数图象的对称性可知,P1(﹣1,y1)与(3,y1)关于对称轴对称,故y1=y2>y3,故选D.【点评】本题考查了函数图象上的点的坐标与函数解析式的关系,同时考查了函数的对称性及增减性.3.(2016•贺州)抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为()A.B.C.D.【分析】根据二次函数图象与系数的关系确定a>0,b<0,c<0,根据一次函数和反比例函数的性质确定答案.【解答】解:由抛物线可知,a>0,b<0,c<0,∴一次函数y=ax+b的图象经过第一、三、四象限,反比例函数y=的图象在第二、四象限,故选:B.【点评】本题考查的是二次函数、一次函数和反比例函数的图象与系数的关系,掌握二次函数、一次函数和反比例函数的性质是解题的关键.4.(2016•临沂)二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:下列说法正确的是()A.抛物线的开口向下B.当x>﹣3时,y随x的增大而增大C.二次函数的最小值是﹣2D.抛物线的对称轴是x=﹣【分析】选出3点的坐标,利用待定系数法求出函数的解析式,再根据二次函数的性质逐项分析四个选项即可得出结论.【解答】解:将点(﹣4,0)、(﹣1,0)、(0,4)代入到二次函数y=ax2+bx+c 中,得:,解得:,∴二次函数的解析式为y=x2+5x+4.A、a=1>0,抛物线开口向上,A不正确;B、﹣=﹣,当x≥﹣时,y随x的增大而增大,B不正确;C、y=x2+5x+4=﹣,二次函数的最小值是﹣,C不正确;D、﹣=﹣,抛物线的对称轴是x=﹣,D正确.故选D.【点评】本题考查了待定系数求函数解析式以及二次函数的性质,解题的关键是利用待定系数法求出函数解析式.本题属于基础题,难度不大,解决该题型题目时,结合点的坐标利用待定系数法求出函数解析式是关键.5.(2016•宁波)已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是()A.当a=1时,函数图象过点(﹣1,1)B.当a=﹣2时,函数图象与x轴没有交点C.若a>0,则当x≥1时,y随x的增大而减小D.若a<0,则当x≤1时,y随x的增大而增大【分析】把a=1,x=﹣1代入y=ax2﹣2ax﹣1,于是得到函数图象不经过点(﹣1,1),根据△=8>0,得到函数图象与x轴有两个交点,根据抛物线的对称轴为直线x=﹣=1判断二次函数的增减性.【解答】解:A、∵当a=1,x=﹣1时,y=1+2﹣1=2,∴函数图象不经过点(﹣1,1),故错误;B、当a=﹣2时,∵△=42﹣4×(﹣2)×(﹣1)=8>0,∴函数图象与x轴有两个交点,故错误;C、∵抛物线的对称轴为直线x=﹣=1,∴若a>0,则当x≥1时,y随x的增大而增大,故错误;D、∵抛物线的对称轴为直线x=﹣=1,∴若a<0,则当x≤1时,y随x的增大而增大,故正确;故选D.【点评】本题考查的是二次函数的性质,熟练掌握二次函数的性质是解题的关键.6.(2016•达州)如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A (﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0②4a+2b+c>0③4ac﹣b2<8a④<a<⑤b>c.其中含所有正确结论的选项是()A.①③B.①③④C.②④⑤D.①③④⑤【分析】根据对称轴为直线x=1及图象开口向下可判断出a、b、c的符号,从而判断①;根据对称轴得到函数图象经过(3,0),则得②的判断;根据图象经过(﹣1,0)可得到a、b、c之间的关系,从而对②⑤作判断;从图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间可以判断c的大小得出④的正误.【解答】解:①∵函数开口方向向上,∴a>0;∵对称轴在y轴右侧∴ab异号,∵抛物线与y轴交点在y轴负半轴,∴c<0,∴abc>0,故①正确;②∵图象与x轴交于点A(﹣1,0),对称轴为直线x=1,∴图象与x轴的另一个交点为(3,0),∴当x=2时,y<0,∴4a+2b+c<0,故②错误;③∵图象与x轴交于点A(﹣1,0),∴当x=﹣1时,y=(﹣1)2a+b×(﹣1)+c=0,∴a﹣b+c=0,即a=b﹣c,c=b﹣a,∵对称轴为直线x=1∴=1,即b=﹣2a,∴c=b﹣a=(﹣2a)﹣a=﹣3a,∴4ac﹣b2=4•a•(﹣3a)﹣(﹣2a)2=﹣16a2<0∵8a>0∴4ac﹣b2<8a故③正确④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间,∴﹣2<c<﹣1∴﹣2<﹣3a<﹣1,∴>a>;故④正确⑤∵a>0,∴b﹣c>0,即b>c;故⑤正确;故选:D.【点评】主要考查图象与二次函数系数之间的关系.解题关键是注意掌握数形结合思想的应用.7.(2016•绍兴)抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是()A.4 B.6 C.8 D.10【分析】根据抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,可以得到c的取值范围,从而可以解答本题.【解答】解:∵抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,∴解得6≤c≤14,故选A.【点评】本题考查二次函数的性质、解不等式,解题关键是明确题意,列出相应的关系式.8.(2016•泸州)已知二次函数y=ax2﹣bx﹣2(a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为()A.或1 B.或1 C.或D.或【分析】首先根据题意确定a、b的符号,然后进一步确定a的取值范围,根据a﹣b为整数确定a、b的值,从而确定答案.【解答】解:依题意知a>0,>0,a+b﹣2=0,故b>0,且b=2﹣a,a﹣b=a﹣(2﹣a)=2a﹣2,于是0<a<2,∴﹣2<2a﹣2<2,又a﹣b为整数,∴2a﹣2=﹣1,0,1,故a=,1,,b=,1,,∴ab=或1,故选A.【点评】本题考查了二次函数的性质,解题的关键是能够根据图象经过的点确定a+b+c的值和a、b的符号,难度中等.9.(2016•株洲)已知二次函数y=ax2+bx+c(a>0)的图象经过点A(﹣1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是()A.c<3 B.m≤C.n≤2 D.b<1【分析】根据已知条件得到,解方程组得到c=3﹣2a<3,b=1﹣a<1,求得二次函数的对称轴为x=﹣=﹣=﹣<,根据二次函数的顶点坐标即可得到结论.【解答】解:由已知可知:,消去b得:c=3﹣2a<3,消去c得:b=1﹣a<1,对称轴:m=x=﹣=﹣=﹣<,∵A(﹣1,2),a>0,那么顶点的纵坐标为函数的最小值,∴n≤2,故B错.【点评】本题考查了二次函数的性质,二次函数图象上点的坐标特征,熟记二次函数的性质是解题的关键.10.(2015•南昌)已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()A.只能是x=﹣1B.可能是y轴C.可能在y轴右侧且在直线x=2的左侧D.可能在y轴左侧且在直线x=﹣2的右侧【分析】根据题意判定点(﹣2,0)关于对称轴的对称点横坐标x2满足:﹣2<x2<2,从而得出﹣2<<0,即可判定抛物线对称轴的位置.【解答】解:∵抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,∴点(﹣2,0)关于对称轴的对称点横坐标x2满足:﹣2<x2<2,∴﹣2<<0,∴抛物线的对称轴可能在y轴左侧且在直线x=﹣2的右侧.故选:D.【点评】本题考查了二次函数的性质,根据点坐标判断出另一个点的位置是解题的关键.11.(2007•临沂)如图,某厂有许多形状为直角梯形的铁皮边角料,为节约资源,现要按图中所示的方法从这些边角料上截取矩形(阴影部分)片备用,当截取的矩形面积最大时,矩形两边长x、y应分别为()A.x=10,y=14 B.x=14,y=10 C.x=12,y=15 D.x=15,y=12【分析】由直角三角形相似得,得x=•(24﹣y),化简矩形面积S=xy 的解析式为S=﹣(y﹣12)2+180,再利用二次函数的性质求出S 的最大值,以及取得最大值时x、y的值.【解答】解:以直角梯形的下底直角边端点为原点,两直角边方向为x,y轴建立直角坐标系,过点D作DE⊥x轴于点E,∵NH∥DE,∴△CNH∽△CDE,∴=,∵CH=24﹣y,CE=24﹣8,DE=OA=20,NH=x,∴,得x=•(24﹣y),∴矩形面积S=xy=﹣(y﹣12)2+180,∴当y=12时,S有最大值,此时x=15.故选D.【点评】本题考查的是直角梯形以及矩形的性质的相关知识点.12.(2015•玉林)如图,反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点(﹣,m)(m>0),则有()A.a=b+2k B.a=b﹣2k C.k<b<0 D.a<k<0【分析】把(﹣,m)代入y=ax2+bx图象的顶点坐标公式得到顶点(﹣,﹣),再把(﹣,﹣)代入得到k=,由图象的特征即可得到结论.【解答】解:∵y=ax2+bx图象的顶点(﹣,m),∴﹣=﹣,即b=a,∴m==﹣,∴顶点(﹣,﹣),把x=﹣,y=﹣代入反比例解析式得:k=,由图象知:抛物线的开口向下,∴a<0,∴a<k<0,故选D.【点评】本题考查了二次函数的性质,反比例函数图象上点的坐标特征,熟练掌握反比例函数图象上点的坐标特征是解题的关键.二.填空题(共9小题)13.(2016•厦门)已知点P(m,n)在抛物线y=ax2﹣x﹣a上,当m≥﹣1时,总有n≤1成立,则a的取值范围是﹣≤a<0.【分析】依照题意画出图形,结合函数图形以及已知条件可得出关于a的一元一次不等式组,解不等式组即可得出a的取值范围.【解答】解:根据已知条件,画出函数图象,如图所示.由已知得:,解得:﹣≤a<0.故答案为:﹣≤a<0【点评】本题考查了二次函数图象上点的坐标特征以及二次函数的性质,解题的关键是画出函数图象,依照数形结合得出关于a的不等式组.本题属于基础题,难度不大,解决该题型题目时,根据二次函数的性质画出函数图象,利用数形结合解决问题是关键.14.(2016•镇江)a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是b<c(用“>”或“<”号填空)【分析】求出二次函数的对称轴,再根据二次函数的增减性判断即可.【解答】解:∵二次函数y=x2﹣2ax+3的图象的对称轴为x=a,二次项系数1>0,∴抛物线的开口向上,在对称轴的右边,y随x的增大而增大,∵a+1<a+2,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,∴b<c,故答案为:<.【点评】本题考查了二次函数图象上点的坐标特征,求出对称轴解析式,然后利用二次函数的增减性求解更简便.15.(2016•内江)二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b﹣2c|,Q=|2a﹣b|﹣|3b+2c|,则P,Q的大小关系是P>Q.【分析】由函数图象可以得出a<0,b>0,c>0,当x=1时,y=a+b+c>0,x=﹣1时,y=a﹣b+c<0,由对称轴得出2a+b=0,通过确定绝对值中的数的符号后去掉绝对值再化简就可以求出P、Q的值.【解答】解:∵抛物线的开口向下,∴a<0,∵﹣>0,∴b>0,∴2a﹣b<0,∵﹣=1,∴b+2a=0,x=﹣1时,y=a﹣b+c<0.∴﹣b﹣b+c<0,∴3b﹣2c>0,∵抛物线与y轴的正半轴相交,∴c>0,∴3b+2c>0,∴p=3b﹣2c,Q=b﹣2a﹣3b﹣2c=﹣2a﹣2b﹣2c,∴Q﹣P=﹣2a﹣2b﹣2c﹣3b+2c=﹣2a﹣5b=﹣4b<0∴P>Q,故答案为:P>Q.【点评】本题考查了二次函数的图象与系数的关系,去绝对值,二次函数的性质.熟记二次函数的性质是解题的关键.16.(2016•梅州)如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+,2)或(1﹣,2).【分析】当△PCD是以CD为底的等腰三角形时,则P点在线段CD的垂直平分线上,由C、D坐标可求得线段CD中点的坐标,从而可知P点的纵坐标,代入抛物线解析式可求得P点坐标.【解答】解:∵△PCD是以CD为底的等腰三角形,∴点P在线段CD的垂直平分线上,如图,过P作PE⊥y轴于点E,则E为线段CD的中点,∵抛物线y=﹣x2+2x+3与y轴交于点C,∴C(0,3),且D(0,1),∴E点坐标为(0,2),∴P点纵坐标为2,在y=﹣x2+2x+3中,令y=2,可得﹣x2+2x+3=2,解得x=1±,∴P点坐标为(1+,2)或(1﹣,2),故答案为:(1+,2)或(1﹣,2).【点评】本题主要考查等腰三角形的性质,利用等腰三角形的性质求得P点纵坐标是解题的关键.17.(2014•宁德)如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为6.【分析】设P(x,y)(2>x>0,y>0),根据矩形的周长公式得到C=﹣2(x﹣1)2+6.根据二次函数的性质来求最值即可.【解答】解:∵y=﹣x2+x+2,∴当y=0时,﹣x2+x+2=0即﹣(x﹣2)(x+1)=0,解得x=2或x=﹣1故设P(x,y)(2>x>0,y>0),∴C=2(x+y)=2(x﹣x2+x+2)=﹣2(x﹣1)2+6.=6,.∴当x=1时,C最大值即:四边形OAPB周长的最大值为6.故答案是:6.【点评】本题考查了二次函数的最值,二次函数图象上点的坐标特征.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.本题采用了配方法.18.(2016•泰州)二次函数y=x2﹣2x﹣3的图象如图所示,若线段AB在x轴上,且AB为2个单位长度,以AB为边作等边△ABC,使点C落在该函数y轴右侧的图象上,则点C的坐标为(1+,3)或(2,﹣3).【分析】△ABC是等边三角形,且边长为2,所以该等边三角形的高为3,又点C在二次函数上,所以令y=±3代入解析式中,分别求出x的值.由因为使点C落在该函数y轴右侧的图象上,所以x>0.【解答】解:∵△ABC是等边三角形,且AB=2,∴AB边上的高为3,又∵点C在二次函数图象上,∴C的纵坐标为±3,令y=±3代入y=x2﹣2x﹣3,∴x=1或0或2∵使点C落在该函数y轴右侧的图象上,∴x>0,∴x=1+或x=2∴C(1+,3)或(2,﹣3)故答案为:(1+,3)或(2,﹣3)【点评】本题考查二次函数的图象性质,涉及等边三角形的性质,分类讨论的思想等知识,题目比较综合,解决问题的关键是根据题意得出C的纵坐标为±3.19.(2016•大庆)直线y=kx+b与抛物线y=x2交于A(x1,y1)、B(x2,y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为(0,4).【分析】根据直线y=kx+b与抛物线y=x2交于A(x1,y1)、B(x2,y2)两点,可以联立在一起,得到关于x的一元二次方程,从而可以得到两根之和与两根之积,再根据OA⊥OB,可以求得b的值,从而可以得到直线AB恒过的定点的坐标.【解答】解:∵直线y=kx+b与抛物线y=x2交于A(x1,y1)、B(x2,y2)两点,∴kx+b=,化简,得x2﹣4kx﹣4b=0,∴x1+x2=4k,x1x2=﹣4b,又∵OA⊥OB,∴=,解得,b=4,即直线y=kx+4,故直线恒过顶点(0,4),故答案为:(0,4).【点评】本题考查二次函数的性质、一次函数的性质,解题的关键是明确题意,找出所求问题需要的条件,知道两条直线垂直时,它们解析式中的k的乘积为﹣1.20.(2016•长春)如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为15.【分析】设D(x,﹣x2+6x),根据勾股定理求得OC,根据菱形的性质得出BC,=×5×(﹣x2+6x﹣3)=﹣(x﹣3)2+15,然后根据三角形面积公式得出∴S△BCD根据二次函数的性质即可求得最大值.【解答】解:∵D是抛物线y=﹣x2+6x上一点,∴设D(x,﹣x2+6x),∵顶点C的坐标为(4,3),∴OC==5,∵四边形OABC是菱形,∴BC=OC=5,BC∥x轴,∴S=×5×(﹣x2+6x﹣3)=﹣(x﹣3)2+15,△BCD∵﹣<0,∴S有最大值,最大值为15,△BCD故答案为15.【点评】本题考查了菱形的性质,二次函数的性质,注意数与形的结合是解决本题的关键.21.(2016•自贡)抛物线y=﹣x2+4ax+b(a>0)与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.(1)a=时,求抛物线的解析式和BC的长;(2)如图a>1时,若AP⊥PC,求a的值.【分析】(1)根据抛物线经过原点b=0,把a=、b=0代入抛物线解析式,即可求出抛物线解析式,再求出B、C坐标,即可求出BC长.(2)利用△PCB∽△APM,得=,列出方程即可解决问题.【解答】解:(1)∵抛物线y=﹣x2+4ax+b(a>0)经过原点O,∴b=0,∵a=,∴抛物线解析式为y=﹣x2+6x,∵x=2时,y=8,∴点B坐标(2,8),∵对称轴x=3,B、C关于对称轴对称,∴点C坐标(4,8),∴BC=2.(2)∵AP⊥PC,∴∠APC=90°,∵∠CPB+∠APM=90°,∠APM+∠PAM=90°,∴∠CPB=∠PAM,∵∠PBC=∠PMA=90°,∴△PCB∽△APM,∴=,∴=,整理得a2﹣4a+2=0,解得a=2±,∵a>1,∴a=2+.【点评】本题考查二次函数性质、相似三角形的判定和性质、待定系数法等知识,解题的关键是利用相似三角形性质列出方程解决问题,学会转化的思想,属于中考常考题型.三.解答题(共12小题)22.(2016•黔南州)已知二次函数y=x2+bx+c的图象与y轴交于点C(0,﹣6),与x轴的一个交点坐标是A(﹣2,0).(1)求二次函数的解析式,并写出顶点D的坐标;(2)将二次函数的图象沿x轴向左平移个单位长度,当y<0时,求x的取值范围.【分析】(1)将点A和点C的坐标代入抛物线的解析式可求得b、c的值,从而得到抛物线的解析式,然后依据配方法可求得抛物线的顶点坐标;(2)依据抛物线的解析式与平移的规划规律,写出平移后抛物线的解析式,然后求得抛物线与x轴的交点坐标,最后依据y<0可求得x的取值范围.【解答】解:(1)∵把C(0,﹣6)代入抛物线的解析式得:C=﹣6,把A(﹣2,0)代入y=x2+bx﹣6得:b=﹣1,∴抛物线的解析式为y=x2﹣x﹣6.∴y=(x﹣)2﹣.∴抛物线的顶点坐标D(,﹣).(2)二次函数的图形沿x轴向左平移个单位长度得:y=(x+2)2﹣.令y=0得:(x+2)2﹣=0,解得:x1=,x2=﹣.∵a>0,∴当y<0时,x的取值范围是﹣<x<.【点评】本题主要考查的是抛物线与x轴的交点、待定系数法求二次函数的解析式,掌握相关知识是解题的关键.23.(2016•无锡)已知二次函数y=ax2﹣2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B 且垂直于x轴的直线交于点D,且CP:PD=2:3(1)求A、B两点的坐标;(2)若tan∠PDB=,求这个二次函数的关系式.【分析】(1)由二次函数的解析式可求出对称轴为x=1,过点P作PE⊥x轴于点E,所以OE:EB=CP:PD;(2)过点C作CF⊥BD于点F,交PE于点G,构造直角三角形CDF,利用tan∠PDB=即可求出FD,由于△CPG∽△CDF,所以可求出PG的长度,进而求出a 的值,最后将A(或B)的坐标代入解析式即可求出c的值.【解答】解:(1)过点P作PE⊥x轴于点E,∵y=ax2﹣2ax+c,∴该二次函数的对称轴为:x=1,∴OE=1∵OC∥BD,∴CP:PD=OE:EB,∴OE:EB=2:3,∴EB=,∴OB=OE+EB=,∴B(,0)∵A与B关于直线x=1对称,∴A(﹣,0);(2)过点C作CF⊥BD于点F,交PE于点G,令x=1代入y=ax2﹣2ax+c,∴y=c﹣a,令x=0代入y=ax2﹣2ax+c,∴y=c∴PG=a,∵CF=OB=,∴tan∠PDB=,∴FD=2,∵PG∥BD∴△CPG∽△CDF,∴==∴PG=,∴a=,∴y=x2﹣x+c,把A(﹣,0)代入y=x2﹣x+c,∴解得:c=﹣1,∴该二次函数解析式为:y=x2﹣x﹣1.【点评】本题考查二次函数,涉及待定系数法求出二次函数解析式,相似三角形的性质与判定,锐角三角函数等知识内容,解题的关键是利用作垂线构造直角三角形,再利用相似三角形的对应边的比相等即可得出答案.24.(2016•淄博)已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0,),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q 的纵坐标为.(1)求a的值;(2)当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;(3)当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF.【分析】(1)设Q(m,),F(0,),根据QO=QF列出方程即可解决问题.(2)设M(t,t2),Q(m,),根据K OM=K OQ,求出t、m的关系,根据QO=QM 列出方程即可解决问题.(3)设M(n,n2)(n>0),则N(n,0),F(0,),利用勾股定理求出MF 即可解决问题.【解答】解:(1)∵圆心Q的纵坐标为,∴设Q(m,),F(0,),∵QO=QF,∴m2+()2=m2+(﹣)2,∴a=1,∴抛物线为y=x2.(2)∵M在抛物线上,设M(t,t2),Q(m,),。
