几种时频分析方法及其工程应用
信号的时频域检测方法及在频谱监测中的应用

信号的时频域检测方法及在频谱监测中的应用引言:一、时频分析方法STFT将信号分成多个时间窗口,对每个窗口进行傅里叶变换,以得到每个时刻的频谱信息。
STFT是一种常用的时频域分析方法,可用于信号的时频特征提取和信号的时频分布分析。
2. 小波变换(Wavelet Transform)小波变换是一种多分辨率分析方法,它可以将信号分解成不同频率的小波系数,从而得到信号在不同频带上的时频特征。
小波变换可以提取信号的瞬时频率和瞬时振幅,并可用于信号降噪、特征提取和边缘检测等应用。
3. Wigner-Ville分布(Wigner-Ville Distribution,WVD)WVD是一种高分辨率的时频分析方法,它可以提供信号的瞬时频率、瞬时幅度和瞬时相位等信息。
WVD通过在时频平面上绘制信号的二维时频图像来描述信号的时频特性,对于非线性和非平稳信号具有较好的分析效果。
1.无线通信系统中的频谱监测在无线通信系统中,频谱监测是保障无线通信质量和避免频谱干扰的重要手段。
时频域检测方法可以用于对通信信号进行监测,从而提供通信信号的时频特征和频谱分布情况。
通过对频谱进行实时监测和分析,可以及时发现频谱异常和干扰信号,并采取相应的措施来保障通信质量。
2.频谱资源管理频谱资源是有限的,如何合理分配和管理频谱资源是频谱监测的另一个重要应用。
时频域检测方法可以用于对频谱资源的现状进行评估和分析,包括频率利用率、频谱效益、频谱利用方式等。
通过对频谱资源进行分析,可以优化频谱分配方案,提高频谱利用效率。
3.频谱监测中的信号识别和分类时频域检测方法对于信号的识别和分类具有重要意义。
不同类型的信号在时频域上具有不同的特征,如调制方式、调制参数、调制深度等。
时频域检测方法可以提取信号的特征,从而实现信号的自动识别和分类。
通过信号的识别和分类,可以对频谱进行合理管理和优化利用。
结论:时频域检测方法是信号处理领域中的重要技术之一,能够提取信号的时频特征,并在频谱监测中得到广泛应用。
时频分析方法

傅里叶变换分析信号的缺点基于傅里叶(Fourier)变换的信号频域表示,揭示了时间函数和频港函数之间的内在联系,在传统的平稀信号分析和处理中发挥了极其重要的作用,很多理论研究和应用研究都把傅里叶变换当作最基本的经典「具来使用.但是傅里叶变换存在着严重的缺点:1.傅里叶变换缺乏时间和频率的定位功能傅里叶变换及其逆变换表示如下:S ㈣=f[s(t)]=匚S(t)e*dt (1)r-Kos(t) = — [ S(c)e*d/ (2)In A由以上两式可知,傅里叶变换是一种整体变换,对信号的表征要么完全在时域内,要么完全在频域内,u)和t是互相排斥的两个变量.用傅里叶变换的方法得到某-个频率/的频谱分吊S (国J),必须从-8〜+8的整个时间轴上进行积分.如果要从频谱得到信号在某一时刻t0的ffis(t0),则需要对S(co)在整个频率轴上进行积分.因此,傅里叶变换得到的是信号s(t) 在整个时间范围内的频率特性,它不能告诉人们在某段时间里信号发生了什么变化,也无法获得某一频率出现的时刻信息,因此,它不具有时间和频率的定位功能2.傅里叶变换对于非平稳信号的局限性信号的瞬时频率,表示了信号的谱峰在时间-频率平而上的位置及其随时间的变化情况,一般平稳信号的瞬时频率为常数,而非平稳信号的瞬时频率是时间t的函数.从傅里叶变换变换的表达式可以看出,S(U) )是单变量3的函数,信号的傅里叶变换不随时间的变化而变化, 因此,傅里叶变换仅仅适用于平稳信号.但是,在实际工作中,我们分析和处理的往往是时变的或非平稳的信号,它们的频率随时间变化而变化,其相关函数、功率谱等也是时变信号,用傅里叶变换进行分析,得到的信号频谱反映的是整体信号中包含的某一频率分最的平均值. 所以傅里叶变换不能反映信号瞬时频率随时间的变化情况,仅仅诂用于分析平稳信号.对频率随时间变化的非平稳信号,傅里叶变换只能给出其总体效果,不能完整地把握信号在某一时刻的本质特征3.傅里叶变换在时间和频率分辨率上的局限性分辨率是信号处理的基本概念之一,包括频率分辨率和时间分辨率.在时域分析中,信号处理的目标是尽"能地同时获得高的时间分辨率和频率分辨率.然而,订以证明时域窗和频域窗乘积恒定且大于等于12,也即不可能同时获得高的时频分辨率,这就是著名的不确定性原理.傅里叶变换在这方面的表现尤其不尽如人意.傅里叶变换可以改写成内积的形式,即= (3)由于傅里叶变换等效于s(t)和基函数做内积,而彳顼对不同的3构成一族正交基,因此S(co)精确地反映了s(t)在该频率点的分量大小.基函数彳侦在频域是位于co处的。
现代信号处理第八章基于EMD的时频分析方法及其应用

目前EMD方法主要应用于一元信号处理领域,未来研究将拓展其在多元信号处理中的应用,如多 通道信号分析、多维数据融合等。
EMD在复杂系统故障诊断中的应用
复杂系统的故障诊断是信号处理领域的重要研究方向之一,未来研究将探索将EMD方法应用于复 杂系统的故障诊断中,以提高诊断的准确性和可靠性。
01 基于EMD的时频分析方 法概述
EMD方法简介
EMD(Empirical Mode Decomposition)即经验模态分解,是 一种自适应的信号处理方法。
EMD方法能够将复杂信号分解为一系列固有 模态函数(Intrinsic Mode Functions, IMFs),这些IMFs表征了信号在不同时间 尺度上的局部特征。
THANKS FOR WATCHING
感谢您的观看
图像去噪与增强技术
EMD去噪原理
基于经验模态分解(EMD) 的去噪方法通过分解图像信号 为多个固有模态函数(IMF),
有效去除噪声成分。
自适应阈值处理
结合EMD与自适应阈值技术, 实现图像噪声的智能抑制,提
高图像质量。
对比度增强
利用EMD方法对图像进行分 层处理,调整各层对比度,实
现图像整体对比度的增强。
边界效应问题
EMD方法在分解过程中,对信号两端的数据处理存在不确 定性,容易产生边界效应,影响分解结果的精度和可靠性。
发展趋势预测
自适应噪声抑制技术
针对噪声干扰问题,未来研究将更加注重自适应噪声抑制 技术的发展,以提高EMD方法在噪声环境下的性能。
改进EMD算法
为解决模态混叠问题,研究者将致力于改进EMD算法,如引入 掩膜信号、优化筛选过程等,以提高分解的准确性和稳定性。
测试技术3x新时频分析
1
2020/11/26
2
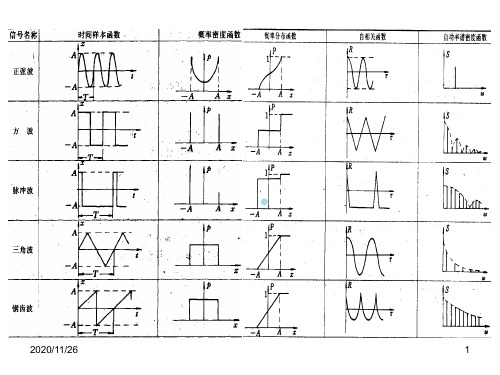
四、信号的时频分析
时频分析的基本任务是建立一个函数,要 求这个函数不仅能够同时用时间和频率描述信 号的能量分布密度,还能够以同样的方式来计 算信号的其他特征量。这里只是简单介绍当前 广泛采用的时频分析方法:短时傅里叶变换 (STFT)、小波变换(WT)及时频分析的一些 应用。
22
STFT方法的精度分析 由以上分析可 知,窗函数宽度的选择将会直接影响时域 或频域的精度。为改进时域精度可以选择 一个较短的窗,但是短窗将会导致傅氏变 换计算时采样点数目的减少,因此,频域 中离散频率数也将减少,从而引起频域精 度的降低。
2020/11/26
23
可以证明时域精度的提高将以损失频 域精度为代价,而提高频域精度将以损失 时域精度为代价,二者不可兼得。对STFT 来说.重要的是窗函数一经选定,则时频 精度在整个时频表面都是固定的,因为同 一个窗函数将被用于信号中所有频率。所 以STFT的窗函数对时频分析是刚性的。
得信号谱估计可以在很短的时间内完成,从而实现
对观测信号的实时分析。频谱估计现已成为信号分
析与处理领域中十分重要的特征分析工具。傅里叶
变换的不足之处在于它只适用于稳态信号分析,而
非稳态信号在工程领域中是广泛存在的,另外,非
稳态信号很可能在一个短时瞬间发生变化.即具有
很强的时间局部性,并对整个频谱产生影响,很难
这个声音的频谱告诉我们频率范围大约从
175Hz到325Hz。这个信息是有意义而且重要的,
但是根据这个频谱告诉无法知道这些频率什么时
候存在。例如,不可能通过观察频谱确切知道
300Hz声音在什么时候产生,或者产生这个声音
的总持续时间,或产生了多少次。主图反映了信
参数化时频分析理论方法及应用_2016_西北工大

短时傅立叶变换
定义: ST FTx ( , ) x(t ) g (t )e jt dt
0.35 0.3 0.25 0.2 0.15 0.1 0.05 0 -5 0 t/sec 5
a=1
窗函数
本质:加窗傅立叶变换 适用对象:分段平稳信号
3 2 1 0 -1 -2 -3 0 1 2 t/sec 3 4
ψ2
参数化时频分析-方法
多频率分量信号分析-时频融合法
高通 滤波
0.1111 0.1111 0.1111 H 0.1111 0.8889 0.1111 0.1111 0.1111 0.1111
示例-SCT
STFT SCT CWT
WVD
PCT
参数化时频分析-方法
广义Warblet变换 (GWT)
旋转算子
R (t ) e
t j ( ) d 0
(t ) (i )e
i 1
N
几种时频分析方法及其工程应用

几种时频分析方法及其工程应用时频分析是一种将时间和频率维度综合起来分析信号的方法,广泛应用于信号处理、通信、音频处理、图像处理等领域。
在实际工程应用中,根据不同的需求和应用场景,可以采用多种不同的时频分析方法。
本文将介绍几种常见的时频分析方法及其工程应用。
短时傅里叶变换是一种将信号分为多个小片段,并对每个小片段进行傅里叶变换的方法。
它在时域上采用滑动窗口的方式将信号分段,然后进行傅里叶变换得到频域信息。
STFT方法具有时间和频率分辨率可调的特点,可用于信号的频域分析、谱估计、声音的频谱显示等。
工程应用:STFT广泛应用于语音处理、音频编解码、信号分析等领域。
例如在音频编解码中,可以利用STFT分析音频信号的频谱特征,进行数据压缩和编码。
2. 小波变换(Wavelet Transform)小波变换是一种时频分析方法,它通过将信号与一系列基函数(小波)进行卷积来分析信号的时间和频率特性。
小波变换具有多分辨率分析的特点,可以在不同尺度上对信号进行分析。
工程应用:小波变换可以用于信号处理、图像压缩等领域。
在图像处理中,小波变换被广泛应用于图像的边缘检测、图像去噪等处理过程中。
3. Wigner-Ville分布(Wigner-Ville Distribution,WVD)Wigner-Ville分布是一种在时间-频率平面上分析信号的方法,它通过在信号的时域和频域上进行傅里叶变换得到瞬时频率谱。
WVD方法可以展现信号在时间和频率上的瞬时变化特性。
工程应用:Wigner-Ville分布在通信领域中被广泛应用于信号的调制识别、通信信号的自适应滤波等方面。
例如在调制识别中,可以利用WVD方法对调制信号的频谱特征进行分析,从而判断信号的调制类型。
4. Cohen类分析(Cohen's class of distributions)Cohen类分析是一种将信号在时间-频率域上进行分析的方法,它结合了瞬时频率和瞬时能量的信息。
信号处理中的时频分析方法研究

信号处理中的时频分析方法研究一、引言在信号处理领域,时频分析是一种重要的分析方法,它可以展示信号在时间和频率两个维度上的变化规律。
时频分析方法可以被广泛应用于许多领域,例如通信、医学、音乐和地震学等领域。
本文将介绍一些常见的时频分析方法,并探讨它们的应用与优缺点。
二、短时傅里叶变换(STFT)短时傅里叶变换是时频分析中最常见的一种方法。
它可以通过将信号分解成不同时间窗口内的频率成分来获得时域和频域分布。
在STFT中,信号被乘以一个窗口函数,然后在每个时间点上窗口的长度和形状都保持不变。
然后,使用快速傅里叶变换在每个时间窗口内计算频域分量。
由于不同的时间窗口可以为其提供不同的频率分辨率,因此可以选择窗口长度以平衡时间和频率分辨率之间的折衷。
STFT的优点是可以清晰地看到信号随时间和频率的变化。
它在信号处理和地震学分析方面得到了广泛的应用。
但它也有一些局限性,例如窗口函数的选择对分析结果有很大的影响,一般情况下只能得到离散的时频信息,无法获得连续的时频特性。
三、连续小波分析(CWT)连续小波分析是一种时变滤波器的应用,是一种常用的时频分析方法。
它采用一组母小波(通常称为分析小波),在不同的时刻对输入信号进行滤波。
这些分析小波可以缩放和平移,以便提供不同的频率和时间精度,并且可以在尺度和时间轴上提供常规分析不能提供的信息。
相较于STFT,CWT可以获得更连续的时频信息,而且由于可以根据需要改变小波的尺度和位置,因此比STFT更加灵活。
然而,CWT计算时需要进行大量的计算,处理大量的数据将导致算法效率较低。
四、峭度尺度分析(KSA)峭度尺度分析是一种基于二阶统计的非参数时频分析方法。
它利用峭度作为指标来计算信号在不同尺度下的频率分解表达。
KSA通过计算每个尺度下信号的二阶矩来确定信号的局部频率,因此不需要进行时域和频域的分析。
此外,KSA可以提供高频率分辨率和极低频的有效处理,因此可以获得有关信号的更广泛的信息。
数字信号处理中的时频分析算法

数字信号处理中的时频分析算法时频分析是数字信号处理领域中一种重要的信号分析方法,它能够同时提供信号在时间和频率上的特性信息。
在许多应用中,时频分析被广泛应用于信号识别、通信系统、雷达和生物医学工程等领域。
本文将介绍几种常见的数字信号处理中的时频分析算法。
1. 短时傅里叶变换(STFT)短时傅里叶变换是时频分析中最基本的方法之一。
它将信号分成一段段的小片段,并对每个小片段进行傅里叶变换,从而得到该时间段内信号的频谱。
由于信号随时间的变化,STFT能够提供信号在各个时刻的频谱特性。
然而,由于STFT使用固定的时间窗口宽度,无法在时间和频率上同时获得高分辨率。
2. 连续小波变换(CWT)连续小波变换是时频分析中一种基于小波理论的算法。
它与STFT类似,也将信号分成一段段的小片段,但不同之处在于小波变换使用了不同尺度的小波基函数进行变换。
这使得连续小波变换可以在时间和频率上自适应地调整分辨率,并能够对信号的瞬时频率进行较好的估计。
3. 峭度分析方法峭度分析方法通过计算信号的高阶统计moments,如峭度和偏度等,来提取信号的时频特征。
峭度反映了信号在短时间尺度上的频率成分,能够用于检测信号中的瞬时频率变化。
然而,峭度分析方法在实际应用中对信号的平稳性和高斯性有一定的要求。
4. Wigner-Ville变换(WVT)Wigner-Ville变换是一种经典的时频分析方法,它通过计算信号的时域和频域的自相关函数之间的关系,得到信号的时频表示。
WVT能够提供更精确的时频信息,但也存在交叉项干扰和分辨率衰减的问题。
为了克服这些问题,后续的研究提出了改进的时频分析方法,如Cohen's class分布和Cohen's class分布等。
5. 累积频谱分析方法累积频谱分析方法通过将多个STFT结果累积,从而提高分辨率和信噪比。
累积频谱分析方法包括短时傅里叶变换累积、小波包累积、Wigner-Ville累积等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程测试技术文献综述教师:***班级:10级城轨1班姓名:***学号:********西南交通大学峨眉校区2013年4月16日几种时频分析方法及其工程应用罗昌华(西南交通大学峨眉校区,城轨车辆一班)摘要:时频分析时频分析(JTFA)即时频联合域分析(Joint Time-Frequency Analysis)的简称,作为分析时变非平稳信号的有力工具,成为现代信号处理研究的一个热点,它作为一种新兴的信号处理方法,近年来受到越来越多的重视。
时频分析方法提供了时间域与频率域的联合分布信息,清楚地描述了信号频率随时间变化的关系。
时频分析的基本思想是:设计时间和频率的联合函数,用它同时描述信号在不同时间和频率的能量密度或强度。
时间和频率的这种联合函数简称为时频分布。
利用时频分布来分析信号,能在每一时间指示出信号在瞬时频率串附近的能量聚集情况,并且能够进行时频滤波和时变信号综合。
关键词:时频;短时傅里叶变换;小波变换;希尔伯特——黄变换;信号盲源一.短时傅里叶变换短时距傅里叶变换是傅里叶变换的一种变形,为时频分析中其中一个重要的工具。
其与傅里叶变换的区别是:傅里叶转换只提供了有哪些频率成份的信息,却没有提供时间信息;而短时傅里叶转换则清楚的提供这两种信息。
这种时频分析的方法有利于频率会随着时间改变的信号分析。
在连续时间的例子中,一个函数可以先乘上仅在一段时间不为零的窗函数再进行一维的傅里叶变换。
再将这个窗函数沿着时间轴挪移,所得到一系列的傅里叶变换结果排开则成为二维表象。
所以短时傅里叶变换具有:比起傅里叶转换更能观察出信号瞬时频率的信息的优点。
但其计算复杂度高。
应用:应用单边指数窗的短时傅里叶变换建立了对数化的OTDR数据的事件分析算法。
通过对不同的光纤链路进行事件检测处理,准确的定位了光纤链路事件的位置。
相对于传统的具有较强噪声容纳能力,能够对受噪声污染较严重的信号进行事件分析,提高了ODTR算法的效率,具有较高的实用价值。
短时傅里叶变换作为一种新颖的时频分析工具已经得到了研究人员越来越多的关注,因此在国内推广到地震监测、电力系统、防盗系统以及很多故障检测系统等。
二.小波变换缩放滤波器小波完全通过缩放滤波器g ——一个低通有限脉冲响应(FIR)长度为2N和为1的滤波器——来定义。
在双正交小波的情况,分解和重建的滤波器分别定义。
高通滤波器的分析作为低通的QMF来计算,而重建滤波器为分解的时间反转。
例如Daubechies 和Symlet小波。
缩放函数小波由时域中的小波函数ψ(t)和缩放函数Ф(t)来定义。
小波函数实际上是带通滤波器,每一级缩放将带宽减半。
这产生了一个问题,如果要覆盖整个谱需要无穷多的级。
缩放函数滤掉变换的最低级并保证整个谱被覆盖到。
对于有紧支撑的小波,Ф(t)可以视为有限长,并等价于缩放滤波器g。
例如Meyer小波。
小波函数小波只有时域表示,作为小波函数ψ(t)。
小波的应用通常来讲,DWT用于信号编码而CWT 用于信号分析。
所以,DWT通常用于工程和计算机科学而CWT经常用于科学研究。
小波变换现在被大量不同的应用领域采纳,经常取代了傅里叶变换的位置。
很多物理学的领域经历了这个範式的转变,包括分子动力学,从头计算(ab initio calculations),天文物理学,密度矩阵局部化,地震地质物理学,光学,湍流,和量子力学。
其他经历了这种变化的学科有图像处理,血压,心率和心电图分析,DNA分析,蛋白质分析,气象学,通用信号处理,语言识别,计算机图形学,和多分形分析。
小波的一个用途是数据压缩。
和其他变换一样,小波变换可以用于原始数据(例如图像),然后将变换后的数据编码,得到有效的压缩。
JPEG 2000 是采用小波的图像标准。
数据压缩是小波变换的一个成功应用领域,特别是对二维图像数据压缩更为有效.采用小波变换进行数据压缩的优点是不仅压缩比可以提高,而且可以避免其他压缩编码方法由于数据分块造成的方块效应0和/蚊式噪声0,因而质量较好.随着多媒体、信息高速公路等技术的发展,数据压缩已成为信息传输中的瓶颈问题,因此其重要性愈见显著.基于小波分析的压缩方法很多,比较成功的有小波包最好基方法、小波域纹理模型方法、小波变换零树压缩、小波变换向量压缩等.把小波变换、图像分割、二维建模、自适应量化等技术综合起来,并结合人类视觉的特点,对图像中的不同区域(轮廓和纹理)采用不同的压缩方法,即所谓/第二代图像压缩技术0是图像压缩技术发展的必然趋势。
由于分形和小波变换在尺度性能上表现出的类似性,因此小波变换被认为是分析、刻画物理学中许多有关分形现象的有力工具.傅氏变换虽然能看到湍流信号的频率特性,但是却不能表现其相干结构;直观的图形(例如二维湍流场的旋涡图)虽能粗略观察到它的相干结构,但却不能给出各尺度间能量和熵交换情况的定量描述.小波变换恰能把这两方面结合起来,弥补了上述缺点,而且它本身又包含有时间概念,因此还可以表现出湍流发展的过程,即如何由初始状态发展成充分成熟的涡流[28].Arneodo和Argoul[29]则以小波变换为/数学显微镜0,对非平衡系统的模式形成现象,包括分维生长过程,如何向混沌过渡、分形聚集体等多分形现象作了分析。
三.希尔伯特——黄变换希尔伯特——黄变换主要内容包含两部分,第一部分为经验模态分解(Empirical Mode Decomposition,简称EMD),它是由Huang提出的;第二部分为Hilbert谱分析(Hilbert Spectrum Analysis,简称HAS)。
简单说来,希尔伯特——黄变换处理非平稳信号的基本过程是:首先利用EMD方法将给定的信号分解为若干固有模态函数(以Intrinsic Mode Function或IMF表示,也称作本征模态函数),这些IMF是满足一定条件的分量;然后,对每一个IMF进行Hilbert 变换,得到相应的Hilbert谱,即将每个IMF 表示在联合的时频域中;最后,汇总所有IMF 的Hilbert谱就会得到原始信号的Hilbert谱。
与传统的信号或数据处理方法相比,希尔伯特——黄变换具有如下特点:(1)希尔伯特——黄变换能分析非线性非平稳信号传统的数据处理方法,如傅立叶变换只能处理线性非平稳的信号,小波变换虽然在理论上能处理非线性非平稳信号,但在实际算法实现中却只能处理线性非平稳信号。
历史上还出现过不少信号处理方法,然而它们不是受线性束缚,就是受平稳性束缚,并不能完全意义上处理非线性非平稳信号。
希尔伯特——黄变换则不同于这些传统方法,它彻底摆脱了线性和平稳性束缚,其适用于分析非线性非平稳信号。
(2)希尔伯特——黄变换具有完全自适应性希尔伯特——黄变换能够自适应产生“基”,即由“筛选”过程产生的IMF。
这点不同于傅立叶变换和小波变换。
傅立叶变换的基是三角函数,小波变换的基是满足“可容性条件”的小波基,小波基也是预先选定的。
在实际工程中,如何选择小波基不是一件容易的事,选择不同的小波基可能产生不同的处理结果。
我们也没有理由认为所选的小波基能够反映被分析数据或信号的特性。
(3)希尔伯特——黄变换不受Heisenberg 测不准原理制约——适合突变信号傅立叶变换、短时傅立叶变换、小波变换都受Heisenberg测不准原理制约,即时间窗口与频率窗口的乘积为一个常数。
这就意味着如果要提高时间精度就得牺牲频率精度,反之亦然,故不能在时间和频率同时达到很高的精度,这就给信号分析处理带来一定的不便。
而希尔伯特——黄变换不受Heisenberg测不准原理制约,它可以在时间和频率同时达到很高的精度,这使它非常适用于分析突变信号。
(4)希尔伯特——黄变换的瞬时频率是采用求导得到的傅立叶变换、短时傅立叶变换、小波变换有一个共同的特点,就是预先选择基函数,其计算方式是通过与基函数的卷积产生的。
希尔伯特——黄变换不同于这些方法,它借助Hilbert变换求得相位函数,再对相位函数求导产生瞬时频率。
这样求出的瞬时频率是局部性的,而傅立叶变换的频率是全局性的,小波变换的频率是区域性的。
四.盲源分离盲源分离是指在信号的理论模型和源信号无法精确获知的情况下,如何从混迭信号(观测信号)中分离出各源信号的过程。
盲源分离和盲辨识是盲信号处理的两大类型。
盲源分离的目的是求得源信号的最佳估计,盲辨识的目的是求得传输通道混合矩阵。
应用领域盲源信号分离是一种功能强大的信号处理方法,在生物医学信号处理,阵列信号处理,语音信号识别,图像处理及移动通信等领域得到了广泛的应用。
盲源分离(BSS:Blind source separation),是信号处理中一个传统而又极具挑战性的问题,BSS指仅从若干观测到的混合信号中恢复出无法直接观测的各个原始信号的过程,这里的“盲”,指源信号不可测,混合系统特性事先未知这两个方面。
在科学研究和工程应用中,很多观测信号都可以看成是多个源信号的混合,所谓“鸡尾酒会”问题就是个典型的例子。
其中独立分量分析ICA(Independent component analysis)是一种盲源信号分离方法,它已成为阵列信号处理和数据分析的有力工具,而BSS比ICA适用范围更宽。
参考文献[1] 维基百科.小波变换.[J/OL][2013-4-14]./wiki/%E5%B0%8F%E 6%B3%A2%E5%8F%98%E6%8D%A2[2] 维基百科.短时傅里叶变换[J/OL].[2013-4-14].http://zh.wikipedia.o rg/wiki/%E7%9F%AD%E6%97%B6%E5%82%85%E9%8 7%8C%E5%8F%B6%E5%8F%98%E6%8D%A2[3] 李春峰,Liner C.基于小波多尺度分析的奇性指数:一种新地震属性[J].地球物理报,2005,48(4):882~888.[4] 印兴耀,张奎,张广智.联合时频分布及其矩属性的应用[J].石油地球物理勘探,2003,38(5):521~526.[5] Q.Chen,N.E.Huang,5.瓦emensclmeider,Y.Xu.AB一sPlineaPProachPu t.Math.Vol24[6] 钟佑明,金涛,秦树人.希尔伯特黄变换中的一种新包络线算法.2005[7] 钟伯成.基于小波变换的脑电信号瞬态特征提取[J].模式识别与人工智能,2000[8] Zhang Q. Using wavelet network innonparametric estimation[J]. IEEETransactions on Neural Networks, 1997 [9] 钟佑明,金涛,秦树人.希尔伯特黄变换中的一种新包络线算法.2005[10] 郑君里,应启晰,杨为理.信号与系统.高等教育出版社,2002[11] TAYLOR T S. Turbulence simulation andoptical processing through turbulencemedia[J]. SPIE, 1997, 3073: 404-415.[12]张东.吴晓琳短时傅立叶变换在振动信号处理中的应用[J]-计算机与数字工程 2011 [13] 陈文静,苏显渝,谭松新. Fourier变换轮廓术中对测量系统的基本要求[J].光电子#激光,1999[14] 百度百科.盲源分离.[J/OL].[2013-4-14]./view/3819359.htm[15] 百度文库.盲源分离.[M/OL].[2013-4-14]./view/c41a225c804d2b160b4ec033.html。
