万有引力与航天
高考物理知识点专题之万有引力与航天 专题04 神州飞船(解析版)
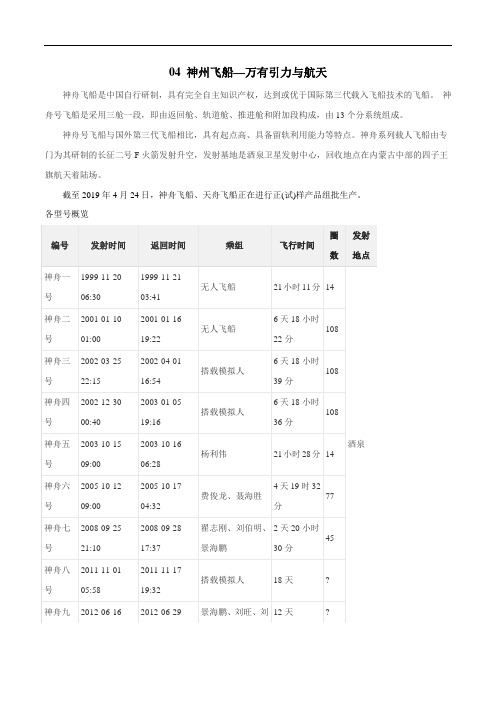
04 神州飞船—万有引力与航天神舟飞船是中国自行研制,具有完全自主知识产权,达到或优于国际第三代载入飞船技术的飞船。
神舟号飞船是采用三舱一段,即由返回舱、轨道舱、推进舱和附加段构成,由13个分系统组成。
神舟号飞船与国外第三代飞船相比,具有起点高、具备留轨利用能力等特点。
神舟系列载人飞船由专门为其研制的长征二号F火箭发射升空,发射基地是酒泉卫星发射中心,回收地点在内蒙古中部的四子王旗航天着陆场。
截至2019年4月24日,神舟飞船、天舟飞船正在进行正(试)样产品组批生产。
各型号概览1. 一质量为8.00×104 kg 的太空飞船从其飞行轨道返回地面。
飞船在离地面高度1.60×105 m 处以7.5×103 m/s 的速度进入大气层,逐渐减慢至速度为100 m/s 时下落到地面。
取地面为重力势能零点,在飞船下落过程中,重力加速度可视为常量,大小取为9.8 m/s 2。
(结果保留2位有效数字) (1)分别求出该飞船着地前瞬间的机械能和它进入大气层时的机械能;(2)求飞船从离地面高度600 m 处至着地前瞬间的过程中克服阻力所做的功,已知飞船在该处的速度大小是其进入大气层时速度大小的2.0%。
【解析】(1)飞船着地前瞬间的机械能为20021mv E k =① 式中,m 和v 0分别是飞船的质量和着地前瞬间的速率。
由①式和题给数据得8kp 4.010J E =⨯②设地面附近的重力加速度大小为g ,飞船进入大气层时的机械能为212h h E m mgh =+③ 式中,v h 是飞船在高度1.6×105m 处的速度大小。
由③式和题给数据得122.410J h E =⨯④(2)飞船在高度h' =600 m 处的机械能为21 2.0()2100h h E m v mgh ''=+⑤由功能原理得k0h W E E '=-⑥式中,W 是飞船从高度600m 处至着地瞬间的过程中克服阻力所做的功。
《万有引力与航天》知识点总结

万有引力与航天知识点总结一、人类认识天体运动的历史1、“地心说”的内容及代表人物: 托勒密 (欧多克斯、亚里士多德)2、“日心说”的内容及代表人物: 哥白尼 (布鲁诺被烧死、伽利略) 二、开普勒行星运动定律的内容开普勒第二定律:v v >远近开普勒第三定律:K —与中心天体质量有关,与环绕星体无关的物理量;必须是同一中心天体的星体才可以列比例,太阳系: 333222===......a a a T T T 水火地地水火 三、万有引力定律1、内容及其推导:应用了开普勒第三定律、牛顿第二定律、牛顿第三定律。
KT R =23 ① r T m F 224π= ② 22π4=r m K F 2m F r ∝ F F '= ③ 2r M F ∝' 2r Mm F ∝ 2r MmG F =2、表达式:221r m m GF = 3、内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1,m2的乘积成正比,与它们之间的距离r 的二次方成反比。
4.引力常量:G=6.67×10-11N/m 2/kg 2,牛顿发现万有引力定律后的100多年里,卡文迪许在实验室里用扭秤实验测出。
5、适用条件:①适用于两个质点间的万有引力大小的计算。
②对于质量分布均匀的球体,公式中的r 就是它们球心之间的距离。
③一个均匀球体与球外一个质点的万有引力也适用,其中r 为球心到质点间的距离。
④两个物体间的距离远远大于物体本身的大小时,公式也近似的适用,其中r 为两物体质心间的距离。
6、推导:2224mM G m R R T π= ⇒ 3224R GMT π= 四、万有引力定律的两个重要推论1、在匀质球层的空腔内任意位置处,质点受到地壳万有引力的合力为零。
2、在匀质球体内部距离球心r 处,质点受到的万有引力就等于半径为r 的球体的引力。
五、万有引力的成就1、测量中心天体的质量法一:在天体表面找一个物体m ,不计天体自转,万有引力=重力(=G F F 引)2Mm G mg R=⇒M = 黄金代换式中心天体的密度:233443gR M gG V GR R ρππ===法二:在中心天体周围找一颗卫星绕中心天体做圆周运动,万有引力提供向心力(=n F F 引)2Mm G r= 22232223224v v r m M r Gr mr M G r mr M T GT ωωππ⇒=⇒=⎛⎫⇒=⎪⎝⎭以 2324r M GT π=为例求中心天体的密度 2332233433r M r GT V GT R R ππρπ=== 若为近地卫星,则r=R ,则23GT πρ= T 为近地卫星的公转周期六、双星系统两颗质量可以相比的恒星相互绕着旋转的现象,叫双星。
专题05 万有引力与航天—备战2023年高考物理母题题源解密(全国通用)(解析版)

A.火星的公转周期大约是地球的 倍
B.在冲日处,地球上的观测者观测到火星的运动为顺行
C.在冲日处,地球上的观测者观测到火星的运动为逆行
D.在冲日处,火星相对于地球的速度最小
【答案】CD
【解析】A.由题意根据开普勒第三定律可知
火星轨道半径大约是地球轨道半径的1.5倍,则可得
故A错误;
BC.根据
可得
由于火星轨道半径大于地球轨道半径,故火星运行线速度小于地球运行线速度,所以在冲日处火星相对于地球由东向西运动,为逆行,故B错误,C正确;D.由于火星和地球运动的线速度大小不变,在冲日处火星和地球速度方向相同,故相对速度最小,故D正确。故选CD。
A. B.
C. D.
【答案】C
【解析】地球表面的重力加速度为g,根据牛顿第二定律得
解得
根据题意可知,卫星的运行周期为
根据牛顿第二定律,万有引力提供卫星运动的向心力,则有
联立解得 ,故选C。
【母题来源六】2022年高考浙江卷
【母题题文】(2022·浙江6月卷·T6)神州十三号飞船采用“快速返回技术”,在近地轨道上,返回舱脱离天和核心舱,在圆轨道环绕并择机返回地面。则( )
A.天和核心舱所处的圆轨道距地面高度越高,环绕速度越大
B.返回舱中的宇航员处于失重状态,不受地球的引力
C.质量不同的返回舱与天和核心舱可以在同一轨道运行
万有引力与航天知识点总结

万有引力与航天知识点总结————————————————————————————————作者:————————————————————————————————日期:ﻩ332T=2.GM GM GM r M v a Gr r r ωπ=== , , ,万有引力定律①内容:自然界中任何两个物体都相互吸引,引力的大小与物体的质量1m 和2m 的乘积成正比,与它们之间的距离r 的二次方成反比。
即: 其中G =6. 67×10-11N·m 2/kg 2②适用条件1.可看成质点的两物体间,r 为两个物体质心间的距离。
2.质量分布均匀两球体间,r为两球体球心间距离。
③运用万有引力与重力的关系:重力是万有引力的一个分力,一般情况下, 可认为重力和万有引力相等。
忽略地球自转可得:二. 重力和地球的万有引力:1.地球对其表面物体的万有引力产生两个效果:(1)物体随地球自转的向心力: F 向=m ·R ·(2π/T 0)2,很小。
由于纬度的变化,物体做圆周运动的向心力不断变化,因而表面物体的重力随纬度的变化而变化。
(2)重力约等于万有引力:在赤道处:mg F F +=向,所以R m R GMm F F mg 22自向ω-=-=,因地球自转角速度很小,R m R GMm 22自ω>>,所以2R GM g =。
说明:如果有些星球的自转角速度非常大,那么万有引力的向心力分力就会很大,重力就相应减小,就不能再认为重力等于万有引力了。
如果星球自转速度相当大,使得在它赤道上的物体所受的万有引力恰好等于该物体随星球自转所需要的向心力,那么这个星球就处于自行崩溃的临界状态了。
在地球的同一纬度处,g 随物体离地面高度的增大而减小,即2)('h R GM g +=。
强调:g =G ·M /R 2不仅适用于地球表面,还适用于其它星球表面。
2.绕地球运动的物体所受地球的万有引力充当圆周运动的向心力,万有引力、向心力、重力三力合一。
学生学习“万有引力与航天”困难成因及教学策略お共4页word资料

学生学习“万有引力与航天”困难成因及教学策略お历来学生对“万有引力与航天”这章内容很恐惧,往往是听着都懂,做起题目没有头绪,即便到了高三复习,仍有一部分学生头脑混乱,无从下手.那么是什么原因导致学生学习该内容如此困难?作为教师又可以从哪些地方作出改进从而达到更好的教学效果呢?笔者通过教学实践总结如下:1学生学习困难成因1.1概念抽象、公式繁多万有引力是自然界普遍存在的规律,但万有引力不像弹力、摩擦力那样具体、贴合学生实际生活,由于万有引力作用使天体做圆周运动,对学生来说是个抽象概念和物理模型.另外,万有引力公式与圆周运动公式结合之后,使得公式繁多、结论琐碎,学生很难将公式之间的联系、结论的来龙去脉等彻底弄清楚,往往重公式轻理解,死代公式,一代一个错,造成了学习上的困难.1.2科学前沿、高不可攀学生往往认为航天活动是一项高精尖的事业,与自己的距离较远,把天体运动看的过于神秘和高不可攀,在心理上产生了距离和畏难情绪,缺乏学好本章内容的自信心.1.3空间想象能力、建立物理模型能力欠缺本章的运动模型仍然是圆周运动模型,用到的是分析圆周运动的常规方法,学生前面牛顿运动定律和圆周运动基础不扎实,那么学习这章会非常吃力.况且本章题目往往题意复杂、材料新颖,无疑对学生的能力提出更高的要求,要求学生能在看似复杂的题目中提炼有用信息,建立正确的物理模型,选择恰当的解题思路和方法.另外,学好本章还需要一定的空间思维能力和地理知识.总之,两种能力欠缺,都会感觉学习困难.1.4能量知识缺乏初中时学生有一些能量知识储备,但还不足以解决本章涉及到的相关能量问题,较系统的功和能量知识是在《机械能守恒定律》这一章,恰在《万有引力与航天》之后,因此在一定程度上也造成了学生学习的困难.2教学策略2.1拉近与生活的距离,克服畏难情绪,提高学习兴趣本章知识与我们的生活息息相关,教学时可以适时拓展学生知识面,比如航天事业是如何影响我们的生活,还可以鼓励学生通过网络搜集相关信息,了解当前航天事业科技前沿,并做交流展示.总之,让学生明白学习本章知识的重要意义.2.2帮助学生理清本章与前面力学知识的逻辑关系本章安排在运动学、力学之后,是圆周运动的延续,内容并不复杂.尽管本章是从万有引力的发现历史展开教学,但通篇来看,将天体运动看做匀速圆周运动,实质就是圆周运动的力学规律和运动学规律,因此在教学中,时时处处向学生渗透处理天体运动问题需从受力分析和运动分析入手,始终灌输圆周运动处理方法,从向心力来源入手,即万有引力提供向心力.2.3深入理解两个基本原理两个基本原理即万有引力提供天体运动所需向心力、物体在某处的万有引力等于物体在该处重力.首先,要帮助学生建立物理模型,万有引力等于向心力是适用于一个天体围绕中心天体做匀速圆周运动的情境;万有引力等于重力是在涉及重力加速度的情况下首先想到的规律,可以假设某物体在某处,其受到的万有引力等于该处重力.其次,重复强调两个原理运用时的注意点.比如,万有引力等于重力,学生运用时往往忽视等式两边必须地理位置一致这个前提条件.再比如,运用万有引力等于向心力时学生往往面对众多公式不知所措,因此在平时教学中一定要培养学生良好的审题习惯,在众多文字和条件中提炼匀速圆周运动模型和相关物理量,从而选择合适的向心力公式.第三,重基本公式轻二级结论.比如,所谓“黄金代换式”是万有引力等于重力这一基本关系的二级结论,然而学生容易记住这个“黄金代换式”,却忽视了其本源,运用时就容易死套结论.笔者在教学中不会给出这个结论,而是强调万有引力等于重力这一基本关系,避免学生犯舍本求末的错误.2.4引领学生审题,帮助学生建立物理模型本章题目的特点是条件繁多,信息量大,学生往往会被题目样式所吓住,丧失进一步审题分析的信心,因此在平时教学中更要注重学生审题能力的培养,引导他们如何去辩识和提取有用信息,如何将文字信息转换成图形信息,从而构建出正确的运动模型,运用恰当的物理规律和方法去处理.2.5降低教学难度,增强学习信心对于高一学生来说,普遍感觉物理难学,尤其是本章知识,所以在本章教学时,仍要以基础为主,难度切不可大,否则极大挫伤学生学习的积极性和自信心.比如,卫星变轨问题是本章的一个难点,也是学生综合运用能力的体现,但对高一学生来说无论是知识还是能力都还达不到,所以遇到此类问题首先要做好知识的铺垫,浅入深出,也不必要求学生一定要掌握到何种程度,到了高三复习可以拔高要求,那时学生对知识的理解和思维能力水平都有了很大提高.希望以上资料对你有所帮助,附励志名言3条:1、要接受自己行动所带来的责任而非自己成就所带来的荣耀。
万有引力与航天公式总结

万有引力与航天重点规律方法总结一. 三种模型1.匀速圆周运动模型:无论是自然天体(如地球、月亮)还是人造天体(如宇宙飞船、人造卫星)都可看成质点,围绕中心天体(视为静止)做匀速圆周运动2.双星模型:将两颗彼此距离较近的恒星称为双星,它们相互之间的万有引力提供各自转动的向心力。
3.“天体相遇”模型:两天体相遇,实际上是指两天体相距最近。
二. 两种学说1.地心说:代表人物是古希腊科学家托勒密2/日心说:代表人物是波兰天文学家哥白尼三. 两个定律1.幵普勒定律:第一定律(又叫椭圆定律):所有的行星围绕太阳运动的轨道都是椭圆,太阳位于椭圆的一个焦点上第二定律(又叫面积定律):对每一个行星而言,太阳和行星的连线,在相等时间内扫过相同的面积。
第三定律(又叫周期定律):所有行星绕太阳运动的椭圆轨道的半长轴R的三次方跟公转周期T的二次方的比值都相等。
表达式为: 3 R-K(K GM )k只与中心天体质量T 4 二2.牛顿万有引力定律1687年在《自然哲学的数学原理》正式提出万有引力定律⑴.内容:宇宙间的一切物体都是相互吸引的.两个物体间引力的方向在它们的连线上,引力的大小跟它们的质量的乘积成正比,跟它们之间的距离的二次方成反比.⑵.数学表达式:F万二G Mm mr⑶.适用条件:a.适用于两个质点或者两个均匀球体之间的相互作用。
(两物体为均匀球体时,r为两球心间的距离)b.当r > 0时,物体不可以处理为质点,不能直接用万有引力公式计算c.认为当r > 0时,引力F—;•匚的说法是错误的⑷.对定律的理解a. 普遍性:任何客观存在的有质量的物体之间都有这种相互作用力b. 相互性:两个物体间的万有引力是一对作用力和反作用力,而不是平衡力 关系。
c. 宏观性:在通常情况下万有引力非常小,只有在质量巨大的星球间或天体与天体附近的物体间,它的存在才有实际意义.d. 特殊性:两个物体间的万有引力只与它们本身的质量、它们之间的距离有关.与所在空间的性质无关,与周期及有无其它物体无关.(5)引力常数G: ① 大小:G = 6.67 10J1N m 2/kg 2,由英国科学家卡文迪许利用扭秤测出② 意义:表示两个质量均为1kg 的物体,相距为1米时相互作用力为:6.671QJ1N四. 两条思路:即解决天体运动的两种方法1. 万有引力提供向心力:F 万二F向即: F 万=G Mm ^ =ma “ =ml =mr 4l_ =mrco 22. 天体对其表面物体的万有引力近似等于重力:即GM =gR 2(又叫黄金代换式)2③ 关系:gJ g (R+h )五. 万有引力定律的应用1. 计算天体运动的线速度、角速度、 c.周期:T =2二、和2. 计算中心天体的质量: 方法一:根据转动天体运动周期 T 和转动半径r 计算:234nr M 占 GT方法二:根据中心天体半径 R 和其表面的重力加速度g 计算:2M 二9R(适合于没有行星、卫星转动的中心天体) G注意:转动天体的质量是求不出来的。
高中物理周测——万有引力与航天
高中物理周测——万有引力与航天学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图所示,A、B、C是在地球大气层外圆形轨道上运动的三颗人造地球卫星,下列说法中正确的是()A.B、C的线速度大小相等,且大于A的线速度B.B、C的周期相等,且大于A的周期C.B、C的向心加速度大小相等,且大于A的向心加速度D.C加速(速率增大)可追上同一轨道上的B2.我国“天舟1号”货运飞船于2017年4月20日19时41分在海南文昌航天发射中心由长征7号遥2运载火箭成功发射,4月27日19时07分,“天舟一号”货运飞船与“天宫二号”空间实验室成功完成首次推进剂在轨补加试验等上系列任务,标志“天舟一号”飞行任务取得圆满成功。
在“天舟一号”完成任务期间,位于地球同步轨道的我国4颗数据中继卫星“天链一号”卫星(01星、02星、03星与04星全球组网运行),为此次任务提供数据中继服务,测控支持等方面起到了极为重要的作用。
若设“天链一号”卫星距地面的高度为H,“天舟一号”与“天宫二号”对接成功所在轨道距地面高为h,地球的半径为R,重力加速度为g,地球自转周期为T自,忽略“天舟一号”运行轨道与赤道平面的倾角,则下列说法正确的是A.“天舟一号”在海南文昌航天发射中心的发射架上等待发射时的速度v1与“天链一号”卫星运行速度v2之比为B.“天舟一号”在海南文昌航天发射中心的发射架上等待发射时的速度v1与“天宫一号”空间站运行速度v3之比为C.“天舟一号”在海南文昌航天发射中心的发射架上等待发射时的加速度a1与“天链一号”卫星运行的加速度a2之比为)D.“天舟一号”对接成功后在一昼夜的运行中,因为地球的遮挡而无法直接与“天链一号”卫星中01星通讯的次数为自3.火星探测项目是我国继载人航天天工程、嫦娥工程之后又一个重大太空探索项日。
已知地球公转周期为T,与太日的别距离为R1,运行速率为v1,火星到太旧的距离为R2,运行速率为v2,太阳质量为M,引力常量为G。
高一物理万有引力与航天试题答案及解析
高一物理万有引力与航天试题答案及解析1.把太阳系各行星的运动近似看做匀速圆周运动,则离太阳越远的行星A.周期越大B.线速度越小C.角速度越大D.加速度越小【答案】A【解析】设太阳的质量为M,行星的质量为m,轨道半径为r.行星绕太阳做圆周运动,万有引力提供向心力,则由牛顿第二定律得:G=m,G=mω2r,G=ma,解得:v=,ω=,a=,周期T==2π,可知,行星离太远越近,轨道半径r越小,则周期T越小,线速度、角速度、向心加速度越大,故BCD错误;故选:A.2.发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图所示。
则在卫星分别在1、2、3轨道上正常运行时,以下说法正确的是A.卫星在轨道3上的速率大于在轨道1上的速率B.卫星在轨道3上的角速度小于在轨道1上的角速度C.卫星在轨道1上运动一周的时间小于于它在轨道2上运动一周的时间D.卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度【答案】BCD【解析】根据公式,解得,即轨道半径越大,线速度越小,A错误;根据公式可得,即轨道半径越大,角速度越小,故B正确;根据开普勒第三定律可得轨道半径或半长轴越大,运动周期越大,故卫星在轨道1上运动一周的时间小于它在轨道2上运动一周的时间,故C正确;在轨道2和3上经过P点时卫星到地球的距离相等,根据,可得,半径相同,即加速度相等,D正确。
3.关于第一宇宙速度,下列说法正确的是A.它是人造地球卫星绕地球飞行的最小速度B.它是同步卫星的运行速度C.它是使卫星进入近地圆轨道的最大发射速度D.它是人造卫星在圆形轨道的最大运行速度【答案】D【解析】第一宇宙速度又称为环绕速度,是指在地球上发射的物体绕地球飞行作圆周运动所需的最小发射速度,为环绕地球运动的卫星的最大速度,即近地卫星的环绕速度,同步卫星轨道要比近地卫星的大,所以运行速度小于该速度,故D正确。
万有引力与航天公式总结归纳
万有引力与航天重点规律方法总结一.三种模型1.匀速圆周运动模型:无论是自然天体(如地球、月亮)还是人造天体(如宇宙飞船、人造卫星)都可看成质点,围绕中心天体(视为静止)做匀速圆周运动2.双星模型:将两颗彼此距离较近的恒星称为双星,它们相互之间的万有引力提供各自转动的向心力。
3.“天体相遇”模型:两天体相遇,实际上是指两天体相距最近。
二.两种学说1.地心说:代表人物是古希腊科学家托勒密2/日心说:代表人物是波兰天文学家哥白尼三.两个定律1.开普勒定律:第一定律(又叫椭圆定律):所有的行星围绕太阳运动的轨道都是椭圆,太阳位于椭圆的一个焦点上 第二定律(又叫面积定律):对每一个行星而言,太阳和行星的连线,在相等时间内扫过相同的面积。
第三定律(又叫周期定律):所有行星绕太阳运动的椭圆轨道的半长轴R 的三次方跟公转周期T 的二次方的比值都相等。
表达式为:)4(223πGM K K T R ==k 只与中心天体质量有关的定值与行星无关2.牛顿万有引力定律1687年在《自然哲学的数学原理》正式提出万有引力定律⑴.内容:宇宙间的一切物体都是相互吸引的.两个物体间引力的方向在它们的连线上,引力的大小跟它们的质量的乘积成正比,跟它们之间的距离的二次方成反比.⑵.数学表达式:r F Mm G 2=万⑶.适用条件:a.适用于两个质点或者两个均匀球体之间的相互作用。
(两物体为均匀球体时,r 为两球心间的距离)b.当0→r 时,物体不可以处理为质点,不能直接用万有引力公式计算c.认为当0→r 时,引力∞→F 的说法是错误的⑷.对定律的理解a.普遍性:任何客观存在的有质量的物体之间都有这种相互作用力b.相互性:两个物体间的万有引力是一对作用力和反作用力,而不是平衡力关系。
c.宏观性:在通常情况下万有引力非常小,只有在质量巨大的星球间或天体与天体附近的物体间,它的存在才有实际意义.d.特殊性:两个物体间的万有引力只与它们本身的质量、它们之间的距离有关.与所在空间的性质无关,与周期及有无其它物体无关.(5)引力常数G :①大小:kg m N G 2211/67.610⋅⨯=-,由英国科学家卡文迪许利用扭秤测出 ②意义:表示两个质量均为1kg 的物体,相距为1米时相互作用力为:N 101167.6-⨯四.两条思路:即解决天体运动的两种方法1.万有引力提供向心力:F F向万=即:222224n Mm v F G ma m mr mr r r T πω=====万 2.天体对其表面物体的万有引力近似等于重力: 即2gR GM =(又叫黄金代换式)注意:①地面物体的重力加速度:R GM g 2=≈9.8m/s 2 ②高空物体的重力加速度:〈+=2')(h R GM g 9.8m/s 2 ③关系:22')(h R g R g +=五.万有引力定律的应用1.计算天体运动的线速度、角速度、周期、向心加速度。
第六章第一节 开普勒定律
【答案】
BD
栏目 导引
第六章
万有引力与航天
跟踪训练1 (2013· 高考江苏卷)火星和木星沿各自的椭圆轨道绕太阳运
行,根据开普勒行星运动定律可知(
A.太阳位于木星运行轨道的中心
)
B.火星和木星绕太阳运行速度的大小始终相等 C.火星与木星公转周期之比的平方等于它们轨道半长轴 之比的立方
D.相同时间内,火星与太阳连线扫过的面积等于木星与
;火星与太阳连线在相同时间内扫过的面积相等,木星与
太阳连线在相同时间内扫过的面积相等,但这两个面积不 相等,选项D错误.
栏目 导引
第六章
万有引力与航天
要点二 行星运动的一般处理方法 1.天体虽做椭圆运动,但它们的轨道一般接近圆.为 简化运算,一般把天体的运动看成匀速圆周运动,椭圆 的半长轴即为圆半径. 2.在处理天体运动时,开普勒第三定律表述为:天体 轨道半径 R 的三次方跟它的公转周期 T 的二次方的比 R3 值为常数,即 2 =k.据此可知,绕同一天体运动的多个 T 天体,轨道半径 R 越大的天体,其周期越长.
kg,它的轨道半径是地球绕太阳运动半径的2.77倍,求谷 神星绕太阳一周所需要的时间.
【解析】 设地球的轨道半径为 R0,则谷神星绕太阳 运行的轨道半径为 Rn=2.77R0 又知地球绕太阳运行周期为 T0=365 天
栏目 导引
第六章
万有引力与航天
R3 R3 0 n 据 2 = 2 得:谷神星绕太阳的运行周期 T0 Tn Tn= R3 n T0= 2.773×365 天=1 683 天=1 R3 0
的一个焦点上
C.水星的半长轴最短,所以公转周期最长 D.海王星离太阳“最远”,所以绕太阳运动的公转周期 最长
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 4.3 万有引力与航天 一、基础知识回顾 (一)万有引力定律及其应用 1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比,与它们之间距离r的平方成反比.
2.表达式:F=Gm1m2r2,G为引力常量, G=6.67×10-11 N·m2/kg2.
3.适用条件 (1)公式适用于质点间的相互作用.当两个物体间的距离远远大于物体本身的大小时,物体可视为质点. (2)质量分布均匀的球体可视为质点,r是两球心间的距离. (二)宇宙速度 1.第一宇宙速度 (1)第一宇宙速度又叫环绕速度. 推导过程为:由mg=mv2/R=GMm/R2得:
v=GMR=gR=7.9 km/s.
(2)第一宇宙速度是人造地球卫星在地面附近环绕地球做匀速圆周运动时具有的速度. (3)第一宇宙速度是人造卫星的最大环绕速度,也是人造地球卫星的最小发射速度. 2.第二宇宙速度(脱离速度):v2=11.2 km/s,使物体挣脱地球引力束缚的最小发射速度. 3.第三宇宙速度(逃逸速度):v3=16.7 km/s,使物体挣脱太阳引力束缚的最小发射速度. (三)经典时空观和相对论时空观 1.经典时空观 (1)在经典力学中,物体的质量是不随运动状态而改变的. (2)在经典力学中,同一物理过程发生的位移和对应时间的测量结果在不同的参考系中是相同的.
2.相对论时空观 (1)在狭义相对论中,物体的质量是随物体运动速度的增大而增大的,用公式表示为m=m01-v2c2.
(2)在狭义相对论中,同一物理过程发生的位移和对应时间的测量结果在不同的参考系中是不同的. 2
例1.关于第一宇宙速度,下列说法正确的是( ) A.它是人造地球卫星绕地球运行的最小速度 B.它是近地圆形轨道上人造地球卫星的运行速度 C.它是使卫星进入近地圆形轨道的最小发射速度 D.它是卫星在椭圆轨道上运行时在近地点的速度 例2.关于同步卫星(它相对于地面静止不动),下列说法中正确的是( ) A.它一定在赤道上空 B.同步卫星的高度、周期是一个确定的值 C.所有的同步卫星具有相同的速度和加速度 D.它运行的线速度一定介于第一宇宙速度和第二宇宙速度之间
例3.(2012·山东理综卷)2011年11月3日,“神舟八号”飞船与“天宫一号”目标飞行器成功实施了首次交会对接.任务完成后“天宫一号”经变轨升到更高的轨道,等待与“神舟九号”交会对接.变轨前和变轨完成后“天宫一号”的运行轨道均可视为圆轨道,对应的轨道半径分别为R1、
R2,线速度大小分别为v1、v2.则v1v2等于( )
A.R31R32 B.R2R1 C.R22R21 D.R2R1
4.2012年6月24日,天宫神九组合体在轨飞行六天后短暂分离,并于12时成功实施首次手控对接,意味着中国完整掌握空间交会技术,具备了建设空间站的基本能力.假如“神舟九号”与“天宫一号”对接前所处的轨道如图甲所示,图乙是它们在轨道上即将对接时的模拟图.当它们处于图甲所示的轨道运行时,下列说法正确的是( ) A.“神舟九号”的加速度比“天宫一号”的大 B.“神舟九号”的运行速度比“天宫一号”的小 C.“神舟九号”的运行周期比“天宫一号”的长 D.“神舟九号”适度加速后有可能与“天宫一号”实现对接
5.地球表面的重力加速度为g,地球半径为R,万有引力常量为G,则由此估算地球的平均密度为( )
A.3g4πRG B.3g4πR2G
C.gRG D.gR2G 二、考点、热点解析 3
考点一 万有引力定律的理解及应用 例1:(2012·课标全国卷)假设地球是一半径为R、质量分布均匀的球体.一矿井深度为d.已知质量分布均匀的球壳对壳内物体的引力为零.矿井底部和地面处的重力加速度大小之比为( ) A.1-dR B.1+dR
C.R-dR2 D.
R
R-d2
题后反思:星体表面及其某一高度处的重力加速度的求法 (1)设天体表面的重力加速度为g,天体半径为R,则mg=GMmR2,即g=GMR2(或GM=gR2)
(2)若物体距星体表面高度为h,则重力mg′=GMmR+h2,即g′=GMR+h2=R2R+h2g. 变式1-1:近地人造卫星1和2绕地球做匀速圆周运动的周期分别为T1和T2.设在卫星1、卫
星2各自所在的高度上的重力加速度大小分别为g1、g2,则( ) A.g1g2=T1T24/3 B.g1g2=T2T14/3
C.g1g2=T1T22 D.g1g2=
T2
T1
2
考点二 天体质量、密度的估算
例2:(2012·福建卷)一卫星绕某一行星表面附近做匀速圆周运动,其线速度大小为v.假设宇航员在该行星表面上用弹簧测力计测量一质量为m的物体重力,物体静止时,弹簧测力计的示数为N.已知引力常量为G,则这颗行星的质量为( )
A.mv2GN B.mv4GN
C.Nv2Gm D.Nv4Gm 借题发挥:天体质量和密度的估算 (1)利用天体表面的重力加速度g和天体的半径R
由GMmR2=mg,得M=R2gG,
ρ=MV=M43πR3=3g4πRG.
(2)利用天体的卫星,已知卫星的周期T(或线速度v)和卫星的轨道半径r 4
建立GMmr2=mv2r=mr4π2T2, 则M= 4π2r3GT2v2rG 测天体的密度:将天体的质量M代入ρ=M43πR3得:
ρ= 3πr3GR3T2 表面卫星3πGT23v2r4GπR3 变式2-1:一行星绕恒星做圆周运动.由天文观测可得,其运行周期为T,速度为v.引力常
量为G,则( ) A.恒星的质量为v3T2πG
B.行星的质量为4π2v3GT2 C.行星运动的轨道半径为vT2π D.行星运动的加速度为2πvT
考点三 卫星的轨道参量随轨道半径变化分析及计算 1.卫星的轨道参量随轨道半径变化的规律 动力学特征 GMmr2=man=mv2r=mω2r=m(2πT)2r
向心加速度an an=GMr2,即an∝1r2
线速度v v=GMr,即v∝1r 5
角速度ω ω=GMr3,即ω∝1r3 周期T T=4π2r3GM,即T∝r
3
由上表分析可知:随卫星轨道半径的增加,卫星的向心加速度、线速度、角速度都减小,其运行周期将增加. 2.几种常见卫星 (1)近地卫星 近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫星,其运行的轨道半径可近似认为等于
地球的半径,其运行线速度v=GMR=gR,约为7.9 km/s,其运行周期T=2πRv,约为84 min. (2)同步卫星 同步卫星与地球自转同步,相对地球静止,可用作为通讯卫星,其特点如下: ①轨道平面一定:轨道平面和赤道平面重合. ②周期一定:与地球自转周期相同, 即T=24 h=86 400 s. ③角速度一定:与地球自转的角速度相同.
④高度一定:据GMmr2=m4π2T2r得r=3GMT24π2=4.24×104 km,卫星离地面高度h=r-R≈6R(为恒量). ⑤速率一定:运动速度v=2πr/T=3.08 km/s(为恒量). ⑥绕行方向一定:与地球自转的方向一致.
例3:(2012·安徽卷)我国发射的“天宫一号”和“神舟八号”在对接前,“天宫一号”的运行轨道高度为350 km,“神舟八号”的运行轨道高度为343 km.它们的运行轨道均视为圆周,则( ) A.“天宫一号”比“神舟八号”速度大 B.“天宫一号”比“神舟八号”周期长 C.“天宫一号”比“神舟八号”角速度大 D.“天宫一号”比“神舟八号”加速度大 题后反思:利用万有引力定律解决卫星运动的方法是:一个模型两条思路 模型:人造天体的运动看做绕中心天体做匀速圆周运动,它受到的万有引力提供向心力. 思路:
(1)当天体运动时,由万有引力提供向心力GMmr2=mv2r=mω2r=mr2πT2.这是万有引力定律这一章的主线索. 6
(2)在地面附近万有引力近似等于物体的重力,GMmR2=mg.这是万有引力定律这一章的副线索. 变式3-1:如图所示,a、b是两颗绕地球做匀速圆周运动的人造卫星,它们距地面的高度分
别是R和2R(R为地球半径).下列说法中正确的是( ) A.a、b的线速度大小之比是 2∶1 B.a、b的周期之比是1∶22 C.a、b的角速度大小之比是36∶4 D.a、b的向心加速度大小之比是9∶4 三、重难点、易混点、典型例题
难点 一:卫星变轨问题 名师支招:卫星变轨的实质 若GMmr2=mv2r,供求平衡——卫星做匀速圆周运动,稳定运行;
若GMmr2若GMmr2>mv2r,供过于求——卫星做近心运动; 在同一椭圆轨道上,近地点速度大于远地点速度;不管在哪一个轨道上,由a=GMR2知,同一点加速度相同.
典例1:“嫦娥一号”探月卫星沿地月转移轨道直奔月球,在距月球表面200 km的P点进行第一次变轨后被月球捕获,先进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点又经过两次变轨,最后在距月球表面200 km的圆形轨道Ⅲ上绕月球做匀速圆周运动.对此,下列说法正确的是( ) A.卫星在轨道Ⅲ上运动的速度小于月球的第一宇宙速度 B.卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上短 C.卫星在轨道Ⅲ上运动的加速度大于沿轨道Ⅰ运动到P点时的加速度 D.Ⅰ、Ⅱ、Ⅲ三种轨道运行相比较,卫星在轨道Ⅲ上运行的机械能最小
难点二 双星问题 名师支招:◎ 双星问题的处理方法 在天体运动中,将两颗彼此相距较近的行星称为双星.星体在万有引力提供向心
