3.4单筋矩形截面梁正截面承载力验算
钢筋混凝土受弯构件正截面承载力计算 (2)_OK

合力作用点相同
x=βxc
合力大小相同
fce=αfc
27
混凝土受压区等效矩形应力图系数
≤ C50
C55
C60
C6 5
C70
C75
C80
α
1.0
0.99
0.98
0.97
0.96
0.95
0.94
β
0.8
0.79
0.78
0.77
0.76
0.75
0.74
水工结构中,常常只使用较低等级的混凝土,因此规范 规定:
10
四、梁内钢筋的直径和净距
架立钢筋——设置在梁受压区,用以固定箍筋的正确位置, 并能承受混凝土收缩和温度变化产生的内应力。 箍筋——承受梁的剪力;固定纵向钢筋位置,形成钢筋笼。 侧向构造钢筋——增加梁内钢筋骨架的刚性,增强梁的抗 扭能力,承受侧向发生的温度及收缩变形。
11
四、梁内钢筋的直径和净距
Mu
fyAs
计算简图
fcbx fy As
M
D
Mu
fcbx(h0
x) 2
fy As (h0
x) 2
KM S
Mu
fcbx(h0
x) 2
fy As (h0
x) 2
32
六、基本公式的适用条件
防止发生超筋破坏
max
As fcbx x fc fc
bh0 fybh0 h0 fy
fy
相对受压区高度
x fy As fcb
x
h0
若
1
:
b
Mu
f c b x ( h0
x) 2
f y As (h0
x) 2
若
第四章 受弯构件正截面承载力计算

因此得出
b
1
1
fy
cu E s
第四章 受弯构件正截面承载力计算
由平衡条件: 1 fcbxb= fyAs
可得出 1fcbbh0fyAs,max ---(4-15)
可推出适筋受弯构件最大配筋率max与 b
的表达式
maxAbs,m 0 hax b
1fc fy
---(4-16)
fy h0
360 465
0.2% h 0.2% 500 0.215%,可以。
h0
465
例题2
第四章 受弯构件正截面承载力计算
已知一单跨简支板,计算跨L0=2.34m,承受均 布荷载qk=3kN/m2(不包括板自重);混凝土 强度等级为C30;钢筋采用HPB235级钢筋。可
最小配筋率ρmin
第四章 受弯构件正截面承载力计算
4.2.2适筋受弯构件截面受力的几个阶段
第一阶段 —— 截面开裂前阶段。
第二阶段 —— 从截面开裂到纵向受拉钢筋屈服前阶段。
第三阶段 —— 钢筋屈服到破坏阶段。
第四章 受弯构件正截面承载力计算
各阶段和各特征点的截面应力 — 应变分析:
第四章 受弯构件正截面承载力计算
由式(4-16)可知,当构件按最大配筋率配筋时,由式
M1fcb(xh02 x) (4-9a)
可以求出适筋受弯构件所能承受的最大弯矩为
M m a1 x fc b 0 2b h ( 1 0 .5 b )sb b 0 2h 1 fc
其中, sb ----截面最大的抵抗矩系数,可查表。
坏。
第四章 受弯构件正截面承载力计算
受弯构件的配筋形式
P
P
钢筋等截面代换公式

钢筋代换计算公式一、抗弯承载力(强度)验算:单筋矩形截面受弯构件正截面受弯承载力计算基本公式为:M≤Mu=fyAs(ho-fyAs/2a1fcb)当砼强度等级超过C50,a1取1.0.钢筋代换后的截面强度:fy2As2(ho2-fy2As2/2fcb)≥fy1As1(ho1-fy1As1/2fcb)fy2---拟代换钢筋的抗拉强度设计值fy1---原设计钢筋的抗拉强度设计值As2---拟代换钢筋的截面面积As1---原设计钢筋的截面面积ho2---拟代换钢筋合力作用点至构件截面受压边缘的距离ho1---原设计钢筋合力作用点至构件截面受压边缘的距离fc---砼抗压强度设计值b---构件截面宽度二、钢筋代换抗剪承载力(强度)验算:钢筋砼受弯构件,当配有箍筋和弯起钢筋时,其:斜截面受剪承载力的计算公式为:v≤0.7ftbho+1.25fyvAsvho/s+0.8fyAstysinαs,αs---斜截面上弯起钢筋与构件纵向轴向的夹角,一般取αs=45°,当梁截面较高时取αs=60°即钢筋砼受弯斜截面所承受的剪力主要由三部分组成:1.砼承担的剪力;2、箍筋承担的剪力;3、弯起钢筋承担的剪力。
其中:箍筋所承担的剪力为:vsv=1.25fyvAsvho/s, 所以,(1)、箍筋代换应满足:fyv2Asv2/s2≥fyv1Asv1/s1fyv2---拟代箍筋换的抗拉强度设计值fyv1---原设计箍筋的抗拉强度设计值Asv2---拟代换箍筋截面积Asv1---原设计箍筋截面积s2---拟代换箍筋沿构件长度方向上的距离s1---原设计箍筋沿构件长度方向上的距离弯起钢筋所能承载的剪力为:vsb=0.8fyAsbsinαs,所以,(2)、弯起钢筋代换后应满足:fy2Asb2≥fy1Asb1fy2---拟代换弯起钢筋的抗拉强度设计值fy1---原设计弯起钢筋的抗拉强度设计值Asb2---同一弯起平面内拟代换弯起钢筋的截面积Asb1---同一弯起平面内原设计弯起钢筋的截面积当fy2Asb2<fy1Asb1时,即拟代换弯起钢筋抗力小于原设计弯起钢筋的抗力时,可通过适当增强箍筋的方法补强。
3-钢筋混凝土受弯构件正截面承载力计算

3.3.1 线弹性梁截面正应力计算原理
一.基本假定
1. 平截面假定成立-变形前的平截面在变形后保持平截面 不变,即截面上的正应变沿截面高度呈线形分布-给出 了截面变形的几何条件或变形协调条件。
2. 材料的应力-应变关系符合Hook定律,即应力应变之间 呈线性关系-给出了材料的物理关系。
有三种基本形式
延性破坏:配筋合适的构件,具有较高的承载力,同时破 坏时具有一定的延性,钢筋的抗拉强度和混凝土的抗压强度 都得到发挥,如适筋梁。 受拉脆性破坏:承载力很小,取决于混凝土的抗拉强度,混 凝土的抗压强度未能发挥,破坏特征与素混凝土构件类似。 虽然由于配筋使构件在破坏阶段表现出很长的破坏过程,但 这种破坏是在混凝土一开裂就产生,没有预兆,如少筋梁。 受压脆性破坏:具有较高的承载力,取决于混凝土抗压强度, 其延性能力取决于混凝土的受压塑性,因而较差,钢筋的受 拉强度没有发挥,如超筋梁 。
正常使用阶段的裂缝宽度和挠度变形验算;
绘制施工图。
桥梁工程系-杨 剑
3.2 试验研究
桥梁工程系-杨 剑
3.2.1 配筋率对正截面破坏形态的影响
一.两个名词
As’
as'
as'
h0 h
AS b
as
桥梁工程系-杨 剑
1.截面的有效高度h0及有效面积 bh0
截面的有效高度h0-截面内纵向受拉钢筋重心至 截面受压边缘的距离;
M/Mu
1.0 Mu 0.8 My
0.6
0.4
Mcr
0
fcr
fy
fu f
桥梁工程系-杨 剑
(a) (b) (c)
(d)
(e) (f) ε cu
钢筋混凝土受弯构件正截面承载力计算

结性能,钢筋的混凝土保护层厚度c一般不小于 25mm;
并符合附录四附表4—1的规定。 截面有效高度 h0 h as
Ý¡ 30mm
1.5d cݡ cmin
d
混凝土保护层计算厚度as:
h0
钢筋一层布置时 as=c+d/2 ,
钢筋二层布置时 as=c+d+e/2, a
其中e为钢筋之间净距。
Ý¡ cmin 1.5d
4.1 概述
第三章 钢筋混凝土受弯构件正截面承载力计算
3.2 受弯构件正载面的试验研究
b
一、适筋梁正截面受力过程
As
ec f
xn
h h0
a
h0:有效截面高度 es 平截面假定
应变片
第三章 钢筋混凝土受弯构件正截面承载力计算
应变图
ec max
应力图 M
et max
Mcr
M
ey
My
M
xf D
Mu Z
现浇梁板:常用C15~C25级混凝土 预制梁板:常用C20~C30级混凝土
● 另一方面,RC受弯构件是带裂缝工作的,由于裂缝宽度 和挠度变形的限制,高强钢筋的强度也不能得到充分利用。
梁常用Ⅱ~Ⅲ级钢筋,板常用Ⅰ~Ⅱ级钢筋。
第三章 钢筋混凝土受弯构件正截面承载力计算
◆截面尺寸确定 ● 截面应具有一定刚度,满足正常使用阶段的验算能
基本公式: fcbx f y As
KM
fcbx(h0
x) 2
f y As (h0
x) 2
x≥bh0时, 会产生超筋破坏。此时截面承载力用
bh0 代入计算 KM
第三章 钢筋混凝土受弯构件正截面承载力计算
单筋矩形
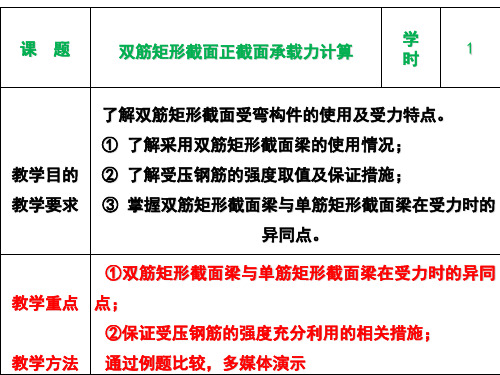
' x 2as
注意:双筋截面一般不会出现少筋破坏,故可不必验算ρmin。 单筋截面与双筋截面的不同在于同时在受拉、受压区 增配了钢筋,相应的承载力得到提高,而此部分的用钢量 对构件的破坏形式影响不大。
截面设计:
计
算
二、双筋矩形截面正截面承载力计算实例讲述
例4.6已知梁的截面bxh=200x400,弯矩的设计值 M=120KN.m,混凝土C20,钢筋HRB335级 设计梁的截面。 解:见黑板
课
题
双筋矩形截面正截面承载力计算
学 时
1
了解双筋矩形截面受弯构件的使用及受力特点。 ① 了解采用双筋矩形截面梁的使用情况;
教学目的
教学要求
② 了解受压钢筋的强度取值及保证措施;
③ 掌握双筋矩形截面梁与单筋矩形截面梁在受力时的 异同点。
①双筋矩形截面梁与单筋矩形截面梁在受力时的异同
教学重点 点; ②保证受压钢筋的强度充分利用的相关措施; 教学方法 通过例题比较,多媒体演示
cu s s s s
s1
s
c
c
s
s
s2
y s
y
5、基本公式及适用条件
◆适用条件
防止超筋脆性破坏
x b h0 或 b
As1 f max b c bh0 fy
M 1 s ,max f cbh02 或 s1 s ,max
保证受压钢筋强度充分利用
一 、双筋矩形截面正截面承载力计算理论
1. 定义:双筋截面是指同时配置受拉和受压钢筋 的情况。
受压钢筋
As'
As
受拉钢筋
2、适用情况:
①
2 Mu M u,max 1 fcbh0 b (1 0.5b ) ,而梁截面尺寸受到限制, fc不能提高时;在受压区配置钢筋可补充混凝土受压
钢筋混凝土受弯构件正截面承载力计算
由相对界限受压区高度b可推出最大配筋率 b及单筋矩形截面的最大受弯承载力Mumax。
As bh0
b
1
f
fc
y
4.3.5 适筋和少筋破坏的界限条件
min.h/h0 b min —— 最小配筋率, 根据钢筋混凝土梁的破坏弯
矩等于同样截面尺寸素砼梁的开裂弯矩 确定的。
确定的理论依据为:
Mu = Mcr
《规范》对min作出如下规定:
(1)受弯构件、偏心受拉、轴心受拉构件其 一侧纵向受拉钢筋的配筋百分率不 应小于0.2%和0.45ft/fy中的较大值 ;
梁的宽度和高度
宽度 :b = 120、150、(180)、200、(220)、 250、300、350、…(mm)
高度:h=250、300、350、400、……、750、800、 900、…(mm)。
二、 截面尺寸和配筋构造
2. 板
c15mm d
分布钢筋
h0
h
d 6 ~ 12mm
h0 h 20
(2)卧置于地基上的混凝土板,板的受拉钢 筋的最小配筋百分率可适当降低, 但不应小于0.15%。
4.4 单筋矩形截面的承载力计算
4.4.1 基本计算公式及适用条件
1fc
x
Mu
C=1fc bx
Ts = fyAs
1. 基本计算公式
N 0
M 0
1 fcbx fyAs (3 - 20)
架立
箍筋
弯矩引起的 垂直裂缝
钢筋混凝土受弯构件正截面承载力计算
为保证钢筋混凝土结构的耐久性、防火性以及钢
筋与混凝土的粘结性能,钢筋的混凝土保护层厚
5度、一配般筋不率小于2A 5msm% ; ....4...2()
bh0
用下述公式表示
As bh0
%
公式中各符号含义:
As为受拉钢筋截面面积; b为梁宽;h0为梁的有效 高度,h0=h-as;as为所有受拉钢筋重心到梁底面 的距离,单排钢筋as= 35mm ,双排钢筋as= 55~60mm 。
M/ M u
Mu
1.0
0.8 My
0.6
II
0.4
III III a II a
M cr I a
I
0
f cr
fy
fu f
加载过程中弯矩-曲率关系
说明:
对于配筋合适的梁,在III
阶段,其承载力基本保持不 变而变形可以很大,在完全
M/ M u
Mu
1.0
破坏以前具有很好的变形能 力,破坏预兆明显,我们把
0.8 My
通常采用两点对称集中加荷,加载点位于梁跨度 的1/3处,如下图所示。这样,在两个对称集中荷载间 的区段(称“纯弯段”)上,不仅可以基本上排除剪力的 影响(忽略自重),同时也有利于在这一较长的区段上(L /3)布置仪表,以观察粱受荷后变形和裂缝出现与开 展的情况。在“纯弯段”内,沿梁高两侧布置多排测 点,用仪表量测梁的纵向变形。
梁破坏时的极限弯矩Mu小于在正常情况下的开
裂弯矩Mcr。梁配筋率越小, Mcr -Mu的差值越大; 越大(但仍在少筋梁范围内), Mcr -Mu的差值越小。
当Mcr -Mu =0时,它就是少筋梁与适筋梁的界限。这
时的配筋率就是适筋梁最小配筋率的理论值min。
建筑结构答案重大2010年造价1221
一、填空题1.建筑结构应满足的三项功能要求是 安全性 、 适用性 、 耐久性 。
2.衡量有明显屈服点钢筋的力学性能指标有① 屈服强度 、 ② 极限强度 、 ③ 伸长率 、④ 冷弯性能 。
3.预加应力的方法有 先张 法和 后张 法 。
4.室内正常环境下,砼强度等级≥C 25时,梁的砼保护层最小厚度为 25 mm 。
5.砼的基本强度有:立方抗压强度、 轴心抗压强度 、 轴心抗拉强度 , 6.《砼结构设计规范》根据 立方体抗压强度标准值 将砼划分为 14 个等级。
7.《建筑结构设计统一标准》将极限状态分为两类,即 承载力 极限状态和 正常使用 极限状态。
8.钢筋级别越高,强度越 高 ,塑性越 低 。
9. h=500 mm 的矩形截面梁中,常见的钢筋有:纵向受力钢筋、弯起钢筋、 侧向构造钢筋 、 箍筋 、 架立筋 。
10. 受弯构件斜截面破坏形态有斜压破坏、 剪压 破坏、 斜拉 破坏,斜截面抗剪承载力计算以 剪压 破坏为计算依据。
11. 受弯构件正截面计算要求b ξξ≤是为了防止 斜拉 破坏。
12. 钢筋冷加工的方法有 冷拉 和冷拔,冷加工后的钢筋 强度 提高,塑性降低 。
13. 钢筋砼轴心受压构件的b l 0越大,ϕ值越 小 。
14. 计算轴心受压构件正截面承载力时,其计算公式为 Nu=0.9Ψ(fc As+fy`As`) 。
15. 受弯构件正截面破坏形态有 适筋 破坏、 超筋 破坏、 少筋 破坏,16. 混凝土在荷载的长期作用下,随正常时间而增长的变形称为徐变。
17. 没有明显屈服点钢筋的条件屈服强度取残余应变为0.2%时所对应的应力σ0.2。
18. 受弯构件斜截面破坏形态有三种,即: 斜压 破坏、 剪压 破坏和 斜拉 破坏;验算ρsv ≥ρsvmin 则是为了防止 斜拉 破坏。
19. 钢筋砼大偏心受压构件破坏的特征是,先受拉一侧钢筋 先屈服 ,而后受压一侧砼___被压碎_。
20. 钢筋按其外表形状不同,可分为 光圆钢筋和 变形 钢筋两种。
T形截面梁讲解
fyAs 1fcb'f x
M
Mu
1fcb'f
x
h0
x 2
M —— 外荷载所产生的弯矩设计值
Mu —— 截面自身的抗弯承载力
f y —— 钢筋抗拉强度设计值(屈服强度)
As —— 受拉钢筋截面面积
fc —— 砼的轴心抗压强度设计值。 b —— 梁截面宽
x —— 砼受压区高度
适用条件
x bh0
1、截面设计
第一类T形截面
M
1fcb'f h'f h0
h'f 2
第二类T形截面
M
1fcb'f h'f
h0
h'f 2
2、截面复核
第一类T形截面
fyAs 1fcb'f h'f
第二类T形截面
fyAs 1fcb'f h'f
三、基本公式及适用条件 (一)第一类T形截面
按单筋矩形截面梁承载力计算公式
As1
M1 fysh0
D、求 AS
As As1 As2
(二)截面复核
已知:内力M,梁截面尺寸 b h ,b'f h'f
纵向受力钢筋截面积 As , 砼等级( fc ) ,钢筋级别( fy )
求:试校核该梁是否安全?(Mu)
设计步骤:
1、判别截面类型
当 fyAs 1fcb'f h'f 第一类T形截面 当 fyAs 1fcb'f h'f 第二类T形截面
砼C20
例2、有一独立T形截面梁,bf´=600mm, b=300mm,
h'f =120mm,承受 M 45.4 107 N mm ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单筋矩形截面梁承载力验算主讲教师:吕文晓
截面验算工程案例
某钢筋混凝土矩形截面梁,跨中弯矩设计值M=150kN·m,梁的截面尺寸b×h=250×500mm,采用C30级混凝土,HRB400级钢筋。
已在受拉区配置有4根直径为20mm的钢筋,试验算该梁承载力是否满足要求。
单筋矩形截面梁
承载力计算基本公式
s y c 1A f bx f =α()
201x h bx f M M c u -=≤α
y c b s b
b b f f bh A h x x 1max 00
αξρρξξξ=≤=≤=≤防止超筋破坏:防止少筋破坏:bh
A A S S min min ,min
ρρρ=≥≥适用条件
案例解析计算步骤:
1.验算是否少筋梁
2.由基本公式1求得x
3.验算是否为超筋梁
4.由基本公式2求得M U
案例解析
1.查取相关系数
查表得f c=14.3N/mm2,f t=1.43 N/mm2,f y=360N/mm2,α1=1.0,ξ
=0.518,钢筋面积A s=1256mm2
b
纵向受力钢筋为单排,
则h0=h-40=500-40=460mm
案例解析
2.验算是否为少筋梁
0.45f t/f y=0.45×1.43/360=0.19%<0.2%,取ρmin=0.2%
A
=0.2%×250×500=250mm2 s,min
<A s=1256mm2不属少筋梁。
3.利用基本公式1求得x
案例解析
mm b f A f x c s
y 48.126250
3.140.112563601=⨯⨯⨯==α
4.验算是否为超筋梁
案例解析
满足不超筋的要求
∴<==⨯==b
b b x mm x mm h x 48.12628.238460518.00Θξ
5.利用基本公式2求得M u
案例解析
m kN mm N x h x b f M c u ⋅=⋅⨯=-⨯⨯⨯⨯=-⋅=4.179104.179)2/48.126460(48.1262503.140.1)
2/(601α满足承载力要求∴<⋅=u
M m kN M 150Θ
思考题
某钢筋混凝土矩形截面梁,梁的截面尺寸b×h=200×500mm,采用C30级混凝土,HRB400级钢筋。
已在受拉区配置有5根直径为25mm的钢筋,试求该梁的极限承载力。
小结
1.正截面承载力验算又称为截面复核
2.截面复核和截面设计异同点
3.两个公式两个条件必不可少。
