chp2 fundamentals of probability
Chp_

示功图(功的图示法)
F dA F dx
FX
A F dx 面积
Xb Xa
O
xa
dx
xb
x
力 位移曲线下的面积表示力F所作的功的大小
P.22/75
质点动力学
例2-6. 设作用力的方向沿 Ox 轴,其大小与 x 的关系 如图所示,物体在此作用力的作用下沿 Ox 轴运动。求 物体从O 运动到 2m的过程中,此作用力作的功 A。
例2-4.一质点做圆周运动,有一力 F F0 xi yj 作 用于质点,在质点由原点至P(0,2R)点过程中,力 F 做的功 A = ?
P
C
y
R
.
m
F
解:
r
x
O
dr dxi dyj
r xi yj
F F0 xi F0 yj
R
2
mg
cos sin
则有:
g
g cos g sin 2 R cos 2 R sin
g sin 2 R cos g cos 2 R sin
对给定的
ω
μ
P.19/75
、R和 值, 不能小于此值,否则最大静摩擦力不足以维持m在斜面上不动.
两边积分:
R dt 2 dv v
t
0
dt
v 3 v
R dv 2 v
P.10/75
质点动力学
例2-2. 一质量为 m 的小球最初位于如图所示的 A 点, 然后沿半径为 r 的光滑圆弧的内表面ADCB下滑。试求 小球在C 时的角速度和对圆弧表面的作用力。 解:取自然坐标系,小球受力如图 r O A B eτ en Ft v C D G mg
数学毕业论文---常见分布的性质及其应用

数学毕业论文---常见分布的性质及其应用目录第一章:绪论------------------------------------------------------------------- 31.1 随机变量------------------------------------------------------------------------------31.2 离散型随机变量及其分布---------------------------------------------------------31.3 连续型随机变量及其分布---------------------------------------------------------4 第二章:常见离散型分布及其应用-----------------------------------------42.1 0-1分布及其应用---------------------------------------------------------------- ----42.2 几何分布及其应用-------------------------------------------------------------------52.3 二项分布及其应用-------------------------------------------------------------------62.4 泊松分布及其应用-------------------------------------------------------------------7 第三章:常见连续型分布及其应用-----------------------------------------113.1 均匀分布及其应用-----------------------------------------------------------------113.2 指数分布及其应用-----------------------------------------------------------------123.3 正态分布及其应用-----------------------------------------------------------------13 参考文献------------------------------------------------------------------------23常见分布的性质及其应用张久恩,数学计算机学院摘要:在概率论领域里,我们研究的概率分布大体分为两种,离散型概率分布和连续性概率分布。
英文版概率论与数理统计重点单词
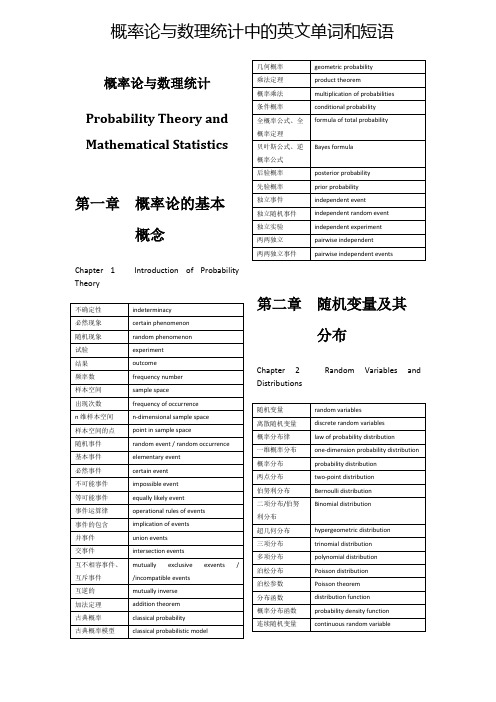
概率论与数理统计Probability Theory and Mathematical Statistics第一章概率论的基本概念Chapter 1 Introduction of Probability Theory不确定性indeterminacy必然现象certain phenomenon随机现象random phenomenon试验experiment结果outcome频率数frequency number样本空间sample space出现次数frequency of occurrencen维样本空间n-dimensional sample space样本空间的点point in sample space随机事件random event / random occurrence基本事件elementary event必然事件certain event不可能事件impossible event等可能事件equally likely event事件运算律operational rules of events事件的包含implication of events并事件union events交事件intersection events互不相容事件、互斥事件mutually exclusive exvents / /incompatible events互逆的mutually inverse加法定理addition theorem古典概率classical probability古典概率模型classical probabilistic model 几何概率geometric probability乘法定理product theorem概率乘法multiplication of probabilities条件概率conditional probability全概率公式、全概率定理formula of total probability贝叶斯公式、逆概率公式Bayes formula后验概率posterior probability先验概率prior probability独立事件independent event独立随机事件independent random event独立实验independent experiment两两独立pairwise independent两两独立事件pairwise independent events第二章随机变量及其分布Chapter 2 Random Variables and Distributions随机变量random variables离散随机变量discrete random variables概率分布律law of probability distribution一维概率分布one-dimension probability distribution 概率分布probability distribution两点分布two-point distribution伯努利分布Bernoulli distribution二项分布/伯努利分布Binomial distribution超几何分布hypergeometric distribution三项分布trinomial distribution多项分布polynomial distribution泊松分布Poisson distribution泊松参数Poisson theorem分布函数distribution function概率分布函数probability density function连续随机变量continuous random variable概率论与数理统计中的英文单词和短语概率密度probability density概率密度函数probability density function 概率曲线probability curve均匀分布uniform distribution指数分布exponential distribution指数分布密度函数exponential distribution density function正态分布、高斯分布normal distribution标准正态分布standard normal distribution正态概率密度函数normal probability density function正态概率曲线normal probability curve标准正态曲线standard normal curve柯西分布Cauchy distribution分布密度density of distribution第三章多维随机变量及其分布Chapter 3 Multivariate Random Variables and Distributions二维随机变量two-dimensional random variable联合分布函数joint distribution function二维离散型随机变量two-dimensional discrete random variable二维连续型随机变量two-dimensional continuous random variable联合概率密度joint probability variablen维随机变量n-dimensional random variablen维分布函数n-dimensional distribution functionn维概率分布n-dimensional probability distribution 边缘分布marginal distribution边缘分布函数marginal distribution function边缘分布律law of marginal distribution边缘概率密度marginal probability density二维正态分布two-dimensional normal distribution二维正态概率密two-dimensional normal probability 度density二维正态概率曲线two-dimensional normal probabilitycurve条件分布conditional distribution条件分布律law of conditional distribution条件概率分布conditional probability distribution条件概率密度conditional probability density边缘密度marginal density独立随机变量independent random variables第四章随机变量的数字特征Chapter 4 Numerical Characteristics fo Random Variables数学期望、均值mathematical expectation期望值expectation value方差variance标准差standard deviation随机变量的方差variance of random variables均方差mean square deviation相关关系dependence relation相关系数correlation coefficient协方差covariance协方差矩阵covariance matrix切比雪夫不等式Chebyshev inequality第五章大数定律及中心极限定理Chapter 5 Law of Large Numbers and Central Limit Theorem大数定律law of great numbers切比雪夫定理的special form of Chebyshev theorem特殊形式依概率收敛convergence in probability伯努利大数定律Bernoulli law of large numbers同分布same distribution列维-林德伯格定理、独立同分布中心极限定理independent Levy-Lindberg theorem辛钦大数定律Khinchine law of large numbers利亚普诺夫定理Liapunov theorem棣莫弗-拉普拉斯定理De Moivre-Laplace theorem第六章样本及抽样分布Chapter 6 Samples and Sampling Distributions统计量statistic总体population个体individual样本sample容量capacity统计分析statistical analysis统计分布statistical distribution统计总体statistical ensemble随机抽样stochastic sampling / random sampling 随机样本random sample简单随机抽样simple random sampling简单随机样本simple random sample经验分布函数empirical distribution function样本均值sample average / sample mean样本方差sample variance样本标准差sample standard deviation标准误差standard error样本k阶矩sample moment of order k样本中心矩sample central moment样本值sample value样本大小、样本容量sample size样本统计量sampling statistics随机抽样分布random sampling distribution抽样分布、样本分布sampling distribution自由度degree of freedomZ分布Z-distributionU分布U-distribution第七章参数估计Chapter 7 Parameter Estimations统计推断statistical inference参数估计parameter estimation分布参数parameter of distribution参数统计推断parametric statistical inference点估计point estimate / point estimation总体中心距population central moment总体相关系数population correlation coefficient总体分布population covariance总体协方差population covariance点估计量point estimator估计量estimator无偏估计unbiased estimate / unbiasedestimation估计量的有效性efficiency of estimator矩法估计moment estimation总体均值population mean总体矩population moment总体k阶矩population moment of order k总体参数population parameter极大似然估计maximum likelihood estimation极大似然估计量maximum likelihood estimator极大似然法maximum likelihood method /maximum-likelihood method似然方程likelihood equation似然函数likelihood function区间估计interval estimation置信区间confidence interval置信水平confidence level置信系数confidence coefficient单侧置信区间one-sided confidence interval置信上限confidence upper limit置信下限confidence lower limitU估计U-estimator正态总体normal population总体方差的估计estimation of population variance 置信度degree of confidence方差比variance ratio第八章假设检验Chapter 8 Hypothesis Testings参数假设parametric hypothesis假设检验hypothesis testing两类错误two types of errors统计假设statistical hypothesis统计假设检验statistical hypothesis testing检验统计量test statistics显著性检验test of significance统计显著性statistical significanceone-sided test单边检验、单侧检验one-sided hypothesis单侧假设、单边假设双侧假设two-sided hypothesis双侧检验two-sided testing显著水平significant levelrejection region拒绝域/否定区域接受区域acceptance regionU检验U-testF检验F-test方差齐性的检验homogeneity test for variances 拟合优度检验test of goodness of fit。
An Introduction to Probability Theory - Geiss

5
6 Secondly, we take a function f :Ω→R
CONTENTS
which gives for all ω the difference f (ω ) = T − S . From properties of this function we would like to get useful information of our thermometer and, in particular, about the correctness of the displayed values. So far, the things are purely abstract and at the same time vague, so that one might wonder if this could be helpful. Hence let us go ahead with the following questions: Step 1: How to model the randomness of ω , or how likely an ω is? We do this by introducing the probability spaces in Chapter 1. Step 2: What mathematical properties of f we need to transport the randomness from ω to f (ω )? This yields to the introduction of the random variables in Chapter 2. Step 3: What are properties of f which might be important to know in practice? For example the mean-value and the variance, denoted by
a level 概率统计学 词汇

1111- Probability 概率- Random variable 随机变量- Distribution 分布- Binomial distribution 二项分布- Poisson distribution 泊松分布- Normal distribution 正态分布- Standard deviation 标准差- Sample mean 样本均值- Hypothesis testing 假设检验- Confidence interval 置信区间- Central limit theorem 中心极限定理- Correlation 相关性- Regression 回归- ANOVA 方差分析- Chi-squared test 卡方检验- Independence 独立性- Random sample 随机样本- Population 参数- Sample statistic 样本统计量- Sampling distribution 抽样分布- Statistical inference 统计推断- p-value p 值- Margin of error 误差幅度- Statistical significance 统计显著性- Cumulative distribution function 累积分布函数- Probability density function 概率密度函数- Expected value 期望值- Variance 方差- Moments 矩- Skewness 偏度- Kurtosis 峰度- Time series 时间序列- Stationarity 平稳性- Autocorrelation 自相关- Linear regression 线性回归- Multiple regression 多元回归- Logistic regression 逻辑回归- Residuals 残差- ANOVA table 方差分析表- Factor analysis 因子分析- Cluster analysis 聚类分析- Principal component analysis 主成分分析这些词汇是 A-Level 概率统计学科的基础,掌握它们对于理解和解决相关问题至关重要。
南京大学随机过程练习题附中文解释及答案

8、(3.8)An unbiased die is successively rolled. Let X and Y denote, respectively, the number of rolls necessary to obtain a six and a five. Find (a) E[X], (b) E[X|Y=1] 相继地掷一颗不均匀的骰子。令 X 和 Y 分别记得到一个 6 和一个 5 所必须的抛 掷次数。求(a)E[X],(b)E[X|Y=1]。 重要:E[E[X|Y]]=E[X]
3、(4.32) Each of two switches is either on or off during a day. On day n, each switch will independently be on with probability [1+#of on switches during day n-1]/4. For instance, if both switches are on during day n-1, then each will independently be on during day n with probability3/4. What fraction of days are both switches on? What fractions are both off? 在一天中两个开关或者开或者关。在第 n 天,每个开关独立地处于开的概率是[1+ 第 n-1 天是开的开关数]/4。例如,如果在第 n-1 天两个开关都是开的,那么在第 n 天,每个开关独立地处于开的概率是 3/4。问两个开关都是开的天数的比例是 多少?两个开关都是关的天数的比例是多少?
(完整word版)英文版概率论与数理统计重点单词
Bayes formula
后验概率
posterior probability
先验概率
prior probability
独立事件
independent event
独立随机事件
independent random event
独立实验
independent experiment
两两独立
classical probabilistic model
几何概率
geometric probability
乘法定理
product theorem
概率乘法
multiplication of probabilities
条件概率
conditional probability
全概率公式、全概率定理
formula of total probability
基本事件
elementary event
必然事件
certain event
不可能事件
impossible event
等可能事件
equally likely event
事件运算律
operational rules of events
事件的包含
implication of events
并事件
union events
似然方程
likelihood equation
似然函数
likelihood function
区间估计
interval estimation
置信区间
confidence interval
置信水平
confidence level
fundamentalsofmu...
Chapter 15International Portfolio Theory and DiversificationT QuestionsDiversification benefits1. How does the diversification of a portfolio change its expected returns and expected risks? Is this inprinciple any different for internationally diversified portfolios?The diversification of a portfolio results primarily in the reduction of risk. For a domestic portfolio, the diversification of the portfolio results in a weighted average expected return, but a reduction in risk as the returns of individual securities will be less than perfectly correlated.This principle also applies to international diversification, but the definition of the “market” isexpanded with many new securities with their respective risks, returns, and correlations being added.The other added component of international diversification is the introduction of currency risk.Risk reduction2. What types of risk are present in a diversified portfolio? Which type of risk remains after theportfolio has been diversified?A diversified portfolio has systematic risk and unsystematic risk. Systematic risk is the risk of themarket itself. Unsystematic risk is the risk of individual securities within the market and the portfolio.Increasing the number of securities in the portfolio reduces and ultimately eliminates theunsystematic risk—the risk of the individual securities—leaving only the risk of the market, the systematic risk.Measurement of risk3. How, according to portfolio theory, is the risk of the portfolio measured exactly?If we assume a portfolio consists of two assets, asset 1 and asset 2, The weights of investment in thetwo assets are w1 and w2respectively, and w1+ w2= 1. The risk of the portfolio (σp), usuallyexpressed in terms of the standard deviation of the portfolio’s expected return, is given by the following equation:pσ=where σ12and σ22 are the variances of the expected returns of risky assets 1 and 2, respectively. σ1andσ2are their respective standard deviations. ρ12is the correlation coefficient between the two assets’returns.Chapter 15 International Portfolio Theory and Diversification 281Market risk4. If all national markets have market risk, is all market risk the same?All market risk is not the same because all markets, like individual assets, are not perfectly correlated in their returns. The addition of additional markets to the potential portfolio of the investor reduces the overall market risk below that of any individual market.Currency risk5. The currency risk associated with international diversification is a serious concern for portfoliomanagers. Is it possible for currency risk ever to benefit the portfolio’s return?Currency risk for a portfolio, like currency risk for a firm or a currency speculator, can be positive or negative. If an individual investors buys a security denominated in a currency, which then appreciates against the home currency of the investor, it increases the expected returns of the investor in home currency terms. Different international portfolios and portfolio managers deal with this concern very differently. Some international portfolios wish to hedge the currency risk as much as possible,focusing on the expected returns and risks of the individual assets for their portfolio goals. Other managers, however, use the currency of denomination of the asset as part of the expected returns and risks from which the manager is trying to profit.Optimal domestic portfolio6. Define in words (without graphics) how the optimal domestic portfolio is constructed.An investor may choose any portfolio of assets which lie within the domestic portfolio opportunity set. In order to maximize expected return while minimizing expected risk, the investor will find a combination of the risk-free asset available in the market with some portfolio of risky assets as found in the domestic portfolio opportunity set. The optimal domestic portfolio is then found as thatportfolio which provides the highest expected return when combined with the riskless asset and the lowest possible expected portfolio risk.Minimum risk portfolios7. If the primary benefit of portfolio diversification is risk reduction, is the investor always better offchoosing the portfolio with the lowest expected risk?The portfolio with the lowest expected risk is not the same thing as the optimal portfolio. Theportfolio with minimum risk is measured only on that basis—risk—and does not consider the relative amount of expected return per unit of expected risk. Modern portfolio theory assumes that investors are risk averse, but are in search of the highest expected return per unit of risk which they canachieve.International risk8. Many portfolio managers, when asked why they do not internationally diversify their portfolios,answer that “the risks are not worth the expected returns.” Using the theory of internationaldiversification, how would you evaluate this statement?This means that, at least from their perspective, they do not expect that international diversification will result in any net reduction in the potential portfolio opportunity set’s risk. This is equivalent to saying that internationally diversifying the portfolio does not cause an inward shift of the portfolio opportunity set as illustrated in Exhibits 19.4 and 19.5.282 Moffett • Fundamentals of Multinational Finance, Second EditionCorrelation coefficients9. The benefits of portfolio construction, domestically or internationally, arise from the lack ofcorrelation among assets and markets. The increasing globalization of business is expected to change these correlations over time. How do you believe they will change and why?Many experts have expected the correlations between markets to slowly but steadily increase over time as the world “globalizes.” There are, however, many political and institutional frictions and barriers which may cause this to be a very, very long process.One important development over the past decade complicates this process. While more and more countries have opened their markets to foreign investors and firms, more and more of the world’s publicly traded firms are listing and trading in the world’s primary equity markets of London and New York in addition to their individual domestic equity markets. This reduces market segmentation, increases correlation, and increases liquidity.Relative risk and return10. Conceptually, how do the Sharpe and Treynor performance measures define risk differently? Whichdo you believe is a more useful measure in an internationally diversified portfolio?The Sharpe measure (SHP) defines risk as the standard deviation of the returns of the portfolio. The Treynor measure (TRN) uses a measure of risk which measures the systematic risk of the portfolio versus the world market portfolio. If a portfolio is poorly diversified, it is possible for it to show a high ranking on the basis of the Treynor measure, but a lower ranking on the basis of the Sharpe measure. The two measures provide different information, but are useful in their own ways when evaluating portfolios which are not always adequately diversified.International equities and currencies11. As the newest member of the asset allocation team in your firm, you constantly find yourself beingquizzed by your fellow group members. The topic this morning is international diversification. One analyst asks you the following question:Security prices are driven by a variety of factors, but corporate earnings are clearly one of theprimary drivers. And corporate earnings—on average—follow business cycles. Exchange rates, as they taught you back in college, reflect the market’s assessment of the growth prospects forthe economy behind the currency. So if securities go up with the business cycle, and currenciesgo up with the business cycle, why do we see currencies and securities prices across the globenot going up and down together?Answer her questionWhat sounds so simple at first glance is not. First, exchange rate values change as a result of many factors (as described in earlier chapters of this book), not just business cycles. Expected changes in inflation, real interest rates, political and country risk, current account balances, to name a few, all influence the movement of exchange rates. Secondly, even if business cycles were a primary driver of currency values, business cycles are not perfectly correlated globally. In fact, one way to appreciate this phenomenon is to consider that in 2001–2002 most of the major industrial economies were either in recession or near-recession, but currencies still fluctuated widely. For example, the Japanese yen first depreciated against the dollar in the early part of 2002, but still appreciated significantly by mid-year.Chapter 15 International Portfolio Theory and Diversification 283Are MNEs global investments?12. Firms with operations and assets across the globe, true MNEs, are in many ways as international incomposition as the most internationally diversified portfolio of unrelated securities. Why do investors not simply invest in MNEs traded on their local exchanges and forego the complexity of purchasing securities traded on foreign exchanges?Actually, many investors do consider ownership in the securities of a MNE listed on their localexchange as a substitute for international diversification. Although generating its earnings partially in different countries and currencies, its results are reported in the home currency of the parentcompany. The MNE bears the currency risk of ‘international diversification’ internally, rather than the investor bearing the explicit risk of international diversification.ADRs versus direct holdings13. When you are constructing your portfolio, you know you want to include Cementos de Mexico(Mexico) in it, but you cannot decide whether you wish to hold it in the form of ADRs traded on the NYSE or directly through purchases on the Mexico City Bolsa.(a) Does it make any difference in regard to currency risk? The currency risk is the same.(b) List the pros and cons of ADRs and direct purchases. ADRs convey certain technical advantagesto U.S. shareholders. Dividends paid by a foreign firm are passed to its custodial bank and then to the bank that issued the ADR. The issuing bank exchanges the foreign currency dividends forU.S. dollars and sends the dollar dividend to the ADR holders. ADRs are in registered form,rather than in bearer form. Transfer of ownership is facilitated because it is done in the UnitedStates in accordance with U.S. laws and procedures. In the event of death of a shareholder, theestate need not to go through probate in a foreign court system. Normally, trading costs are lower than when buying or selling the underlying shares in their home market. Settlement is usuallyfaster in the United States. Withholding taxes are simpler because they’re handled by thedepositary bank.(c) What would you recommend if you were an asset investor for a corporation with no internationaloperations or internationally diversified holdings? Discussion question.T Mini-Case: Strategic Hedging1. According to Exhibit 1, were there a significant number of portfolio managers able to add value tointernational portfolios through active (selective) currency management consistently over the time period studied?The top 25th percentile were consistently able to outperform the median and mean significantly with respect to active return. However, this does not show the risk that needed to be acquired or accepted to achieve those returns, at least not in exhibit 1.2. According to Exhibit 2, would the international investor in an Australia portfolio be better off, onaverage, with a completely hedged or unhedged portfolio?It is not possible to determine if an international investor would be better off being hedged orunhedged. An Australian-only investor would have had a higher return unhedged (4.44% versus3.30%), but a higher level of risk (15.60% versus 14.10%). However, an international investor wouldbe able to reduce they Australian equities’ risk, both hedged and unhedged, through international portfolio diversification.284 Moffett • Fundamentals of Multinational Finance, Second Edition3. If you were Sean, what would you conclude from this specific study?Sean may have learned a number of different things. First, that although a portfolio is internationally diversified, that is not the same thing as ‘hedged.’ Secondly, that hedging does not—at least on the basis of the data provided—guarantee any better or worse returns over time. In fact, Sean might come to the same conclusion that traditional corporate treasurers have for many years, that selectivehedging may protect the firm or the portfolio from significant losses in value from unforseenexchange rate changes, but that in the long run, the risks and returns to hedging do appear to average out.Chapter 15 International Portfolio Theory and Diversification 285 T ProblemsWhat is the return on this investment in foreign securities?Jan 1st Dec 31stElement Purchase Sale DistributionsShare price, euros P135.00 P157.60 P15.00Exchange rate, US$/euro $1.0660 $1.1250Gain inLocal Currency Percentagea. Return on the security in local currency termsCapital appreciation 22.60 16.74%Dividend distribution 15.00 11.11%Total return 37.60 27.85%b. Return on the security in US$ termsInitial investment in US$ $100,000.00Converted to euros P93,808.63Purchases shares at initial price P135.00Holding this number of shares 694.88Which earn this dividend per share P15.00Total dividend income P10,423.18Ending share price P157.60Total euro proceeds, Dec 31 P119,936.07End of period exchange rate, US$/euro $1.1250End of period proceeds, US$ $134,928.08Rate of return in US$ terms 34.93%(ending/beginning) −1c. Although both returns appear to be very good for a one year period, the relative returnon an individual security should always be compared to that of the market as a whole(or some index of the market).286 Moffett • Fundamentals of Multinational Finance, Second EditionAssumptions Expected Return Expected Risk (σ) Correlation (ρ) Boeing (US) 18.60% 22.80% 0.60 Unilever (UK) 16.00% 24.00%PORTFOLIO ANALYSISWeight of Weight of Expected ExpectedBoeing in Unilever in Risk ReturnPortfolio Portfolio (percent) (percent)1.00 0.00 22.80% 18.60%0.95 0.05 22.40% 18.47%0.90 0.10 22.04% 18.34%0.85 0.15 21.73% 18.21%0.80 0.20 21.47% 18.08%0.75 0.25 21.25% 17.95%0.70 0.30 21.08% 17.82%0.65 0.35 20.97% 17.69%0.60 0.40 20.90% 17.56%0.55 0.45 20.89% 17.43%0.50 0.50 20.93% 17.30%0.45 0.55 21.02% 17.17%0.40 0.60 21.17% 17.04%0.35 0.65 21.36% 16.91%0.30 0.70 21.61% 16.78%0.25 0.75 21.90% 16.65%0.20 0.80 22.24% 16.52%0.15 0.85 22.62% 16.39%0.10 0.90 23.04% 16.26%0.05 0.95 23.50% 16.13%0.00 1.00 24.00% 16.00%Expected Return Expected Risk Correlationa. Equally weighted 17.30% 20.93% +0.6portfolio hasb. 70% Boeing & 17.82% 21.08% +0.630% Unileverc. Optimal portfolio 17.43% 20.89% +0.655% Boeing, 45% Unilever(assume ‘optimal’ is minimum risk)292 Moffett •Fundamentals of Multinational Finance, Second EditionWhat were the returns on the Brazilian diversification?April 10, 2002 April 10, 2003 Element Purchase SaleShare price of SPYDERS (US dollars) $112.60 $87.50Exchange rate (Reais/$) 2.27 3.22Index Price Percentagea. Return on the security in US dollar termsInitial price 112.60Ending price 87.50Total change in price (25.10) −22.29%b. Return on the security in Brazilian reais termsInitial investment in Brazilian reais R$ 500,000Initial exchange rate (R$/$) 2.27Converted to dollars $220,264.32Purchases shares at initial price $112.60Holding this number of shares 1,956.17Ending share price $87.50Ending proceeds in US$ $171,164.54End of period exchange rate, R$/$ 3.22End of period proceeds, R$ R$ 551,149.83Rate of return in Brazilian reais 10.23%(ending/beginning) −1c. The Brazilian investor did indeed make a positive return on its investment. However,the return was positive only because of the fall in the value of the Brazilian real, as the SPYDERS themselves lost more than 22% of their value over this period of the bearmarket. If the Brazilian investors could have invested its R$500,000 in an interestbearing deposit in Brazil and earn 12%, it would have actually made a higher return(12% > 10.23%), but there would have been no up-side potential as offered by the USequity market possessed (but didn’t deliver).。
probability_theory_and_examples_课后解答
probability theory and examples 课后解答1. 引言1.1 概述概率论是一门研究随机事件发生的可能性及其规律的数学分支。
随机性存在于我们日常生活中的各个方面,从天气预报到股市波动,从飞机失事的概率到买彩票中奖的概率,无处不在。
因此,了解和应用概率论对我们做出正确决策、推断和预测至关重要。
本篇长文旨在深入讲解概率论的基本理论和主要计算方法,并通过实际应用例子进行解析。
文章将介绍概率论的基本概念和定义,探讨概率公理化系统及其在随机变量与概率分布中的应用。
同时,我们将详细介绍组合与排列的计算方法、条件概率和全概率公式、独立事件和乘法法则等重要内容。
另外,我们还将深入讨论常见的概率分布模型,包括二项分布、泊松分布、正态分布等连续型和离散型随机变量,并探讨它们的特征参数与统计推断方法。
最后,我们将通过实际案例展示如何应用所学知识进行数据分析和推断。
1.2 文章结构本文共分为五个主要部分。
首先,在概率论的概述中,我们将介绍本文的背景和目的,解释概率论在现实生活中的重要性。
其次,在概率理论概述部分,我们将详细讨论概率论的基本定义和基本概念,并介绍随机变量与概率分布的关系。
然后,在概率计算方法部分,我们将深入探讨组合与排列的计算方法、条件概率和全概率公式以及独立事件和乘法法则等内容。
接下来,在常见的概率分布模型部分,我们将详细介绍二项分布、泊松分布、正态分布等常见模型,并说明它们在实际应用中的意义。
最后,在结论部分,我们将总结文章主要观点和发现,并提出对未来研究的展望和建议。
1.3 目的本篇长文旨在帮助读者全面了解并掌握概率论及其应用方法。
通过学习本文所述内容,读者将能够理解概率论相关术语和定理,并能够应用这些知识进行数据统计、推断和预测。
无论是从事科学研究、金融投资还是进行决策分析,概率论都提供了一种强大而必不可少的工具。
在完成本篇长文阅读后,我们相信读者将能够更加自信地应对各种概率相关问题,并在实践中获得更好的成果。
[理学]概率论与数理统计英文 第四章-精品文档
(b) Select 5 bulbs randomly from the product of company X, what is the probability that at least 3 of them has life longer than 450 hrs.
, (4.1.4)
Where is the mean ofX, is referred to as thestandard deviation.
We easily get
.(4.1.5)
Example4.1.5
Determining the mean and variance using the probability density function
Note Equation (4.5.1) really gives a density function, since
Theorem4.5.1The mean and variance of a continuous random variableXhaving exponential distribution with parameter is given by
.
ProofSince the probability density function ofXis (4.5.1), we have
Example4.5.1.
Assume that the lifeYof bulbs produced by company X has exponential distribution with mean .
