三角形等积变形 Microsoft Office PowerPoint 演示文稿 2
相似三角形复习——比例式等积式的几种常见证明方法PPT课件
利用等积 式代换
G
C
D
A
E
B
第4页/共13页
第5页/共13页
D F
C E
A
B
BE2=EA·E
C
A
B D
E C
F
P AC:AB=AD:BD
G
C
D
A
B
E
EC2=EA·EB
第6页/共13页
C
A
D
B
在这一个图形中,有两个垂直,有
____对相似,三有___对互余的角,有
_分四__别__是组对应成比例的线段,五它们
第9页/共13页
1.通过本节课的学习,你有什么 收获?还有什么困惑吗?
2.你对自己本节课的表现满意吗? 为什么?
第10页/共13页
作业纸
老师寄语:若希望成功,当以恒心为 良友,以经验为参谋,以信心为光荣, 以希望为哨兵。
第11页/共13页
再见
欢迎多提宝贵意见
第12页/共13页
感谢您的观看!
第13页/共13页
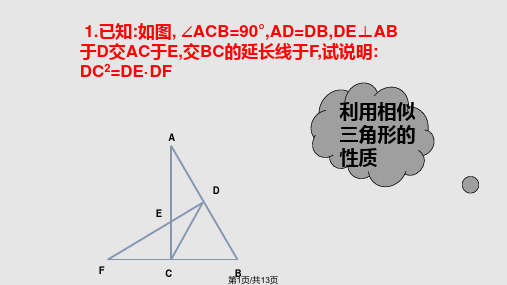
1.已知:如图, ∠ACB=90°,AD=DB,DE⊥AB 于D交AC于E,交BC的延长线于F,试说明: DC2=DE·DF
利用相似
A
三角形的
性质
D E
F
C
第B1页/共13页
2. 如图,在直角梯形ABCD中,AB∥CD, AB⊥BC,对角线AC⊥BD,垂足为E,AD=BD, 过点E作EF∥AB交AD于F, 试说明 (1)AF=BE (2) AF2=AE·EC
利用等线 段代换
D F
C E
A
B
第2页/共13页
3.已知,如图,在△ABC中, ∠BAC=90°, AD⊥BC,垂足为D,E是AC的中点,ED的延 长线交AB的延长线于点F. 试说明:AB:AC=DF:AF
第三讲 等积变形

第三讲等积变形
第三讲等积变形
思考一:三角形按角度大小课分为哪几类?三角形的面积怎噩梦计算?一个三角形有几个底几个高?你会作三角形的高吗?(尤其是钝角三角形的高)
思考二:三角形的高不变,底变,面积会不会变?怎么变?反过来呢?
思考三:你能把一个三角形分成面积相等的两份吗?如果是三份、四份……n份你还会吗?
(想想还有别的分法么?)
思考四:找等高三角形
例如在上图中,若以BC所在的直线为底,发现∆
,为等高三角形,你能找出思考三中画出的三∆,
ABD∆
ABC
ADC
角形中有哪些等高三角形吗?
思考五:你会画辅助线吗?什么时候需要画辅助线?该怎么画辅助线呢?(例3,例4,例5)
(辅助线的做法:找到有倍数关系的边,以它们所在的直线为底,找等高三角形)
思考六:你还记得一半模型吗?如果变一变你还会吗?(提高学案四)
思考七:(1)下面平行线间的三个三角形有什么关系呢?
(2)下面梯形中有几组三角形面积相等,你能找出来
吗?
思考八:两个并排的正方形,同方向的一组对角线平行吗?阴影部分的面积怎么求?(例6,尖子班学案4,超常挑战)。
最新五大模型——三角形等积变形、共角模型说课讲解

(★★★)已知三角形DEF的面积为18,AD∶BD=2∶3,AE∶CE=1∶2,BF∶CF=3∶2,则三角形ABC的面积为?小升初几何重点考查内容(★★★)如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积。
(★★★★)如图将四边形ABCD四条边AB、CB、CD、AD分别延长两倍至点E、F、G、H,若四边形ABCD的面积为5cm2,则四边形EFGH的面积是多少?(★★★)图中三角形ABC的面积是180平方厘米,D是BC的中点,AD的长是AE长的3倍,EF的长是BF长的3倍。
那么三角形AEF的面积是多少平方厘米(★★★★)如图,大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成。
求阴影部分的面积。
(★★★★★)(2009年“学而思杯”六年级)如图BC=45,AC=21,△ABC被分成9个面积相等的小三角形,那么DI+FK=_____。
在线测试题温馨提示:请在线作答,以便及时反馈孩子的薄弱环节。
1.★★★★设111,,,345AD AB BE BC FC AC===如果三角形DEF的面积为19平方厘米,那么三角形ABC的面积是多少平方厘米?A.46.7 B.45.3 C.45.6 D.46.5FEDCBA2.★★★如下图,将三角形ABC 的BA 边延长1倍到D ,CB 的边延长2倍到E ,AC 边延长1倍到F 。
如果三角形ABC 的面积等于1,那么三角形DEF 的面积是多少? A .10 B .8 C .9 D .11EFDCBA3.★★★★★如图,把四边形ABCD 的各边都延长3倍,得到一个新四边形EFGH ,如果ABCD 的面积是6,则EFGH 的面积是( )? A .130 B .145 C .160 D .1504.★★★★如图, D 是BC 的中点,AD 的长是AE 长的3倍,EF 的长是BF 长的3倍.三角形AEF 的面积是18平方厘米,三角形ABC 的面积是( )平方厘米? A .144 B .168 C .72 D .1005.★★图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是( ) A .50 B .48 C .56 D .45EGC B6.★★★如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =。
面积法与等积变换(PPT)5-3

思考 3.如图,在四边形 ABCD 中, △ABD,△BCD,△ABC 的 面 积 比 是 3:4:1, 点 M , N 分 别 在 AC,CD 上 , 满 足 AM : AC CN : CD,并且 B, M , N 共线,求证: M 与 N 分 别是 AC 和 CD的中点.(1983 年全国高中联赛题)
提示:设 AM CN r 0 AC CD
利用面积得图中的一些线段比. 对△DEC 运用梅涅劳斯定理可得 关于 r 的方程,解方程即可.
思考4
3.等积变换
一个图形经过变形,但面积保持不变,这种变形称为
等积变换.
叫脖领子。 【脖子】?名头和躯干相连接的部分。 【博】①(量)多;丰富:渊~|地大物~|~而不精。②通晓:~古通今。③〈书〉大:宽衣~带。④ ()名姓。 【博】(②簙)①博取;取得:聊~一笑|以~欢心。②古代的一种棋戏,后来泛指:~徒|~局。 【博爱】’动指普遍地爱世间所有的人:~ 众生。 【博采众长】广泛地采纳各家的;BBQ电影 BBQ电影 ;长处。 【博彩】名指、摸彩、抽奖一类活动:~业。 【博大】形宽广;丰 富(多用于抽象事物):~的胸怀|学问~而精深。 【博大精深】ī(思想、学说等)广博高深。 【博导】名博士研究生导师的简称。 【博得】动取得;得 到(好感、同情等):~群众的信任|这个电影~了观众的好评。 【博古】①动通晓古代的事情:~多识|~通今。②名指古器物,也指以古器物为题材的 国画。 【博古通今】ī通晓古今的事情,形容知识渊博。 【博览】动广泛阅览:~群书。 【博览会】名组织许多国家参加的大型产品展览会。有时也指一国 的大型产品展览会。 【博洽】〈书〉形(学识)渊博:~多闻。 【博取】动用言语、行动取得(信任、重视等):~欢心|~人们的同情。 【博识】形学 识丰富:多闻~。 【博士】名①学位的最高一级:文学~。②古时指专精某种技艺或专司某种职业的人:茶~|酒~。③古代的一种传授经学的官员。 【博 士后】名获得博士学位后在高等院校或研究机构从事研究工作并继续深造的阶段。也指博士后研究人员。 【博闻强记】博闻强识。 【博闻强识】见闻广博, 记忆力强。也说博闻强记。 【博物】名动物、植物、矿物、生理等学科的总称。 【博物馆】名搜集、保管、研究、陈列、展览有关、历史、文化、艺术、自 然科学、技术等方面的文物或标本的机构。 【博物院】名博物馆:故宫~。 【博学】形学问广博精深:~多才。 【博雅】〈书〉形渊博:~之士|~精深。 【博弈】动①古代指下围棋,也指。②比喻为谋取利益而竞争。 【博引】动广泛地引证:旁征~|~众说。 【葧】见页[蒡葧]。 【鹁】(鵓)见下。 【鹁鸽】名家鸽。 【鹁鸪】名鸟,羽毛黑褐色,天要下雨或刚晴的时候,常在树上咕咕地叫。也叫水鸪鸪。 【渤】渤海,在山东半岛和辽东半岛之间。 【搏】①搏斗;对打:拼~|肉~。②扑上去抓:狮子~兔。③跳动:脉~。 【搏动】动有节奏地跳动(多指心脏或血脉):心脏起搏器能模拟心脏的自 然~,改善病跟敌人~。②比喻激烈地斗争:与暴风雪~|新旧思想的大~。
三角形等积变形

三角形等积变形
三角形是几何学中的一个基本形状,具有三条边和三个角。
在数学中,我们学习过三角形的性质和各种定理,但在生活中,三角形的形状也经常出现在我们的眼前。
而在艺术中,三角形等积变形是一种常见的设计元素,可以为作品增添美感和动感。
在建筑设计中,三角形等积变形常常被用来设计建筑的外观和结构。
例如,许多现代建筑采用了三角形的形状,不仅可以增加建筑的美感,还可以提高建筑的稳定性和结构强度。
这种设计不仅具有美学上的价值,还具有实用性,体现了建筑师对结构和功能的兼顾。
在艺术作品中,三角形等积变形也经常被运用。
艺术家们通过将三角形等积变形组合在一起,创造出各种美丽的图案和设计。
这些作品不仅具有装饰性,还可以传达出艺术家的情感和思想。
三角形等积变形的组合可以产生无穷无尽的可能性,让人们在欣赏作品的同时,感受到艺术家的创意和灵感。
在日常生活中,三角形的形状也随处可见。
比如,许多家具和装饰品都采用了三角形的设计,为家居空间增添动感和现代感。
此外,一些日常用品如餐具、文具等也常常采用三角形的形状,方便使用的同时也美观大方。
总的来说,三角形等积变形在各个领域都有着重要的作用。
无论是在建筑设计、艺术创作还是日常生活中,三角形的形状都能给人带
来美的享受和视觉上的愉悦。
通过运用三角形等积变形,人们可以创造出无限的可能性,展现出自己的创意和想象力。
让我们一起欣赏和探索三角形等积变形的魅力,感受美的力量和无限的可能性。
三角形的等积变形

胜利教育教案教学内容第十讲三角形的等积变形授课类型新授所需时间110分教学时间教学目标:知识目标:利用三角形的面积与底和高关系解决稍复杂的图形。
能力目标:培养学生的观察,分析能力。
情感目标:激发学习的斗志和情趣。
教学重点及教学难点:重点及难点:利用三角形的面积与底和高的关系解决稍复杂的图形。
教学方法讲授法教具准备教师活动学生活时间动一、引入:回顾:1、两个三角形底(高)相等,高(底)成几倍关系?面积成几倍关系?2、等底等高的的两三角形的面积相等。
二、新授:1、出示例1分析:看图,根据所给的条件作辅助线。
解法一:连接BD,在ΔABD中:∵ BE=3AE∴SΔABD=4SΔADB=4cm2在ΔABC中,∵ CD=2AD又∵SΔADB=SΔABC-SΔBDCSΔABC=3SΔABD=3×4=12cm2解法二:略作业:P36 72题2、出示例2:分析:连接BG,在ΔABG中:∵ BD=2AD∴SΔADG=1/3SΔABG在SΔABC中AG=2CG∴SΔABG=2/3SΔABG∴SΔADG=1/3×2/3SΔABG=2/9SΔABC同理:SΔBDE=1/9SΔABCSΔCFG=1/9SΔABCSΔADG+SΔBDE+SΔCFG=(2/9+2/9+1/9)SΔABC=5/9SΔABC阴影部分面积=(1-5/9)SΔABC=4/9SΔABC作业:P3671例3:分析:连接AF、CF∴SΔADE=SΔACESΔCDF=∴SΔACF又∵ AC与EF平行∴SΔACE=SΔACF∴SΔADE=SΔCDF=4cm2作业:P36 74例4:分析:连接AC,∵ AB∥CD∴SΔADE=SΔACE而SΔACF=SΔACE+SΔAEFSΔABF=SΔBEF+SΔAEF∴SΔACE=SΔBEF∴SΔBEF=SΔADE=1cm2三、总结四、作业板书设计:三角形等积变形(二)例1------------------------- 例2------------------------- 例3-------------------------。
一、三角形的等积变形
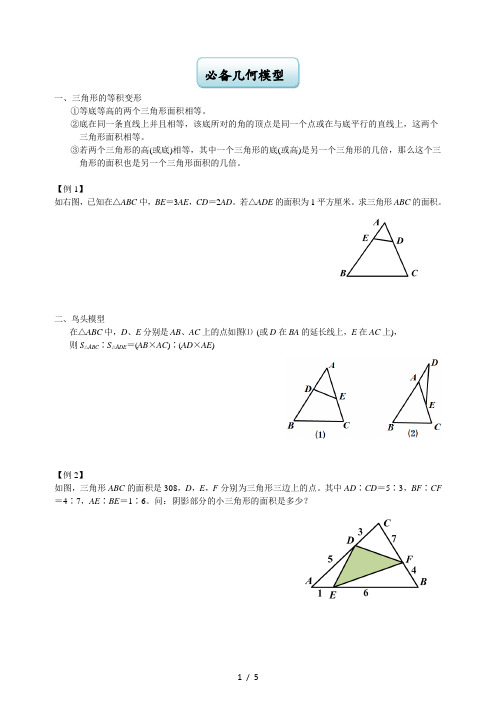
一、三角形的等积变形①等底等高的两个三角形面积相等。
②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等。
③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
【例1】如右图,已知在△ABC中,BE=3AE,CD=2AD。
若△ADE的面积为1平方厘米。
求三角形ABC的面积。
二、鸟头模型在△ABC中,D、E分别是AB、AC上的点如图⑴(或D在BA的延长线上,E在AC上),则S△ABC∶S△ADE=(AB×AC)∶(AD×AE)【例2】如图,三角形ABC的面积是308,D,E,F分别为三角形三边上的点。
其中AD∶CD=5∶3,BF∶CF =4∶7,AE∶BE=1∶6。
问:阴影部分的小三角形的面积是多少?必备几何模型【例3】如图,三角形两边上的点都是各边上的五等分点。
问:阴影部分与空白部分的面积比为多少?三、相似三角形性质(沙漏模型):①AD AE DE AF AB AC BC AG ===②S△ADE∶S△ABC=AF2∶AG2所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;【例4】如图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积。
四、蝴蝶模型任意四边形中的比例关系(“蝴蝶定理”)①S1×S3=S2×S4②AO∶OC=(S1+S2)∶(S4+S3)①S1∶S3=a2∶b2②S1∶S2∶S3∶S4=a2∶ab∶b2∶ab③梯形面积S的对于份数是(a+b)2【例5】如图面积为12平方厘米的正方形ABCD中,E、F是BC边上的三等分点,求阴影部分的面积。
第三讲 等积变形

根据蝶形定理, ,故 ,
所以 (平方厘米).
2.右图中 是梯形, 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.
答案:连接 .由于 与 是平行的,所以 也是梯形,那么 .
∵在正方形 中, 边上的高,
∴ (三角形面积等于与它等底等高的平行四边形面积的一半)
同理, .
∴正方形 与长方形 面积相等. 长方形的宽 (厘米).
2.在边长为6厘米的正方形 内任取一点 ,将正方形的一组对边二等分,另一组对边三等分,分别与 点连接,求阴影部分面积.
答案;(法1)特殊点法.由于 是正方形内部任意一点,可采用特殊点法,假设 点与 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的 和 ,所以阴影部分的面积为 平方厘米.
答案;连接 .
∵ ,
∴ ,
又∵ ,
∴ ,∴ , .
B
6.如图,以正方形的边 为斜边在正方形内作直角三角形 , , 、 交于 .已知 、 的长分别为 、 ,求三角形 的面积.
答案;如图,连接 ,以 点为中心,将 顺时针旋转 到 的位置.
那么 ,而 也是 ,所以四边形 是直角梯形,且 ,
所以梯形 的面积为:
根据面积比例模型, 的面积为 .
A
1.如图所示,正方形 的边长为 厘米,长方形 的长 为 厘米,那么长方形的宽为几厘米?
答案;本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半.
证明:连接 .(我们通过 把这两个长方形和正方形联系在一起).
