北京市西城区2014年高三下学期4月模拟考试(一模)数学(文科)试卷(word版)
北京市西城区高三4月统一测试(一模)数学(文)---精校Word版含答案
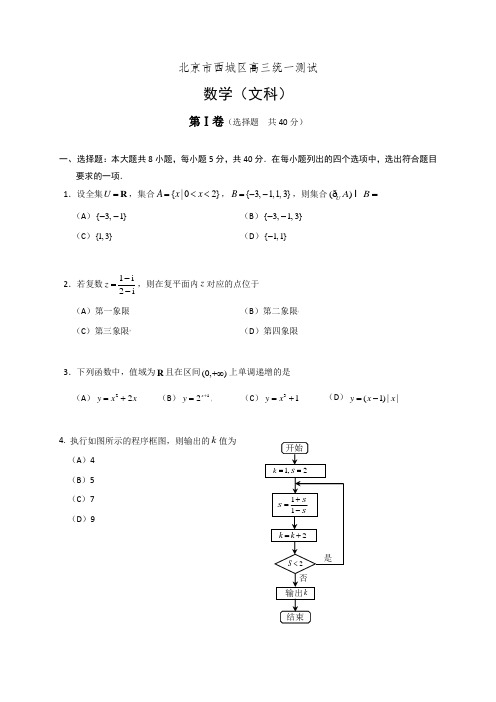
北京市西城区高三统一测试数学(文科)第Ⅰ卷(选择题 共40分)一、 选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设全集U =R ,集合{|02}A x x =<<,{3,1,1,3}B =--,则集合()U A B =ð(A ){3,1}-- (B ){3,1,3}-- (C ){1,3} (D ){1,1}-2.若复数1i2iz -=-,则在复平面内z 对应的点位于 (A )第一象限 (B )第二象限[](C )第三象限[][(D )第四象限3.下列函数中,值域为R 且在区间(0,)+∞上单调递增的是 (A )22y x x =+ (B )12x y +=[](C )31y x =+ (D )(1)||y x x =-4. 执行如图所示的程序框图,则输出的k 值为 (A )4 (B )5 (C )7 (D )92S <2k k =+ 输出k 开始否 结束11S S S+=-是1,2k S ==5. 在△ABC 中,已知2a =,1sin()3A B +=,1sin 4A =,则c = (A )4 (B )3(C )83 (D )436. 设 ,,a b m 均为正数,则“b a >”是“a m ab m b+>+”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件 (D )既不充分也不必要条件7.如图,阴影表示的平面区域W 是由曲线0x y -=,222x y +=所围成的. 若点(,)P x y 在W 内(含边界),则43z x y =+的最大值和最小值分别为 (A )52,7- [][][][](B )52,52- (C )7,52- (D )7,7-8. 如果把一个平面区域内两点间的距离的最大值称为此区域的直径,那么曲线2||2y x =-围成的平面区域的直径为 (A )2 (B )4 (C )22 (D )26x OyW第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.设向量a ,b 满足||2=a ,||3=b ,,60>=<a b ,则()⋅+=a a b ____.10.设1F ,2F 为双曲线2222 1(0,0)x y C a b a b-=>>:的两个焦点,若双曲线C 的两个顶点恰好将线段12F F 三等分,则双曲线C 的离心率为____.11.能说明“在△ABC 中,若sin2sin2A B =,则A B =”为假命题的一组A ,B 的值是____. 12.某四棱锥的三视图如图所示,那么该四棱锥的体积为____.13.设函数ln(2), ()1,24, 1.x x f x x x +⎧=⎨⎩---<-≥ 当()1f a =-时,a =____;如果对于任意的x ∈R 都有()f x b ≥,那么实数b 的取值范围是____. 14.团体购买公园门票,票价如下表:购票人数 1~50 51~100 100以上 门票价格13元/人11元/人9元/人现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a 和b ()a b ≥,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数a =____;b =____.侧(左)视图正(主)视图俯视图 221三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()sin (cos 3sin )f x x x x =-. (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)求函数()f x 在区间π5π[,]312-上的最小值和最大值.16.(本小题满分13分)已知数列{}n a 的前n 项和(1)2n S n n =++,其中*n ∈N . (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若2232,,k k a a a ++(k *∈N )为等比数列{}n b 的前三项,求数列{}n b 的通项公式.17.(本小题满分13分)为培养学生的阅读习惯,某校开展了为期一年的“弘扬传统文化,阅读经典名著”活动. 活动后,为了解阅读情况,学校统计了甲、乙两组各10名学生的阅读量(单位:本),统计结果用茎叶图记录如下,乙组记录中有一个数据模糊,无法确认,在图中以a 表示.(Ⅰ)若甲组阅读量的平均值大于乙组阅读量的平均值, 求图中a 的所有可能取值; (Ⅱ)将甲、乙两组中阅读量超过..15本的学生称为“阅读达人”. 设3a =,现从所有的“阅读达人”里任取2人,求至少有1人来自甲组的概率;(Ⅲ)记甲组阅读量的方差为20s . 若在甲组中增加一个阅读量为10的学生,并记新得到的甲组阅读量的方差为21s ,试比较20s ,21s 的大小.(结论不要求证明)(注:2222121[()()()]n s x x x x x x n=-+-++-,其中x 为数据12,,,n x x x 的平均数)乙12 07 2 2 1 0 1 2 3 6 6 a8 6 2 1 0 1 2 4 4 甲18.(本小题满分14分)如图,在多面体ABCDEF 中,底面ABCD 为矩形,侧面ADEF 为梯形,//AF DE ,DE AD ⊥,DC DE =.(Ⅰ)求证:AD CE ⊥; (Ⅱ)求证://BF 平面CDE ;(Ⅲ)判断线段BE 上是否存在点Q ,使得平面ADQ ⊥平面BCE ?并说明理由.19.(本小题满分13分)设函数2()e 3x f x m x =-+,其中∈m R .(Ⅰ)当()f x 为偶函数时,求函数()()h x xf x =的极值;(Ⅱ)若函数()f x 在区间[2,4]-上有两个零点,求m 的取值范围.20.(本小题满分14分)已知椭圆W : 2214x y m m+=的长轴长为4,左、右顶点分别为,A B ,经过点(1,0)P 的动直线与椭圆W 相交于不同的两点,C D (不与点,A B 重合). (Ⅰ)求椭圆W 的方程及离心率; (Ⅱ)求四边形ACBD 面积的最大值;(Ⅲ)若直线CB 与直线AD 相交于点M ,判断点M 是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)DA BCEF北京市西城区高三统一测试 数学(文科)参考答案及评分标准 2019.4一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.D 3.C 4.D 5.C 6.C 7.A 8.B 二、填空题:本大题共6小题,每小题5分,共30分. 9.710.311.答案不唯一,如60A =,30B = 12.4313.32-;(,2]-∞-14.70;40注:第13题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)解:(Ⅰ)2()sin cos 3sin f x x x x =-13sin 2(1cos2)22x x =-- ……………… 4分 π3sin(2)32x =+-, ……………… 6分所以函数()f x 的最小正周期πT =. ……………… 8分(Ⅱ)因为π5π312x -≤≤,所以 ππ7π2336x -+≤≤. ……………… 9分所以当ππ232x +=,即π12x =时,()f x 取得最大值312-. 当ππ233x +=-,即π3x =-时,()f x 取得最小值3-. ……………… 13分16.(本小题满分13分)解:(Ⅰ)当1n =时,114S a ==, ……………… 2分当2n ≥时,由题意,得(1)2n S n n =++,○1 1(1)2n S n n -=-+,○2由○1-○2,得2n a n =,其中2n ≥. ……………… 5分所以数列{}n a 的通项公式4, 1,2, 2.n n a n n =⎧=⎨⎩≥ ……………… 7分(Ⅱ)由题意,得22232k k a a a ++=⋅.……………… 9分 即2[2(2)]42(32)k k +=⨯+. 解得0k =(舍)或2k =.……………… 10分所以公比222k a q a +==. ……………… 11分 所以111122n n n n b b q a q --+===. ……………… 13分17.(本小题满分13分)解:(Ⅰ)甲组10名学生阅读量的平均值为12681011121217211010+++++++++=,乙组10名学生阅读量的平均值为124412131616(10)20981010a a+++++++++++=. ……………… 2分由题意,得981010a+>,即2a <. ……………… 3分 故图中a 的取值为0或1. ……………… 4分 (Ⅱ)记事件“从所有的“阅读达人”里任取2人,至少有1人来自甲组”为M . … 5分由图可知,甲组“阅读达人”有2人,在此分别记为1A ,2A ;乙组“阅读达人”有3人,在此分别记为1B ,2B ,3B .则从所有的 “阅读达人” 里任取2人,所有可能结果有10种,即12(,)A A ,11(,)A B ,12(,)A B ,13(,)A B ,21(,)A B ,22(,)A B ,23(,)A B ,12(,)B B ,13(,)B B ,23(,)B B . …… 7分而事件M 的结果有7种,它们是12(,)A A ,11(,)A B ,12(,)A B ,13(,)A B ,21(,)A B ,22(,)A B ,23(,)A B , ……………… 8分所以7()10P M =. 即从所有的‘阅读达人’里任取2人,至少有1人来自甲组的概率为710. … 10分 (Ⅲ)2201s s >. ……………… 13分 18.(本小题满分14分)解:(Ⅰ)由底面ABCD 为矩形,知AD CD ⊥.……………… 1分又因为DE AD ⊥,DECD D =, ……………… 2分所以AD ⊥平面CDE .……………… 3分又因为CE ⊂平面CDE ,所以AD CE ⊥. ……………… 4分 (Ⅱ)由底面ABCD 为矩形,知//AB CD ,又因为AB ⊄平面CDE ,CD ⊂平面CDE , 所以//AB 平面CDE . ……………… 6分 同理//AF 平面CDE , 又因为ABAF A =,所以平面//ABF 平面CDE . ……………… 8分 又因为BF ⊂平面ABF ,所以//BF 平面CDE . ……………… 9分(Ⅲ)结论:线段BE 上存在点Q (即BE 的中点),使得平面ADQ ⊥平面BCE . … 10分证明如下:取CE 的中点P ,BE 的中点Q ,连接,,AQ DP PQ ,则//PQ BC . 由//AD BC ,得//PQ AD .所以,,,A D P Q 四点共面. ……………… 11分 由(Ⅰ),知AD ⊥平面CDE , 所以AD DP ⊥,故BC DP ⊥.在△CDE 中,由DC DE =,可得DP CE ⊥. 又因为BCCE C =,所以DP ⊥平面BCE . ……………… 13分 又因为DP ⊂平面ADPQ所以平面ADPQ ⊥平面BCE (即平面ADQ ⊥平面BCE ).即线段BE 上存在点Q (即BE 中点),使得平面ADQ ⊥平面BCE . ……… 14分19.(本小题满分13分)DABC EFPQ解:(Ⅰ)由函数()f x 是偶函数,得()()f x f x -=,即22e()3e 3xx m x m x ---+=-+对于任意实数x 都成立,所以0m =. ……………… 2分此时3()()3h x xf x x x ==-+,则2()33h x x '=-+.由()0h x '=,解得1x =±. ……………… 3分 当x 变化时,()h x '与()h x 的变化情况如下表所示:x (,1)-∞-1-(1,1)-1(1,)+∞()h x '-0 +0 -()h x↘极小值↗极大值↘所以()h x 在(,1)-∞-,(1,)+∞上单调递减,在(1,1)-上单调递增. …………… 5分 所以()h x 有极小值(1)2h -=-,()h x 有极大值(1)2h =. ……………… 6分(Ⅱ)由2()e 30xf x m x =-+=,得23ex x m -=.所以“()f x 在区间[2,4]-上有两个零点”等价于“直线y m =与曲线23()ex x g x -=,[2,4]x ∈-有且只有两个公共点”. ……………… 8分对函数()g x 求导,得223()exx x g x -++'=. ……………… 9分 由()0g x '=,解得11x =-,23x =. ……………… 10分 当x 变化时,()g x '与()g x 的变化情况如下表所示:x (2,1)--1-(1,3)-3(3,4)()g x '-0 +0 -()g x↘极小值↗极大值↘所以()g x 在(2,1)--,(3,4)上单调递减,在(1,3)-上单调递增. …………… 11分 又因为2(2)e g -=,(1)2e g -=-,36(3)(2)e g g =<-,413(4)(1)eg g =>-, 所以当4132e e m -<<或36e m =时,直线y m =与曲线23()ex x g x -=,[2,4]x ∈-有且只有两个公共点. 即当4132e em -<<或36e m =时,函数()f x 在区间[2,4]-上有两个零点. …… 13分20.(本小题满分14分)解:(Ⅰ)由题意,得244a m == , 解得1m =. ……………… 1分所以椭圆W 方程为2214x y +=. ……………… 2分故2a =,1b =,223c a b =-=. 所以椭圆W 的离心率32c e a ==. ……………… 4分 (Ⅱ)当直线CD 的斜率k 不存在时,由题意,得CD 的方程为1x =, 代入椭圆W 的方程,得3(1,)2C ,3(1,)2D -, 又因为||24AB a ==,AB CD ⊥, 所以四边形ACBD 的面积1||||232S AB CD =⨯=. ……………… 6分 当直线CD 的斜率k 存在时,设CD 的方程为(1)(0)y k x k =-≠,11(,)C x y ,22(,)D x y ,联立方程22(1), 1,4y k x x y =-⎧⎪⎨+=⎪⎩ 消去y ,得2222(41)8440k x k x k +-+-=. …… 7分 由题意,可知0∆>恒成立,则2122841k x x k +=+,21224441k x x k -=+.………… 8分 四边形ACBD 的面积ABC ABD S S S ∆∆=+1211||||||||22AB y AB y =⨯+⨯ ……… 9分121||||2AB y y =⨯-122|()|k x x =-2222121222(31)2[()4]8(41)k k k x x x x k +=+-=+,设241k t +=,则四边形ACBD 的面积21223S t t =--+,1(0,1)t∈, 所以212(1)423S t=-++<.综上,四边形ACBD 面积的最大值为23. ……………… 11分 (Ⅲ)结论:点M 在一条定直线上,且该直线的方程为4x =. ……………… 14分。
2024年北京市西城区高三一模数学答案

2024.4 第1页(共6页)西 城 区 高 三 统 一 测 试 试 卷数学答案及评分参考 2024.4一、选择题(共10小题,每小题4分,共40分) ( 1 )B ( 2 )D ( 3 )A ( 4 )C ( 5 )C( 6 )A( 7 )A( 8 )B( 9 )D(10)C二、填空题(共5小题,每小题5分,共25分)(11(12)π3 π3(答案不唯一) (13)y =(14)6−n 13−(15)① ③ ④三、解答题(共6小题,共85分) (16)(共14分) 解:(Ⅰ)连接1A B ,设11A BAB E =,连接DE .………1分因为在三棱柱111ABC A B C −中,四边形11A ABB 是平行四边形, 所以E 为1A B 的中点.………2分因为D 为BC 的中点, 所以1//DE A C .………3分又因为1A C ⊄平面1AB D ,⊂DE 平面1AB D , 所以1//AC 平面1AB D . ………5分(Ⅱ)因为1AB AC ⊥,AB AC ⊥,所以AB ⊥平面11A ACC .………6分所以1AB AA ⊥.又1AA AC ⊥,所以1,,AB AC AA 两两相互垂直. 如图建立空间直角坐标系A x yz −.………7分 则(0,0,0)A ,1(2,0,2)B ,(1,1,0)D ,(0,2,0)C . 所以1(,,)202AB =,(,,)110AD =.2024.4 第2页(共6页)设平面1AB D 的法向量为(,,)x y z =m ,则10,0,AB AD =⎧⎪⎨=⎪⎩⋅⋅m m 即220,0.x z x y +=⎧⎨+=⎩令1x =−,则1y =,1z =.于是(1,1,1)=−m . ………10分因为AC ⊥平面11A ABB ,所以(0,2,0)AC =是平面11A ABB 的一个法向量. ………11分 所以3cos ,3||||AC AC AC 〈〉==⋅m m m .………13分由题设,二面角11D ABA −−的平面角为钝角, 所以二面角11D AB A −−的余弦值为 ………14分(17)(共13分)解:(Ⅰ)由tan 2sin a B b A =,得sin 2sin cos a B b A B =.………1分 在ABC △中,由正弦定理得sin sin 2sin sin cos A B A B B =.………3分因为sin 0,sin 0A B >>, 所以1cos 2B =. ………4分 又0πB <∠<, ………5分 所以π3B ∠=.………6分 (Ⅱ)选条件①:BC………7分设BC 边中点为M ,连接AM ,则AM =,4BM =.在ABM △中,由余弦定理得2222cos AM AB BM AB BM B =+−⋅⋅,………9分 即2π21168cos3AB AB =+−⋅. 整理得2450AB AB −−=. 解得5AB =或1AB =−(舍).………11分 所以ABC △的面积为1sin 2ABC S AB BC B =⋅⋅=△.………13分2024.4 第3页(共6页)选条件③:7b =.………7分 在ABC △中,由余弦定理得2222cos b a c ac B =+−,………9分即222π7816cos3c c =+−⋅. 整理得28150c c −+=. 解得3c =或5c =.………11分当3c =时,ABC △的面积为1sin 2ABC S ac B ==△ 当5c =时,ABC △的面积为1sin 2ABC S ac B ==△.………13分(18)(共13分)解:(Ⅰ)甲进入决赛,理由如下:丙射击成绩的总环数为26471081892610542⨯+⨯+⨯+⨯+⨯=,甲射击成绩的总环数为16171082492410549⨯+⨯+⨯+⨯+⨯=. 因为549542>,所以甲进入决赛.………3分(Ⅱ)根据题中数据,“甲命中9环”的概率可估计为242605=; “甲命中10环” 的概率可估计为242605=; “乙命中9环” 的概率可估计为301602=; “乙命中10环” 的概率可估计为151604=.………5分所以这4次射击中出现2个“9环”和2个“10环”的概率可估计为:222212122212121113()()()()C ()C ()5452524100⨯+⨯+⨯⨯=. ………10分 (Ⅲ)7a =和8.(写出一个即可)………13分2024.4 第4页(共6页)(19)(共15分)解:(Ⅰ)由题设,2222,1,2.a c a abc =⎧⎪⎪=⎨⎪⎪−=⎩………3分解得224,3a b ==.所以椭圆G 的方程为22143x y +=. ………5分(Ⅱ)由题设,直线l 的斜率存在,设其方程为y kx m =+.则(2,2)E k m +,直线OE 的方程为()2my k x =+. ………6分 由22,3412,y kx m x y =+⎧⎨+=⎩ 得222(43)84120k x kmx m +++−=.………7分由2248(43)0=−+>Δk m ,得2243<+m k .设11(,)C x y ,22(,)D x y ,则122843kmx x k +=−+,212241243m x x k −=+. ………8分直线AC 的方程为11(2)2yy x x =++. ………9分联立直线AC 和OE 得11(2)()22y mx k x x +=++. 解得1111111244()44()(2)2M y y kx m x mmx k mx kk x y +===++++−.………11分同理可得224()4N kx m x mx k +=+.所以122112()(4)()(4)4(4)(4)M N kx m mx k kx m mx k x x mx k mx k ++++++=⨯++.………12分因为1221()(4)()(4)+++++kx m mx k kx m mx k22121222222222(4)()82(412)8(4)8(43)4343430kmx x k m x x kmkm m km k m km k k k k =++++−++=−++++=,所以0M N x x +=,即点M 和点N 关于原点O 对称. 所以||||=OM ON .………15分2024.4 第5页(共6页)(20)(共15分)解:(Ⅰ)当1a =时,()ln e =++x f x x x x ,所以1()1(1)e '=+++x f x x x. ………2分所以(1)2e 2f '=+.所以曲线()y f x =在点(,())11f 处切线的斜率为2e 2+.………4分(Ⅱ)当1a =−时,()ln()e =+−−x f x x x x ,()f x 的定义域为(,0)−∞.11()1(1)e (1)(e )'=+−+=+−x x f x x x x x. ………6分因为1e 0xx−<, 所以(,1)x ∈−∞−时,()0f x '>;(1,0)x ∈−时,()0f x '<.所以()f x 的单调递增区间为(,1)−∞−;单调递减区间为(1,0)−. ………9分 (Ⅲ)1e ()(1)()'=++xf x x x a.当0a >时,()f x 的定义域为(0,)+∞. 所以()0'>f x ,()f x 在(0,)+∞上单调递增.因为1()0>f a ,所以0a >不合题意.………11分当0a <时,()f x 的定义域为(,0)−∞.因为(,1)x ∈−∞−时,()0f x '>;(1,0)x ∈−时,()0f x '<. 所以()f x 的单调递增区间为(,1)−∞−;单调递减区间为(1,0)−. 所以max 1()(1)1ln()e=−=−+−−f x f a a . ………13分设1()1ln()e =−+−−g x x x ,则2211e 1()e e +'=+=x g x x x x , 因为1(,)e ∈−∞−x 时,()0'<g x ;1(,0)e∈−x 时,()0'>g x ,所以()g x 的单调递减区间为1(,)e −∞−;单调递增区间为1(,0)e −.所以min 1()()1e=−=−g x g .所以集合{|()1}−≥x f x 有且只有一个元素时1ea =−.………15分2024.4 第6页(共6页)(21)(共15分) 解:(Ⅰ)记1122i i i n in t a b a b a b =+++.因为1233,2,0t t t ===, ………3分 所以2=K .………4分(Ⅱ)(ⅰ)B 不满足3m r =,理由如下:假设B 满足3m r =.因为B 的每行恰有三个1,故B 中满足1==i p i q b b 的(,,)i p q 的个数共有3m 个. 另一方面,从B 中任选两列共有2C n 种可能,且对任意两列,都恰有r 行使得 这两列的数均为1,故B 中满足1==i p i q b b 的(,,)i p q 的个数共有2C n r 个. 所以23C n m r =.当3m r =时,得2C 9n =,此方程无解. 所以B 不满足3m r =.………9分(ⅱ)由(ⅰ)可得23C nm r =,即2C 3nr m =.下面考虑满足1==i p i q b b ,但p q a a ≠的(,,)i p q 的个数:对B 中满足0≠i t 和3的−m K 行,每行恰有两组(,)p q 使1==i p i q b b 且p q a a ≠,所以满足1==i p i q b b ,但p q a a ≠的(,,)i p q 的个数为2C 2()2()3−=−n r m K K .………11分设数列A 中有x 项为1,−n x 项为0.满足1==i p i q b b ,但p q a a ≠的(,)p q 的个数为()−x n x . 所以满足1==i p i q b b ,但p q a a ≠的(,,)i p q 的个数为()−rx n x .………13分所以2C ()2()3−=−n r rx n x K .所以222C ()(33)326−=−=−+−nr rx n x r K x nx n n 22222331()()(4)6426424−+−=−−≥≥r n n r n n n n n n . ………15分。
2014年北京高三模考数学文科试题分类汇编---概率统计

2014年北京高三模拟考试数学文科试题分类汇编—概率统计(6)(2104年丰台一模文)某企业开展职工技能比赛,并从参赛职工中选1人参加该行业全国技能大赛.经过6轮选拔,甲、乙两人成绩突出,得分情况如茎叶图所示.若甲乙两 人的平均成绩分别是x 甲,x 乙,则下列说法正确的是 (A )x x >甲乙,乙比甲成绩稳定,应该选乙参加比赛 (B )x x >甲乙,甲比乙成绩稳定,应该选甲参加比赛 (C )x x <甲乙,甲比乙成绩稳定,应该选甲参加比赛(D )x x <甲乙,乙比甲成绩稳定,应该选乙参加比赛11、(2014年东城一模文)如图所示茎叶图记录了甲、乙两组各5名同学在期末考试中的数学成绩,则甲组数据的中位数是 ;乙组数据的平均数是 .2. (2014年顺义一模文)某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为A. 8万元B. 10万元C. 12万元D. 15万12.(2014年延庆一模文)某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作为样本.用系统抽样的方法将全体职工随机按1~200编号,并按编号顺序分为40组(1~5号,6~10号,,,,,196~200号),若第5组抽出的号码为22,则第8组抽出的号码应是 ,若改用分层抽样的方法,则40岁以下年龄段应抽取 人.8 7 5 6 982 6 甲 乙55 72 585 频率/组距9. (2014顺义二模文)某学校有初中生1200人,高中生900人,教师120人,现采用分层抽样的方法, 从所有师生中抽取一个容量为n 的样本进行调查.如果从高中生中抽取60人,则样本容量_________n =.(9)(2014房山二模文)某校高三年级共400名学生,现用分层抽样的方法随机抽取32人进行健康调查.若男生抽取了12人,则高三年级共有女生 人. (12)(2014房山二模文)设不等式组01,01x y ⎧⎨⎩≤≤≤≤表示的平面区域为D ,在区域D 内任取一点(9)(2014丰台二模文)已知一个样本容量为100的样本数据的频率分布直方图如图所示,样本数据落在[40,60)内的频数为 .(11)(2014年东城二模文)在区间[0,6]上随机取两个实数x ,y ,则事件“26x y +≤”的概率为_________. (6)(2014年朝阳二模文)在区间[],ππ-上随机取一个实数x ,则事件:"cos 0"x ≥的概率为( ). (A )14 (B ) 34 (C ) 23 (D )12(13)(2014昌平二模文)已知矩形ABCD 中,2,1AB BC ==,在矩形ABCD 内随机取一点M ,则90AMB ︒∠≤的概率为__________ .16(2014西城一模文).(本小题满分13分)某批次的某种灯泡共200个,对其寿命进行追踪调查,将结果列成频率分布表如下. 根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.样本数据(Ⅰ)根据频率分布表中的数据,写出a ,b ,c 的值;(Ⅱ)某人从这200个灯泡中随机地购买了1个,求此灯泡恰好不.是次品的概率; (Ⅲ)某人从这批灯泡中随机地购买了()*∈n n N 个,如果这n 个灯泡的等级情况恰好与按.三个..等级..分层抽样....所得的结果相同,求n 的最小值.16(2014年石景山一模文).(本小题满分13分)某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.(Ⅰ)求分数在[5060),的频率及全班人数; (Ⅱ)求分数在[8090),之间的频数,并计算频率分布直方图中[8090),间矩形的高; (Ⅲ)若要从分数在[80100),之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90100),之间的概率.(16)(2104年丰台一模文)(本题共13分)年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”。
2014北京西城高考一模数学文(word解析)

北京市西城区2014年高三一模试卷 数 学(文科) 2014.4 第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设全集{|02}U x x =<<,集合{|0}1A x x =<≤,则集合U A =ð() A .(0,1)B .(0,1]C .(1,2)D .[1,2)2.已知平面向量(2,1)=-a ,(1,3)=b ,那么|a +b |等于() A .5 B .13C .17D .133.已知双曲线2222:1(0,0)x y C a b a b-=>>的虚轴长是实轴长的2倍,则此双曲线的离心率为()A .2B .2C .3D .54.某几何体的三视图如图所示,则该几何体的体积为() A .2 B .43 C .4D .56.设0a >,且1a ≠,函数log a y x =在(0,)+∞上是减函数”是“函数3(2)y a x =-在R 上是增函数”的().A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7.某企业为节能减排,用9万元购进一台新设备用于生产.第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加2万元,该设备每年生产的收入均为11万元.设该设备使用了()n n *∈N 年后,盈利总额达到最大值(盈利额等于收入减去成本),则n 等于(). A .4B .5C .6D .75.下列函数中,对于任意x ∈R ,同时满足条件()()f x f x =-和(π)()f x f x -=的函数是() A .()sin f x x = B .()sin 2f x x = C .()cos f x x = D .()cos 2f x x =正(主)视图俯视图 侧(左)视图2312518.如图,设P 为正四面体A BCD -表面(含棱)上与顶点不重合的一点,由点P 到四个顶点的距离组成的集合记为M ,如果集合M 中有且只有2个元素,那么符合条件的点P 有(). A .4个B .6个C .10个D .14个第Ⅱ卷(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.设复数1ii 2ix y -=++,其中,x y ∈R ,则x y +=______.10.若抛物线2:2C y px =的焦点在直线20x y +-=上,则p =_____;C 的准线方程为_____.11.已知函数3, 0,()1, 0,1x x f x x x +⎧⎪=⎨>⎪+⎩≤若0()2f x =,则实数0x =______;函数()f x 的最大值为_____.12.执行如图所示的程序框图,如果输入2,2a b ==,那么输出的a 值为______.13.若不等式组0,26,1,x y x y x y a⎧⎪⎪⎨+⎪⎪+⎩≤≥≥≤表示的平面区域是一个四边形,则实数a 的取值范围是__________.14.如图,在直角梯形ABCD 中,//AB CD ,AB BC ⊥,2AB =,1CD =,2BC =,P 为线段AD (含端点)上一个动点.设AP xAD =uu u r uuu r ,PB PC y ⋅=uu r uu ur ,记()y f x =,则(1)f =____;函数()f x 的值域为_________.A B D C P BADC. P开始 b a a =3log 4a >输出a结束否是输入a , b三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)在△ABC中,角A,B,C所对的边分别为a,b,c.已知222b c a bc+=+.(Ⅰ)求A的大小;(Ⅱ)如果6cos3B=,2b=,求a的值.16.(本小题满分13分)某批次的某种灯泡共200个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.寿命(天) 频数频率[100,200)10 0.05[200,300) 30 a[300,400) 700.35 [400,500) b0.15[500,600)60 c合计 2001(Ⅰ)根据频率分布表中的数据,写出a ,b ,c 的值;(Ⅱ)某人从这200个灯泡中随机地购买了1个,求此灯泡恰好不.是次品的概率; (Ⅲ)某人从这批灯泡中随机地购买了()n n *∈N 个,如果这n 个灯泡的等级情况恰好与按三个等级分......层抽样...所得的结果相同,求n 的最小值.17.(本小题满分14分)如图,在四棱锥ABCD S -中,底面ABCD 是矩形,2AD AB =,SA SD =,SA AB ⊥,N 是棱AD的中点.(Ⅰ)求证://AB 平面SCD ; (Ⅱ)求证:SN ⊥平面ABCD ;(Ⅲ)在棱SC 上是否存在一点P ,使得平面PBD ⊥平面ABCD ?若存在,求出SPPC的值;若不存在,说明理由.BCA D SN18.(本小题满分13分)已知函数()ln af x x x=-,其中a ∈R . (Ⅰ)当2a =时,求函数()f x 的图象在点(1,(1))f 处的切线方程;(Ⅱ)如果对于任意(1,)x ∈+∞,都有()2f x x >-+,求a 的取值范围.19.(本小题满分14分)已知椭圆22221(0)x y W a b a b+=>>:的焦距为2,过右焦点和短轴一个端点的直线的斜率为1-,O 为坐标原点.(Ⅰ)求椭圆W 的方程.(Ⅱ)设斜率为k 的直线l 与W 相交于,A B 两点,记AOB ∆面积的最大值为k S ,证明:12S S =.20.(本小题满分13分)在数列{}n a 中,1()n a n n*=∈N .从数列{}n a 中选出(3)k k ≥项并按原顺序组成的新数列记为{}n b ,并称{}n b 为数列{}n a 的k 项子列.例如数列1111,,,2358为{}n a 的一个4项子列.(Ⅰ)试写出数列{}n a 的一个3项子列,并使其为等比数列;(Ⅱ)如果{}n b 为数列{}n a 的一个5项子列,且{}n b 为等差数列,证明:{}n b 的公差d 满足104d -<<; (Ⅲ)如果{}n c 为数列{}n a 的一个6项子列,且{}n c 为等比数列,证明:1234566332c c c c c c +++++≤.北京市西城区2014年高三一模试卷参考答案及评分标准高三数学(文科) 2014.4一、选择题:本大题共8小题,每小题5分,共40分.1.C 2.B 3.D 4.C 5.D 6.A 7.B 8.C 二、填空题:本大题共6小题,每小题5分,共30分. 9.25- 10.42x =-11.1-,3 12.25613.(3,5) 14.14[,4]5注:第10、11、14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分.其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分) (Ⅰ)解:因为222b c a bc +=+,所以2221cos 22b c a A bc +-==, ……………… 4分又因为(0,π)A ∈,所以π3A =. ……………… 6分 (Ⅱ)解:因为6cos 3B =,(0,π)B ∈, 所以23sin 1cos 3B B =-=, ………………8分 由正弦定理sin sin a bA B =, ………………11分 得sin 3sin b Aa B==. ………………13分 16.(本小题满分13分)(Ⅰ)解:0.15a =,30b =,0.3c =. ……………… 3分 (Ⅱ)解:设“此人购买的灯泡恰好不是次品”为事件A . ……………… 4分由表可知:这批灯泡中优等品有60个,正品有100个,次品有40个,所以此人购买的灯泡恰好不是次品的概率为100604()2005P A +==. …………… 8分 (Ⅲ)解:由(Ⅱ)得这批灯泡中优等品、正品和次品的比例为60:100:403:5:2=.……………… 10分所以按分层抽样法,购买灯泡数35210()n k k k k k *=++=∈N ,所以n 的最小值为10. ……………… 13分 17.(本小题满分14分)(Ⅰ)证明:因为底面ABCD 是矩形,所以//AB CD , ……………… 1分又因为AB ⊄平面SCD ,CD ⊂平面SCD ,所以//AB 平面SCD . ……………… 3分 (Ⅱ)证明:因为, , AB SA AB AD SA AD A ⊥⊥= ,所以⊥AB平面SAD , ……………… 5分又因为SN ⊂平面SAD ,所以AB SN ⊥. ……………… 6分 因为SA SD =,且N 为AD 中点, 所以SN AD ⊥. 又因为AB AD A = ,所以SN ⊥平面ABCD . ……………… 8分(Ⅲ)解:如图,连接BD 交NC 于点F ,在平面SNC 中过F 作//FP SN 交SC 于点P ,连接PB ,PD .因为SN ⊥平面ABCD ,所以FP ⊥平面ABCD . …………… 11分 又因为FP ⊂平面PBD , 所以平面PBD⊥平面ABCD . …………… 12分在矩形ABCD 中,因为//ND BC ,所以12NF ND FC BC ==. 在SNC ∆中,因为//FP SN ,所以12NF SP FC PC ==. 则在棱SC 上存在点P ,使得平面⊥PBD 平面ABCD ,此时12SPPC=. ……… 14分 18.(本小题满分13分) (Ⅰ)解:由2()ln f x x x =-,得212()f x x x'=+, ……………… 2分 所以(1)3f '=, 又因为(1)2f =-,所以函数()f x 的图象在点(1,(1))f 处的切线方程为350x y --=. ……………… 4分 (Ⅱ)解:由()2f x x >-+,得ln 2ax x x->-+, 即2ln 2a x x x x <+-. ……………… 6分 设函数2()ln 2g x x x x x =+-,则()ln 21g x x x '=+-, ……………… 8分 因为(1,)x ∈+∞,所以ln 0x >,210x ->,所以当(1,)x ∈+∞时,()ln 210g x x x '=+->, ……………… 10分 故函数()g x 在(1,)x ∈+∞上单调递增,所以当(1,)x ∈+∞时,()(1)1g x g >=-. ……………… 11分 因为对于任意(1,)x ∈+∞,都有()2f x x >-+成立, 所以对于任意(1,)x ∈+∞,都有()a g x <成立.BCADSN FP N所以1a -≤. ……………… 13分 19.(本小题满分14分)(Ⅰ)解:由题意,得椭圆W 的半焦距1c =,右焦点(1,0)F ,上顶点(0,)M b ,…… 1分 所以直线MF 的斜率为0101MF b k -==--, 解得1b =, ……………… 3分由222a b c =+,得22a =,所以椭圆W 的方程为2212x y +=. ……………… 5分(Ⅱ)证明:设直线l 的方程为y kx m =+,其中1k =或2,11(,)A x y ,22(,)B x y .… 6分由方程组2212y kx m x y =+⎧⎪⎨+=⎪⎩得222(12)4220k x kmx m +++-=, ……………… 7分 所以2216880k m ∆=-+>,(*)由韦达定理,得122412km x x k -+=+, 21222212m x x k-=+. ……………… 8分 所以22222422||1()41212km m AB kk k --=+-⨯=++22228(21)112k k k m -+++. …… 9分因为原点O 到直线y kx m =+的距离2||1m d k +=, ……………… 10分所以1||2AOB S AB d ∆=⋅22222(21)12m k m k =-++, ……………… 11分当1k =时,因为222(3)3AOB S m m ∆=-, 所以当232m =时,AOB S ∆的最大值122S =, 验证知(*)成立; ……………… 12分 当2k =时,因为222(9)9AOB S m m ∆=-, 所以当292m =时,AOB S ∆的最大值222S =; 验证知(*)成立.所以12S S =. ……………… 14分 注:本题中对于任意给定的k ,AOB ∆的面积的最大值都是22.20.(本小题满分13分)(Ⅰ)解:答案不唯一.如3项子列:12,14,18. ……………… 2分 (Ⅱ)证明:由题意,知1234510b b b b b >>>>>≥, 所以210d b b =-<. ……………… 4分因为514b b d =+,151,0b b >≤, 所以514011d b b =->-=-,解得14d >-.所以104d -<<. ……………… 7分(Ⅲ)证明:由题意,设{}n c 的公比为q ,则23451234561(1)c c c c c c c q q q q q +++++=+++++. 因为{}n c 为{}n a 的一个6项子列,所以q 为正有理数,且1q <,11()1c a a*=∈N ≤. ……………… 8分 设(,K q K L L*=∈N ,且,K L 互质,2L ≥).当1K =时,因为112q L =≤,所以23451234561(1)c c c c c c c q q q q q +++++=+++++2345111111()()()()22222+++++≤,所以1234566332c c c c c c +++++≤. ……………… 10分当1K ≠时,因为556151K c c q a L==⨯是{}n a 中的项,且,K L 互质,所以5*()a K M M =⨯∈N ,所以23451234561(1)c c c c c c c q q q q q +++++=+++++543223*********()M K K L K L K L KL L=+++++. 因为2L ≥,*,K M ∈N ,所以234512345611111631()()()()2222232c c c c c c ++++++++++=≤. 综上,1234566332c c c c c c +++++≤. ……………… 13分北京市西城区2014年高三一模试卷数学(文科)选填解析一、 选择题 1.【答案】C【解析】解:如图所以全集U 和集合A ,则集合(1,2)U A =ð 故选C .2.【答案】B【解析】解:由已知得(3,2)+=a b ,所以223213+=+=a b . 故选B .3.【答案】D【解析】解:由已知得2b a =,则222245c a b a a a =+=+=,所以5ce a==. 故选D4.【答案】C【解析】解:该几何的直观图如图所示是一个底面为直角梯形的直四棱柱,故起底面积1(13)122S =+⋅⋅=, 高2h =,所以体积224V S h =⋅=⋅= 故选C .5.【答案】D【解析】解:由题意得()f x 是周期为π的偶函数, 对于A ,()sin f x x =是周期为2π的奇函数,故不选; 对于B ,()sin 2f x x =是周期为π的奇函数,故不选; 对于C ,()cos f x x =是周期为2π的偶函数,故不选; 对于D ,()cos 2f x x =周期为π的偶函数, 故选D .AUO 12352116.【答案】A【解析】解:若命题p :函数log a y x =在(0,)+∞上是减函数,则01a <<;命题q :函数3(2)y a x =-在R 上是增函数,则(2)0a ->,则2a <,所以p 是q 的充分不必要条件.故答案为A .7.【答案】B【解析】解:设总收入为R ,总成本为C ,由题意得11R n =;企业每年的运营费用为2n 万元,该设备使用了()n n *∈N 年后的运营成本符合等差数列的前n 项和为(1)n n +万元,所以9(1)C n n =++;所以该企业的盈利总额为[]22119(1)109(5)16R C n n n n n n -=-++=-+-=--+,所以当5n =时盈利总额最大.故答案选B8.【答案】C【解析】解:若集合M 中有且只有2个元素,由点P 到四个顶点的距离有两个值.当点P 位于正四面体四个面的几何中心时,其到这个面的三个顶点距离相等且不等于到平面外的另一个顶点的距离,符合此条件的点有4个;当点P 位于正四面体每条棱的中点时,其到这条棱的两个顶点距离相等,到两外两个点距离相等,并且这两个距离不等,所以满足条件的点有6个;故共有10个点符合条件. 故答案选C .二、 填空题 9.【答案】25-【解析】解:()()()()1i 2i 1i 13i 13i i 2i 2i 2i 555x y ----===-=+++-,所以13,55x y ==-,所以25x y +=-. 故答案为25-.10.【答案】4,2x =-【解析】解:抛物线焦点,02p ⎛⎫⎪⎝⎭在直线20x y +-=上,所以得4p =,准线方程为22p x =-=-.故答案为4,2x =-.11.【答案】1-,3【解析】解:当00x ≤时,00()32f x x =+=,所以01x =-; 当00x >时,001()21f x x ==+,所以0102x =-<不符合题意舍,综上01x =-; 当0x ≤时,max ()3f x =,当0x >时,()(0,1)f x ∈,所以()f x 的最大值为3 故答案为1-,3.12.【答案】256【解析】解:计算步骤如下:输入2,2a b ==,23log 24,24a <==,23log 44,416a <==,23log 164,16256a <==,3log 2564>所以输出256a =故答案为25613.【答案】(3,5)【解析】解:如图所示,当直线x y a +≤介于直线l 与直线m 之间时,不等式组表示的平面区域是一个平行四边形,所以将点(3,0)A 及点(1,4)C 坐标带入直线x y a +≤中算出a 的取值范围,切不能取等号, 故答案为(3,5).14.【答案】1,4,45⎡⎤⎢⎥⎣⎦【解析】解:建立如图所示平面直角坐标系,则各点坐标为(0,0),A(2,0),C(0,2),D(1,2)B --,因为AP xAD =uu u r uuu r,得点P 的坐标(2,2)x x -,(2,2)PB x x =--u u r ,(2,22)PC x x =--u u u r ,所以22()(2)2(22)584=5(01)y f x PB PC x x x x x x ==⋅=---=-+≤≤u u r u u u r,所以(1)5841f =-+=; 2244()5845()55f x x x x =-+=-+,min 44()()55f x f ==,(0)4(1)1f f =>=,所以max ()4f x =,故()f x 的值域为4,45⎡⎤⎢⎥⎣⎦故答案为1,4,45⎡⎤⎢⎥⎣⎦lmx+y ≤ayx2x+y ≤6x ≥1C (1,4)A (3,0)OyxBD CAP。
北京市西城区2014年高三下学期4月模拟考试(一模)英语试题(word版)

北京市西城区2014年高三下学期4月模拟考试(一模)英语试题(word版)本试卷共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分:听力理解(共三节,30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你将有10秒钟的时间回答有关小题和阅读下一小题。
每段对话你将听一遍。
1.What will the man and woman probably do?A.Stay where they are. B.Go for a walk.C.Go to a coffee shop.2.What is the woman probably doing?A.Asking for help.B.Making an appointment.C.Giving advice.3.What does the man want to do now?A.Prepare the schedule.B.Talk about the schedule.C.Take a rest.4.What does the woman feel about the US?A.Bored.B.Curious.C.Disappointed.5.When will the woman meet with Mr.Smith?A.12 00.B.1:30.C.2:OO.第二节(共10小题;每小题1.5分,共15分)听下面4段对话或独白。
每段对话或独白后有几道小题,从每题所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有5秒钟的时间阅读每小题。
听完后,每小题将给出5秒钟的作答时间。
每段对话或独白你将听两遍。
听第6段材料,回答第6至7题。
6.What does the man recommend?A.A chocolate cake.B.An apple pie.C.Some ice cream.7.What's the probable relationship between the two speakers?A.Boss and employee. B.Waiter and customer.C.Husband and wife.听第7段材料,回答第8至9题。
数学_2014年北京市高考数学模拟试卷(文科)(含答案)

2014年北京市高考数学模拟试卷(文科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合A={x||x|<2},B={x|x2−4x+3<0},则A∩B=()A {x|−2<x<1}B {x|1<x<2}C {x|2<x<3}D {x|−2<x<3}2. 设a=30.5,b=log32,c=cos23π,则()A c<b<aB c<a<bC a<b<cD b<c<a3. 已知函数f(x)是定义在R上的偶函数,且当x>0时,f(x)=ln(x+1),则函数f(x)的大致图象为()A B C D4. 程序框图如图所示,若输入a的值是虚数单位i,则输出的结果是()A −1B i−1C 0D −i5. 命题“∃x0∈R,log2x0≤0”的否定为()A ∃x0∈R,log2x0>0B ∃x0∈R,log2x0≥0C ∀x∈R,log2x≥0D ∀x∈R,log2x>06. 记集合A={(x, y)|x2+y2≤4}和集合B={(x, y)|x+y−2≤0, x≥0, y≥0}表示的平面区域分别为Ω1,Ω2,若在区域Ω1内任取一点M(x, y),则点M落在区域Ω2内的概率为()A 12π B 1πC 14D π−24π7. 在△ABC中,若tan A−B2=a−ba+b,则△ABC的形状是()A 直角三角形B 等腰三角形C 等腰直角三角形D 等腰三角形或直角三角形8. 一四面体的三视图如图所示,则该四面体四个面中最大的面积是()A 2B 2√2C √3D 2√3二、填空题:本大题共6小题,每小题5分,共30分.9. 已知抛物线y2=4x上一点M与该抛物线的焦点F的距离|MF|=4,则点M的横坐标x=________.10. 为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为________.(用“>”连接)11. 已知等差数列{a n}的前n项和为S n,若a2=1,S5=10,则S7=________.12. 已知函数f(x)={2−x−1,x≤0−x2−2x,x>0,若f(a2−2)>f(a),则实数a的取值范围是________.13. 设不等式组{x≥0y≥0y≤−kx+4k在直角坐标系中所表示的区域的面积为S,则当k>1时,ksk−1的最小值为________.14. 在平面直角坐标系xOy中,若直线y=kx+1与曲线y=|x+1x |−|x−1x|有四个公共点,则实数k的取值范围是________.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15. 已知函数f(x)=sin2x+√3sinxcosx−12.(1)求f(−π12)的值;(2)若x ∈[0,π2],求函数y =f(x)的最小值及取得最小值时的x 值.16. 某学校餐厅新推出A 、B 、C 、D 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示: 满意 一般 不满意(1)若同学甲选择的是A 款套餐,求甲的调查问卷被选中的概率;(2)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D 款套餐的概率.17. 如图,菱形ABCD 的边长为6,∠BAD =60∘,AC ∩BD =O .将菱形ABCD 沿对角线AC 折起,得到三棱锥B −ACD ,点M 是棱BC 的中点,DM =3√2.(1)求证:OM // 平面ABD ;(2)求证:平面ABC ⊥平面MDO ; (3)求三棱锥M −ABD 的体积.18. 已知函数f(x)=alnx −4x ,g(x)=−x 2−3. (1)求函数f(x)在x =1处的切线方程;(2)若存在x 0∈[e, e 2],使得f(x 0)<g(x 0)成立,求实数a 的取值范围.19. 在平面直角坐标系xoy 中,已知F 1,F 2分别是椭圆G:x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,椭圆G 与抛物线y 2=−8x 有一个公共的焦点,且过点(−2, √2). (1)求椭圆G 的方程;(2)设直线l 与椭圆G 相交于A 、B 两点,若OA →⊥OB →(O 为坐标原点),试判断直线l 与圆x 2+y 2=83的位置关系,并证明你的结论.20. 已知数列{a n }满足a 1=a(a ∈N ∗),S n =pa n+1(p ≠0, p ≠−1, n ∈N ∗). (1)求数列{a n }的通项公式;(2)对任意k ∈N ∗,若将a k+1,a k+2,a k+3按从小到大的顺顺序排列后,此三项均能构成等差数列,且记公差为d k .(I)求p 的值以及数列{d k }的通项公式;(II)记数列{d k }的前k 项和为S k ,问是否存在正整数a ,使得S k <30恒成立,若存在,求出a 的最大值;若不存在说明理由.2014年北京市高考数学模拟试卷(文科)答案1. B2. A3. C4. A5. D6. A7. D8. D9. 310. s 1>s 2>s 3 11. 2112. −1<a <2 13. 3214. {−18,0,18}15. 解:(1)∵ f(x)=sin 2x +√3sinxcosx −12=√32sin2x −12cos2x =sin(2x −π6),… ∴ f(−π12)=sin(−2×π12−π6)=sin(−π3)=−√32.… (2)∵ 0≤x ≤π2, ∴ 0≤2x ≤π. ∴ −π6≤2x −π6≤5π6. …∴ −12≤sin(2x −π6)≤1, 即−12≤f(x)≤1.… ∴ f(x)min =−12, 此时2x −π6=−π6,∴ x=0.…∴ 当x=0时,f(x)min=−12.…16. 若甲选择的是A款套餐,甲被选中调查的概率是0.1.(2)由图表可知,选A,B,C,D四款套餐的学生分别接受调查的人数为4,5,6,5.其中不满意的人数分别为1,1,0,2个.…记对A款套餐不满意的学生是a;对B款套餐不满意的学生是b;对D款套餐不满意的学生是c,d.…设事件N=“从填写不满意的学生中选出2人,至少有一人选择的是D款套餐”…从填写不满意的学生中选出2人,共有(a, b),(a, c),(a, d),(b, c),(b, d),(c, d)6个基本事件,…而事件N有(a, c),(a, d),(b, c),(b, d),(c, d)5个基本事件,…则P(N)=56.…答:这两人中至少有一人选择的是D款套餐的概率是56.17. (1)证明:因为点O是菱形ABCD的对角线的交点,所以O是AC的中点.又点M是棱BC的中点,所以OM是△ABC的中位线,OM // AB.因为OM⊄平面ABD,AB⊂平面ABD,所以OM // 平面ABD.(2)证明:由题意,OM=OD=3,因为DM=3√2,所以∠DOM=90∘,OD⊥OM.又因为菱形ABCD,所以OD⊥AC.因为OM∩AC=O,所以OD⊥平面ABC.因为OD⊂平面MDO,所以平面ABC⊥平面MDO.(3)解:三棱锥M−ABD的体积等于三棱锥D−ABM的体积.由(2)知,OD⊥平面ABC,所以OD=3为三棱锥D−ABM的高.△ABM的面积为12BA×BM×sin120∘=12×6×3×√32=9√32,所求体积等于13×S△ABM×OD=9√32.18. 解:(1)∵ f(x)=alnx−4x,∴ f′(x)=ax −4,…∴ f′(1)=a −4,…故切线方程为y =(a −4)x −a ; … (2)ℎ(x)=alnx +x 2−4x +3, ∴ ℎ′(x)=2x 2−4x+ax,…①若△=16−8a ≤0,即a ≥2,则ℎ′(x)≥0,则ℎ(x)在(1, +∞)上单调递增,又ℎ(1)=0,不符舍去. … ②若△>0,则a <2, 令ℎ′(x)>0得x >1+√4−2a2,令ℎ′(x)<0得0<x <1+√4−2a2, 则ℎ(x)在(0, 1+√4−2a 2)上单调递减,在(1+√4−2a2, +∞)单调递增,… 又ℎ(1)=0,则必有ℎ(e)<0,…即a +e 2−4e +3<0,∴ a <−e 2+4e −3. … 19. 解:(1)∵ F 1,F 2分别是椭圆G:x 2a2+y 2b 2=1(a >b >0)的左、右焦点,椭圆G 与抛物线y 2=−8x 有一个公共的焦点,且过点(−2, √2),∴ {c =24a 2+2b 2=1a 2=b 2+c 2,… 解得a 2=8,b 2=4, ∴ 椭圆C 的方程为x 28+y 24=1.…(2)结论:直线l 与圆x 2+y 2=83相切.证明:由题意可知,直线l 不过坐标原点,设A ,B 的坐标分别为(x 1, y 1),(x 2, y 2),y 1>y 2,(1)当直线l ⊥x 轴时,直线l 的方程为x =m ,(m ≠0),且−2√2<m <2√2, 则x 1=m ,y 1=√1−m 22,x 2=m ,y 2=−√4−m 22,∵ OA →⊥OB →,∴ x 1x 2+y 1y 2=0,∴ m 2−(4−m 22)=0,解得m =±2√63,故直线l 的方程为x =±2√63, 因此,点O(0, 0)到直线l 的距离为d =2√63, 又圆x 2+y 2=83的圆心为O(0, 0), 半径r =2√63=d ,∴ 直线l 与圆x 2+y 2=83相切.…(2)当直线l 不垂直于x 轴时,设直线l 的方程为y =kx +n ,联立直线和椭圆方程消去y 得: (1+2k 2)x 2+4knx +2n 2−8=0, ∴ x 1+x 2=−4kn 1+2k 2,x 1x 2=2n 2−81+2k 2,y 1y 2=(kx 1+n)(kx 2+n) =k 2x 1x 2+nk(x 1+x 2)+n 2 =n 2−8k 21+2k 2,∵ OA →⊥OB →,∴ x 1x 2+y 1y 2=0, ∴ 2n 2−81+2k 2+n 2−8k 21+2k 2=0,3n 2−8k 2−8=0, 3n 2=8k 2+8,①又圆x 2+y 2=83的圆心为O(0, 0),半径r =2√63, 圆心O 到直线l 的距离为d =√1+k 2, ∴ d 2=(√1+k2)2=n 21+k2=3n 23(1+k 2),②将①式带入②式得:d 2=8k 2+83(1+k 2)=83, ∴ d =2√63=r ,∴ 直线l 与圆x 2+y 2=83相切.…20. 解:(1)∵ S n =pa n+1(p ≠0, p ≠−1, n ∈N ∗), ∴ 当n ≥2时,有S n−1=pa n ,∴ a n+1a n=p+1p,n ≥2,∴ 数列{a n }从第二项起是公比为p+1p的等比数列,当n =1时,a 1=pa 2,而p ≠0,a 1=a ,得a 2=ap , ∴ a n ={a,n =1a p(p+1p)n−2,n ≥2.(2)(I)由(1)知a k+1=a p (p+1p)k−1, a k+2=a p (p+1p)k,a k+3=a p (p+1p)k+1, 若a k+1为等差中项,则2a k+1=a k+2+a k+3,解得:p =−13, 若a k+2为等差中项,则2a k+2=a k+1+a k+3,解得:p ∈⌀, 若a k+3为等差中项,则2a k+3=a k+1+a k+2,解得:p =−23, 综上所述p =−13或p =−23.当p =−13时,a k+1=−3a(−2)k−1,a k+2=−3a(−2)k ,注意到(−2)k−1与(−2)k 异号,d k =|a k+1−a k+2|=9a ⋅2k−1. 当p =−23时,a k+1=−3a 2(−12)k−1,a k+3=−3a 2(−12)k ,注意到(−12)k−1与(−12)k+1同号,d k =|a k+1−a k+3|=9a 8(12)k−1. 综上所述:当p =−13时,d k =9a ⋅2k−1;当p =−23时,d k =9a 8(12)k−1. (II)当p =−13时,∵ d k =9a ⋅2k−1,∴ S k =9a(2k −1), 则由S k <30,得a <103(2k −1),当k ≥3时,103(2k −1)<1, ∴ a <1,这时不存在符合题意的最大正整数a . 当p =−23时,∵ d k =9a 8⋅(12)k−1,∴ S k =9a 4(1−(12)k ),则由S k <30,得a <403(1−(12)k ),∵403(1−(12)k )>403,∴ a =13时,满足S k <30恒成立,当a ≥14时,存在k ∈N ∗,使得a >403(1−(12)k ),即S k >30,所以当a ≥14时,S k <30不恒成立综上所述:当p =−23时存在满足题意的最大正整数a =13.。
北京市西城区2024届高三下学期4月统一测试数学试卷(解析版)
西城区高三统一测试试卷数学2024.4本试卷共6页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知全集U =R ,集合{}{}3,22A x x B x x =<=-≤≤,则U A B =I ð()A.()2,3 B.()(),22,3-∞-⋃ C.[)2,3 D.][(),22,3-∞-⋃【答案】B【解析】【分析】利用补集和交集运算求解即可.【详解】因为集合{}22B x x =-≤≤,所以{2U B x x =<-ð或}2x >,又集合{}3A x x =<,所以U A B =I ð{2x x <-或}23x <<=()(),22,3∞--⋃.故选:B2.下列函数中,既是偶函数又在区间()0,∞+上单调递增的是()A.2y x x=+ B.cos y x =C.2xy = D.2log y x =【答案】D【解析】【分析】利用奇偶函数的判断方法及基本函数的单调性,对各个选项逐一分析判断,即可得出结果.【详解】对于选项A ,当1x =时,112y =+=,当=1x -时,110y =-=,即(1)(1)f f -≠,所以选项A 不满足题意,对于选项B ,因cos y x =在区间()0,∞+上不单调,所以选项B 不满足题意,对于选项C ,因为2x y =图象不关于y 轴对称,所以选项C 不满足题意,对于选项D ,因为2log y x =的定义域为()(),00,∞-+∞U ,关于原点对称,又22()log log ()f x x x f x -=-==,所以2log y x =为偶函数,当0x >时,22log log y x x ==,又2log y x =在区间()0,∞+上单调递增,所以选项D 满足题意,故选:D.3.622x x ⎛⎫- ⎪⎝⎭的展开式中,常数项为A.60- B.15-C.15D.60【答案】D【解析】【分析】写出二项式展开通项,整理后令x 的指数为0,得到相应的项数,然后算出常数项.【详解】622x x ⎛⎫- ⎪⎝⎭的展开式的通项为()663166222rr r r r r r T C x C x x --+⎛⎫=-=- ⎪⎝⎭,令630r -=,得到2r =所以622x x ⎛⎫- ⎪⎝⎭展开式中常数项为()226260C -=,故选D 项.【点睛】对二项式展开通项的考查,题目难度不大,考查内容比较单一,属于简单题.4.已知抛物线C 与抛物线24y x =关于直线y x =对称,则C 的准线方程是()A.=1x - B.2x =-C.1y =- D.=2y -【答案】C【解析】【分析】由对称性可得曲线C 方程,求出准线方程即可.【详解】因为抛物线C 与抛物线24y x =关于直线y x =对称,所以将,x y 互换后可得抛物线C 方程为24x y =,即242p p =⇒=,所以C 的准线方程为12p y =-=-,故选:C.5.设()11,,2a t b t c t t t t =-=+=+,其中10t -<<,则()A.b a c <<B.c<a<bC.b<c<aD.c b a<<【答案】C【解析】【分析】借助正负性、对勾函数的性质及二次函数的性质判断即可得.【详解】由10t -<<,故()1,1t ∈-∞-,故10a t t =->,由对勾函数性质可得()1112b t t =+<-+=-,()20c t t =+<,且()()2222111c t t t t t =⋅+=+=+-≥-,综上所述,有b<c<a .故选:C.6.已知向量,,a b c 在正方形网格中的位置如图所示.若网格纸上小正方形的边长为1,则()A.1- B.1 C.7- D.7【答案】A【解析】【分析】得出()1,3a b -=- 、()2,1c = 后借助向量数量积的坐标运算法则计算即可得.【详解】由图可得()1,3a b -=- ,()2,1c = ,故()()12311c a b ⋅-=⨯+-⨯=- .故选:A.7.已知函数()2,20x x x f x x c ⎧+-<<⎪=⎨≤<⎪⎩,若()f x 存在最小值,则c 的最大值为()A.116 B.18 C.14 D.12【答案】A【解析】【分析】运用二次函数的性质求得20x -<<的最小值,再结合幂函数的单调性,由题意列出不等式,求解即可.【详解】当20x -<<时,2211()24f x x x x ⎛⎫=+=+- ⎪⎝⎭,故当12x =-时,()f x 有最小值为14-;0x c ≤<时,()f x =()0f x <≤,由题意()f x 存在最小值,则14≥-,解得1016c <≤,即c 的最大值为116.故选:A8.在等比数列{}n a 中,00n a >.则“001n n a a +>”是“0013n n a a ++>”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【解析】【分析】结合等比数列的性质与充分条件与必要条件的定义判断即可的.【详解】设等比数列{}n a 的公比为0q ≠,当001n n a a +>时,即有00n n a q a >⋅,又00n a >,故1q <且0q ≠,当1q <-时,有0002311n n n a q a a +++=>,故不能得到0013n n a a ++>,即“001n n a a +>”不是“0013n n a a ++>”的充分条件;当0013n n a a ++>时,即有0002311n n n a q a a +++=<,即21q <且0q ≠,则001n n a q a +=⋅,当()1,0q ∈-时,由00n a >,故010n a +<,故001n n a a +>,当()0,1q ∈时,0001n n n a q a a +=⋅<,亦可得001n n a a +>,故“001n n a a +>”是“0013n n a a ++>”的必要条件;综上所述,“001n n a a +>”是“0013n n a a ++>”的必要不充分条件.故选:B.9.关于函数()sin cos2f x x x =+,给出下列三个命题:①()f x 是周期函数;②曲线()y f x =关于直线π2x =对称;③()f x 在区间[)0,2π上恰有3个零点.其中真命题的个数为()A.0B.1C.2D.3【答案】D【解析】【分析】选项①,根据条件得到()2π()f x f x +=,即可判断出①的正误;选项②,根据条件得出(π)()f x f x -=,根据对称轴的定义,即可得出②的正误;选项③,令()0f x =,直接求出x 的值,即可得出③的正误,从而得出结果.【详解】对于①,因为()sin cos2f x x x =+,所以()2πsin(2π)cos2(2π)sin cos2()f x x x x x f x +=+++=+=,故2πT =,所以选项①正确,对于②,因为(π)sin(π)cos2(π)sin cos2()f x x x x x f x -=-+-=+=,由对称轴的定义知,π2x =为函数()f x 的一条对称轴,所以选项②正确,对于③,因为()2sin cos22sin sin 1f x x x x x =+=-++,令()0f x =,得到22sin sin 10x x -++=,解得1sin 2x =-或sin 1x =,又[)0,2πx ∈,由1sin 2x =-,得到7π6x =或11π6x =,由sin 1x =,得到π2x =,所以选项③正确,故选:D.10.德国心理学家艾·宾浩斯研究发现,人类大脑对事物的遗忘是有规律的,他依据实验数据绘制出“遗忘曲线”.“遗忘曲线”中记忆率y 随时间t (小时)变化的趋势可由函数0.2710.6y t =-近似描述,则记忆率为50%时经过的时间约为()(参考数据:lg20.30,lg30.48≈≈)A.2小时B.0.8小时C.0.5小时D.0.2小时【答案】C【解析】【分析】根据题设得到0.2756t =,两边取对数求解,即可得出结果.【详解】根据题意得0.27110.62t =-,整理得到0.2756t =,两边取以10为底的对数,得到5lg 0.27lg 6t =,即1lg 32lg 20.27lg t --=,又lg20.30,lg30.48≈≈,所以8lg 27t =-,得到827100.5t -=≈,故选:C.第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.若复数z 满足(12i)3i z +=+,则z =______【答案】【解析】【分析】利用复数的除法公式计算1i z =-,再计算模长即可.【详解】(12i)3i z +=+,则()()()()3i 12i 3i 55i 1i 12i 12i 12i 5z +-+-====-++-,故z ==..12.已知(),0,παβ∈.使()()tan tan αβαβ+<-成立的一组,αβ的值为α=__________;β=__________.【答案】①.π3②.π3(答案不唯一)【解析】【分析】任取一组(),0,παβ∈,验证是否满足()()tan tan αβαβ+<-即可得.【详解】取π3αβ==,此时()2πtan tan 03αβ+=<,()tan tan00αβ-==,故()()tan tan αβαβ+<-,符合要求.故答案为:π3;π3(答案不唯一).13.双曲线22:13y M x -=的渐近线方程为__________;若M 与圆222:()0O x y r r +=>交于,,,A B C D 四点,且这四个点恰为正方形的四个顶点,则r =__________.【答案】①.y =②.【解析】【分析】结合双曲线渐近线的定义与正方形的性质计算即可得.【详解】由22:13y M x -=,故其渐近线方程为1y x =±=;令(),A m n ,由题意可得m n =,即有2213m m -=,解得232m =,故222232r m n m ===+,即r =.故答案为:y =14.在数列{}n a 中,122,3a a ==-.数列{}n b 满足()*1n n n b a a n +=-∈N.若{}nb 是公差为1的等差数列,则{}n b 的通项公式为n b =______,n a 的最小值为______.【答案】①.6n -②.13-【解析】【分析】求出等差数列{}n b 的首项,直接求出{}n b 的通项公式即可,利用数列{}n a 的单调性得最小项为6a ,利用累加法即可求解.【详解】由题意1215b a a =-=-,又等差数列{}n b 的公差为1,所以()5116n b n n =-+-⋅=-;故16n n a a n +-=-,所以当6n ≤时,10n n a a +-≤,当6n >时,10n n a a +->,所以123456789a a a a a a a a a >>>>>=<<<⋅⋅⋅,显然n a 的最小值是6a .又16n n a a n +-=-,所以()()()()()612132435465a a a a a a a a a a a a =+-+-+-+-+-()()()()()25432113=+-+-+-+-+-=-,即n a 的最小值是13-.故答案为:6n -,13-15.如图,正方形ABCD 和矩形ABEF 所在的平面互相垂直.点P 在正方形ABCD 及其内部运动,点Q 在矩形ABEF 及其内部运动.设2,1AB AF ==,给出下列四个结论:①存在点,P Q ,使3PQ =;②存在点,P Q ,使//CQ EP ;③到直线AD 和EF 的距离相等的点P 有无数个;④若PA PE ⊥,则四面体PAQE 体积的最大值为13.其中所有正确结论的序号是__________.【答案】①③④【解析】【分析】建立适当空间直角坐标系后,借助空间向量研究位置关系,结合距离公式、三棱锥体积公式逐项判断即可得.【详解】建立如图所示空间直角坐标系A FBD -,则有()0,0,0A 、()1,0,0F 、()0,2,0B 、()0,0,2D 、()0,2,2C 、()1,2,0E ,设()0,,P m n ,(),,0Q s t ,其中0,,2m n t ≤≤,01s ≤≤,对①:(),,PQ s t m n =-- ,则()222PQ s t m n =+-+ ,当1s =,2t n ==,0m =时,有1443PQ =++=,故存在点,P Q ,使3PQ =,故①正确;对②:(),2,2CQ s t =-- ,()1,2,EP m n =-- ,若//CQ EP ,则有()()222s m t sn ⎧-=--⎨=⎩,由0,,2m n t ≤≤,01s ≤≤,故当2sn =时,1s =,2n =,此时有()22m t -=--,即4m t +=,即2m t ==,此时Q 与E 重合,P 与C 重合,故不存在点,P Q ,使//CQ EP ,故②错误;对③:点P 到直线AD 的距离为m ,点P 到直线EF 的距离为,即有m =221m n -=,由0,2m n ≤≤,故其轨迹为双曲线的一部分,即点P 有无数个,故③正确;对④:()0,,AP m n = ,()1,2,EP m n =-- ,由PA PE ⊥,故有()220m m n -+=,则()[]22110,1n m =--∈,又1112122AB AQE FE S S ≤=⨯⨯= 矩形,故11113313P AQE AQE V S n -⨯≤⨯⨯==⨯ ,故④正确.故答案为:①③④.【点睛】关键点点睛:第④个结论的关键点在于借助四面体的体积公式,分别求出高与底面三角形的最大值.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.如图,在三棱柱111ABC A B C -中,侧面11A ACC 为正方形,AB AC ⊥,2AB AC ==,D 为BC 的中点.(1)求证:1//A C 平面1AB D ;(2)若1A C AB ⊥,求二面角11D AB A --的余弦值.【答案】(1)证明见解析(2)3-【解析】【分析】(1)根据线线平行证明面面平行;(2)向量法求二面角.【小问1详解】如图,连接1A B ,设11A B AB E = ,连接DE .因为在三棱柱111ABC A B C -中,四边形11A ABB 是平行四边形,所以E 为1A B 的中点.因为D 为BC 的中点,所以1//DE AC .又因为1A C ⊄平面1AB D ,DE ⊂平面1AB D ,所以1AC 平面1AB D .【小问2详解】因为1AB A C ⊥,AB AC ⊥,又1AC AC C ⋂=,1AC ⊂平面11A ACC ,AC ⊂平面11A ACC ,所以AB ⊥平面11A ACC ,又因1AA ⊂平面11A ACC ,所以1AB AA ⊥.又1AA AC ⊥,所以AB ,AC ,1AA 两两相互垂直.如图建立空间直角坐标系A xyz -,则()0,0,0A ,()12,0,2B ,()1,1,0D ,()0,2,0C .所以()12,0,2AB = ,()1,1,0AD = .设平面1AB D 的法间量为(),,m x y z = ,则100m AB m AD ⎧⋅=⎪⎨⋅=⎪⎩ 即2200x z x y +=⎧⎨+=⎩,令=1x -,则1y =,1z =于是()1,1,1m =- .因为AC ⊥平面11A ABB ,所以()0,2,0AC = 是平面11A ABB 的一个法向量.所以cos ,3m AC m AC m AC⋅== .由题设,二面角11D AB A --的平面角为钝角,所以二面角11D AB A --的余弦值为3-.17.在ABC 中,tan 2sin a B b A =.(1)求B ∠的大小;(2)若8a =,再从下列三个条件中选择一个作为已知,使ABC 存在,求ABC 的面积.条件①:BC ;条件②:2cos 3A =-;条件③:7b =.注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.【答案】(1)π3B ∠=(2)答案见解析【解析】【分析】(1)借助正弦定理计算即可得;(2)选条件①或③:借助余弦定理与面积公式计算即可得;不可选条件②,不存在这样的ABC .【小问1详解】由tan 2sin a B b A =,得sin 2sin cos a B b A B =,在ABC 中,由正弦定理得sin sin 2sin sin cos A B A B B =,因为sin 0,sin 0A B >>,所以1cos 2B =,又0πB <∠<,所以π3B ∠=;【小问2详解】选条件①:BC :设BC 边中点为M ,连接AM,则4AM BM ==,在ABM 中,由余弦定理得2222cos AM AB BM AB BM B =+-⋅⋅,即2π21168cos 3AB AB =+-⋅,整理得2450AB AB --=,解得5AB =或1AB =-(舍),所以ABC的面积为11πsin 58sin 223ABC S AB BC B =⋅⋅=⨯=,选条件③:7b =:在ABC 中,由余弦定理得2222cos b a c ac B =+-,即222π7816cos3c c =+-⋅,整理得28150c c -+=,解得3c =或5c =,当3c =时,ABC的面积为11πsin 83sin 223ABC S ac B ==⨯⨯= .当5c =时,ABC的面积为11πsin 85sin 223ABCS ac B ==⨯⨯=△.不可选条件②,理由如下:若2cos 3A =-,故A为钝角,则5sin 3A ==,则38sin 12152sin 53a Bb A ⨯===,224325b a =>,即b a >,其与A 为钝角矛盾,故不存在这样的ABC .18.10米气步枪是国际射击联合会的比赛项目之一,资格赛比赛规则如下:每位选手采用立姿射击60发子弹,总环数排名前8的选手进入决赛.三位选手甲、乙、丙的资格赛成绩如下:环数6环7环8环9环10环甲的射出频数11102424乙的射出频数32103015丙的射出频数24101826假设用频率估计概率,且甲、乙、丙的射击成绩相互独立.(1)若丙进入决赛,试判断甲是否进入决赛,说明理由;(2)若甲、乙各射击2次,估计这4次射击中出现2个“9环”和2个“10环”的概率;(3)甲、乙、丙各射击10次,用()1,2,3i X i =分别表示甲、乙、丙的10次射击中大于a 环的次数,其中{}6,7,8,9a ∈.写出一个a 的值,使()()()321D X D X D X >>.(结论不要求证明)【答案】(1)甲进入决赛,理由见解析(2)13100(3)7a =或8【解析】【分析】(1)分别计算出甲和丙射击成绩的总环数,进行比较即可判断.(2)先根据题中数据,用频率估计概率分别得出甲、乙命中9环的概率和甲、乙命中10环的概率;再根据互斥事件的概率加法公式和相互独立事件的概率公式即可求解.(3)根据题意可知()1,2,3i X i =服从二项分布,利用二项分布求出每一个a 对应的()()()321,,D X D X D X 即可解答.【小问1详解】甲进入决赛,理由如下:丙射击成绩的总环数为26471081892610542⨯+⨯+⨯+⨯+⨯=,甲射击成绩的总环数为16171082492410549⨯+⨯+⨯+⨯+⨯=.因为549542>,所以用样本来估计总体可得甲进入决赛.【小问2详解】根据题中数据:“甲命中9环”的概率可估计为242605=;“甲命中10环”的概率可估计为242605=;“乙命中9环”的概率可估计为301602=;“乙命中10环”的概率可估计为156041=.所以这4次射击中出现2个“9环”和2个“10环”的概率可估计为:222221122212121113.5452524100C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⨯+⨯+⨯⨯⨯⨯= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭【小问3详解】7a =或8.根据题中数据:当6a =时,在每次射击中,甲击中大于6环的的概率为5960p =;在每次射击中,乙击中大于6环的的概率为5760p =;在每次射击中,丙击中大于6环的的概率为5860p =;由题意可知:15910,60X B ⎛⎫~ ⎪⎝⎭,25710,60X B ⎛⎫~ ⎪⎝⎭,35810,60X B ⎛⎫~ ⎪⎝⎭.此时()15915901060603600D X =⨯⨯=,()257317101060603600D X =⨯⨯=,()358211601060603600D X =⨯⨯=,不满足()()()321D X D X D X >>.当7a =时,在每次射击中,甲击中大于7环的的概率为5860p =;在每次射击中,乙击中大于7环的的概率为5560p =;在每次射击中,丙击中大于7环的的概率为5460p =;由题意可知:15810,60X B ⎛⎫~ ⎪⎝⎭,25510,60X B ⎛⎫~ ⎪⎝⎭,35410,60X B ⎛⎫~ ⎪⎝⎭.此时()158211601060603600D X =⨯⨯=,()255527501060603600D X =⨯⨯=,()354632401060603600D X =⨯⨯=,满足()()()321D X D X D X >>.当8a =时,在每次射击中,甲击中大于8环的的概率为4860p =;在每次射击中,乙击中大于8环的的概率为4560p =;在每次射击中,丙击中大于8环的的概率为4460p =;由题意可知:14810,60X B ⎛⎫~ ⎪⎝⎭,24510,60X B ⎛⎫~ ⎪⎝⎭,34410,60X B ⎛⎫~ ⎪⎝⎭.此时()1481257601060603600D X =⨯⨯=,()2451567501060603600D X =⨯⨯=,()3441670401060603600D X =⨯⨯=,满足()()()321D X D X D X >>.当9a =时,在每次射击中,甲击中大于9环的的概率为2460p =;在每次射击中,乙击中大于9环的的概率为1560p =;在每次射击中,丙击中大于9环的的概率为2660p =;由题意可知:12410,60X B ⎛⎫~ ⎪⎝⎭,21510,60X B ⎛⎫~ ⎪⎝⎭,32610,60X B ⎛⎫~ ⎪⎝⎭.此时()1243686401060603600D X =⨯⨯=,()2154567501060603600D X =⨯⨯=,()3263488401060603600D X =⨯⨯=,不满足()()()321D X D X D X >>.所以7a =或8.19.已知椭圆2222:1(0)x y G a b a b+=>>的一个顶点为()2,0A -,离心率为12.(1)求椭圆G 的方程;(2)设O 为原点.直线l 与椭圆G 交于,C D 两点(,C D 不是椭圆的顶点),l 与直线2x =交于点E ,直线,AC AD 分别与直线OE 交于点,M N .求证:=OM ON .【答案】(1)22143x y +=(2)证明见解析【解析】【分析】(1)结合题意,列出方程组计算即可得;(2)设直线l 为y kx m =+,联立椭圆方程可得与横坐标有关韦达定理,借助C 、D 两点坐标可表示出M x 、N x ,计算可得0M N x x +=,即可得解.【小问1详解】由题意可得222212a c a a b c=⎧⎪⎪=⎨⎪-=⎪⎩,解得21a b c =⎧⎪=⎨⎪=⎩所以椭圆G 的方程为22143x y +=;【小问2详解】由题意可知直线l 的斜率存在,设其方程为y kx m =+.则()2,2E k m +,直线OE 的方程为2m y k x ⎛⎫=+ ⎪⎝⎭,由223412y kx m x y =+⎧⎨+=⎩,得()2224384120k x kmx m +++-=,由()22Δ48430k m =-+>,得2243m k <+,设()()1122,,,C x y D x y ,则21212228412,4343km m x x x x k k -+=-=++,直线AC 的方程为()1122y y x x =++,联立直线AC 和OE 得()11222y m x k x x ⎛⎫+=+ ⎪+⎝⎭,解得()()11111114244422M kx m y y x m mx k mx k k x y +===++⎛⎫++- ⎪⎝⎭,同理可得()2244N kx m x mx k +=+,所以()()()()()()12211244444M N kx m mx k kx m mx k x x mx k mx k ++++++=⨯++,因为()()()()122144kx m mx k kx m mx k +++++()()221212248kmx x k m x x km =++++()()()22222222412848430434343km m km k m km k k k k -++=-+=+++,所以0M N x x +=,即点M 和点N 关于原点O 对称,所以OM ON =..【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:(1)设直线方程,设交点坐标为()()1122,,,x y x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,注意∆的判断;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x (或12y y +、12y y )的形式;(5)代入韦达定理求解.20.已知函数()()1ln e x f x x ax x a=++.(1)当1a =时,求曲线()y f x =在点()()1,1f 处切线的斜率;(2)当1a =-时,讨论()f x 的单调性;(3)若集合(){}1xf x ≥-∣有且只有一个元素,求a 的值.【答案】(1)2e 2+(2)单调递增区间为(),1-∞-;单调递减区间为()1,0-(3)1a e =-【解析】【分析】(1)根据条件,利用导数的几何意义,即可求出结果;(2)对函数求导得到()()11e x f x x x ⎛⎫=+-⎪⎝⎭',由函数()f x 定义域知1e 0x x -<,再利用导数与函数单调性间的关系,即可求出结果;(3)对函数求导得到()()1e 1x f x x x a ⎛⎫=++ ⎪⎝⎭',再分0a >和a<0两种情况讨论,利用导数与函数单调性间的关系,求出函数的单调区间,结合条件,即可求出结果.【小问1详解】当1a =时,()ln e xf x x x x =++,所以()()111e x f x x x=+++',得到()12e 2f '=+,所以曲线()y f x =在点()(1,)1f 处切线的斜率为2e 2+.【小问2详解】当1a =-时,()()ln e xf x x x x =+--,易知()f x 的定义域为(),0∞-,又()()()1111e 1e x x f x x x x x ⎛⎫=+-+=+- ⎪⎝⎭',因为(),0x ∈-∞,所以1e 0x x -<,所以(),1x ∈-∞-时,()0f x ¢>,()1,0x ∈-时,()0f x '<所以()f x 的单调递增区间为(),1-∞-;单调递减区间为()1,0-.【小问3详解】因为()()1ln e x f x x ax x a =++,所以()()1e 1x f x x x a ⎛⎫=++ ⎪⎝⎭',易知0a ≠,当0a >时,()f x 的定义域为()0,∞+,所以()0f x ¢>恒成立,故()f x 在()0,∞+上单调递增,又12111e 0a f a a a⎛⎫=+> ⎪⎝⎭,所以0a >不合题意,当0a <时,()f x 的定义域为(),0∞-,此时1e 0xx a+<,所以(),1x ∈-∞-时,()0f x ¢>,()1,0x ∈-时,()0f x '<,故()f x 的单调递增区间为(),1-∞-,单调递减区间为()1,0-,所以()()max 1()11ln ef x f a a =-=-+--.设()()11ln (0)e g x x x x =-+--<,则()2211e 1e e x g x x x x +=+=',当1,e x ∞⎛⎫∈-- ⎪⎝⎭时,()0g x '<,1,0e x ⎛⎫∈- ⎪⎝⎭时,()0g x '>,所以()g x 的单调递减区间为1,e ⎛⎫-∞- ⎪⎝⎭;单调递增区间为1,0e ⎛⎫- ⎪⎝⎭.所以min 1()1e g x g ⎛⎫=-=- ⎪⎝⎭,所以集合(){}1xf x ≥-∣有且只有一个元素时1a e =-.【点睛】方法点睛:对于求不等式成立时的参数范围问题,一般有三个方法:一是分离参数法,使不等式一端是含有参数的式子,另一端是一个区间上具体的函数,通过对具体函数的研究确定含参式子满足的条件;二是讨论分析法,根据参数取值情况分类讨论;三是数形结合法,将不等式转化为两个函数,通过两个函数图像确定条件.21.对正整数3,6m n ≥≥,设数列{}()12:,,,,0,11,2,,n i A a a a a i n ∈= .B 是m 行n 列的数阵,ij b 表示B 中第i 行第j 列的数,{}()0,11,2,,;1,2,,ij b i m j n ∈== ,且B 同时满足下列三个条件:①每行恰有三个1;②每列至少有一个1;③任意两行不相同.记集合{11220i i n in i a b a b a b +++= 或}3,1,2,,i m = 中元素的个数为K .(1)若111000:1,1,1,0,0,0,101100000111A B ⎛⎫ ⎪= ⎪ ⎪⎝⎭,求K 的值;(2)若对任意{},1,2,,(),p q n p q B ∈< 中都恰有r 行满足第p 列和第q 列的数均为1.①B 能否满足3m r =?说明理由;②证明:()21424K n n ≥-.【答案】(1)2K =(2)①不满足,理由见解析;②证明见解析【解析】【分析】(1)记1122i i i n in t a b a b a b =+++ ,计算出1t 、2t 、3t 即可得;(2)①由题意可得B 中满足1ip iq b b ==的(),,i p q 的个数共有3m 个,亦可得其为2n rC 个,当3m r =时,可得2C 9n=,此方程无解,故不满足;②满足1ip iq b b ==,但p q a a ≠的(),,i p q 的个数为2C 23n r K ⎛⎫- ⎪⎝⎭,亦可得其为()rx n x -,即有()2C 23n r rx n x K ⎛⎫-=- ⎪⎝⎭,借助该等式表示出K 后放缩即可得.【小问1详解】记1122i i i n in t a b a b a b =+++ ,则11112123134145156163t a b a b a b a b a b a b +=+++=+,21212223234245256262t a b a b a b a b a b a b +=+++=+,31312323334345356360t a b a b a b a b a b a b +=+++=+,故2K =;【小问2详解】①B 不满足3m r =,理由如下:假设B 满足3m r =,因为B 的每行恰有三个1,故B 中满足1ip iq b b ==的(),,i p q 的个数共有3m 个,另一方面,从B 中任选两列共有2C n 种可能,且对任意两列,都恰有r 行使得这两列的数均为1,故B 中满足1ip iq b b ==的(),,i p q 的个数共有2n rC 个,所以23C n m r =,当3m r =时,得2C 9n =,此方程无解,所以B 不满足3m r =;②由①可得23C nm r =,即2C 3n r m =,下面考虑满足1ip iq b b ==,但p q a a ≠的(),,i p q 的个数:对B 中满足0i t ≠和3的m K -行,每行恰有两组(),p q 使1ip iq b b ==且p q a a ≠,所以满足1ip iq b b ==,但p q a a ≠的(),,i p q 的个数为()2C 223n r m K K ⎛⎫-=- ⎪⎝⎭,设数列A 中有x 项为1,n x -项为0,满足1ip iq b b ==,但p q a a ≠的(),p q 的个数为()x n x -,所以满足1ip iq b b ==,但p q a a ≠的(),,i p q 的个数为()rx n x -,所以()2C 23n r rx n x K ⎛⎫-=- ⎪⎝⎭,所以()()222C 33326n rx n x r r K x nx n n -=-=-+-()2222233146426424r n n r n n n n n n ⎛⎫⎛⎫≥-+-=-≥- ⎪ ⎪⎝⎭⎝⎭.【点睛】关键点点睛:本题考查新定义,关键点在于结合定义,得到满足1ip iq b b ==,但p q a a ≠的(),,i p q 的个数为2C 23n r K ⎛⎫- ⎪⎝⎭且为()rx n x -.。
2014年北京西城区高三一模数学试题解析
2014年北京西城区高三一模数学试题解析拿到西城一模数学试卷,隐隐觉得有点“不详”的预感。
通观全卷,感觉这份卷子出得有点让人哭笑不得。
【选择分析】8个选择,题型设计非常常规。
需要提一下的是第7题,一个函数应用题,此题的出现基本上和考试说明中提出的“考察实际能力”的精神是相符合的。
但其实,真要纠结于这一点的话,函数应用题,并不是一个特别生僻的点,即使把它勉强算成较少考察大的点,那么整张卷子,也没有第二道题出现了所谓的考察实际能力。
此题难度一般。
第8题,传统意义上的选择压轴。
题目本身没有设置特别大的难度,但是题干的用语却十分复杂纠结。
一个正四面体、任意一点到定点距离、距离构成的集合、集合元素还有限。
如果考生被这些或有用或无用的条件耽误太多时间,那么可能此题真的就成了一个难点。
但只要是有一个比较良好的审题习惯,并且对于高中的一百多知识点都非常熟悉,此题其实难度也没有想象中那么大。
【选择解读】逃离第八题本身的难度讨论,但是从第八题的出题方式也许能成为某种信号:绝对难度值降下来了,但是难度方式却发生了转移,更强调对于数学术语和数学逻辑的理解的考察。
如果命题者真是把这样的考察方式理解为考察数学思想。
那么本题的参考价值或许真的不小。
(当然,平心而论,笔者并不觉得这种出题方式和所谓的数学思想有多大关系,但或多或少,为数学思想提供了一个试题出口。
这个信号对于考生的价值其实还是比较大的。
)【填空分析】6个填空也没有太大的变化,平稳为主。
值得注意的是14题,和前面所说的第8题在某种程度上,如出一辙:绕!直角梯形,向量,内积加上莫名其妙的函数,或许会让部分学生有点晕头转向。
但其实,如果我们把这个题稍稍做调整,把函数换成“对应关系”四个字,也许晕的同学会减少不少,在很多同学考后给我的信息是:在考场上纠结函数大的解析式是什么纠结了很久,然后无果只能放弃。
这或许正式出题人的意图,用复杂的“条件们”去阻碍思路。
【填空解读】其实,14题算是一道好题,对于数学思想的考察明显比第8题要好很多。
2014年北京市数学(文)高考真题含答案带解析(超完美word版)
2014年普通高等学校招生全国统一考试北京卷文科数学一、选择题共8小题,每小题5分,共40分。
在每小题列出的4个选项中,选出符合题目要求的一项。
1.若集合{}0,1,2,4A =,{}1,2,3B =,则A B = ( )A.{}0,1,2,3,4B.{}0,4C.{}1,2D.{}3 2.下列函数中,定义域是R 且为增函数的是( )A.x y e -=B.y x =C.ln y x =D.y x =3.已知向量()2,4a = ,()1,1b =-,则2a b -= ( )A.()5,7B.()5,9C.()3,7D.()3,9 4.执行如图所示的程序框图,输出的S 值为( )A.1B.3C.7D.155.设a 、b 是实数,则“a b >”是“22a b >”的( )A.充分而不必要条件B.必要而不必要条件C.充分必要条件D.既不充分不必要条件 6.已知函数()26log f x x x=-,在下列区间中, 包含()f x 零点的区间是( ) A.()0,1B.()1,2C.()2,4D.()4,+∞7.已知圆()()22:341C x y -+-=和两点(),0A m -,()(),00B m m >,若圆C 上存在点P , 使得90APB ∠=,则m 的最大值为( )A.7B.6C.5D.4 8.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”. 在特定条件下,可食用率p 与加工时间t (单位:分钟) 满足的函数关系2p at bt c =++(a 、b 、c 是常数), 图中记录了三次实验的数据.根据上述函数模型和实验数据, 可以得到最佳加工时间为( )A.3.50分钟B.3.75分钟C.4.00分钟D.4.25分钟二、填空题共6小题,每小题5分,共30分。
9.若()()12x i i i x R +=-+∈,则x = . 10.设双曲线C的两个焦点为(),),一个顶点式()1,0,则C 的方程为.11.某三棱锥的三视图如图所示,则该三棱锥的最长棱的棱长为.侧(左)视图正(主)视图12.在ABC ∆中,1a =,2b =,1cos 4C =,则c = ;sin A = . 13.若x 、y 满足11010y x y x y ≤⎧⎪--≤⎨⎪+-≥⎩,则z y +的最小值为 .14.顾客请一位工艺师把A 、B 两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这 项任务,每件颜料先由徒弟完成粗加工,再由工艺师进行精加工完成制作,两件工艺品都 完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:则最短交货期为 工作日.三、解答题共6小题,共80分。
北京市西城区届高三4月第一次模拟考试数学(文)试题.pdf
课题1 金属材料 教学目标: 过日常生活中广泛使用金属材料等具体事例,认识金属材料与人类生活和社会发展的密切联系。
2、了解常见金属的物理性质,知道物质的性质很大程度上决定物质的用途,但还需考虑价格等因素。
3、认识合金,知道生铁和钢等重要合金,以及合金比纯金属具有更广泛的用途。
重点:1、知道物质的性质很大程度上决定物质的用途,但还需考虑价格等因素。
2、认识合金。
难点:采用活动与探究的方式来研究金属及合金的物理性质上的差异 教学过程: 教师先展示一些物品,然后设问:这些物品是由什么材料制成?教师引导学生,如何根据金属的一些用途,推断金属的物理性质。
使学生明白:物质的性质、资源、价格、美观等决定其用途Ag Cu Au Al Zn Fe Pb 导电性逐渐减弱密度Au Pb Ag Cu Fe Zn Al 密度逐渐减少熔点W Fe Cu Au Ag Al Sn 熔点由高到低硬度 Cr Fe Ag Cu Au Al Pb 硬度由大到小 合金:合金是由一种金属跟其它一种或几种金属(或金属跟非金属)一起熔合而成的具有金属特性的物质。
【讲述】合金的简单命名。
【引入】我们在日常生活中接触到的钢铁都是铁碳合金。
根据含碳量的不同,铁碳合金又分为生铁和钢。
一些合金和组成它们的纯金属性质比较 性质比较 现象黄铜铜焊锡锡光泽和颜色硬度结论实验8-2比较焊锡、锡和铅的熔化温度 现象结论最近一些学者研究发现,古罗马人的遗骸中含有大量铅,古罗马帝国的灭亡竟与铅中毒有关。
原来古罗马贵族惯用铅制器皿(瓶、杯、壶等)和含铅化合物的化妆品,甚至输送饮水的水管也是用铅做的,从而导致慢性铅中毒死亡。
根据上述材料回答下列问题: (1)人们日常接触的哪些物质中含铅? (2)铅对人体有哪些危害? (3)为防止铅中毒,请你提出几条合理建议。
(4)以小组的形式组织一项调查活动:到附近的加油站,调查汽油的种类,是否还在使用含铅汽油?是什么时候停止使用含铅汽油的?并进行环保宣传。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市西城区2014年高三下学期4月模拟考试(一模)数学(文科)试卷2014.4第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设全集{|02}U x x =<<,集合1{|0}A x x =<≤,则集合U A =ð( ) (A )(0,1) (B )(0,1](C )(1,2)(D )[1,2)2.已知平面向量(2,1)=-a ,(1,3)=b ,那么|a +b |等于( ) (A )5 (B(C(D )133.已知双曲线2222:1(0,0)x y C a b a b-=>>的虚轴长是实轴长的2倍,则此双曲线的离心率为( ) (A(B )2(C(D4.某几何体的三视图如图所示,则该几何体的体积为( ) (A )2 (B )43(C )4 (D )5正(主)视图俯视图侧(左)视图6. 设0a >,且1a ≠,则“函数log a y x =在(0,)+∞上是减函数”是“函数3(2)y a x =-在R 上是增函数”的( )(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件7.某企业为节能减排,用9万元购进一台新设备用于生产. 第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加2万元,该设备每年生产的收入均为11万元. 设该设备使用了()n n *∈N 年后,盈利总额达到最大值(盈利额等于收入减去成本),则n 等于( ) (A )4 (B )5(C )6(D )78. 如图,设P 为正四面体A BCD -表面(含棱)上与顶点不重合的一点,由点P 到四个顶点的距离组成的集合记为M ,如果集合M 中有且只有2个元素,那么符合条件的点P 有( )(A ) 4个 (B )6个(C )10个(D )14个5.下列函数中,对于任意x ∈R ,同时满足条件()()f x f x =-和(π)()f x f x -=的函数是( )(A )()sin =f x x (B )()sin 2=f x x (C )()cos =f x x (D )()cos 2=f x x BADC. P第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.设复数1ii 2ix y -=++,其中,x y ∈R ,则x y +=______.10.若抛物线2:2C y px =的焦点在直线20x y +-=上,则p =_____;C 的准线方程为_____.11.已知函数3, 0,()1, 0,1≤+⎧⎪=⎨>⎪+⎩x x f x x x 若0()2=f x ,则实数0=x ______;函数()f x 的最大值为_____.12.执行如图所示的程序框图,如果输入2,2a b ==,那么输出的a 值为______.13.若不等式组1,0,26,ax y x y x y ⎧⎪⎪⎨+⎪⎪+⎩≥≥≤≤表示的平面区域是一个四边形,则实数a 的取值范围是__________.14.如图,在直角梯形ABCD 中,//AB CD ,AB BC ⊥,2AB =,1CD =,2BC =,P 为线段AD (含端点)上一个动点. 设AP xAD = ,PB PC y ⋅=,记()=y f x ,则(1)=f ____; 函数()f x 的值域为_________.D C P三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 已知222b c a bc +=+.(Ⅰ)求A 的大小;(Ⅱ)如果cos =B 2b =,求a 的值. 16.(本小题满分13分)某批次的某种灯泡共200个,对其寿命进行追踪调查,将结果列成频率分布表如下. 根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.(Ⅰ)根据频率分布表中的数据,写出a ,b ,c 的值;(Ⅱ)某人从这200个灯泡中随机地购买了1个,求此灯泡恰好不.是次品的概率; (Ⅲ)某人从这批灯泡中随机地购买了()*∈n n N 个,如果这n 个灯泡的等级情况恰好与按.三个..等级分层抽样......所得的结果相同,求n 的最小值.17.(本小题满分14分)如图,在四棱锥ABCD S -中,底面ABCD 是矩形,2AD AB =,SA SD =,SA AB ⊥, N 是棱AD 的中点.(Ⅰ)求证://AB 平面SCD ; (Ⅱ)求证:SN ⊥平面ABCD ;(Ⅲ)在棱SC 上是否存在一点P ,使得平面⊥PBD 平面ABCD ?若存在,求出SPPC的值;若不存在,说明理由. 18.(本小题满分13分)已知函数()ln af x x x=-,其中a ∈R . (Ⅰ)当2a =时,求函数()f x 的图象在点(1,(1))f 处的切线方程; (Ⅱ)如果对于任意(1,)x ∈+∞,都有()2f x x >-+,求a 的取值范围. 19.(本小题满分14分)已知椭圆22221(0)x y W a b a b+=>>:的焦距为2,过右焦点和短轴一个端点的直线的斜率为1-,O 为坐标原点.(Ⅰ)求椭圆W 的方程.(Ⅱ)设斜率为k 的直线l 与W 相交于,A B 两点,记AOB ∆面积的最大值为k S ,证明:12S S =.20.(本小题满分13分)在数列{}n a 中,1()n a n n*=∈N . 从数列{}n a 中选出(3)k k ≥项并按原顺序组成的新数列记为{}n b ,并称{}n b 为数列{}n a 的k 项子列. 例如数列1111,,,2358为{}n a 的一个4项子列.(Ⅰ)试写出数列{}n a 的一个3项子列,并使其为等比数列;(Ⅱ)如果{}n b 为数列{}n a 的一个5项子列,且{}n b 为等差数列,证明:{}n b 的公差d 满足104d -<<; (Ⅲ)如果{}n c 为数列{}n a 的一个6项子列,且{}n c 为等比数列,证明:1234566332c c c c c c +++++≤.北京市西城区2014年高三一模试卷参考答案及评分标准高三数学(文科) 2014.4一、选择题:本大题共8小题,每小题5分,共40分.1.C 2.B 3.D 4.C 5.D 6.A 7.B 8.C 二、填空题:本大题共6小题,每小题5分,共30分. 9.25-10.4 2=-x 11.1- 3 12.25613. (3,5) 14.1 4[,4]5注:第10、11、14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:因为 222b c a bc +=+,所以 2221cos 22b c a A bc +-==, ……………… 4分又因为 (0,π)∈A ,所以 π3A =. ……………… 6分(Ⅱ)解:因为 cos =B (0,π)∈B ,所以 sin B ==, ………………8分由正弦定理sin sin =a bA B, (11)得 sin 3sin ==b Aa B. ………………13分16.(本小题满分13分)(Ⅰ)解:0.15a =,30b =,0.3=c . ……………… 3分(Ⅱ)解:设“此人购买的灯泡恰好不是次品”为事件A . ……………… 4分由表可知:这批灯泡中优等品有60个,正品有100个,次品有40个, 所以此人购买的灯泡恰好不是次品的概率为100604()2005+==P A . …………… 8分(Ⅲ)解:由(Ⅱ)得这批灯泡中优等品、正品和次品的比例为60:100:403:5:2=. (10)分所以按分层抽样法,购买灯泡数 35210()*=++=∈n k k k k k N ,所以n 的最小值为10. ……………… 13分17.(本小题满分14分)(Ⅰ)证明:因为底面ABCD 是矩形,所以 //AB CD , ……………… 1分又因为 AB ⊄平面SCD ,CD ⊂平面SCD ,所以 //AB 平面SCD . ……………… 3分(Ⅱ)证明:因为 , , AB SA AB AD SA AD A ⊥⊥= ,所以⊥AB 平面SAD , (5)又因为 SN ⊂平面SAD ,所以 AB SN ⊥. ……………… 6分因为 SA SD =,且N 为AD 中点, 所以 SN AD ⊥. 又因为 AB AD A = ,所以 SN ⊥平面ABCD . ……………… 8分(Ⅲ)解:如图,连接BD 交NC 于点F ,在平面SNC 中过F 作//FP SN 交SC 于点P ,连接PB ,PD .因为 SN ⊥平面ABCD ,所以 FP ⊥平面ABCD . (11)又因为 FP ⊂平面PBD ,所以平面PBD ⊥平面ABCD . …………… 12在矩形ABCD 中,因为//ND BC , 所以12NF ND FC BC ==. 在SNC ∆中,因为//FP SN , 所以12NF SP FC PC ==. 则在棱SC 上存在点P ,使得平面⊥PBD 平面ABCD ,此时12SP PC =. ……… 14分18.(本小题满分13分) (Ⅰ)解:由2()ln f x x x=-,得212()f x x x '=+, ……………… 2分所以 (1)3f '=, 又因为 (1)2f =-,所以函数()f x 的图象在点(1,(1))f 处的切线方程为350x y --=. ……………… 4分(Ⅱ)解:由 ()2f x x >-+,得ln 2ax x x->-+, 即 2ln 2a x x x x <+-. ……………… 6分设函数2()ln 2g x x x x x =+-,则 ()ln 21g x x x '=+-, ……………… 8分因为(1,)x ∈+∞,所以ln 0x >,210x ->,所以当(1,)x ∈+∞时,()ln 210g x x x '=+->, ……………… 10分故函数()g x 在(1,)x ∈+∞上单调递增,所以当(1,)x ∈+∞时,()(1)1g x g >=-. ……………… 11分因为对于任意(1,)x ∈+∞,都有()2f x x >-+成立, 所以对于任意(1,)x ∈+∞,都有()a g x <成立.所以1a -≤. ……………… 13分19.(本小题满分14分)(Ⅰ)解:由题意,得椭圆W 的半焦距1c =,右焦点(1,0)F ,上顶点(0,)M b ,…… 1分 所以直线MF 的斜率为0101-==--MF b k , 解得 1b =, ……………… 3分由 222a b c =+,得22a =,所以椭圆W 的方程为2212x y +=. (5)分(Ⅱ)证明:设直线l 的方程为y kx m =+,其中1k =或2,11(,)A x y ,22(,)B x y .… 6分由方程组2212y kx m x y =+⎧⎪⎨+=⎪⎩ 得222(12)4220k x kmx m +++-=, ……………… 7分所以 2216880k m ∆=-+>, (*)由韦达定理,得122412kmx x k -+=+, 21222212m x x k -=+. (8)分所以||AB == (9)分因为原点O 到直线y kx m =+的距离d =, (10)分所以 1||2AOB S AB d ∆=⋅= ……………… 11分当1k =时,因为AOB S ∆=所以当232m =时,AOB S ∆的最大值1S =,验证知(*)成立; ……………… 12分当2k =时,因为AOB S ∆=,所以当292m =时,AOB S ∆的最大值2S =;验证知(*)成立.所以 12S S =. ……………… 14分注:本题中对于任意给定的k ,AOB ∆.20.(本小题满分13分)(Ⅰ)解:答案不唯一. 如3项子列:12,14,18. ……………… 2分(Ⅱ)证明:由题意,知1234510b b b b b >>>>>≥,所以 210d b b =-<. ……………… 4分因为 514b b d =+,151,0b b >≤, 所以 514011d b b =->-=-,解得 14d >-. 所以104d -<<. ……………… 7分(Ⅲ)证明:由题意,设{}n c 的公比为q ,则 23451234561(1)c c c c c c c q q q q q +++++=+++++. 因为{}n c 为{}n a 的一个6项子列, 所以 q 为正有理数,且1q <,111()c a a*=∈N ≤. ……………… 8分设 (,Kq K L L*=∈N ,且,K L 互质,2L ≥). 当1K =时,因为 112q L =≤, 所以 23451234561(1)c c c c c c c q q q q q +++++=+++++ 2345111111()()()()22222+++++≤, 所以 1234566332c c c c c c +++++≤. ……………… 10分当1K ≠时,因为 556151==⨯K c c q a L是{}n a 中的项,且,K L 互质,所以 5*()a K M M =⨯∈N ,所以 23451234561(1)c c c c c c c q q q q q +++++=+++++543223*********()M K K L K L K L KL L=+++++. 因为 2L ≥,*,K M ∈N ,所以 234512345611111631()()()()2222232c c c c c c ++++++++++=≤. 综上, 1234566332c c c c c c +++++≤. ……………… 13分。
