关于x、y轴及原点对称PPT教学课件
合集下载
双曲线的几何性质PPT课件
解 (1)依题意可知,双曲线的焦点在 y 轴上,且 c=13,
又ac=153, ∴a=5,b= c2-a2=12,故其标准方程为5y22-1x222=1.
(2)法一 ∵双曲线的渐近线方程为 y=±12x, 若焦点在 x 轴上,设所求双曲线的标准方程为xa22-by22=1(a>0,
b>0),则ba=12.
课前探究学习
课堂讲练互动
活页规范训练
为 深 入 学 习 习近平 新时代 中国特 色社会 主义思 想和党 的十九 大精神 ,贯彻全 国教育 大会精 神,充分 发挥中 小学图 书室育 人功能
②与双曲线xa22-by22=1
有共同渐近线的双曲线方程为ax22-yb22=
λ(λ≠0).
2.直线与双曲线的位置关系
[思路探索] 可先把方程化成标准方程,确定a,b,c,再 求其几何性质.
解 把方程 16x2-9y2=-144 化为标准方程y422-3x22=1, 由此可知,半实轴长 a=4, 半虚轴长 b=3,c= a2+b2=5.
课前探究学习
课堂讲练互动
活页规范训练
为 深 入 学 习 习近平 新时代 中国特 色社会 主义思 想和党 的十九 大精神 ,贯彻全 国教育 大会精 神,充分 发挥中 小学图 书室育 人功能
为 深 入 学 习 习近平 新时代 中国特 色社会 主义思 想和党 的十九 大精神 ,贯彻全 国教育 大会精 神,充分 发挥中 小学图 书室育 人功能
自学导引
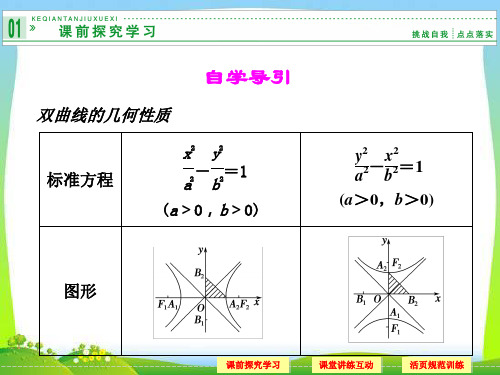
双曲线的几何性质
标准方程
x2 y2
- =1
a2 b2
(a>0,b>0)
ya22-bx22=1 (a>0,b>0)
图形
课前探究学习
课堂讲练互动
《轴对称现象》生活中的轴对称优质课件

鼓励学生将所学的轴对称知识应用到实际 生活中,如设计具有对称美的图案、分析 工程结构的稳定性等。
THANKS
谢谢您的观看
例子
正方形、圆形、等腰三角形等都是 常见的轴对称图形。
解析几何中的轴对称
定义
在解析几何中,如果一个点关于 原点对称,那么这个点被称为关
于x轴、y轴或z轴的对称点。
性质
关于x轴对称的点,横坐标相等 ,纵坐标互为相反数;关于y轴 对称的点,横坐标互为相反数, 纵坐标相等;关于z轴对称的点 ,横、纵坐标都互为相反数。
02
生活中的轴对称现象
自然界中的轴对称现象
蝴蝶
蝴蝶的翅膀在飞行时呈现明显的轴对 称,这种对称性有助于保持飞行稳定 。
植物叶子
许多植物的叶子在生长过程中呈现出 轴对称的特点,如枫叶、银杏叶等。
雪花
雪花是自然界中轴对称的典型例子, 其形状由冰晶按照一定规律生长而成 。
建筑中的轴对称现象
01
02
03
轴对称现象的特性
详细描述
轴对称现象具有以下特性
2. 轴线唯一性
每个轴对称现象都有一个唯一 的对称轴,且对称轴两侧的形 状、大小等完全一致。
总结词
全面、深入
1. 对称性
物体或图形在轴对称下,其两 侧形状、大小、排列等完全相 同。
3. 旋转不变性
若将物体或图形绕对称轴旋转 180度,其形状、大小等不会 发生变化。
雕塑
许多雕塑作品采用轴对称 的设计,如罗丹的《思想 者》雕塑,呈现出优雅的 平衡感。
音乐
音乐作品中的旋律和和声 有时会采用轴对称的结构 ,使音乐听起来更加和谐 和平衡。
03
轴对称现象的数学解释
平面几何中的轴对称
《平面直角坐标系》复习课件(共32张PPT)

x=-y
特殊位置点的特殊坐标:
坐标轴上点P
(x,y)
连线平行于坐标轴 的点
点P(x,y)在各象限的
坐标特点
象限角平分线 上的点
x轴 y轴 原点 平行于 平行于y 第一 第二 第三 第四 一三象 二四象
x轴
轴
象限 象限 象限 象限 限
限
纵坐标相 横坐标相 x>0
(x,0) (0,y) (0,0) 同
.
6.点A(x,y),且x+y>0,
x 那0 么点A在第___象限 y
特殊点的坐标 y
(0,y)
在平面平直行角于坐x轴标的系直内线描上出(2,2),(的0,各2),点(2的,2)纵,(4坐,2)标,依相次连 接各点同,,从横中坐标你不发同现. 了什么?
1
-1 0 1 -1
在平面直角坐标系内描
出平(行-2于,3)y,轴的直线上的
x
1
2
.
C
3
4
5
1.点P的坐标是(2,-3),则点P在第 四象限.
2.若点P(x,y)的坐标满足xy﹥0,则点P
象限; 一或三
在第
若点P(x,y)的坐标满足xy﹤0,且在x轴上方,则点P
在第
象二限.
3.若点A的坐标是(-3,5),则它到x轴的距离是
,
到y轴的距离是
.
5
3
4.若点B在x轴上方,y轴右侧,并且到x轴、y轴距离分别是2、
1
-4 -3 -2 -1 0 -1 -2 -3
-4
A的横坐标为4
A的纵坐标为2
有序数对(4, 2)就叫做A的坐标
记作:(A ·4,2)
横坐轴 写在前面 1 2 3 4 5 x 横轴
特殊位置点的特殊坐标:
坐标轴上点P
(x,y)
连线平行于坐标轴 的点
点P(x,y)在各象限的
坐标特点
象限角平分线 上的点
x轴 y轴 原点 平行于 平行于y 第一 第二 第三 第四 一三象 二四象
x轴
轴
象限 象限 象限 象限 限
限
纵坐标相 横坐标相 x>0
(x,0) (0,y) (0,0) 同
.
6.点A(x,y),且x+y>0,
x 那0 么点A在第___象限 y
特殊点的坐标 y
(0,y)
在平面平直行角于坐x轴标的系直内线描上出(2,2),(的0,各2),点(2的,2)纵,(4坐,2)标,依相次连 接各点同,,从横中坐标你不发同现. 了什么?
1
-1 0 1 -1
在平面直角坐标系内描
出平(行-2于,3)y,轴的直线上的
x
1
2
.
C
3
4
5
1.点P的坐标是(2,-3),则点P在第 四象限.
2.若点P(x,y)的坐标满足xy﹥0,则点P
象限; 一或三
在第
若点P(x,y)的坐标满足xy﹤0,且在x轴上方,则点P
在第
象二限.
3.若点A的坐标是(-3,5),则它到x轴的距离是
,
到y轴的距离是
.
5
3
4.若点B在x轴上方,y轴右侧,并且到x轴、y轴距离分别是2、
1
-4 -3 -2 -1 0 -1 -2 -3
-4
A的横坐标为4
A的纵坐标为2
有序数对(4, 2)就叫做A的坐标
记作:(A ·4,2)
横坐轴 写在前面 1 2 3 4 5 x 横轴
3.2.2双曲线的简单几何性质 课件(共24张PPT)

2
2
=λ(λ≠0).
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
跟踪训练 求适合下列条件的双曲线的标准方程:
5
(1)焦点在x轴上,虚轴长为8,离心率为3 ;ห้องสมุดไป่ตู้
跟踪训练
A.
1
4
双曲线x2-my2=1的实轴长是虚轴长的2倍,则m等于
B.
1
2
C.2
D.4
(D)
二、求双曲线方程
例2
根据下列条件,求双曲线方程:
(1)双曲线 x
2
9
y2
1 有共同渐近线,且过点 ( 3, 2 3) ;
16
(2)与双曲线 x
2
16
解
y2
1 有公共焦点,且过点 (3 2 , 2) .
第三章
3.2
双曲线
3.2.2 双曲线的简单几何性质
学习目标
1.理解双曲线的简单几何性质(范围、对称性、顶点、渐近线、离心率).
2.能用双曲线的简单性质解决一些简单的问题
核心素养:数学运算、数学建模
新知学习
复习引入
定义
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
y
y
M
M
F2
(2)焦点在 y 轴上的双曲线的标准方程可设为
2
(3)与双曲线
2
2 +
2
−
2
2
2
−
=1(a>0,b>0).
2
2
=1 共焦点的双曲线方程可设为
2
=λ(λ≠0).
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
跟踪训练 求适合下列条件的双曲线的标准方程:
5
(1)焦点在x轴上,虚轴长为8,离心率为3 ;ห้องสมุดไป่ตู้
跟踪训练
A.
1
4
双曲线x2-my2=1的实轴长是虚轴长的2倍,则m等于
B.
1
2
C.2
D.4
(D)
二、求双曲线方程
例2
根据下列条件,求双曲线方程:
(1)双曲线 x
2
9
y2
1 有共同渐近线,且过点 ( 3, 2 3) ;
16
(2)与双曲线 x
2
16
解
y2
1 有公共焦点,且过点 (3 2 , 2) .
第三章
3.2
双曲线
3.2.2 双曲线的简单几何性质
学习目标
1.理解双曲线的简单几何性质(范围、对称性、顶点、渐近线、离心率).
2.能用双曲线的简单性质解决一些简单的问题
核心素养:数学运算、数学建模
新知学习
复习引入
定义
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
y
y
M
M
F2
(2)焦点在 y 轴上的双曲线的标准方程可设为
2
(3)与双曲线
2
2 +
2
−
2
2
2
−
=1(a>0,b>0).
2
2
=1 共焦点的双曲线方程可设为
关于原点对称的点的坐标课件

02
原点对称点的坐标规律
规律
规律一
如果点$P(x, y)$关于原点对称,则其对称点$P^{prime}(-x, -y)$。
规律二
如果点$P(x, y)$关于原点对称,则其对称点$P^{prime}(-x, -y)$与原点的距离 相等,即$OP = OP^{prime}$。
证明
证明一
设点$P(x, y)$关于原点对称,则其对称点$P^{prime}(-x, -y)$。根据两点之间的 距离公式,有$OP = sqrt{x^2 + y^2}$,$OP^{prime} = sqrt{(-x)^2 + (y)^2} = sqrt{x^2 + y^2}$。因此,$OP = OP^{prime}$。
举例2
余弦函数y=cos(x)的图像也关于原点 对称,因为对于任意x,有cos(x)=cos(x)。
05
原点对称点的计算方法
计算方法
设原点为 $(x_0, y_0)$,则关于原点对称的点坐标为 $(-x_0, -y_0)$。
若原点为 $(0, 0)$,则任意一点 $(x, y)$ 关于原点的对称点 坐标为 $(-x, -y)$。
原点对称的点与原点的距离相等 ,即$|OP| = |OP'|$。
性质2
原点对称的点与原点连线的中点 是原点,即线段$OP$与线段 $OP'$的中点是原点。
举例
举例1
点$P(2, 3)$关于原点的对称点$P'$ 的坐标为$(-2, -3)$。
举例2
点$Q(-4, -1)$关于原点的对称点$Q'$ 的坐标为$(4, 1)$。
原点对称点在函数图像上的表现
要点二
原点对称点与函数值的关系
人教版八年级数学上册《画轴对称图形》轴对称PPT精品课件

画点B、C的对称点F、G,然后顺次连接E、F、G得△
EFG,则△ EFG就是所求.
方法二:也可以利用全等知识进行作图,即先出A、C
的对称点E、G,然后分别以E、G为圆心,AB、CB为
半径作弧,两弧交于点F,则△ EFG就是所求.
知识拓展
二、确定对称点:四边形ABCD和四边形EFGH关于直线MN对称,连
知识梳理
例2:(2)画出△ ABC关于y轴对称的△ A2B2C2;
(3)是否存在点E,使△ ACE和△ ACB全等?若存在,直接写
出所有点E的坐标。
【结论】轴对称变换的作图的步骤是:①
求特殊点的坐标;②描点;③连线.
知识梳理
例3:在平面直角坐标系中,已知点
A( − 3,1),B( −
1,0),C( − 2, − 1),请在下图中画出△ ABC,并画出与
分别为何值.
(1)A、B关于x轴对称;
(2)A、B关于y轴对称。
知识梳理
例2:(1)根据关于x轴对称点的坐标特点横坐标不变、纵坐标互为
相反数可得
2m + n = 1
=1
,解得
− = −2
= −1
(2)根据关于y轴对称点的坐标特点纵坐标不变、横坐标互为
2m + n = −1
= −1
又∵点P(m,n),关于y轴的对称点的坐标为(1,b)
∴m=-1,n=b.
∴m=-1,n=2,故m+n=1.
知识梳理
例4:若点A(m + 2,3)与点B( − 4,n + 5)关于y轴对称,则
m+n= 0 .
+2=4
=2
根据
;解得
;故m + n = 0
EFG,则△ EFG就是所求.
方法二:也可以利用全等知识进行作图,即先出A、C
的对称点E、G,然后分别以E、G为圆心,AB、CB为
半径作弧,两弧交于点F,则△ EFG就是所求.
知识拓展
二、确定对称点:四边形ABCD和四边形EFGH关于直线MN对称,连
知识梳理
例2:(2)画出△ ABC关于y轴对称的△ A2B2C2;
(3)是否存在点E,使△ ACE和△ ACB全等?若存在,直接写
出所有点E的坐标。
【结论】轴对称变换的作图的步骤是:①
求特殊点的坐标;②描点;③连线.
知识梳理
例3:在平面直角坐标系中,已知点
A( − 3,1),B( −
1,0),C( − 2, − 1),请在下图中画出△ ABC,并画出与
分别为何值.
(1)A、B关于x轴对称;
(2)A、B关于y轴对称。
知识梳理
例2:(1)根据关于x轴对称点的坐标特点横坐标不变、纵坐标互为
相反数可得
2m + n = 1
=1
,解得
− = −2
= −1
(2)根据关于y轴对称点的坐标特点纵坐标不变、横坐标互为
2m + n = −1
= −1
又∵点P(m,n),关于y轴的对称点的坐标为(1,b)
∴m=-1,n=b.
∴m=-1,n=2,故m+n=1.
知识梳理
例4:若点A(m + 2,3)与点B( − 4,n + 5)关于y轴对称,则
m+n= 0 .
+2=4
=2
根据
;解得
;故m + n = 0
13.2画轴对称图形(第2课时)课件ppt

谢谢观赏
You made my day!
我们,还在路上……
八年级 上册
13.2 画轴对称图形 (第2课时)
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
如图,如果以天安门为原点,分别以长安街和中 轴线为x轴和y 轴建立平面直角坐标系,对应于东直门 的坐标,你能找到西直门 的位置,说出西直门的坐 标吗?
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
解:关于x 轴对称的点的坐标:(-2, -6), (1,2),(-1, -3),(-4,2),(1,0) .
关于y 轴对称的点的坐标:(2,6), (-1,-2),(1,3),(4,-2),(-1,0) .
课堂练习
练习2 若点P(2a+b,-3a)与点P′(8,b+2) 关于x 轴对称,则a = 2 ,b= 4 ;若关于y 轴对 称,则a = 6 ,b=__-_2_0__.
O
1
D′
E E′
x
B′
C
A
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
观察下图中关于x 轴对称的每对对称点的坐标有怎
样的变化规律?
y
C′ 关于x 轴对称的每对对 称点的横坐标相等,纵坐标 互为相反数.
C
A′ B
1D
O
1
D′
B′
A
E E′
x
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
在平面直角坐标系中,画出下列已知点及其关于 y 轴对称的点,把它们的坐标填入表格中.
C y C′
D
D′
为: A′( 5 , 1 ), B′( 2 , 1 ),
A
B
1
O
You made my day!
我们,还在路上……
八年级 上册
13.2 画轴对称图形 (第2课时)
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
如图,如果以天安门为原点,分别以长安街和中 轴线为x轴和y 轴建立平面直角坐标系,对应于东直门 的坐标,你能找到西直门 的位置,说出西直门的坐 标吗?
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
解:关于x 轴对称的点的坐标:(-2, -6), (1,2),(-1, -3),(-4,2),(1,0) .
关于y 轴对称的点的坐标:(2,6), (-1,-2),(1,3),(4,-2),(-1,0) .
课堂练习
练习2 若点P(2a+b,-3a)与点P′(8,b+2) 关于x 轴对称,则a = 2 ,b= 4 ;若关于y 轴对 称,则a = 6 ,b=__-_2_0__.
O
1
D′
E E′
x
B′
C
A
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
观察下图中关于x 轴对称的每对对称点的坐标有怎
样的变化规律?
y
C′ 关于x 轴对称的每对对 称点的横坐标相等,纵坐标 互为相反数.
C
A′ B
1D
O
1
D′
B′
A
E E′
x
探究并归纳已知点关于坐标轴对称的点 的坐标变化规律
在平面直角坐标系中,画出下列已知点及其关于 y 轴对称的点,把它们的坐标填入表格中.
C y C′
D
D′
为: A′( 5 , 1 ), B′( 2 , 1 ),
A
B
1
O
《平面直角坐标系》PPT课件

8.若点(a,b-1)在第二象限,则a的取值范
围是__a_<_0_,b的取值范围_b__>_1____。
9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在
【 B 】.
(A)原点
(B)x轴正半轴
(C)第一象限 (D)任意位置
雁塔
钟楼
中心广场
碑林
大成殿
科技大学
影月湖
各个景点的坐标为: 雁塔(0,3) 碑林(3,1) 钟楼(-2,1) 大成殿(-2,-2) 科技大学(-5,-7) 影月湖(0,-5) 中心广场(0,0)
A(-4,3)
4
· ·3 C(-2,3)
1
· ·B(4,3)
D(2,3)
观察所得的图
形,你觉得它
象什么?
-4 -3 -2 -1 o
1234
x
-1
-2
做
· E(-2,-3)
-3
·F(2,-3)
一 做
各象限内的点的坐标有何特征?
y
(-,+)(C-2,3)45 3
(+,+)
B (5,3)
F(-7,2)
则a=_4__,b=_5___。
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在__第__二__或__四__象__限。
7.如果同一直角坐标系下两个点的横坐标相同,
那么过这两点的直线( B )
(A)平行于x轴 (B)平行于y轴 (C)经过原点 (D)以上都不对
Y 5
· A(-4,3) 4 3 2
· P(4,3)
1
· -4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、写出下列各点关于x轴、y轴、原点对称的 点的坐标: ⑴A(1,2) ; ⑵B(2,-3); ⑶C(-3,-4);⑷D(-4,5);
已知圆O的半径为3,以圆O的圆心O为 坐标原点,交两条坐标轴为A、B、C、 D 四点,写出A 、B、C、D的坐标.
y
B (0,3)
(-3,0)
C O
A (3,0) x
B (-4,0) O
_(1_,_1_)__,_(_-4_,_-3_)_,_(_2,-_3)_. • 若BC的坐标不变, △ABC的面
y
A
积为6,点A的横坐标为-1,那么点
A的坐标为__(_-1_,_2_)_或_(_-_1_,-_2_) ___.
(-4,0B)
C (2,0x )
(2,0)
Cx
1.在 y轴上的点的横坐标是( 0 ), 在 x轴上的点的纵坐标是( 0 ). 2.点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是(2,3). 3.点 B( - 2,1)关 于 y 轴 对 称 的 点 的 坐 标 是(2,1).
歌剧是把戏剧、诗歌、音 乐、舞蹈和美术结合在一起的一 种综合艺术,起源于十六世纪末 的意大利。欧洲传统歌剧分为: 正歌剧、意大利喜歌剧、法国音 歌剧和法国大歌剧等几种体裁。
一种以歌唱为主,并综合 以器乐、诗歌、舞蹈等艺术为一 体的戏剧形式,称歌剧。歌剧是 西洋音乐舞台上最重要的综合艺 术形式。西洋歌剧的故乡是意大 利,第一部歌剧《达芙妮》在那 里产生。
提高题: 1.若 mn = 0,则点 P(m,n)必定 在 坐标_轴___上 2.已知点 P( a,b),Q(3,6)
且 PQ ∥ x轴,则 b的值为( 6 )
3.点(m,- 1)和点(2,n)关于 x 轴对称,则 mn等于【 B 】 (A)- 2 (B)2 (C)1 (D)- 1
y
y
P (x,y)
4.点 (a, b) 关于 y 轴的对称点的坐标是( D ).
A(a,b) B(a,-b) C(a,b) D(-a,b)
5.点 M(- 8,12)到 x轴的距离是 (12),到 y轴的距离是(8 )
6.点(4,3)与点(4,- 3)的关系 是【B 】. (A)关于原点对称 (B)关于 x轴对称 (C)关于 y轴对称 (D)不能构成对称关系
一.三象限角平分线上的点的横坐标与纵坐标相同;
二.四象限角平分线上的点的横坐标与纵坐标相反;
• 如图,点A的坐标为(2,5)
• 点A关于x轴的对称点的坐标
是__(2_,_-_5_)_;
想一想
• 点A关于y轴的对称点的坐标
是__(-_2_,_5_)_;
• 点A关于原点对称点的坐标为 7个单位y A(2,5)
复习
在平面直角坐标系中分别描出下列点的坐标
A(3,2) B(3,-2) C(-3,2) D(-3,-2) E(4,2)
想一想
点A与点B的横坐标相同, 线段AB的位置有什么特点?
y
C(-3,2)
3
2
A(3,2) E(4,2)
1
-4 -3 -2 -1 0 1 2 3 4
x
-1
点A与点C的纵坐标相同, D(-3,-2) 线段AC的位置有什么特点?
中国宋元以来形成的各种 戏曲,也有歌剧的性质。五四以 后特别是延安时期,音乐工作者 开始尝试借鉴西洋歌剧的创作方 式来创作具有中国特色的歌剧。 参见新歌剧条。
韦伯
(1786-1826)
德国作曲家。他出生于一个戏剧之家,从小 随父母在各地旅行演出,对戏剧非常熟悉,对德 国民间音乐、风俗也有很深的体验。这对他以后 的音乐创作具有重要的意义。韦伯十岁学钢琴, 以后又学作曲,十二岁开始写作歌剧音乐。
1
O 1x
x
点p(x,y)
点p到x轴的距离为 y 点p到y轴的距离为 x
2、在直角坐标系中,描出下列各点:A(4,3), B(-2,3),C(-4,-1),D(2,-2), E(0,-1)
纵轴 y 5
· B
4
3
A
·
2
1
·-4
C
-3
-2
-1
0 -1 E
1
-2
-3
-4
2 3 4 5 x 横轴
·
D点B到x轴的距离为__3__ 点B到y轴的距离为__2__
克拉拉舞会上波希米亚人歌舞与西 班牙斗牛士表演 --- 选自第二幕, 第一、二、三场,这一段主要是为 及后的男女主角会面产生的冲突, 作场面气氛上的渲染和情节上的铺 垫,但金碧辉煌的舞台,光彩夺目 的华丽服饰,热烈的歌舞,把这些 元素独立出来以后,本身也是极富 欣赏价值的。
比捷
(1838-1875)
(5)如果点 E(a, a) 在第一象限,那么点 (a2 , 2a)
在( C ).
A、第四象限 C、第二象限
B、第三象限 D、第一象限
小练习:
1)若已知点P(-8,-6),则点p到x轴的距离为 6 ,
到y轴的距离为 8
。
2)点A(5,-2) 关于y轴对称点为B,则AB= 10 。
3) 距若离已的知2点倍P,(则3aa为-2,0 4或-a)8到. x轴的距离等于它到y轴的
-2
B(3,-2)
-3
-4
横坐标相同的点在平行于y轴的同一直线上
纵坐标相同的点在平行于x轴的同一直线上
在平面直角坐标系中分别描出下列点的坐标
想一想
A(3,2) B(3,-2) C(-3,2) D(-3,-2) E(4,2)
y
C(-3,2)
3
A(3,2)
点A与点B的坐标有什么关系? 点A与点B的位置有什么特点?
(0,-3) D
3.实数 x,y满足 x2+ y2= 0,则
点 P( x,y)在【 A 】. (A)原点(B)x轴正半轴(C)
第一象限 (D)任意位置
4.点 A 在第一象限,当 m 为何
值( 3m -
51)51 到)x时轴,的点距A离(是m它+到1y,
轴距离的一半 .
• 5.矩形ABCD中,三点的坐标分别是 (0,0),(5,0),(5,3),D点的坐标为( C ) A.(0,5) B (5,0) C (0,3) D(3,0)
猎人合唱是德国作曲家韦伯的著名歌剧 《自由射手》第三幕里的一段选曲。这部 歌剧创作于1820年。故事取材于德国和捷 克斯洛伐克广为流传的、一个名叫《黑猎 人》的民间传说。它描写年轻的猎人马克 斯与守林人的女儿阿格泰相爱,并战胜重 重困难,最后结为夫妻的故事。
威尔第
(1813-1901)
意大利作曲家。作有29部歌剧,代表作《博尼法乔 伯爵奥贝尔托》《纳布科》《弄臣》《茶花女》 《游吟诗人》《假面舞会》《命运的力量》《阿依 达》《奥塞罗》和《福斯塔夫》等歌剧,至今仍在 舞台上久演不衰。
• 已知A(1,4),B(-4,0),C(2,0). • △ABC的面积是__12___.
• 将△ABC向左平移三个单位后, 点A、B、C的坐标分别变为 (_-_2_,4_)__,_(_-7_,_0_)_,_(_-1_,0)_.
y
A(1,4)
•
将△ABC向下平移三个单位后, 点A、B、C的坐标分别变为
法国作曲家。10岁进巴黎音乐学院学习,19岁获罗马大 奖,是19世纪法国具有鲜明个性的作曲家。主要作品有《采 珠人》《扎米雷》《罗马》《阿莱城的姑娘》等,歌剧《卡 门》是其代表作。也是世界上演率最高的剧目之一。
四幕歌剧《卡门》取材于法国作家梅里美同名小说。这部歌剧因题材 新奇、风格独特,1875年首演曾失败。在这部歌剧中,作者塑造了烟厂女 工——卡门这个追求个性解放的女性形象。通过她在爱情生活上的不幸遭 遇,反映了吉普赛人的悲惨生活,生活气息颇浓。《卡门序曲》的音乐建 立在第四幕斗牛士上场音乐及第二幕《斗牛士之歌》等素材的基础上,它 的结构简炼,既描写了欢乐的节日气氛,也刻画了斗牛士的英勇形象。
• 6.已知P(x,y),Q(m,n),如果x+m=0,y+n=0,那么 点P、Q( A )
A、关于原点对称 B、关于 x 轴对称
C、关于 y 轴对称 D、关于过点(0, 0), (1,1) 的直线对称
7、如果同一直角坐标系下两个点的横坐标相同,那么
过这两点的直线( B )
(A)平行于 x轴 (B)平行于 y轴 (C)经过原点 (D)以上都不对
表斗门行光副了既奏都上的群米
现 众 人 对 他 的 赞 美 和 颂 扬 。
牛 士 的 胜 利 激 情 。 爱 情 的 喜 悦 , 也
等 人 的 五 重 唱 加 男 声 合 唱 , 既 表 现
曲 , 先 由 埃 斯 卡 米 洛 独 唱 , 后 接 卡
辉 , 豪 迈 的 旋 律 , 犹 如 一 首 凯 旋 进
2
E(4,2)
1
点A与点C的坐标有什么关系? -4 -3 -2 -1 0 1 2 3 4
x
点A与点C的位置有什么特点?D(-3,-2)
-1 -2
点B与点C的坐标有什么关系?
B(3,-2)
点B与点C的位置有什么特点?
-3 -4
关于x轴对称的点的横坐标相同,纵坐标相反
关于y轴对称的点的纵坐标相同,横坐标相反 关于原点对称的点的横坐标、纵坐标都相反
二.四象限角平分线上的点的横坐标与纵坐标相反;
y
知识小结
3
2
X轴上的点纵坐标为0
1
y轴上的点2 3 4
x
-1
纵坐标相同的点在平行于x轴的同一直线上 -2
横坐标相同的点在平行于y轴的同一直线上 -3
-4
关于x轴对称的点的横坐标相同,纵坐标相反
关于y轴对称的点的纵坐标相同,横坐标相反 关于原点对称的点的横坐标、纵坐标都相反
已知圆O的半径为3,以圆O的圆心O为 坐标原点,交两条坐标轴为A、B、C、 D 四点,写出A 、B、C、D的坐标.
y
B (0,3)
(-3,0)
C O
A (3,0) x
B (-4,0) O
_(1_,_1_)__,_(_-4_,_-3_)_,_(_2,-_3)_. • 若BC的坐标不变, △ABC的面
y
A
积为6,点A的横坐标为-1,那么点
A的坐标为__(_-1_,_2_)_或_(_-_1_,-_2_) ___.
(-4,0B)
C (2,0x )
(2,0)
Cx
1.在 y轴上的点的横坐标是( 0 ), 在 x轴上的点的纵坐标是( 0 ). 2.点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是(2,3). 3.点 B( - 2,1)关 于 y 轴 对 称 的 点 的 坐 标 是(2,1).
歌剧是把戏剧、诗歌、音 乐、舞蹈和美术结合在一起的一 种综合艺术,起源于十六世纪末 的意大利。欧洲传统歌剧分为: 正歌剧、意大利喜歌剧、法国音 歌剧和法国大歌剧等几种体裁。
一种以歌唱为主,并综合 以器乐、诗歌、舞蹈等艺术为一 体的戏剧形式,称歌剧。歌剧是 西洋音乐舞台上最重要的综合艺 术形式。西洋歌剧的故乡是意大 利,第一部歌剧《达芙妮》在那 里产生。
提高题: 1.若 mn = 0,则点 P(m,n)必定 在 坐标_轴___上 2.已知点 P( a,b),Q(3,6)
且 PQ ∥ x轴,则 b的值为( 6 )
3.点(m,- 1)和点(2,n)关于 x 轴对称,则 mn等于【 B 】 (A)- 2 (B)2 (C)1 (D)- 1
y
y
P (x,y)
4.点 (a, b) 关于 y 轴的对称点的坐标是( D ).
A(a,b) B(a,-b) C(a,b) D(-a,b)
5.点 M(- 8,12)到 x轴的距离是 (12),到 y轴的距离是(8 )
6.点(4,3)与点(4,- 3)的关系 是【B 】. (A)关于原点对称 (B)关于 x轴对称 (C)关于 y轴对称 (D)不能构成对称关系
一.三象限角平分线上的点的横坐标与纵坐标相同;
二.四象限角平分线上的点的横坐标与纵坐标相反;
• 如图,点A的坐标为(2,5)
• 点A关于x轴的对称点的坐标
是__(2_,_-_5_)_;
想一想
• 点A关于y轴的对称点的坐标
是__(-_2_,_5_)_;
• 点A关于原点对称点的坐标为 7个单位y A(2,5)
复习
在平面直角坐标系中分别描出下列点的坐标
A(3,2) B(3,-2) C(-3,2) D(-3,-2) E(4,2)
想一想
点A与点B的横坐标相同, 线段AB的位置有什么特点?
y
C(-3,2)
3
2
A(3,2) E(4,2)
1
-4 -3 -2 -1 0 1 2 3 4
x
-1
点A与点C的纵坐标相同, D(-3,-2) 线段AC的位置有什么特点?
中国宋元以来形成的各种 戏曲,也有歌剧的性质。五四以 后特别是延安时期,音乐工作者 开始尝试借鉴西洋歌剧的创作方 式来创作具有中国特色的歌剧。 参见新歌剧条。
韦伯
(1786-1826)
德国作曲家。他出生于一个戏剧之家,从小 随父母在各地旅行演出,对戏剧非常熟悉,对德 国民间音乐、风俗也有很深的体验。这对他以后 的音乐创作具有重要的意义。韦伯十岁学钢琴, 以后又学作曲,十二岁开始写作歌剧音乐。
1
O 1x
x
点p(x,y)
点p到x轴的距离为 y 点p到y轴的距离为 x
2、在直角坐标系中,描出下列各点:A(4,3), B(-2,3),C(-4,-1),D(2,-2), E(0,-1)
纵轴 y 5
· B
4
3
A
·
2
1
·-4
C
-3
-2
-1
0 -1 E
1
-2
-3
-4
2 3 4 5 x 横轴
·
D点B到x轴的距离为__3__ 点B到y轴的距离为__2__
克拉拉舞会上波希米亚人歌舞与西 班牙斗牛士表演 --- 选自第二幕, 第一、二、三场,这一段主要是为 及后的男女主角会面产生的冲突, 作场面气氛上的渲染和情节上的铺 垫,但金碧辉煌的舞台,光彩夺目 的华丽服饰,热烈的歌舞,把这些 元素独立出来以后,本身也是极富 欣赏价值的。
比捷
(1838-1875)
(5)如果点 E(a, a) 在第一象限,那么点 (a2 , 2a)
在( C ).
A、第四象限 C、第二象限
B、第三象限 D、第一象限
小练习:
1)若已知点P(-8,-6),则点p到x轴的距离为 6 ,
到y轴的距离为 8
。
2)点A(5,-2) 关于y轴对称点为B,则AB= 10 。
3) 距若离已的知2点倍P,(则3aa为-2,0 4或-a)8到. x轴的距离等于它到y轴的
-2
B(3,-2)
-3
-4
横坐标相同的点在平行于y轴的同一直线上
纵坐标相同的点在平行于x轴的同一直线上
在平面直角坐标系中分别描出下列点的坐标
想一想
A(3,2) B(3,-2) C(-3,2) D(-3,-2) E(4,2)
y
C(-3,2)
3
A(3,2)
点A与点B的坐标有什么关系? 点A与点B的位置有什么特点?
(0,-3) D
3.实数 x,y满足 x2+ y2= 0,则
点 P( x,y)在【 A 】. (A)原点(B)x轴正半轴(C)
第一象限 (D)任意位置
4.点 A 在第一象限,当 m 为何
值( 3m -
51)51 到)x时轴,的点距A离(是m它+到1y,
轴距离的一半 .
• 5.矩形ABCD中,三点的坐标分别是 (0,0),(5,0),(5,3),D点的坐标为( C ) A.(0,5) B (5,0) C (0,3) D(3,0)
猎人合唱是德国作曲家韦伯的著名歌剧 《自由射手》第三幕里的一段选曲。这部 歌剧创作于1820年。故事取材于德国和捷 克斯洛伐克广为流传的、一个名叫《黑猎 人》的民间传说。它描写年轻的猎人马克 斯与守林人的女儿阿格泰相爱,并战胜重 重困难,最后结为夫妻的故事。
威尔第
(1813-1901)
意大利作曲家。作有29部歌剧,代表作《博尼法乔 伯爵奥贝尔托》《纳布科》《弄臣》《茶花女》 《游吟诗人》《假面舞会》《命运的力量》《阿依 达》《奥塞罗》和《福斯塔夫》等歌剧,至今仍在 舞台上久演不衰。
• 已知A(1,4),B(-4,0),C(2,0). • △ABC的面积是__12___.
• 将△ABC向左平移三个单位后, 点A、B、C的坐标分别变为 (_-_2_,4_)__,_(_-7_,_0_)_,_(_-1_,0)_.
y
A(1,4)
•
将△ABC向下平移三个单位后, 点A、B、C的坐标分别变为
法国作曲家。10岁进巴黎音乐学院学习,19岁获罗马大 奖,是19世纪法国具有鲜明个性的作曲家。主要作品有《采 珠人》《扎米雷》《罗马》《阿莱城的姑娘》等,歌剧《卡 门》是其代表作。也是世界上演率最高的剧目之一。
四幕歌剧《卡门》取材于法国作家梅里美同名小说。这部歌剧因题材 新奇、风格独特,1875年首演曾失败。在这部歌剧中,作者塑造了烟厂女 工——卡门这个追求个性解放的女性形象。通过她在爱情生活上的不幸遭 遇,反映了吉普赛人的悲惨生活,生活气息颇浓。《卡门序曲》的音乐建 立在第四幕斗牛士上场音乐及第二幕《斗牛士之歌》等素材的基础上,它 的结构简炼,既描写了欢乐的节日气氛,也刻画了斗牛士的英勇形象。
• 6.已知P(x,y),Q(m,n),如果x+m=0,y+n=0,那么 点P、Q( A )
A、关于原点对称 B、关于 x 轴对称
C、关于 y 轴对称 D、关于过点(0, 0), (1,1) 的直线对称
7、如果同一直角坐标系下两个点的横坐标相同,那么
过这两点的直线( B )
(A)平行于 x轴 (B)平行于 y轴 (C)经过原点 (D)以上都不对
表斗门行光副了既奏都上的群米
现 众 人 对 他 的 赞 美 和 颂 扬 。
牛 士 的 胜 利 激 情 。 爱 情 的 喜 悦 , 也
等 人 的 五 重 唱 加 男 声 合 唱 , 既 表 现
曲 , 先 由 埃 斯 卡 米 洛 独 唱 , 后 接 卡
辉 , 豪 迈 的 旋 律 , 犹 如 一 首 凯 旋 进
2
E(4,2)
1
点A与点C的坐标有什么关系? -4 -3 -2 -1 0 1 2 3 4
x
点A与点C的位置有什么特点?D(-3,-2)
-1 -2
点B与点C的坐标有什么关系?
B(3,-2)
点B与点C的位置有什么特点?
-3 -4
关于x轴对称的点的横坐标相同,纵坐标相反
关于y轴对称的点的纵坐标相同,横坐标相反 关于原点对称的点的横坐标、纵坐标都相反
二.四象限角平分线上的点的横坐标与纵坐标相反;
y
知识小结
3
2
X轴上的点纵坐标为0
1
y轴上的点2 3 4
x
-1
纵坐标相同的点在平行于x轴的同一直线上 -2
横坐标相同的点在平行于y轴的同一直线上 -3
-4
关于x轴对称的点的横坐标相同,纵坐标相反
关于y轴对称的点的纵坐标相同,横坐标相反 关于原点对称的点的横坐标、纵坐标都相反
